Figure 1.
Two maps showing the location of the radar. (a) Overview map showing where in Norway the radar is located. (b) Shows a detailed map of the studied area. The circle to the left marks the location of the radar, and the 6 circles to the right marks the monitored mountain area. The black line marks the pointing direction of the radar.
Figure 1.
Two maps showing the location of the radar. (a) Overview map showing where in Norway the radar is located. (b) Shows a detailed map of the studied area. The circle to the left marks the location of the radar, and the 6 circles to the right marks the monitored mountain area. The black line marks the pointing direction of the radar.
Figure 2.
Illustration of the measurement setup at Hegguraksla. There are three sites in the mountain with two reflectors at each. The numbering of the six reflectors is indicated below each reflector. The radar is located roughly 3 km from the mountain. The triangular corner reflectors are located from 740 to 1000 m AMSL.
Figure 2.
Illustration of the measurement setup at Hegguraksla. There are three sites in the mountain with two reflectors at each. The numbering of the six reflectors is indicated below each reflector. The radar is located roughly 3 km from the mountain. The triangular corner reflectors are located from 740 to 1000 m AMSL.
Figure 3.
(a) Hegguraksla Mountain viewed from Fjørå where the radar is located. The three areas (Sites 1–3) are marked with white circles. (b) is a close-up picture of Site 1, showing the vertical fault and the location of reflector 1 and 2. Reflector 1 is the main reflector, and 2 is the reference reflector. The white arrow indicates the anticipated motional direction of the block.
Figure 3.
(a) Hegguraksla Mountain viewed from Fjørå where the radar is located. The three areas (Sites 1–3) are marked with white circles. (b) is a close-up picture of Site 1, showing the vertical fault and the location of reflector 1 and 2. Reflector 1 is the main reflector, and 2 is the reference reflector. The white arrow indicates the anticipated motional direction of the block.
Figure 4.
Variation in refractive index as a function of air temperature and relative humidity. The pressure is kept constant at 1013.25 mbar. The International Standard Atmosphere according to ISO 2314 is marked with a red cross-hair (The ISO 1314 Standard Atmosphere is defined as Temperature = 15°C, Humidity = 60% and Pressure = 1013.25 mbar at Sea Level).
Figure 4.
Variation in refractive index as a function of air temperature and relative humidity. The pressure is kept constant at 1013.25 mbar. The International Standard Atmosphere according to ISO 2314 is marked with a red cross-hair (The ISO 1314 Standard Atmosphere is defined as Temperature = 15°C, Humidity = 60% and Pressure = 1013.25 mbar at Sea Level).
Figure 5.
Time-Amplitude plot showing the amplitude of the reflected energy from the six reflectors as a function of time. Most of the attenuation is in the winter-months, which for this part of Norway and this elevation is from November to March.
Figure 5.
Time-Amplitude plot showing the amplitude of the reflected energy from the six reflectors as a function of time. Most of the attenuation is in the winter-months, which for this part of Norway and this elevation is from November to March.
Figure 6.
Phasor plot illustrating the amplitude and phase contribution. A is the amplitude of the measured backscatter from one range-cell. N is the sum of the noise and Y the actual backscatter from the reflector. ϕA is the measured angle and ϕN the angle of the noise contribution. The red circle illustrates the circular sample space of the noise.
Figure 6.
Phasor plot illustrating the amplitude and phase contribution. A is the amplitude of the measured backscatter from one range-cell. N is the sum of the noise and Y the actual backscatter from the reflector. ϕA is the measured angle and ϕN the angle of the noise contribution. The red circle illustrates the circular sample space of the noise.
Figure 7.
A section of the range–amplitude plot showing the distinct reflections from the six triangular corner reflectors. Note that the first peak contains both reflectors 1 and 3, as they are separated by just three range-cells. The range plot is range-compensated for by a range factor of R
4 according to the radar equation [
8]. The corner reflectors are in a range from 2900 to 3400 m. The radar cross section of the reflectors is 36.2 dBsm at 9.65 GHz.
Figure 7.
A section of the range–amplitude plot showing the distinct reflections from the six triangular corner reflectors. Note that the first peak contains both reflectors 1 and 3, as they are separated by just three range-cells. The range plot is range-compensated for by a range factor of R
4 according to the radar equation [
8]. The corner reflectors are in a range from 2900 to 3400 m. The radar cross section of the reflectors is 36.2 dBsm at 9.65 GHz.
Figure 8.
The percentage of time per month that the signal has fallen below the cut-off value for the measurement period. Most of the fall-outs occur in the winter.
Figure 8.
The percentage of time per month that the signal has fallen below the cut-off value for the measurement period. Most of the fall-outs occur in the winter.
Figure 9.
The variation of the amplitude reflects the signal-to-clutter level of each corner reflector. Panel (
a) and (
b) are from Site 1, panel (
c) and (
d) are from Site 2, and panel (
e) and (
f) are from Site 3. High signal-to-clutter level produces low variation. The amplitude of the backscattered energy from the reflectors shows a Rayleigh distribution as stated in [
9], while the clutter from the mountain is normally distributed.
Figure 9.
The variation of the amplitude reflects the signal-to-clutter level of each corner reflector. Panel (
a) and (
b) are from Site 1, panel (
c) and (
d) are from Site 2, and panel (
e) and (
f) are from Site 3. High signal-to-clutter level produces low variation. The amplitude of the backscattered energy from the reflectors shows a Rayleigh distribution as stated in [
9], while the clutter from the mountain is normally distributed.
Figure 10.
Meteorological data showing pressure, temperature, and relative humidity from March 2010 to March 2018. The meteorological data are from The Norwegian Meteorological Institute’s measurement station in Tafjord, located approximately 8.5 km from the radar.
Figure 10.
Meteorological data showing pressure, temperature, and relative humidity from March 2010 to March 2018. The meteorological data are from The Norwegian Meteorological Institute’s measurement station in Tafjord, located approximately 8.5 km from the radar.
Figure 11.
Panel (a) shows the estimated variation in path length between the radar and reflector 1 at Site 1 due to variations in the radio refractivity. Panel (b) shows the path length variations between the two reflectors at Site 1. The blue line is the raw-data, while the magenta line is 3-month moving mean. The variation in path length due to radio refractivity is reduced by a factor of approximately 66 when using the differential technic.
Figure 11.
Panel (a) shows the estimated variation in path length between the radar and reflector 1 at Site 1 due to variations in the radio refractivity. Panel (b) shows the path length variations between the two reflectors at Site 1. The blue line is the raw-data, while the magenta line is 3-month moving mean. The variation in path length due to radio refractivity is reduced by a factor of approximately 66 when using the differential technic.
Figure 12.
(
a) Variation in path length and estimated temperature profile as a function of time at Site 1 during the first four months of 2011. This variation is believed to be caused by build-up of snow inside the reflector. Please note that even though the variation at the end of January seems to be instantaneous, the maximum measured velocity is in the order of 2 mrad·s
−1, which is about half the maximum unambiguous velocity of the radar (vmax = 4.2mrad·s
−1). The temperature profile is based on the meteorological data presented in
Figure 10. Even though the meteorological data is from a station 8.5 km away, it gives an indication of the temperature at Site 1. There is a good correlation between the temperature profile and the measured displacement of the reflector. (
b) Picture of build-up of snow inside one of the reflectors during the winter of 2011. The photo is from Åknes-Tafjord IKS.
Figure 12.
(
a) Variation in path length and estimated temperature profile as a function of time at Site 1 during the first four months of 2011. This variation is believed to be caused by build-up of snow inside the reflector. Please note that even though the variation at the end of January seems to be instantaneous, the maximum measured velocity is in the order of 2 mrad·s
−1, which is about half the maximum unambiguous velocity of the radar (vmax = 4.2mrad·s
−1). The temperature profile is based on the meteorological data presented in
Figure 10. Even though the meteorological data is from a station 8.5 km away, it gives an indication of the temperature at Site 1. There is a good correlation between the temperature profile and the measured displacement of the reflector. (
b) Picture of build-up of snow inside one of the reflectors during the winter of 2011. The photo is from Åknes-Tafjord IKS.
Figure 13.
Diurnal variation in measured path length between the two reflectors at Site 2. The blue line is the raw data, the magenta line is the 6-h moving mean, and the green line is the calculated variation in the radio refractivity. As the plot shows, there is a good correlation between the measured path length variation and the calculated radio refractivity.
Figure 13.
Diurnal variation in measured path length between the two reflectors at Site 2. The blue line is the raw data, the magenta line is the 6-h moving mean, and the green line is the calculated variation in the radio refractivity. As the plot shows, there is a good correlation between the measured path length variation and the calculated radio refractivity.
Figure 14.
Time–Displacement diagram for the three sites during 8 years of monitoring. Note that negative values indicate shorter distance between the radar and the reflectors. The blue line is the raw-data, while the red line is the 3-months moving mean. The figure shows annual cyclic variations, which correlate with the annual temperature variations.
Figure 14.
Time–Displacement diagram for the three sites during 8 years of monitoring. Note that negative values indicate shorter distance between the radar and the reflectors. The blue line is the raw-data, while the red line is the 3-months moving mean. The figure shows annual cyclic variations, which correlate with the annual temperature variations.
Figure 15.
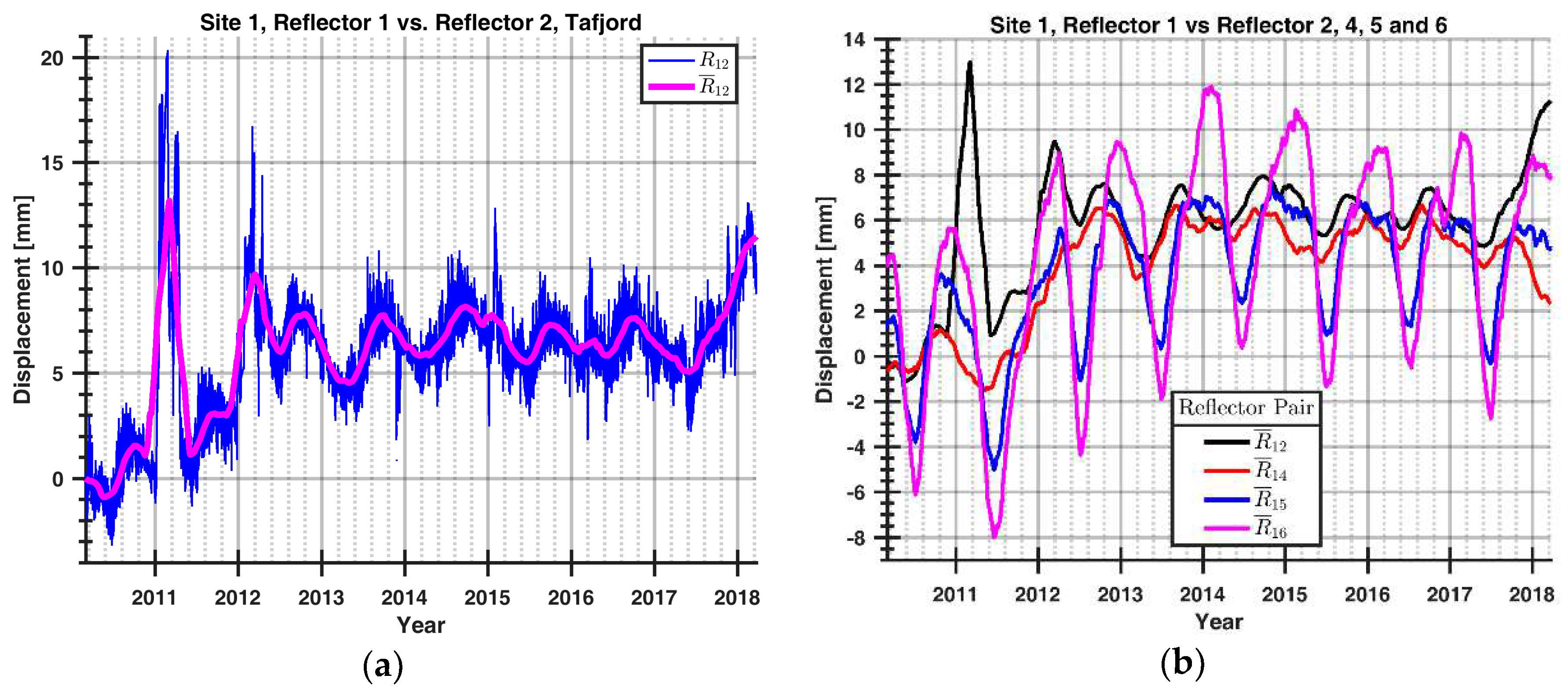
(a) The displacement as a function of time for Site 1, reflector 1 referenced to reflector 2. There are three large displacements visible in the plot during the winters of 2011, 2012, and 2018. All three displacements are believed to be caused by build-up of snow inside the reference reflector. The blue line is the raw-data, while the magenta line is the 3-month moving mean. (b) The displacement of reflector 1 at Site 1 referenced to all the reference reflectors. They all show similar motion, the major difference being the variation in the amplitude of the annual cyclic motions. The variation in amplitude increases with the distance between reflector 1 and the reference reflectors.
Figure 15.
(a) The displacement as a function of time for Site 1, reflector 1 referenced to reflector 2. There are three large displacements visible in the plot during the winters of 2011, 2012, and 2018. All three displacements are believed to be caused by build-up of snow inside the reference reflector. The blue line is the raw-data, while the magenta line is the 3-month moving mean. (b) The displacement of reflector 1 at Site 1 referenced to all the reference reflectors. They all show similar motion, the major difference being the variation in the amplitude of the annual cyclic motions. The variation in amplitude increases with the distance between reflector 1 and the reference reflectors.
Figure 16.
(a) The displacement as a function of time for Site 2 from 2010 to 2018, reflector 3 referenced to reflector 4. The blue line is the raw-data, while the magenta line is the 3-months moving mean. The results show a displacement of −1.2 mm for the whole timespan. The displacement from 2013 to 2018 is in the order of −2.0 mm. (b) The displacement as a function of time for reflector 3 referenced to the four reference reflectors (reflectors 2, 4, 5, and 6). They all show similar motion, the major difference being the variation in the amplitude of the annual cyclic motion. The standard deviation increases with the distance between reflector 3 and the reference reflectors.
Figure 16.
(a) The displacement as a function of time for Site 2 from 2010 to 2018, reflector 3 referenced to reflector 4. The blue line is the raw-data, while the magenta line is the 3-months moving mean. The results show a displacement of −1.2 mm for the whole timespan. The displacement from 2013 to 2018 is in the order of −2.0 mm. (b) The displacement as a function of time for reflector 3 referenced to the four reference reflectors (reflectors 2, 4, 5, and 6). They all show similar motion, the major difference being the variation in the amplitude of the annual cyclic motion. The standard deviation increases with the distance between reflector 3 and the reference reflectors.
Figure 17.
Displacement as a function of time for Site 3; reflector 5 referenced to reflector 6. The blue line is the raw-data while the red line is the three-months moving average. There is no displacement detected of Site 3 except for the annual cyclic motion.
Figure 17.
Displacement as a function of time for Site 3; reflector 5 referenced to reflector 6. The blue line is the raw-data while the red line is the three-months moving average. There is no displacement detected of Site 3 except for the annual cyclic motion.
Figure 18.
Three months moving average of the measured displacement adjusted with radio refractivity estimated from the meteorological data. (a) is Site 1, (b) is Site 2, (c) is Site 3, and (d) is all three sites combined. The blue line is the differential interferometric displacement. The red line is the variation in path length estimated from radio refractivity. The black line is the radio refractivity-corrected displacement. This shows that meteorological data can be used to reduce the path length variation due to variations in radio refractivity, in the case of Site 3 by approximately 35%. Note the different scaling of the y-axis on the four figures.
Figure 18.
Three months moving average of the measured displacement adjusted with radio refractivity estimated from the meteorological data. (a) is Site 1, (b) is Site 2, (c) is Site 3, and (d) is all three sites combined. The blue line is the differential interferometric displacement. The red line is the variation in path length estimated from radio refractivity. The black line is the radio refractivity-corrected displacement. This shows that meteorological data can be used to reduce the path length variation due to variations in radio refractivity, in the case of Site 3 by approximately 35%. Note the different scaling of the y-axis on the four figures.
Figure 19.
(a) Displacement as a function of time from the two extensometers mounted at Site 1. The trends show a displacement of −0.7 mm for extensometer 1 and of −6.0 mm for extensometer 2 from 6th February 2012 to 10th March 2017. The motion of extensometer 2 is believed to be partly due to failure of the mounting rods at one end. (b) Displacement as a function of time for the data from RADARSAT-2. The blue diamonds are the data samples, the red line is a 4th order polynomial fit, and the green line is a linear fit. The magenta line is a linear fit covering the same measurement period as the extensometers. Note that the satellite data are line-of-sight displacement and not vertical displacement.
Figure 19.
(a) Displacement as a function of time from the two extensometers mounted at Site 1. The trends show a displacement of −0.7 mm for extensometer 1 and of −6.0 mm for extensometer 2 from 6th February 2012 to 10th March 2017. The motion of extensometer 2 is believed to be partly due to failure of the mounting rods at one end. (b) Displacement as a function of time for the data from RADARSAT-2. The blue diamonds are the data samples, the red line is a 4th order polynomial fit, and the green line is a linear fit. The magenta line is a linear fit covering the same measurement period as the extensometers. Note that the satellite data are line-of-sight displacement and not vertical displacement.
Figure 20.
Displacement as a function of time from the extensometers and crack meters at Site 2. (a) The extensometers show a displacement varying from −0.08 mm to 0.45 mm. (b) The crack meters show a displacement varying from −0.04 mm to 0.95 mm.
Figure 20.
Displacement as a function of time from the extensometers and crack meters at Site 2. (a) The extensometers show a displacement varying from −0.08 mm to 0.45 mm. (b) The crack meters show a displacement varying from −0.04 mm to 0.95 mm.
Table 1.
Key radar parameters.
Table 1.
Key radar parameters.
| FMCW Radar Parameters | Value |
|---|
| Frequency, fc [GHz] | 9.65 |
| Bandwidth, BW [MHz] | 300 |
| Range Resolution, ΔR [m] | 0.5 |
| Pulse Repetition Frequency, PRF [Hz] | 1/60 |
| Wave Length, λ [mm] | 31.1 |
| Antenna Gain [dB] | 24 |
| RCS of the Reflectors, [dBsm] @ 9.65 GHz | 36.2 |
Table 2.
Mean amplitude value and standard deviation of the amplitude for the measurement period. The higher variation at Site 3 is believed to be caused by the longer distance, which gives a greater susceptibility to atmospheric attenuation.
Table 2.
Mean amplitude value and standard deviation of the amplitude for the measurement period. The higher variation at Site 3 is believed to be caused by the longer distance, which gives a greater susceptibility to atmospheric attenuation.
| Site | Reflector | Mean Amplitude [dB] | Standard Deviation [dB] |
|---|
| 1 | 1 | 38.0 | 2.8 |
| 2 | 38.8 | 2.2 |
| 2 | 3 | 37.6 | 2.5 |
| 4 | 35.6 | 2.1 |
| 3 | 5 | 38.1 | 3.9 |
| 6 | 38.0 | 4.0 |
Table 3.
Key parameters for each site. The maximum variation in path length for both radar-to-site and reflector-to-reflector per site are listed.
Table 3.
Key parameters for each site. The maximum variation in path length for both radar-to-site and reflector-to-reflector per site are listed.
| Site | Reflector Number | Radar to Reflector Distance[m] | Height (AMSL) [m] | Inter Reflector Distance Per Site [m] | Difference in Reflector Elevation [m] | Maximum Variation in Path Length between Radar and Reflector [mm] | Maximum Variation in Path Length between Reflectors Per Site [mm] |
|---|
| 1 | 1 | 2918.9 | 734 | 52 | 20 | 395.2 | 6.0 |
| 2 | 2970.9 | 754 | 401.3 |
| 2 | 3 | 2920.4 | 837 | 22.5 | 16 | 389.4 | 2.6 |
| 4 | 2942.9 | 853 | 391.8 |
| 3 | 5 | 3283.1 | 957 | 141.6 | 38 | 430.1 | 16.1 |
| 6 | 3424.7 | 995 | 446.3 |
Table 4.
Measured displacement of Reflector 1 at Site 1, referenced to the four reference reflectors.
Table 4.
Measured displacement of Reflector 1 at Site 1, referenced to the four reference reflectors.
| Site | Reference Reflector | Total Motion 2010–2018 [mm] | Standard Deviation [mm] | Motion 2013–2018 [mm] |
|---|
| 1 | 2 | 4.7 | 3.1 | 1.7 |
| 2 | 4 | 5.3 | 2.9 | −0.9 |
| 3 | 5 | 5.2 | 4.5 | −0.2 |
| 6 | 6.1 | 6.5 | −0.5 |
Table 5.
Measured displacement of reflector 3, referenced to the four reference reflectors.
Table 5.
Measured displacement of reflector 3, referenced to the four reference reflectors.
| Site | Reference Reflector | Standard Deviation [mm] | Total Motion [mm] | Motion 2013–2018 [mm] |
|---|
| 1 | 2 | 3.2 | −2.2 | 0.6 |
| 2 | 4 | 1.2 | −1.6 | −2.0 |
| 3 | 5 | 4.0 | −1.6 | −1.3 |
| 6 | 6.3 | −0.9 | −1. 8 |