Detection of Differential Settlement of Man-Made Structures Coupled with Urban Development by Using Persistent Scatterer Interferometry (PSI)
Abstract
:1. Introduction
2. Study Area and Dataset
3. Methods
3.1. Master-Image Selection
3.2. PS Selection
3.3. PS Classification
4. Results
4.1. Differential Settlement in Bangkok
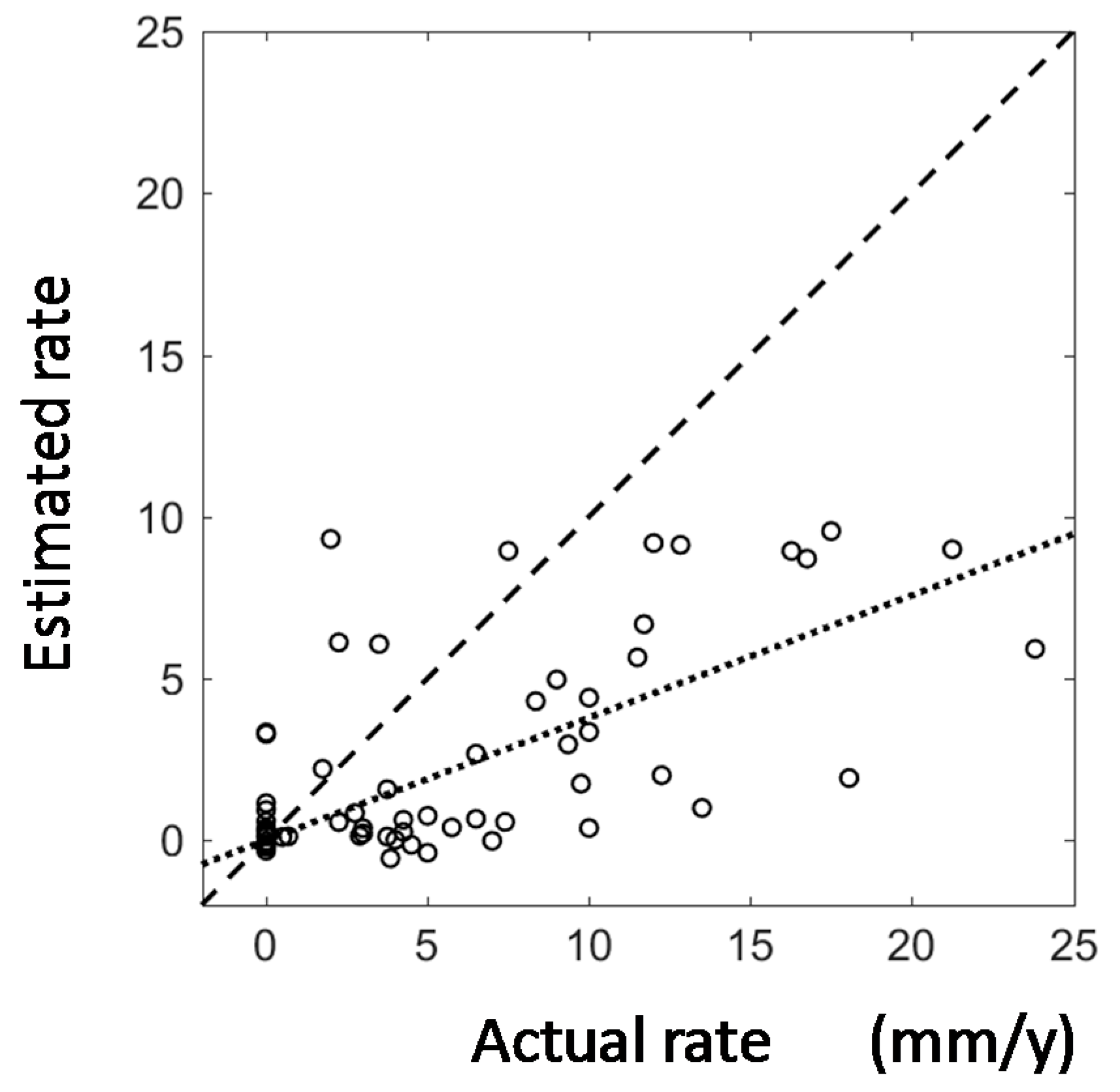
4.2. Validation
5. Discussion
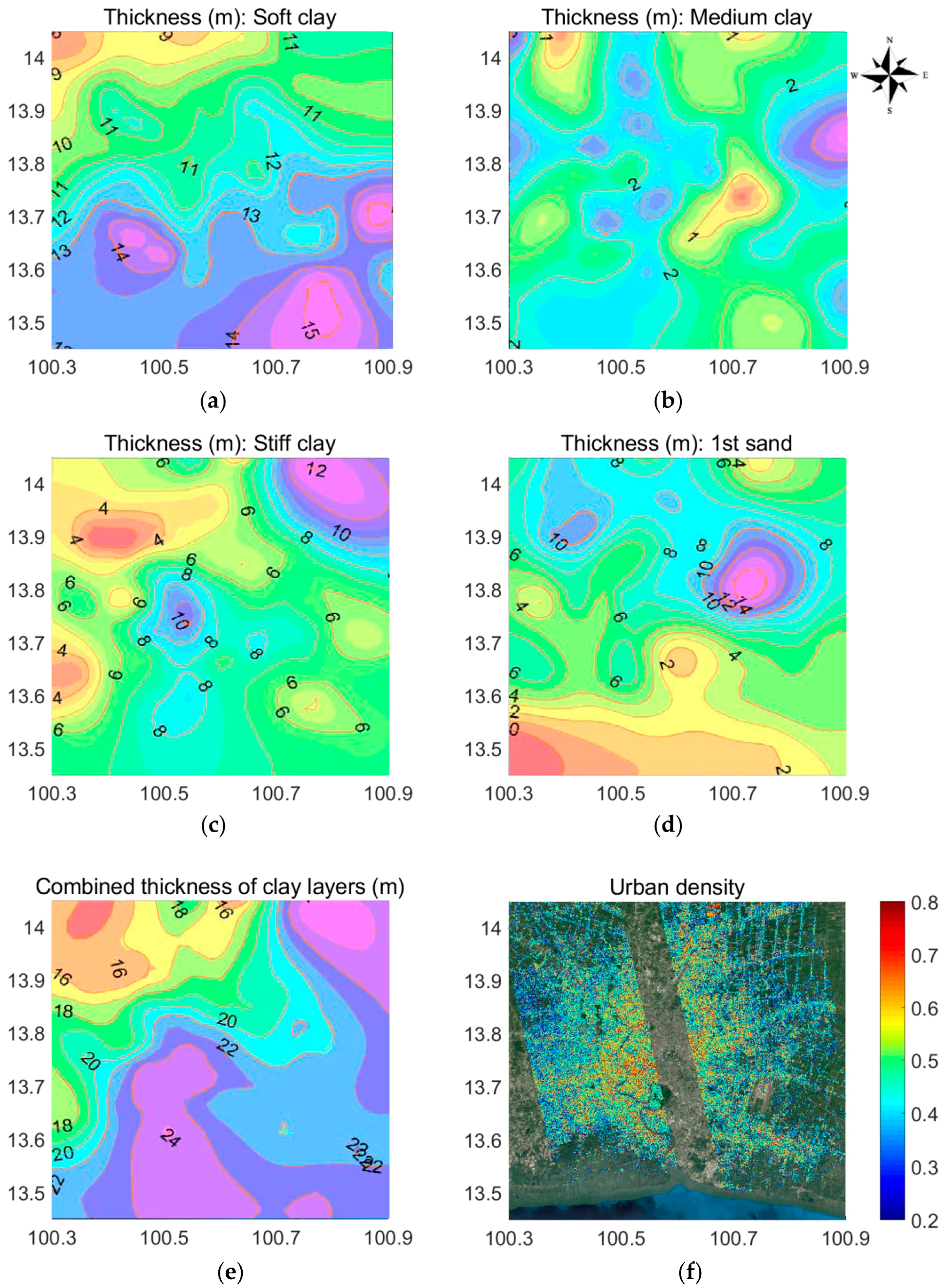
5.1. Effect of Geological Strata and Building Density
5.2. Validity of the Proposed Method
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Erban, L.E.; Gorelick, S.M.; Zebker, H.A. Groundwater extraction, land subsidence, and sea-level rise in the Mekong Delta, Vietnam. Environ. Res. Lett. 2014, 9, 084010. [Google Scholar] [CrossRef] [Green Version]
- Caló, F.; Notti, D.; Galve, J.P.; Abdikan, S.; Görüm, T.; Pepe, A.; Balik Şanli, F. DInSAR-based detection of land subsidence and correlation with groundwater depletion in Konya Plain, Turkey. Remote Sens. 2017, 9, 83. [Google Scholar] [CrossRef]
- Reul, O.; Randolph, M.F. Piled rafts in overconsolidated clay: Comparison of in situ measurements and numerical analyses. Géotechnique 2003, 53, 301–305. [Google Scholar] [CrossRef]
- Arapakou, A.E.; Papadopoulos, V.P. Factors affecting differential settlements of framedstructures. Geotech. Geol. Eng. 2012, 30, 1323–1333. [Google Scholar] [CrossRef]
- Phien-wej, N.; Giao, H.P.; Nutalaya, P. Land subsidence in Bangkok, Thailand. Eng. Geol. 2006, 82, 187–201. [Google Scholar] [CrossRef]
- Boonyatee, T.; Tongjarukae, J.; Uaworakunchai, T.; Ukritchon, B. A review on design of pile foundations in Bangkok. Geotech. Eng. 2015, 46, 76–85. [Google Scholar]
- Anuphao, A. InSAR Time Series Analysis for Land Subsidence Monitoring in Bangkok and Its Vicinity Area. Ph.D. Thesis, Department of Survey Engineering, Chulalongkorn University, Bangkok, Thailand, 2012. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef] [Green Version]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometricdata-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Non-linear subsidence rate estimation using permanent scatterers in differential SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Stramondo, S.; Bozzano, F.; Marra, F.; Wegmuller, U.; Cinti, F.R.; Moro, M.; Saroli, M. Subsidence induced by urbanisation in the city of Rome detected by advanced InSAR technique and geotechnical investigations. Remote Sens. Environ. 2008, 112, 3160–3172. [Google Scholar] [CrossRef]
- Perissin, D.; Wang, T. Time-series InSAR applications over urban areas in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 4, 92–100. [Google Scholar] [CrossRef]
- Chaussard, E.; Wdowinski, S.; Cabral-Cano, E.; Amelung, F. Land subsidence in central Mexico detected by ALOS InSAR time-series. Remote Sens. Environ. 2014, 140, 94–106. [Google Scholar] [CrossRef]
- Goel, K.; Adam, N. A distributed scatterer interferometry approach for precision monitoring of known surface deformation phenomena. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5454–5468. [Google Scholar] [CrossRef]
- Lv, X.; Yazici, B.; Zeghal, M.; Bennett, V.; Abdoun, T. Joint-scatterer processing for time-series InSAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7205–7221. [Google Scholar]
- Devanthéry, N.; Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Crippa, B. An approach to persistent scatterer interferometry. Remote Sens. 2014, 6, 6662–6679. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent scatterer interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- German Aerospace Center (DLR). TerraSAR-X—Germany’s Radar Eye in Space. Available online: http://www.dlr.de/dlr/en/desktopdefault.aspx/tabid-10377/565_read-436/#/gallery/350 (accessed on 2 February 2018).
- U.S. Geological Survey (USGS). Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global. Available online: https://lta.cr.usgs.gov/SRTM1Arc (accessed on 2 February 2018).
- The Royal Thai Survey Department. International union of geodesy and geophysics—Thailand reported on the geodetic work period 1999–2002. In Proceedings of the the XXIII General Assembly of the International Union of Geodesy and Geophysics, Sapporo, Japan, 30 June–11 July 2003. [Google Scholar]
- Earth Observation Research Cente (EORC). Japan Aerospace Exploration Agency (JAXA), About ALOS—PALSAR. Available online: http://www.eorc.jaxa.jp/ALOS/en/about/palsar.htm (accessed on 2 February 2018).
- Colesanti, C.; Ferretti, A.; Locatelli, R.; Savio, G. Multi-platform permanent scatterers analysis: First result. In Proceedings of the Second GRSS/ISPRS Joint Workshop on Data Fusion and Remote Sensing over Urban Areas, Berlin, Germany, 22–23 May 2013; pp. 52–56. [Google Scholar]
- Kampes, B.M. Radar Interferometry; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hooper, A.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. 2007, 112, B07407. [Google Scholar] [CrossRef]
- Susaki, J. Adaptive slope filtering of airborne LiDAR data in urban areas for digital terrain model (DTM) Generation. Remote Sens. 2012, 4, 1804–1819. [Google Scholar] [CrossRef] [Green Version]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum-likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B. 1977, 39, 1–38. [Google Scholar]
- Redner, R.; Walker, H. Mixture densities, maximum likelihood and the EM algorithm. SIAM Rev. 1984, 26, 195–239. [Google Scholar] [CrossRef]
- MATLAB. MathWorks. Available online: https://www.mathworks.com/products/matlab.html (accessed on 5 May 2018).
- Google Earth, Google. Available online: https://www.google.com/earth/ (accessed on 5 May 2018).
- Amornfa, K.; Phienwej, N.; Kitpayuck, P. Current practice on foundation design of high-rise building in Bangkok, Thailand. Lowl. Technol. Int. 2012, 14, 70–83. [Google Scholar]
- Ngamcharoen, K.; Likitlersuang, S.; Boonyatee, T. Development of 3D geological modelling for Bangkok subsoils. In Proceedings of the Twenty-Ninth KKHTCNN Symposium on Civil Engineering, Hong Kong, China, 3–5 December 2016. [Google Scholar]
- RockWorks. RockWare. Available online: https://www.rockware.com/product/rockworks/ (accessed on 5 May 2018).
- Gambolati, G.; Teatini, P. Geomechanics of subsurface water withdrawal and injection. Water Resour. Res. 2015, 51, 3922–3955. [Google Scholar] [CrossRef] [Green Version]
- Kajimoto, K.; Susaki, J. Urban density estimation from polarimetric SAR images based on a POA correction method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1418–1429. [Google Scholar] [CrossRef] [Green Version]
- Susaki, J.; Kajimoto, M.; Kishimoto, M. Urban density mapping of global megacities from polarimetric SAR images. Remote Sens. Environ. 2014, 155, 334–348. [Google Scholar] [CrossRef] [Green Version]
- Bru, G.; Herrera, G.; Tomás, R.; Duro, J.; De la Vega, R.; Mulas, J. Control of deformation of buildings affected by subsidence using persistent scatterer interferometry. Struct. Infrastruct. Eng. 2013, 9, 188–200. [Google Scholar] [CrossRef]
- Bianchini, S.; Pratesi, F.; Nolesini, T.; Casagli, N. Building deformation assessment by means of persistent scatterer interferometry analysis on a landslide-affected area: The Volterra (Italy) case study. Remote Sens. 2015, 7, 4678–4701. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley and Sons: New York, NY, USA, 1944. [Google Scholar]
- Land Subsidence Status of Kansai International Airport for the Island 1. Available online: http:// www.kansai-airports.co.jp/efforts/our-tech/kix/sink/sink3/sink3_c.html (accessed on 18 February 2018). (In Japanese).
- Land Subsidence Status of Kansai International Airport for the Island 2. Available online: http:// www.kansai-airports.co.jp/efforts/our-tech/kix/sink/sink3/sink3_e.html (accessed on 18 February 2018). (In Japanese).



| NO. | YEAR | MONTH | DAY | NO. | YEAR | MONTH | DAY |
|---|---|---|---|---|---|---|---|
| 1 | 2009 | 9 | 5 | 11 | 2010 | 5 | 5 |
| 2 | 2009 | 9 | 16 | 12 | 2010 | 5 | 27 |
| 3 | 2009 | 10 | 30 | 13 | 2010 | 6 | 18 |
| 4 | 2009 | 11 | 21 | 14 | 2010 | 11 | 19 |
| 5 | 2009 | 12 | 24 | 15 | 2011 | 1 | 2 |
| 6 | 2010 | 1 | 15 | 16 | 2011 | 2 | 15 |
| 7 | 2010 | 2 | 6 | 17 | 2011 | 9 | 12 |
| 8 | 2010 | 4 | 13 | 18 | 2011 | 10 | 4 |
| 9 | 2010 | 2 | 28 | 19 | 2011 | 10 | 26 |
| 10 | 2010 | 3 | 22 | 20 | 2011 | 12 | 9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Susaki, J.; Maruo, N.; Tsujino, M.; Boonyatee, T. Detection of Differential Settlement of Man-Made Structures Coupled with Urban Development by Using Persistent Scatterer Interferometry (PSI). Remote Sens. 2018, 10, 1048. https://doi.org/10.3390/rs10071048
Susaki J, Maruo N, Tsujino M, Boonyatee T. Detection of Differential Settlement of Man-Made Structures Coupled with Urban Development by Using Persistent Scatterer Interferometry (PSI). Remote Sensing. 2018; 10(7):1048. https://doi.org/10.3390/rs10071048
Chicago/Turabian StyleSusaki, Junichi, Naoyuki Maruo, Masahiro Tsujino, and Tirawat Boonyatee. 2018. "Detection of Differential Settlement of Man-Made Structures Coupled with Urban Development by Using Persistent Scatterer Interferometry (PSI)" Remote Sensing 10, no. 7: 1048. https://doi.org/10.3390/rs10071048
APA StyleSusaki, J., Maruo, N., Tsujino, M., & Boonyatee, T. (2018). Detection of Differential Settlement of Man-Made Structures Coupled with Urban Development by Using Persistent Scatterer Interferometry (PSI). Remote Sensing, 10(7), 1048. https://doi.org/10.3390/rs10071048






