Validation of Improved Significant Wave Heights from the Brown-Peaky (BP) Retracker along the East Coast of Australia
Abstract
:1. Introduction
2. Data and Study Area
2.1. Study Area
2.2. Data
3. Methods
3.1. Estimation of SWH
3.2. Methods for the SWH Evaluation and Validation
- Using Jason-1 nominal tracks provided by the Centre for Topographic studies of the Ocean and Hydrosphere (CTOH, http://ctoh.legos.obs-mip.fr/altimetry/satellites), the altimetric SWHs are linearly interpolated to the corresponding nominal track;
- The buoy wave heights are interpolated to the same time as the altimeter SWH data;
- The difference (i.e., bias) between the buoy and 1 Hz altimeter SWHs is calculated at each along-track point for all cycles;
- The mean and STD of the SWH differences, and correlation coefficient between the altimeter and buoy wave heights are calculated at each along-track point.
4. Evaluation of BP-Estimated SWHs
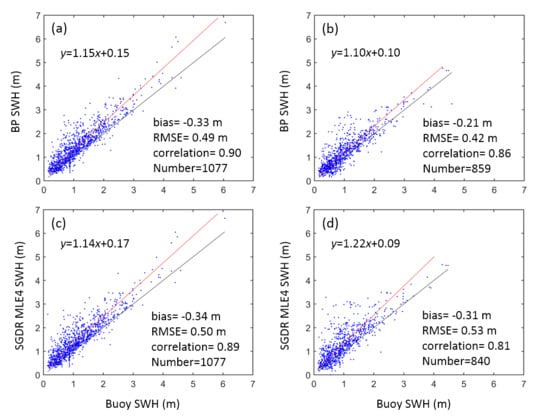
4.1. Comparison between BP and SGDR MLE4 SWHs
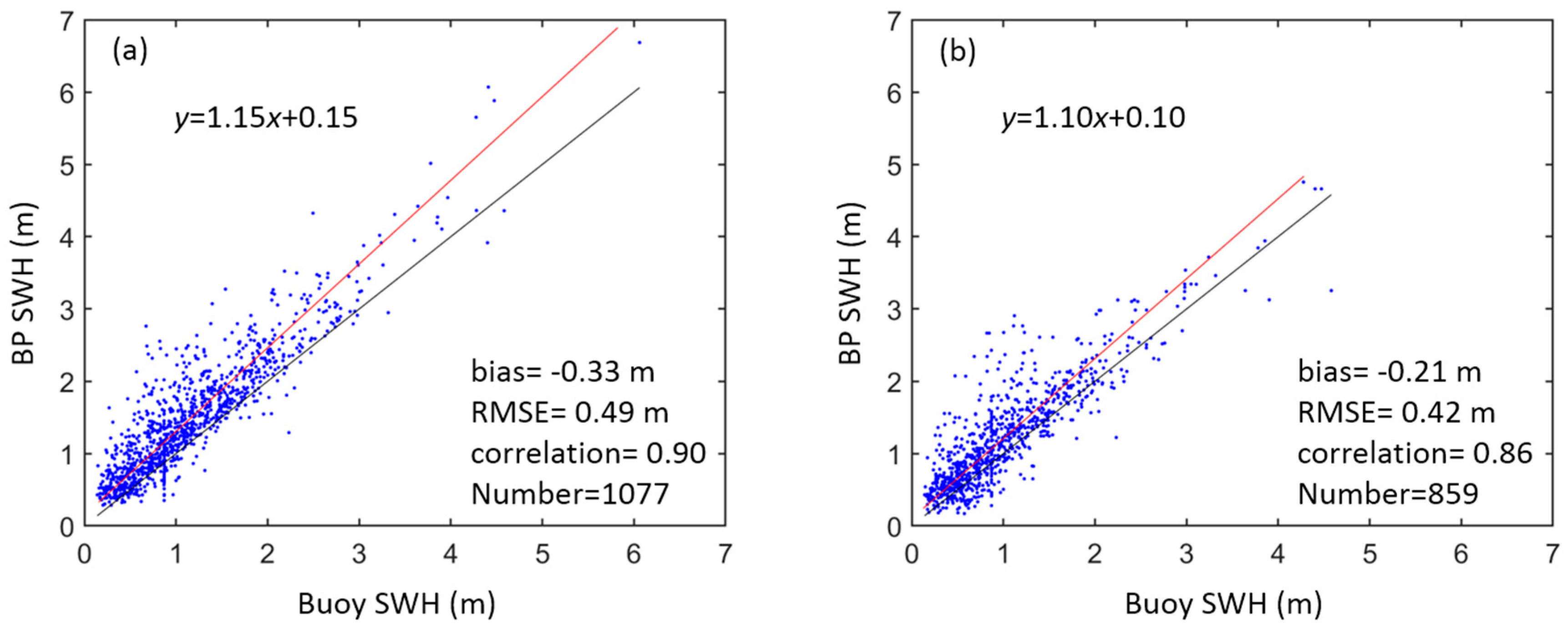
4.2. Comparison Between BP-Estimated SWHs and Buoy Wave Heights
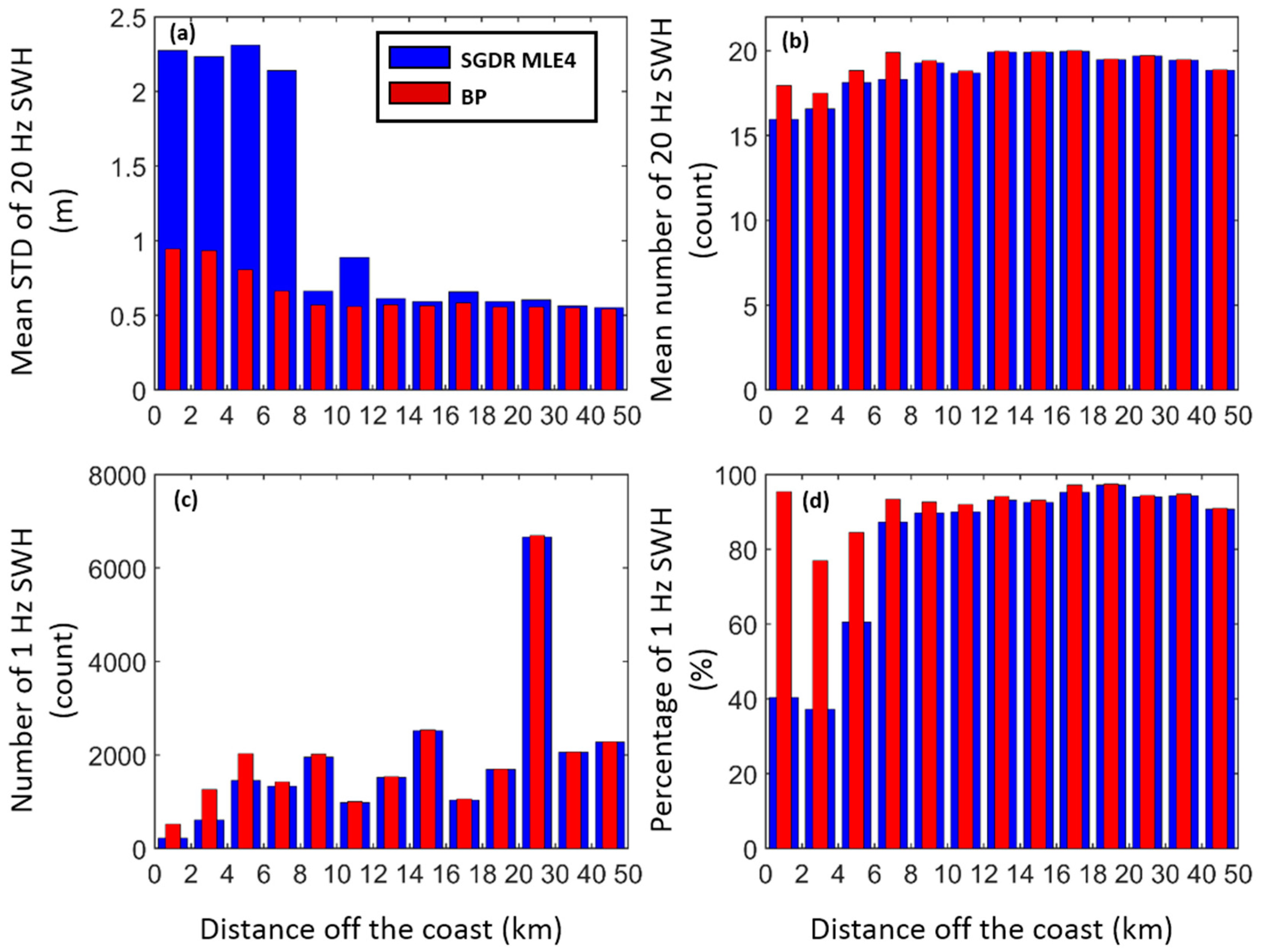
5. Validation of 1 Hz Along-Track SWHs
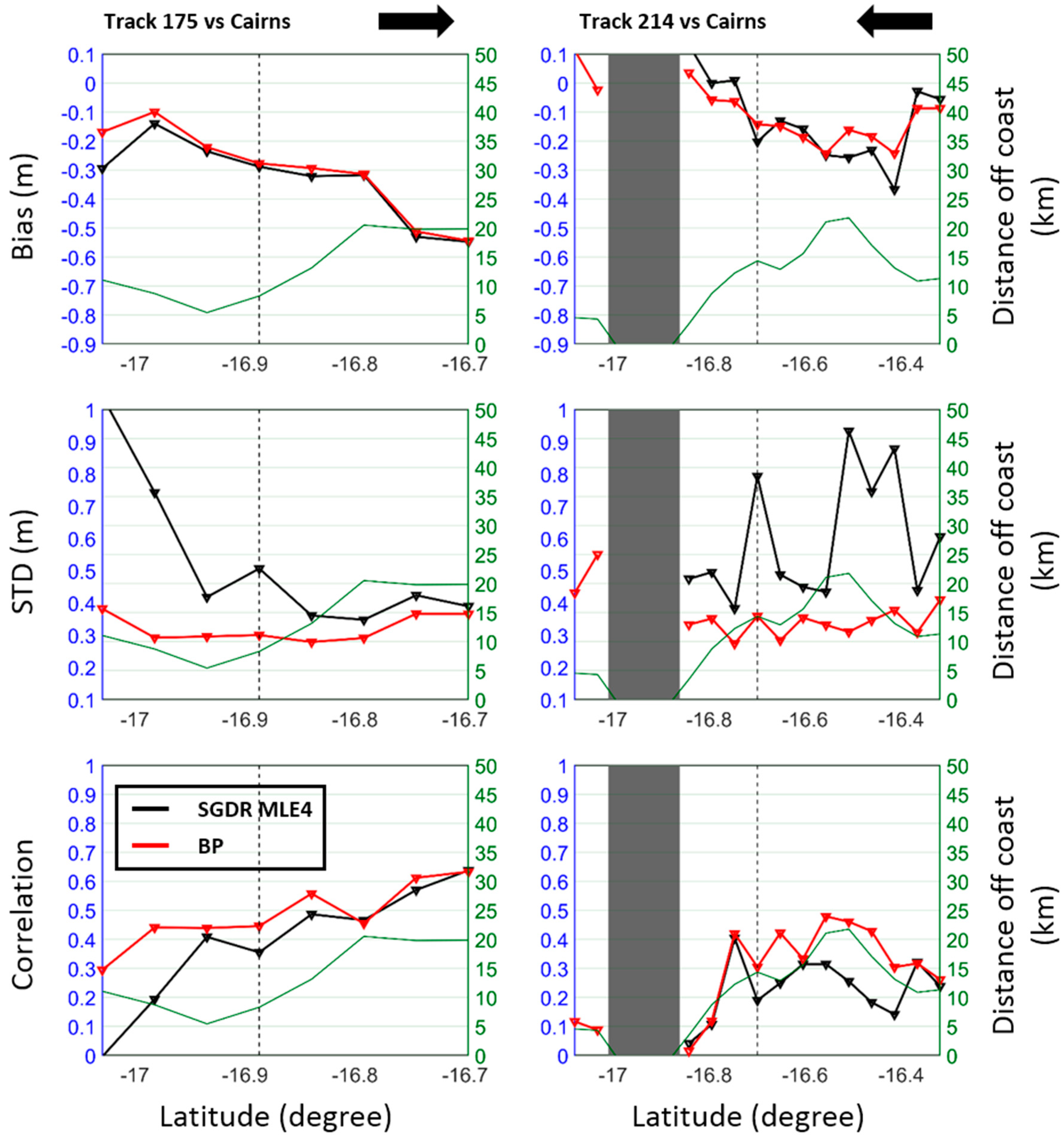
5.1. North Queensland
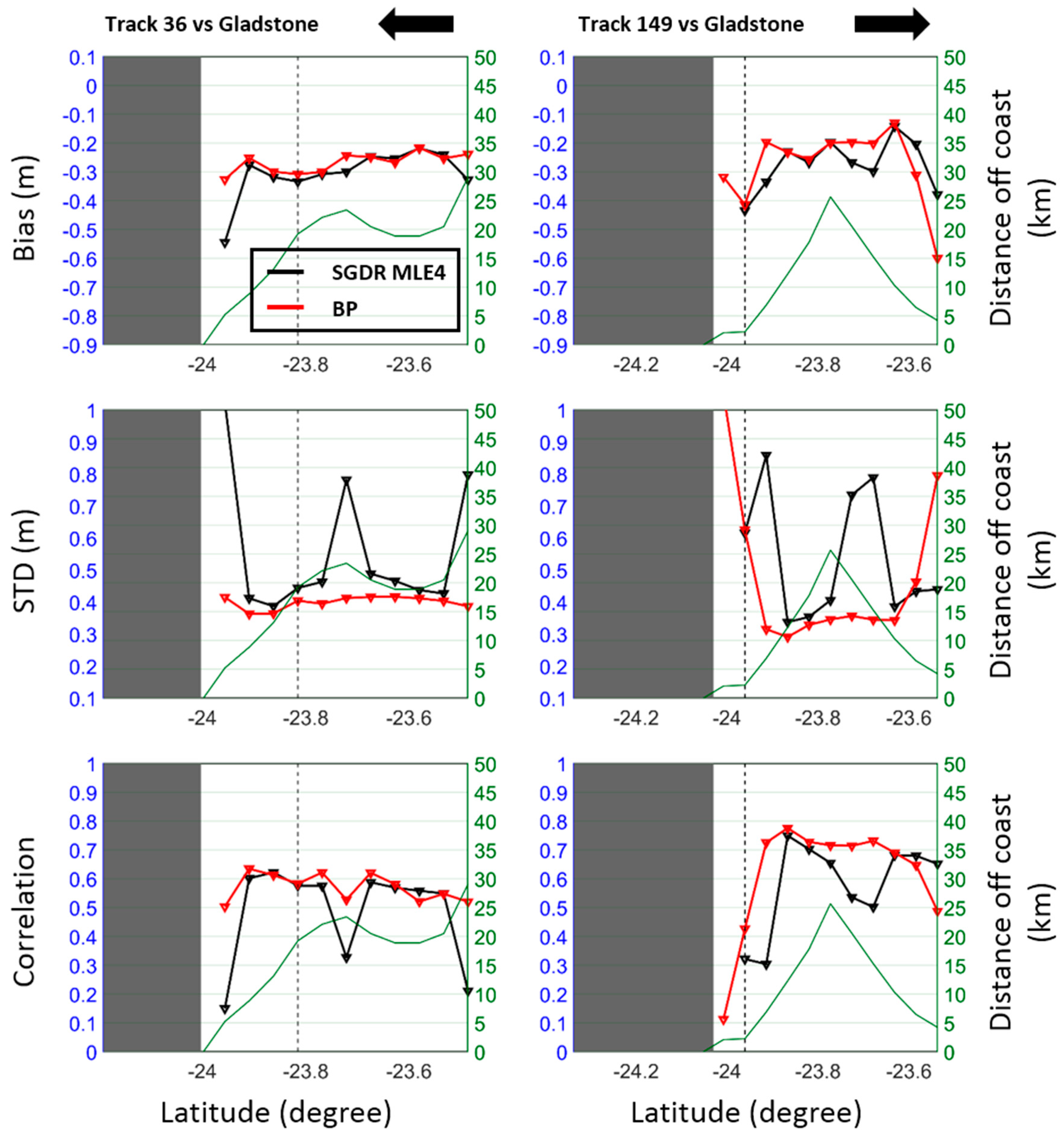
5.2. Central Queensland
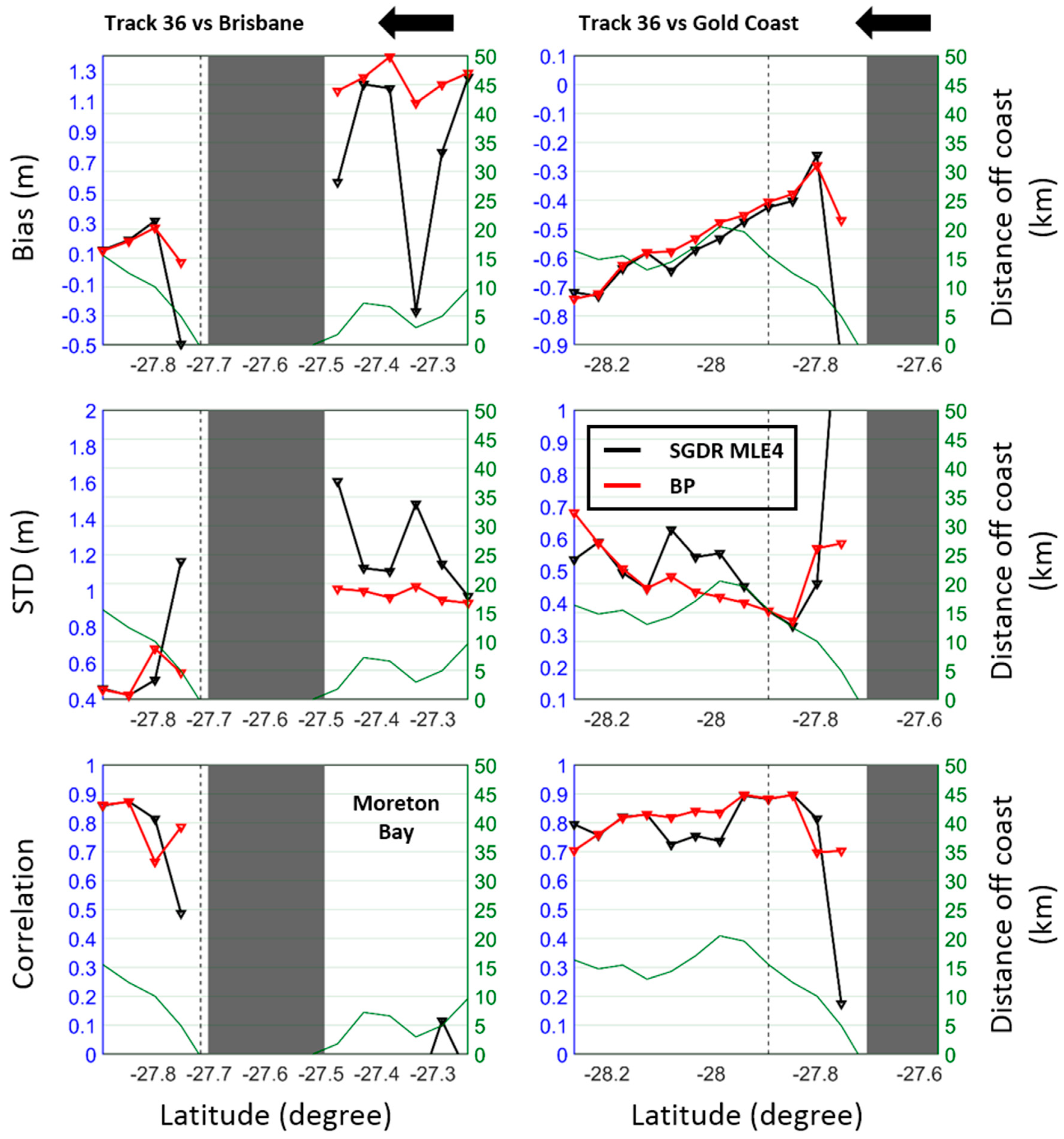
5.3. South Queensland
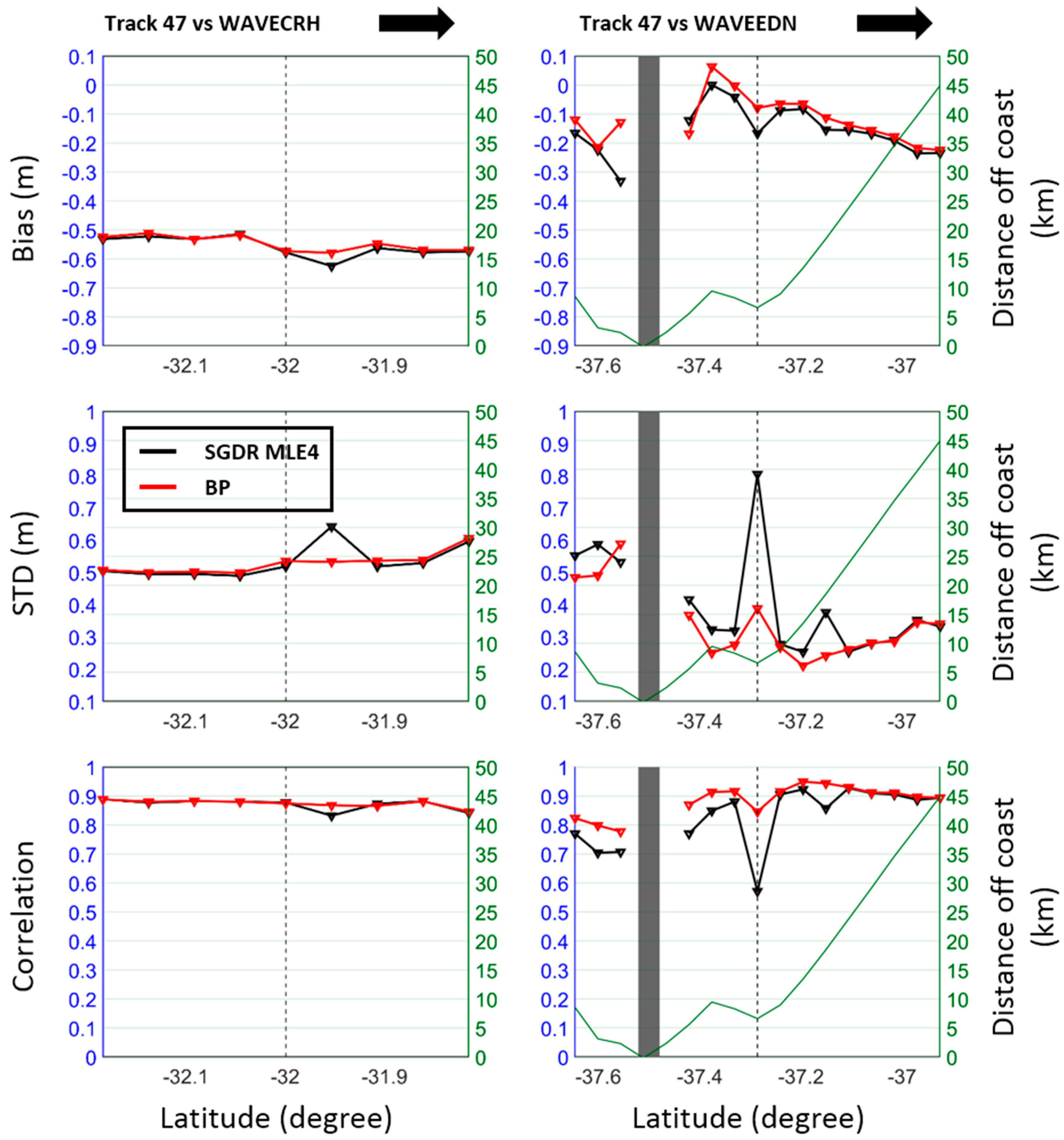
5.4. New South Wales
5.5. Discussion of Common Issues
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bhatt, V.; Kumar, R.; Basu, S.; Agarwal, V.K. Assimilation of altimeter significant wave height into a third-generation global spectral wave model. IEEE Trans. Geosci. Remote Sens. 2005, 43, 110–117. [Google Scholar] [CrossRef]
- Caballero, I.; Gómez-Enri, J.; Cipollini, P.; Navarro, G. Validation of high spatial resolution wave data from Envisat RA-2 altimeter in the Gulf of Cádiz. IEEE Geosci. Remote Sens. Lett. 2014, 11, 371–375. [Google Scholar] [CrossRef]
- Dufau, C.; Martin-Puig, C.; Moreno, L. User requirements in the coastal ocean for satellite altimetry. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 51–60. [Google Scholar]
- Young, I.R. An intercomparison of Geosat, Topex and ERS1 measurements of wind speed and wave height. Ocean Eng. 1998, 26, 67–81. [Google Scholar] [CrossRef]
- Passaro, M.; Fenoglio-Marc, L.; Cipollini, P. Validation of significant wave height from improved satellite altimetry in the German Bight. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2146–2156. [Google Scholar] [CrossRef]
- Gommenginger, C.; Thibaut, P.; Fenoglio-Marc, L.; Quartly, G.; Deng, X.; Gómez-Enri, J.; Challenor, P.; Gao, Y. Retracking altimeter waveforms near the coasts. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 61–101. [Google Scholar]
- Cotton, P.D.; Carter, D.J.T. Cross calibration of TOPEX, ERS-1, and Geosat wave heights. J. Geophys. Res. Oceans 1994, 99, 25025–25033. [Google Scholar] [CrossRef]
- Durrant, T.H.; Greenslade, D.J.M.; Simmonds, I. Validation of Jason-1 and Envisat remotely sensed wave heights. J. Atmos. Ocean Technol. 2009, 26, 123–134. [Google Scholar] [CrossRef]
- Zieger, S.; Vinoth, J.; Young, I.R. Joint calibration of multiplatform altimeter measurements of wind speed and wave height over the past 20 years. J. Atmos. Ocean Technol. 2009, 26, 2549–2564. [Google Scholar] [CrossRef]
- Hithin, N.K.; Remya, P.G.; Nair, T.M.B.; Harikumar, R.; Kumar, R.; Nayak, S. Validation and intercomparison of SARAL/Altika and PISTACH-derived coastal wave heights using in-situ measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4120–4129. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Vignudelli, S.; Quartly, G.D.; Snaith, H.M. Ales: A multi-mission adaptive subwaveform retracker for coastal and open ocean altimetry. Remote Sens. Environ. 2014, 145, 173–189. [Google Scholar] [CrossRef] [Green Version]
- Peng, F.K.; Deng, X.L. A new retracking technique for Brown peaky altimetric waveforms. Mar. Geod. 2018, 41, 99–125. [Google Scholar] [CrossRef]
- Gourlay, M.R. Waves, Set-Up and currents on reefs: Cay formation and stability. In Proceedings of the Conference on Engineering in Coral Reef Regions, Townsville, Australia, 1–4 September 1996; pp. 149–264. [Google Scholar]
- Gallop, S.L.; Young, I.R.; Ranasinghe, R.; Durrant, T.H.; Haigh, I.D. The large-scale influence of the Great Barrier Reef matrix on wave attenuation. Coral Reefs 2014, 33, 1167–1178. [Google Scholar] [CrossRef] [Green Version]
- Shand, T.D.; Wasko, C.D.; Goodwin, I.D.; Carley, J.T.; You, Z.J.; Kulmar, M.; Cox, R.J. Long-term trends in NSW coastal wave climate and derivation of extreme design storms. In Proceedings of the 20th New South Wales Coastal Conference, Tweed Heads, Australia, 10–12 November 2011. [Google Scholar]
- Dobson, E.; Monaldo, F.; Goldhirsh, J.; Wilkerson, J. Validation of Geosat altimeter-derived wind speeds and significant wave heights using buoy data. J. Geophys. Res. Oceans 1987, 92, 10719–10731. [Google Scholar] [CrossRef]
- Monaldo, F. Expected differences between buoy and radar altimeter estimates of wind speed and significant wave height and their implications on buoy-altimeter comparisons. J. Geophys. Res. Oceans 1988, 93, 2285–2302. [Google Scholar] [CrossRef]
- Chaudhary, A.; Basu, S.; Kumar, R.; Prasad, K.V.S.R.; Sharma, R. Retrieving significant wave height in the indian ocean near Visakhapatnam using Jason-2 altimeter data. Remote Sens. Lett. 2015, 6, 286–294. [Google Scholar] [CrossRef]
- Queffeulou, P. Long-term validation of wave height measurements from altimeters. Mar. Geod. 2004, 27, 495–510. [Google Scholar] [CrossRef]
- Ray, R.D.; Beckley, B.D. Simultaneous ocean wave measurements by the Jason and Topex satellites, with buoy and model comparisons special issue: Jason-1 calibration/validation. Mar. Geod. 2003, 26, 367–382. [Google Scholar] [CrossRef]
- Brown, G. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Amarouche, L.; Thibaut, P.; Zanife, O.Z.; Dumont, J.P.; Vincent, P.; Steunou, N. Improving the Jason-1 ground retracking to better account for attitude effects. Mar. Geod. 2004, 27, 171–197. [Google Scholar] [CrossRef]
- Thibaut, P.; Amarouche, L.; Zanife, O.Z.; Steunou, N.; Vincent, P.; Raizonville, P. Jason-1 altimeter ground processing look-up correction tables. Mar. Geod. 2004, 27, 409–431. [Google Scholar] [CrossRef]
- Thibaut, P.; Poisson, J.C.; Bronner, E.; Picot, N. Relative performance of the MLE3 and MLE4 retracking algorithms on Jason-2 altimeter waveforms. Mar. Geod. 2010, 33, 317–335. [Google Scholar] [CrossRef]
- Caires, S.; Sterl, A. Validation of ocean wind and wave data using triple collocation. J. Geophys. Res. Oceans 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Caires, S.; Sterl, A.; Bidlot, J.R.; Graham, N.; Swail, V. Intercomparison of different wind–wave reanalyses. J. Clim. 2004, 17, 1893–1913. [Google Scholar] [CrossRef]
- Hemer, M.A.; Church, J.A.; Hunter, J.R. Waves and climate change on the Australian coast. J. Coast. Res. 2007, 50, 432–437. [Google Scholar]
- Middleton, J.H. Low-frequency trapped waves an a wide, reef-fringed continental shelf. J. Phys. Oceanogr. 1983, 13, 1371–1382. [Google Scholar] [CrossRef]
- Middleton, J.H.; Cunningham, A. Wind-forced continental shelf waves from a geographical origin. Cont. Shelf Res. 1984, 3, 215–232. [Google Scholar] [CrossRef]
- Church, J.A.; Freeland, H.J. The energy source for the coastal-trapped waves in the Australian coastal experiment region. J. Phys. Oceanogr. 1987, 17, 289–300. [Google Scholar] [CrossRef]
- Church, J.A.; Freeland, H.J.; Smith, R.L. Coastal-trapped waves on the east Australian continental shelf part i: Propagation of modes. J. Phys. Oceanogr. 1986, 16, 1929–1943. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J.; Clarke, A.J.; Freeland, H.J.; Smith, R.L. Coastal-trapped waves on the east Australian continental shelf part ii: Model verification. J. Phys. Oceanogr. 1986, 16, 1945–1957. [Google Scholar] [CrossRef]
- Mortlock, R.T.; Goodwin, D.I. Directional wave climate and power variability along the Southeast Australian shelf. Cont. Shelf Res. 2015, 98, 36–53. [Google Scholar] [CrossRef]
- Liu, Y.; Kerkering, H.; Weisberg, R.H. (Eds.) Coastal Ocean Observing Systems; Elsevier: London, UK, 2015; p. 461. [Google Scholar]
- Chelton, D.B.; Walsh, E.J.; MacArthur, J.L. Pulse compression and sea level tracking in satellite altimetry. J. Atmos. Ocean. Technol. 1989, 6, 407–438. [Google Scholar] [CrossRef]
- Fenoglio-Marc, L.; Dinardo, S.; Scharroo, R.; Roland, A.; Sikiric, M.D.; Lucas, B.; Becker, M.; Benveniste, J.; Weiss, R. The German Bight: A validation of Cryosat-2 altimeter data in SAR mode. Adv. Space Res. 2015, 55, 2641–2656. [Google Scholar] [CrossRef]
- Phalippou, L.; Enjolras, V. Re-tracking of SAR altimeter ocean power-waveforms and related accuracies of the retrieved sea surface height, significant wave height and wind speed. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 3533–3536. [Google Scholar]
- Sepulveda, H.H.; Queffeulou, P.; Ardhuin, F. Assessment of SARAL/Altika wave height measurements relative to buoy, Jason-2, and Cryosat-2 data. Mar. Geod. 2015, 38, 449–465. [Google Scholar] [CrossRef]
- Shaeb, K.H.B.; Anand, A.; Joshi, A.K.; Bhandari, S.M. Comparison of near coastal significant wave height measurements from SARAL/Altika with wave rider buoys in the Indian region. Mar. Geod. 2015, 38, 422–436. [Google Scholar] [CrossRef]
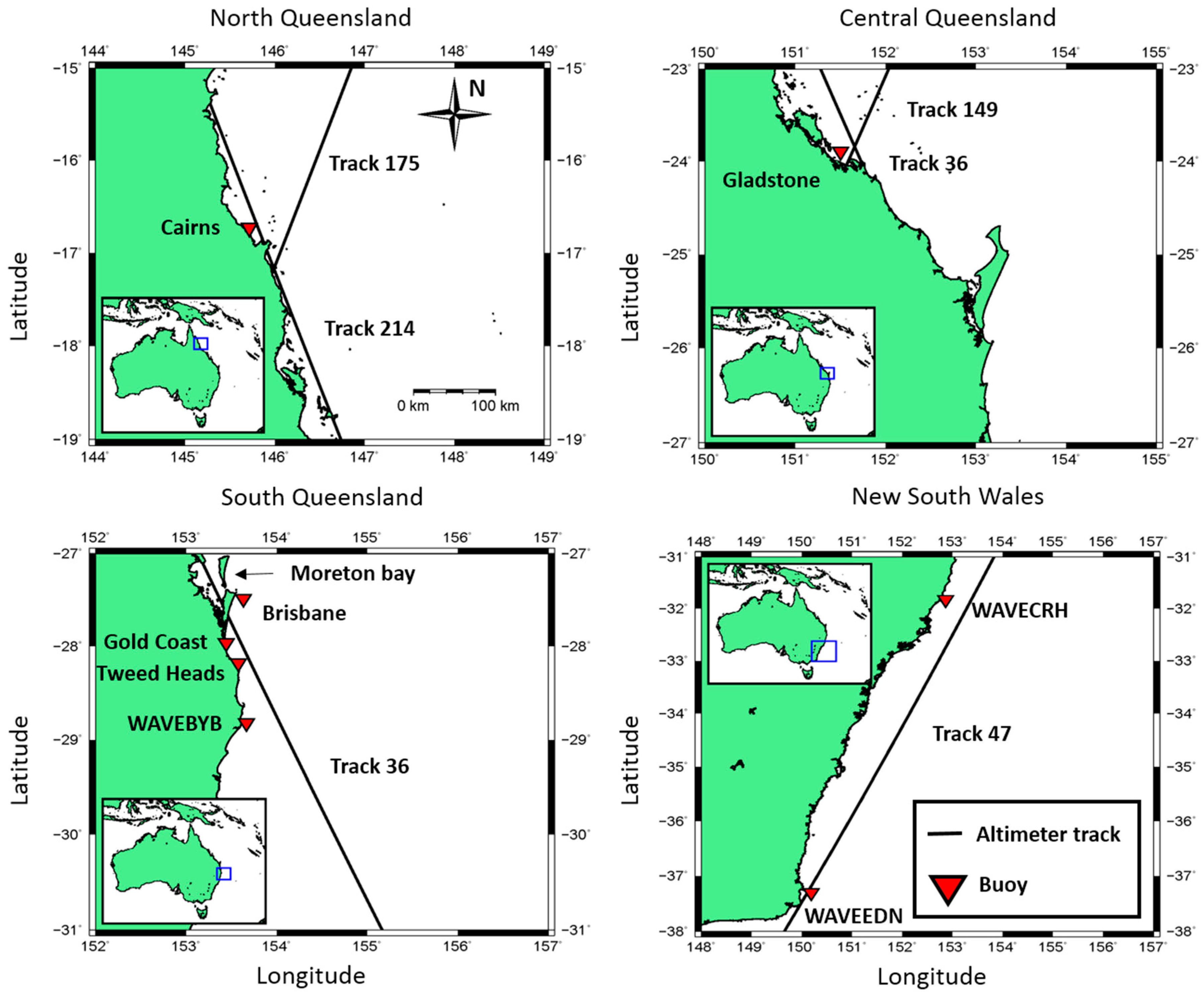


| Buoy | Altimeter Track | Minimum Buoy-Track Distance (km) | Maximum Buoy-Track Distance (km) | Buoy-Coast Distance (km) |
|---|---|---|---|---|
| Cairns | 175 | 44.8 | 49.6 | 2.2 |
| 214 | 9.7 | 46.4 | 2.2 | |
| Gladstone | 36 | 17.1 | 45.9 | 5.0 |
| 149 | 12.6 | 49.7 | 5.0 | |
| Brisbane | 36 | 23.8 | 47.1 | 10.1 |
| Gold Coast | 36 | 14.9 | 45.0 | 1.1 |
| Tweed Heads | 36 | 12.3 | 48.5 | 1.6 |
| WAVEBYB | 36 | 32.9 | 49.5 | 5.6 |
| WAVECRH | 47 | 44.0 | 49.8 | 10.0 |
| WAVEEDN | 47 | 7.0 | 46.9 | 12.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, F.; Deng, X. Validation of Improved Significant Wave Heights from the Brown-Peaky (BP) Retracker along the East Coast of Australia. Remote Sens. 2018, 10, 1072. https://doi.org/10.3390/rs10071072
Peng F, Deng X. Validation of Improved Significant Wave Heights from the Brown-Peaky (BP) Retracker along the East Coast of Australia. Remote Sensing. 2018; 10(7):1072. https://doi.org/10.3390/rs10071072
Chicago/Turabian StylePeng, Fukai, and Xiaoli Deng. 2018. "Validation of Improved Significant Wave Heights from the Brown-Peaky (BP) Retracker along the East Coast of Australia" Remote Sensing 10, no. 7: 1072. https://doi.org/10.3390/rs10071072
APA StylePeng, F., & Deng, X. (2018). Validation of Improved Significant Wave Heights from the Brown-Peaky (BP) Retracker along the East Coast of Australia. Remote Sensing, 10(7), 1072. https://doi.org/10.3390/rs10071072