Flow Duration Curve from Satellite: Potential of a Lifetime SWOT Mission
Abstract
:1. Introduction
2. Materials and Datasets
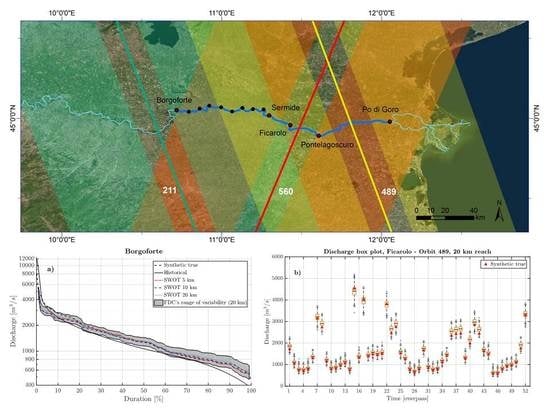
2.1. Study Area and Available Data
2.2. SWOT Mission: Scientific Background and Satellite Coverage
2.3. Hydrodynamic Simulation of the River
3. Methodology
3.1. River Reach Discretization
3.2. Simulation of SWOT Hydraulic Variables and River Discharge Estimation
3.3. Flow Duration Curve
3.4. Performance Indices
4. Results and Discussion
4.1. Discharge Estimation
4.2. Spatial and Temporal Monitoring of the Study Area
4.3. Estimation of Flow Duration Curve (FDC)
4.4. Potential and Limitations of the SWOT Mission for FDC Monitoring
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pugliese, A.; Farmer, W.H.; Castellarin, A.; Archfield, S.A.; Vogel, R.M. Regional flow duration curves: Geostatistical techniques versus multivariate regression. Adv. Water Resour. 2016, 96, 11–22. [Google Scholar] [CrossRef]
- Vogel, R.M.; Fennessey, N.M. Flow duration curves II: A review of applications in water resources planning. JAWRA J. Am. Water Resour. Assoc. 1995, 31, 1029–1039. [Google Scholar] [CrossRef]
- Chow, V.T. Handbook of Applied Hydrology; McGraw-Hill Book Company: New York, NY, USA, 1964. [Google Scholar]
- Castellarin, A.; Galeati, G.; Brandimarte, L.; Montanari, A.; Brath, A. Regional flow-duration curves: Reliability for ungauged basins. Adv. Water Resour. 2004, 27, 953–965. [Google Scholar] [CrossRef]
- Ganora, D.; Claps, P.; Laio, F.; Viglione, A. An approach to estimate nonparametric flow duration curves in ungauged basins. Water Resour. Res. 2009, 45, 1–10. [Google Scholar] [CrossRef]
- Singh, K.P. Model Flow Duration and Streamflow Variability. Water Resour. Res. 1971, 7, 1031–1036. [Google Scholar] [CrossRef]
- Castellarin, A. Regional prediction of flow-duration curves using a three-dimensional kriging. J. Hydrol. 2014, 513, 179–191. [Google Scholar] [CrossRef]
- Tourian, M.J.; Sneeuw, N.; Bárdossy, A. A quantile function approach to discharge estimation from satellite altimetry (ENVISAT). Water Resour. Res. 2013, 49, 4174–4186. [Google Scholar] [CrossRef] [Green Version]
- Alsdorf, D.E.; Rodriguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45, 1–24. [Google Scholar] [CrossRef]
- Wilson, M.D.; Durand, M.; Jung, H.C.; Alsdorf, D. Swath-altimetry measurements of the main stem Amazon River: Measurement errors and hydraulic implications. Hydrol. Earth Syst. Sci. 2015, 19, 1943–1959. [Google Scholar] [CrossRef]
- Schumann, G.J.-P.; Domeneghetti, A. Exploiting the proliferation of current and future satellite observations of rivers. Hydrol. Process. 2016, 30, 2891–2896. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Dingman, S.L.; Bolster, C.H. Comparison of constitutive flow resistance equations based on the Manning and Chezy equations applied to natural rivers. Water Resour. Res. 2005, 41, 1–7. [Google Scholar] [CrossRef]
- Brakenridge, G.R.; Nghiem, S.V.; Andreson, E.; Chien, S. Space-Based Measurement of River Runoff. EOS Trans. Am. Geophys. Union 2005, 86, 185–192. [Google Scholar] [CrossRef]
- Gleason, C.J.; Smith, L.C. Toward global mapping of river discharge using satellite images and at-many-stations hydraulic geometry. Proc. Natl. Acad. Sci. USA 2014. [Google Scholar] [CrossRef] [PubMed]
- Durand, M.; Neal, J.; Rodríguez, E.; Andreadis, K.M.; Smith, L.C.; Yoon, Y. Estimating reach-averaged discharge for the River Severn from measurements of river water surface elevation and slope. J. Hydrol. 2014, 511, 92–104. [Google Scholar] [CrossRef]
- Durand, M.; Gleason, C.J.; Garambois, P.A.; Bjerklie, D.; Smith, L.C.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J.; et al. An intercomparison of remote sensing river discharge estimation algorithms frommeasurements of river height, width, and slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; Moore, P.; Kilsby, C.G.; O’Donnell, G.M.; Hardy, A.J.; Berry, P.A.M. Daily discharge estimation at ungauged river sites using remote sensing. Hydrol. Process. 2014, 28, 1043–1054. [Google Scholar] [CrossRef]
- Garambois, P.A.; Monnier, J. Inference of effective river properties from remotely sensed observations of water surface. Adv. Water Resour. 2015, 79, 103–120. [Google Scholar] [CrossRef]
- Oubanas, H.; Gejadze, I.; Malaterre, P.; Durand, M.; Wei, R.; Frasson, R.P.M.; Domeneghetti, A. Discharge Estimation in Ungauged Basins Through Variational Data Assimilation: The Potential of the SWOT Mission Water Resources Research. Water Resour. Res. 2018, 54, 2405–2423. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Clark, E.A.; Lettenmaier, D.P.; Alsdorf, D.E. Prospects for river discharge and depth estimation through assimilation of swath-altimetry into a raster-based hydrodynamics model. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Amarnath, G.; Brocca, L.; Massari, C.; Moramarco, T. Remote Sensing of Environment Discharge estimation and forecasting by MODIS and altimetry data in Niger-Benue River. Remote Sens. Environ. 2017, 195, 96–106. [Google Scholar] [CrossRef]
- Tourian, M.J.; Tarpanelli, A.; Elmi, O.; Qin, T.; Brocca, L.; Moramarco, T.; Sneeuw, N. Spatiotemporal densification of river water level time series bymultimission satellite altimetry. Water Resour. Res. 2016, 52, 1140–1159. [Google Scholar] [CrossRef]
- Tourian, M.J.; Schwatke, C.; Sneeuw, N. River discharge estimation at daily resolution from satellite altimetry over an entire river basin. J. Hydrol. 2017, 546, 230–247. [Google Scholar] [CrossRef]
- Rodriguez, E. Surface Water and Ocean Topography Mission (SWOT) Project Science Requirements Document; JPL D-61923; JPL: Pasadena, CA, USA, 2016. [Google Scholar]
- De Frasson, R.P.M.; Wei, R.; Durand, M.; Minear, J.T.; Domeneghetti, A.; Schumann, G.; Williams, B.A.; Rodriguez, E.; Picamilh, C.; Lion, C.; et al. Automated River Reach Definition Strategies: Applications for the Surface Water and Ocean TopographyMission. Water Resour. Res. 2017, 53, 8164–8186. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT Mission and Its Capabilities for Land Hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Schumann, G.J.; Frasson, R.P.M.; Wei, R.; Pavelsky, T.M.; Castellarin, A.; Brath, A.; Durand, M.T. Characterizing water surface elevation under different flow conditions for the upcoming SWOT mission. J. Hydrol. 2018, 561, 848–861. [Google Scholar] [CrossRef]
- Fjørtoft, R.; Gaudin, J.M.; Pourthié, N.; Lalaurie, J.C.; Mallet, A.; Nouvel, J.F.; Martinot-Lagarde, J.; Oriot, H.; Borderies, P.; Ruiz, C.; et al. KaRIn on SWOT: Characteristics of near-nadir Ka-band interferometric SAR imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2172–2185. [Google Scholar] [CrossRef]
- Preissmann, A. Propagation of translatory waves in channels and rivers. In Proceedings of the First Congress of French Association for Computation (AFCAL), Grenoble, France, 1961; pp. 433–442. [Google Scholar]
- Castellarin, A.; Di Baldassarre, G.; Brath, A. Floodplain management strategies for flood attenuation in the river Po. River Res. Appl. 2011, 27, 1037–1047. [Google Scholar] [CrossRef]
- Castellarin, A.; Domeneghetti, A.; Brath, A. Identifying robust large-scale flood risk mitigation strategies: A quasi-2D hydraulic model as a tool for the Po River. Phys. Chem. Earth Parts A B C 2011, 36, 299–308. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Tarpanelli, A.; Brocca, L.; Barbetta, S.; Moramarco, T.; Castellarin, A.; Brath, A. The use of remote sensing-derived water surface data for hydraulic model calibration. Remote Sens. Environ. 2014, 149, 130–141. [Google Scholar] [CrossRef]
- Durand, M.; Andreadis, K.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Moller, D.; Wilson, M. Estimation of bathymetric depth and slope from data assimilation of swath altimetry into a hydrodynamic model. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Montanari, A.; Ceola, S.; Baratti, E.; Domeneghetti, A.; Brath, A. Po River Basin. In Handbook of Applied Hydrology, 2nd ed.; Singh, V.P., Ed.; McGraw Hill: New York, NY, USA, 2017; pp. 1–4. [Google Scholar]
- Paiva, R.C.D.; Durand, M.; Hossain, F. Spatiotemporal interpolation of discharge across a river network by using synthetic SWOT satellite data. Water Resour. Res. 2015, 51, 430–449. [Google Scholar] [CrossRef] [Green Version]
- Yoon, Y.; Durand, M.; Merry, C.J.; Rodriguez, E. Improving temporal coverage of the SWOT mission using spatiotemporal kriging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1719–1729. [Google Scholar] [CrossRef]
- Pan, M.; Wood, E.F. Inverse streamflow routing. Hydrol. Earth Syst. Sci. 2013, 17, 4577–4588. [Google Scholar] [CrossRef] [Green Version]
- Schumann, G.J.-P.; Bates, P.; Neal, J.; Andreadis, K. Fight floods on a global scale. Nature 2014, 507, 2014. [Google Scholar] [CrossRef] [PubMed]
- Domeneghetti, A. On the use of SRTM and altimetry data for flood modeling in data-sparse regions. Water Resour. Res. 2016, 52, 2901–2918. [Google Scholar] [CrossRef]














| Historical Data | Three-Year Period: 2008–2010 | |||||||
|---|---|---|---|---|---|---|---|---|
| Starting Year of Obs. (-) | Main Channel Width (m) | Min. Q (m3/s) | Mean Q (m3/s) | Max. Q (m3/s) | Min. Q (m3/s) | Mean Q (m3/s) | Max. Q (m3/s) | |
| Borgoforte | 1923 | 326 | 209 | 1312 | 12,047 | 466 | 1591 | 8060 |
| Sermide | 1994 | 485 | 123 | 1422 | 10,100 | 452 | 1661 | 7660 |
| Ficarolo | 1988 | 357 | 245 | 1557 | 11,200 | 560 | 1766 | 7580 |
| Pontelagoscuro | 1922 | 316 | 156 | 1509 | 10,300 | 534 | 1728 | 7090 |
| Δx [km] | 560 Up | 560 Down | 489 | 211 |
|---|---|---|---|---|
| 5 | 14 | 8 | 16 | 14 |
| 10 | 7 | 4 | 8 | 7 |
| 20 | 4 | 2 | 4 | 4 |
| MAE (m3/s) | RMSE (m3/s) | |||||
|---|---|---|---|---|---|---|
| Swath | 5 km | 10 km | 20 km | 5 km | 10 km | 20 km |
| 560 upstream | 146 | 144 | 118 | 177 | 173 | 175 |
| 560 downstream | 366 | 274 | 373 | 425 | 333 | 429 |
| 489 | 199 | 167 | 151 | 238 | 206 | 190 |
| 211 | 152 | 145 | 117 | 183 | 176 | 174 |
| rMAE (%) | rRMSE (%) | |||||
| 560 upstream | 10.3 | 10.1 | 8.4 | 12.5 | 12.3 | 12.7 |
| 560 downstream | 31.2 | 23.3 | 33.3 | 35.6 | 27.7 | 37.5 |
| 489 | 13.0 | 11.6 | 10.6 | 15.7 | 14.4 | 13.4 |
| 211 | 10.3 | 10.0 | 8.2 | 12.5 | 12.2 | 12.6 |
| rMAE (%) | rRMSE (%) | |||||
|---|---|---|---|---|---|---|
| Station | 5 km | 10 km | 20 km | 5 km | 10 km | 20 km |
| Borgoforte | 4.2 | 4.3 | 4.3 | 6.8 | 6.9 | 6.0 |
| Sermide | 28.3 | 14.6 | 5.7 | 29.2 | 15.2 | 6.6 |
| Ficarolo | 22.4 | 13.3 | 11.9 | 23.8 | 14.1 | 13.0 |
| Pontelagoscuro | 12.3 | 22.0 | 13.3 | 14.5 | 26.3 | 15.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domeneghetti, A.; Tarpanelli, A.; Grimaldi, L.; Brath, A.; Schumann, G. Flow Duration Curve from Satellite: Potential of a Lifetime SWOT Mission. Remote Sens. 2018, 10, 1107. https://doi.org/10.3390/rs10071107
Domeneghetti A, Tarpanelli A, Grimaldi L, Brath A, Schumann G. Flow Duration Curve from Satellite: Potential of a Lifetime SWOT Mission. Remote Sensing. 2018; 10(7):1107. https://doi.org/10.3390/rs10071107
Chicago/Turabian StyleDomeneghetti, Alessio, Angelica Tarpanelli, Luca Grimaldi, Armando Brath, and Guy Schumann. 2018. "Flow Duration Curve from Satellite: Potential of a Lifetime SWOT Mission" Remote Sensing 10, no. 7: 1107. https://doi.org/10.3390/rs10071107
APA StyleDomeneghetti, A., Tarpanelli, A., Grimaldi, L., Brath, A., & Schumann, G. (2018). Flow Duration Curve from Satellite: Potential of a Lifetime SWOT Mission. Remote Sensing, 10(7), 1107. https://doi.org/10.3390/rs10071107