2-D Coherent Integration Processing and Detecting of Aircrafts Using GNSS-Based Passive Radar
Abstract
:1. Introduction
2. Air Target Echo Model in GNSS-Based Passive Radar
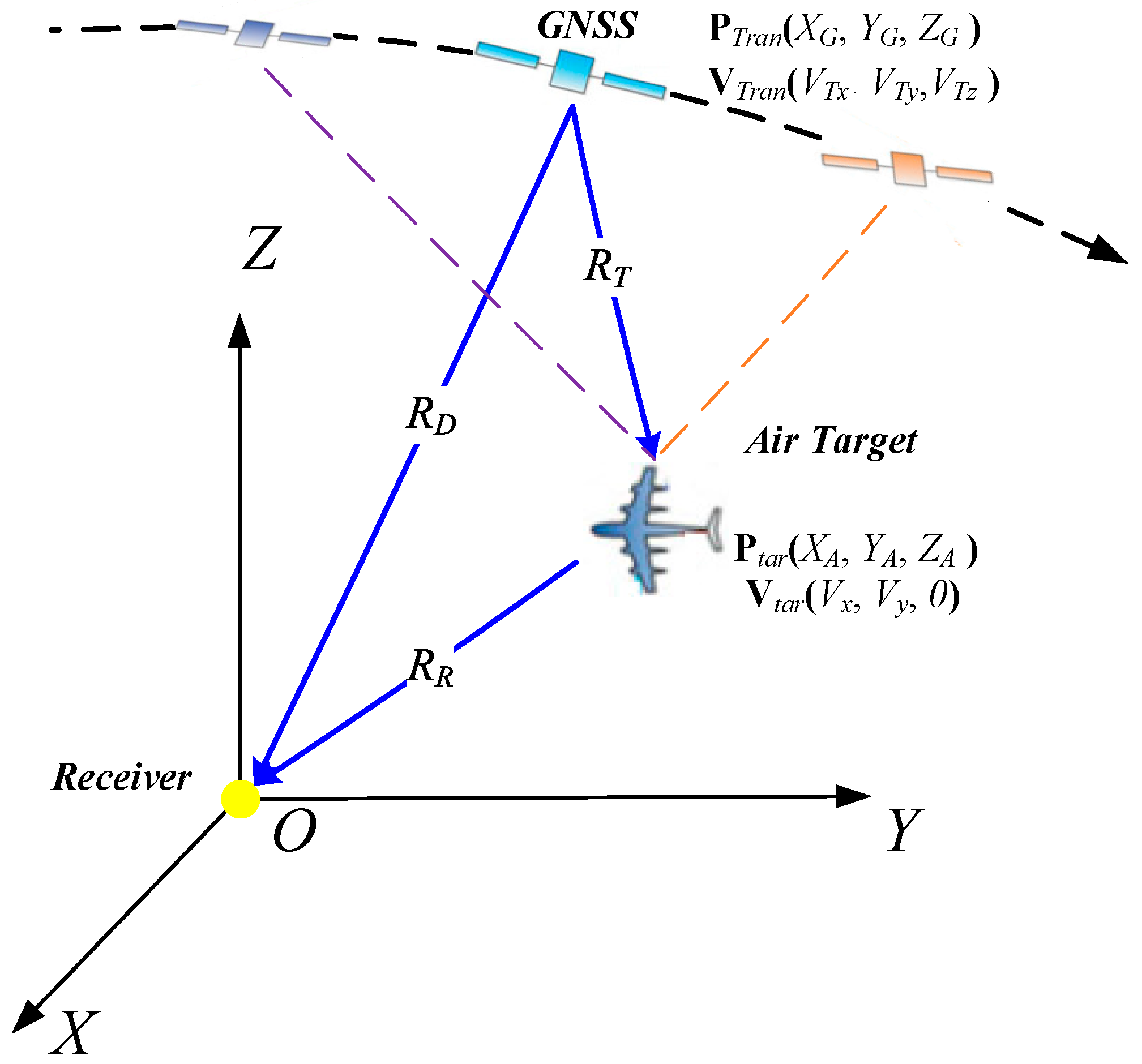
2.1. GNSS-Based Passive Radar Geometry and Doppler Characteristic Analysis
2.2. Air Target Echo Signal Model of GNSS-Based Passive Radar
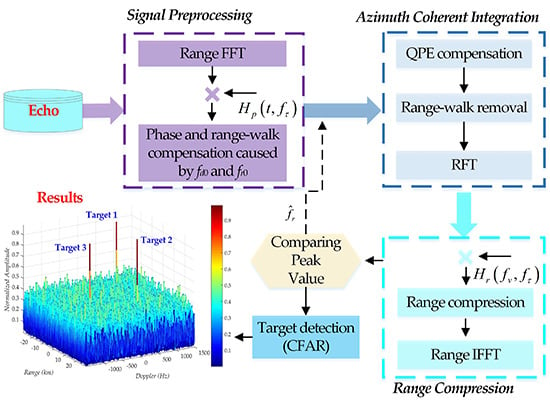
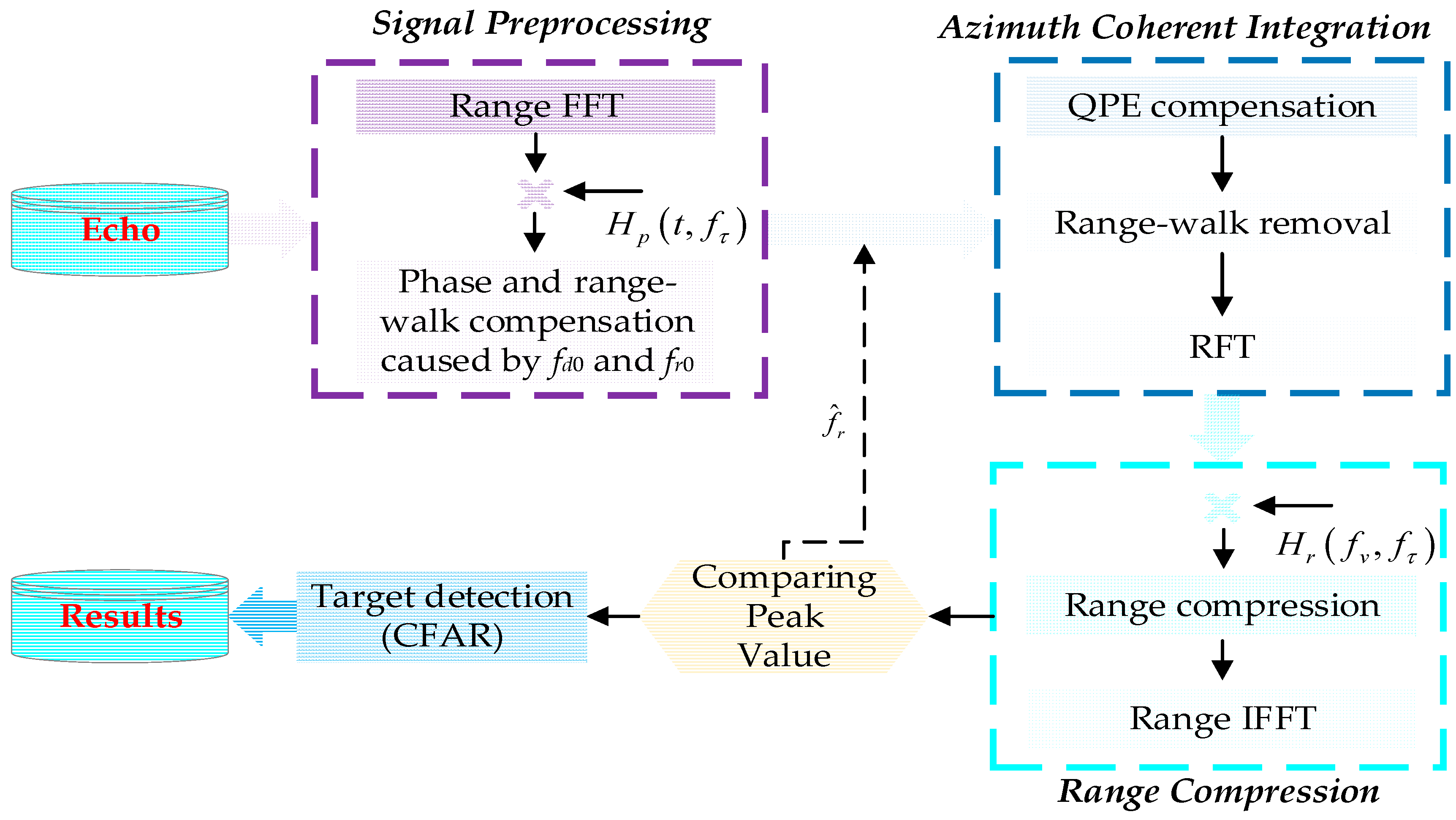
3. The Proposed 2-D Coherent Integration Processing and Target Detection Algorithm
3.1. The Principle of RFT
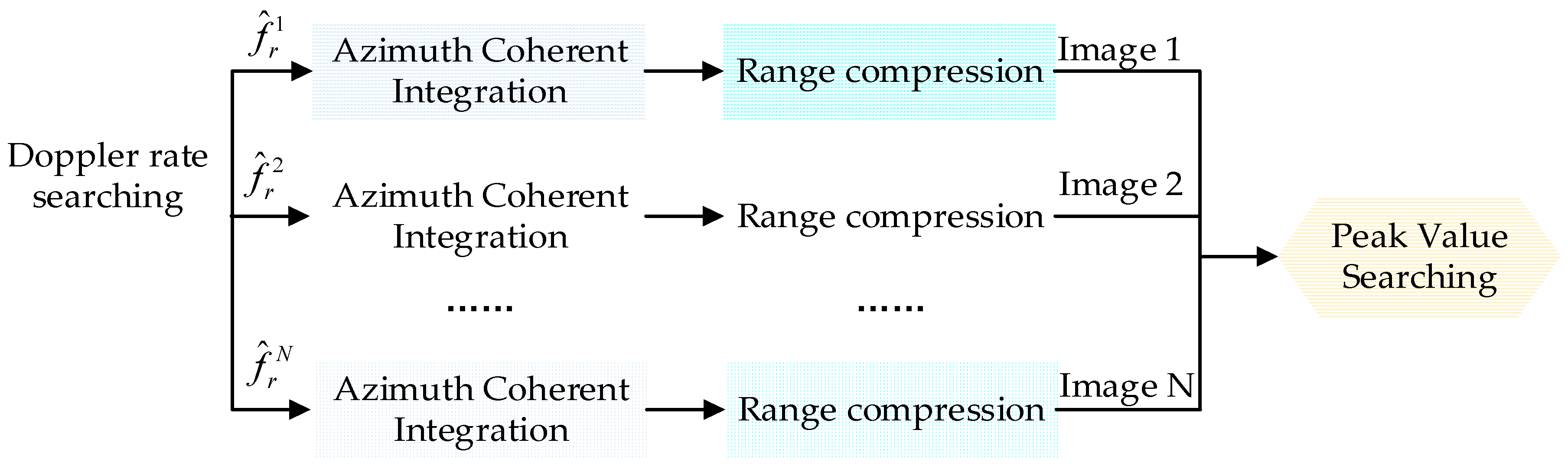
3.2. Air Target Detection Based on 2-D Coherent Integration
3.2.1. Signal Preprocessing
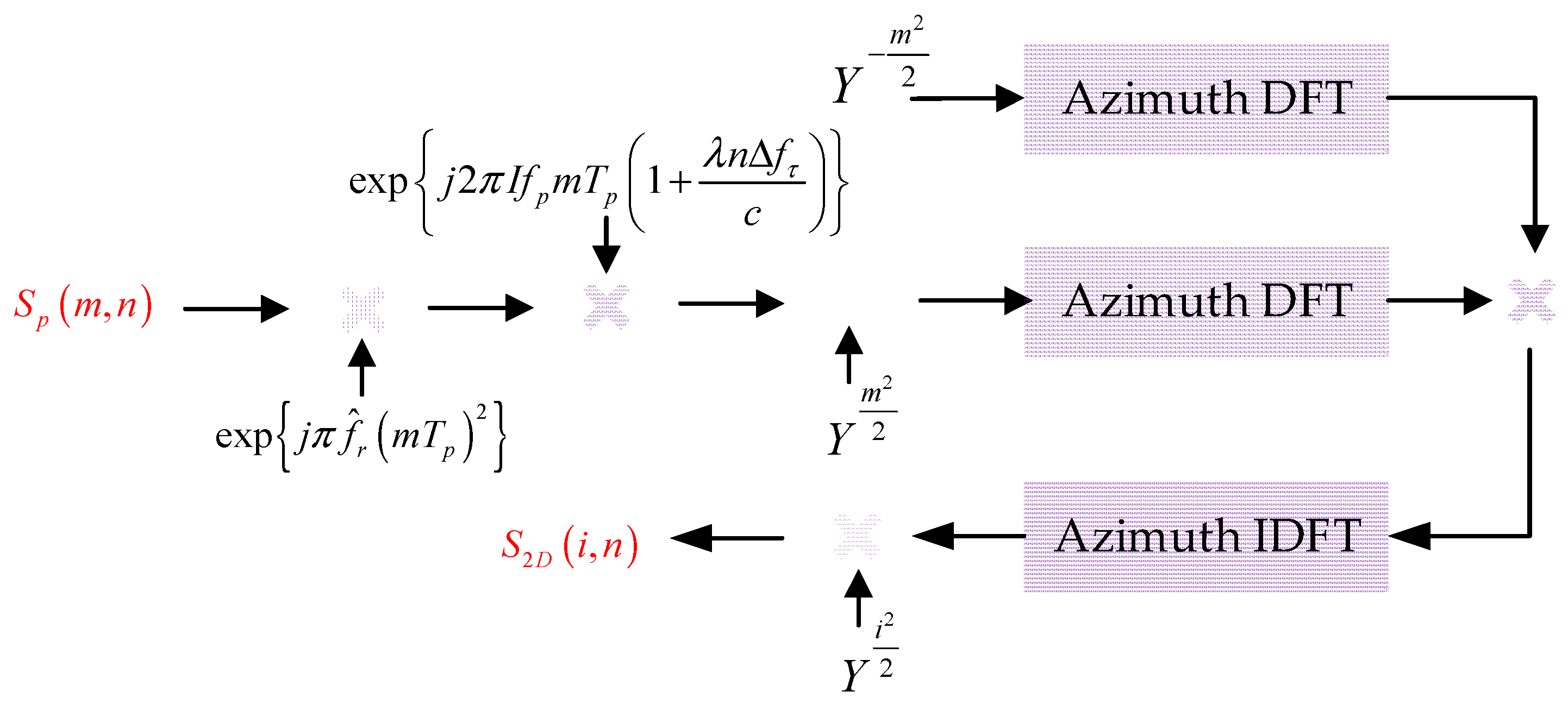
3.2.2. Azimuth Coherent Integration
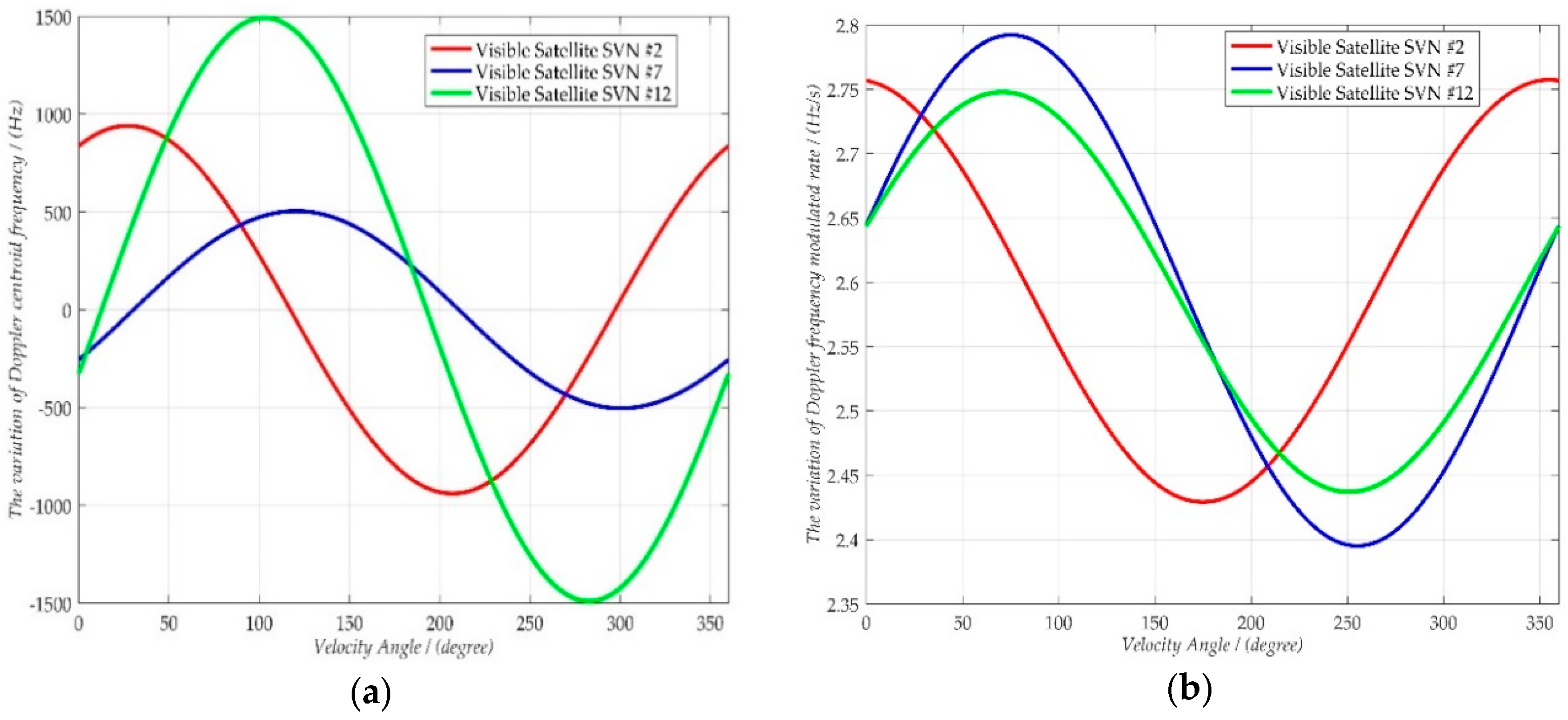
- The first phase term in the first line of Equation (13) is QPE compensation, and is the estimated Doppler rate parameter. As shown in Figure 2b, the variation range of Doppler rate is very small, and the maximum variation value is smaller than 0.6 Hz/s. Hence, we can use parallelized step search to estimate the Doppler rate (as shown in Figure 4), and this method has a high searching efficiency because of the small variation range of fr,v. Normally, the estimated Doppler rate can be expressed as:where , and denote the initial Doppler rate, Doppler rate searching step, and Doppler rate searching number, respectively. Finally, when matches the true value of target Doppler rate or equals zero, the azimuth coherent gain could be achieved and the maximum peak value of target will be obtained.
- The second phase term in the first line of Equation (13) is residual range-walk removal, and fv is the Doppler searching parameter. As shown in Equation (9), non-integer range cell is inevitable during the range history line searching, so range interpolation processing is necessary for traditional RFT. However, in Equation (13), when fv matches the target’s Doppler frequency, fd,v, all range-walk term is removed, and the echo signal will distribute along the line perpendicular to the range direction. Therefore, the non-interpolation processing is needed in the proposed algorithm, and the following azimuth integral processing is greatly simplified.
- The last phase term in the first line of Equation (13) is RFT processing, or called azimuth integral. As the range-walk term is removed, the echo signal is distributed along the azimuth direction. So, the RFT operation is similar to azimuth FFT operation.
3.2.3. Range Compression
3.2.4. Target Detection
4. Experiments and Discussion
4.1. Experiments and Results
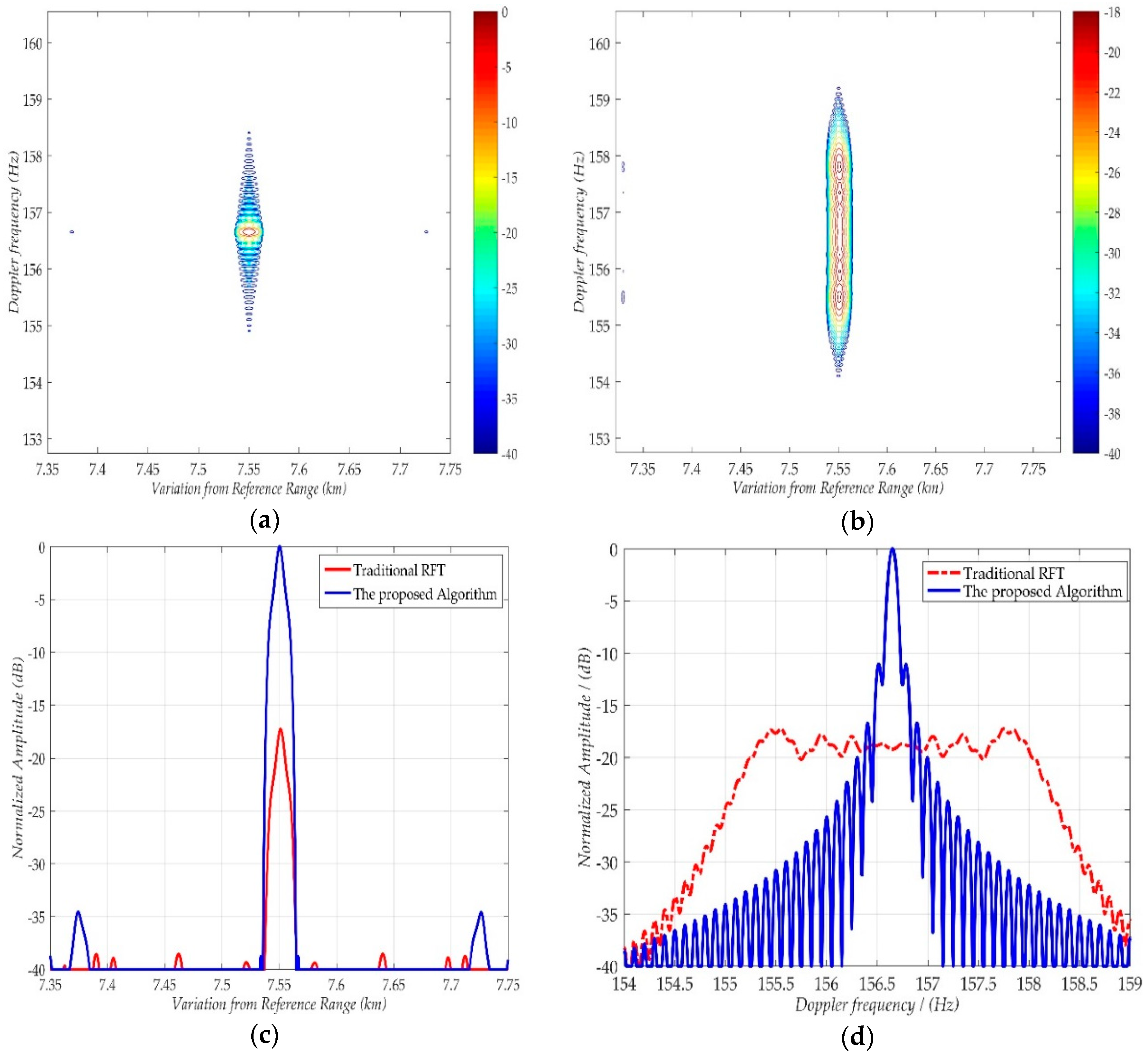
4.1.1. Comparing Results Using the Proposed Algorithm and Traditional RFT
4.1.2. Multi-Static Experiments and Aircrafts Motion Parameters Estimation
4.2. Discussion
4.2.1. Power Budget and Coherent Time
4.2.2. Searching Step of Doppler Rate
4.2.3. Doppler Ambiguity
4.2.4. Computation Analysis about the Azimuth Coherent Processing
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
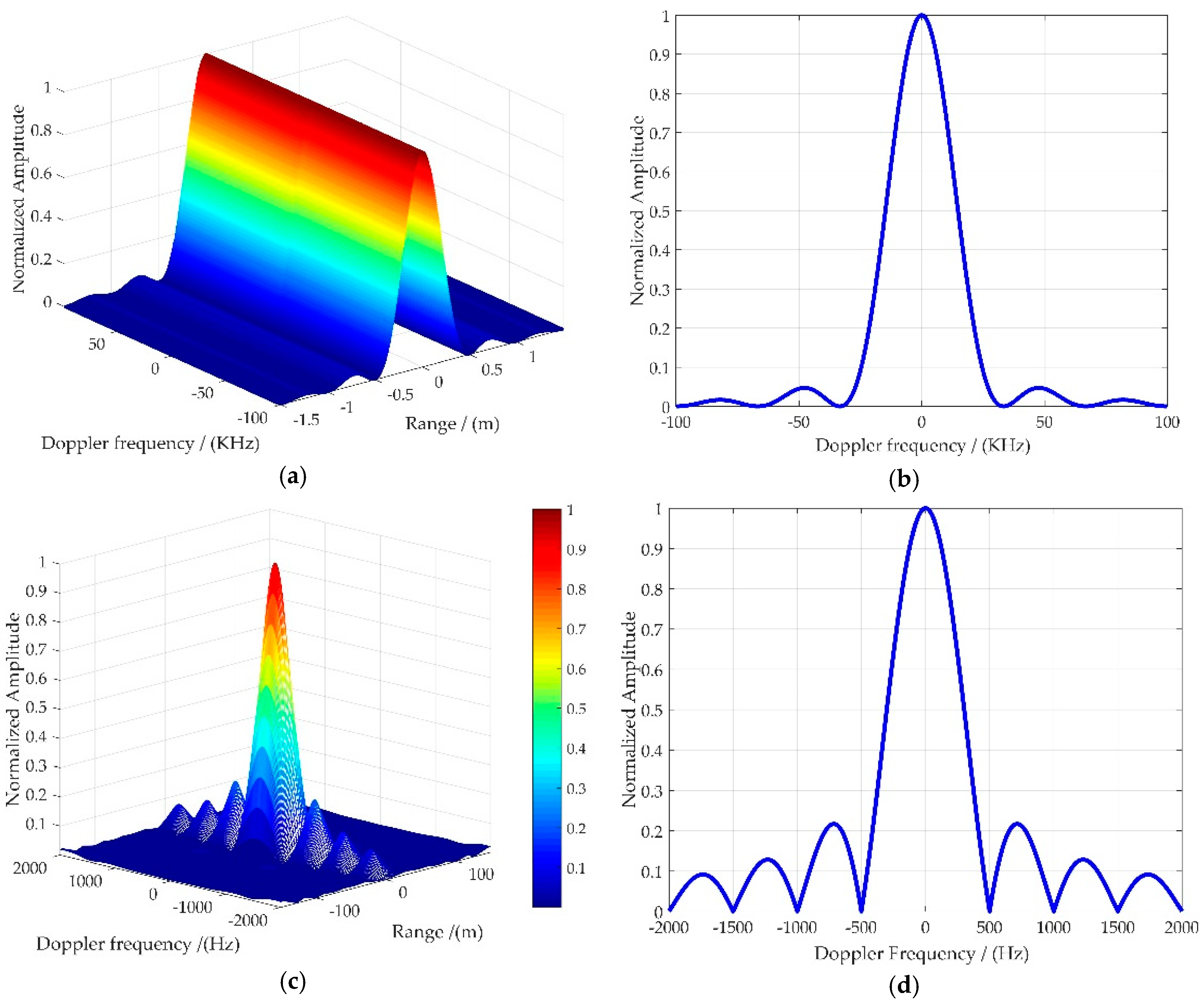
Appendix A. Delay-Doppler Ambiguity Function of GNSS and LFM Signal
Appendix B
References
- Del-Rey-Maestre, N.; Mata-Moya, D.; Jarabo-Amores, M.; Gómez-del-Hoyo, P.; Bárcena-Humanes, J.; Rosado-Sanz, J. Passive Radar Array Processing with Non-Uniform Linear Arrays for Ground Target’s Detection and Localization. Remote Sens. 2017, 9, 756. [Google Scholar] [CrossRef]
- Shang, H.; Jia, L.; Menenti, M. Modeling and reconstruction of time series of passive microwave data by discrete Fourier transform guided filtering and harmonic analysis. Remote Sens. 2016, 8, 970. [Google Scholar] [CrossRef]
- Belfiori, F.; Monni, S.; Rossum, W.V.; Hoogeboom, P. Antenna array characterisation and signal processing for an FM radio-based passive coherent location radar system. IET Radar Sonar Navig. 2012, 6, 687–696. [Google Scholar] [CrossRef]
- Colone, F.; Faclone, P.; Bongioanni, C.; Lombardo, P. WiFi-based passive bistatic radar: Data processing schemes and experimental results. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1061–1079. [Google Scholar] [CrossRef]
- Ribo, S.; Arco, J.C.; Oliveras, S.; Cardellach, E.; Rius, A.; Buck, C. Experimental results of an X-band PARIS reciver using digital satellite TV opportunity signals scattered on the sea surface. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5704–5711. [Google Scholar] [CrossRef]
- Ma, H.; Antoniou, M.; Pastina, D.; Santi, F.; Pieralice, F.; Bucciarelli, M.; Cherniakov, M. Maritime Moving Target Indication Using Passive GNSS-based Bistatic Radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 115–130. [Google Scholar] [CrossRef]
- Clemente, C.; Soraghan, J.J. GNSS-Based Passive Bistatic Radar for Micro-Doppler Analysis of Helicopter Rotor Blades. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 491–500. [Google Scholar] [CrossRef]
- Liu, F.; Antoniou, M.; Zeng, Z.; Cherniakov, M. Coherent change detection using passive GNSS-based BSAR: Experimental proof of concept. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4544–4555. [Google Scholar] [CrossRef]
- He, X.; Zeng, T.; Cherniakov, M. Signal detectability in SS-BSAR with GNSS non-cooperative transmitter. IEE Proc. Radar Sonar Navig. 2005, 152, 124–132. [Google Scholar] [CrossRef]
- Hu, C.; Liu, C.; Wang, R.; Chen, L.; Wang, L. Detection and SISAR Imaging of Aircrafts Using GNSS Forward Scatter Radar: Signal Modeling and Experimental Validation. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2077–2093. [Google Scholar] [CrossRef]
- Suberviola, I.; Mayordomo, I.; Mendizabal, J. Experimental Results of Air Target Detection with a GPS Forward-Scattering Radar. IEEE Geosci. Remote Sens. Lett. 2011, 9, 47–51. [Google Scholar] [CrossRef]
- Kabakchiev, C.; Garvanov, I.; Behar, V.; Kabakchieva, D.; Kabakchiev, K.; Rohling, H.; Kulpa, K.; Yarovoy, A. Detection and classification of objects from their radio shadows of GPS signals. In Proceedings of the 2015 16th International Radar Symposium (IRS), Dresden, Germany, 24–26 June 2015; pp. 906–991. [Google Scholar]
- Glennon, E.P.; Dempster, A.G.; Rizos, C. Feasibility of Air Target Detection Using GPS as a Bistatic Radar. J. Glob. Position. Syst. 2006, 5, 119–126. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, M.; Cherniakov, M. GNSS-based bistatic SAR: A signal processing view. Eurasip J. Adv. Signal Process. 2013, 1, 1–16. [Google Scholar] [CrossRef]
- Ma, H.; Antoniou, M.; Cherniakov, M. Passive GNSS-Based SAR Resolution Improvement Using Joint Galileo E5 Signals. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1640–1644. [Google Scholar] [CrossRef]
- Zeng, H.; Wang, P.; Chen, J.; Liu, W.; Ge, L. A Novel General Imaging Formation Algorithm for GNSS-Based Bistatic SAR. Sensors 2016, 16, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Tao, R.; Zhang, N.; Wang, Y. Analysing and compensating the effects of range and Doppler frequency migrations in linear frequency modulation pulse compression radar. IET Radar Sonar Navig. 2011, 5, 12–22. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier transform for radar target detection, I: Generalized Doppler filter bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Giangregorio, G.; Bisceglie, M.; Addabbo, P.; Beltramonte, T.; D’Addio, S.; Galdi, C. Stochastic modeling and simulation of Delay-Doppler Maps in GNSS-R over the ocean. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2056–2069. [Google Scholar] [CrossRef]
- Colone, F.; Langellotti, D.; Lombardo, P. DVB-T signal ambiguity Function Control for Passive Radars. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 329–347. [Google Scholar] [CrossRef]
- Howland, P.E.; Maksimiuk, D.; Reitsma, G. FM radio based bistatic radar. IET Radar Sonar Navig. 2005, 152, 107–115. [Google Scholar] [CrossRef]
- Saini, R.; Cherniakov, M. DTV signal ambiguity function analysis for radar application. IET Radar Sonar Navig. 2005, 152, 133–142. [Google Scholar] [CrossRef]
- Skolnik, M.; Linde, G.; Meads, K. Senrad: An advanced wideband air-surveillance radar. IEEE Trans. Aerosp. Electron. Syst. 2011, 37, 1163–1175. [Google Scholar] [CrossRef]
- Perry, R.P.; Dipietro, R.C.; Fante, R.L. Coherent integration with range migration using Keystone formatting. In Proceedings of the IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007; pp. 863–868. [Google Scholar]
- Li, G.; Xia, X.G.; Peng, Y.N. Doppler Keystone Transform: An Approach Suitable for Parallel Implementation of SAR Moving Target Imaging. IEEE Geosci. Remote Sens. Lett. 2008, 5, 573–577. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.G.; Ma, J.T.; Zheng, J.B. Ground Maneuvering Target Imaging and High-Order Motion Parameter Estimation Based on Second-Order Keystone and Generalized Hough-HAF Transform. IEEE Trans. Geosci. Remote Sens. 2017, 55, 320–335. [Google Scholar] [CrossRef]
- Satzoda, R.K.; Suchitra, S.; Srikanthan, T. Parallelizing the Hough transform computation. IEEE Signal Process. Lett. 2008, 15, 297–300. [Google Scholar] [CrossRef]
- Xia, J.W.; Zhou, Y.; Jin, X.; Zhou, J.J. A Fast Algorithm of Generalized Radon-Fourier Transform for Weak Maneuvering Target Detection. Int. J. Antennas Propag. 2016, 1–10. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G.; Long, T. Space–time Radon–Fourier transform and applications in radar target detection. IET Radar Sonar Navig. 2012, 6, 846–857. [Google Scholar] [CrossRef]
- Xu, J.; Yan, L.; Zhou, X.; Xia, X.G.; Long, T.; Wang, Y.; Farina, A. Adaptive Radon-Fourier Transform for Weak Radar Target Detection. IEEE Trans. Aerosp. Electron. Syst. 2018, 1. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier Transform for Radar Target Detection, II: Blind Speed Sidelobe Suppression. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2473–2486. [Google Scholar] [CrossRef]
- Chen, X.L.; Guan, J.; Liu, N.B.; He, Y. Maneuvering Target Detection via Radon-Fractional Fourier Transform-Based Long-Time Coherent Integration. IEEE Trans. Signal Process. 2014, 62, 939–953. [Google Scholar] [CrossRef]
- Cheng, Y.; Bao, Z.; Zhao, F.; Lin, Z. Doppler compensation for binary phase-coded waveforms. IEEE Trans. Aerosp. Electron. Syst. 2011, 38, 1068–1072. [Google Scholar] [CrossRef]
- Robey, F.C.; Fuhrmann, D.R.; Nitzberg, R.; Kelly, E.J. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef]
- Gao, H.; Li, J.W. Detection and Tracking of a Moving Target Using SAR Images with the Particle Filter-Based Track-Before-Detect Algorithm. Sensor 2014, 14, 10829–10845. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, W.; Chen, J.; Liu, W.; Wang, P.B. Moving Target Azimuth Velocity Estimation for the MASA Mode Based on Sequential SAR Images. IEEE J.-STARS 2017, 10, 2780–2790. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithm and Implementation; Artech House: Boston, MA, USA, 2005; pp. 380–390. [Google Scholar]
- Yu, J.; Xu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier Transform for Radar Target Detection, III: Optimality and Fast Implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 991–1004. [Google Scholar] [CrossRef]
- Zeng, H.; Chen, J.; Zhang, H.; Yang, W.; Wang, P. A modified imaging formation algorithm for bistatic SAR based on GPS-L5 signal. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4129–4132. [Google Scholar]
- Behar, V.; Kabakchiev, C. Detectability of Air Targets using Bistatic Radar Based on GPS L5 Signals. Int. Radar Symp. 2011, 7–9, 212–217. [Google Scholar]
- Sukharevsky, O.I. Electromagnetic Wave Scattering by Aerial and Ground Radar Objects; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2015; pp. 162–174. [Google Scholar]
- Blunt, S.D.; Mokole, E.L. Overview of Radar Waveform Diversity. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 2–42. [Google Scholar] [CrossRef]
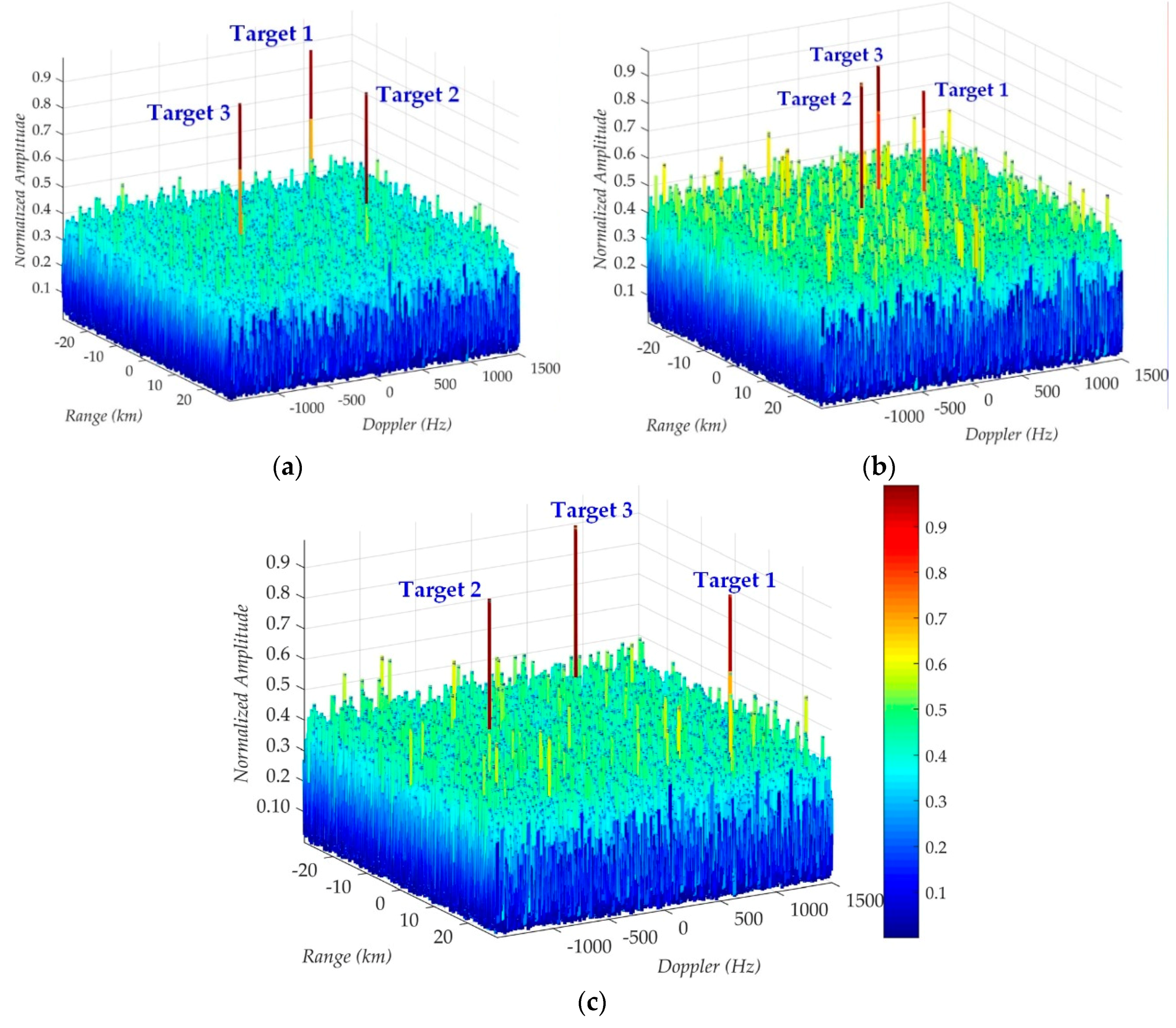

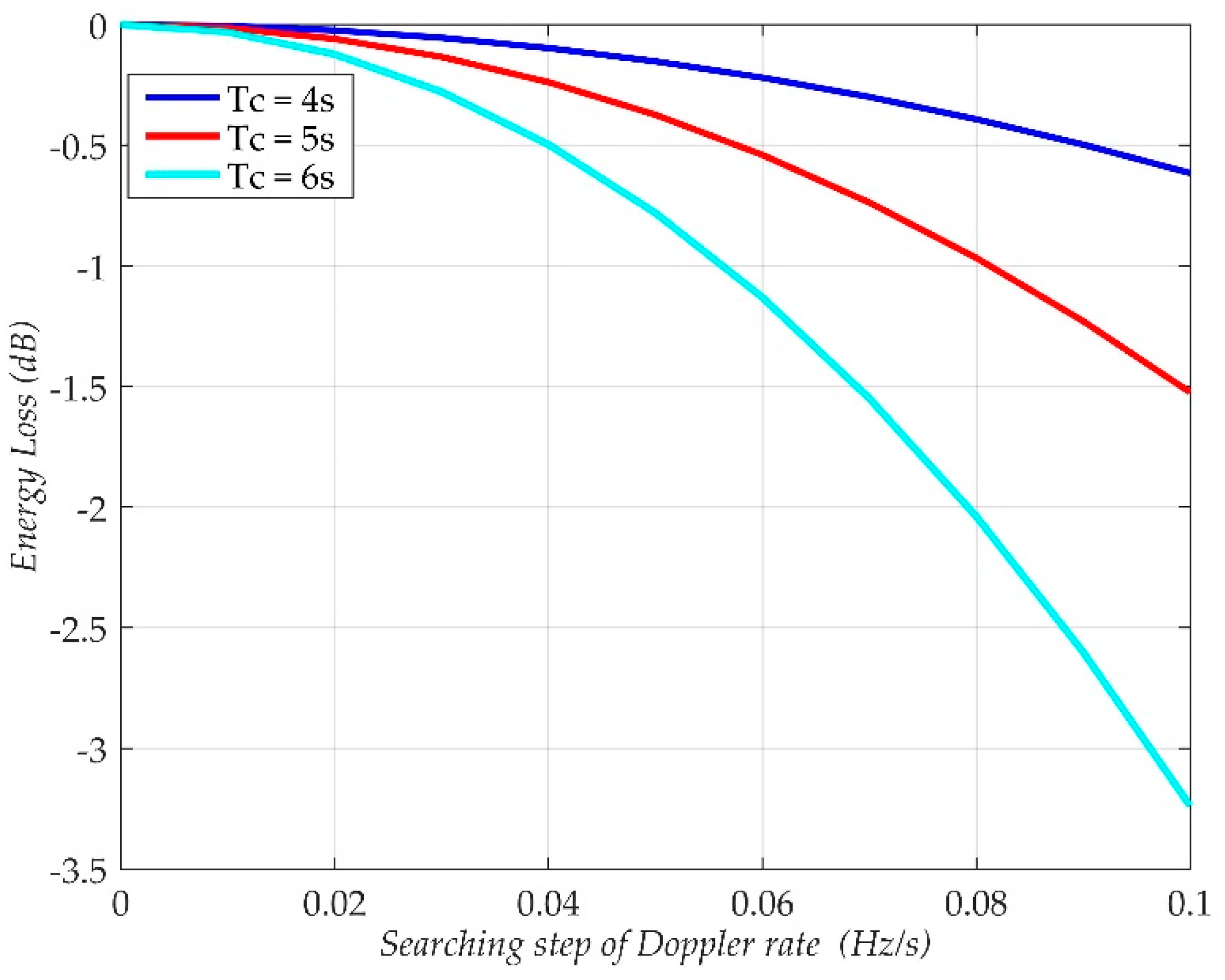
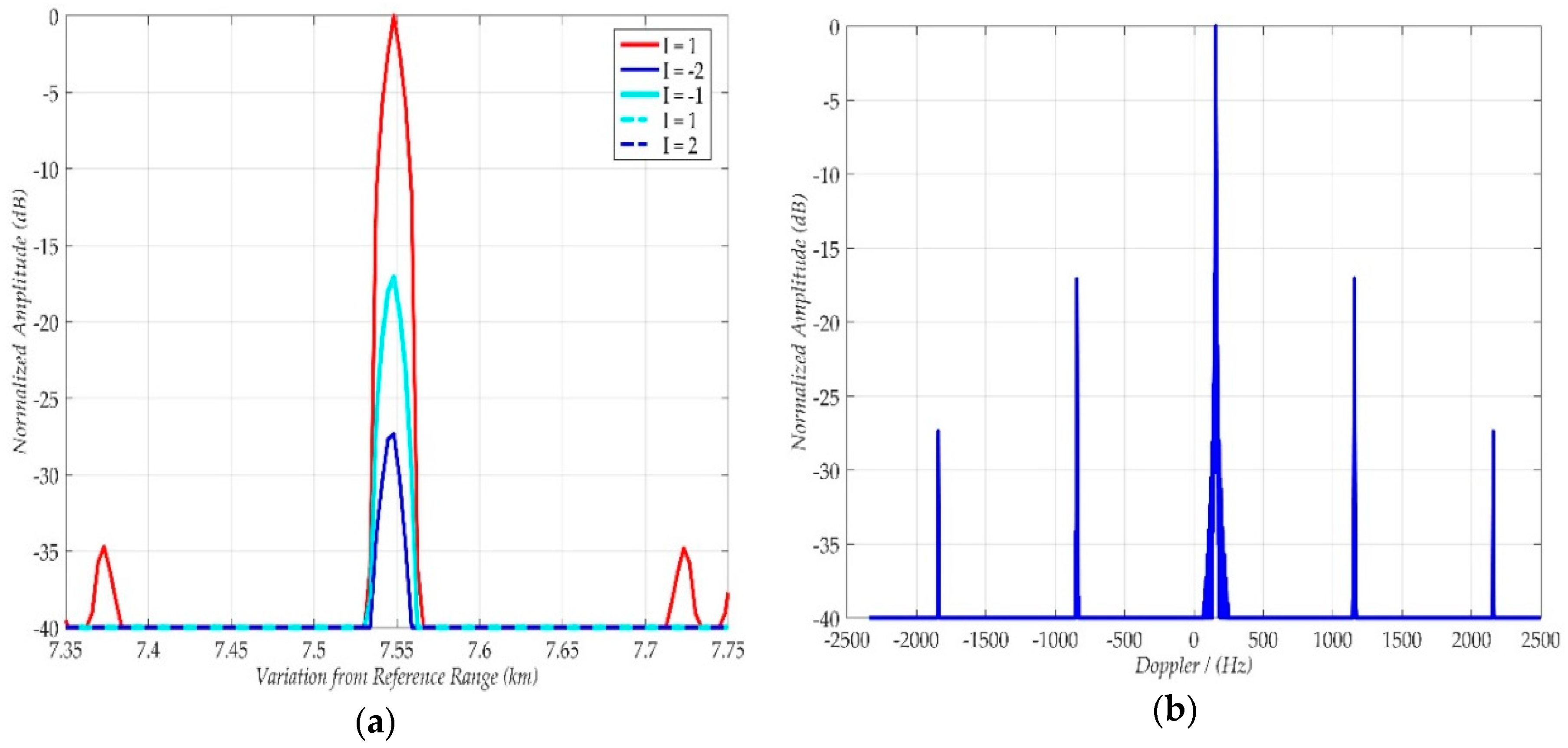
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Wavelength | 0.255 m | SVN #2 position | (1.0234, −1.5530,1.2411) × 104 km |
| Sampling rate | 42.0 MHz | SVN #7 position | (0.9767, 1.2291, 1.4880) × 104 km |
| 0.2 Hz | SVN #12 position | (−1.8017, 1.6150, 0.4690) × 104 km | |
| 0.04 Hz/s | SVN #2 velocity | (187.9, −2113.8, −1799.3) m/s | |
| NV | 15,000 | SVN #7 velocity | (−2398.5, −632.5, 1426.5) m/s |
| fp | 1000 Hz | SVN #12 velocity | (−2097.3, −729.0, −2321.4) m/s |
| Experiment scenario Center | (60, 40, 10) km | Target RCS [41] | 20 dB |
| Antenna gain (Receiver) | 35 dB | Coherent time | 5 s |
| Target 1 position | (70, 20, 10) km | Target 1 velocity | (150, 120) m/s |
| Target 2 position | (65, 30, 10) km | Target 2 velocity | (−135, 140) m/s |
| Target 3 position | (50, 50, 10) km | Target 3 velocity | (100, −170) m/s |
| Target-1 | Target-2 | Target-3 | |||
|---|---|---|---|---|---|
| SVN #2 | fd,v (Hz) | True | 748.87 | 375.28 | −835.72 |
| Estimated | 749.20 | 375.40 | −835.80 | ||
| Variation from reference range (km) | True | −17.79 | −9.76 | 10.13 | |
| Estimated | −17.78 | −9.76 | 10.13 | ||
| SVN #7 | fd,v (Hz) | True | 156.66 | −322.39 | 9.49 |
| Estimated | 156.40 | −322.20 | 9.60 | ||
| Variation from reference range (m) | True | 7.55 | 2.92 | −2.56 | |
| Estimated | 7.55 | 2.92 | −2.56 | ||
| SVN #12 | fd,v (Hz) | True | 812.52 | −995.59 | 531.07 |
| Estimated | 812.60 | −998.60 | 531.20 | ||
| Variation from reference range (m) | True | 21.08 | 9.68 | −15.25 | |
| Estimated | 21.08 | 9.68 | −15.24 |
| Target-1 | Target-2 | Target-3 | ||
|---|---|---|---|---|
| Target Location (XA,YA,ZA) (km) | True | (70, 20, 10) | (65, 30, 10) | (50, 50, 10) |
| Estimated | (70.02, 19.99, 10.00) | (64.98, 30.01, 10.01) | (50.01, 50.02, 10.00) | |
| Target Velocity (Vx,Vy,0) (m/s) | True | (150, 120, 0) | (−135, 140, 0) | (100, −170, 0) |
| Estimated | (150.2, 119.9, 0) | (−135.0, 140.1, 0.0) | (99.9, −170.1, 0) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, H.-C.; Chen, J.; Wang, P.-B.; Yang, W.; Liu, W. 2-D Coherent Integration Processing and Detecting of Aircrafts Using GNSS-Based Passive Radar. Remote Sens. 2018, 10, 1164. https://doi.org/10.3390/rs10071164
Zeng H-C, Chen J, Wang P-B, Yang W, Liu W. 2-D Coherent Integration Processing and Detecting of Aircrafts Using GNSS-Based Passive Radar. Remote Sensing. 2018; 10(7):1164. https://doi.org/10.3390/rs10071164
Chicago/Turabian StyleZeng, Hong-Cheng, Jie Chen, Peng-Bo Wang, Wei Yang, and Wei Liu. 2018. "2-D Coherent Integration Processing and Detecting of Aircrafts Using GNSS-Based Passive Radar" Remote Sensing 10, no. 7: 1164. https://doi.org/10.3390/rs10071164
APA StyleZeng, H.-C., Chen, J., Wang, P.-B., Yang, W., & Liu, W. (2018). 2-D Coherent Integration Processing and Detecting of Aircrafts Using GNSS-Based Passive Radar. Remote Sensing, 10(7), 1164. https://doi.org/10.3390/rs10071164