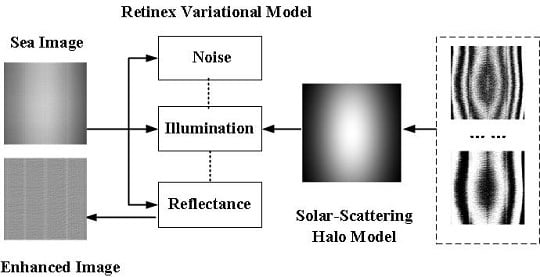
A Variational Model for Sea Image Enhancement
Abstract
:1. Introduction
2. Model and Algorithm
2.1. Retinex Model with Noise Suppression
2.2. Fitting Scattering Halo
2.3. Final Variational Model
| Algorithm 1. Numerical Algorithm for Solving (13) |
| (1) Set the initial guesses , , . (2) Choose appropriate parameters , , , , , . (3) For k = 0, 1, ... ..., iterate the following function until convergence. |
3. Experimental and Discussion
3.1. Experiment Settings
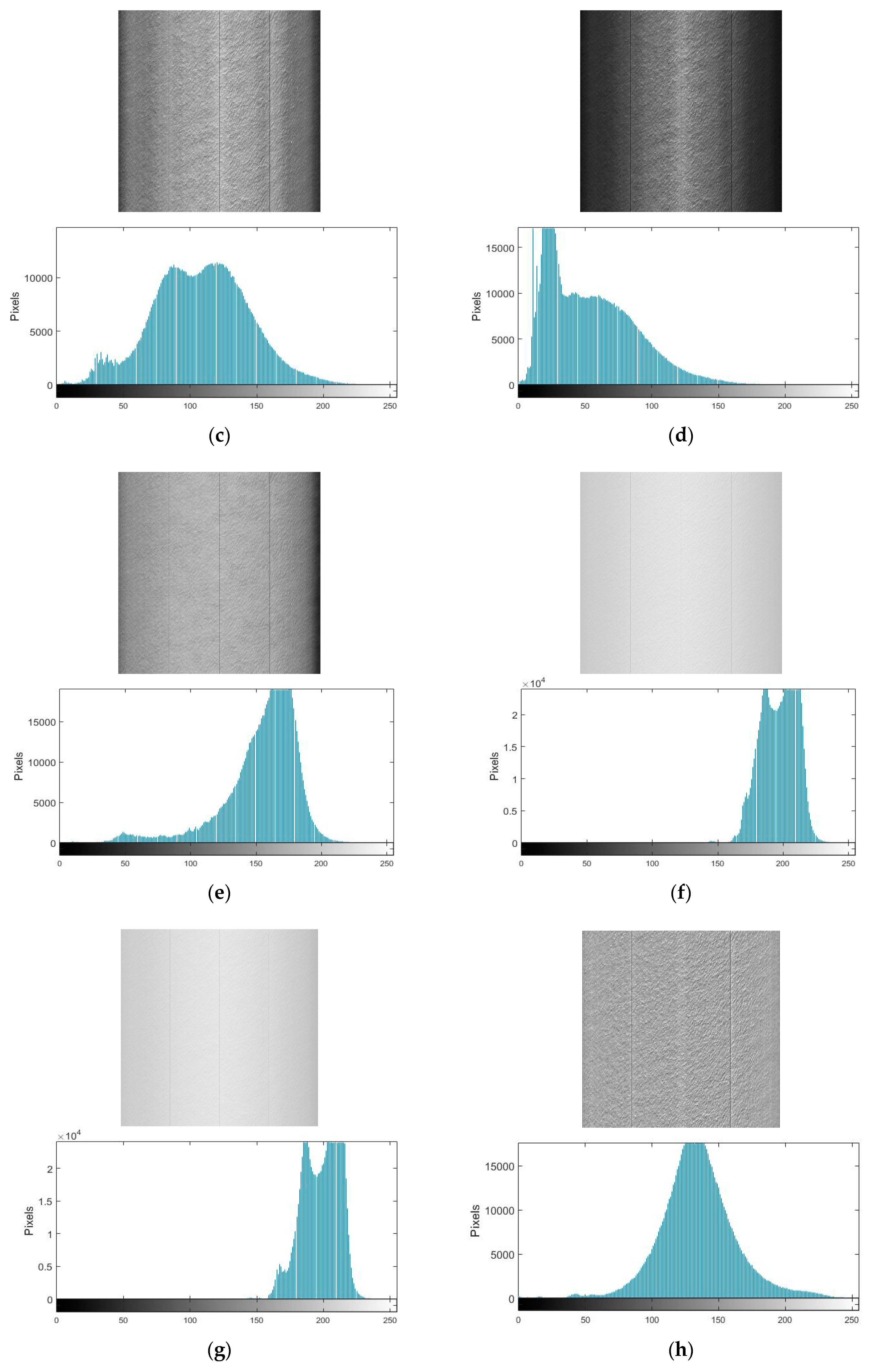
3.2. Sea Image Enhancement
3.3. Objective Quality Assessments
3.4. Noise Suppression
3.5. Convergence Rate and Computational Time
3.6. Further Correction
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Gonzalez, R.C. Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Bovik, A.C. Handbook of Image and Video Processing; Academic: New York, NY, USA, 2010. [Google Scholar]
- Pizer, S.M.; Johnston, R.E.; Ericksen, J.P.; Yankaskas, B.C.; Muller, K.E. Contrast-limited adaptive histogram equalization: Speed and effectiveness. In Proceedings of the First Conference on Visualization in Biomedical Computing, Atlanta, GA, USA, 22–25 May 1990; pp. 337–345. [Google Scholar]
- Nikolova, M.; Steidl, G. Fast hue and range preserving histogram specification: Theory and new algorithms for color image enhancement. IEEE Trans. Image Process. 2014, 23, 4087–4100. [Google Scholar] [CrossRef] [PubMed]
- Polesel, A.; Remponi, G.; Mathews, V.J. Image enhancement via adaptive unsharp masking. IEEE Trans. Image Process. 2000, 9, 505–510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, G. A generalized unsharp masking algorithm. IEEE Trans. Image Process. 2011, 20, 1249–1261. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zheng, J.; Li, B. Parameters-adaptive nighttime image enhancement with multi-scale decomposition. IET Comput. Vis. 2016, 10, 425–432. [Google Scholar] [CrossRef]
- Wang, S.; Luo, G. Naturalness preserved image enhancement using a priori multi-layer lightness statistics. IEEE Trans. Image Process. 2018, 27, 938–948. [Google Scholar] [CrossRef] [PubMed]
- Land, E.H.; McCann, J.J. Lightness and Retinex theory. J. Opt. Soc. Am. 1971, 61, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Hines, G.; Rahman, Z.U.; Jobson, D.; Woodell, G. Singel-scale Retinex using digital signal processors. In Proceedings of the Global Signal Processign Conference, San Jose, CA, USA, 27–30 September 2004. [Google Scholar]
- Jobson, D.J.; Rahman, Z.-U.; Woodell, G.A. A multiscale Retinex for bridging the gap between color images and the human observation of scenes. IEEE Trans. Image Process. 1997, 6, 965–976. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zheng, J.; Hu, H.-M.; Li, B. Naturalness preserved enhancement algorithm for non-uniform illumination images. IEEE Trans. Image Process. 2013, 22, 3538–3548. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Liao, Y.; Zeng, D.; Huang, Y.; Zhang, X.-P.; Ding, X. A probabilistic method for image enhancement with simultaneous illumination and reflectance estimation. IEEE Trans. Image Process. 2015, 24, 4965–4977. [Google Scholar] [CrossRef] [PubMed]
- Ng, M.K.; Wang, W. A total variation model for Retinex. SIAM J. Imaging Sci. 2011, 4, 345–365. [Google Scholar] [CrossRef]
- Kimmel, R.; Elad, M.; Shaked, D.; Keshet, R.; Sobel, I. A variational framework for Retinex. Int. J. Comput. Vis. 2003, 52, 7–23. [Google Scholar] [CrossRef]
- Wang, W.; Ng, M.K. A nonlocal total variation model for image decomposition: Illumination and reflectance. Numer. Math. Theory Method. Appl. 2014, 7, 334–355. [Google Scholar]
- Ma, W.; Morel, J.M.; Osher, S.; Chien, A. An L1-based variational model for Retinex theory and its applications to medical images. In Proceedings of the Computer Vision and Pattern Recognition, Providence, RI, USA, 20–25 June 2011; pp. 153–160. [Google Scholar]
- Ma, W.; Osher, S. A TV bregman iterative model of Retinex theory. Inverse Probl. Imaging 2012, 6, 697–708. [Google Scholar] [CrossRef]
- Fu, X.; Zeng, D.; Huang, Y.; Zhang, X.-P.; Ding, X. A weighted variational model for simultaneous reflectance and illumination estimation. In Proceedings of the Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2782–2790. [Google Scholar]
- Li, M.; Liu, J.; Yang, W.; Sun, X.; Guo, Z. Structure-revealing low-light image enhancement via robust Retinex model. IEEE Trans. Image Process. 2018, 27, 2828–2841. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, T.; Osher, S. The split Bregman alogrithm for L1 regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Wang, H.; Zhong, W.; Wang, J.; Xia, D. Research of measurement for digital image definition. J. Image Graph. 2004, 9, 828–831. [Google Scholar]
- Gadallah, F.L.; Csillag, F.; Smith, E.J.M. Destriping multisensor imagery with moment matching. Int. J. Remote Sens. 2000, 21, 2505–2511. [Google Scholar] [CrossRef]
















| ε = 0.01 | ε = 0.05 | ε = 0.001 | |
|---|---|---|---|
| 1024 × 1024 | 14.86 | 29.32 | 120.66 |
| 512 × 512 | 3.64 | 7.11 | 29.52 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, M.; Qu, H.; Zhang, G.; Tao, S.; Jin, G. A Variational Model for Sea Image Enhancement. Remote Sens. 2018, 10, 1313. https://doi.org/10.3390/rs10081313
Song M, Qu H, Zhang G, Tao S, Jin G. A Variational Model for Sea Image Enhancement. Remote Sensing. 2018; 10(8):1313. https://doi.org/10.3390/rs10081313
Chicago/Turabian StyleSong, Mingzhu, Hongsong Qu, Guixiang Zhang, Shuping Tao, and Guang Jin. 2018. "A Variational Model for Sea Image Enhancement" Remote Sensing 10, no. 8: 1313. https://doi.org/10.3390/rs10081313
APA StyleSong, M., Qu, H., Zhang, G., Tao, S., & Jin, G. (2018). A Variational Model for Sea Image Enhancement. Remote Sensing, 10(8), 1313. https://doi.org/10.3390/rs10081313