Consistent Calibration of VIRR Reflective Solar Channels Onboard FY-3A, FY-3B, and FY-3C Using a Multisite Calibration Method
Abstract
:1. Introduction
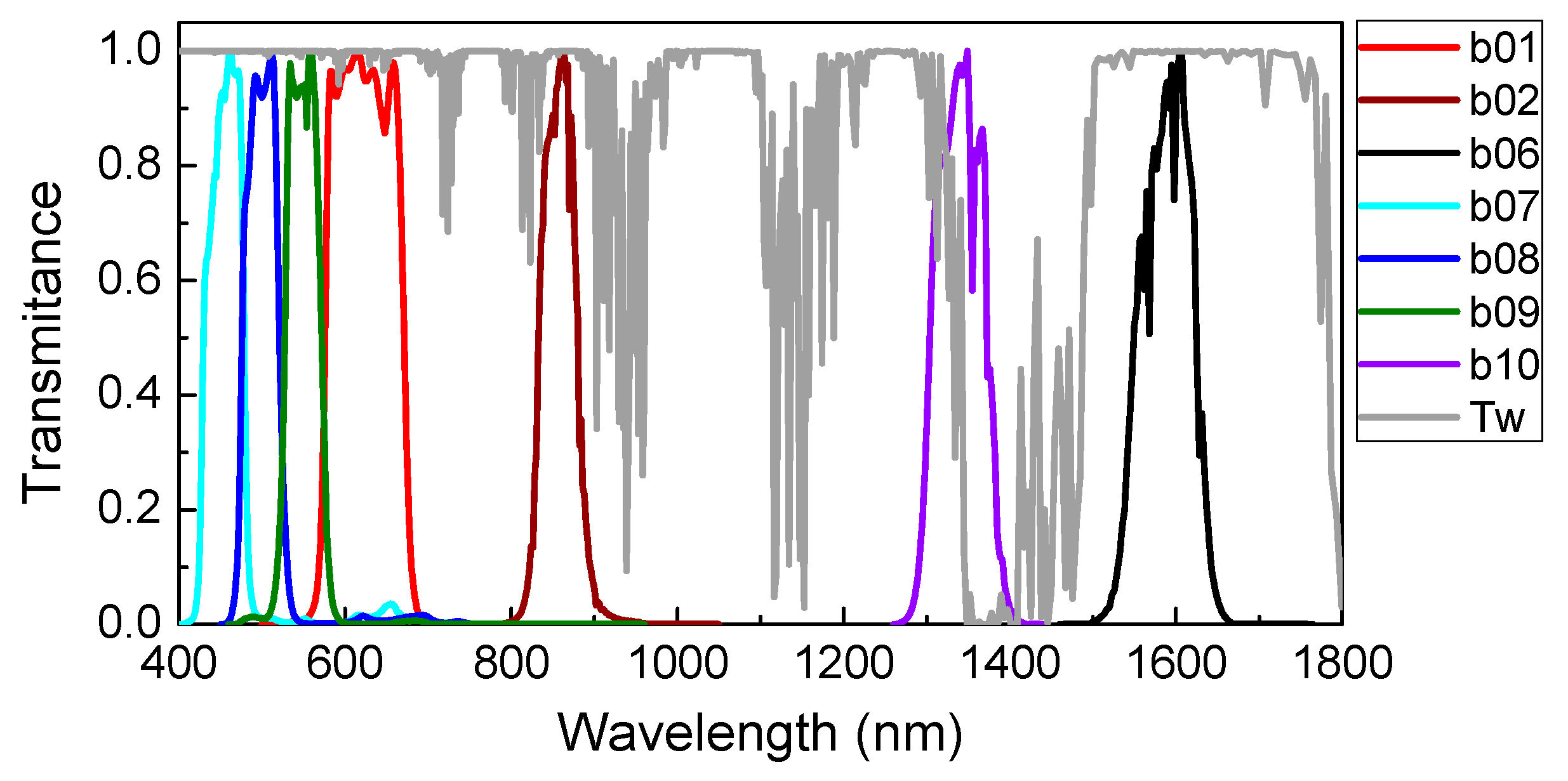
2. Sensor Overview and Current Calibration State
3. Methodology
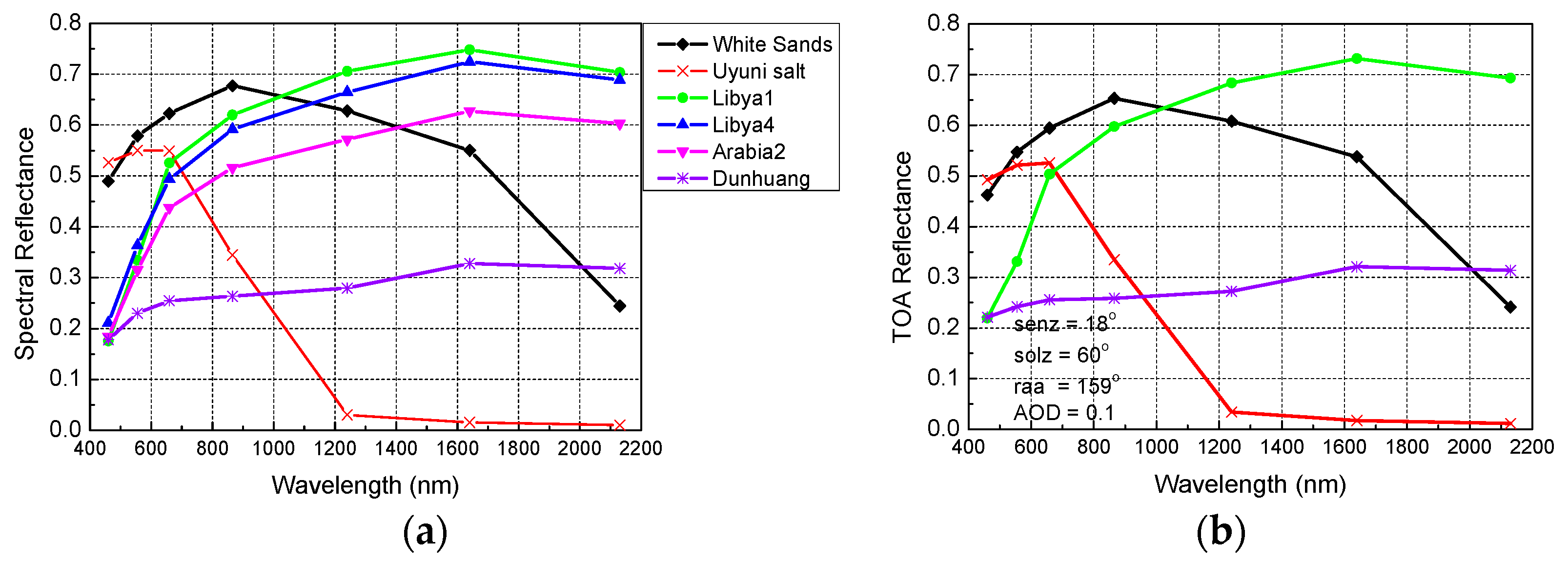
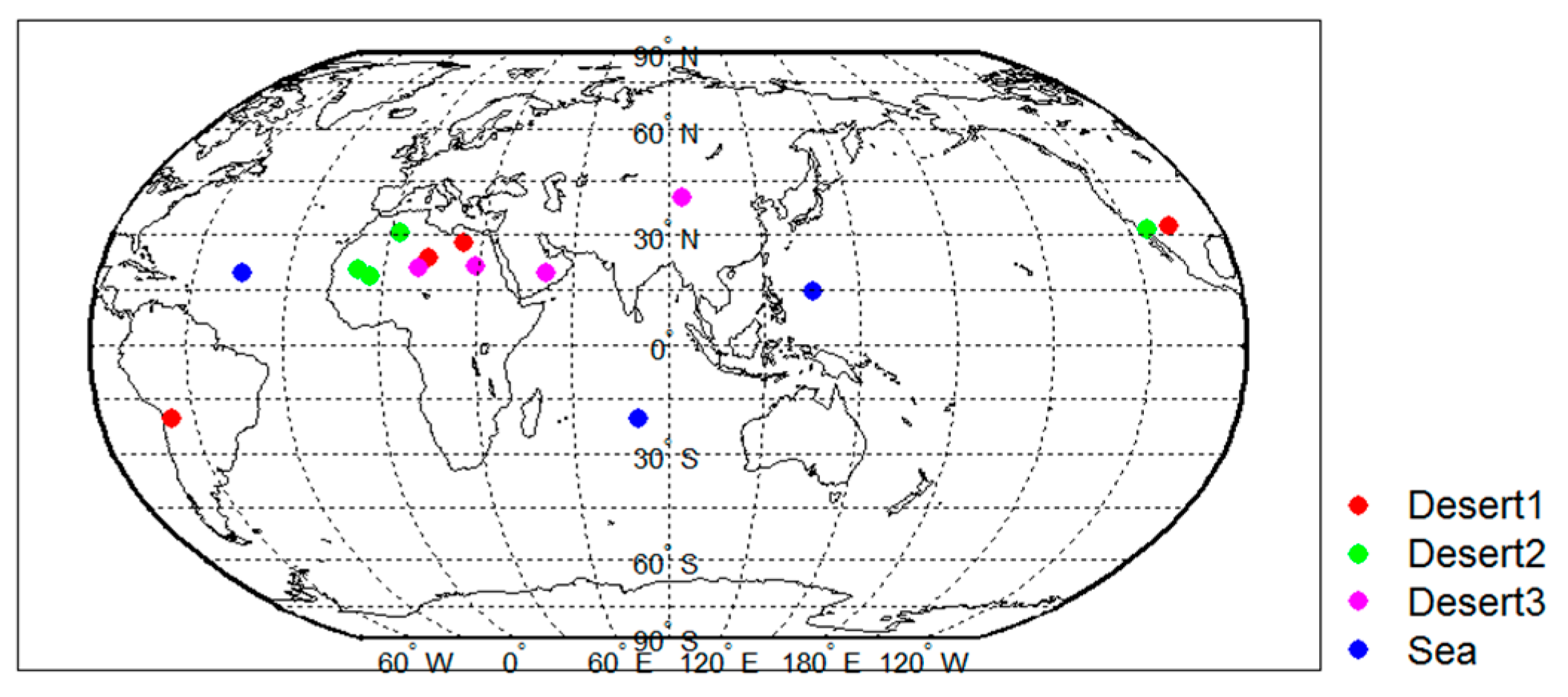
3.1.Selection of Calibration Sites
3.1.1. Calibration Test Sites
3.1.2. Calibration Sites Used for this Study
3.2. Identification of Cloud-Free Sites
3.3. Calibration Reference Calculation
3.4. Determining Calibration Coefficient
4. Results and Discussion
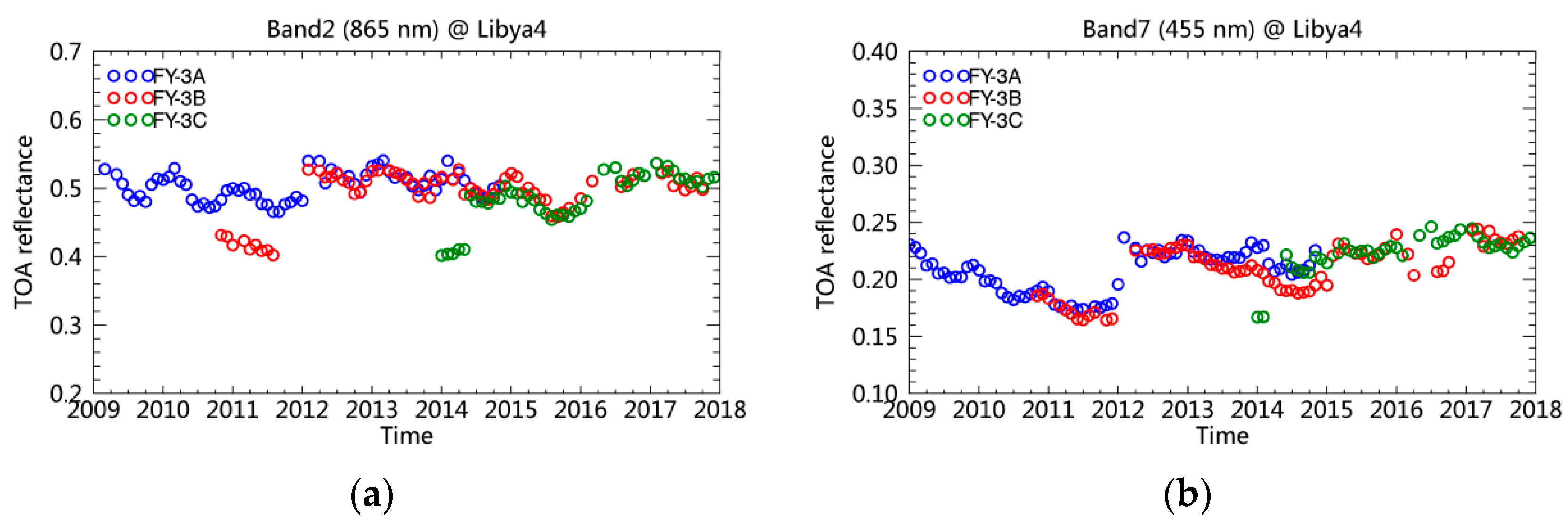
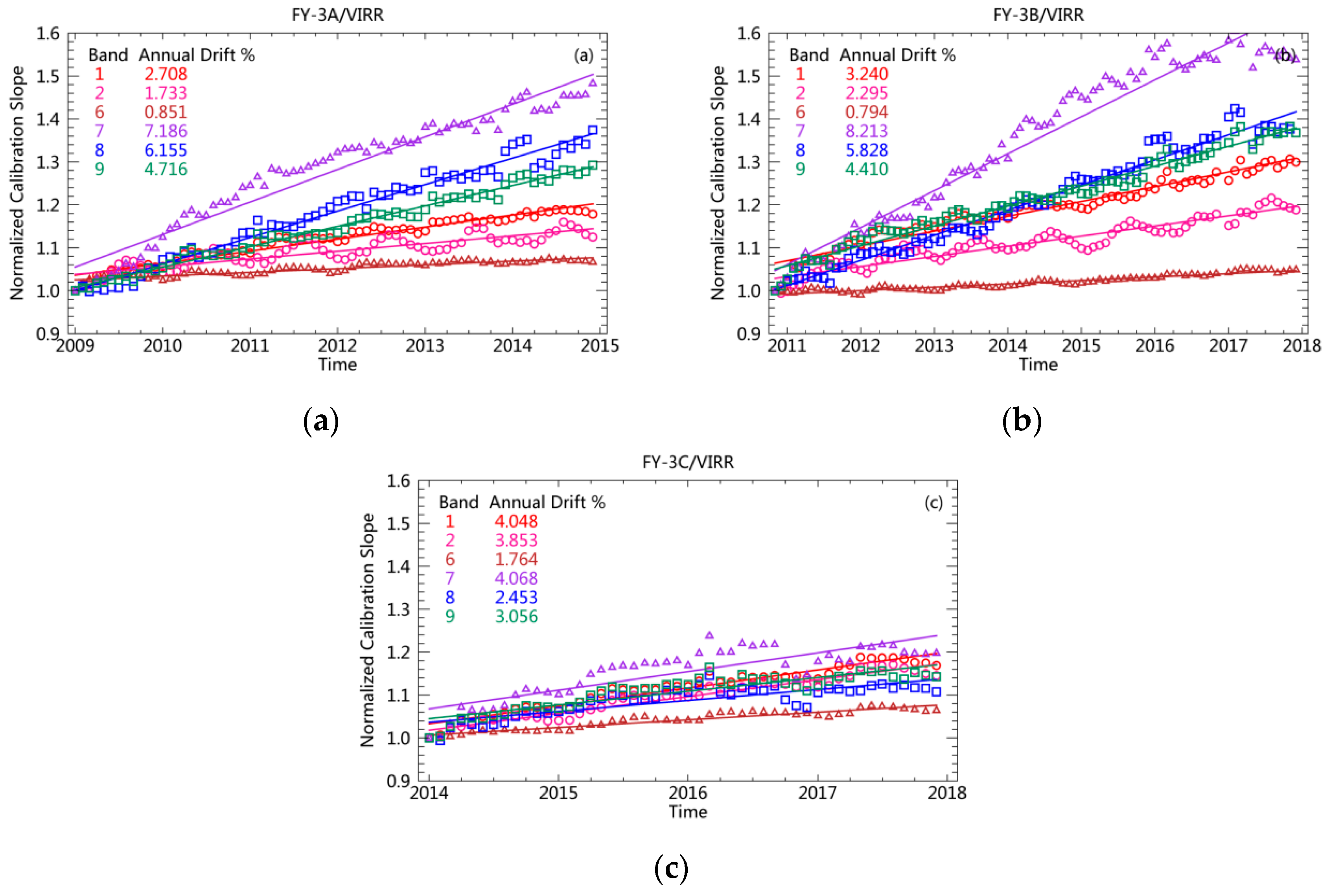
4.1. Time Series of the Calibration Slopes
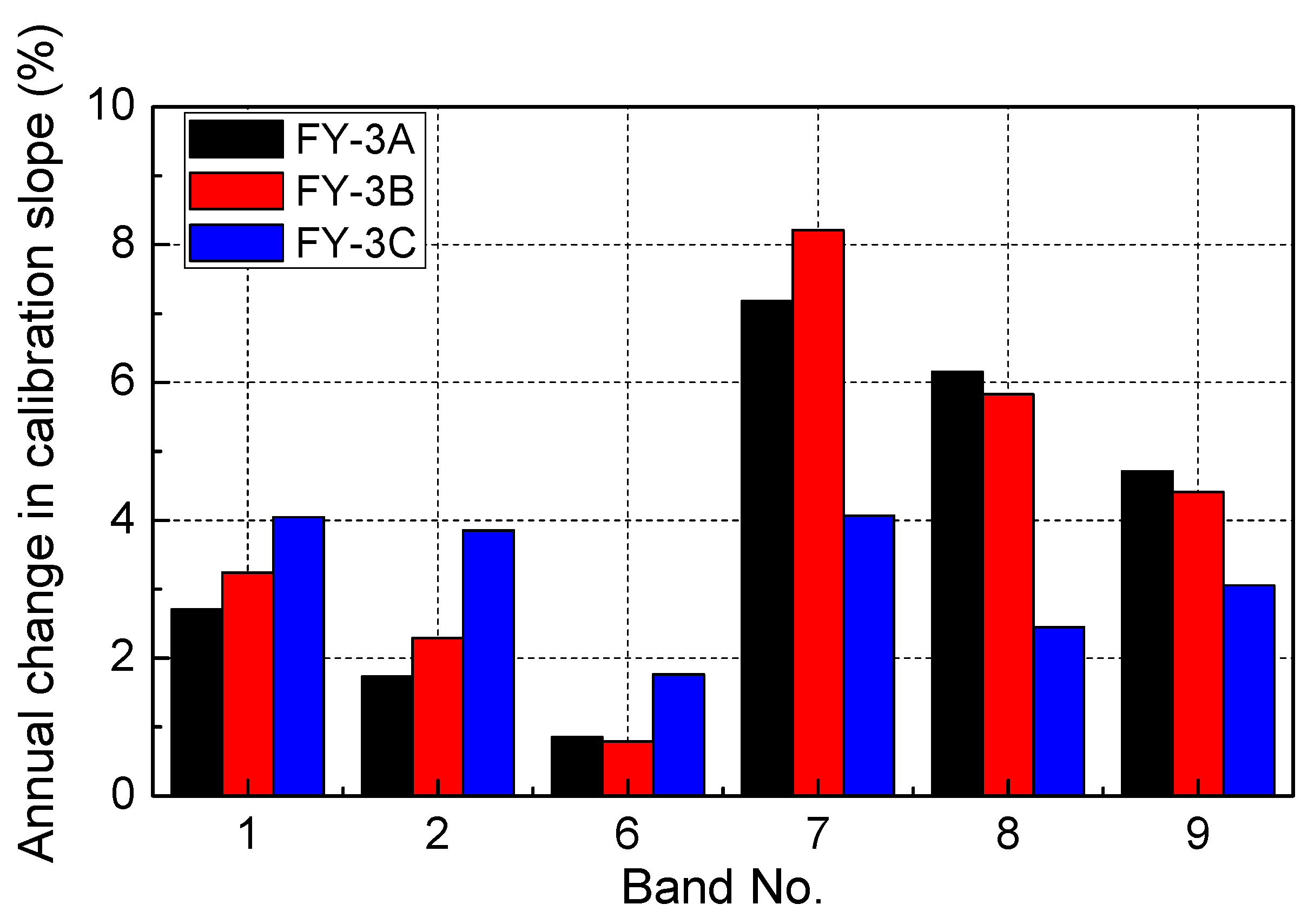
4.2. Annual Change in the Calibration Slope
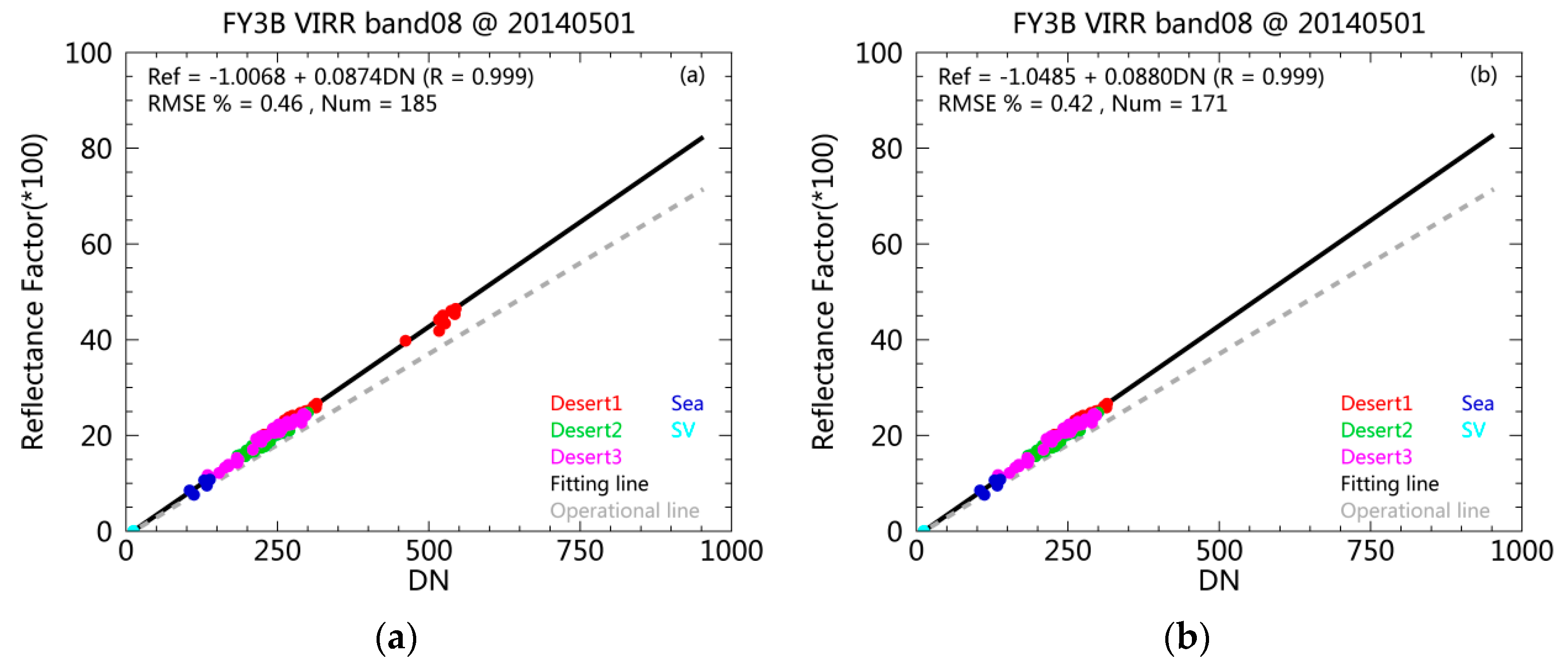
4.3. Comparison of the Reflectance with L1B Operational Products
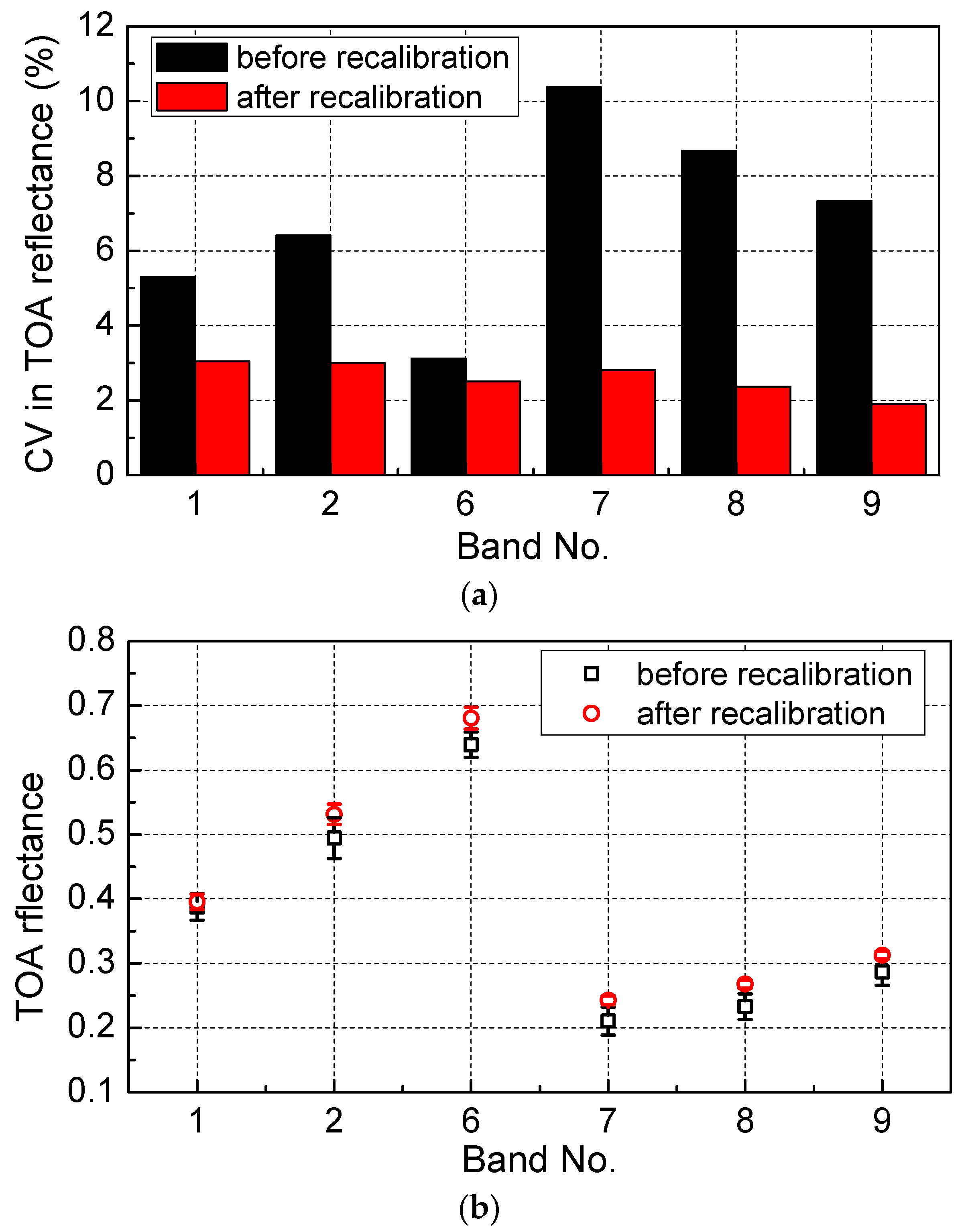
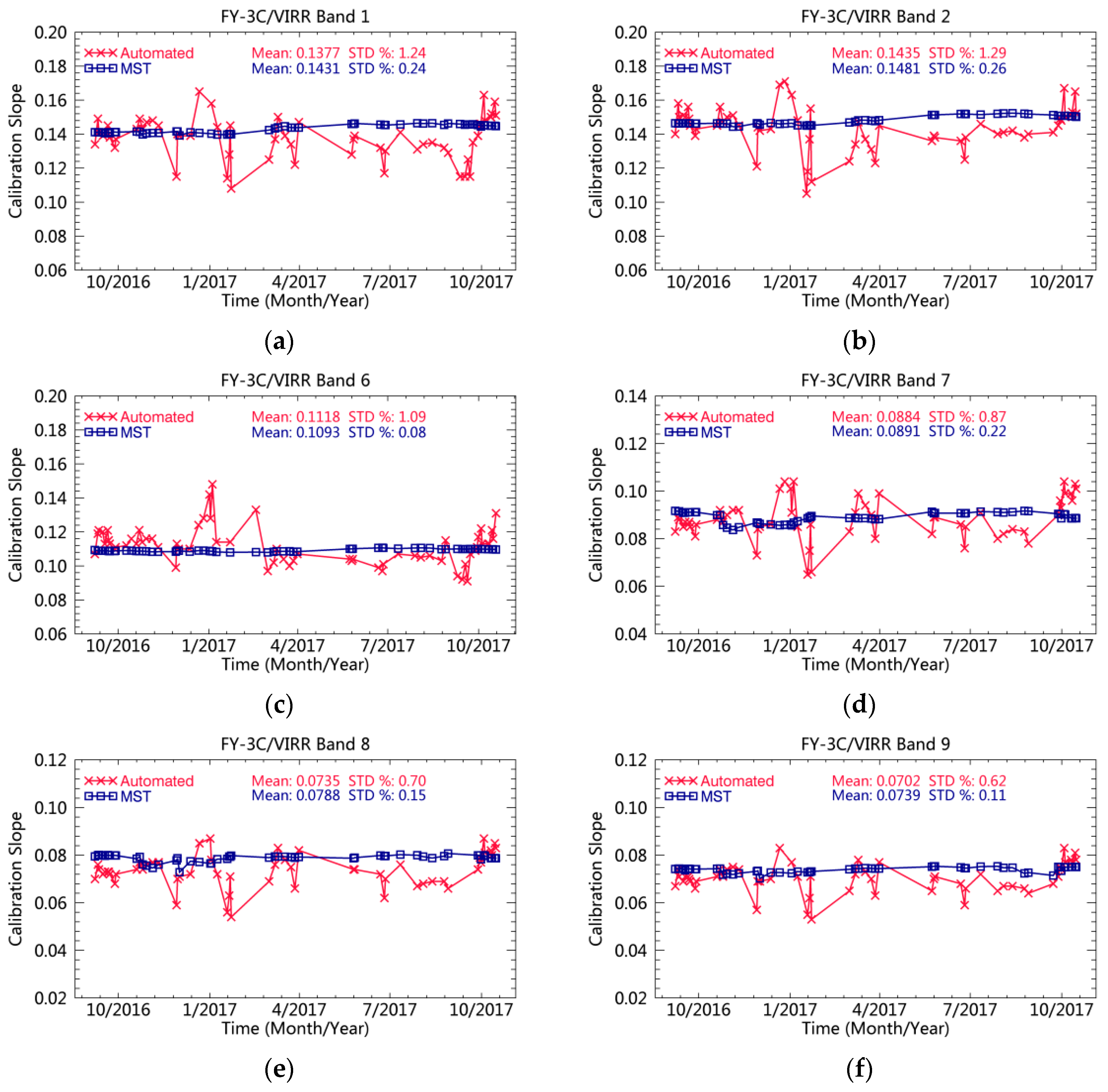
4.4. Comparison of the Calibration Slopes with the Automatic Calibration Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, N.; Chen, L.; Hu, X.; Zhang, L.; Zhang, P. Assessment and correction of on-orbit radiometric calibration for FY-3 VIRR thermal infrared channels. Remote Sens. 2014, 6, 2884–2897. [Google Scholar] [CrossRef]
- Li, Y.; Rong, Z.; Zheng, Z.; Liu, J.; Zhang, L.; Zhang, L.; Hu, X.; Zhang, Y.; Sun, L. Post launch site calibration of visible and near-infrared channels of FY-3A visible and infrared radiometers. Opt. Precis. Eng. 2009, 17, 2966–2973. [Google Scholar]
- Hu, X.; Liu, J.; Sun, L.; Rong, Z.; Li, Y.; Zhang, Y.; Zheng, Z.; Wu, R.; Zhang, L.; Gu, X. Characterization of CRCS Dunhuag test site and vicarious calibration utilization for Fengyun (FY) series sensors. Can. J. Remote Sens. 2010, 36, 566–582. [Google Scholar] [CrossRef]
- Sun, L.; Guo, M.; Xu, N.; Zhang, L.; Liu, J.; Hu, X. On-orbit response variation analysis of FY-3 MERSI reflective solar bands based on Dunhuang site calibration. Spectrosc. Spectr. Anal. 2012, 32, 1869–1877. [Google Scholar]
- Mishra, N.; Helder, D.; Angal, A.; Choi, J.; Xiong, X. Absolute calibration of optical satellite sensors using Libya 4 pseudo invariant calibration site. Remote Sens. 2014, 6, 1327–1346. [Google Scholar] [CrossRef]
- Wu, A.; Xiong, X.; Cao, C.; Angal, A. Monitoring MODIS Calibration Stability of Visible and Near-IR Bands from Observed Top-of-Atmosphere BRDF-Normalized Reflectances over Libyan Desert and Antarctic Surfaces. Available online: https://doi.org/10.1117/12.795296 (accessed on 19 August 2018).
- Bhatt, R.; Doelling, D.; Wu, A.; Xiong, X.; Scarino, B.; Haney, C.; Gopalan, A. Initial stability assessment of S-NPP VIIRS reflective solar band calibration using invariant desert and deep convective cloud targets. Remote Sens. 2014, 6, 2809–2826. [Google Scholar] [CrossRef]
- Heidinger, A.K.; Sullivan, J.T.; Rao, C.R. Calibration of visible and near-infrared channels of the NOAA-12 AVHRR using time series of observations over deserts. Int. J. Remote Sens. 2003, 24, 3635–3649. [Google Scholar] [CrossRef]
- Heidinger, A.K.; Straka, W.C.; Molling, C.C.; Sullivan, J.T.; Wu, X. Deriving an inter-sensor consistent calibration for the AVHRR solar reflectance data record. Int. J. Remote Sens. 2010, 31, 6493–6517. [Google Scholar] [CrossRef]
- Wu, A.; Xiong, X.; Angal, A. Derive a MODIS-Based Calibration for the AVHRR Reflective Solar Channels of the NOAA KLM Operational Satellites. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1405–1413. [Google Scholar] [CrossRef]
- Chen, L.; Hu, X.; Xu, N.; Zhang, P. The application of deep convective clouds in the calibration and response monitoring of the reflective solar bands of FY-3A/MERSI (Medium Resolution Spectral Imager). Remote Sens. 2013, 5, 6958–6975. [Google Scholar] [CrossRef]
- Wu, R.; Yang, J.; Yang, Z.; Liu, J. Impacts of spectral response differences on SNO calibration-study examples of FY-3A/MERSI and EOS/MODIS. Remote Sens. Inf. 2011, 2, 51–57. [Google Scholar]
- Xu, N.; Chen, L.; Wu, R.; Hu, X.; Sun, L.; Zhang, P. In-Flight Intercalibration of FY-3C Visible Channels with AQUA MODIS. In Proceedings of the SPIE, Earth Observing Missions and Sensors: Development, Implementation, and Characterization III, Beijing, China, 26 November 2014. [Google Scholar]
- Hu, X.; Xu, N.; Wu, R.; Chen, L.; Min, M.; Wang, L.; Xu, H.; Sun, L.; Yang, Z.; Zhang, P. Performance Assessment of FY-3C/MERSI on Early Orbit. In Proceedings of the SPIE, Earth Observing Missions and Sensors: Development, Implementation, and Characterization III, Beijing, China, 26 November 2014. [Google Scholar]
- Sun, L.; Hu, X.; Guo, M.; Xu, N. Multisite calibration tracking for FY-3A MERSI solar bands. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4929–4942. [Google Scholar] [CrossRef]
- Chander, G.; Christopherson, J.B.; Stensaas, G.L.; Teillet, P.M. Online Catalogue of World-Wide Test Sites for the Post-Launch Characterization and Calibration of Optical Sensors. In Proceedings of the International Astronautical Federation—58th International Astronautical Congress, Hyderabad, India, 24–28 September 2007. [Google Scholar]
- Teillet, P.M.; Barsi, J.A.; Chander, G.; Thome, K.J. Prime candidate Earth targets for the post-launch radiometric calibration of space-based optical imaging instruments. In Proceedings of the SPIE, Earth Observing Systems XII, San Diego, CA, USA, 5 October 2007. [Google Scholar]
- Smith, D.L.; Mutlow, C.T.; Nagaraja Rao, C.R. Calibration monitoring of the visible and near-infrared channels of the Along-Track Scanning Radiometer-2 by use of stable terrestrial sites. Appl. Opt. 2002, 41, 515–523. [Google Scholar] [CrossRef] [PubMed]
- Chander, G.; Xiong, X.; Choi, T.; Angal, A. Monitoring on-orbit calibration stability of the Terra MODIS and Landsat 7 ETM+ sensors using pseudo-invariant test sites. Remote Sens. Environ. 2010, 114, 925–939. [Google Scholar] [CrossRef]
- Helder, D.; Thome, K.J.; Mishra, N.; Chander, G.; Xiong, X.; Angal, A.; Choi, T. Absolute radiometric calibration of Landsat using a pseudo invariant calibration site. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1360–1369. [Google Scholar] [CrossRef]
- Ross, J.K. The Radiation Regime and Architecture of Plant Stands; Springer Science & Business Media: Norwell, MA, USA, 1981; p. 392. [Google Scholar]
- Li, X.; Strahler, A.H. Geometric-optical bidirectional reflectance modeling of the discrete crown vegetation canopy: effect of crown shape and mutual shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–2922. [Google Scholar] [CrossRef]
- Gao, F.; Schaaf, C.; Strahler, A.; Roesch, A.; Lucht, W.; Dickinson, R. The MODIS BRDF/Albedo Climate Modeling Grid Products and the Variability of Albedo for Major Global Vegetation Types. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Kim, W.; Cao, C.Y.; Liang, S.L. Assessment of Radiometric Degradation of FY-3A MERSI Reflective Solar Bands using TOA Reflectance of Pseudo-Invariant Calibration Sites. IEEE Geosci. Remote Sens. Lett. 2013, 11, 793–797. [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Kotchenova, S.Y.; Vermote, E.F.; Matarrese, R.; Klemm, F.J. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part I: Path radiance. Appl. Opt. 2006, 45, 6762–6774. [Google Scholar] [CrossRef] [PubMed]
- Hubanks, P.A.; King, M.D.; Platnick, S.T.; Pincus, R.O. MODIS Atmosphere L3 Gridded Product Algorithm Theoretical Basis Document. Available online: https://eospso.nasa.gov/sites/default/files/atbd/atbd_mod30.pdf (accessed on 19 August 2018).
- Hsu, N.C.; Jeong, M.J.; Bettenhausen, C.; Sayer, A.M.; Hansell, R.; Seftor, C.S.; Huang, J.; Tsay, S.C. Enhanced Deep Blue aerosol retrieval algorithm: The second generation. J. Geophys. Res. Atmos. 2013, 118, 9296–9315. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, X.; Rong, Z.; Zhang, L.; Hu, X.; Ba, X. China radiometric calibration sites ground-based automatic observing systems for CAL/VAL. In Proceedings of the SPIE, Sensors, Systems, and Next-Generation Satellites XIX, Toulouse, France, 12 October 2015. [Google Scholar]
- Lv, J.; He, M.; Chen, L.; Hu, X.; Li, X. Automated radiation calibration method based on Dunhuang radiometric calibration site. Acta Opt. Sin. 2017, 37, 1–8. [Google Scholar]


| Band | Wavelength Range (μm) | Spectral Bandwidth (μm) | Spatial Resolution (m) | Noise (Δ or ΔK @300 K) | Dynamic ( or K) |
|---|---|---|---|---|---|
| 1 | 0.58–0.68 | 0.10 | 1100 | 0.1% | 0–100% |
| 2 | 0.84–0.89 | 0.05 | 1100 | 0.1% | 0–100% |
| 3 | 3.55–3.93 | 0.38 | 1100 | 0.3 K | 180–350 K |
| 4 | 10.3–11.3 | 1.00 | 1100 | 0.2 K | 180–330 K |
| 5 | 11.5–12.5 | 1.00 | 1100 | 0.2 K | 180–330 K |
| 6 | 1.55–1.64 | 0.09 | 1100 | 0.15% | 0–90% |
| 7 | 0.43–0.48 | 0.05 | 1100 | 0.05% | 0–50% |
| 8 | 0.48–0.53 | 0.05 | 1100 | 0.05% | 0–50% |
| 9 | 0.53–0.58 | 0.05 | 1100 | 0.05% | 0–50% |
| 10 | 1.325–1.395 | 0.07 | 1100 | 0.19% | 0–90% |
| Band | Slope | Annual Drift (%) | Intercept | R | Std (cali) | RMSE | Var |
|---|---|---|---|---|---|---|---|
| FY-3A | |||||||
| 1 | 7.685 × 10−5 | 2.708 | 1.036 | 0.976 | 0.050 | 0.011 | 0.012 |
| 2 | 4.929 × 10−5 | 1.730 | 1.038 | 0.873 | 0.036 | 0.017 | 0.017 |
| 6 | 2.390 × 10−5 | 0.851 | 1.025 | 0.920 | 0.017 | 0.006 | 0.007 |
| 7 | 2.077 × 10−4 | 7.186 | 1.055 | 0.972 | 0.136 | 0.032 | 0.025 |
| 8 | 1.687 × 10−4 | 6.155 | 1.000 | 0.987 | 0.109 | 0.017 | 0.018 |
| 9 | 1.302 × 10−4 | 4.716 | 1.007 | 0.992 | 0.084 | 0.010 | 0.012 |
| FY-3B | |||||||
| 1 | 9.444 × 10−5 | 3.240 | 1.064 | 0.972 | 0.074 | 0.017 | 0.020 |
| 2 | 6.469 × 10−5 | 2.295 | 1.029 | 0.947 | 0.052 | 0.016 | 0.017 |
| 6 | 2.156 × 10−5 | 0.794 | 0.991 | 0.954 | 0.017 | 0.005 | 0.006 |
| 7 | 2.355 × 10−4 | 8.213 | 1.047 | 0.974 | 0.182 | 0.041 | 0.038 |
| 8 | 1.601 × 10−4 | 5.828 | 1.002 | 0.986 | 0.122 | 0.020 | 0.023 |
| 9 | 1.269 × 10−4 | 4.410 | 1.050 | 0.985 | 0.097 | 0.017 | 0.017 |
| FY-3C | |||||||
| 1 | 1.146 × 10−4 | 4.048 | 1.033 | 0.966 | 0.051 | 0.013 | 0.015 |
| 2 | 1.075 × 10−4 | 3.853 | 1.018 | 0.969 | 0.047 | 0.012 | 0.012 |
| 6 | 4.866 × 10−5 | 1.764 | 1.007 | 0.944 | 0.022 | 0.007 | 0.008 |
| 7 | 1.190 × 10−4 | 4.068 | 1.068 | 0.838 | 0.061 | 0.033 | 0.031 |
| 8 | 6.967 × 10−5 | 2.453 | 1.036 | 0.826 | 0.036 | 0.020 | 0.023 |
| 9 | 8.750 × 10−5 | 3.056 | 1.045 | 0.888 | 0.042 | 0.019 | 0.021 |
| Averaged Calibration Slope | STD of Calibration Slopes | Relative Difference in Calibration Slopes (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Band | MST | Auto | MST | Auto | min | max | std | mean |
| 1 | 0.1431 | 0.1377 | 0.24 | 1.24 | −22.78 | 17.29 | 9.03 | −3.74 |
| 2 | 0.1481 | 0.1435 | 0.26 | 1.29 | −27.60 | 17.04 | 8.92 | −3.10 |
| 6 | 0.1093 | 0.1118 | 0.08 | 1.09 | −17.22 | 36.26 | 10.21 | 2.36 |
| 7 | 0.0891 | 0.0884 | 0.22 | 0.87 | −26.61 | 21.18 | 10.79 | −0.67 |
| 8 | 0.0788 | 0.0735 | 0.15 | 0.70 | −32.35 | 13.79 | 9.42 | −6.73 |
| 9 | 0.0739 | 0.0702 | 0.11 | 0.62 | −27.55 | 14.15 | 8.31 | −4.97 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Hu, X.; Chen, L.; He, L. Consistent Calibration of VIRR Reflective Solar Channels Onboard FY-3A, FY-3B, and FY-3C Using a Multisite Calibration Method. Remote Sens. 2018, 10, 1336. https://doi.org/10.3390/rs10091336
Wang L, Hu X, Chen L, He L. Consistent Calibration of VIRR Reflective Solar Channels Onboard FY-3A, FY-3B, and FY-3C Using a Multisite Calibration Method. Remote Sensing. 2018; 10(9):1336. https://doi.org/10.3390/rs10091336
Chicago/Turabian StyleWang, Ling, Xiuqing Hu, Lin Chen, and Lingli He. 2018. "Consistent Calibration of VIRR Reflective Solar Channels Onboard FY-3A, FY-3B, and FY-3C Using a Multisite Calibration Method" Remote Sensing 10, no. 9: 1336. https://doi.org/10.3390/rs10091336
APA StyleWang, L., Hu, X., Chen, L., & He, L. (2018). Consistent Calibration of VIRR Reflective Solar Channels Onboard FY-3A, FY-3B, and FY-3C Using a Multisite Calibration Method. Remote Sensing, 10(9), 1336. https://doi.org/10.3390/rs10091336





