1. Introduction
The Mons Rümker region is centered at 301.9°E, 40.7°N and is comprised of a plateau with an area of ~4000 km
2. Mons Rümker is the primary candidate for the landing region of the Chang’E-5 lunar sample return mission and an accurate digital elevation model (DEM) is indispensable for selecting and assessing the landing site [
1,
2]. First, an accurate DEM improves our knowledge of the lunar surface, aids in the identification and characterization of the topography, and helps us to understand the impact history by evaluating the relative ages of the geological units [
3,
4]. In addition, illumination and communication maps can be simulated based on a DEM for optimizing the potential lunar landing sites [
5,
6].
Laser altimeters are commonly used to map the lunar topography. The Apollo 15 to Apollo 17 missions provided preliminary laser altimeter data for creating maps of the lunar topography [
7]. Subsequently, the laser ranging instrument onboard the Clementine mission obtained lidar data, which were used to produce a global topographic model with a spatial resolution of 0.25° [
8]. Over the last ten years, the knowledge of lunar topography has greatly improved because of the SELenological and ENgineering Explorer (SELENE) mission, the Chang’E-1 (CE-1) mission, and the lunar reconnaissance orbiter (LRO), all of which carried laser altimeters [
9,
10,
11]; thus, new global lunar DEMs have been produced with a variety of resolutions and accuracies.
The SELENE spacecraft was launched in 2007 and carried onboard a laser altimeter (LALT hereafter for SELENE laser altimeter). The LALT has a radial uncertainty of 4 m and a horizontal uncertainty of 77 m, deriving a global DEM with a spatial resolution of 0.625° [
12]. The CE-1 spacecraft was also launched in 2007 and carried a laser altimeter (LAM hereafter for the CE-1 laser altimeter). Ping et al. [
13] processed the initial 3 million LAM points and produced the CE-1 lunar topographic model s01 (CLTM-s01), with a radial uncertainty of 31 m. Li et al. [
14] used 9.12 million LAM points to construct a global DEM with a spatial resolution of 3 km, a plane-positioning accuracy of 445 m (1σ), and a vertical accuracy of 60 m (1σ). The LRO was launched in 2009 and the lunar orbiter laser altimeter (LOLA) onboard the LRO has a vertical accuracy of 1 m. The mode of multi-beams and high frequency and improved satellite orbit accuracy of the LRO increase the resolution and precision of the LOLA data compared to previous lunar missions [
15,
16]. Thus, global DEMs at high resolutions and the most accurate polar DEMs were constructed using the LOLA data [
11].
All laser altimeters collect the altitude of the points of the lunar surface and the points are then used to construct the DEM using an interpolation method. Therefore, the accuracy of the pixels of the constructed DEM varies and is determined by the distance from the points of the grid to the measured points and the lunar topographic relief. Furthermore, LOLA cannot reliably measure laser returns at ranges >120 km. The altimeter data are exclusively concentrated in the Southern Hemisphere when the LRO was placed in an elliptical polar orbit. The coverage of the data restricts the resolution of the constructed DEM. To solve this problem, Barker et al. [
17] used a five-parameter coordinate transformation and a bounded downhill simplex minimization algorithm to register the stereo-derived DEMs (each 1° × 1°) from the SELENE terrain camera (TC) to the LOLA points, thereby obtaining a LOLA + TC merged DEM (SLDEM2015) that covered the latitudes of ±60°. A comparison of the SLDEM2015 and the LOLA DEM indicates the existence of bands with a width of one or two pixels in the SLDEM2015. We believe that the residual errors of the stereo-derived DEMs are responsible for these bands when merging the LOLA points and the stereo-derived DEMs.
Mons Rümker is located in the mid-latitude region of the northern hemisphere and there is little LOLA data coverage in the Mons Rümker region. Merging multisource altimeter data is a direct approach to improve the DEM coverage. In addition, an improvement in the data coverage also provides a better constraint for the study of Barker et al. [
17].
The precision discrepancy is the main issue when merging multisource altimeter data. A crossover adjustment is used to model the error and improve the orbit determination to yield more precise DEMs [
18,
19]. We used the LOLA data as a benchmark and designed a special crossover adjustment to reduce the radial error in the LALT and LAM data. We evaluated the LOLA data using a grid of 1/256° resolution to find the gaps in the LOLA measurement points. If the points in the LAM and LALT data were located in pixels with a sufficient number of LOLA points (>3), then these points were used as crossovers. We used the LOLA data to interpolate the elevation at these points, calculated the residuals, and derived a one-parameter model to fit the systematic error in the LAM and LALT data. The adjusted LAM and LALT data were combined with the LOLA data in order to develop an improved DEM.
In
Section 2, we provide the details of the datasets used in this study. In
Section 3, we discuss the methods of noise elimination and special crossover adjustment. In
Section 4, we describe the valid data distribution and results of the crossover adjustment. In
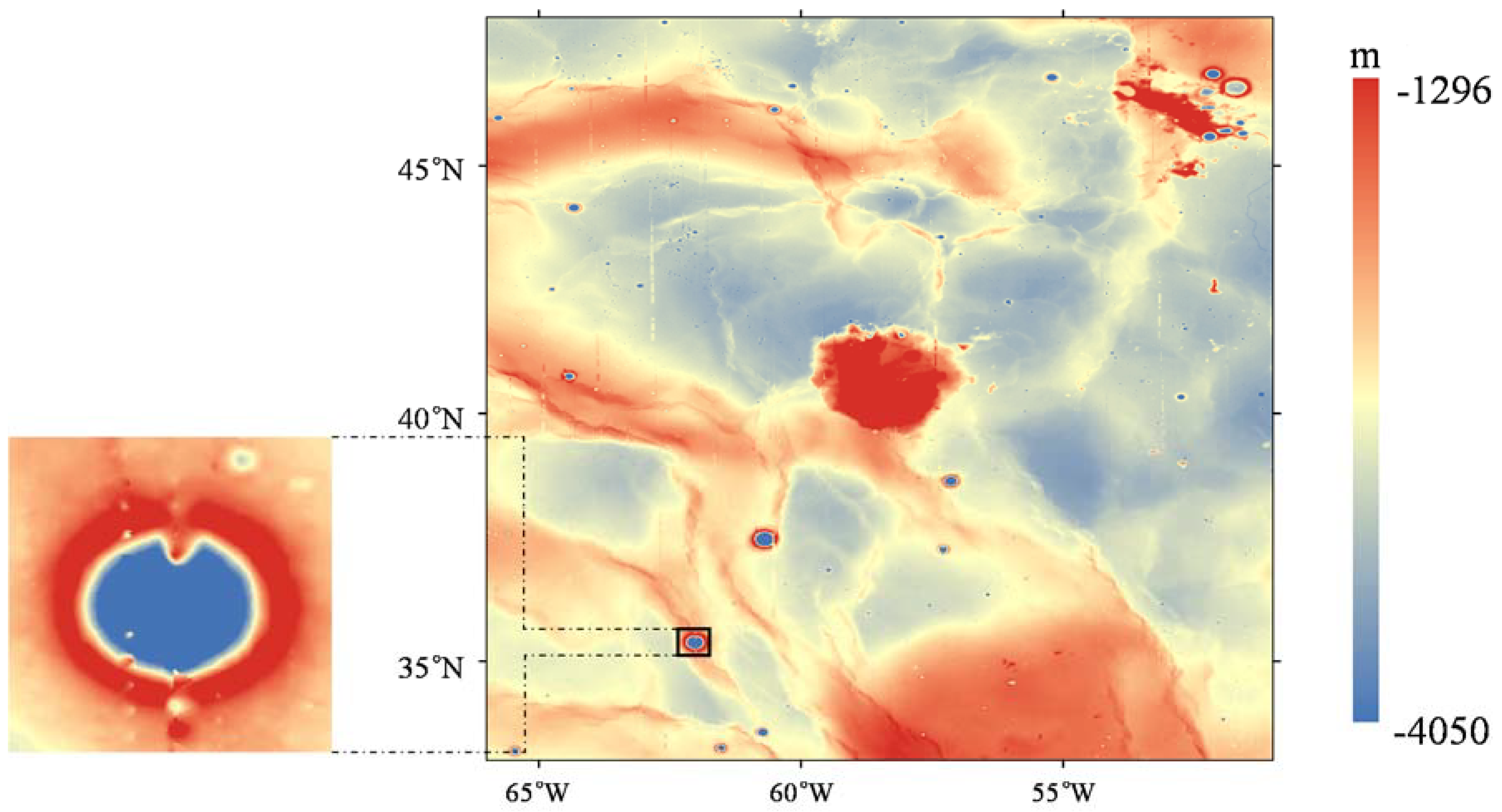
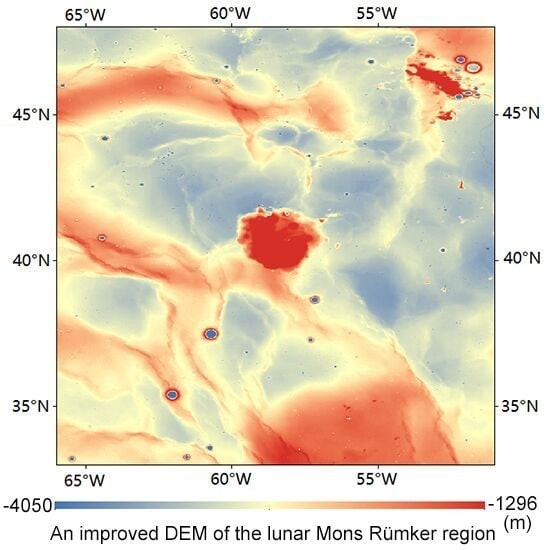
Section 5, we discuss the merged DEMs and SLDEM2015. Finally, the conclusions and future research directions are provided. It is noted that when we consider the use of the DEM, i.e., the simulation of communication and illumination conditions based on the DEM, impact of the surrounding terrain need to be taken into account. We expanded the scope of the calculation and chose the Mons Rümker and its surrounding area as the study area (33°N~48°N, 51°W~66°W).
2. Data
2.1. LOLA Data
The LRO entered the lunar orbit on 27 June 2009 and was placed in a ~30 × 200-km near-polar orbit with a periapsis near the South Pole. Three months later, on 27 September, the spacecraft moved into a near-circular 50-km orbit for a one-year normal mapping mission. On 11 December 2011, the spacecraft was placed back into a quasi-stable elliptical orbit similar to the commissioning orbit to save fuel and extend its lifetime [
20].
The LOLA is a multi-beam laser altimeter onboard the LRO and operates at 28 Hz. A single laser beam is split by a diffractive optical element into five output beams, each of which has a divergence of 100 mrad and illuminates a 5-m diameter spot from an elevation of 50 km in the normal LRO mission. The along-track shot spacing of LOLA are about 50 m. The LOLA sampling strategy produces five parallel profiles along the LRO ground track [
21]. The LOLA Science Team processed the raw data and produced publicly available data sets (
http://pds-geosciences.wustl.edu/).
The LOLA reduced data records (RDR) were used in this study. The RDR comprise time-of-flight ranges to the lunar surface and ancillary data in the geodetic coordinate frame around the center of the lunar mass. After range calibration and orbital processing, the range to each laser spot was located on the surface using the spacecraft trajectory, attitude history, and lunar orientation model. The range profiles were organized into an RDR product containing calibrated, geo-located pulse returns, radii, and energies. The RDR data are divided into serial orbits with increasing numbers at each ascending equator crossing.
The LOLA cannot reliably measure laser returns at ranges larger than 120 km and the altimeter data are exclusively concentrated in the Southern Hemisphere in the elliptical orbit [
22]. Therefore, the period for the data used in this study was from September 2009 to December 2011, covering the entire mapping phase and the first 15 months of the LRO science phase. There were 884 orbits of data collected in the target region.
2.2. LALT Data
The Japanese lunar explorer Kaguya (SELENE) mission to the Moon was launched on 14 September 2007 and entered an elliptical lunar orbit on 4 October 2007. After orbital maneuvers, SELENE reached its nominal 100 km circular orbit on 19 October 2007. The mission ended on 10 June 2009 and the spacecraft was destroyed in a controlled collision onto the lunar surface [
23].
The LALT onboard the SELENE was designed to measure distances to the lunar surface from an altitude of 100 km. The LALT operated at 1 Hz. The beam divergence was 0.4 mrad, resulting in a laser spot size on the lunar surface of typically 40 m from the orbiter altitude of 100 km. The along-track shot spacing of LALT are about 1.4 km [
12]. The SELENE operation and data analysis center (SOAC) processed the raw LALT data from 30 December 2007 to 27 October 2008 and produced publicly available datasets (
http://darts.isas.jaxa.jp/pub/pds3/).
The LALT lunar global topographic data as a time series (LALT_LGT_TS) was used in this study. For the calculations, the SPICE toolkit software developed by the Navigation and Ancillary Information Facility was used to obtain the time series of the data based on the LALT range data, the main orbiter’s position/attitude data, and the ephemeris DE421. The time stamp is in UTC (transmit time). The reference surface is a sphere with a radius of 1737.4 km and its center is the gravity center. There are 149 orbital LALT_LGT_TS profiles in the target region.
2.3. LAM Data
The CE-1 mission was launched on 24 October 2007 and served as a prelude to China’s deep space exploration program. CE-1 entered the lunar orbit on 5 November 2007, remained in orbit for 494 days, and successfully completed a controlled landing on the Moon on 1 March 2009 [
9].
LAM was one of the main payloads onboard the CE-1 and was designed to measure the topography of the lunar surface from the normal altitude of 200 km. The LAM operated at 1 Hz and illuminated a 200-m diameter spot from an elevation of 200 km. The along-track shot spacing of LAM are about 1.4 km [
14]. The National Astronomical Observatories of the Chinese Academy of Sciences processed the raw LALT data and produced publicly available datasets (
http://moon.bao.ac.cn/).
The time series of the LAM level_2B data comprise the geo-located longitude and latitude, the range to the mass center, and the quality status at each laser spot. We calculated the altitude of a reference sphere surface with a radius of 1737.4 km similar to the LOLA and LALT data. There are 156 orbital LAM level_2B profiles in the target region, collected from 27 November 2007 to 4 January 2009. The orbital accuracy of Chang’E-1 is far worse than that of SELENE or LRO. The former is about 200 m, and the latter are about 50 m and 20 m, respectively. In addition, the temperature, voltage, and drift due to aging of the oven-controlled crystal oscillator make the LAM frequency during the mission far different from the standard frequency [
24].
2.4. Data Analysis
The number of tracks of LOLA, LAM and LALT are 884, 156, and 149, respectively, which suggests that the sum of tracks of LAM and LALT is about one third of that of LOLA. Therefore, combining the LOLA with LAM and LALT is indispensable to assemble a new DEM. In fact, the points of LALT and LAM exist near LOLA points or even coincide with LOLA points. Moreover, we think that the contribution of LAM and LALT to the LOLA-only DEM is due to the sampling frequency. LOLA has 19 million points and its multi-beam mode makes the distribution more concentrated. The sampling frequency of LALT and LAM is only 1/28 of that of LOLA. Only a small number of points of LALT and LAM can complement LOLA pixels with data gaps. From another point of view, the distance between each point of the LALT and LAM is about 1.4 km. These points are evenly distributed along the track, which represent the elevation values in different locations. These points can be used to supplement the blank pixels of LOLA-only DEM, which can better describe the relief features and changes of the terrain located far away from the more concentrated points.
3. Methods
3.1. Noise Elimination
Noise is randomly encountered in the signal returning to the receiver during laser altimeter sampling due to the instability of the satellite and other factors. The noise points are irregular and need to be eliminated before creating a DEM. The maximum and minimum elevation of the lunar surface is within the elevations >−10 km or <11 km [
11]. We regarded the points for which elevations were beyond this range as outliers, and they were eliminated. Noise points with elevations within this range were handled by a long-track mean filtering and by comparing the elevation of each point
with the mean elevation
and
(Equation (1)) of several points around the given point (Equation (3)). The threshold of the filtering was the standard deviation of several points around the given point (Equation (2)) or simply a constant [
25,
26].
If an elevation
hi did not satisfy Equation (3), then that point was considered as noise and was eliminated. We used
n = 4 in the mountainous areas and
n = 2 in the maria [
25].
Along-track mean filtering is flawed because the points at small bumps or depressions in local flat areas are eliminated. To overcome the limitation of a long-track mean filtering, a filtering method based on cluster analysis was used. We obtained and of 5 points around the given point, and calculated the residual at each point. Then, we performed a cluster analysis using the residuals, and classified them into noise and normal points.
A k-means clustering was used because it is an appropriate clustering method, in which the classification is performed manually and initial cluster centers are generated randomly [
27]. The classification is performed by calculating and comparing the Euclidean distances to the cluster centers. The geometric centers of each class are used as the next clustering center to classify again until the collections no longer change. Two classes were used: one class comprised the noise points to be eliminated and the other comprised the normal points.
Noise points cannot be eliminated by a combined filtering and cluster analysis method completely at one time. Because the noise points with small errors are included in the normal class, we calculated the residuals by filtering and clustering again until the points no longer had large errors. This process is repeated and does not stop until all noise points are eliminated, however, the number of noise points is unknown and relative. Instead, the number of eliminated points suddenly increases during processing, suggesting that normal points with steep slopes have been wrongly eliminated. At this time, the program stops and uses the normal points obtained in the last step as the result. The normal size of a LOLA profile was about 8000 points, and the average number of eliminated points was about 50. We typically carried out filtering and clustering about 5 or 6 times. At the final time, the number of eliminated points suddenly increased to about 300 to 600 for a majority of profiles, and at this point our program stopped and retained those points. The LALT data are a filtered dataset, and LAM used the above method to remove approximately 15 noise points from every track (about 330 points).
3.2. Crossover Adjustment
Crossover adjustment aims to combine the multisource altimeter data by improving the radial precision of the LAM and LALT data. Treating the LOLA data as a benchmark, a new crossover adjustment method is proposed based on the LOLA multi-beam pattern. We used a grid with a resolution of 256 pixels per degree to count the LOLA points. The data gap and distribution are confirmed using this grid.
Traditional crossovers are locations where two spacecraft ground tracks intersect but this traditional concept is unsuitable for a multi-beam sampling pattern and the high sampling frequency of the LOLA. As
Figure 1 shows, the traditional single-beam crossover is interpolated from the nearest points in the two tracks. The interpolated elevation from the two LAM or LALT points is extremely inaccurate relative to the LOLA points. Thus, the traditional single-beam crossover is inappropriate and we thus define the crossover for an improved use of the LOLA sampling pattern.
As the partial enlargement of
Figure 1 shows, if the LAM and LALT data points are located at the pixels where the LOLA points are >3, we can use them as crossovers and then we interpolate the elevations of the crossover points using the LOLA points in the pixel and the 8 pixels around it with interpolation of inverse distance to a power. At each crossover, the interpolated altitudes entering the altimetry residuals are:
There are two main items in the Equation (4); the former is the elevation of the LAM/LALT points and the latter is the interpolated elevation obtained using LOLA points. The arrow is intended to illustrate the interpolation process.
The target region is small and some tracks have few crossovers. Moreover, from our experimental analysis, we have concluded that the primary error is systematic and that it is stable in such a small region. Thus, we used a one-parameter model as our final adjustment model.
where
i is the track number,
j is the
jth crossover of the
ith track, and
is the parameter of the
ith track. Parameter
of each orbit is obtained by the least squares method and the adjusted elevation is subsequently calculated.
6. Conclusions
A method combining filtering and cluster analysis was used to eliminate the noise points in multisource altimeter data and a special crossover adjustment was used to model the radial errors in the LAM and LALT data. The LAM radial residual RMS was reduced from 154.83 ± 43.60 m to 14.29 ± 27.84 m and the LALT radial residual RMS was reduced from 3.50 ± 5.0 m to 2.75 ± 4.4 m. To fill the gaps in the LOLA data, the adjusted LAM and LALT data were used to produce the merged DEMs. The LAM + LOLA merged DEM shows that there are large horizontal geolocation errors in the adjusted LAM data but the LALT + LOLA merged DEM is more credible than the LOLA-only DEM. The combined multisource altimetry data improves the spatial coverage and helps to create more precise DEMs.
The target region in this study is only 15° × 15° of the lunar surface and the adjustment model has only one parameter. The adjustment model must be replaced by a higher order polynomial when handling an expanded research area. Future work will cover latitudes from 0°N to 60°N, as determined by the LOLA data coverage. The horizontal geolocation of the LALT and LAM data is another problem that must be tackled. The 3-D crossover adjustment is a good way to reduce horizontal and radial errors. In our study, there are few crossover points between a LAM/LALT track and LOLA cloud points. And it is hardly possible to do a 3D match with limited crossover points. If the number of the new data by the future lunar mission becomes as much as LOLA data, horizontal position error can be adjusted as the radial one.