Improvement of Hourly Surface Solar Irradiance Estimation Using MSG Rapid Scanning Service

Abstract

The purpose of this work is to explore the effect of temporal sampling on the accuracy of the hourly mean Surface Solar Irradiance (SSI) estimation. An upgraded version of the Advanced Model for the Estimation of Surface Solar Irradiance from Satellite (AMESIS), exploiting data from the Meteosat Second Generation Rapid Scanning Service (MSG-RSS), has been used to evaluate the SSI. The assessment of the new version of AMESIS has been carried out against data from two pyranometers located in Southern (Tito) and Northern (Ispra) Italy at an altitude of 760 m and 220 m, respectively. The statistical analysis of the comparison between hourly mean SSI estimates based on temporal sampling every five minutes shows a quantitative improvement compared to those based on 15-minute sampling. In particular, for the whole dataset in Tito, the correlation increases from 0.979 to 0.998, the Root Mean Square Error (RMSE) decreases from 45.16 W/m² to 13.19 W/m² and the Mean Bias Error (MBE) is reduced from −0.67 W/m² to −0.02 W/m². For the whole dataset in Ispra, the correlation increases from 0.995 to 0.998, the RMSE decreases from 24.85 W/m² to 15.59 W/m², whereas the MBE increases from 3.84 W/m² to 4.58 W/m². This preliminary assessment shows that higher temporal sampling can improve SSI monitoring over areas featuring frequent and rapid solar irradiance variation.

1. Introduction

Quantitative knowledge of Surface Solar Irradiance (SSI) is required in a wide range of scientific and technological applications. Complete and accurate SSI data at a specific site are highly important for regional crop growth modeling, evapotranspiration estimates and hydrological monitoring [1,2,3,4,5,6,7,8]. Furthermore, SSI is of fundamental importance to Earth’s biosphere and climate [9]; SSI estimation also plays a significant role in the design of photovoltaic power and solar heating systems within the renewable energy industry [10,11,12].

Solar radiation has been historically recorded at ground level by different meteorological agencies in order to provide reliable data for the assessment of the solar resource. Ideally, in situ measurements provide the best method to evaluate solar irradiance at the surface [13]; however, in most cases, ground radiometer networks only cover the area of interest sparsely [14,15], particularly in mountainous areas [16]. In addition, conventional weather stations only measure global irradiance, while only a minority are also equipped to measure either the diffuse or the direct component of solar radiation. Considering the limitations of ground-based instrument networks, especially over complex terrain, other methods have been exploited in the last few years to achieve SSI estimation. One such method exploits the back-scattered solar radiation from the Earth–atmosphere system as detected by meteorological satellites to derive surface solar radiation. Specific models then convert satellite data into SSI, generally resulting in a better accuracy compared to interpolated ground measurements [17,18]. Other methods have been developed to derive the SSI from satellite observations (mainly from geostationary satellites), exploiting normalized reflectance measurements to determine the cloud transmission or cloud index. Subsequently, a clear sky model is generally used to derive the SSI from the retrieved cloud index; an example of this is the Heliosat method [19,20,21]. Several derivations of Heliosat also exist [22], e.g., an operational processing chain for climatological purposes (HelioClim). A different approach retrieves cloud microphysical information and then derives SSI accordingly; e.g., in [23,24,25], cloud physical properties retrieved from a look-up table are exploited in the estimation of SSI. Also, artificial neural networks have been employed to estimate solar irradiation using different sets of inputs [26,27,28].

For many applications, however, the SSI integrated over a specific time interval is the variable of interest. In particular, cumulative sums of hourly, daily and monthly solar irradiance are widely used. The temporal resolution of ground instruments is high enough to provide accurate hourly average values, whereas satellite-based estimates have lower accuracy due to the limited number of measurements per hour. In fact, large variations in solar radiation can occur within an hour, potentially leading to inaccurate estimates of hourly mean estimates. Such variations are well known, and can be calculated in a deterministic manner, because of the seasonal and daily cycles due to Sun–Earth geometry. Additional variability is introduced by atmospheric extinction caused mainly by aerosols, water vapor and other atmospheric trace gases (e.g., ozone), as described in clear sky models. The variability induced by aerosols or water vapor is assumed to be small on a temporal scale shorter than an hour. On the other hand, strong temporal variability occurs within a one-hour temporal scale due to the cloud extinction. Minute-by-minute values show that the passing of opaque cloud fields may lead to changes in the incoming irradiance up to ~80% of the clear-sky value within a minute [13]. Since solar radiation varies rapidly in time and space, instruments with high spatial and temporal resolution are necessary. One of the most suitable temporal and spatial resolution trade-off over Europe is the Spinning Enhanced Visible and InfraRed Imager (SEVIRI) aboard the Meteosat Second Generation (MSG) geostationary satellites. Although SEVIRI was designed to support numerical weather forecasting over Europe and Africa [29], in the last few years it has been used for solar irradiance estimation [19,20,21,22,23,24,25] and short-term forecasting [30]. One SEVIRI is aboard MSG-4 (0°N, 0°E) and provides imagery of the full Earth disk every 15 minutes (normal repeat cycle). However, images are also available at higher temporal resolution (every five minutes) through the Rapid Scanning Service (RSS) from the SEVIRI aboard MSG-3 (0°N, 9.5°E).

This work investigates the effect of temporal resolution on the evaluation of SSI calculated with the Advanced Model for the Estimation of Surface Solar Irradiance from Satellite (AMESIS) based on SEVIRI images from the high temporal resolution (five minutes) Rapid Scanning Service. In particular, hourly mean values of the SSI based on 4 (every fifteen minutes) and 12 (every five minutes) samplings have been compared against the hourly mean solar irradiance obtained with ground-based pyranometers; importantly, we use data from SEVIRI-RSS for both temporal samplings. The evaluation of the upgraded version of AMESIS has been carried out against two pyranometers installed in two different sites: the first one located in Southern Italy (Tito) at an altitude of 760 m, and the second one in the Northern Italy (Ispra) at an altitude of 220 m. The purpose of this paper is to assess whether the use of the RSS images, at higher temporal resolution with respect to the normal scan mode service, can improve the accuracy of the AMESIS-based hourly mean SSI estimation, in particular over cloudy and partially cloudy sky. An upgraded version of AMESIS [24] has been used in order to estimate the surface solar irradiance using data from the RSS. While in a previous work [25] we have demonstrated that the High-Resolution Visible channel in AMESIS improves the spatial accuracy of the SSI estimation, in this work we focus on temporal resolution using the RSS. AMESIS has been developed at the Institute of Methodologies for Environmental Analysis of the National Research Council of Italy (IMAA-CNR) and has been running continuously over Italy since 2017 in support of the monitoring of photovoltaic plants using normal scan mode SEVIRI images (every fifteen minutes). The paper proceeds as follows: Section 2 describes the dataset and tools used in this work for the assessment of the new version of AMESIS; Section 3 provides the statistical analysis evaluation and the results discussion; and Section 4 draws conclusions.

2. Materials and Methods

The SEVIRI radiometer is the main payload on board the MSG geostationary satellite series, operated by the EUropean organization for the exploitation of METeorological SATellites (EUMETSAT). The MSG satellites scan Europe, Africa and part of the Indian Ocean in geostationary orbit at an altitude of 36,000 km above the equator. SEVIRI, a 50-cm-diameter aperture line-by-line scanning radiometer, has twelve spectral channels. Eleven channels cover the infrared and visible region of the spectrum with a spatial sampling of 3 km at nadir, whereas the High-Resolution Visible (HRV) is a broadband (0.3–1.1 μm) channel with 1 km spatial sampling. However, HRV images are acquired over a reduced area of the Earth. The SEVIRI instrument on board the MSG-4 satellite scans the full Earth disc every 15 min; conversely, the SEVIRI on board the MSG-3 operates the Rapid Scanning Service (RSS), offering scans of a third of the Earth disc every 5 min. The baseline scan region is an area corresponding approximately to the top third of a nominal repeat cycle and covers a latitude range from approximately 15° to 70°; Figure 1 shows an example image at one IR channel for the RSS area. RSS data dissemination is identical to normal dissemination: image segments are based on 464 lines, which are compatible with the full disk level 1.5 data scans, and calibration is also operated as done for the full Earth scan mode.

The evaluation of the AMESIS-RSS irradiance data has been carried out against two pyranometers installed in two different sites, as previously stated. The one located in Tito and deployed at IMAA/CNR (latitude: 40.601°N, longitude: 15.724°E, altitude: 760 m) is a CMP11 Kippen and Zonen pyranometer included into a Baseline Solar Radiation Network (BSRN) compliant station measuring the Global Horizontal Irradiance (GHI). The CMP11 instrument, together with its ventilation unit (CVF4), complies with International Organization for Standardization (ISO) 9060:2018 spectrally flat class A (IEC 61724-1:2017 secondary standard). It is classified as “high quality” according to the World Meteorological Organization (WMO) nomenclature [31]. CMP11 is the most widely used in the solar energy industry for site prospecting and plant performance monitoring [32]. We perform data acquisition, processing and quality control at 1 min temporal intervals, following WMO guidelines. Automatic data quality tests have also been implemented. Overall instrument calibration is performed every ~2 years. The uncertainty of the instrument is within 3% in the hourly radiation totals [32], in accordance with WMO standards. The second pyranometer is located at the Joint Research Centre (JRC) in Ispra, Italy (latitude: 45.812°N, longitude: 8.627°E, altitude: 220 m). It is deployed at the European Solar Test Installation (ESTI) [33], which is a European reference laboratory for the verification of the power and energy generation of photovoltaic devices. This pyranometer is a unique product based on modern in-house developed micro-electronics; further specifics can be found in [34].

The SSI values have been estimated by means of AMESIS implemented to work with RSS SEVIRI data. Below we provide a brief overview of AMESIS, while further details and the validation of AMESIS based on normal scan mode SEVIRI data can be found in [24,25]. AMESIS uses retrieved cloud microphysical information derived from SEVIRI data to estimate the SSI. Initially the cloud microphysical parameters retrieval uses radiances in the visible (0.6–0.8 μm), near-infrared (1.6 μm) and infrared (10.8–12.0 μm) spectral regions; in addition, the retrieval process also includes the other channels to improve the accuracy of cloud parameters (e.g., the 3.9 μm band contains useful information on particular types of clouds). Validation of cloud and aerosol microphysical properties has been reported in [24]. The first step of AMESIS methodology consists of classifying the pixels as clear, cloudy or partially cloudy [24] by means of the cloud Classification Mask Coupling of Statistical and Physical methods (C_MACSP) algorithm [35,36,37]. The C_MACSP has been validated against other operational products and also with 2B-GeoProf (CLOUDSAT Geometrical Profiling Product) [38]. Subsequently, AMESIS retrieves the surface solar irradiance on the basis of the correspondent look-up tables, which are periodically updated in order to consider surface albedo/emissivity variations. The update is performed typically once every 8 days. The algorithm works as follows: in the case a HRV pixel is classified as clear, the AMESIS model retrieves the associated coefficient from the correspondent look-up table according to albedo, integrated water vapor, solar zenith, azimuth solar–satellite angles, and the elevation above sea level. Conversely, if both HRV and IR/VIS pixels are classified as cloudy, the model retrieves cloudy microphysical parameters. Depending on the cloud microphysical parameter information obtained from this first step, the surface irradiance is estimated by using the correspondent look-up table. If the HRV and the IR/VIS pixels are classified, respectively, as cloudy and partially cloudy, the method retrieves cloudy microphysical parameters for partially cloudy cases according to the cloud fraction index. In the second step of the algorithm, the surface irradiance is estimated by using the correspondent look-up table for the cloud microphysical parameters. AMESIS also considers the aerosol effect for pixels featuring aerosol presence; microphysical aerosol parameters are retrieved using SEVIRI infrared and visible channels and then used in the look-up tables selection process. Since aerosols are highly variable in time and space, we prefer to use the time and space co-located information of solar visible channels rather than spatially separated ground measurements or temporally distant satellite retrievals derived from other satellite platforms. Aerosol information obtained with AMESIS has been validated through comparisons with Moderate Resolution Imaging Spectroradiometer (MODIS) and Aerosol Robotic Network (AERONET) [24]. It is important to underline that in this work, all the look-up tables have been modified to work with rapid scan data, considering the different projected spatial grid data rectification with respect to the normal scan.

Hourly average surface solar irradiance values have been derived by means of instantaneous AMESIS SSI estimations considering two different temporal sampling, namely 4 (every fifteen minutes) and 12 (every five minutes) estimates, corresponding to the temporal resolution of normal and rapid scanning services, respectively. As previously stated, in this work we use data from AMESIS-RSS for both temporal samplings. The hourly mean is simply calculated as the cumulative sum divided by the total number of samples considered; besides, the sample measurements are symmetrically distributed around the reference hour. The dataset used for comparison is composed of 15 days in March 2018, from the 11th to the 25th. The comparison of the AMESIS products against the ground-based reference is performed through the assessment of statistical scores. In addition to correlation coefficient, four commonly-used statistical measures have been calculated: the Mean Bias Error (MBE), the Root Mean Square Error (RMSE), the Mean Absolute Error (MAE) and the Mean Absolute Percentage Error (MAPE), the normalized RMSE (nRMSE) and MBE (nMBE), defined as follows:

$$corr=\frac{cov\left(p,s\right)}{{\sigma }_p{\sigma }_s}$$

$$MBE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n(s_i-p_i)$$

$$RMSE={\left[\frac{1}{n}{\displaystyle \sum }_{i=1}^n{(s_i-p_i)}^2\right]}^{1/2}$$

$$MAE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n|s_i-p_i|$$

$$MAPE=\frac{100\%}{n}{\displaystyle \sum }_{i=1}^n\left|\frac{\left(p_i-s_i\right)}{p_i}\right|$$

$$nMBE=MBE/\overline{p}$$

$$nRMSE=RMSE/\overline{p}$$

where p denotes ground measured data, s denotes satellite products, n indicates the total number of measurements i, cov is the covariance, σ_p is the standard deviation of p and σ_s is the standard deviation of s.

3. Results and Discussion

In this section, we analyze the comparison between AMESIS estimates (considering both temporal samplings) and the ground-measured SSI data. The dataset is composed overall of 15 days in March, for a total amount of 150 hourly-mean samples. In

Table 1. Qualitative description of the dataset weather conditions.

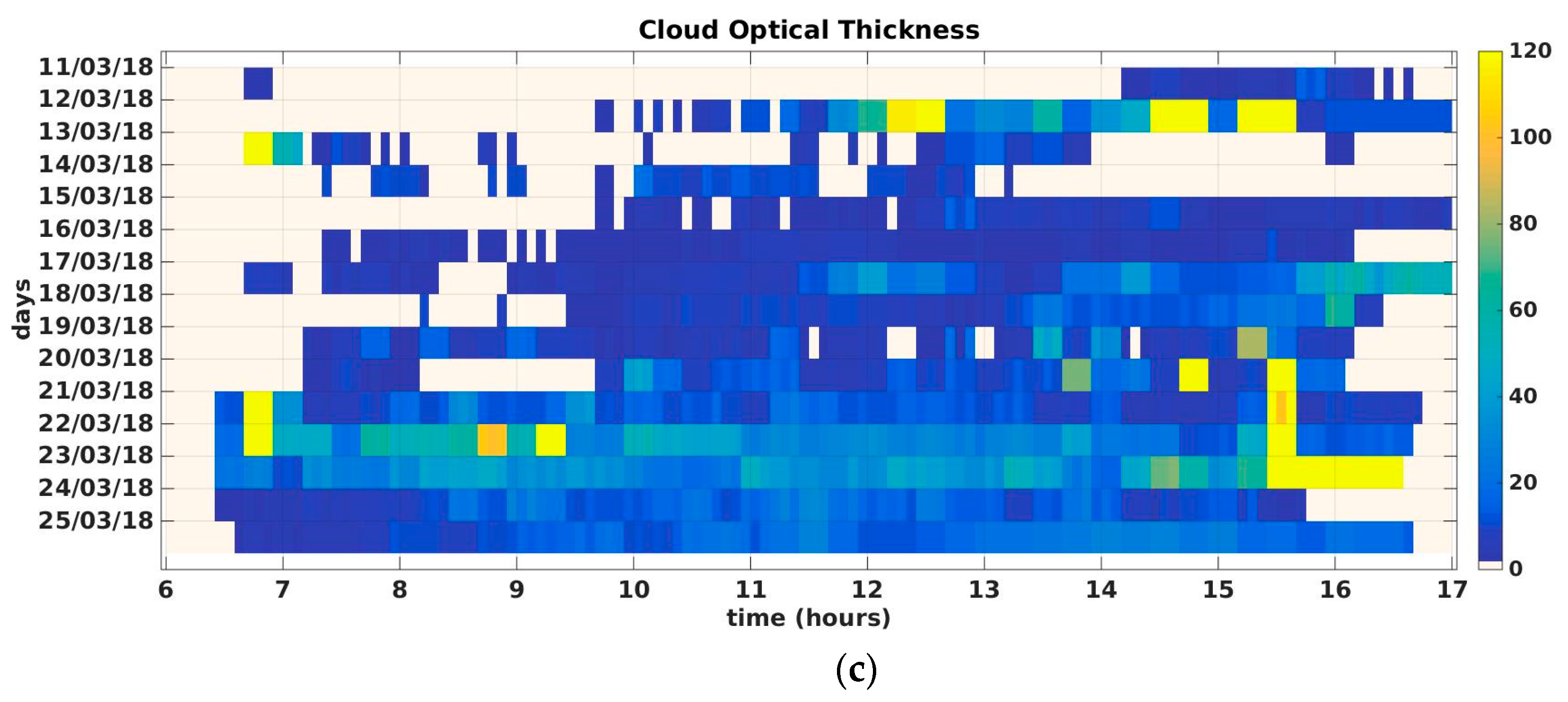
Date (dd/mm/yyyy)	Ispra	Tito
11 March 2018	Cloudy	Clear or broken clouds during the morning, cloud during the afternoon
12 March 2018	Partially cloudy	Clear or broken clouds during the first morning, cloud since 10 a.m.
13 March 2018	Partially cloudy	Partially cloudy
14 March 2018	Clear, small cloud in the afternoon	Partially Clear
15 March 2018	Cloudy	Clear with cloudy passages
16 March 2018	Clear with cloudy passages	Partially cloudy
17 March 2018	Cloudy	Partially cloudy
18 March 2018	Cloudy	Partially cloudy
19 March 2018	Cloudy	Partially cloudy
20 March 2018	Cloudy during the morning, partially cloudy during the afternoon	Partially cloudy during the morning, cloudy during the afternoon
21 March 2018	Cloudy during the morning, partially clear during the afternoon	Cloudy
22 March 2018	Clear during the morning, partially cloudy during the afternoon	Cloudy
23 March 2018	Clear	Cloudy
24 March 2018	Cloudy	Partially cloudy
25 March 2018	Clear with cloudy passages	Partially cloudy

, we report on the general weather condition relative to Tito and Ispra datasets, featuring mainly cloudy and partially cloudy days and few clear day cases.

We firstly analyze the Tito dataset. In Figure 2, we provide a quantitative description of the whole dataset, based on AMESIS-retrieved cloud microphysical parameters. In particular, we show the cloud phase histogram (Figure 2a) and the distributions of cloud top height (Figure 2b) and optical thickness (Figure 2c). We should emphasize that the sample consists overall of 12 (samplings) × 10 (h) × 15 (days), and it is representative of a large variety of cloud types and patterns.

Table 2. Results of the statistical assessment for AMESIS product based on 15-minute temporal sampling against ground measurements at the Tito site. CORR = Correlation, MBE = Mean Bias Error, RMSE = Root Mean Square Error; MAE = Mean Absolute Error; MAPE = Mean Absolute Percentage Error; nMBE = normalized MBE; nRMSE = normalized RMSE.

Date (dd/mm/yyyy)	15-Minute Temporal Sampling
	CORR	MBE (W/m2)	RMSE (W/m2)	MAE (W/m2)	MAPE (%)	nMBE (%)	nRMSE (%)
11 March 2018	0.997	3.205	18.733	13.170	5.821	0.789	4.6
12 March 2018	0.966	35.138	76.460	43.338	25.761	13.863	30.1
13 March 2018	0.930	−11.920	102.627	59.080	14.041	−3.023	26.0
14 March 2018	0.960	19.748	63.218	43.256	10.126	5.592	17.9
15 March 2018	0.991	−9.931	31.714	26.963	7.700	−2.738	8.7
16 March 2018	0.988	6.097	33.029	27.791	6.657	1.725	9.3
17 March 2018	0.992	0.284	23.753	17.834	8.862	0.987	8.2
18 March 2018	0.994	−10.176	25.006	19.093	7.760	−3.702	9.0
19 March 2018	0.962	−21.829	65.298	49.942	17.598	−8.565	25.6
20 March 2018	0.993	−11.307	26.279	21.496	10.622	−4.446	10.3
21 March 2018	0.973	−13.011	24.678	20.722	11.625	−7.595	14.4
22 March 2018	0.996	0.502	2.411	1.875	5.312	1.244	5.9
23 March 2018	0.998	6.118	7.548	6.211	6.175	6.021	7.4
24 March 2018	0.993	5.510	24.147	19.321	5.794	1.686	7.3
25 March 2018	0.987	−8.507	19.126	14.570	7.170	−4.633	10.4

and

Table 3. Results of the statistical assessment for AMESIS product based on five-minute temporal sampling against ground measurements at the Tito site.

Date (dd/mm/yyyy)	Five-Minute Temporal Sampling
	CORR	MBE (W/m2)	RMSE (W/m2)	MAE (W/m2)	MAPE (%)	nMBE (%)	nRMSE (%)
11 March 2018	0.999	2.598	13.160	7.502	2.512	0.640	3.2
12 March 2018	0.998	3.823	16.810	13.365	11.843	1.508	6.6
13 March 2018	0.999	1.616	9.191	6.859	2.813	0.411	2.3
14 March 2018	0.996	4.749	17.873	14.459	4.411	1.345	5.0
15 March 2018	0.999	0.936	8.045	7.009	2.502	0.258	2.2
16 March 2018	0.999	0.056	6.416	4.619	1.594	0.158	1.8
17 March 2018	0.999	3.584	8.489	6.701	3.634	1.246	2.9
18 March 2018	0.999	1.950	5.071	3.983	3.351	0.709	1.8
19 March 2018	0.993	−21.596	32.291	22.008	7.190	−8.473	12.6
20 March 2018	0.999	−2.782	10.896	7.677	3.632	−1.094	4.2
21 March 2018	0.988	−0.552	13.881	9.908	6.850	−0.322	8.1
22 March 2018	0.999	0.544	1.423	1.130	3.078	1.348	3.5
23 March 2018	0.998	2.260	4.727	3.896	4.667	2.224	4.6
24 March 2018	0.999	6.069	9.667	7.227	2.171	1.857	2.9
25 March 2018	0.997	−3.599	8.714	5.512	2.660	−1.960	4.7

report the statistical scores related to the first site (IMAA/CNR—Tito), located in Southern Italy at an altitude of 763 m. The correlation, MBE, MAPE and MAE, based on the higher sampling frequency, outperform the correspondent statistics based on normal scan SEVIRI images in all cases examined except for MBE on the 17th, 22nd and 24th of March.

The case on 13 March 2018 features the highest improvement in correlation, from 0.930 to 0.999, with a relative RMSE reduction from 102.63 W/m² to 9.19 W/m² and a MBE change from −11.92 W/m² to 1.62 W/m². This case is shown in Figure 3, reporting the time series and the scatter plot of the instantaneous SSI measured by the pyranometer and the one estimated by AMESIS for both temporal samplings. As previously stated, statistical scores based on AMESIS-RSS are generally significantly better than those obtained using normal scan mode. Even the MBE tends to improve in each case except on the 22nd and 24th of March where it remains substantially unaffected, and on the 17th of March where it increases from 0.28 W/m² to 3.58 W/m². Figure 4 shows the same analysis (as in Figure 3) relative to the case on 17 March 2018, which features a smooth improvement in the correlation using AMESIS-RSS as well as a strong improvement in the other statistical scores (see Table 2 and Table 3). This is a case featuring strong variability in terms of solar irradiance, as demonstrated from the several dips in the temporal evolution of the SSI.

With regard to the second pyranometer considered for comparison, Figure 5 reports the cloud parameters (phase, top height and optical thickness) retrieved by AMESIS for the JRC site in Ispra, in order to quantitatively characterize the dataset considered.

Table 4. Results of the statistical assessment for AMESIS product based on 15-minute temporal sampling against ground measurements at the Ispra site.

Date (dd/mm/yyyy)	15-Minute Temporal Sampling
	CORR	MBE (W/m2)	RMSE (W/m2)	MAE (W/m2)	MAPE (%)	nMBE (%)	nRMSE (%)
11 March 2018	0.960	2.404	5.596	2.910	14.595	7.015	16.3
12 March 2018	0.965	−18.481	43.777	26.023	9.695	−8.033	19.0
13 March 2018	0.997	12.219	20.962	16.032	5.982	3.433	5.9
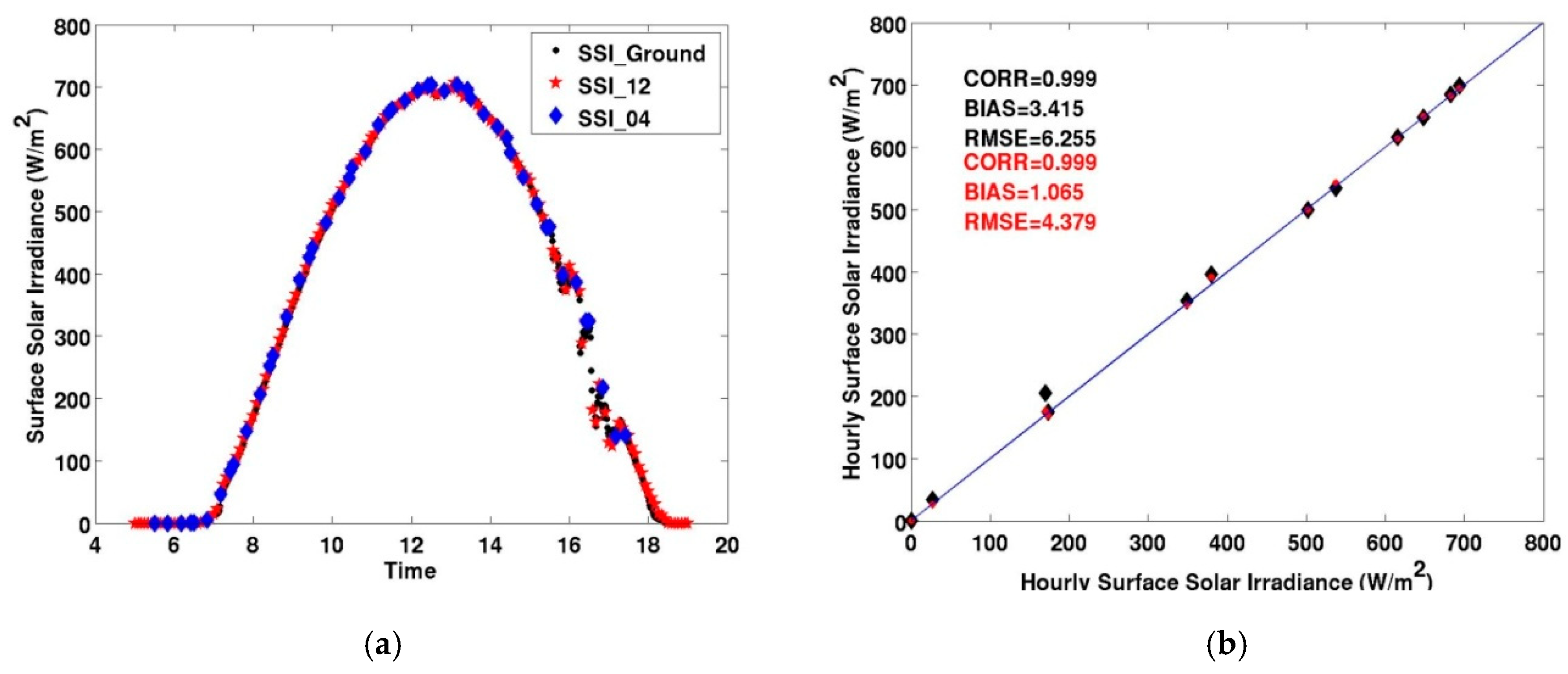
14 March 2018	0.999	3.415	6.255	4.426	3.550	0.763	1.4
15 March 2018	0.976	−0.751	5,079	3.468	8.922	−1.809	12.0
16 March 2018	0.999	2.922	7.387	4.683	1.649	0.650	1.6
17 March 2018	0.989	4.967	9.435	6.386	18.140	8.441	16.0
18 March 2018	0.995	4.328	7.715	5.486	7.874	6.289	11.2
19 March 2018	0.991	1.095	3.261	2.603	4.890	2.257	6.7
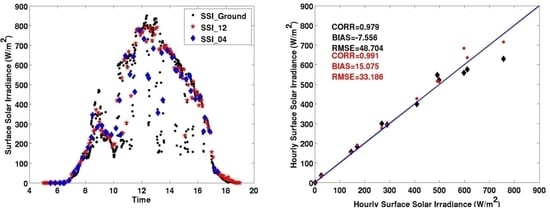
20 March 2018	0.979	−7.556	48.704	34.514	10.580	−1.941	12.5
21 March 2018	0.995	22.518	35.452	25.894	5.249	5.229	8.2
22 March 2018	0.995	18.637	29.296	20.479	4.692	4.448	6.9
23 March 2018	0.999	1.269	3.519	3.114	1.044	0.270	0.8
24 March 2018	0.993	−6.310	26.834	17.879	8.972	−2.350	9.9
25 March 2018	0.992	16.987	37.139	20.930	4.516	4.083	8.9

and

Table 5. Results of the statistical assessment for AMESIS product based on five-minute temporal sampling against ground measurements at the Ispra site.

Day (dd/mm/yyyy)	Five-Minute Temporal Sampling
	CORR	MBE (W/m2)	RMSE (W/m2)	MAE (W/m2)	MAPE (%)	nMBE (%)	nRMSE (%)
11 March 2018	0.972	1.772	4.651	2.314	14.245	5.171	13.6
12 March 2018	0.993	−6.851	19.684	10.711	3.649	−2.978	8.5
13 March2018	0.999	3.942	9.261	6.066	3.254	1.108	2.6
14 March 2018	0.999	1.065	4.379	3.026	0.907	0.238	0.9
15 March 2018	0.996	0.776	2.122	1.866	5.998	1.869	5.1
16 March 2018	0.999	2.694	7.625	5.111	2.861	0.599	1.6
17 March 2018	0.989	3.169	8.419	6.492	19.550	5.386	14.3
18 March 2018	0.997	2.619	5.217	3.770	4.932	3.805	7.5
19 March 2018	0.998	0.683	1.657	1.350	3.187	1.408	3.4
20 March /2018	0.991	15.075	33.186	23.250	7.267	3.873	8.5
21 March 2018	0.997	19.061	27.882	20.131	4.118	4.426	6.4
22 March 2018	0.998	11.550	17.735	12.589	3.313	2.757	4.2
23 March 2018	0.999	0.349	4.473	3.860	1.132	0.742	0.9
24 March 2018	0.996	5.742	18.398	13.628	5.777	2.138	6.8
25 March 2018	0.997	7.122	20.447	10.083	2.490	1.711	4.9

report the statistical scores related to the JRC site in Ispra, located in Northern Italy at an altitude of 220 m. The correlation coefficient and the RMSE of the high frequency-based irradiance estimates are generally better than the lower frequency ones. All the other statistical scores have very close values, except on 20 March 2018, in which case the MBE increases from −7.56 W/m² to 15.08 W/m², while the RMSE decreases from 48.70 W/m² to 33.19 W/m² and the correlation coefficient increases from 0.979 to 0.991.

In Figure 6, we show the diurnal evolution and the scatter plot of the SSI for the case on 20 March 2018, which features strong fluctuations that hinder an accurate monitoring of the SSI, even with five minute sampling. The scatter plot shows larger MBE for the five minute sampling. We also report a clear sky case (14 March 2018) in Figure 7; here, an improvement of all statistical scores is observed when using RSS instead of normal scan mode. The MBE and RMSE decrease from 3.41 W/m² to 1.06 W/m² and from 6.25 W/m² to 1.06 W/m² respectively, while the correlation coefficient is unaffected.

The analysis of the whole dataset, obtained by aggregating 150-hourly mean estimates for each site, shows a general improvement in the statistical assessment of the AMESIS estimates based on RSS with respect to the normal scan mode. In fact, the higher sampling frequency mode may allow us to obtain more accurate and representative mean values than normal scan mode ones, as it is more likely that the rapid scan catches the solar irradiance variations induced by cloud passages. This is demonstrated in

Table 6. Statistical analysis for the 15-minute AMESIS temporal sampling product against ground measurements at the IMAA/CNR—Tito site, considering the whole dataset. N = the total number of hourly mean irradiance values.

N	15-Minute Temporal Sampling
	CORR	MBE (W/m2)	RMSE (W/m2)	MAE (W/m2)	MAPE (%)	nMBE (%)	nRMSE (%)
150	0.979	−0.672	45.157	25.644	10.068	−0.273	18.3

,

Table 7. Statistical analysis for the five-minute AMESIS temporal sampling product against ground measurements at the IMAA/CNR—Tito site, considering the whole dataset. N = the total number of hourly mean irradiance values.

N	Five-Minute Temporal Sampling
	CORR	MBE (W/m2)	RMSE (W/m2)	MAE (W/m2)	MAPE (%)	nMBE (%)	nRMSE (%)
150	0.998	−0.023	13.194	8.124	4.194	−0.009	5.3

,

Table 8. Statistical analysis for the 15-minute AMESIS temporal sampling product against ground measurements at the JRC (Ispra) site, considering the whole dataset. N = the total number of hourly mean irradiance values.

N	15-Minute Temporal Sampling
	CORR	MBE (W/m2)	RMSE (W/m2)	MAE (W/m2)	MAPE (%)	nMBE (%)	nRMSE (%)
150	0.995	3.844	24.853	12.988	7.357	1.516	9.8

and

Table 9. Statistical analysis for the five-minute AMESIS temporal sampling product against ground measurements at the JRC (Ispra) site, considering the whole dataset. N = the total number of hourly mean irradiance values.

N	Five-Minute Temporal Sampling
	CORR	MBE (W/m2)	RMSE (W/m2)	MAE (W/m2)	MAPE (%)	nMBE (%)	nRMSE (%)
150	0.998	4.584	15.593	8.283	5.512	1.809	6.1

, showing the statistical analysis relative to Tito and Ispra, respectively. The higher temporal sampling frequency clearly yields better performances: for Tito, correlation increases from 0.979 to 0.998, the RMSE decreases from 45.16 W/m² to 13.19 W/m² and the MBE reduces from −0.67 W/m² to −0.02 W/m²; for Ispra, correlation increases from 0.995 to 0.998, the RMSE decreases from 24.85 W/m² to 15.59 W/m² and the MBE increases from 3.84 W/m² to 4.58 W/m². Figure 8 shows scatter plots of the two datasets. The higher temporal resolution improves the statistical scores, especially in Tito. Here, orographic features play an important role, leading to strong variations of the SSI throughout the day, even on clear days from mid-morning onwards. The complex orography in Tito is also responsible for the strongly variable weather conditions over this site, leading to the formation of cloud patterns quite often during the day. Besides, the dataset used for Tito is characterized by much higher variability in terms of cloudiness as opposed to the more steady conditions observed in Ispra; this might explain the overall stronger improvement in Tito than in Ispra provided by the higher sampling frequency. In particular, with regard to cloudy cases, the improvement observed is due to the higher probability that the RSS catches the solar irradiance variation caused by the continuous change of cloud patterns and microphysical parameters. Concerning clear sky cases, the RSS increases the chance to capture the irradiance variation due to sporadic cloud passages, therefore improving the estimates in such cases too. The above factors, together with the scarcity of observations in elevated areas, often cause large modeling uncertainties.

The sources of uncertainties related to solar radiation measurements can be classified in two categories: instrument uncertainty and operation related problems [39]. With regard to the former, the largest source of uncertainty is the cosine response, as the pyranometer response depends on the angle of incidence [40]; this uncertainty tends to increase for solar elevation angles below 6°. Another source of uncertainty is the pyranometer response dependence on the azimuthal angle, namely the azimuth response. This uncertainty is labeled as directional according to [31]. The CMP11 pyranometer directional uncertainty is lower than 10 W/m² for zenith angles up to 80° and 1000 W/m² radiation beam [32]. To keep the uncertainty within the above threshold, we only use data with solar zenith angles below 80°.

Air temperature also affects the measurements, since the pyranometer has a temperature response uncertainty caused by large and/or rapid changes in external temperature [41]. Another uncertainty is the instability of the instrument over time, which may result in sensitivity drifts since its initial calibration. We therefore use data measured in the air temperature range between 10 °C and 20 °C to minimize the temperature-related uncertainty.

Other sources of uncertainty fall into the second category, e.g., effects caused by snow, dew, and dust over the lens as well as inaccurate sensor leveling and shading. The CMP11 used in this work undergoes systematic cleaning, general maintenance and calibration according to WMO standards, and it is far from structures that may cause shading. Automatic quality control has also been implemented following WMO standards in order to reject erroneous measurements. Measurements have been compared against satellite estimates (operational AMESIS with the DISORT radiative transfer model) and Numerical Weather Prediction model output (WRF-SOLAR v3.9.1); the resulting agreement is in line with the expected combined uncertainties.

4. Conclusions

In this work, an upgraded version of the Advanced Model for the Estimation of Surface Solar Irradiance from Satellite (AMESIS) has been used to estimate the Surface Solar Irradiance (SSI) by means of data from the SEVIRI Rapid Scanning Service. In particular, we evaluate the improvement obtained in the hourly mean SSI estimates due to the higher temporal resolution. The AMESIS model has been running at the Institute of Methodologies for Environmental Analysis of the National Research Council of Italy (IMAA-CNR) continuously over Italy since 2017 in support of the monitoring of photovoltaic plants with normal scan SEVIRI data. We compare AMESIS results against data from two pyranometers located in Southern (Tito) and Northern (Ispra) Italy at an altitude of 760 m and 220 m, respectively. Considering the whole datasets of 15 days (corresponding to 150 hourly mean SSI estimates), for Tito, the correlation increases from 0.979 to 0.998, the RMSE decreases from 45.16 W/m² to 13.19 W/m², and the MBE from −0.67 W/m² to −0.02 W/m², whereas for Ispra, the correlation increases from 0.995 to 0.998, the RMSE decreases from 24.85 W/m² to 15.59 W/m² and the MBE increases from 3.84 W/m² to 4.58 W/m². The uncertainty estimation is a fundamental step of the measurement process. The uncertainty of AMESIS irradiance estimates has been assessed in previous work [24]. Concerning the instrument uncertainty, measurements (in clear sky conditions) have been compared against satellite estimates (operational AMESIS and the DISORT radiative transfer model) and NWP model output (WRF-SOLAR v3.9.1) since the installation of the CMP11 pyranometer. The resulting error is within 3% on hourly totals, in line with the instrument manual specifications [32]. Besides, the difference between the normalised RMSE based on 12- and 4- hourly samplings (13% and 3.7% for Tito and Ispra, respectively) is larger than the uncertainty level; thus, we deem the improvement brought by the RSS as quite significant. The results show that higher temporal resolution improves the statistical scores. The greatest improvement occurs in Tito, probably related to the complex orography. Accurate solar radiation estimates in mountainous areas represent a challenging task, because of the strong variability arising from orographic effects and mountain weather. The higher temporal sampling is demonstrated to be a valid tool to improve the accuracy of hourly mean SSI estimates and to monitor SSI over those areas where solar irradiance varies rapidly. Although the run time and storage load increase by a factor of three, this initial assessment shows that it is worth the higher effort to add the RSS into the operative chain for solar irradiance monitoring over areas featuring strong surface solar irradiance variability due to dynamic weather conditions.