Evaluating the Potential of Multi-Seasonal CBERS-04 Imagery for Mapping the Quasi-Circular Vegetation Patches in the Yellow River Delta Using Random Forest

Abstract

High-resolution satellite imagery enables decametric-scale quasi-circular vegetation patch (QVP) mapping, which greatly aids the monitoring of vegetation restoration projects and the development of theories in pattern evolution and maintenance research. This study analyzed the potential of employing five seasonal fused 5 m spatial resolution CBERS-04 satellite images to map QVPs in the Yellow River Delta, China, using the Random Forest (RF) classifier. The classification accuracies corresponding to individual and multi-season combined images were compared to understand the seasonal effect and the importance of optimal image timing and acquisition frequency for QVP mapping. For classification based on single season imagery, the early spring March imagery, with an overall accuracy (OA) of 98.1%, was proven to be more adequate than the other four individual seasonal images. The early spring (March) and winter (December) combined dataset produced the most accurate QVP detection results, with a precision rate of 66.3%, a recall rate of 43.9%, and an F measure of 0.528. For larger study areas, the gain in accuracy should be balanced against the increase in processing time and space when including the derived spectral indices in the RF classification model. Future research should focus on applying higher resolution imagery to QVP mapping.

1. Introduction

In arid and semi-arid regions of the world, vegetation usually appears as patches due to the environmental constraints such as a limited water supply, soil salinization or local microtopography. According to size, area and spatial distribution, vegetation patches are characterized as banded (i.e., tiger vegetation) or spotted (i.e., leopard vegetation) [1]. Compared with banded vegetation patterns, the spotted vegetation pattern has not as yet attracted equivalent attention [2]. Patchy vegetation patterns have been reported in America, Africa, Asia, Australia, and Spain [3,4,5,6,7,8,9,10,11,12,13,14,15,16], where the range of annual precipitation is from 50 to 750 mm, and appears to be unrelated to any particular soil type or plant species [14]. In general, it is considered as the result of plant-oil feedback occurring in water-limited regions [12,14,15,16]. Although there is an ongoing debate concerned with the mechanisms for the formation of patchy vegetation patterns, vegetation patchiness can generally increase primary production, influence biodiversity, affect surface runoff and soil erosion, and suggest key indices for ecosystem function and for the management of arid and semi-arid lands [1,16,17,18]. Mapping vegetation patches is, therefore, important for a better understanding of patch patterns, mechanisms for formation and evolution, and function. Moreover, such mapping can provide valuable information for the development of adaptive vegetation recovery and re-establishment strategies for increasingly degraded ecosystems in arid and semi-arid zones [19].

Remote sensing is an effective technology for the creation of vegetation maps. Due to the relatively small size, vegetation patch mapping most frequently involves the application of aerial photographs and high-resolution satellite images. Aerial photographs have long been recognized as an important data source for mapping patchy vegetation patterns since aerial photographs first became accessible in the early 1940s [2,20]. The circular patches (with an area of approximately <90 m² to >3000 m²) of Spartina patens on Cox Island, Siuslaw Estuary, Oregon were mapped using sequential air photos (scale 1:1500) from 1939 to 1980 and their area determined by planimetry [9]. Vegetation patches (with spatial scales of 2–3 m) on the eastern flanks of Mt. Carmel were derived from orthorectified aerial photographs with a 75 cm pixel resolution using a Maximum Likelihood Classifier (MLC) [20]. The fairy circles (with an average diameter of 5–8 m) of Kaokoland, Namibia were detected from a set of aerial photographs (Scale 1:78,000) [21]. Two-dimensional wavelet combined with a 1 m aerial photograph was used to identify individual juniper trees (crown diameter of 2–9 m) and thereby to analyze the encroachment of juniper plants on to a sagebrush steppe landscape [22]. A set of historical aerial photographs have also been used to analyze the onset and trends of an invasion by Pteronia incana into the dry Karoo region of South Africa [19]. Multi-temporal aerial color infrared high-resolution images with a spatial resolution of 1 m were used to validate a distinct discrimination of Pteronia incana from other surfaces in an invaded area in Eastern Cape, South Africa [23]. Previous studies have proved that aerial photograph with a pixel size of 2 m are sufficient to study decametric-scale vegetation patch patterns [24,25]. With the launch of high spatial resolution civil commercial satellites in 1999, increasing numbers of studies have been carried out concerning the dynamics of vegetation patch patterns either by combining historical aerial photographs with multi-temporal high-resolution satellite images in recent years, or with the sole use of multi-temporal high-resolution satellite images. For example, a set of historical aerial photographs with a spatial resolution of 86 cm and a QuickBird satellite image with a spatial resolution of 60 cm were used to monitor shrub encroachment from 1937 to 2003 in southern New Mexico using the Object-Based Image Analysis method (OBIA), and approximately 87% of all shrubs of more than 2 m² were identified [26]. Shekede et al. [25] used a discrete wavelet transform to map dynamics in the encroachment of woody patches (with an average diameter of between 8 m and 32 m) onto Zimbabwean savanna through the integration of multi-temporal aerial photographs (Scale 1:20,000) with the resample high spatial resolution (a spatial resolution of 2 m) GeoEye satellite images. High spatial resolution SPOT 5 (for which sharpened imagery has a spatial resolution of 2.5 m), QuickBird and IKONOS (with a spatial resolution of 80 cm) satellite imagery has been successfully used to map tree canopy cover patterns in savannas, and tree canopy sizes mapped with SPOT 5 imagery using the OBIA method had a similar distribution to those observed with QuickBird detection [27]. SPOT 5 (a spatial resolution of 2.5 m), ALOS (a spatial resolution of 2.5 m), ZY-3(a spatial resolution of 5.8 m), and QuickBird imagery have been also successfully used to detect the quasi-circular vegetation patches (QVPs, with an area of 115 m² to more than 1200 m²) in the Yellow River Delta (YRD), China [28,29,30]. The WorldView-2 satellite imagery (with a spatial resolution of 2 m) was recognized as more appropriate for the mapping to be used for a global estimation of giant reed invasion [31].

The above-mentioned studies use single-date high-resolution imagery to map vegetation patches. Multi-date images are not generally used for the detection of such patches, but are mainly used to analyze the dynamics of vegetation patch patterns according to differences between the bi-temporal images. The phenological information for vegetation derived from multi-seasonal imagery is very useful for mapping tree species [32,33,34,35,36,37,38,39], forest cover [40,41,42], crop types [43,44,45,46,47,48,49], bush encroachment [25], grassland [50,51,52,53,54], and land use/land cover and changes [55,56,57,58,59,60,61,62]. Despite the different conclusions obtained from a few studies [36,63,64], generally, multi-spectral and seasonal imagery can largely support higher classification accuracy than single-date imagery. During the temporal series classification procedure, it is necessary to find the optimal number of images and the optimal seasonal composition periods for mapping the target research objects in a region [46,58,65], because the acquisition of a large number of images may not be feasible due to cloud contamination, the satellite revisiting cycle, the high price, and the fact that long image composition periods may be less informative and lead to information redundancy [43,48,66].

Temporal series approaches involve the pixel-based and OBIA classification using several algorithms: principal component analysis, multi-temporal tasseled cap transformation, ISODATA, K-Means, maximum likelihood classification, linear discriminant analysis, multinomial logistic regression, discrete wavelet transform, deep neural network, spectral unmixing, spectral angle mapping, decision trees (DT), classification and regression trees, k-nearest neighbor (KNN), support vector machine (SVM), and random forest (RF). Accuracy assessments from previous studies suggest that there were inconsistent conclusions on the respective performance of these algorithms [34,56,67]. Fassnacht et al. [36] stated that the selection of the classifier itself was usually of low significance if the remotely sensed data met the demands of the classifier and study subject. Among these temporal series approaches, the RF classifier has been the most often used in recent years, and was demonstrated to produce higher classification accuracy with multi-seasonal images for a range of applications, including tree species detection [38,68,69], identification of crop types [48,66,70], and land cover classification [56,58,59]. In addition to the spectral bands, the spectral indices, temporal anomalies of spectral indices, biophysical variables, texture information, and topographic data were often stacked and used as input to the RF classifier. After random forest variable importance measures and the repeated classification accuracy assessment procedure were implemented, the optimal composition for input variables was determined as the input to the RF classifier to produce the final high classification result. Although temporal series approaches have received increasing attention, the multi-spectral and seasonal imagery-based classification for vegetation patches is still lacking.

The QVPs are visible with various composition components and spatial structures within the unused land of the YRD and were initially found through high spatial resolution SPOT 5 fusion-ready imagery in 2011 [71]. The QVPs appear to have a rapid succession rate and are ideal for studying the mechanism of spontaneous plant colonization and growth in this region, which will benefit the adaptive active restoration strategies implementation in the degraded wetland ecosystem of the YRD initiated in July 2002 [72]. Mapping QVPs is therefore important for a better understanding of vegetation patch patterns, formation and evolution mechanisms, and patch functioning. The single-date high-resolution imagery from different satellites such as SPOT 5, ALOS, ZY-3, QuickBird, China-Brazil Earth Resource Satellite (CBERS) 04, Gaofen (GF) 1 and GF-2 has been used to map the QVPs [16,28,29,30,71]. CBERS-04 imagery (with a spatial resolution of 5 m) is suitable for detecting the QVPs that are commonly found in an area of 25 km from the Bohai Sea of the YRD [16]. However, the classification accuracies for K-Means, DT, and SVM, are not stable, and are low in some cases [16,73]. Although comparison of the different seasonal CBERS-04 images for mapping QVPs has been carried out [73], the multi-spectral and seasonal imagery-based classification of QVPs remains unclear. For these reasons, the aim of this study was to explore the potential of multi-seasonal CBERS-04 images for mapping QVPs using the widely used RF classifier. CBERS-04 imagery acquired in the early spring, spring, summer, late autumn, and winter was used individually and the results were compared to provide insights into the optimal season for image acquisition. The different combinations of the different seasonal images were then used to evaluate the potential for using a multi-seasonal approach for mapping the QVPs.

2. Materials and Methods

2.1. Study Area

The study site is located 63 km northeast of Dongcheng District of Doongying City (118°7′ E–119°10′ E and 36°55′ N–38°10′ N) in Shandong Province, China (Figure 1a) and covers an area of 2.85 km² (Figure 1b). This area is a low and flat unused land formed after the cofferdam of the Gudong Oil Field was built to prevent sea water erosion and facilitate oil exploration in 1988. The soil types in this area are Fluvisols and Solonchaks, and the soil textures vary from sandy loam to silty clay [74]. This area has a warm temperate continental monsoon climate, with distinct seasons, a mean annual evaporation of 1962 mm, and a mean annual rainfall of 580 mm; about 70% of the rain falls during the summer [74]. It has an aridity index (the ratio between mean annual rainfall and mean annual evaporation) taken by the United Nations Convention to Combat desertification (UNCCD) of 0.30, which belongs to semi-arid areas [75]. Suaeda salsa (the growing season from late April to middle November), Tamarix chinensis (the growing season from late March to early December), and Phragmites australis (the growing season from early April to middle November) are the three most common and widely distributed types of native plant species over the study area, and are also the main plant species in the QVPs (photo in Figure 1a). The landscape of this area is characterized by a two-phase mosaic composed of the QVPs interspersed in the bare soil matrix (Figure 1b). The formation mechanisms on the QVPs and pattern is under study now, the hypotheses of QVP occurrence attributed to the seismic exploration of Gudong Oil Field in the YRD still needs to be confirmed [76,77].

A total of 32 georeferenced data from three field surveys carried out in October 2013 [76], August 2017 [77], and May 2018 were used to identify the QVPs in the CBERS-04 imagery for inclusion in the reference dataset. The collection of georeferenced data were equally divided into a training dataset (the number of QVPs, bare soil, and bodies of water were 816 pixels, 1875 pixels, and 609 pixels, respectively) and an independent validation dataset (the number of the QVPs, bare soil, and the water area were 516 pixels, 536 pixels, and 358 pixels, respectively) for the RF classification and accuracy assessment.

2.2. CBERS-04 Data

The CBERS-04 satellite launched on 7 December 2014 has four sensors, one of which is a panchromatic and multispectral camera, characterized by a 5 m spatial resolution panchromatic band (band 1, 510–850 nm), three 10 m spatial resolution multispectral bands (band 2, 520–590 nm; band 3, 630–690 nm; band 4, 770–890 nm), and a swath width of 60 km [78]. Due to the limitation of cloud coverage and data acquisition, and considering image quality, only five CBERS-04 images acquired in 2015, 2016, and 2017 were used in the study, including an image from the early spring in March, one from the spring in May, one from the summer in July, one from the late autumn in October, and one from the winter in December (

Table 1. Acquisition dates of the CBERS-04 imagery used in this study.

Sensor	Acquisition Date	Season
a panchromatic and multispectral camera	27 March 2017	early spring
	18 May 2017	spring
	10 July 2016	summer
	24 October 2015	late autumn
	13 December 2016	winter

).

Twenty GCPs selected by the image-to-image approach (with a mean root mean square error of 0.35 pixels) were used to register the multispectral bands at 10 m × 10 m pixel size to the panchromatic bands at 5 m × 5 m pixel size using a quadratic polynomial near neighbor method in ENVI v5.1. Pan-sharpened 5 m multispectral images were then produced for the five acquisition dates using the Gram–Schmidt spectral sharpening technique, which is one of the usual image sharpening methods used for preserving the spectral information of images [38,73,79], embedded in ENVI v5.1. The quick atmospheric correction method embedded in ENVI v5.1 was used to convert the digital numbers of the CBERS-04 images to the spectral reflectance, which needs no extra aided data, and implements significantly faster than the physics-based approaches, generally creating spectral reflectance within approximately 15% of the most widely used physics-based approach, fast line-of-sight atmospheric analysis of spectral hypercubes [80]. To reduce data processing time, a subset of the CBERS-04 fusion imagery was clipped to focus on the study site (Figure 1b), which included QVPs, bare soil and bodies of water.

Due to the flat terrain and the difficulty in obtaining fine resolution digital elevation model data for the research area, topographic data were not used in this study. The variables from texture information were often low on the list of variable importance [33,34]. The spectral bands and the derived spectral indices were, therefore, most commonly applied [35,46,56]. In this study, three bands of pan-sharpened 5 m multispectral imagery, and nine spectral indices were used as predictive variables for the RF classification of the QVPs (

Table 2. Predictive variables used in mapping the quasi-circular vegetation patches.

Predictive Variables	Description	Wavelength (nm)/Formula	Reference
CBERS-04 bands	Green (G)	520–590
	Red (R)	630–690
	Near-infrared (NIR)	770–890
Spectral indices	Normalized difference vegetation index (NDVI)	(NIR − R)/(NIR + R)	[81]
	Two-band enhanced vegetation index (EVI2)	2.5 (NIR − R)/(NIR + 2.4 R + 1)	[81]
	Optimized soil adjusted vegetation index (OSAVI)	1.16 (NIR − R)/(NIR + R + 0.16)	[81]
	Modified triangular vegetation index (MTVI2)	1.5 (1.2 (NIR − G) − 2.5 (R − G))/Square ((2 NIR + 1)2 − (6 NIR − 5 square (R)) − 0.5)	[81]
	Red-Green (RG)	R/G	[64]
	Normalized difference water index (NDWI)	(G − NIR)/(G + NIR)	[84]
	Green chlorophyll vegetation index (GCVI)	NIR/G − 1	[47]
Tasseled cap component	Tasseled cap brightness (TCB)	0.447 × G+0.540 × R + 0.713 × NIR	Proposed in this paper
	Tasseled cap greenness (TCG)	0.699 × NIR − 0.507 × G − 0.504 × R	Proposed in this paper

Notes: NDVI is sensitive to green vegetation even for low vegetation covered areas, and was first used in 1973 by Rouse et al. [86]. EVI2 is sensitive to green vegetation and can simultaneously reduce soil and atmospheric effects [87]. OSAVI is proposed to minimize the effects of soil background [88]. MTVI2 is sensitive to high leaf area index, and relatively insensitive to leaf chlorophyll content and soil effect [89]. RG emphasizes the spectral change in foliage color from green to red [90]. NDWI is sensitive to water features and eliminates the effects of soil and vegetation features [91]. GCVI is related to total pigment concentration in the canopy at plant community level [92]. TCB is sensitive to surface brightness, and TCG is sensitive to vegetation greenness [93].

), which can be derived from three multispectral bands (Near infrared (band 4), Red (band 3), and Green (band 2)) of CBERS-04, and have repeatedly been demonstrated to improve classification accuracy due to sensitivity to vegetation characteristics, insensitivity to soil effect, and the ability to capture both land surface features and the seasonal changes in the growth of vegetation [47,64,81,82,83,84]. Because there are no tasseled cap coefficients for spectral reflectance in the fusion CBERS-04 imagery for deriving the tasseled cap brightness (TCB) and greenness (TCG), the combined coefficients from five-date images used in this study were derived (Table 2) according to the Gram-Schmidt orthogonalization based method used in the previous study [85], and the TCB and TCG components were, thus, produced.

2.3. Random Forest Classification

As described in Section 1, the RF classifier was selected to classify the QVPs in this study. The RF classifier consists of an ensemble of multiple decision trees, each of which is built using a bootstrapped sample of the reference data and is assessed from the remaining sample of the reference data. The RF classifier has four main advantages, such as the small number of parameters that need to be adjusted, a low tendency to over-fit data, no data distribution assumptions that need to be met, and an ability to measure the importance of the input variables. The detailed introduction and theories on the RF classifier can be found in literature [94,95,96]. The RF classification was implemented using the ImageRF embedded in the EnMAP-Box v2.02, which is a freely available processing and analysis toolbox and can be integrated into the ENVI v5.1 classic menu to enhance the range of available applications [97]. The two main tuning parameters in RF, ntree (number of trees to be grown, the default value in ntree = 500) and mtry (number of possible splitting variables to be considered at each tree node, the default value of mtry = the number of the square root of the total predictive variables), were set to their default values because previous studies have demonstrated that the default values are generally a good choice [34,35,98].

The use of combined multi-season images for detecting QVPs has been lacking, and the potential of multi-seasonal CBERS-04 images remain unclear. It is necessary to compare the differences between the data acquisition periods and to find optimal composition periods, classifications were carried out on the CBERS-04 data separately from the five different dates and the twenty-six combined datasets (all possible combinations of the five images were the ten two-season combined images, the ten three-season combined images, the five four-season combined images, and the one five-season combined image) in a multi-date approach. A backward variable removing procedure was used to select the optimal feature datasets for every dataset for building a RF model through an assessment of variable importance produced by the RF model based on mean decrease in classification accuracy and the minimum mean square error calculated from the out-of–bag data and RF model classification accuracy. On the basis of ranking the importance of predictive variables, firstly, the least important predictive variable was removed, and the remaining variables were used to reclassify, then, the second least important predictive variable was removed, and the remaining variables were used to reclassify. This process was repeated until only the three most important predictive variables for single season image (the predictive variables at least containing one variable of every image for multi-season combined images) were left and the classification was stopped. Finally, the variables that can obtain the highest classification accuracy were selected as the predictive variables for the final RF classification model. During the process of classification and accuracy assessment, the same training and validation dataset was used to avoid differences induced by the reference dataset variability. Accuracy assessment of the classification results was presented in a confusion matrix and measured according to the producer’s (PA) and user’s accuracy (UA), overall accuracy (OA), and the Kappa coefficient.

Next a successive identification was performed, where a majority analysis with a 3 × 3 kernel size was first used to match the salt and pepper noise pixels within a large single class with a large single class, followed by a change in the classification to vector analysis in order to separate the QVPs from the non-QVP vegetation based on the thresholds of area (less than 3000 m²) and perimeter/area (less than 0.54), as determined by previous results [16,28,73]. The precision rate (A_d), recall rate (A_r), and F measure (F) were then used to analyze the final detection accuracy of the QVPs; these factors have often been used for performance measures in pattern recognition, information retrieval, machine learning and binary classification [73,99].

3. Results

3.1. Single Season Image

3.1.1. Predictive Variable Importance

The effects of the different predictive variables on the land cover classification results from five single season data are listed in Figure 2. The importance of the predictive variables diverges considerably between the seasons of image acquisition. The best important variable for the classification success was the green band (G) for the early spring month of March, the TCG for the spring and summer months of May–July, and the MTVI2 for the late autumn and winter months of October–December. This reflects the seasonal characteristics of the two-phase mosaic of the study area and the best spectral indices for monitoring them. This may be explained by the fact that in early spring the vegetation begins to grow, and the original spectral bands can reflect the landscape features well. In spring and summer, the vegetation becomes green and dense, and the TCG can better monitor QVPs and bare soils. In late autumn and winter, the vegetation becomes yellow and sparse, and the MTVI2 is sensitive to high leaf area index and relatively insensitive to leaf chlorophyll content and soil effect [81,89], and therefore, can effectively monitor landscape features.

3.1.2. Predictive Variable Selection

The outcome of the predictive variable selection is listed in

Table 3. Variable selection results for the final RF classification model for the five single season datasets.

Dataset	No. Variables	Selected Variables
27 March 2017	3	G, R, TCG
18 May 2017	4	TCB, NIR, G, R
10 July 2016	3	TCB, RG, G
24 October 2015	3 1	R, NIR, G
13 December 2016	3 1	NIR, G, R

¹ Indicates that the overall classification accuracy and Kappa coefficient derived from the original spectral bands are better than those from all twelve predictive variables and the minimum predictive variable datasets.

. Several of the predictive variables were identified as redundant in each of the datasets, and were therefore, removed from the final RF classification model. The number of predictive variables included in the final RF classification models was similar between the five datasets. Another observation was that the green band (G) was included in all of the five final RF classification models. The NDVI, NDWI, EVI2, OSAVI, MTVI2 and GCVI vegetation indices appeared to contribute relatively little to the classification success for all of five datasets. For the late autumn October and the winter December datasets, the three original spectral bands (red, near-infrared, and green bands) were slightly better for RF classification (for the October image, OA = 92.8%, Kappa = 0.890; for the December image, OA = 93.9%, Kappa = 0.906) than all twelve predictive variables and the minimum predictive variable datasets derived from all twelve predictive variables (for the October image, OA = 91.3%, Kappa = 0.867; for the December image, OA = 93.7%, Kappa = 0.903). Therefore, only the three original spectral bands were used in the final RF classification model for the October and December image.

3.1.3. The QVP Classification Results

The overall classification accuracies and Kappa coefficients resulting from the use of the five predictive variable datasets are presented in Figure 3. The results show that land cover classification based on the early spring data acquired on 27 March 2017 (OA = 98.1%, Kappa = 0.971) was more accurate than the classification based on the other four seasonal data. The lowest classification accuracy was obtained from the late autumn data, acquired on 24 October 2015 image (OA = 92.8%, Kappa = 0.890). Due to limited space, only the confusion matrix of the 27 March 2017 is presented in

Table 4. Confusion matrix showing the producer’s and user’s classification accuracies for three land cover classes obtained from the selected early spring (27 March 2017) predictive variable datasets.

Reference Classified	The QVPs	Bare Soil	Water	Sum	Producer’s Accuracy (%)	User’s Accuracy (%)
The QVPs	493	4	0	497	95.5	99.2
Bare soil	23	532	0	555	99.3	95.9
Water	0	0	358	358	100	100
Sum	516	536	358	1410

. The error of commission and omission was mainly because of the confusion between the QVPs and the bare soil, and the error of commission and omission between the QVPs and bodies of water were only found in the May and July images. This may be attributed to growth of aquatic plants during these periods. The error of commission and omission between the bare soil and the bodies of water existed only in the December image.

Through the visual interpretation of the Quickbird image (with a spatial resolution of 0.6 m) carried out with ENVI 5.1 software with the multi-temporal finer spatial resolution images from Google Earth and the multi-temporal CBERS-04 images, we identified 139 QVPs distributed in the study area [16,73], which was used as the correct number of QVPs to calculate the precision rate, recall rate, and F measure for assessing the final detection accuracy of the QVPs. The precision rate, recall rate, and F measure resulting from the use of the five predictive variable datasets are presented in Figure 4, which displays a similar curve to the overall classification accuracies and Kappa coefficients for land cover classification presented in Figure 3. The results show that the QVP detection based on the early spring data acquired on 27 March 2017 (A_d = 56.1%, A_r = 43.2%, F = 0.488) was more accurate than the classification based on the other four seasonal datasets. The lowest detection accuracy was obtained from the late autumn data acquired on the image from the 24 October 2015 (A_d = 40.7%, A_r = 25.2%, F = 0.311).

3.2. Two-Season Combined Images

3.2.1. Predictive Variable Importance and Selection

There were ten combined datasets in a two-season approach. The influence of the different predictive variables on land cover classification results from the ten combined datasets and the outcome of the predictive variable selection are shown in Figure 5 and

Table 5. Variable selection results for the final RF classification model for the ten two-season combined datasets.

Dataset	Selected Variables	No. Variables
March+ May	G5, TCG3, NIR3, TCB5, R5, NIR5, TCB3, GCVI3, NDWI3, G3, GCVI5, OSAVI5, EVI25, NDWI5, NDVI5, NDVI3, R3, EVI23, OSAVI3	19
March + July	TCB7, G7, G3, RG7, TCG3, OSAVI3, EVI23, R3, NDVI3, NIR3, TCB3, GCVI3, NDWI3	13
March + October	OSAVI3, EVI23, R3, NDVI3, TCG3, MTVI23, TCB10, G3, TCB3, NIR3, TCG10, EVI210, MTVI210, OSAVI10, NDVI10, R10, NIR10, GCVI3, GCVI10, NDWI3	20
March + December	EVI23, R3, OSAVI3, NDVI3, TCG3, G3, NIR3, TCB3, RG12, OSAVI12, NDWI12	11
May + July	TCB5, NIR5, G5, G7	4
May + October	TCB5, NIR5, G5, R5, TCB10, RG5, TCG10, MTVI210, R10, NIR10	10
May + December	TCB5, NIR5, G5, NDWI12, R5, GCVI12, RG12, MTVI212, OSAVI12, NDVI12, TCG5, TCG12, NDWI5, RG5, OSAVI5, EVI25, GCVI5, NDVI5	18
July + October	TCB7, R7, G7, TCG10, RG7, NIR7, OSAVI10, NDVI10, MTVI210, EVI210, NDWI10, R10, RG10 1	13
July + December	R7, TCB7, G7, OSAVI12, EVI212, NDVI12, TCG12, NDWI12, NIR7	9
October + December	TCB12, RG12, R12, TCG10, NDWI10, R10, NIR12, GCVI10, TCG12, MTVI212, GCVI12, TCB10, OSAVI10, G10, NDWI12, MTVI210, EVI210, G12, NDVI10, NIR10	20

¹ RG₁₀ is Red-Green spectral index derived from 24 October 2015, where the subscript 10 stands for the acquisition month of 24 October 2015.

. The number of predictive variables included in the final classification models differs considerably between the ten datasets (Table 5). The four datasets, including the March image, showed that the importance of the predictive variables for March was similar to that for May, and was relatively higher than for the July, October, and December images. From the three datasets, including the May image, it appeared that the importance of the predictive variables for May was relatively higher than those for the July, October, and December images. The number of predictive variables for the October and December images, including in the final classification models of the two datasets with the July image, exceeded that associated with the July image. For the October–December combined dataset, the number of predictive variables for the October image exceeded that of the December image. These results demonstrate the different effects that the different seasonal images have on the classification success.

3.2.2. The QVP Classification Results

The overall classification accuracies and Kappa coefficients resulting from the use of the ten predictive variable datasets are presented in Figure 6. The results show that land cover classification based on the combined March–October dataset (OA = 99.4%, Kappa = 0.990) was more accurate than the classification based on the other nine combined two-season datasets. The lowest classification accuracy was obtained from the combined May–December dataset (OA = 96.8%, Kappa = 0.951). Due to limited space, only the confusion matrix of the combined March–October dataset is presented in

Table 6. Confusion matrix showing the producer’s and user’s classification accuracies for three land cover classes obtained from the selected predictive variable datasets of the combined March–October images.

Reference Classified	The QVPs	Bare SOIL	Water	Sum	Producer’s Accuracy (%)	User’s Accuracy (%)
The QVPs	508	1	0	509	98.5	99.8
Bare soil	8	535	0	543	99.8	98.5
Water	0	0	358	358	100	100
Sum	516	536	358	1410

. The error of commission and omission was mainly from the confusion between the QVPs and bare soils.

The precision rate, recall rate, and F measure resulting from the ten combined two-season datasets are presented in Figure 7. The highest precision rate, recall rate, and F measure were from the combined March–December image (A_d = 66.3%), the combined March–July image (A_r = 47.5%), and the combined March–December image (F = 0.528), respectively. The lowest precision rate, recall rate, and F measure were from the combined May–December image (A_d = 37.2%), the combined October–December image (A_r = 23.7%), and the combined October–December image (F = 0.313), respectively. The results show that the detection of QVPs based on the combined March–December image (A_d = 66.3%, A_r = 43.9%, F = 0.528) was more accurate than the classification based on the other nine two-season datasets.

3.3. Three-Season Combined Images

There were ten combined datasets in the three-season approach. The number of predictive variables included in the final RF classification models was 34 for March–May–July, 17 for March–May–October, 35 for March–May–December, 24 for March–July–October, 27 for March–July–December, 25 for March–October–December, 27 for May–July–October, 17 for May–July–December, 35 for May–October–December, and 31 for July–October–December combined datasets, respectively. The overall classification accuracies and Kappa coefficients resulting from the use of the ten predictive variable datasets are presented in Figure 8. The results show that land cover classification based on the combined March–July–December dataset (OA = 99.8%, Kappa = 0.997) was more accurate than the classification based on the other nine combined two-season datasets. The lowest classification accuracy was obtained from the combined March–May–December dataset (OA = 97.0%, Kappa = 0.954). Due to limited space, only the confusion matrix for the combined March–July–December dataset is presented in

Table 7. Confusion matrix showing the producer’s and user’s classification accuracies for three land cover classes obtained from the selected predictive variable datasets of the combined March–July–December images.

Reference Classified	The QVPs	Bare soil	Water	Sum	Producer’s Accuracy (%)	User’s Accuracy (%)
The QVPs	515	2	0	517	99.8	99.6
Bare soil	1	534	0	535	99.6	99.8
Water	0	0	358	358	100	100
Sum	516	536	358	1410

. The error of commission and omission was mainly from the confusion between the QVPs and bare soils.

The precision rate, recall rate, and F measure resulting from the ten combined three-season datasets are presented in Figure 9. The results show that the detection of QVPs based on the combined March–October–December dataset (A_d = 64.0%, A_r = 41.0%, F = 0.500) was more accurate than the classification based on the other nine three-season datasets. The lowest detection accuracy was obtained from the combined Match–May–October dataset (A_d = 37.5%, A_r = 28.1%, F = 0.321).

3.4. Four-Season Combined Images

There were five combined datasets for the four-season approach. The number of predictive variables included in the final RF classification models was 46 for March–May–July–October, 21 for March–May–July–December, 27 for March–May–October–December, 26 for March–July–October–December, and 42 for May–July–October–December, respectively.

The overall classification accuracies and Kappa coefficients resulting from the use of the five predictive variable datasets are presented in Figure 10. The results show that land cover classification based on the combined March–July–October–December dataset (OA = 99.8%, Kappa = 0.997) was more accurate than the classification based on the other four combined two-season datasets. The lowest classification accuracy was obtained from the combined March–May–October–December dataset (OA = 97.8%, Kappa = 0.967). The confusion matrix, Producer’s and User’s accuracies of the three land cover classes from the combined March–July–October–December dataset were similar to those of the combined March–July–December dataset displayed in Table 7. The error of commission and omission was mainly from the confusion between the QVPs and bare soils.

The precision rate, recall rate, and F measure resulting from the five combined four-season datasets are presented in Figure 11. The results show that the QVP detection based on the combined March–July–October–December dataset (A_d = 60.2%, A_r = 40.3%, F = 0.483) was more accurate than the classification based on the other four four-season datasets. The lowest precision rate, recall rate, and F measure were from the combined May–July–October–December dataset (A_d = 38.2%), the combined March–May–July–October dataset (A_r = 26.6%), and the combined March–May–July–October dataset (F = 0.316), respectively.

3.5. Five-Season Combined Image

The number of predictive variables included in the final RF classification models was fifty-eight for the combined five-season dataset. The land cover classification accuracy was OA = 98.7%, Kappa = 0.978. The confusion matrix for the combined March–May–July–October–December dataset is presented in

Table 8. Confusion matrix showing the producer’s and user’s classification accuracies for three land cover classes obtained from the selected predictive variable datasets of the combined March–May–July–October–December images.

Reference Classified	The QVPs	Bare Soil	Water	Sum	Producer’s Accuracy (%)	User’s Accuracy (%)
The QVPs	501	3	0	504	97.1	99.4
Bare soil	15	533	0	548	99.4	97.3
Water	0	0	358	358	100	100
Sum	516	536	358	1410

. The error of commission and omission was mainly from the confusion between the QVPs and bare soils. The precision rate, recall rate, and F measure resulting from the combined five-season dataset were A_d = 37.3%, A_r = 27.3%, and F = 0.315, respectively.

3.6. Comparisons

Table 9. A summary of the QVP classification accuracies from the individual season imagery and season combined images using the random forest classifier.

Index Imagery	OA	Kappa	Precision Rate (%)	Recall Rate (%)	F Measure	No. Predictive Variables
March	98.1	0.971	56.1	43.2	0.488	3
March + October/March + December	99.4	0.990	66.3	43.9	0.528	20/13
March + July + December/March + October + December	99.8	0.997	64.0	41.0	0.500	27/25
March + July + October + December	99.8	0.997	60.2	40.3	0.483	26
March + May + July + October + December	98.7	0.978	37.3	27.3	0.315	58

shows the comparison analyses of the optimal classification results for the five different combinations in the number of seasons using the overall accuracy (OA), Kappa coefficient (Kappa), precision rate, recall rate, and F measure values. The comparison in the results indicates that the influence from the March image is significant. The OA and Kappa values increased slightly from the optimal individual seasonal imagery to season combined image datasets, and the precision rate, recall rate, and F measure values increased moderately, except for those associated with the combined five-season dataset. Finally, the results suggest that the March–December combination dataset was the optimal choice for the detection of QVPs (Figure 12).

4. Discussion

Previous research results for the YRD had demonstrated that different seasonal QVP classification from CBERS-04 imagery had variable accuracy, and that the spring imagery could detect the QVPs more precisely and completely when compared with the other seasonal images [73], but the use of combined multi-season images for detecting QVPs has been lacking. In fact, the use of multi-seasonal images has been demonstrated as statistically important for the mapping of tree species [35,37,38]. The importance of this study was in demonstrating that the seasonal influence in multi-season CBERS-04 images for classifying land cover and detecting QVPs was significant. This study showed that accurate land cover classification can be achieved for the distribution of QVPs in the YRD by applying both single season and multi-seasonal fusion CBERS-04 high spatial resolution (5 m) multispectral images (best result OA = 99.8%, Kappa = 0.997). Errors in the classification mainly existed between the QVPs and the bare soil. However, as in previous studies [16,73], the detection accuracy of the QVPs was low (best result precision rate = 66.3%, recall rate = 47.5%, F measure = 0.528). This low detection accuracy may be attributed to the omission of the smaller size QVPs (less than 3 × 3 pixels), or the coalescence between the QVPs with other QVPs or other vegetation.

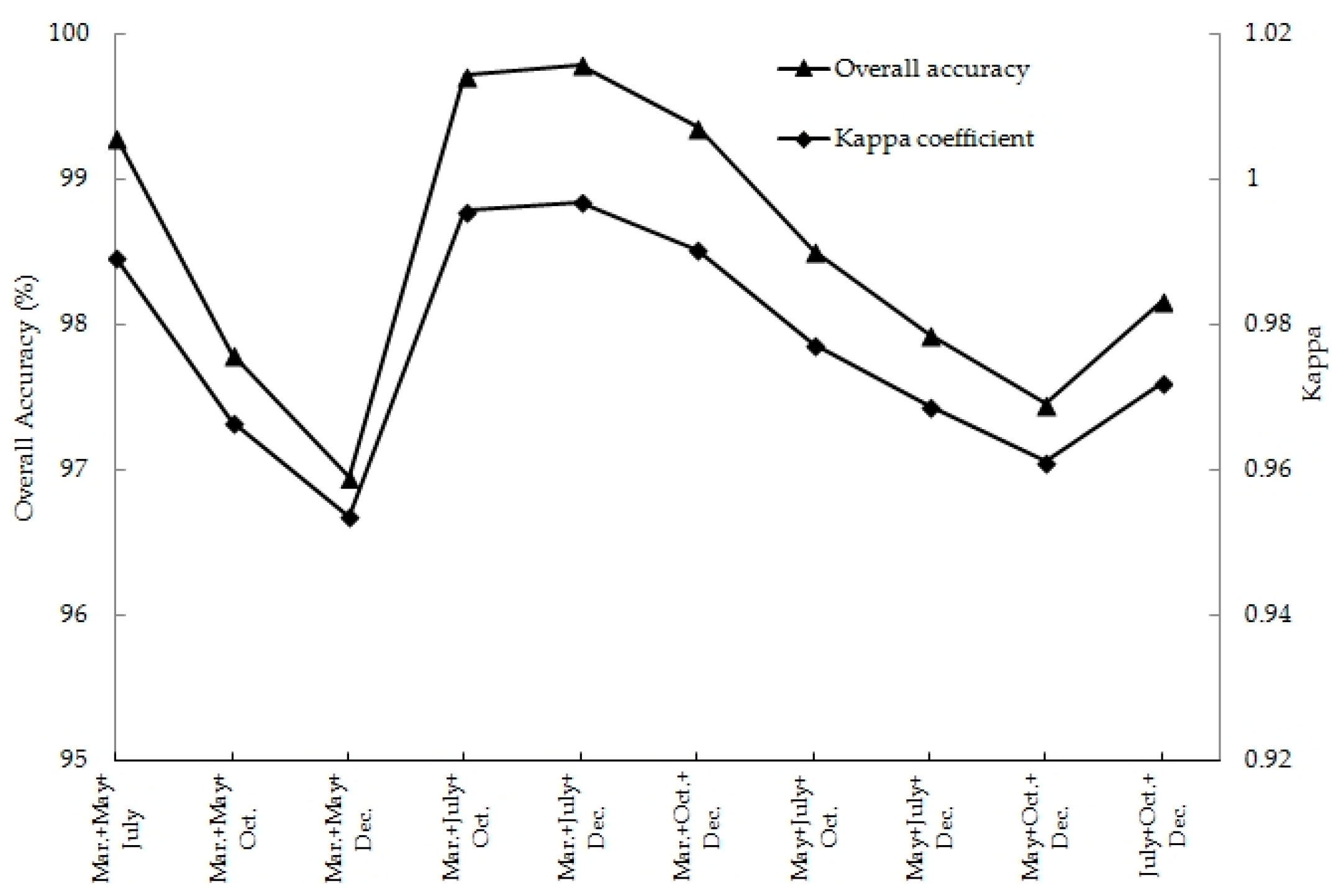
Our comparison analysis demonstrates that both the March image and multi-seasonal fusion CBERS-04 high spatial resolution multispectral images including the March image, can produce high overall classification accuracies for land cover, and the multi-season combined images only increased 0.6–1.7% in overall accuracy as compared to the use of the March image alone. The research result of this study indicated that March and May were more suitable acquisition periods for single date imagery used for land cover mapping and QVP detection in this study area, which was consistent with that of Liu [73]. The reason for the higher accuracies of the spring season classification over the summer season (the peak of growing season of vegetation with the greatest difference between vegetation and bare soil) are unpredictable, but some key observations during the field investigation can be used to explain this phenomenon. (1) Bare soil becomes brighter because of desiccation and soil salt accumulation in the spring, which increases the contrast between QVPs and bare soil, whereas the summer rainfall results in increases in soil moisture, therefore decreasing the contrast between the QVPs and the bare soil. (2) The gap between the QVPs and other strips of vegetation can be blurred due to the coalescence between vegetation elements in either summer or autumn season [73]. For single season imagery, the October (autumn season, the end of growing season of vegetation) produced the lowest overall classification accuracy for land cover, which through visual inspections and comparisons on five images (Figure 13) could be attributed to the small difference between the vegetation and bare soil area and more coalescence between vegetation elements. The highest classification accuracies for land cover from two-season, three-season, and four-season combined datasets were obtained from the May–October (OA = 99.4%), March–July–December (OA = 99.8%), and the March–July–October–December (OA = 99.8%) combined images respectively. The lowest classification accuracies for land cover from two-season, three-season, and four-season combined datasets were obtained from the MayvDecember (OA = 96.8%), March–May–December (OA = 97.0%), and the March–May–October–December (OA = 97.8%) combined images, respectively. These results indicated that adding imagery into classification could help to improve the accuracies for mapping land cover, which is consistent with the previous researches [45,46,55,58], but the increase in accuracy was limited. The March–May–October–December combined data had the lowest classification accuracy of all four-season combined datasets, which indicated that the combined data consisting of images with less contrasts or similar phenological features had the low capability for mapping land cover. It also showed that the combination of different season images with the higher classification accuracy for land cover was not necessarily an optimal combination of multi-season images, whereas the combination of the different season images with the different landscape temporal features, especially the phenological features of vegetation may be an optimal combination of multi-season images, and could further improve the classification accuracy for mapping land cover and detecting the QVPs.

Through one-sample t test analysis on Kappa values in SPSS 19.0 software (SPSS, Chicago, IL., USA), it indicated that the land cover classification results were statistically significant different for among single season images (p = 0.041), among two-season combined data (p = 0.002), and among three-season combined data (p = 0.025), and those from four-season combined data were not statistically significant different (p = 0.243). The independent-samples T test detected statistically significant differences of Kappa values between the single season and two-season (p = 0.039), the single season and three-season (p = 0.025), and the single season and four-season (p = 0.018) combined data, and no significant differences of Kappa values between the other combined data.

In general, the optimal seasonal combination data which had a high accuracy for classifying land cover could produce a high accuracy for detecting the QVPs (shown in Figure 3, Figure 4, Figure 10 and Figure 11). However, for the two-season and three-season combination datasets, the optimal seasonal combination data which had a high accuracy for classifying land cover did not necessarily produce a high accuracy for detecting the QVPs (Figure 6, Figure 7, Figure 8 and Figure 9). The main possible reason may be due to the coalescence between the QVPs and other vegetation elements which made the thresholds of area and shape less effective for detecting the QVPs from land cover map. The March–December spring-winter season combined images had the best result for detecting the QVPs compared to the single season and other multi-season combined images. Except the high difference between the QVPs and bare soil in the two images, one possible reason may be that Tamarix chinensis, one of the main plant species composed of the QVPs, is easier to be identified in late fall and early winter [100]. This is not consistent with the higher classification results for tree species mapping by applying the dry-wet season combined images [35,37,38], which may be due to the different geographical and phenological characteristics, and soil salinization. In general, increasing temporal imagery acquisition frequencies can help to improve the classification accuracies [46,55,58]. However, there still is an optimization of image acquisition timing and frequency for different research objects with different resolution imagery in different regions [58,66]. Our assessment results indicated that the March–December spring-winter season combined images produces optimal multi-season combined data when the multi-season images are to be used for detection of QVPs, and that the combined images including those of more than two seasons could not effectively improve the classification accuracy, which is in line with the conclusion that adding more images could not increase the value for classifying tree species [36]. This finding must be interpreted with caution because there were only five images used in this study.

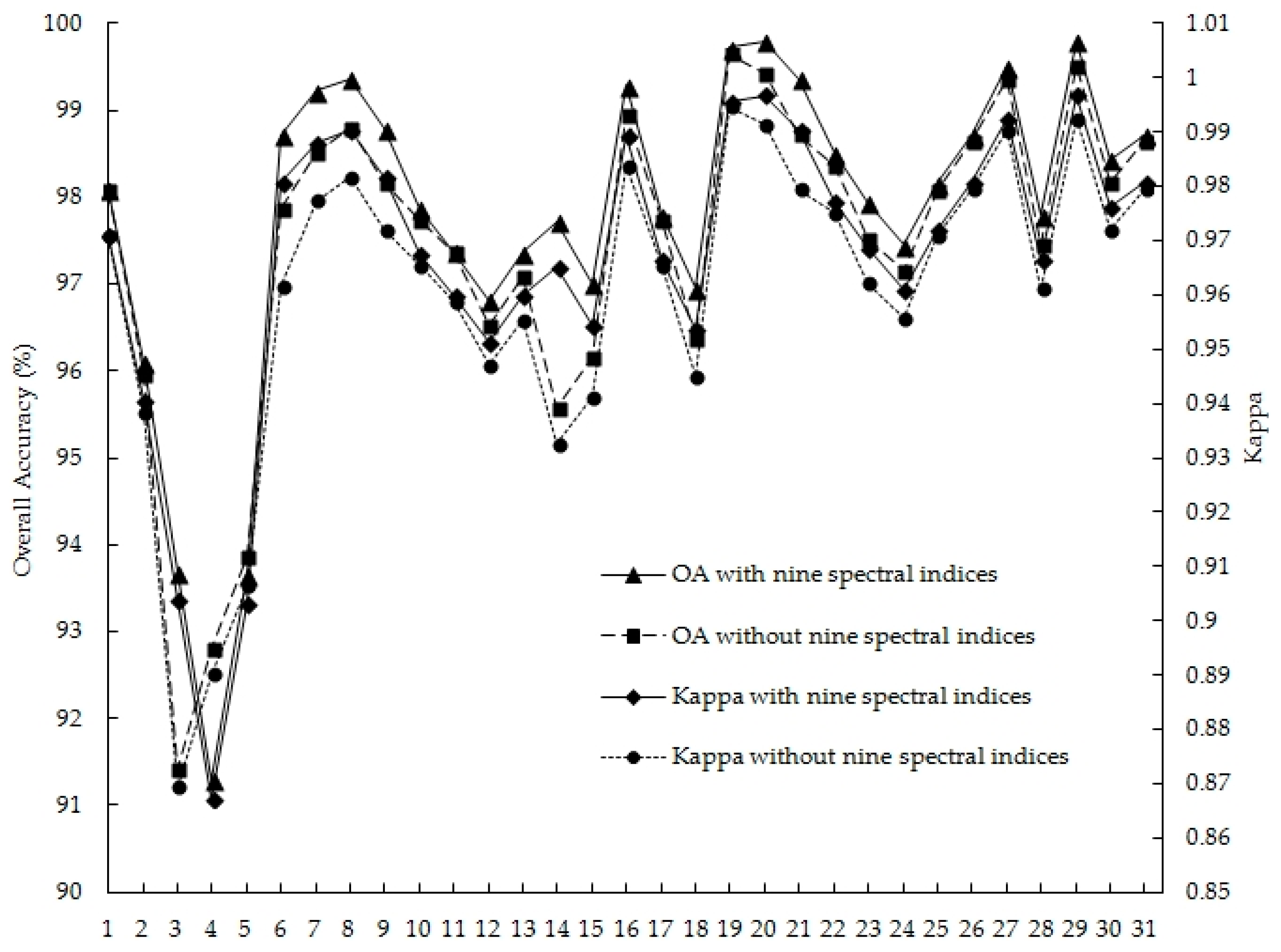
Figure 14 shows the thirty-one pairs of comparison analyses of the optimal classification results for mapping land covers with and without nine spectral indices using the overall accuracy (OA) and Kappa coefficient (Kappa). The optimal classification results for mapping land covers including nine spectral indices had higher OA and Kappa values than those without nine spectral indices, except for the October and December images. However, the difference of 0–2.3% for OA and 0–0.035 for Kappa was small between the thirty-one pairs with and without those indices, and twenty-eight of the thirty-one pairs had less than 1% OA difference and less than 0.02 Kappa difference. The paired-sample t test detected no statistically significant differences of Kappa values between the land cover classification results from the combined data with and without nine spectral indices (p = 0.003). This result indicated that the nine spectral indices derived from the three original spectral bands contributed low value for land cover classification. It must be especially considered that when a classification is to be carried out over a large study area, larger data storage and longer processing times are required.

Although the optimal seasonal CBERS-04 images along with effective predictive variable datasets were used, the low detection accuracies presented in this study are similar to previous research results where the individual seasonal high spatial resolution data, including those from CBERS-04, have been used for detecting QVPs using the OBIA classification with K-Means, KNN and SVM classifiers [16,73]. This indicated that the choice of the classifier itself could not greatly improve the classification accuracy of the QVPs, which is in line with the opinion that the selection of the classifier itself was of low significance if the data is adequate in meeting the demands of the classifier [36].

It is possible to improve QVP mapping through three approaches in the future. (1) Additional texture features are included in the RF classification for the QVPs. Texture features have been proved important in the mapping of invasive Fallopia japonica [32], larch plantations [33], urban tree species [34] and plastic-mulched farmland [101]. (2) The sub-meter level resolution data are applied. When the gaps between QVPs or between QVPs and other strips of vegetation are less than 5 m, or the diameter of a QVP is less than 10 m, the 5 m spatial resolution of CBERS-04 imagery is not enough to detect the QVPs. Therefore, it is necessary to further improve spatial resolution [16,38]. (3) Higher spectral resolution data are applied. The WorldView-2 imagery has higher spectral resolution and unique spectral bands such the red edge band, shortwave bands, and has therefore demonstrated higher accuracy for the classification of tree species than other images with a similar or higher spatial resolution [35,38]. This is therefore a good choice for detecting QVPs in the YRD in the future.

5. Conclusions

This study has investigated the potential of multi-season CBERS-04 imagery for mapping the QVPs commonly found in the YRD, which extends from the Liaohe Delta to the coastal salt marshes in Northern Jiangsu Province, China. Classification was performed using the RF classification approach. Thirty-one different datasets including three spectral bands and nine spectral indices derived from the five fusion 5 m CBERS-04 multispectral images were compared for their capabilities of classifying land covers and detecting QVPs to evaluate the seasonal influences on classification accuracy. The main conclusions resulting from this research are as follows:

The early spring season image (March) produced a higher classification accuracy compared to all other individual season CBERS-04 images.

All of the optimal classifications resulted from the different combinations that include the early spring season image, which indicated that the early spring season image contributed much to classification success.

A typical early spring-winter (December and March) combined CBERS-04 images performed better for mapping the QVPs than the other multi-season combined image datasets.

The five-season combination images (March, May, July, October, and December) had the lowest classification accuracy for mapping QVPs.

Although the optimal classification results including nine spectral indices had higher OA and Kappa values than those without those indices, the improvement in overall accuracy was small. Therefore, the gain in accuracy should be balanced against the increase in processing time and storage space when using the derived spectral indices.

The choice of the classifier itself could not greatly improve classification accuracy from the CBERS-04 imagery. Improved classification accuracy will most likely be achieved through use of the higher spatial and spectral resolution data such as GF-2, WorldView-2, and WordView-3. The improvement in spectral resolution is more important for mapping QVPs than the improvement in spatial resolution.

Our work shows that it is important to choose suitable seasonal imagery for mapping of QVPs. The research results from this study also indicated that there is an optimization of image acquisition timing and frequency, and that adding more seasonal data for mapping the QVPs may not be worth the gain in classification accuracy, and may even reduce the classification accuracy. Future research should focus on (1) comparison analysis based on more seasonal data and more areas, (2) applying higher spatial and spectral resolution imagery to map the QVPs, and (3) map the components and structure of the QVPs, which is important for studying the evolution models of the QVPs.