Tree Height Estimation of Forest Plantation in Mountainous Terrain from Bare-Earth Points Using a DoG-Coupled Radial Basis Function Neural Network
Abstract
:1. Introduction
2. Study Area and Materials
2.1. Test Site
2.2. Field Measurements
2.3. UAV Remotely Sensed Image Acquisition
3. Method
3.1. UAV-Based Photogrammetry
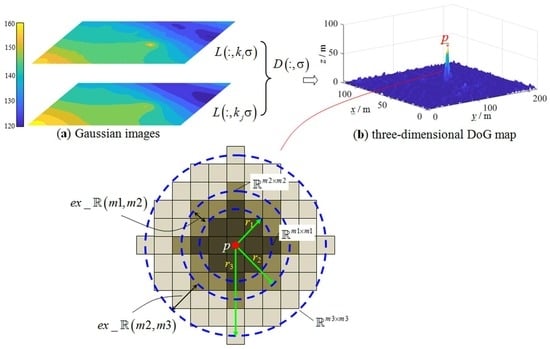
3.2. DTM Generation
| Algorithm 1: RBF neural network against noisy data |
| Parameters: and are the width and height of the DSM, respectively; and correspond to the mean and standard deviation of the height values ; r is the radius centered on candidate ; is a multiple factor; is the residual value; and is a given threshold. |
| Generate the DTM using the RBF neural network from the ground points. |
| Compute the DoG map using the DTM. |
| for to do |
| for to do |
| if is the local maxima or minima, then |
| while !() or !() |
| end while |
| end if |
| if then |
| is regarded as a noisy point. |
| is then derived from the fitted quadratic surface model. |
| Update the height value of the ground points. |
| end if |
| end for |
| end for |
| Generate the DTM using the RBF neural network from the updated ground points again. |
3.3. CHM Generation
3.4. Tree Height Estimation
3.5. Evaluation Criteria for Tree Height Estimation Performance
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tuanmu, M.N.; Viña, A.; Bearer, S.; Xu, W.; Ouyang, Z.; Zhang, H.; Liu, J. Mapping understory vegetation using phenological characteristics derived from remotely sensed data. Remote Sens. Environ. 2010, 114, 1833–1844. [Google Scholar] [CrossRef]
- Takahashi, M.; Shimada, M.; Tadono, T.; Watanabe, M. Calculation of trees height using PRISM-DSM. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 6495–6498. [Google Scholar]
- Lin, Y.; Holopainen, M.; Kankare, V.; Hyyppa, J. Validation of mobile laser scanning for understory tree characterization in urban forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3167–3173. [Google Scholar] [CrossRef]
- Latifi, H.; Heurich, M.; Hartig, F.; Müller, J.; Krzystek, P.; Jehl, H.; Dech, S. Estimating over- and understorey canopy density of temperate mixed stands by airborne LiDAR data. Forestry 2015, 89, 69–81. [Google Scholar] [CrossRef] [Green Version]
- Puliti, S.; Ørka, H.O.; Gobakken, T.; Næsset, E. Inventory of small forest areas using an unmanned aerial system. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Jing, L.; Hu, B.; Li, J.; Noland, T.; Guo, H. Automated tree crown delineation from imagery based on morphological techniques. In Proceedings of the International Symposium on Remote Sensing of Environment, Beijing, China, 22–26 April 2013; pp. 1–6. [Google Scholar]
- Chianucci, F.; Disperati, L.; Guzzi, D.; Bianchini, D.; Nardino, V.; Lastri, C.; Rindinella, A.; Corona, P. Estimation of canopy attributes in beech forests using true colour digital images from a small fixed-wing UAV. Int. J. Appl. Earth Obs. 2016, 47, 60–68. [Google Scholar] [CrossRef] [Green Version]
- Nilson, T. A theoretical analysis of the frequency of gaps in plant stands. Agric. Meteorol. 1971, 8, 25–38. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Chiteculo, V. Determining tree height and crown diameter from high-resolution UAV imagery. Int. J. Remote Sens. 2017, 38, 2392–2410. [Google Scholar] [CrossRef]
- Wing, B.M.; Ritchie, M.W.; Boston, K.; Cohen, W.B.; Gitelman, A.; Olsen, M.J. Prediction of understory vegetation cover with airborne lidar in an interior ponderosa pine forest. Remote Sens. Environ. 2012, 124, 730–741. [Google Scholar] [CrossRef]
- Wallace, L.; Musk, R.; Lucieer, A. An assessment of the repeatability of automatic forest inventory metrics derived from UAV-borne laser scanning data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7160–7169. [Google Scholar] [CrossRef]
- Wallace, L.; Watson, C.; Lucieer, A. Detecting pruning of individual stems using airborne laser scanning data captured from an unmanned aerial vehicle. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 76–85. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. Vertical stratification of forest canopy for segmentation of understory trees within small-footprint airborne LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 130, 385–392. [Google Scholar] [CrossRef] [Green Version]
- Heinzel, J.; Ginzler, C. A single-tree processing framework using terrestrial laser scanning data for detecting forest regeneration. Remote Sens. 2018, 11, 60. [Google Scholar] [CrossRef]
- Korpela, I.; Hovi, A.; Morsdorf, F. Understory trees in airborne LiDAR data—Selective mapping due to transmission losses and echo-triggering mechanisms. Remote Sens. Environ. 2012, 119, 92–104. [Google Scholar] [CrossRef]
- Kükenbrink, D.; Schneider, F.D.; Leiterer, R.; Schaepman, M.E.; Morsdorf, F. Quantification of hidden canopy volume of airborne laser scanning data using a voxel traversal algorithm. Remote Sens. Environ. 2017, 194, 424–436. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A photogrammetric workflow for the creation of a forest canopy height model from small unmanned aerial system imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; Tompalski, P.; Crawford, P.; Day, K.J.K. Updating residual stem volume estimates using ALS- and UAV-acquired stereo-photogrammetric point clouds. Int. J. Remote Sens. 2017, 38, 2938–2953. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J.Y. Evaluation of the newly released worldwide AW3D30 DEM over typical landforms of China using two global DEMs and ICESat/GLAS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4430–4440. [Google Scholar] [CrossRef]
- Selkowitz, D.J.; Green, G.; Peterson, B.; Wylie, B. A multi-sensor lidar, multi-spectral and multi-angular approach for mapping canopy height in boreal forest regions. Remote Sens. Environ. 2012, 121, 458–471. [Google Scholar] [CrossRef]
- Birdal, A.C.; Avdan, U.; Türk, T. Estimating tree heights with images from an unmanned aerial vehicle. Geomat. Nat. Hazards Risk 2017, 8, 1144–1156. [Google Scholar] [CrossRef] [Green Version]
- Hirschmüller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Turner, D.; Lucieer, A.; Watson, C. An automated technique for generating georectified mosaics from ultra-hight resolution unmanned aerial vehicle (UAV) imagery, based on structure from motion (SfM) point clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Javernick, L.; Brasington, J.; Caruso, B. Modeling the topography of shallow braided rivers using Structure-from-Motion photogrammetry. Geomorphology 2014, 213, 166–182. [Google Scholar] [CrossRef]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Cook, K.L. An evaluation of the effectiveness of low-cost UAVs and structure from motion for geomorphic change detection. Geomorphology 2017, 278, 195–208. [Google Scholar] [CrossRef]
- Kattenborn, T.; Sperlich, M.; Bataua, K.; Koch, B. Automatic single tree detection in plantations using UAV-based photogrammetric point clouds. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, ISPRS Technical Commission III Symposium, Zurich, Switzerland, 5–7 September 2014; pp. 139–144. [Google Scholar]
- Qiu, Z.; Feng, Z.K.; Wang, M.; Li, Z.; Lu, C. Application of UAV photogrammetric system for monitoring ancient tree communities in Beijing. Forests 2018, 9, 735. [Google Scholar] [CrossRef]
- Krause, S.; Sanders, T.G.M.; Mund, J.P.; Greve, K. UAV-based photogrammetric tree height measurement for intensive forest monitoring. Remote Sens. 2019, 11, 758. [Google Scholar] [CrossRef]
- Marques, P.; Pádua, L.; Adão, T.; Hruška, J.; Peres, E.; Sousa, A.; Sousa, J.J. UAV-based automatic detection and monitoring of chestnut trees. Remote Sens. 2019, 11, 855. [Google Scholar] [CrossRef]
- Sirmacek, B.; Unsalan, C. Damaged building detection in aerial images using shadow information. In Proceedings of the International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 11–13 June 2009; pp. 249–252. [Google Scholar]
- Bullinaria, J.A. Radial basis function networks: Introduction. Neural Comput. Lect. 2004, 13, L13-2–L13-16. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with Lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 2003, 29, 564–577. [Google Scholar] [CrossRef]
- DJI. Phantom 4 Pro/Pro+ User Manual. 2018. Available online: https://dl.djicdn.com/downloads/phantom_4_pro/Phantom+4+Pro+Pro+Plus+User+Manual+v1.0.pdf (accessed on 5 June 2018).
- Open Source Computer Vision Library (OpenCV). 2018. Available online: https://opencv.org/ (accessed on 5 June 2018).
- He, H.; Chen, X.; Liu, B.; Lv, Z. A sub-Harris operator coupled with SIFT for fast images matching in low-altitude photogrammetry. Int. J. Signal Process. Image Process. Pattern Recognit. 2014, 7, 395–406. [Google Scholar] [CrossRef]
- sba: A Generic Sparse Bundle Adjustment C/C++ Package. 2018. Available online: http://users.ics.forth.gr/~lourakis/sba/ (accessed on 5 June 2018).
- Booth, D.T.; Cox, S.E.; Meikle, T.W.; Fitzgerald, C. The accuracy of ground-cover measurements. Rangel. Ecol. Manag. 2006, 59, 179–188. [Google Scholar] [CrossRef]
- He, H.; Zhou, J.; Chen, M.; Chen, T.; Li, D.; Cheng, P. Building extraction from UAV images jointly using 6D-SLIC and multiscale Siamese convolutional networks. Remote Sens. 2019, 11, 1040. [Google Scholar] [CrossRef]
- Schwenker, F.; Kestler, H.A.; Palm, G. Three learning phases for radial-basis-function networks. Neural Netw. 2001, 14, 439–458. [Google Scholar] [CrossRef]
- Lowe, D. Object recognition from local scale-invariant features. In Proceedings of the 7th IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; p. 1150. [Google Scholar]
- Tonkin, T.N.; Midgley, N.G.; Graham, D.J.; Labadz, J.C. The potential of small unmanned aircraft systems and structure-from-motion for topographic surveys: A test of emerging integrated approaches at Cwm Idwal, North Wales. Geomorphology 2014, 226, 35–43. [Google Scholar] [CrossRef] [Green Version]
- Long, N.; Millescamps, B.; Guillot, B.; Pouget, F.; Bertin, X. Monitoring the topography of a dynamic tidal inlet using UAV imagery. Remote Sens. 2016, 8, 387. [Google Scholar] [CrossRef]
- Koci, J.; Jarihani, B.; Leon, J.X.; Sidle, R.C.; Wilkinson, S.N.; Bartley, R. Assessment of UAV and ground-based structure from motion with multi-view stereo photogrammetry in a gullied savanna catchment. ISPRS Int. J. Geo-Inf. 2017, 6, 328. [Google Scholar] [CrossRef]
- Gindraux, S.; Boesch, R.; Farinotti, D. Accuracy assessment of digital surface models from unmanned aerial vehicles’ imagery on glaciers. Remote Sens. 2017, 9, 186. [Google Scholar] [CrossRef]
- Gonçalves, G.R.; Pérez, J.A.; Duarte, J. Accuracy and effectiveness of low cost UASs and open source photogrammetric software for foredunes mapping. Int. J. Remote Sens. 2018, 39, 5059–5077. [Google Scholar] [CrossRef]












| Parameters | Value |
|---|---|
| Image size | 4000 × 3000 |
| 2687.62 | |
| 2686.15 | |
| 1974.34 | |
| 1496.10 | |
| −0.13097076 | |
| 0.10007409 | |
| 0.00141688 | |
| −0.00020433 |
| Site | RMSE X (cm) | RMSE Y (cm) | RMSE Z (cm) | Total RMSE (cm) |
|---|---|---|---|---|
| Plantation 1 | 4.61 | 5.12 | 9.77 | 6.79 |
| Plantation 2 | 5.37 | 5.62 | 8.70 | 6.63 |
| Study | Terrain Characteristic | Platform | AGL (m) | Height RMSE (cm) |
|---|---|---|---|---|
| Tonkin et al., 2014 [43] | Moraine–mound | Hexacopter | 117 | 51.7 |
| Long et al., 2016 [44] | Coastal | Fixed-wing | 149 | 17 |
| Koci et al., 2017 [45] | Gullied | Quadcopter | 86/97/99 | >30 |
| Gindraux et al., 2017 [46] | Glacier | Fixed-wing | 115 | 10–25 |
| Gonçalves et al., 2018 [47] | Dune | Quadcopter | 80/100 | 12 |
| Our study | Mountainous | Quadcopter | 120 | 9.24 |
| Plantation 1 | Plantation 2 | |||
|---|---|---|---|---|
| Measured Height | Estimated Height | Measured Height | Estimated Height | |
| min | 11.70 | 10.84 | 11.94 | 11.69 |
| p25 | 14.68 | 13.19 | 16.83 | 15.39 |
| median | 16.83 | 17.16 | 19.48 | 19.62 |
| p75 | 19.57 | 20.34 | 22.64 | 22.48 |
| max | 26.73 | 27.08 | 26.83 | 29.62 |
| mean | 17.52 | 17.31 | 19.60 | 19.46 |
| std | 3.85 | 4.20 | 4.31 | 4.84 |
| MAE | 1.45 | 1.73 | ||
| ① | ② | Ours | |
|---|---|---|---|
| Plantation 1 | 2.80 | 2.19 | 1.95 |
| Plantation 2 | 2.74 | 2.31 | 2.02 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Yan, Y.; Chen, T.; Cheng, P. Tree Height Estimation of Forest Plantation in Mountainous Terrain from Bare-Earth Points Using a DoG-Coupled Radial Basis Function Neural Network. Remote Sens. 2019, 11, 1271. https://doi.org/10.3390/rs11111271
He H, Yan Y, Chen T, Cheng P. Tree Height Estimation of Forest Plantation in Mountainous Terrain from Bare-Earth Points Using a DoG-Coupled Radial Basis Function Neural Network. Remote Sensing. 2019; 11(11):1271. https://doi.org/10.3390/rs11111271
Chicago/Turabian StyleHe, Haiqing, Yeli Yan, Ting Chen, and Penggen Cheng. 2019. "Tree Height Estimation of Forest Plantation in Mountainous Terrain from Bare-Earth Points Using a DoG-Coupled Radial Basis Function Neural Network" Remote Sensing 11, no. 11: 1271. https://doi.org/10.3390/rs11111271
APA StyleHe, H., Yan, Y., Chen, T., & Cheng, P. (2019). Tree Height Estimation of Forest Plantation in Mountainous Terrain from Bare-Earth Points Using a DoG-Coupled Radial Basis Function Neural Network. Remote Sensing, 11(11), 1271. https://doi.org/10.3390/rs11111271