Comparing Remotely-Sensed Surface Energy Balance Evapotranspiration Estimates in Heterogeneous and Data-Limited Regions: A Case Study of Tanzania’s Kilombero Valley
Abstract
1. Introduction
2. Materials and Methods
2.1. Kilombero Valley (KV) River Basin: Site Description and Ancillary Datasets
2.2. Overview of Remotely-Sensed Surface Energy Balance Products
2.2.1. MODIS Program
2.2.2. Preprocessing of MODIS Land Products
2.3. The Surface Energy Balance Algorithm for Land model
2.3.1. Net Radiation (Rn)
2.3.2. Soil Heat Flux (G)
2.3.3. Sensible Heat Flux (H)
2.3.4. Instantaneous Evaporative Fraction ()
2.3.5. The Daily (24-Hour) Actual ET ()
2.4. The Operational Simplified Surface Energy Balance Model
2.5. The Simplified Surface Energy Balance Index Model
2.6. Model Implementation and Comparison
3. Results
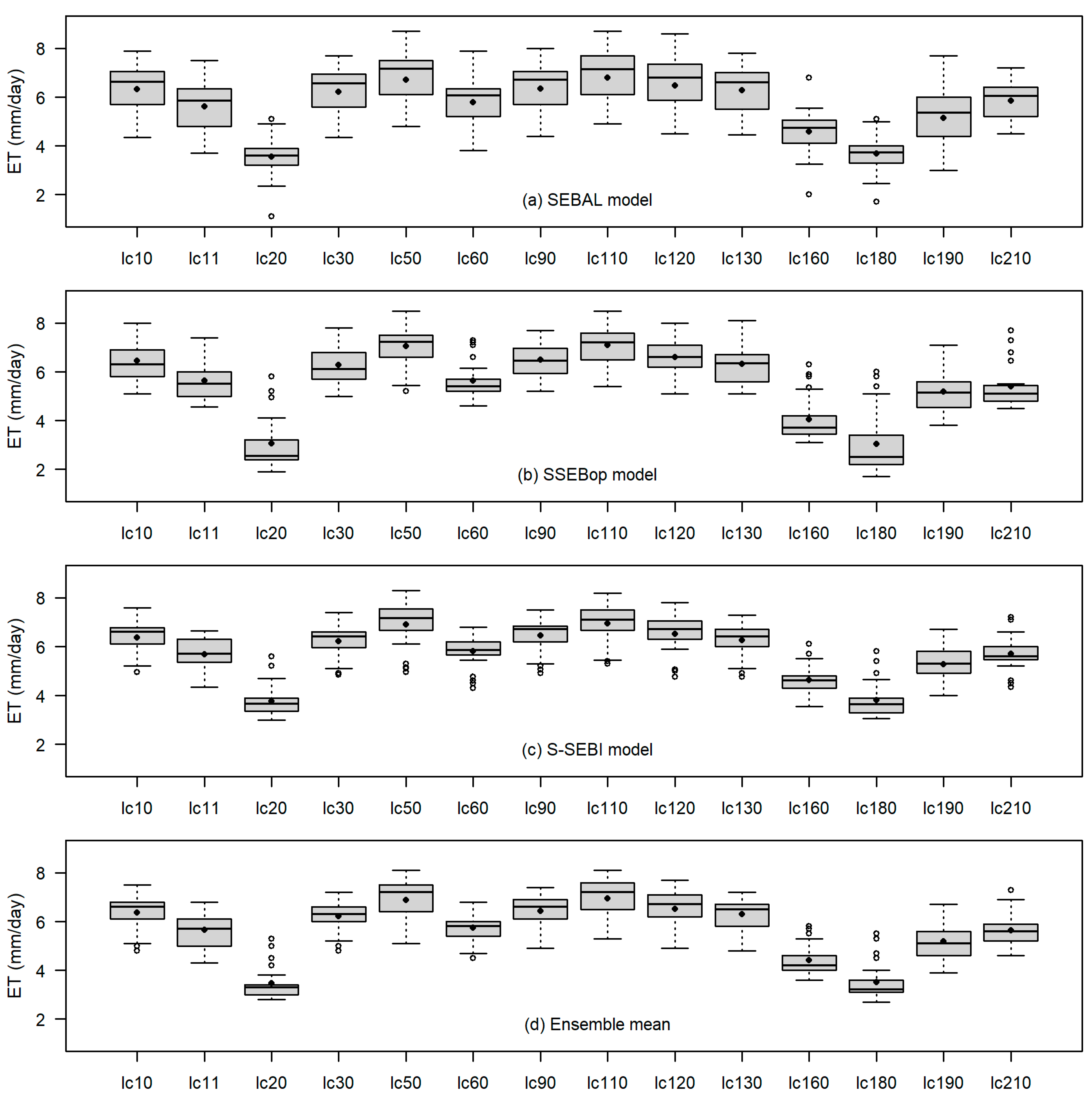
3.1. Actual ET Comparisons Based on Land Cover Classes
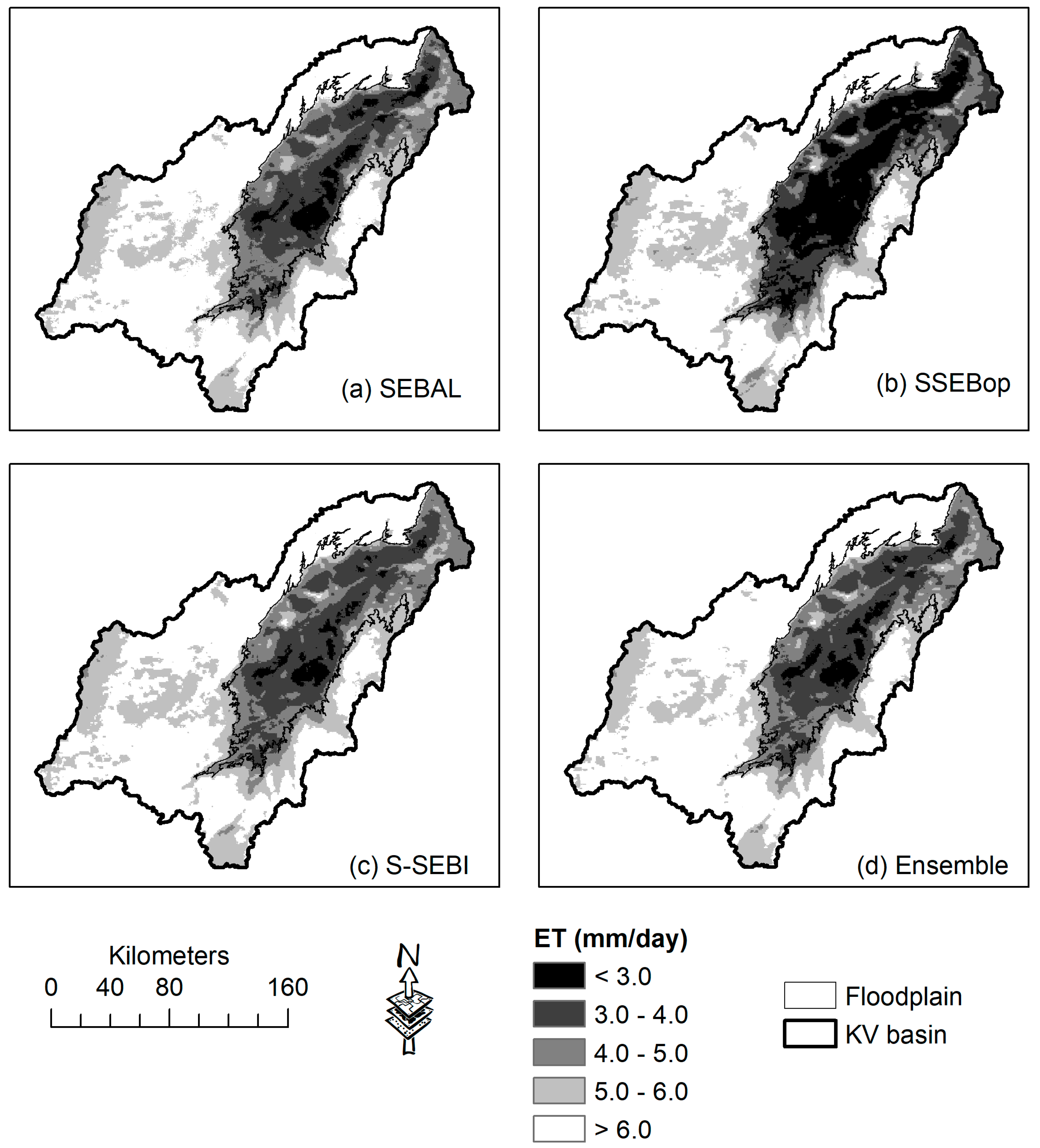
3.2. Graphical and Visual Comparisons of the Actual ET
3.3. Pre-Post SAGCOT Comparisons of the Actual ET
Pre-post SAGCOT Comparisons across Land Cover Classes
4. Discussion
4.1. Implications for Sustainability of a Ramsar site (Kilombero Valley Floodplain)
4.2. On the Applicability of the Approach
4.3. On Limitations and Potential Uncertainties of ET Estimates
4.4. Implications for Hydrological Modeling
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Katul, G.G.; Oren, R.; Manzoni, S.; Higgins, C.; Parlange, M.B. Evapotranspiration: A process driving mass transport and energy exchange in the soil-plant-atmosphere-climate system. Rev. Geophys. 2012, 50, RG3002. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Burba, G.G.; Verma, S.B. Seasonal and interannual variability in evapotranspiration of native tallgrass prairie and cultivated wheat ecosystems. Agric. For. Meteorol. 2005, 135, 190–201. [Google Scholar] [CrossRef]
- Kiptala, J.K.; Mohamed, Y.; Mul, M.L.; Van Der Zaag, P. Mapping evapotranspiration trends using MODIS and SEBAL model in a data scarce and heterogeneous landscape in Eastern Africa. Water Resour. Res. 2013, 49, 8495–8510. [Google Scholar] [CrossRef]
- Alemayehu, T.; van Griensven, A.; Senay, G.B.; Bauwens, W. Evapotranspiration Mapping in a Heterogeneous Landscape Using Remote Sensing and Global Weather Datasets: Application to the Mara Basin, East Africa. Remote Sens. 2017, 9, 390. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. Atmos. 2007, 112, D10117. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Ahmad, M.-U.-D.; Chemin, Y. Satellite surveillance of evaporative depletion across the Indus Basin. Water Resour. Res. 2002, 38, 91–99. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: II. Recommended documentation. Agric. Water Manag. 2011, 98, 921–929. [Google Scholar] [CrossRef]
- Jaramillo, F.; Destouni, G. Developing water change spectra and distinguishing change drivers worldwide. Geophys. Res. Lett. 2014, 41, 8377–8386. [Google Scholar] [CrossRef]
- Yang, Y.; Shang, S.; Jiang, L. Remote sensing temporal and spatial patterns of evapotranspiration and the responses to water management in a large irrigation district of North China. Agric. For. Meteorol. 2012, 164, 112–122. [Google Scholar] [CrossRef]
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef]
- Wright, J.L. New evapotranspiration crop coefficients. J. Irrig. Drain. Div. ASCE 1982, 108, 57–74. [Google Scholar]
- Zhang, B.; Kang, S.; Li, F.; Zhang, L. Comparison of three evapotranspiration models to Bowen ratio-energy balance method for a vineyard in an arid desert region of northwest China. Agric. For. Meteorol. 2008, 148, 1629–1640. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional Evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth Part B Hydrol. Oceans Atmos. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Gowda, P.H.; Chavez, J.L.; Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. ET mapping for Agric. Water Manag.: Present status and challenges. Irrig. Sci. 2008, 26, 223–237. [Google Scholar] [CrossRef]
- Karimi, P.; Bastiaanssen, W.G.M. Spatial evapotranspiration, rainfall and land use data in water accounting—Part 1: Review of the accuracy of the remote sensing data. Hydrol. Earth Syst. Sci. 2015, 19, 507–532. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Tr. Akad. Nauk SSSR Geophiz. Inst. 1954, 24, 163–187. [Google Scholar]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Senkondo, W.; Tumbo, M.; Lyon, S.W. On the evolution of hydrological modelling for water resources in Eastern Africa. CAB Rev. 2018, 13, 1–26. [Google Scholar] [CrossRef]
- Alavaisha, E.; Lyon, S.W.; Lindborg, R. Assessment of Water Quality across Irrigation Schemes: A Case Study of Wetland Agriculture Impacts in Kilombero Valley, Tanzania. Water (Switzerland) 2019, 11, 671. [Google Scholar] [CrossRef]
- Koutsouris, A.J.; Chen, D.; Lyon, S.W. Comparing global precipitation data sets in eastern Africa: A case study of Kilombero Valley, Tanzania. Int. J. Climatol. 2016, 36, 2000–2014. [Google Scholar] [CrossRef]
- Koutsouris, A.J.; Lyon, S.W. Advancing understanding in data-limited conditions: Estimating contributions to streamflow across Tanzania’s rapidly developing kilombero valley. Hydrol. Sci. J. 2018, 63, 197–209. [Google Scholar] [CrossRef]
- Näschen, K.; Diekkrüger, B.; Leemhuis, C.; Steinbach, S.; Seregina, L.S.; Thonfeld, F.; van der Linden, R. Hydrological modeling in data-scarce catchments: The Kilombero floodplain in Tanzania. Water (Switzerland) 2018, 10, 599. [Google Scholar] [CrossRef]
- Lyon, S.W.; Koutsouris, A.; Scheibler, F.; Jarsjo, J.; Mbanguka, R.; Tumbo, M.; Robert, K.K.; Sharma, A.N.; van der Velde, Y. Interpreting characteristic drainage timescale variability across Kilombero Valley, Tanzania. Hydrol. Process. 2015, 29, 1912–1924. [Google Scholar] [CrossRef]
- Bonarius, H. Physical Properties of Soils in the Kilombero Valley (Tanzania); German Agency for Technical Cooperation (GTZ): Eschborn, Germany, 1975; p. 36.
- Leemhuis, C.; Thonfeld, F.; Näschen, K.; Steinbach, S.; Muro, J.; Strauch, A.; López, A.; Daconto, G.; Games, I.; Diekkrüger, B. Sustainability in the food-water-ecosystem nexus: The role of land use and land cover change for water resources and ecosystems in the Kilombero Wetland, Tanzania. Sustainability (Switzerland) 2017, 9, 1513. [Google Scholar] [CrossRef]
- Beck, A.D. The Kilombero valley of South-Central Tanganyika. East Afr. Geograph. Rev. 1964, 2, 37–43. [Google Scholar]
- Senkondo, W.; Tuwa, J.; Koutsouris, A.; Tumbo, M.; Lyon, S.W. Estimating aquifer transmissivity using the recession-curve-displacement method in Tanzania’s Kilombero valley. Water (Switzerland) 2017, 9, 948. [Google Scholar] [CrossRef]
- McClain, M.E.; Williams, K. Environmental Flows in Rufiji River Basin Assessed from the Perspective of Planned Development in Kilombero and Lower Rufiji Sub-Basins; CDM International, Inc. (CDM Smith): Boston, MA, USA, 2016; p. 148. [Google Scholar]
- Burghof, S.; Gabiri, G.; Stumpp, C.; Chesnaux, R.; Reichert, B. Development of a hydrogeological conceptual wetland model in the data-scarce north-eastern region of Kilombero Valley, Tanzania. Hydrogeol. J. 2018, 26, 267–284. [Google Scholar] [CrossRef]
- Dewitte, O.; Jones, A.; Spaargaren, O.; Breuning-Madsen, H.; Brossard, M.; Dampha, A.; Deckers, J.; Gallali, T.; Hallett, S.; Jones, R.; et al. Harmonisation of the soil map of africa at the continental scale. Geoderma 2013, 211–212, 138–153. [Google Scholar] [CrossRef]
- Al Zayed, I.S.; Elagib, N.A.; Ribbe, L.; Heinrich, J. Satellite-based evapotranspiration over Gezira Irrigation Scheme, Sudan: A comparative study. Agric. Water Manag. 2016, 177, 66–76. [Google Scholar] [CrossRef]
- Bhattarai, N.; Shaw, S.B.; Quackenbush, L.J.; Im, J.; Niraula, R. Evaluating five remote sensing based single-source surface energy balance models for estimating daily evapotranspiration in a humid subtropical climate. Int. J. Appl. Earth Observ. Geoinf. 2016, 49, 75–86. [Google Scholar] [CrossRef]
- Singh, R.K.; Senay, G.B. Comparison of four different energy balance models for estimating EvapoTranspiration in the Midwestern United States. Water (Switzerland) 2016, 8, 9. [Google Scholar] [CrossRef]
- Wagle, P.; Bhattarai, N.; Gowda, P.H.; Kakani, V.G. Performance of five surface energy balance models for estimating daily evapotranspiration in high biomass sorghum. ISPRS J. Photogramm. Remote Sens. 2017, 128, 192–203. [Google Scholar] [CrossRef]
- Kite, G.W.; Droogers, P. Comparing evapotranspiration estimates from satellites, hydrological models and field data. J. Hydrol. 2000, 229, 3–18. [Google Scholar] [CrossRef]
- Mohamed, Y.A.; Bastiaanssen, W.G.M.; Savenije, H.H.G. Spatial variability of evaporation and moisture storage in the swamps of the upper Nile studied by remote sensing techniques. J. Hydrol. 2004, 289, 145–164. [Google Scholar] [CrossRef]
- Mahmoud, S.H.; Alazba, A.A. A coupled remote sensing and the Surface Energy Balance based algorithms to estimate actual evapotranspiration over the western and southern regions of Saudi Arabia. J. Asian Earth Sci. 2016, 124, 269–283. [Google Scholar] [CrossRef]
- Sun, Z.; Wei, B.; Su, W.; Shen, W.; Wang, C.; You, D.; Liu, Z. Evapotranspiration estimation based on the SEBAL model in the Nansi Lake Wetland of China. Math. Comput. Model. 2011, 54, 1086–1092. [Google Scholar] [CrossRef]
- Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.; Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS Land data processing and product status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Roy, D.P.; Borak, J.S.; Devadiga, S.; Wolfe, R.E.; Zheng, M.; Descloitres, J. The MODIS Land product quality assessment approach. Remote Sens. Environ. 2002, 83, 62–76. [Google Scholar] [CrossRef]
- Van Der Kwast, J.; Timmermans, W.; Gieske, A.; Su, Z.; Olioso, A.; Jia, L.; Elbers, J.; Karssenberg, D.; De Jong, S. Evaluation of the Surface Energy Balance System (SEBS) applied to ASTER imagery with flux-measurements at the SPARC 2004 site (Barrax, Spain). Hydrol. Earth Syst. Sci. 2009, 13, 1337–1347. [Google Scholar] [CrossRef]
- Colditz, R.R.; Conrad, C.; Wehrmann, T.; Schmidt, M.; Dech, S. TiSeG: A flexible software tool for time-series generation of MODIS data utilizing the quality assessment science data set. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3296–3308. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Chen, K.-S.; Jia, Y.; Li, C.; Sun, X. Spatial-scale effect on the SEBAL model for evapotranspiration estimation using remote sensing data. Agric. For. Meteorol. 2013, 174–175, 28–42. [Google Scholar] [CrossRef]
- Conrad, C.; Dech, S.W.; Hafeez, M.; Lamers, J.; Martius, C.; Strunz, G. Mapping and assessing water use in a Central Asian irrigation system by utilizing MODIS remote sensing products. Irrig. Drain. Syst. 2007, 21, 197–218. [Google Scholar] [CrossRef]
- Hijmans, R.J. Raster: Geographic Analysis and Modeling with Raster Data. R Package Version 2.8-4. Available online: https://cran.r-project.org/web/packages/raster/ (accessed on 14 December 2018).
- Weiss, D.J.; Atkinson, P.M.; Bhatt, S.; Mappin, B.; Hay, S.I.; Gething, P.W. An effective approach for gap-filling continental scale remotely sensed time-series. ISPRS J. Photogramm. Remote Sens. 2014, 98, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Zeng, C.; Shen, H.; Zhang, L. Recovering missing pixels for Landsat ETM+ SLC-off imagery using multi-temporal regression analysis and a regularization method. Remote Sens. Environ. 2013, 131, 182–194. [Google Scholar] [CrossRef]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Teixeira, A.H.d.C.; Bastiaanssen, W.G.M.; Ahmad, M.D.; Bos, M.G. Reviewing SEBAL input parameters for assessing evapotranspiration and water productivity for the Low-Middle São Francisco River basin, Brazil. Part A: Calibration and validation. Agric. For. Meteorol. 2009, 149, 462–476. [Google Scholar] [CrossRef]
- Chen, H.; Huo, Z.; Dai, X.; Ma, S.; Xu, X.; Huang, G. Impact of agricultural water-saving practices on regional evapotranspiration: The role of groundwater in sustainable agriculture in arid and semi-arid areas. Agric. For. Meteorol. 2018, 263, 156–168. [Google Scholar] [CrossRef]
- French, A.N.; Jacob, F.; Anderson, M.C.; Kustas, W.P.; Timmermans, W.; Gieske, A.; Su, Z.; Su, H.; McCabe, M.F.; Li, F.; et al. Surface energy fluxes with the Advanced Spaceborne Thermal Emission and Reflection radiometer (ASTER) at the Iowa 2002 SMACEX site (USA). Remote Sens. Environ. 2005, 99, 55–65. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res. 2013, 49, 2601–2618. [Google Scholar] [CrossRef]
- Wang, Z.; Mao, D.; Li, L.; Jia, M.; Dong, Z.; Miao, Z.; Ren, C.; Song, C. Quantifying changes in multiple ecosystem services during 1992–2012 in the Sanjiang Plain of China. Sci. Total Environ. 2015, 514, 119–130. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.; Irmak, A.; Trezza, R.; Hendrickx, J.M.H.; Bastiaanssen, W.; Kjaersgaard, J. Satellite-based ET estimation in agriculture using SEBAL and METRIC. Hydrol. Process. 2011, 25, 4011–4027. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X.; Yang, K.; Zhou, J. Assessing the impacts of an ecological water diversion project on water consumption through high-resolution estimations of actual evapotranspiration in the downstream regions of the Heihe River Basin, China. Agric. For. Meteorol. 2018, 249, 210–227. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Farah, H.O.; Bastiaanssen, W.G.M. Impact of spatial variations of land surface parameters on regional evaporation: A case study with remote sensing data. Hydrol. Process. 2001, 15, 1585–1607. [Google Scholar] [CrossRef]
- Owusu, G. Sebkc: The Surface Energy Balance and Crop Coefficient Estimation with R. R Package Version 1.0-1. Available online: https://rdrr.io/github/gowusu/sebkc/ (accessed on 14 December 2018).
- Allen, R.G.; Burnett, B.; Kramber, W.; Huntington, J.; Kjaersgaard, J.; Kilic, A.; Kelly, C.; Trezza, R. Automated calibration of the METRIC-Landsat evapotranspiration process. J. Am. Water Resources Assoc. 2013, 49, 563–576. [Google Scholar] [CrossRef]
- Bhattarai, N.; Quackenbush, L.J.; Im, J.; Shaw, S.B. A new optimized algorithm for automating endmember pixel selection in the SEBAL and METRIC models. Remote Sens. Environ. 2017, 196, 178–192. [Google Scholar] [CrossRef]
- Brutsaert, W.; Sugita, M. Application of self-preservation in the diurnal evolution of the surface energy budget to determine daily evaporation. J. Geophys. Res. 1992, 97, 18377–18382. [Google Scholar] [CrossRef]
- Farah, H.O.; Bastiaanssen, W.G.M.; Feddes, R.A. Evaluation of the temporal variability of the evaporative fraction in a tropical watershed. Int. J. Appl. Earth Observ. Geoinf. 2004, 5, 129–140. [Google Scholar] [CrossRef]
- Peng, J.; Borsche, M.; Liu, Y.; Loew, A. How representative are instantaneous evaporative fraction measurements of daytime fluxes? Hydrol. Earth Syst. Sci. 2013, 17, 3913–3919. [Google Scholar] [CrossRef]
- Singh, R.K.; Irmak, A.; Irmak, S.; Martin, D.L. Application of SEBAL model for mapping evapotranspiration and estimating surface energy fluxes in South-Central Nebraska. J. Irrig. Drain. Eng. 2008, 134, 273–285. [Google Scholar] [CrossRef]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
- Muthuwatta, L.P.; Ahmad, M.-U.-D.; Bos, M.G.; Rientjes, T.H.M. Assessment of water availability and consumption in the Karkheh river basin, Iran-using remote sensing and geo-statistics. Water Resources Manag. 2010, 24, 459–484. [Google Scholar] [CrossRef]
- Chen, M.; Senay, G.B.; Singh, R.K.; Verdin, J.P. Uncertainty analysis of the Operational Simplified Surface Energy Balance (SSEBop) model at multiple flux tower sites. J. Hydrol. 2016, 536, 384–399. [Google Scholar] [CrossRef]
- ASCE-EWRI. The ASCE Standardized Reference Evapotranspiration Equation: ASCE-EWRI Standardization of Reference Evapotranspiration Task Committe Report; ASCE: Reston, VA, USA, 2005. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; p. 15. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Levene, H. Contributions to Probability and Statistics; Stanford University Press: Redwood City, CA, USA, 1960. [Google Scholar]
- Khan, M.S.; Coulibaly, P.; Dibike, Y. Uncertainty analysis of statistical downscaling methods. J. Hydrol. 2006, 319, 357–382. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Munishi-Kongo, S. Ground and Satellite-Based Assessment of Hydrological Responses to land cover change in the Kilombero river basin, Tanzania. Ph.D. Dissertation, University of KwaZulu-Natal, Pietermaritzburg, South Africa, 2013. [Google Scholar]
- Mombo, F.M.; Speelman, S.; Huylenbroeck, G.V.; Hella, J.; Pantaleo, M.; Moe, S. Ratification of the Ramsar convention and sustainable wetlands management: Situation analysis of the Kilombero Valley wetlands in Tanzania. J. Agric. Ext. R. Dev. 2011, 3, 153–164. [Google Scholar]
- Seki, H.A.; Shirima, D.D.; Courtney Mustaphi, C.J.; Marchant, R.; Munishi, P.K.T. The impact of land use and land cover change on biodiversity within and adjacent to Kibasira Swamp in Kilombero Valley, Tanzania. Afr. J. Ecol. 2017, 56, 518–527. [Google Scholar] [CrossRef]
- Alemu, H.; Senay, G.B.; Kaptue, A.T.; Kovalskyy, V. Evapotranspiration variability and its association with vegetation dynamics in the Nile Basin, 2002–2011. Remote Sens. 2014, 6, 5885–5908. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Alemayehu, T.; Van Griensven, A.; Woldegiorgis, B.T.; Bauwens, W. An improved SWAT vegetation growth module and its evaluation for four tropical ecosystems. Hydrol. Earth Syst. Sci. 2017, 21, 4449–4467. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Savenije, H.H.G.; Bastiaanssen, W.G.M. Constraining model parameters on remotely sensed evaporation: Justification for distribution in ungauged basins? Hydrol. Earth Syst. Sci. 2008, 12, 1403–1413. [Google Scholar] [CrossRef]
- McCabe, M.F.; Ershadi, A.; Jimenez, C.; Miralles, D.G.; Michel, D.; Wood, E.F. The GEWEX LandFlux project: Evaluation of model evaporation using tower-based and globally gridded forcing data. Geosci. Model. Dev. 2016, 9, 283–305. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P.; Li, Z.-L. How sensitive is SEBAL to changes in input variables, domain size and satellite sensor? J. Geophys. Res. Atmos. 2011, 116, D21107. [Google Scholar] [CrossRef]
- Gokmen, M.; Vekerdy, Z.; Verhoef, A.; Verhoef, W.; Batelaan, O.; van der Tol, C. Integration of soil moisture in SEBS for improving evapotranspiration estimation under water stress conditions. Remote Sens. Environ. 2012, 121, 261–274. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Parajuli, P.B.; Jayakody, P.; Ouyang, Y. Evaluation of Using Remote Sensing Evapotranspiration Data in SWAT. Water Resour. Manag. 2018, 32, 985–996. [Google Scholar] [CrossRef]
- Kiptala, J.K.; Mul, M.L.; Mohamed, Y.A.; Van Der Zaag, P. Modelling stream flow and quantifying blue water using a modified STREAM model for a heterogeneous, highly utilized and data-scarce river basin in Africa. Hydrol. Earth Syst. Sci. 2014, 18, 2287–2303. [Google Scholar] [CrossRef]
- Aerts, J.C.J.H.; Kriek, M.; Schepel, M. STREAM (Spatial Tools for River basins and Environment and Analysis of Management options): “Set up and requirements”. Phys. Chem. Earth Part B Hydrol. Oceans Atmos. 1999, 24, 591–595. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Immerzeel, W.W.; Bastiaanssen, W.G.M. Spatial quantification of groundwater abstraction in the irrigated indus basin. Groundwater 2014, 52, 25–36. [Google Scholar] [CrossRef]
- Wambura, F.J.; Dietrich, O.; Lischeid, G. Improving a distributed hydrological model using evapotranspiration-related boundary conditions as additional constraints in a data-scarce river basin. Hydrol. Process. 2018, 32, 759–775. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen, “SHE”, 2: Structure of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 61–77. [Google Scholar] [CrossRef]
- Schultz, G.A. Hydrological modeling based on remote sensing information. Adv. Space Res. 1993, 13, 149–166. [Google Scholar] [CrossRef]
- Savenije, H.H.G. HESS opinions “topography driven conceptual modelling (FLEX-Topo)”. Hydrol. Earth Syst. Sci. 2010, 14, 2681–2692. [Google Scholar] [CrossRef]
- Koutsouris, A.J.; Seibert, J.; Lyon, S.W. Utilization of global precipitation datasets in data limited regions: A case study of Kilombero Valley, Tanzania. Atmosphere 2017, 8, 246. [Google Scholar] [CrossRef]
- Campo, L.; Caparrini, F.; Castelli, F. Use of multi-platform, multi-temporal remote-sensing data for calibration of a distributed hydrological model: An application in the Arno basin, Italy. Hydrol. Process. 2006, 20, 2693–2712. [Google Scholar] [CrossRef]
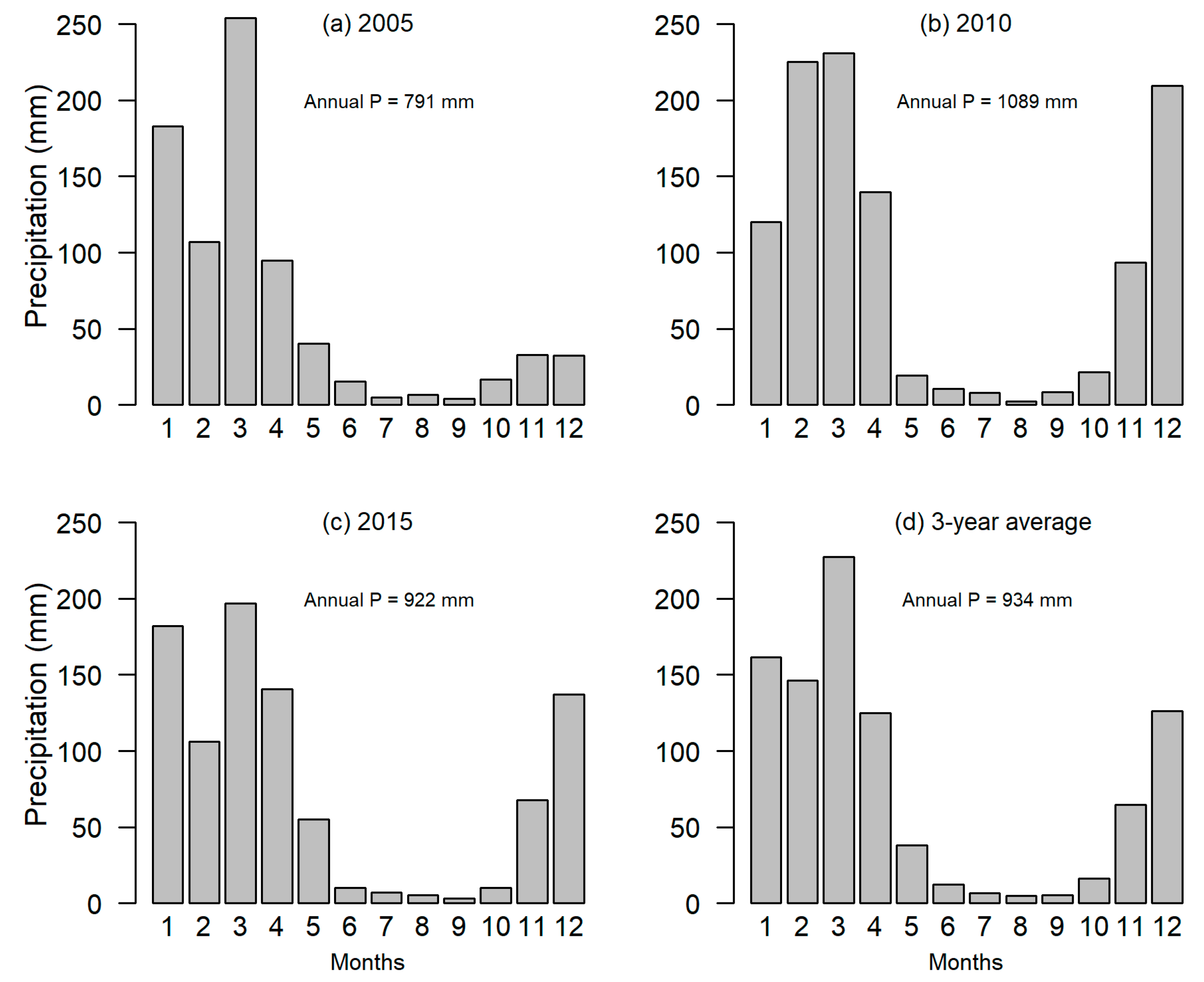

| Data | Properties and Source | ||||
|---|---|---|---|---|---|
| Spatial Resolution | Temporal Resolution | Units | Period of Record | Source | |
| Digital Elevation Model (DEM) | 90 m | Not applicable | m | 2005, 2010, 2015 | SRTM |
| Max and Min air temperature | Points | Daily | °C | 2005, 2010, 2015 | RBWO |
| Relative humidity | Points | Instantaneous * | % | 2005, 2010, 2015 | RBWO |
| Wind speed | Points | Instantaneous * | m/s | 2005, 2010, 2015 | RBWO |
| Precipitation | Points | Daily * | mm | 2005, 2010, 2015 | RBWO |
| Features | Characteristics/Types | Catchment Name | ||
|---|---|---|---|---|
| Entire Basin | Uplands (Mountain-Forests) | Wetland-Valley (Floodplain) | ||
| Topographic | Area (km2) | 34,285 | 18,267 | 16,018 |
| Average slope (%) | 13 | 18 | 7 | |
| Vegetation | Forest (%) | 55 | 30 | 25 |
| Shrubs (%) | 10 | 8 | 2 | |
| Herbaceous (%) | 21 | 8 | 13 | |
| Soil | Nitisols (%) | 15 | 12 | 3 |
| Acrisols (%) | 46 | 24 | 22 | |
| Fluvisols (%) | 18 | 1 | 17 | |
| Others * (%) | 21 | 16 | 5 | |
| Value | Land Cover Classes | Area (km2) |
|---|---|---|
| 10 | Cropland | 411.8 |
| 11 | Herbaceous cover | 3005.0 |
| 20 | Post-flooding cropland | 2371.3 |
| 30 | Mosaic cropland | 1425.2 |
| 50 | Broadleaved evergreen forest | 2696.6 |
| 60 | Broadleaved deciduous forest | 12,555.1 |
| 90 | Mixed leaf forest | 2158.7 |
| 110 | Mosaic herbaceous cover | 963.6 |
| 120 | Shrubland | 2567.8 |
| 130 | Grassland | 545.4 |
| 160 | Flooded tree cover | 348.8 |
| 180 | Flooded herbaceous cover | 3716.0 |
| 190 | Urban areas | 11.7 |
| 210 | Water bodies | 22.5 |
| Satellite Imagery | Product (Sensor) | Spatial Scale | Temporal Scale | Scaling Factor |
|---|---|---|---|---|
| LST/Emissivity | MOD11A2 (Terra) and MYD11A2 (Aqua) | 1 km | 8-day | 0.02/0.002 |
| NDVI | MOD13Q1 (Terra) and MYD13Q1 (Aqua) | 250 m | 16-day | 0.0001 |
| LAI | MOD15A2H (Terra) and MYD15A2H (Aqua) | 500 m | 8-day | 0.1 |
| Albedo | MCD43A3 (combined Terra and Aqua) | 500 m | Daily | 0.001 |
| DOY 2005 | DOY 2010 | DOY 2015 |
|---|---|---|
| 17 | 97 | 153 |
| 121 | 129 | 161 |
| 129 | 185 | 185 |
| 161 | 225 | 193 |
| 193 | 233 | 225 |
| 233 | 249 | 233 |
| 241 | 265 | 249 |
| 249 | 273 | 257 |
| 257 | 281 | 265 |
| 265 | 289 | 281 |
| 273 | 297 | 321 |
| 281 | 305 | 337 |
| 289 | 329 | |
| 313 | 345 | |
| 321 | ||
| 329 | ||
| 337 | ||
| 353 |
| Model (References) | Evaporative Fraction (-) | Daily Actual ET |
|---|---|---|
| SEBAL (Bastiaanssen et al., 1998) | ||
| S-SEBI (Roerink et al., 2000) | ||
| SSEBop (Senay et al., 2013) | ||
| Land Cover Classes | Parameter | Models | |||
|---|---|---|---|---|---|
| SEBAL | SSEBop | S-SEBI | Ensemble Mean | ||
| Cropland | Mean (mm/day) | 6.3 | 6.4 | 6.4 | 6.4 |
| Stdev (mm/day) | 1.0 | 0.8 | 0.7 | 0.7 | |
| Herbaceous cover | Mean (mm/day) | 5.6 | 5.6 | 5.7 | 5.6 |
| Stdev (mm/day) | 1.0 | 0.8 | 0.7 | 0.7 | |
| Post-flooding cropland | Mean (mm/day) | 3.5 | 3.1 | 3.8 | 3.5 |
| Stdev (mm/day) | 0.8 | 1.1 | 0.7 | 0.7 | |
| Mosaic cropland | Mean (mm/day) | 6.2 | 6.3 | 6.2 | 6.2 |
| Stdev (mm/day) | 1.0 | 0.8 | 0.7 | 0.7 | |
| Broadleaved evergreen forest | Mean (mm/day) | 6.7 | 7.0 | 6.9 | 6.9 |
| Stdev (mm/day) | 1.1 | 0.9 | 0.9 | 0.9 | |
| Broadleaved deciduous forest | Mean (mm/day) | 5.8 | 5.6 | 5.8 | 5.7 |
| Stdev (mm/day) | 1.0 | 0.7 | 0.7 | 0.6 | |
| Mixed Leaf forest | Mean (mm/day) | 6.4 | 6.5 | 6.4 | 6.4 |
| Stdev (mm/day) | 1.0 | 0.7 | 0.7 | 0.7 | |
| Mosaic herbaceous cover | Mean (mm/day) | 6.8 | 7.1 | 6.9 | 6.9 |
| Stdev (mm/day) | 1.1 | 0.9 | 0.8 | 0.8 | |
| Shrubland | Mean (mm/day) | 6.5 | 6.6 | 6.5 | 6.5 |
| Stdev (mm/day) | 1.1 | 0.8 | 0.8 | 0.8 | |
| Grassland | Mean (mm/day) | 6.3 | 6.3 | 6.3 | 6.3 |
| Stdev (mm/day) | 1.0 | 0.8 | 0.7 | 0.7 | |
| Flooded tree cover | Mean (mm/day) | 4.6 | 4.0 | 4.6 | 4.4 |
| Stdev (mm/day) | 0.9 | 0.9 | 0.6 | 0.6 | |
| Flooded herbaceous cover | Mean (mm/day) | 3.7 | 3.0 | 3.8 | 3.5 |
| Stdev (mm/day) | 0.8 | 1.3 | 0.7 | 0.7 | |
| Urban areas | Mean (mm/day) | 5.1 | 5.2 | 5.3 | 5.2 |
| Stdev (mm/day) | 1.1 | 0.9 | 0.8 | 0.8 | |
| Water bodies | Mean (mm/day) | 5.9 | 5.4 | 5.7 | 5.6 |
| Stdev (mm/day) | 0.8 | 0.9 | 0.8 | 0.7 | |
| Pair of Model Comparison | Land Cover Classes | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 11 | 20 | 30 | 50 | 60 | 90 | 110 | 120 | 130 | 160 | 180 | 190 | 210 | |
| Wilcoxon’s test p-values (at 95% confidence) | ||||||||||||||
| (SBL vs SOP) | 0.98 | 0.66 | 0.01 | 0.88 | 0.38 | 0.25 | 0.95 | 0.48 | 0.91 | 0.71 | 0.02 | 0.01 | 0.89 | 0.07 |
| (SBL vs SSB) | 0.83 | 0.84 | 0.68 | 0.63 | 0.63 | 0.70 | 0.88 | 0.83 | 0.80 | 0.45 | 0.55 | 0.82 | 0.81 | 0.21 |
| (SOP vs SSB) | 0.95 | 0.53 | 0.00 | 0.83 | 0.68 | 0.07 | 0.81 | 0.59 | 0.88 | 0.98 | 0.00 | 0.00 | 0.50 | 0.03 |
| (SBL vs ESB) | 0.91 | 0.89 | 0.14 | 0.70 | 0.64 | 0.43 | 0.95 | 0.76 | 0.93 | 0.73 | 0.15 | 0.11 | 0.90 | 0.17 |
| (SOP vs ESB) | 0.98 | 0.66 | 0.00 | 0.84 | 0.62 | 0.19 | 0.95 | 0.69 | 1.00 | 0.79 | 0.00 | 0.01 | 0.74 | 0.06 |
| (SSB vs ESB) | 0.83 | 0.88 | 0.02 | 0.85 | 0.97 | 0.76 | 0.95 | 0.79 | 0.82 | 0.65 | 0.08 | 0.03 | 0.73 | 0.95 |
| Levene’s test p-values (at 95% confidence) | ||||||||||||||
| (SBL vs SOP) | 0.23 | 0.48 | 0.43 | 0.27 | 0.24 | 0.33 | 0.21 | 0.22 | 0.13 | 0.27 | 0.97 | 0.14 | 0.49 | 0.79 |
| (SBL vs SSB) | 0.07 | 0.15 | 0.35 | 0.07 | 0.38 | 0.21 | 0.13 | 0.14 | 0.12 | 0.05 | 0.27 | 0.53 | 0.16 | 0.49 |
| (SOP vs SSB) | 0.39 | 0.43 | 0.14 | 0.36 | 0.78 | 0.81 | 0.64 | 0.72 | 0.84 | 0.27 | 0.33 | 0.06 | 0.43 | 0.76 |
| (SBL vs ESB) | 0.09 | 0.27 | 0.27 | 0.08 | 0.36 | 0.19 | 0.17 | 0.21 | 0.17 | 0.10 | 0.21 | 0.56 | 0.26 | 0.37 |
| (SOP vs ESB) | 0.52 | 0.70 | 0.11 | 0.42 | 0.80 | 0.75 | 0.81 | 0.95 | 0.95 | 0.52 | 0.27 | 0.07 | 0.64 | 0.65 |
| (SSB vs ESB) | 0.83 | 0.64 | 0.82 | 0.89 | 0.97 | 0.93 | 0.82 | 0.77 | 0.81 | 0.65 | 0.82 | 1.00 | 0.73 | 0.87 |
| Land Cover Classes | Criteria | Pair of Model Comparison | |||||
|---|---|---|---|---|---|---|---|
| (SBL vs SOP) | (SBL vs SSB) | (SOP vs SSB) | (SBL vs ESB) | (SOP vs ESB) | (SSB vs ESB) | ||
| Cropland | r | 0.35 | 0.79 | 0.69 | 0.87 | 0.75 | 0.95 |
| Pbias (%) | 2.00 | 1.00 | −1.00 | 1.00 | −1.00 | 0.00 | |
| Herbaceous cover | r | 0.34 | 0.78 | 0.73 | 0.84 | 0.78 | 0.96 |
| Pbias (%) | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | −1.00 | |
| Post-flooding cropland | r | 0.02 | 0.52 | 0.71 | 0.59 | 0.78 | 0.95 |
| Pbias (%) | −14.00 | 6.00 | 24.00 | −3.00 | 13.00 | −8.00 | |
| Mosaic cropland | r | 0.25 | 0.75 | 0.67 | 0.84 | 0.72 | 0.96 |
| Pbias (%) | 1.00 | 0.00 | −1.00 | 0.00 | −1.00 | 0.00 | |
| Broadleaved evergreen forest | r | 0.68 | 0.90 | 0.86 | 0.93 | 0.89 | 0.98 |
| Pbias (%) | 5.00 | 3.00 | −2.00 | 2.00 | −2.00 | 0.00 | |
| Broadleaved deciduous forest | r | 0.21 | 0.75 | 0.67 | 0.83 | 0.70 | 0.96 |
| Pbias (%) | −2.00 | 0.00 | 3.00 | −1.00 | 2.00 | −1.00 | |
| Mixed Leaf forest | r | 0.37 | 0.82 | 0.69 | 0.88 | 0.75 | 0.96 |
| Pbias (%) | 2.00 | 1.00 | −1.00 | 1.00 | −1.00 | 0.00 | |
| Mosaic herbaceous cover | r | 0.60 | 0.90 | 0.79 | 0.92 | 0.85 | 0.98 |
| Pbias (%) | 4.00 | 2.00 | −2.00 | 2.00 | −2.00 | 0.00 | |
| Shrubland | r | 0.54 | 0.86 | 0.80 | 0.91 | 0.82 | 0.98 |
| Pbias (%) | 2.00 | 1.00 | −1.00 | 1.00 | −1.00 | 0.00 | |
| Grassland | r | 0.38 | 0.82 | 0.70 | 0.87 | 0.76 | 0.96 |
| Pbias (%) | 1.00 | 0.00 | −1.00 | 0.00 | −1.00 | 0.00 | |
| Flooded tree cover | r | 0.07 | 0.57 | 0.64 | 0.66 | 0.69 | 0.95 |
| Pbias (%) | −12.00 | 1.00 | 14.00 | −4.00 | 9.00 | −5.00 | |
| Flooded herbaceous cover | r | 0.04 | 0.46 | 0.82 | 0.52 | 0.86 | 0.96 |
| Pbias (%) | −18.00 | 4.00 | 26.00 | −5.00 | 16.00 | −8.00 | |
| Urban areas | r | 0.41 | 0.80 | 0.75 | 0.86 | 0.81 | 0.96 |
| Pbias (%) | 1.00 | 2.00 | 2.00 | 1.00 | 0.00 | −1.00 | |
| Water bodies | r | 0.32 | 0.69 | 0.81 | 0.77 | 0.84 | 0.97 |
| Pbias (%) | −8.00 | −3.00 | 6.00 | −4.00 | 5.00 | −1.00 | |
| Land Cover Classes | Parameter | Model/Year | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SEBAL | SSEBop | S-SEBI | Ensemble Mean | ||||||
| 2005 | 2015 | 2005 | 2015 | 2005 | 2015 | 2005 | 2015 | ||
| Cropland (lc10) | Mean (mm/day) | 6.1 | 6.3 | 6.0 | 6.1 | 6.1 | 6.2 | 6.1 | 6.2 |
| Stdev (mm/day) | 1.0 | 1.1 | 0.7 | 0.8 | 0.8 | 0.8 | 0.7 | 0.8 | |
| Wilcoxon’s p-value | 0.69 | 0.60 | 0.72 | 0.66 | |||||
| Levene’s p-value | 0.93 | 1.00 | 0.77 | 0.93 | |||||
| Herbaceous cover (lc11) | Mean (mm/day) | 5.2 | 5.7 | 5.1 | 5.3 | 5.3 | 5.4 | 5.2 | 5.5 |
| Stdev (mm/day) | 0.9 | 1.0 | 0.6 | 0.9 | 0.6 | 0.6 | 0.6 | 0.7 | |
| Wilcoxon’s p-value | 0.31 | 1.00 | 0.54 | 0.54 | |||||
| Levene’s p-value | 0.65 | 0.35 | 0.82 | 0.56 | |||||
| Post-flooding cropland (lc20) | Mean (mm/day) | 3.4 | 3.3 | 2.8 | 2.3 | 3.6 | 3.2 | 3.3 | 2.9 |
| Stdev (mm/day) | 0.6 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.4 | 0.4 | |
| Wilcoxon’s p-value | 0.79 | 0.11 | 0.15 | 0.23 | |||||
| Levene’s p-value | 0.13 | 0.96 | 0.88 | 0.24 | |||||
| Mosaic cropland (lc30) | Mean (mm/day) | 5.9 | 6.2 | 5.8 | 5.9 | 5.9 | 6.1 | 5.9 | 6.1 |
| Stdev (mm/day) | 1.0 | 1.1 | 0.7 | 0.8 | 0.7 | 0.8 | 0.7 | 0.8 | |
| Wilcoxon’s p-value | 0.60 | 0.57 | 0.54 | 0.53 | |||||
| Levene’s p-value | 0.84 | 0.82 | 0.89 | 0.96 | |||||
| Broadleaved evergreen forest (lc50) | Mean (mm/day) | 6.5 | 6.6 | 6.7 | 6.7 | 6.8 | 6.7 | 6.7 | 6.6 |
| Stdev (mm/day) | 1.1 | 1.1 | 0.8 | 1.0 | 1.0 | 1.0 | 0.9 | 1.0 | |
| Wilcoxon’s p-value | 0.93 | 1.00 | 0.66 | 1.00 | |||||
| Levene’s p-value | 0.94 | 0.44 | 0.83 | 0.92 | |||||
| Broadleaved deciduous forest (lc60) | Mean (mm/day) | 5.5 | 5.7 | 5.2 | 5.2 | 5.5 | 5.5 | 5.4 | 5.5 |
| Stdev (mm/day) | 0.9 | 1.0 | 0.5 | 0.7 | 0.7 | 0.7 | 0.6 | 0.7 | |
| Wilcoxon’s p-value | 0.48 | 0.86 | 0.89 | 0.79 | |||||
| Levene’s p-value | 0.64 | 0.22 | 0.61 | 0.53 | |||||
| Mixed Leaf forest (lc90) | Mean (mm/day) | 6.1 | 6.3 | 6.1 | 6.1 | 6.3 | 6.3 | 6.2 | 6.3 |
| Stdev (mm/day) | 1.0 | 1.1 | 0.7 | 0.8 | 0.8 | 0.8 | 0.7 | 0.8 | |
| Wilcoxon’s p-value | 0.63 | 0.72 | 0.96 | 0.76 | |||||
| Levene’s p-value | 0.87 | 0.82 | 0.75 | 0.93 | |||||
| Mosaic herbaceous cover (lc110) | Mean (mm/day) | 6.6 | 6.7 | 6.7 | 6.7 | 6.7 | 6.8 | 6.7 | 6.7 |
| Stdev (mm/day) | 1.1 | 1.1 | 0.7 | 1.0 | 0.8 | 0.8 | 0.8 | 0.9 | |
| Wilcoxon’s p-value | 0.72 | 0.79 | 0.93 | 0.76 | |||||
| Levene’s p-value | 0.93 | 0.52 | 0.86 | 0.75 | |||||
| Shrubland (lc120) | Mean (mm/day) | 6.2 | 6.4 | 6.2 | 6.2 | 6.3 | 6.3 | 6.2 | 6.3 |
| Stdev (mm/day) | 1.1 | 1.2 | 0.8 | 0.9 | 0.9 | 0.9 | 0.8 | 0.9 | |
| Wilcoxon’s p-value | 0.66 | 0.96 | 0.96 | 0.86 | |||||
| Levene’s p-value | 0.91 | 0.70 | 0.80 | 0.84 | |||||
| Grassland (lc130) | Mean (mm/day) | 5.9 | 6.4 | 5.7 | 6.1 | 5.8 | 6.2 | 5.8 | 6.2 |
| Stdev (mm/day) | 1.0 | 1.2 | 0.6 | 1.0 | 0.7 | 0.8 | 0.7 | 0.9 | |
| Wilcoxon’s p-value | 0.21 | 0.43 | 0.15 | 0.23 | |||||
| Levene’s p-value | 0.72 | 0.35 | 0.52 | 0.38 | |||||
| Flooded tree cover (lc160) | Mean (mm/day) | 4.4 | 4.4 | 3.7 | 3.5 | 4.4 | 4.2 | 4.2 | 4.0 |
| Stdev (mm/day) | 0.7 | 0.9 | 0.6 | 0.7 | 0.5 | 0.6 | 0.4 | 0.6 | |
| Wilcoxon’s p-value | 0.96 | 0.42 | 0.59 | 0.42 | |||||
| Levene’s p-value | 0.17 | 0.47 | 0.64 | 0.17 | |||||
| Flooded herbaceous cover (lc180) | Mean (mm/day) | 3.5 | 3.4 | 2.7 | 2.3 | 3.6 | 3.2 | 3.3 | 3.0 |
| Stdev (mm/day) | 0.5 | 0.8 | 0.8 | 0.7 | 0.4 | 0.5 | 0.3 | 0.4 | |
| Wilcoxon’s p-value | 0.86 | 0.13 | 0.20 | 0.18 | |||||
| Levene’s p-value | 0.22 | 0.96 | 0.89 | 0.28 | |||||
| Urban areas (lc190) | Mean (mm/day) | 4.8 | 5.2 | 4.8 | 4.8 | 4.9 | 5.0 | 4.9 | 5.0 |
| Stdev (mm/day) | 0.9 | 1.1 | 0.6 | 0.9 | 0.7 | 0.6 | 0.7 | 0.8 | |
| Wilcoxon’s p-value | 0.45 | 0.86 | 0.79 | 0.79 | |||||
| Levene’s p-value | 0.54 | 0.23 | 0.91 | 0.55 | |||||
| Water bodies (lc210) | Mean (mm/day) | 5.5 | 5.8 | 4.9 | 5.1 | 5.2 | 5.5 | 5.2 | 5.5 |
| Stdev (mm/day) | 0.6 | 0.9 | 0.5 | 0.8 | 0.4 | 0.7 | 0.4 | 0.7 | |
| Wilcoxon’s p-value | 0.40 | 0.59 | 0.21 | 0.27 | |||||
| Levene’s p-value | 0.29 | 0.32 | 0.32 | 0.16 | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senkondo, W.; Munishi, S.E.; Tumbo, M.; Nobert, J.; Lyon, S.W. Comparing Remotely-Sensed Surface Energy Balance Evapotranspiration Estimates in Heterogeneous and Data-Limited Regions: A Case Study of Tanzania’s Kilombero Valley. Remote Sens. 2019, 11, 1289. https://doi.org/10.3390/rs11111289
Senkondo W, Munishi SE, Tumbo M, Nobert J, Lyon SW. Comparing Remotely-Sensed Surface Energy Balance Evapotranspiration Estimates in Heterogeneous and Data-Limited Regions: A Case Study of Tanzania’s Kilombero Valley. Remote Sensing. 2019; 11(11):1289. https://doi.org/10.3390/rs11111289
Chicago/Turabian StyleSenkondo, William, Subira E. Munishi, Madaka Tumbo, Joel Nobert, and Steve W. Lyon. 2019. "Comparing Remotely-Sensed Surface Energy Balance Evapotranspiration Estimates in Heterogeneous and Data-Limited Regions: A Case Study of Tanzania’s Kilombero Valley" Remote Sensing 11, no. 11: 1289. https://doi.org/10.3390/rs11111289
APA StyleSenkondo, W., Munishi, S. E., Tumbo, M., Nobert, J., & Lyon, S. W. (2019). Comparing Remotely-Sensed Surface Energy Balance Evapotranspiration Estimates in Heterogeneous and Data-Limited Regions: A Case Study of Tanzania’s Kilombero Valley. Remote Sensing, 11(11), 1289. https://doi.org/10.3390/rs11111289







