Utilizing Satellite Surface Soil Moisture Data in Calibrating a Distributed Hydrological Model Applied in Humid Regions Through a Multi-Objective Bayesian Hierarchical Framework
Abstract
:1. Introduction
2. Study Area and Datasets
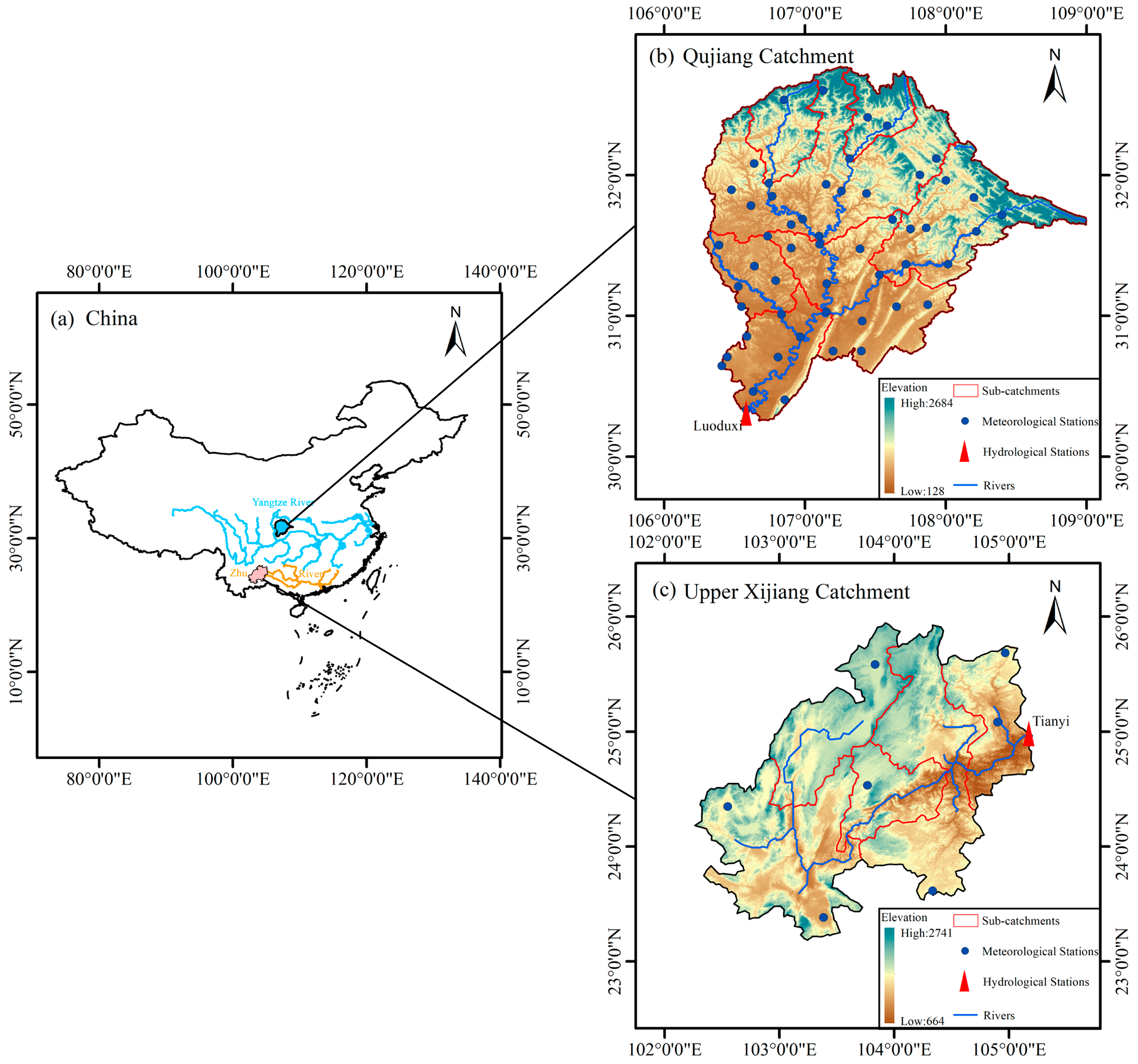
2.1. Study Area
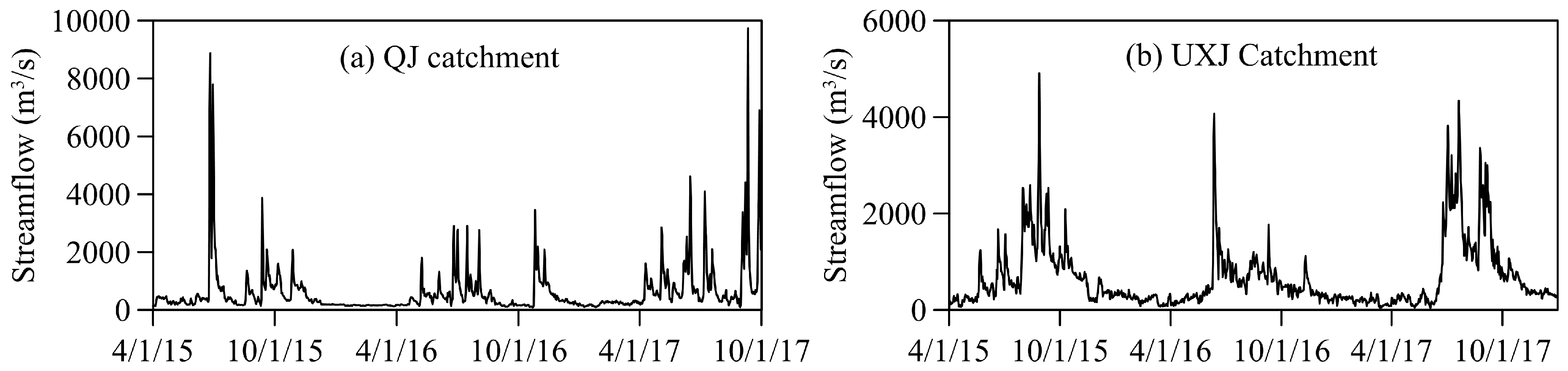
2.2. Hydro-Meteorological Data
2.3. Satellite Soil Moisture Data
3. Methodology
3.1. The DEM-Based Distributed Hydrological Model
3.1.1. Model Structure
3.1.2. Model Parameters
3.2. Multi-Objective Bayesian Hierarchical Framework
3.2.1. Multi-Objective Likelihood Function
3.2.2. Prior Information
3.3. Pre-Processing for Calibration Data
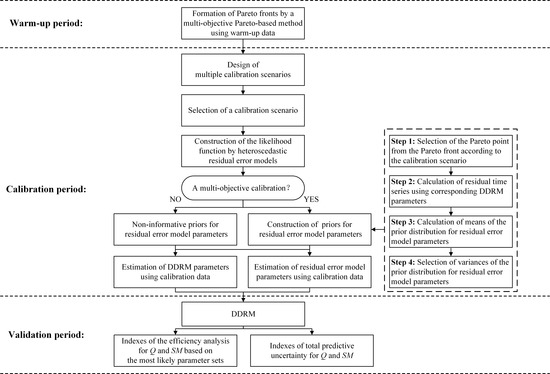
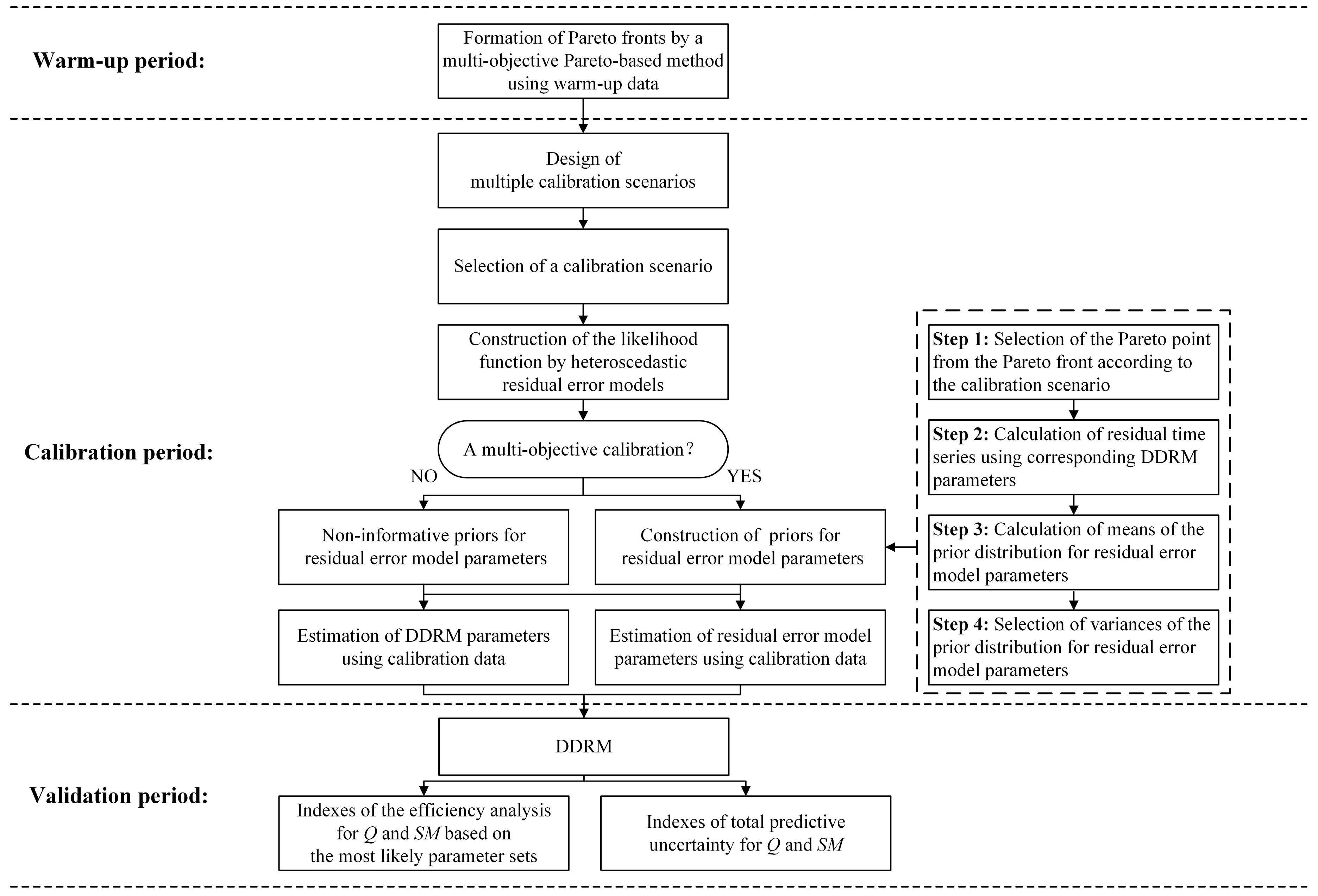
3.4. Procedures for Calibration and Validation
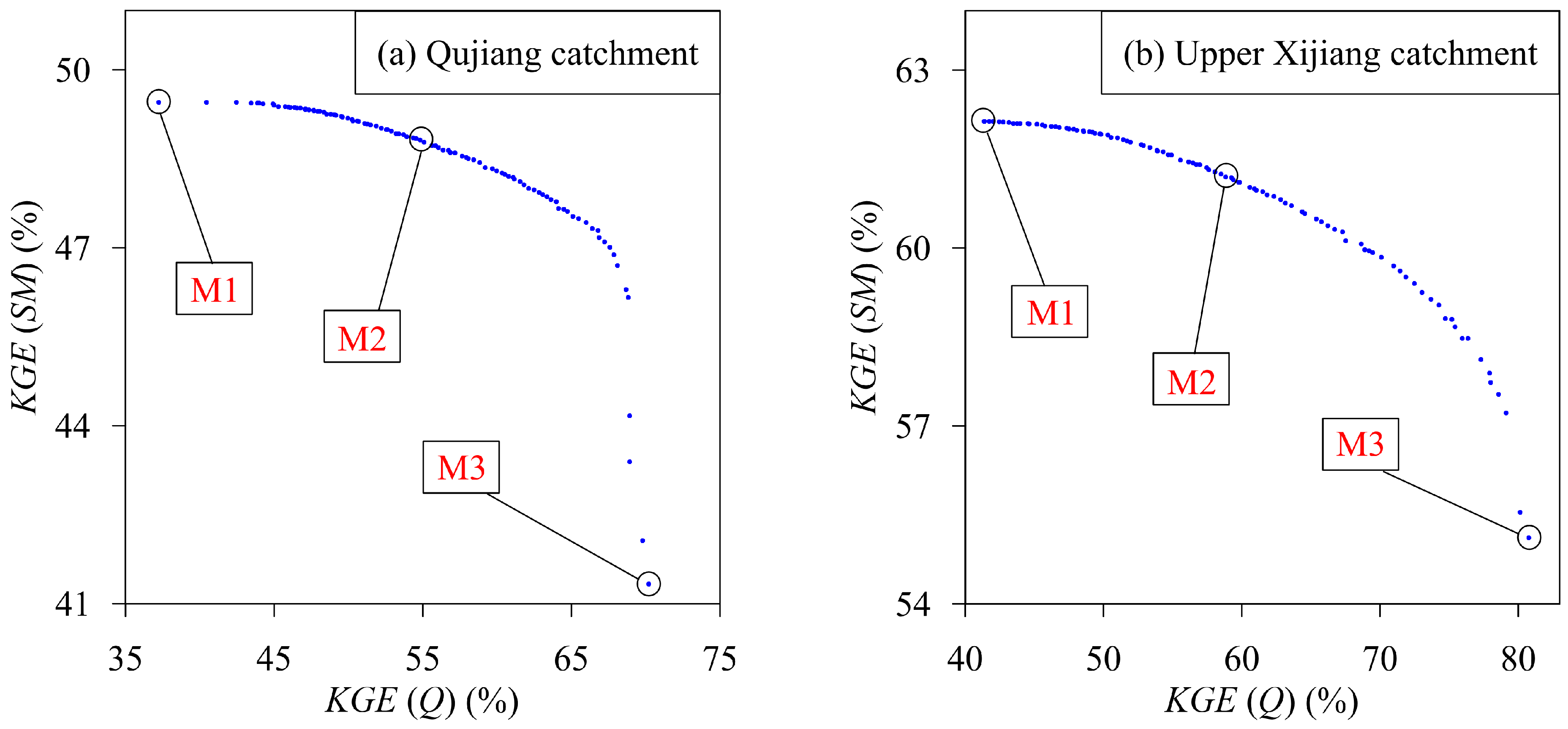
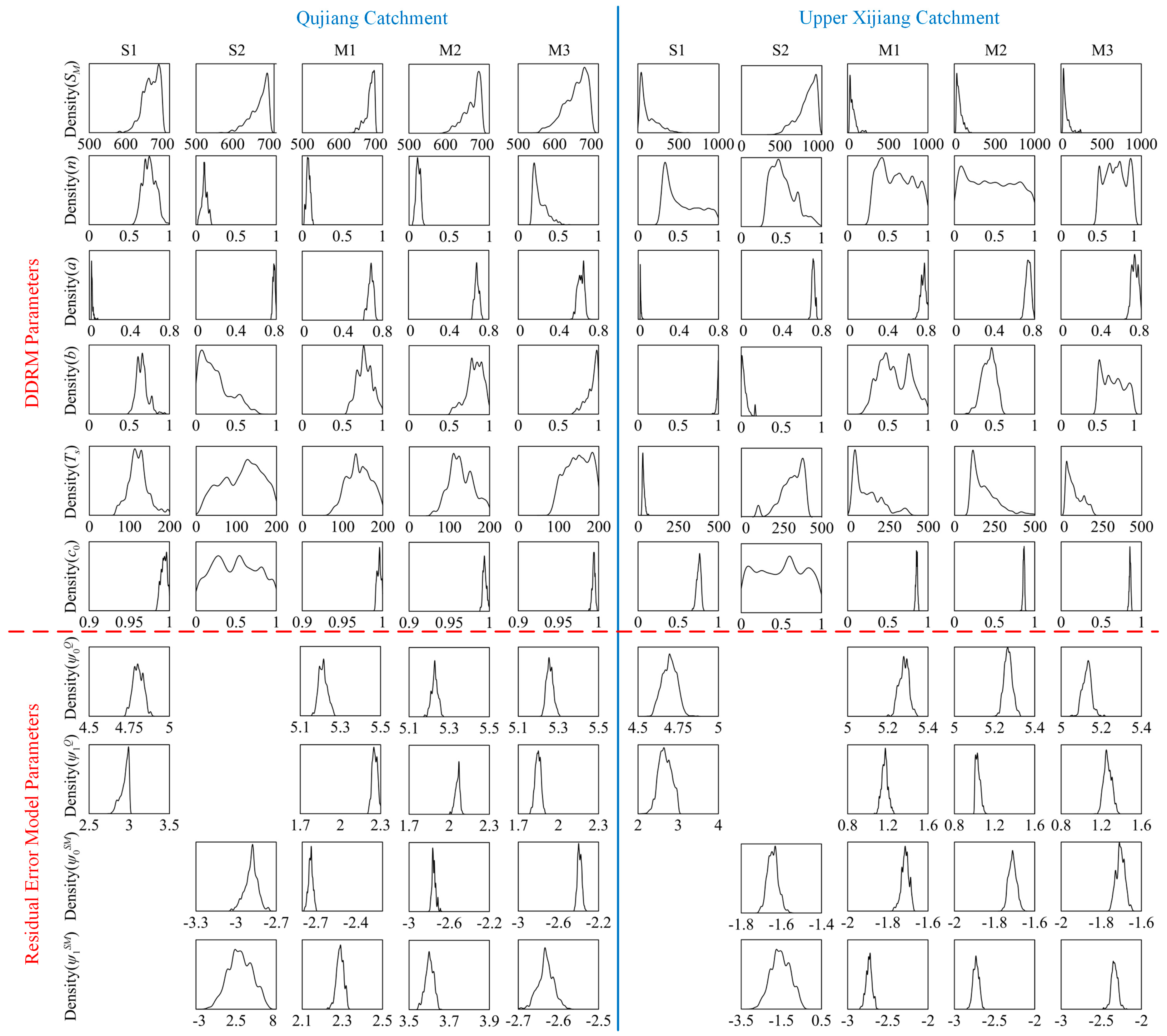
4. Results and Discussion
4.1. Prior Information for Residual Error Model Parameters
4.2. Posterior Information for Parameters
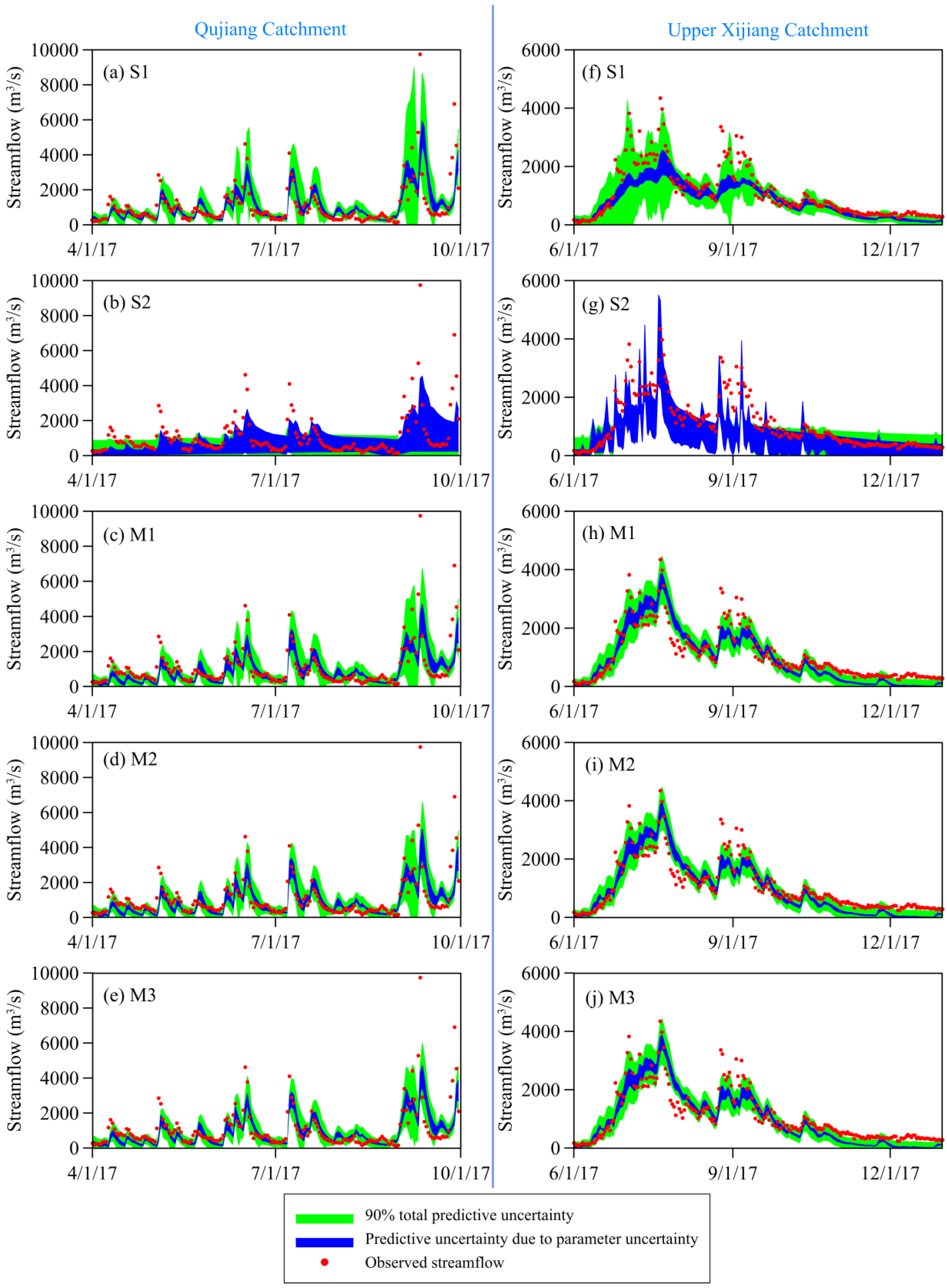
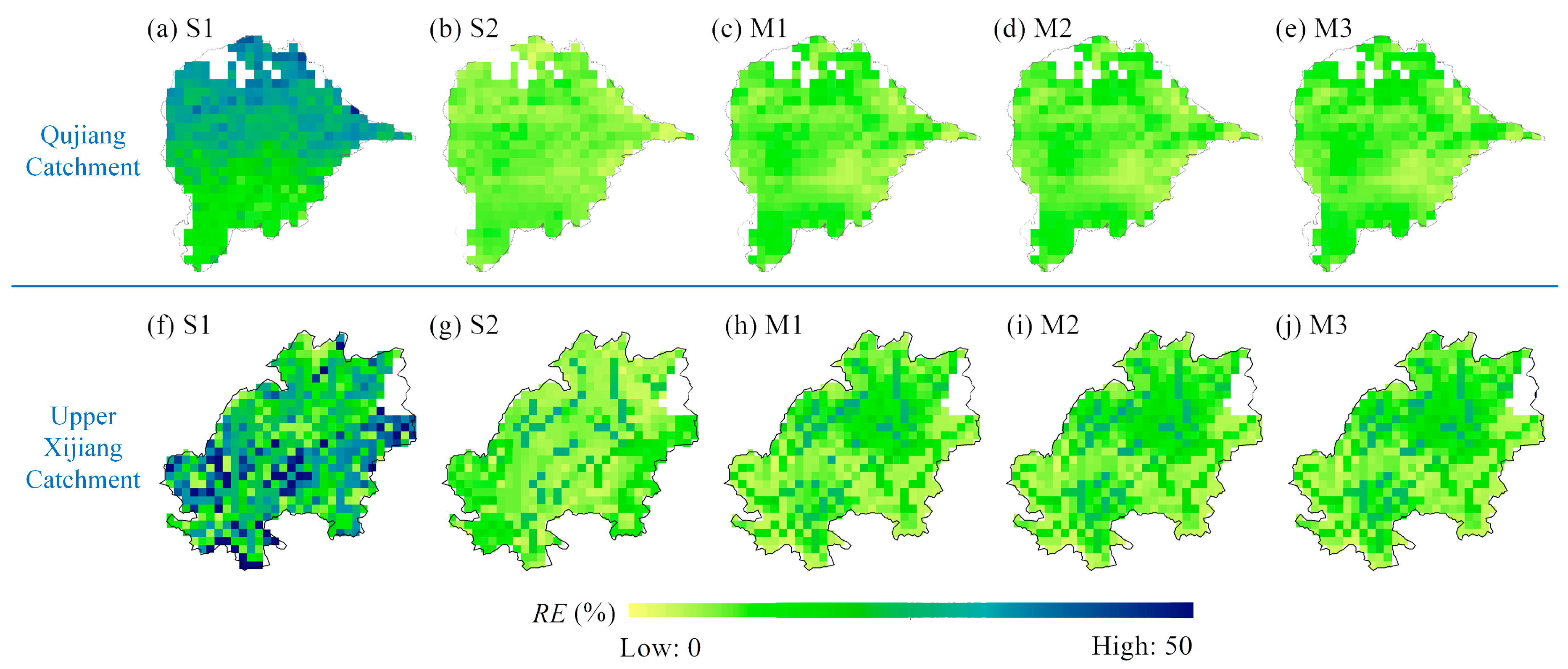
4.3. Observed and Model-Simulated Daily Streamflow and Soil Moisture Data
4.3.1. Observed and Model-Simulated Daily Streamflow
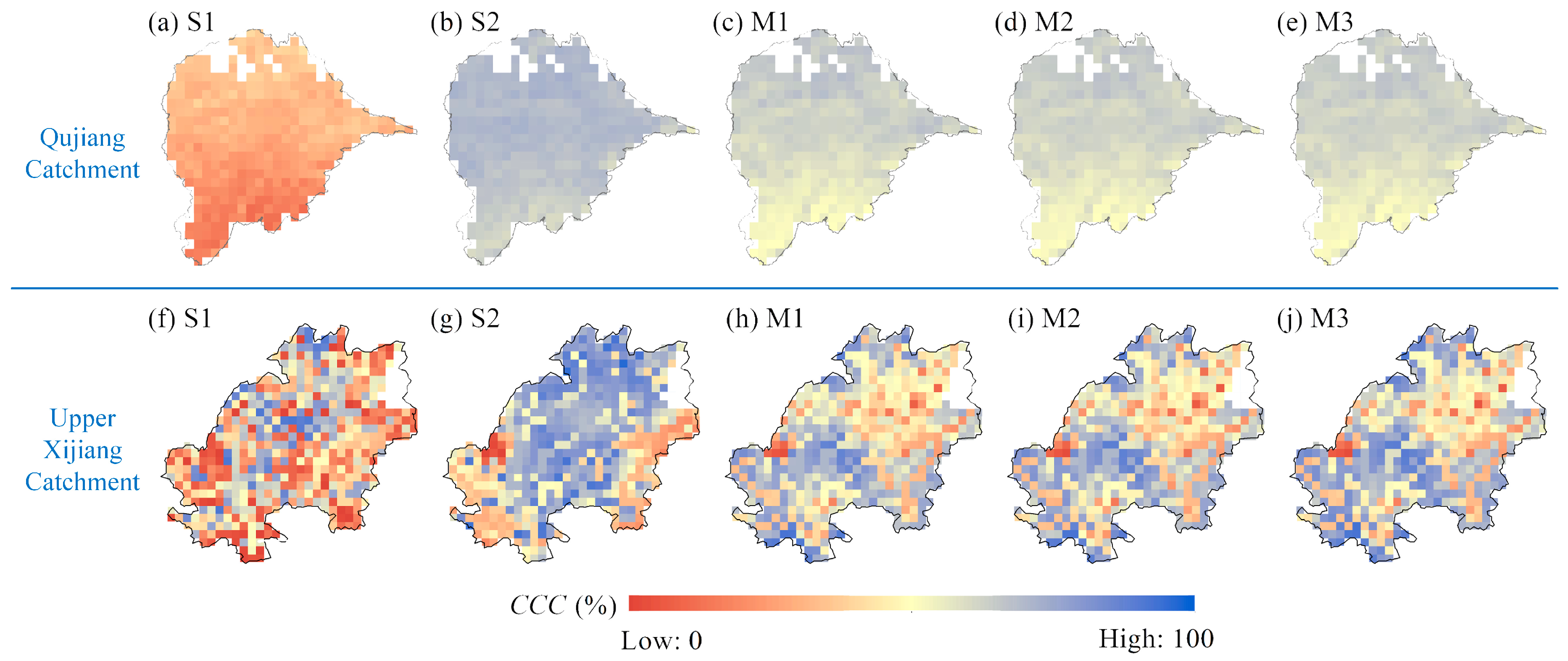
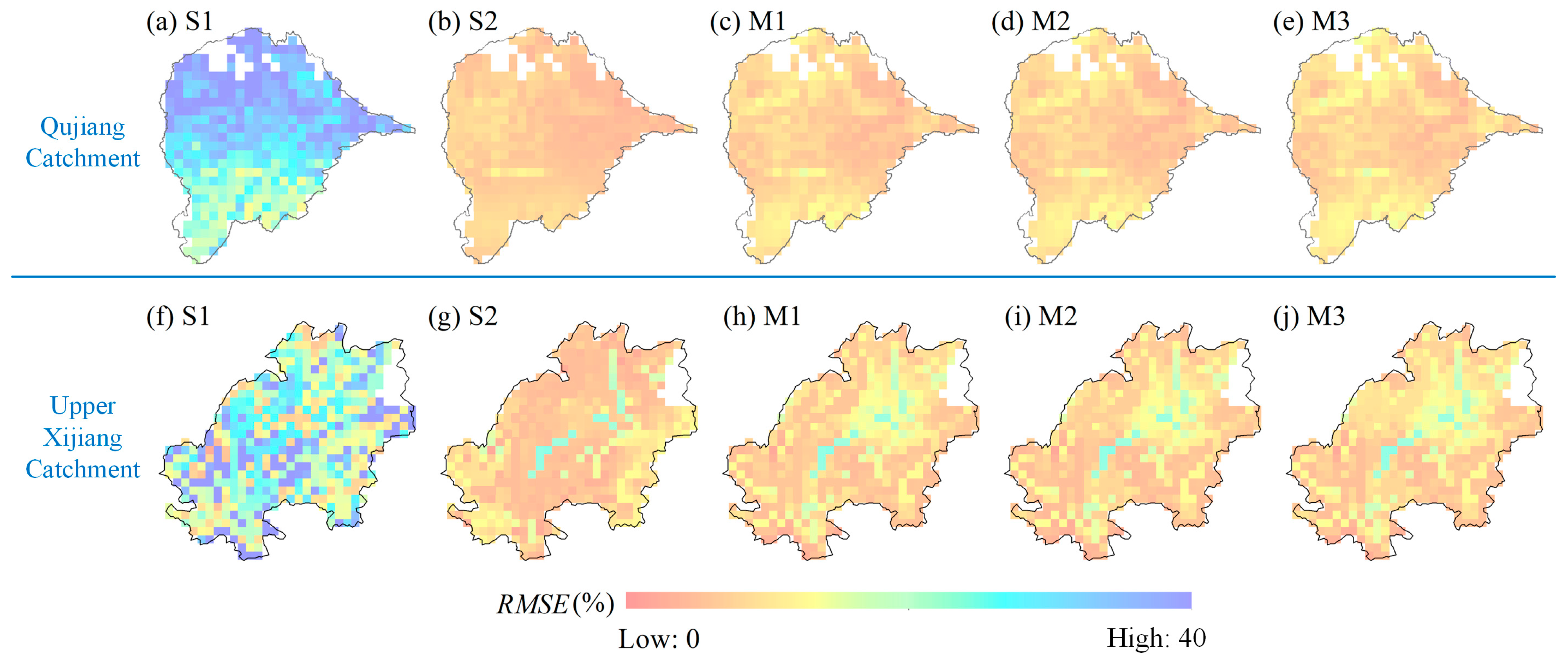
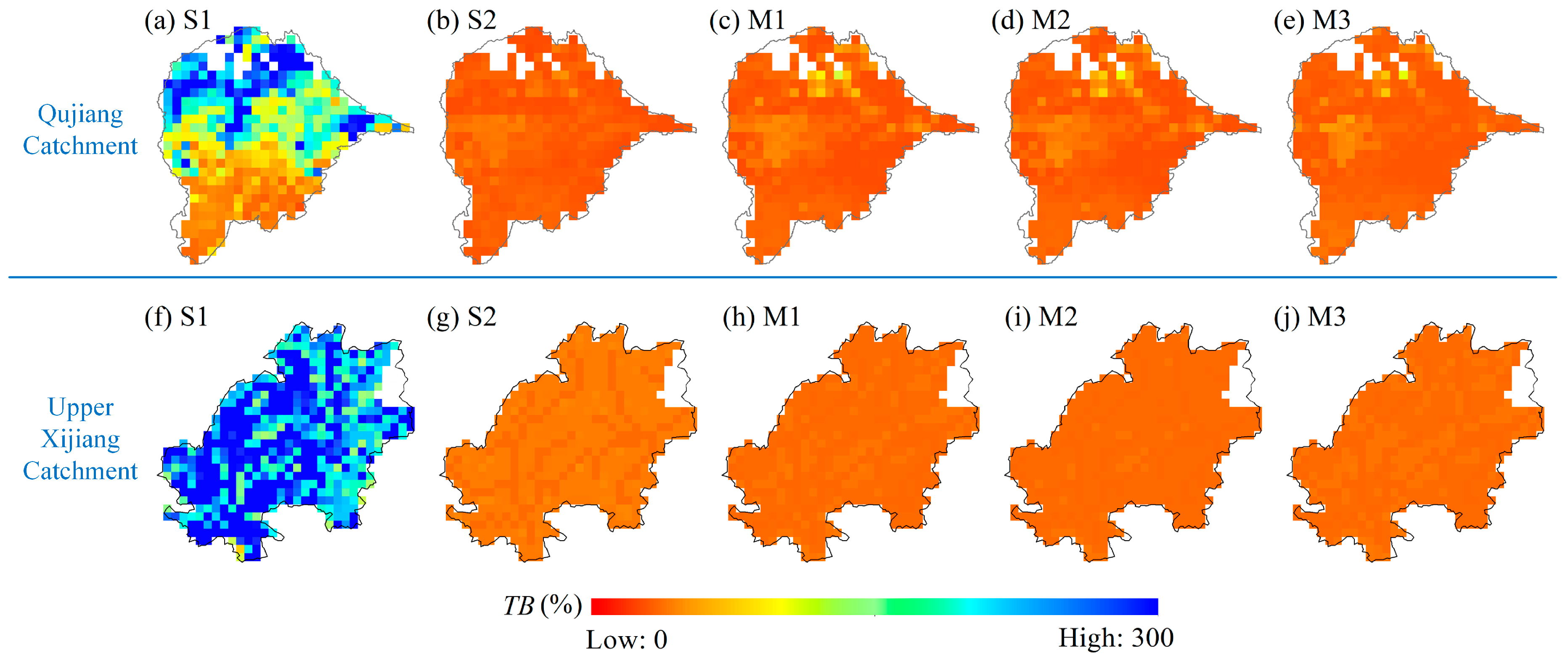
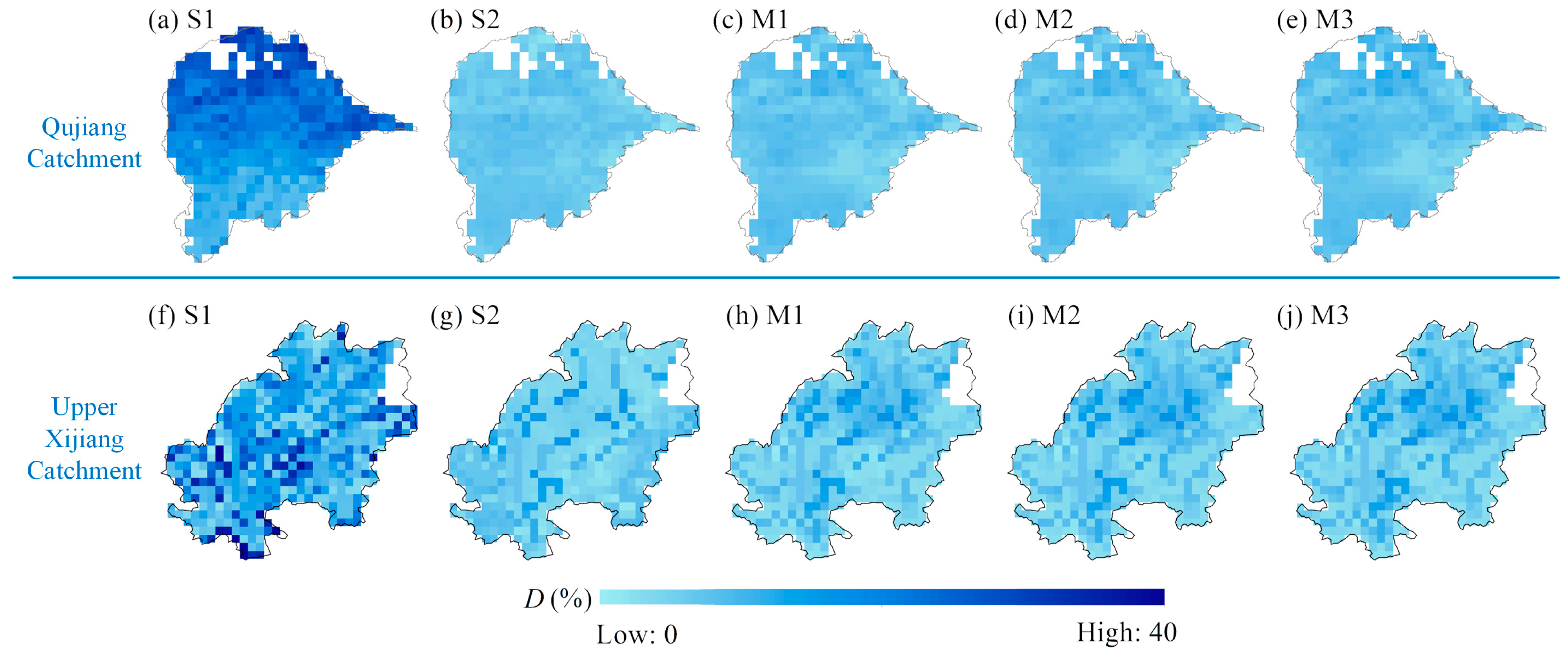
4.3.2. Observed and Model-Simulated Daily Soil Moisture
4.4. Discussion
4.4.1. Uncertainty Caused by Adding Satellite Data for Calibration
4.4.2. Importance of the Calibration Results in Understanding Catchment Hydrology
4.4.3. Limitation and Further Challenges of the Multi-Objective Bayesian Hierarchical Framework
5. Conclusions
- Compared to the streamflow-based single objective calibration, adding satellite soil moisture data in model calibration reduces total predictive uncertainty of streamflow for both catchments and greatly improves performances of soil moisture simulations both in time and space.
- When adding satellite soil moisture data in model calibration, different emphases of objectives have visible influences on streamflow simulations but have slight influences on soil moisture simulations.
Author Contributions
Funding
Conflicts of Interest
References
- Rajib, M.A.; Merwade, V.; Yu, Z. Multi-objective calibration of a hydrologic model using spatially distributed remotely sensed/in-situ soil moisture. J. Hydrol. 2016, 536, 192–207. [Google Scholar] [CrossRef] [Green Version]
- Jackson, T.J.; Bindlish, R.; Cosh, M.H.; Zhao, T.; Starks, P.J.; Bosch, D.D.; Seyfried, M.; Moran, M.S.; Goodrich, D.C.; Kerr, Y.H.; et al. Validation of Soil Moisture and Ocean Salinity (SMOS) soil moisture over watershed networks in the US. Ieee Trans. Geosci. Remote Sens. 2012, 50, 1530–1543. [Google Scholar] [CrossRef]
- Yee, M.S.; Walker, J.P.; Monerris, A.; Rüdiger, C.; Jackson, T.J. On the identification of representative in situ soil moisture monitoring stations for the validation of SMAP soil moisture products in Australia. J. Hydrol. 2016, 537, 367–381. [Google Scholar] [CrossRef]
- Li, Y.; Grimaldi, S.; Walker, J.P.; Pauwels, V. Application of remote sensing data to constrain operational rainfall-driven flood forecasting: A review. Remote Sens. 2016, 8, 456. [Google Scholar] [CrossRef]
- Bartalis, Z.; Wagner, W.; Naeimi, V.; Hasenauer, S.; Scipal, K.; Bonekamp, H.; Figa, J.; Anderson, C. Initial soil moisture retrievals from the METOP-A Advanced Scatterometer (ASCAT). Geophys. Res. Lett. 2007, 34, L20401. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Birchera, S.; Mahmoodia, A.; Mialona, A.; Richaumea, P.; et al. Overview of SMOS performance in terms of global soil moisture monitoring after six years in operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Aubert, D.; Loumagne, C.; Oudin, L. Sequential assimilation of soil moisture and streamflow data in a conceptual rainfall–runoff model. J. Hydrol. 2003, 280, 145–161. [Google Scholar] [CrossRef]
- Rüdiger, C. Streamflow Data Assimilation for Soil Moisture Prediction. Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 29 October 2006. [Google Scholar]
- Chen, F.; Crow, W.T.; Ryu, D. Dual forcing and state correction via soil moisture assimilation for improved rainfall–runoff modeling. J. Hydrometeorol. 2014, 15, 1832–1848. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Crow, W.T.; Robertson, D.E. The impacts of assimilating satellite soil moisture into a rainfall–runoff model in a semi-arid catchment. J. Hydrol. 2014, 519, 2763–2774. [Google Scholar] [CrossRef]
- Ridler, M.E.; Madsen, H.; Stisen, S.; Bircher, S.; Fensholt, R. Assimilation of SMOS-derived soil moisture in a fully integrated hydrological and soil-vegetation-atmosphere transfer model in Western Denmark. Water Resour. Res. 2014, 50, 8962–8981. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Tarpanelli, A.; Moramarco, T. Data assimilation of satellite soil moisture into rainfall-runoff modelling: A complex recipe? Remote Sens. 2015, 7, 11403–11433. [Google Scholar] [CrossRef]
- Laiolo, P.; Gabellani, S.; Campo, L.; Cenci, L.; Silvestro, F.; Delogu, F.; Pisani, A.R. Assimilation of remote sensing observations into a continuous distributed hydrological model: Impacts on the hydrologic cycle. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1308–1311. [Google Scholar] [CrossRef]
- Lievens, H.; Tomer, S.K.; Al Bitar, A.; De Lannoy, G.J.; Drusch, M.; Dumedah, G.; Hendricks Franssen, H.J.; Kerr, Y.H.; Martens, B.; Roundy, J.K. SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia. Remote Sens. Environ. 2015, 168, 146–162. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Crow, W.T.; Su, C.H.; Robertson, D.R. Dual assimilation of satellite soil moisture to improve streamflow prediction in data-scarce catchments. Water Resour. Res. 2016, 52, 5357–5375. [Google Scholar] [CrossRef] [Green Version]
- Nair, A.; Indu, J. Enhancing Noah land surface model prediction skill over Indian subcontinent by assimilating SMOPS blended soil moisture. Remote Sens. 2016, 8, 976. [Google Scholar] [CrossRef]
- Loizu, J.; Massari, C.; Alvarez-Mozos, J.; Tarpanelli, A.; Brocca, L.; Casali, J. On the assimilation set-up of ASCAT soil moisture data for improving streamflow catchment simulation. Adv. Water Resour. 2018, 111, 86–104. [Google Scholar] [CrossRef]
- Silvestro, F.; Gabellani, S.; Rudari, R.; Delogu, F.; Laiolo, P.; Boni, G. Uncertainty reduction and parameter estimation of a distributed hydrological model with ground and remote-sensing data. Hydrol. Earth Syst. Sci. 2015, 19, 1727–1751. [Google Scholar] [CrossRef] [Green Version]
- Wanders, N.; Bierkens, M.F.; de Jong, S.M.; de Roo, A.; Karssenberg, D. The benefits of using remotely sensed soil moisture in parameter identification of large-scale hydrological models. Water Resour. Res. 2014, 50, 6874–6891. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Grimaldi, S.; Pauwels, V.R.; Walker, J.P. Hydrologic model calibration using remotely sensed soil moisture and discharge measurements: The impact on predictions at gauged and ungauged locations. J. Hydrol. 2018, 557, 897–909. [Google Scholar] [CrossRef]
- Sutanudjaja, E.H.; Van Beek, L.P.H.; De Jong, S.M.; Van Geer, F.C.; Bierkens, M.F.P. Calibrating a large-extent high-resolution coupled groundwater-land surface model using soil moisture and discharge data. Water Resour. Res. 2014, 50, 687–705. [Google Scholar] [CrossRef]
- Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Parajka, J.; Naeimi, V.; Blöschl, G.; Komma, J. Matching ERS scatterometer based soil moisture patterns with simulations of a conceptual dual layer hydrologic model over Austria. Hydrol. Earth Syst. Sci. 2009, 13, 259–271. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Gupta, H.V.; Bastidas, L.A.; Bouten, W.; Sorooshian, S. Effective and efficient algorithm for multiobjective optimization of hydrologic models. Water Resour. Res. 2003, 39, 1–19. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Improved evolutionary optimization from genetically adaptive multimethod search. Proc. Natl. Acad. Sci. USA 2007, 104, 708–711. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yapo, P.; Sorooshian, S.; Gupta, V.K. Multi-objective global optimization for hydrologic models. J. Hydrol. 1998, 204, 83–97. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Marshall, L.; Sharma, A.; Ajami, H. A Bayesian alternative for multi-objective ecohydrological model specification. J. Hydrol. 2018, 556, 25–38. [Google Scholar] [CrossRef]
- Bates, B.C.; Campbell, E.P. A Markov chain Monte Carlo scheme for parameter estimation and inference in conceptual rainfall-runoff modeling. Water Resour. Res. 2001, 37, 937–947. [Google Scholar] [CrossRef]
- Reichert, P.; Schuwirth, N. Linking statistical bias description to multiobjective model calibration. Water Resour. Res. 2012, 48, W09543. [Google Scholar] [CrossRef]
- Ter Braak, C.J. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44, W00B09. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar]
- Tomczak, M. Spatial interpolation and its uncertainty using automated anisotropic inverse distance weighting (IDW)-cross-validation/jackknife approach. J. Geogr. Inf. Decis. Anal. 1998, 2, 18–30. [Google Scholar]
- O’Neill, P.E.; Chan, S.; Njoku, E.G.; Jackson, T.; Bindlish, R. SMAP Enhanced L3 Radiometer Global Daily 9 km EASE-Grid Soil Moisture, version 2; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2018. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Jackson, T.J.; O’Neill, P.; De Lannoy, G.; De Rosnay, P.; Walker, J.P.; Kurum, M. Modelling the passive microwave signature from land surfaces: A review of recent results and application to the L-band SMOS & SMAP soil moisture retrieval algorithms. Remote Sens. Environ. 2017, 192, 238–262. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, K.S.; Bi, H.; Chen, Q. A preliminary evaluation of the SMAP radiometer soil moisture product over United States and Europe using ground-based measurements. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4929–4940. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Asanuma, J. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Cai, X.; Pan, M.; Chaney, N.W.; Colliander, A.; Misra, S.; Cosh, M.H.; Wood, E.F. Validation of SMAP soil moisture for the SMAPVEX15 field campaign using a hyper-resolution model. Water Resour. Res. 2017, 53, 3013–3028. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, S.; Ma, J.; Li, J.; Li, X.; Wang, H.; Zang, W. Preliminary evaluation of the smap radiometer soil moisture product over china using in situ data. Remote Sens. 2017, 9, 292. [Google Scholar] [CrossRef]
- Chan, S.K.; Bindlish, R.; O’Neill, P.; Jackson, T.; Njoku, E.; Dunbar, S.; Colliander, A. Development and assessment of the SMAP enhanced passive soil moisture product. Remote Sens. Environ. 2018, 204, 931–941. [Google Scholar] [CrossRef]
- Xiong, L.; Yang, H.; Zeng, L.; Xu, C.Y. Evaluating Consistency between the Remotely Sensed Soil Moisture and the Hydrological Model-Simulated Soil Moisture in the Qujiang Catchment of China. Water 2018, 10, 291. [Google Scholar] [CrossRef]
- Xiong, L.; Guo, S.L.; Tian, X.R. DEM-based distributed hydrological model and its application. Adv. Water Sci. 2004, 15, 517–520. (In Chinese) [Google Scholar]
- Xiong, L.; Guo, S.L.; Chen, H.; Lin, K.R.; Cheng, J.Q. Application of the hydro-network model in the distributed hydrological modeling. J. China Hydrol. 2007, 2, 005. (In Chinese) [Google Scholar]
- Long, H.F.; Xiong, L.; Wan, M. Application of DEM-based distributed hydrological model in Qingjiang river basin. Resour. Environ. Yangtze Basin 2012, 21, 71–78. (In Chinese) [Google Scholar]
- Melching, C.S.; Yoon, C.G. Key sources of uncertainty in QUAL2E model of passaic river. J. Water Resour. Plan. Manag. 1996, 122, 105–113. [Google Scholar] [CrossRef]
- Minet, J.; Laloy, E.; Tychon, B.; François, L. Bayesian inversions of a dynamic vegetation model at four European grassland sites. Biogeosciences 2015, 12, 2809–2829. [Google Scholar] [CrossRef] [Green Version]
- Stasinopoulos, D.M.; Rigby, R.A. Generalized additive models for location scale and shape (GAMLSS) in R. J. Stat. Softw. 2007, 23, 1–46. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Tang, Y.; Marshall, L.; Sharma, A.; Smith, T. Tools for investigating the prior distribution in Bayesian hydrology. J. Hydrol. 2016, 538, 551–562. [Google Scholar] [CrossRef]
- Porporato, A.; Daly, E.; Rodriguez-Iturbe, I. Soil water balance and ecosystem response to climate change. Am. Nat. 2004, 164, 625–632. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, I.; Lin, K. A concordance correlation coefficient to evaluate reproducibility. Int. Biom. Soc. 1989, 45, 255–268. [Google Scholar]
- Xiong, L.; Wan, M.; Wei, X.J.; O’Connor, K.M. Indices for assessing the prediction bounds of hydrological models and application by generalized likelihood uncertainty estimation. Hydrol. Sci. J. 2009, 54, 852–871. [Google Scholar] [CrossRef]
- Kundu, D.; Vervoort, R.W.; van Ogtrop, F.F. The value of remotely sensed surface soil moisture for model calibration using SWAT. Hydrol. Process. 2017, 31, 2764–2780. [Google Scholar] [CrossRef]
- Pauwels, V.R.; De Lannoy, G.J. Improvement of modeled soil wetness conditions and turbulent fluxes through the assimilation of observed discharge. J. Hydrometeorol. 2006, 7, 458–477. [Google Scholar] [CrossRef]
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 12, 1323–1337. [Google Scholar] [CrossRef]
- Tang, Y.; Marshall, L.; Sharma, A.; Ajami, H. Modelling precipitation uncertainties in a multi-objective Bayesian ecohydrological setting. Adv. Water Resour. 2019, 123, 12–22. [Google Scholar] [CrossRef]
- Savin, N.E.; White, K.J. The Durbin-Watson Test for Serial Correlation with Extreme Sample Sizes or Many Regressors. Econometrica 1977, 45, 1989–1996. [Google Scholar] [CrossRef]


| Parameter | Unit | Ranges | Description | ISM | IQ |
|---|---|---|---|---|---|
| mm | 5–100 | Minimum water storage capacity | 0.01 | 0.03 | |
| mm | 5–700 | Range of water storage capacity across the catchment | 0.10 | 0.27 | |
| - | 0–1 | Empirical parameter, reflecting the relationship between and corresponding topographic index | 0.03 | 0.15 | |
| - | 0–1 | Proportion of residual groundwater in soil water storage capacity | 0.31 | 0.29 | |
| - | 0–1 | Empirical parameter, reflecting the characteristic of ground outflow | 0.15 | 0.03 | |
| h | 2–200 | Time constant, reflecting the characteristic of groundwater | 0.07 | 0.39 | |
| h | 2–200 | Time constant, reflecting the characteristic of surface flow | 0 | 0.01 | |
| - | 0–1 | Grid channel parameters of the Muskingum method | 0 | 0.20 | |
| - | 0–1 | River networks routing parameters of the Muskingum method for sub-catchment | 0 | 0.01 |
| Catchment | Warm-up Period | Calibration Period | Validation Period |
|---|---|---|---|
| Qujiang | April 2015–September 2015 | October 2015–March 2017 | April 2017–September 2017 |
| Upper Xijiang | April 2015–September 2015 | October 2015–May 2017 | June 2017–December 2017 |
| Catchment | Scenario | ||||
|---|---|---|---|---|---|
| QJ | S1 | - | - | ||
| S2 | - | - | |||
| M1 | |||||
| M2 | |||||
| M3 | |||||
| UXJ | S1 | - | - | ||
| S2 | - | - | |||
| M1 | |||||
| M2 | |||||
| M3 |
| Qujiang Catchment | Upper Xijiang Catchment | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | S1 | S2 | M1 | M2 | M3 | S1 | S2 | M1 | M2 | M3 | ||
| Calibration period | 71.25 | –24.79 | 57.32 | 65.04 | 71.57 | 57.22 | 13.05 | 72.52 | 79.52 | 81.70 | ||
| 2.31 | 75.62 | 5.33 | 3.62 | 2.59 | 2.84 | 6.51 | 2.82 | 1.28 | 1.38 | |||
| 5.49 | 50.71 | 7.77 | 5.28 | 3.52 | 11.41 | 38.25 | 0.41 | 0.39 | 0.18 | |||
| 0.46 | 29.36 | 5.11 | 3.32 | 1.97 | 4.05 | 30.85 | 4.32 | 2.52 | 1.79 | |||
| 90.35 | 94.72 | 90.53 | 89.79 | 90.89 | 85.37 | 85.37 | 77.55 | 82.72 | 84.74 | |||
| 610.01 | 1004.85 | 658.74 | 636.90 | 622.49 | 676.35 | 897.48 | 644.94 | 643.59 | 639.08 | |||
| 128.64 | 257.07 | 122.47 | 125.15 | 121.96 | 157.15 | 245.24 | 151.31 | 146.90 | 146.67 | |||
| Validation period | 70.10 | –23.48 | 52.73 | 59.60 | 65.90 | 56.79 | 16.81 | 77.90 | 82.90 | 84.77 | ||
| 2.68 | 67.65 | 5.96 | 4.35 | 3.35 | 1.88 | 4.78 | 1.88 | 0.93 | 0.99 | |||
| 5.81 | 53.52 | 9.43 | 6.89 | 5.16 | 12.09 | 33.65 | 0.01 | 0.05 | 1.02 | |||
| 0.47 | 31.30 | 6.95 | 5.07 | 3.11 | 4.70 | 30.77 | 2.98 | 1.94 | 0.01 | |||
| 80.01 | 69.40 | 74.87 | 77.59 | 80.24 | 77.46 | 66.20 | 58.22 | 60.09 | 63.38 | |||
| 1806.81 | 1611.26 | 1754.37 | 1649.91 | 1569.45 | 1260.93 | 1363.79 | 1176.83 | 1168.31 | 1159.15 | |||
| 412.97 | 580.35 | 407.90 | 407.59 | 396.64 | 345.76 | 511.94 | 298.76 | 297.53 | 296.20 | |||
| Qujiang Catchment | Upper Xijiang Catchment | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | S1 | S2 | M1 | M2 | M3 | S1 | S2 | M1 | M2 | M3 | ||
| Calibration period | –142.17 | 33.63 | 31.22 | 31.11 | 27.40 | –0.95 | 42.32 | 45.07 | 43.56 | 44.21 | ||
| 31.30 | 7.74 | 8.91 | 8.93 | 9.56 | 33.40 | 9.89 | 8.74 | 8.89 | 9.05 | |||
| 28.64 | 59.95 | 52.48 | 51.32 | 50.25 | 25.13 | 55.69 | 69.57 | 70.47 | 68.97 | |||
| 32.81 | 9.04 | 10.17 | 10.19 | 10.82 | 32.92 | 8.62 | 7.99 | 8.10 | 8.23 | |||
| 12.08 | 79.87 | 79.35 | 79.44 | 87.30 | 11.36 | 73.88 | 67.48 | 67.66 | 67.68 | |||
| 687.38 | 23.82 | 28.93 | 29.13 | 32.00 | 589.56 | 26.93 | 28.33 | 29.15 | 29.99 | |||
| 29.66 | 5.42 | 6.68 | 6.72 | 7.59 | 21.33 | 5.93 | 6.87 | 7.09 | 7.15 | |||
| Validation period | –119.05 | 36.74 | 36.00 | 35.89 | 32.94 | 6.58 | 45.62 | 46.74 | 48.35 | 46.68 | ||
| 20.29 | 9.30 | 10.06 | 10.05 | 10.37 | 24.25 | 8.72 | 10.02 | 10.47 | 10.51 | |||
| 23.76 | 63.18 | 56.37 | 55.44 | 54.42 | 36.86 | 64.14 | 58.07 | 58.10 | 61.17 | |||
| 31.33 | 9.91 | 10.97 | 10.99 | 11.57 | 25.66 | 7.80 | 9.10 | 9.45 | 9.54 | |||
| 14.47 | 75.19 | 72.14 | 73.76 | 83.94 | 13.61 | 75.94 | 71.58 | 71.88 | 71.76 | |||
| 161.28 | 26.58 | 28.86 | 29.74 | 29.37 | 389.76 | 27.96 | 24.50 | 23.54 | 24.02 | |||
| 19.68 | 6.67 | 7.20 | 7.19 | 7.61 | 17.88 | 4.98 | 5.16 | 5.25 | 5.29 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Xiong, L.; Ma, Q.; Xia, J.; Chen, J.; Xu, C.-Y. Utilizing Satellite Surface Soil Moisture Data in Calibrating a Distributed Hydrological Model Applied in Humid Regions Through a Multi-Objective Bayesian Hierarchical Framework. Remote Sens. 2019, 11, 1335. https://doi.org/10.3390/rs11111335
Yang H, Xiong L, Ma Q, Xia J, Chen J, Xu C-Y. Utilizing Satellite Surface Soil Moisture Data in Calibrating a Distributed Hydrological Model Applied in Humid Regions Through a Multi-Objective Bayesian Hierarchical Framework. Remote Sensing. 2019; 11(11):1335. https://doi.org/10.3390/rs11111335
Chicago/Turabian StyleYang, Han, Lihua Xiong, Qiumei Ma, Jun Xia, Jie Chen, and Chong-Yu Xu. 2019. "Utilizing Satellite Surface Soil Moisture Data in Calibrating a Distributed Hydrological Model Applied in Humid Regions Through a Multi-Objective Bayesian Hierarchical Framework" Remote Sensing 11, no. 11: 1335. https://doi.org/10.3390/rs11111335
APA StyleYang, H., Xiong, L., Ma, Q., Xia, J., Chen, J., & Xu, C.-Y. (2019). Utilizing Satellite Surface Soil Moisture Data in Calibrating a Distributed Hydrological Model Applied in Humid Regions Through a Multi-Objective Bayesian Hierarchical Framework. Remote Sensing, 11(11), 1335. https://doi.org/10.3390/rs11111335