A Censored Shifted Mixture Distribution Mapping Method to Correct the Bias of Daily IMERG Satellite Precipitation Estimates
Abstract
:1. Introduction
2. Study Area and Data Description
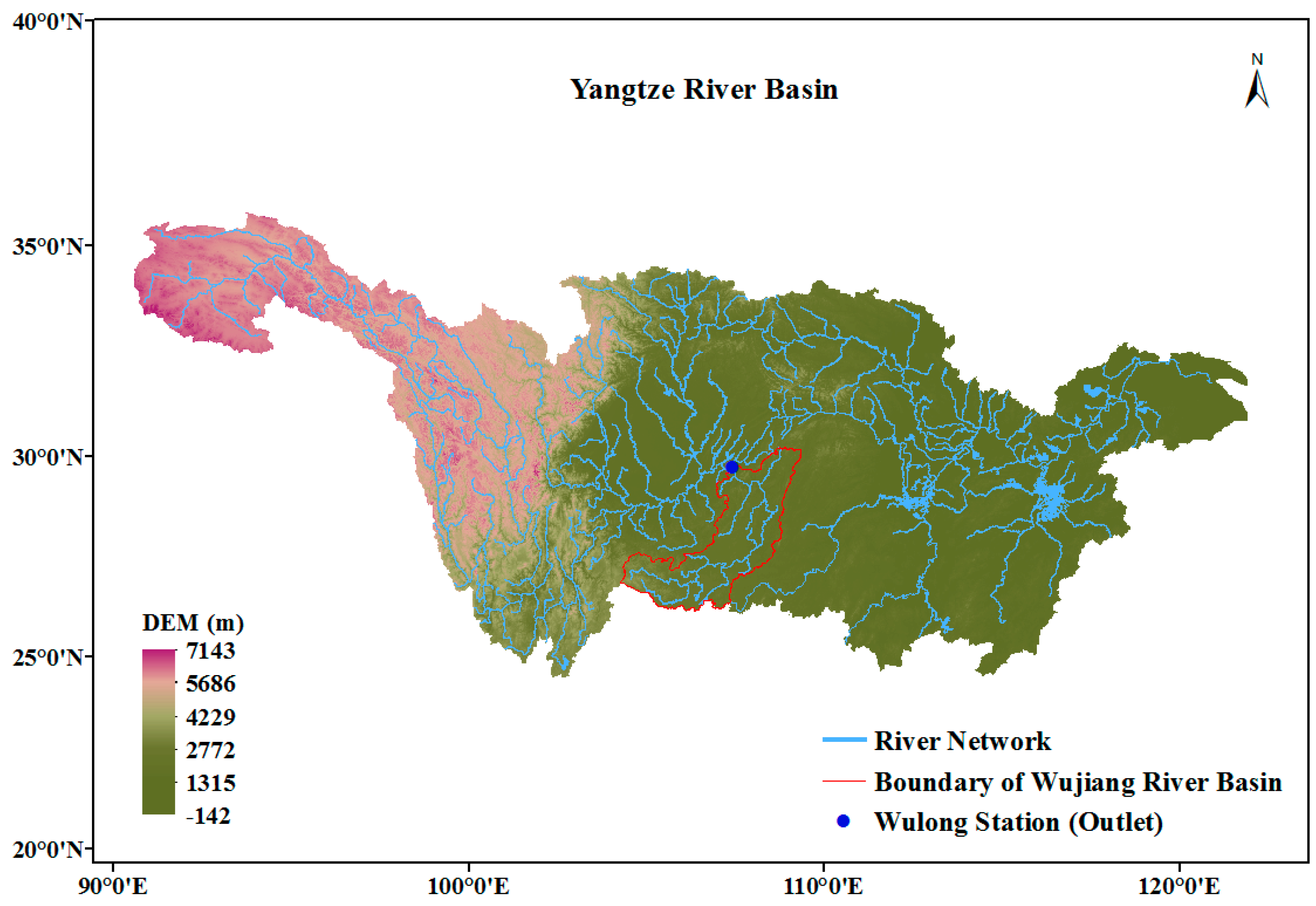
2.1. Yangtze River Basin
2.2. Integrated Multi-Satellite Retrievals for GPM (IMERG) Product
2.3. Gridded Ground Precipitation Data
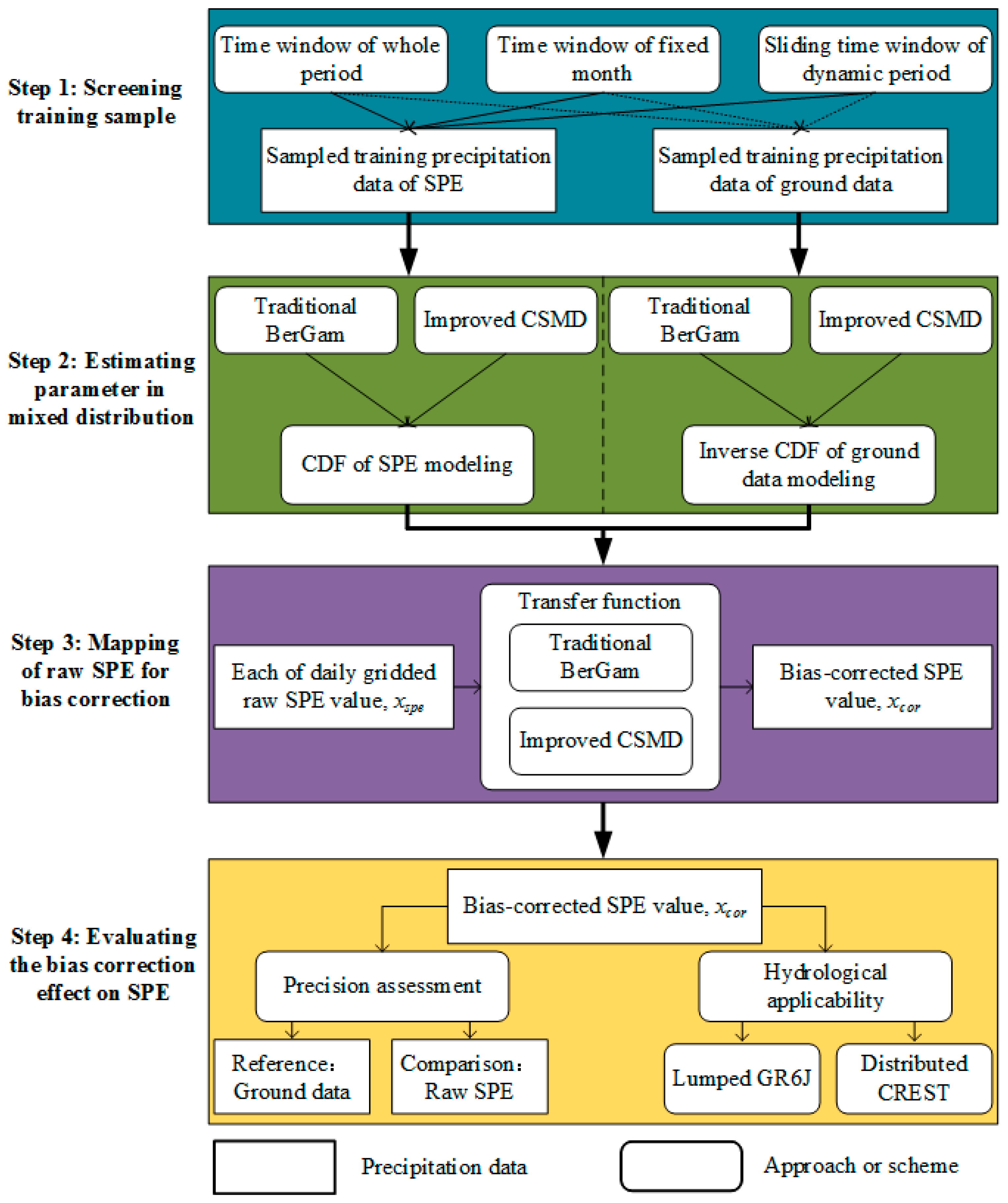
3. Methods
3.1. Bias Correction of SPE Based on Distribution Mapping
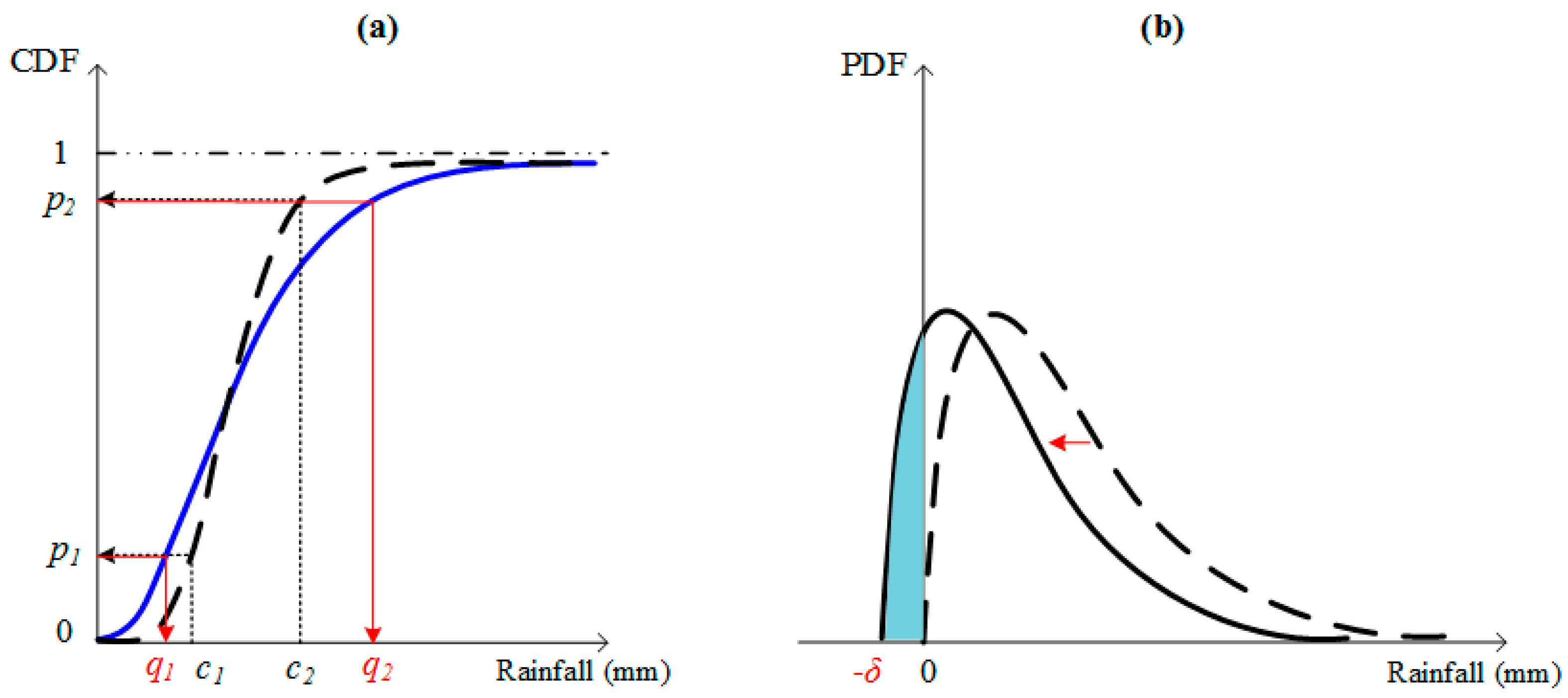
3.1.1. Bernoulli-Gamma (BerGam) Distribution of Traditional Bias Correction
3.1.2. Censored Shifted Mixture Distribution of Improved Bias Correction
3.2. Selection of the Time Window for Screening Precipitation Data
3.3. Streamflow Simulation Driven by Different Precipitation Inputs
3.4. Evaluation Indices
4. Results and Discussion
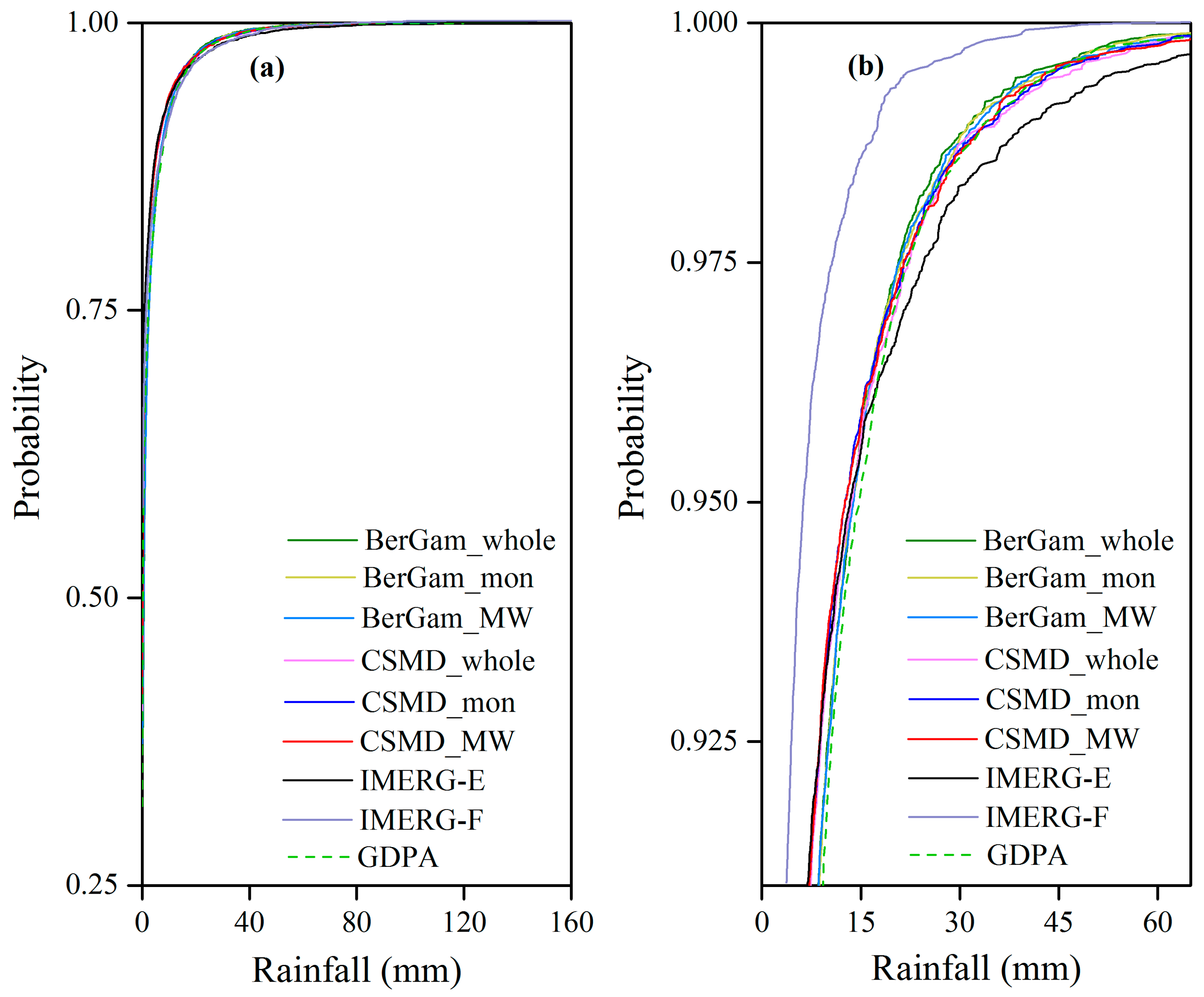
4.1. Assessment of the Raw IMERG-E and IMERG-F Against GDPA Data
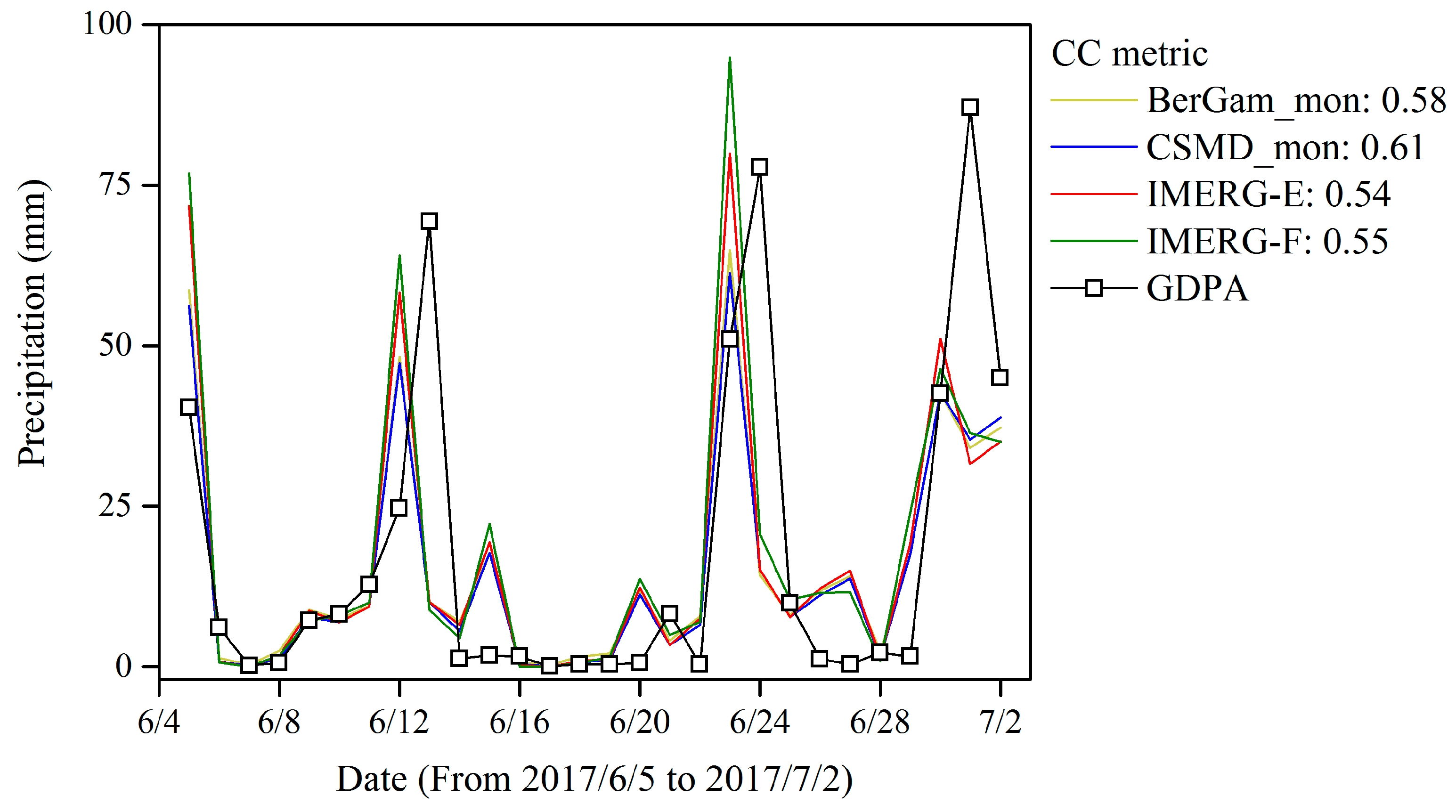
4.2. Performance of Corrected IMERG-E using CSMD and BerGam
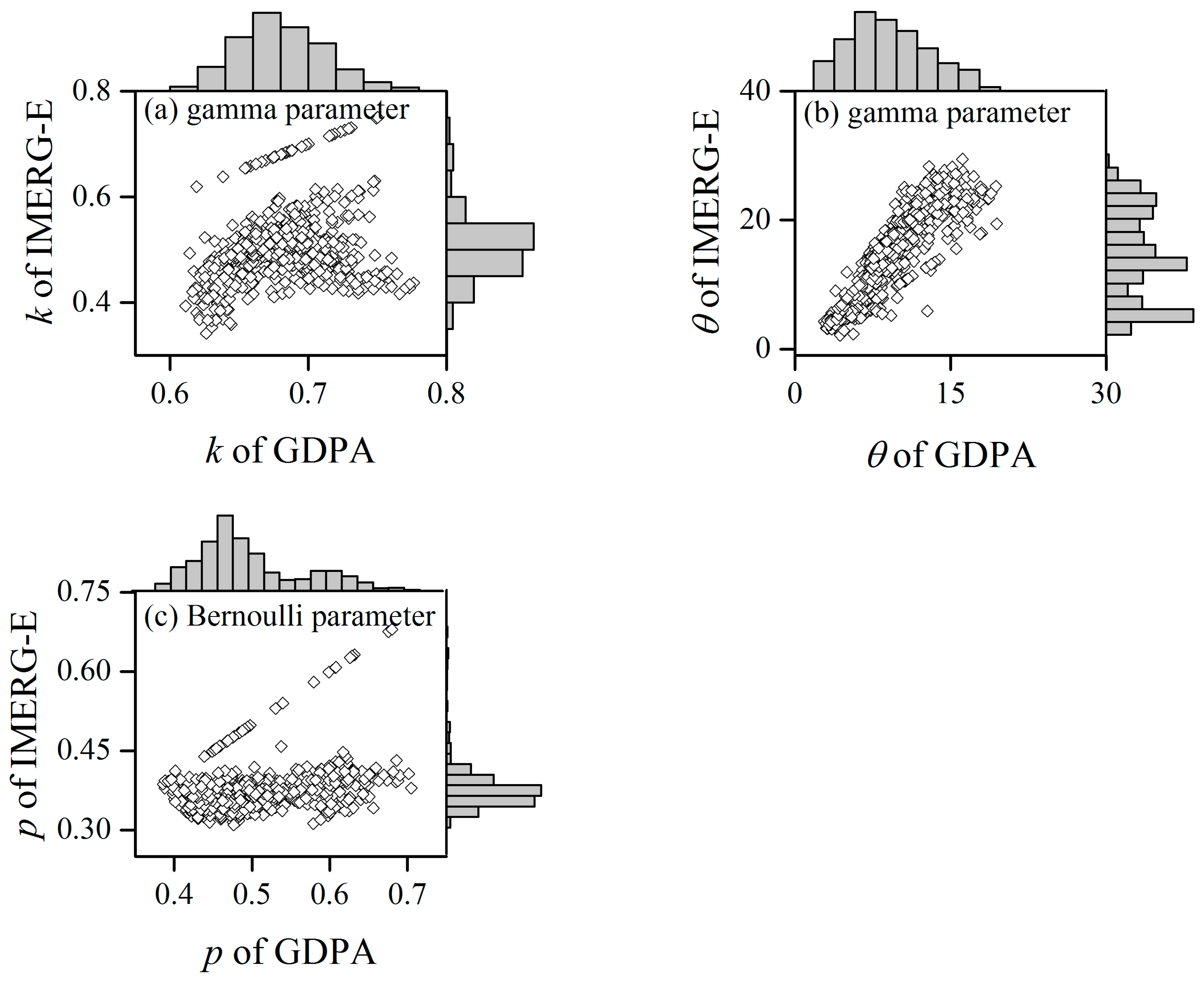
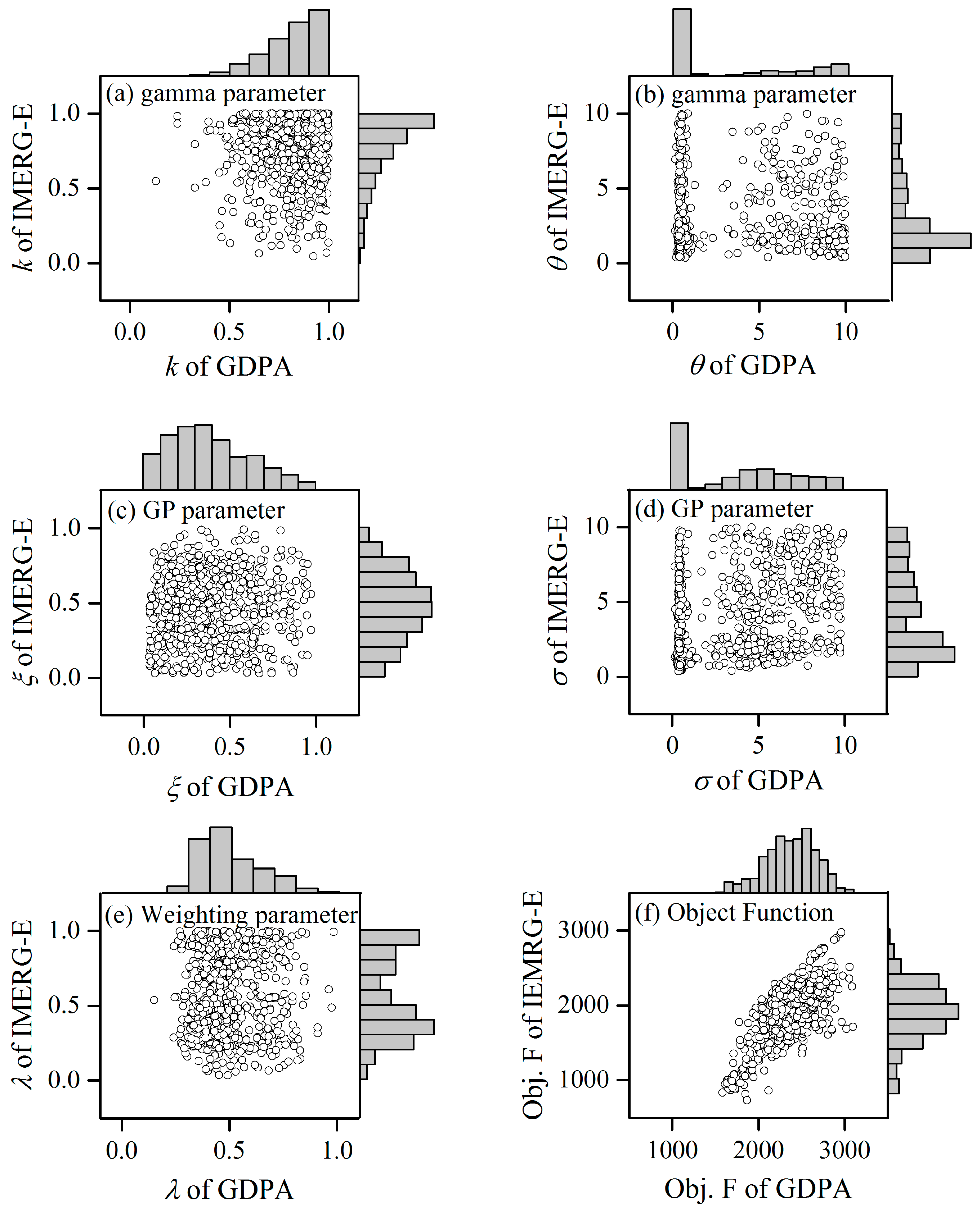
4.2.1. Parameter Estimation of Two Bias Correction Approaches
4.2.2. Comparison of CSMD Correction with BerGam Correction
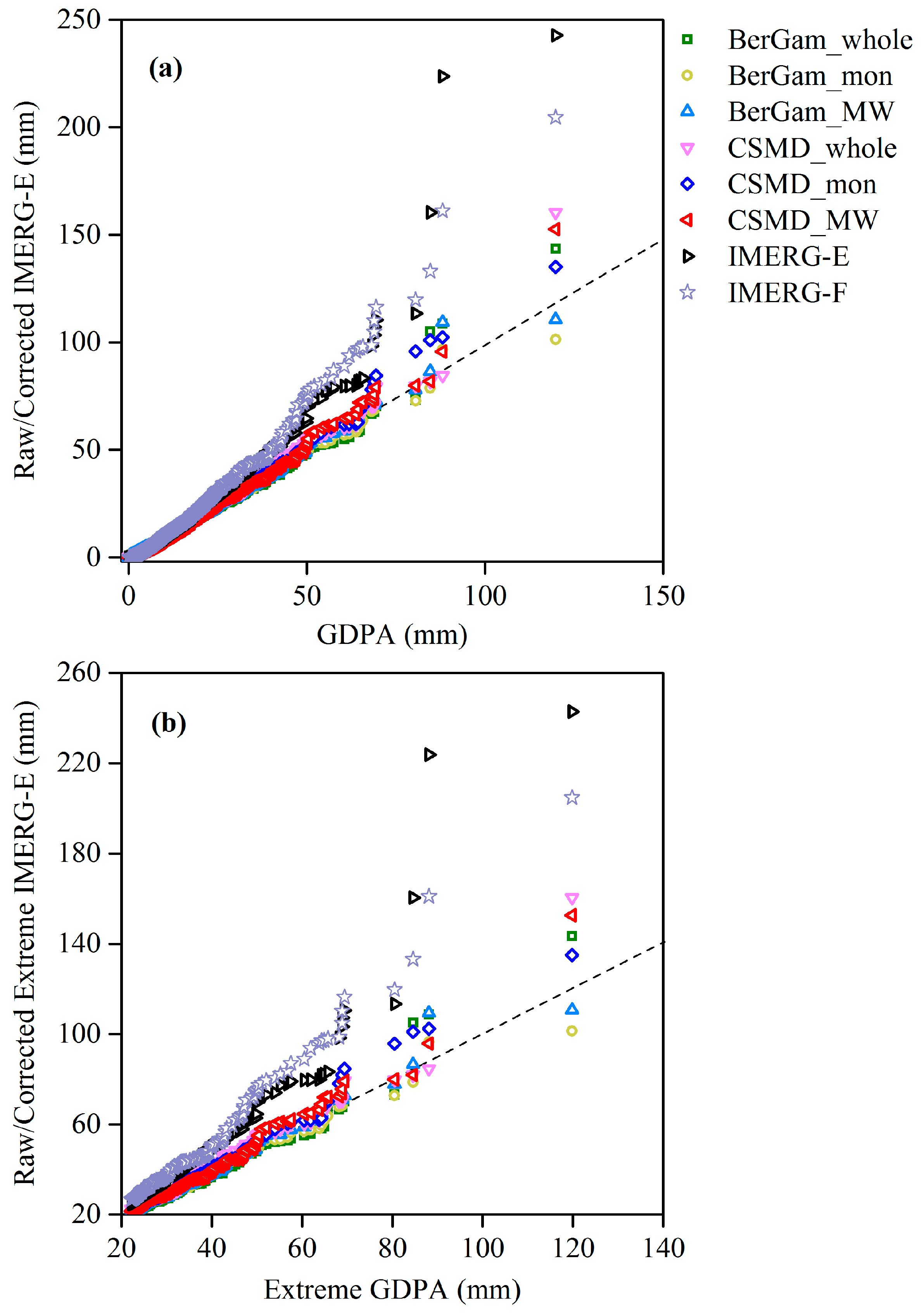
4.2.3. Performance of Corrected Extreme IMERG-E against GDPA
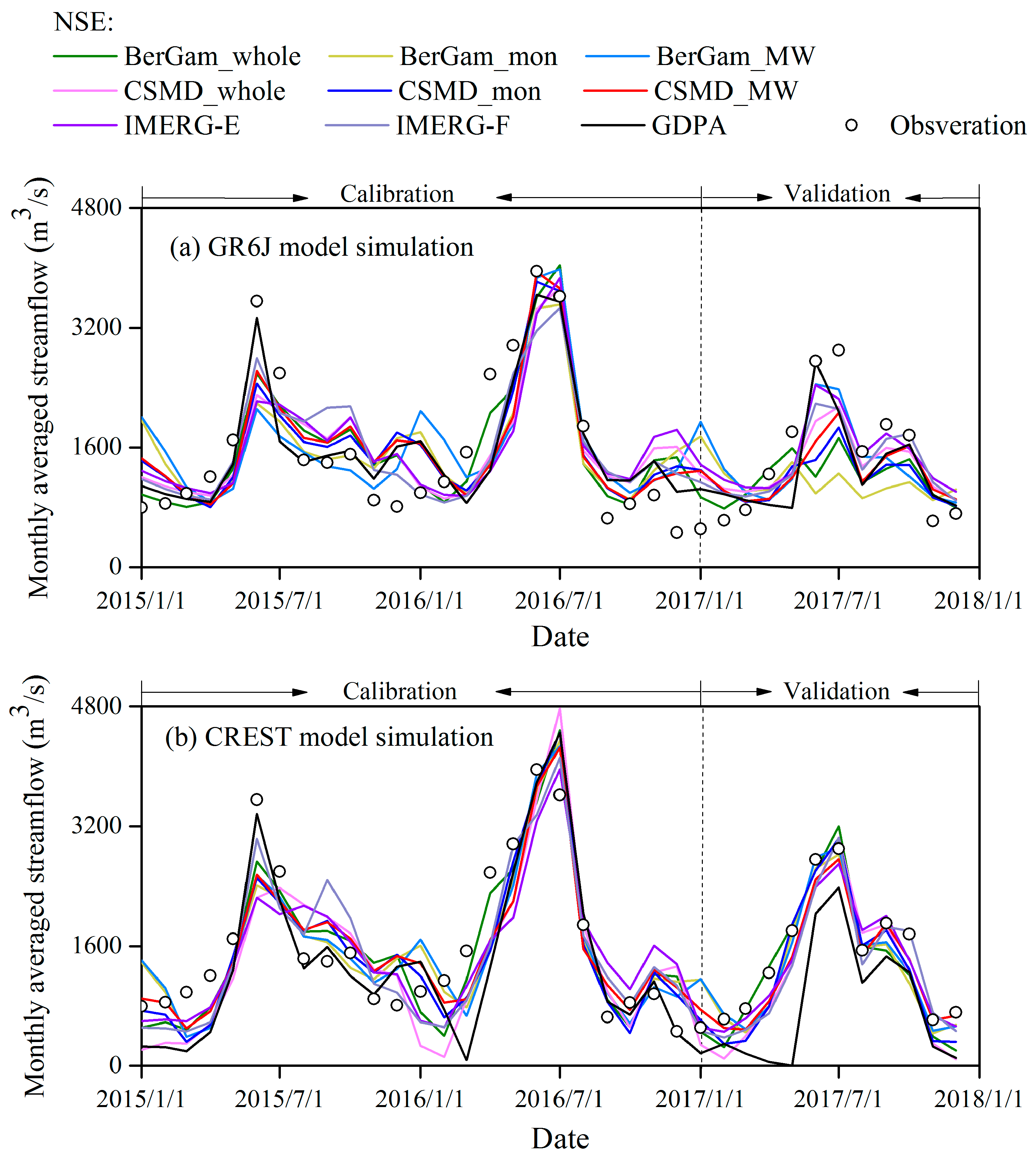
4.3. Evaluation of Simulated Streamflow Driven by Corrected IMERG-E
5. Summary and Conclusions
- (1)
- Both correction approaches of the improved CSMD and the traditional BerGam can significantly reduce the systematic bias of the satellite precipitation product IMERG-E. Furthermore, CSMD was superior to BerGam with respect to the deviation-dependent metrics of MAE, MD, and mNSE for precipitation assessment.
- (2)
- CSMD performed better in correction of the extremely high precipitation, which is the difficulty of the distribution mapping commonly used, as compared to the BerGam correction. This improvement in extreme values is mainly due to the mixture consisting of the generalized Pareto distribution focusing on the extreme value modeling.
- (3)
- The IMERG-E bias correction for CSMD via the sliding window scheme obtained slight improvement, compared to the whole period and monthly period time-window schemes, while there was no significant change among the three time-window schemes for BerGam.
- (4)
- The streamflow simulation driven by the CSMD-corrected IMERG-E outperformed that driven by the BerGam-corrected IMERG-E in more cases of calibration and validation (NSE of GR6J in validation: 0.44–0.51 versus −0.15–0.4 for CSMD and BerGam, respectively. NSE of CREST in validation: 0.62–0.74 versus 0.66–0.68). The distributed CREST model was more robust than the lumped GR6J in verifying the bias correction effect on satellite precipitation IMERG-E for modeling and prediction.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104, 70–97. [Google Scholar] [CrossRef]
- Collins, M.; AchutaRao, K.; Ashok, K.; Bhandari, S.; Mitra, A.K.; Prakash, S.; Srivastava, R.; Turner, A. Observational challenges in evaluating climate models. Nat. Clim. Chang. 2013, 3, 940–941. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Ma, Y.; Hong, Y.; Chen, Y.; Yang, Y.; Tang, G.; Yao, Y.; Long, D.; Li, C.; Han, Z.; Liu, R. Performance of optimally merged multisatellite precipitation products using the dynamic Bayesian model averaging scheme over the Tibetan Plateau. J. Geophys. Res. Atmos. 2018, 123, 814–834. [Google Scholar] [CrossRef]
- Vernimmen, R.; Hooijer, A.; Aldrian, E.; Van Dijk, A. Evaluation and bias correction of satellite rainfall data for drought monitoring in Indonesia. Hydrol. Earth Syst. Sci. 2012, 16, 133–146. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Tang, G.; Long, D.; Yong, B.; Zhong, L.; Wan, W.; Hong, Y. Similarity and error intercomparison of the GPM and its predecessor-TRMM Multisatellite Precipitation Analysis using the best available hourly gauge network over the Tibetan Plateau. Remote Sens. 2016, 8, 569. [Google Scholar] [CrossRef]
- Wright, D.B.; Kirschbaum, D.B.; Yatheendradas, S. Satellite Precipitation Characterization, Error Modeling, and Error Correction Using Censored Shifted Gamma Distributions. J. Hydrometeorol. 2017, 18, 2801–2815. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Ayana, E.K.; Maathuis, B.H.; MacAlister, C.; Philpot, W.D.; Leyton, J.M.O.; Steenhuis, T.S. Performance of bias corrected MPEG rainfall estimate for rainfall-runoff simulation in the upper Blue Nile Basin, Ethiopia. J. Hydrol. 2018, 556, 1182–1191. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.; Yang, L.; Hu, H.; Lu, H.; Hou, A. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network. J. Geophys. Res. Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-satellitE Retrievals for GPM (IMERG) technical documentation. NASA/GSFC Code 2015, 612, 47. [Google Scholar]
- Ma, Q.; Xiong, L.; Liu, D.; Xu, C.; Guo, S. Evaluating the Temporal Dynamics of Uncertainty Contribution from Satellite Precipitation Input in Rainfall-Runoff Modeling Using the Variance Decomposition Method. Remote Sens. 2018, 10, 1876. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.H. Algorithm Theoretical Basis Document (ATBD) Version 5.1. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V5.1b.pdf (accessed on 5 January 2019).
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of integrated multi-satellite retrievals for global precipitation measurement over China. Atmos. Res. 2016, 176, 121–133. [Google Scholar] [CrossRef]
- Gervais, M.; Tremblay, L.B.; Gyakum, J.R.; Atallah, E. Representing extremes in a daily gridded precipitation analysis over the United States: Impacts of station density, resolution, and gridding methods. J. Clim. 2014, 27, 5201–5218. [Google Scholar] [CrossRef]
- Abera, W.; Brocca, L.; Rigon, R. Comparative evaluation of different satellite rainfall estimation products and bias correction in the Upper Blue Nile (UBN) basin. Atmos. Res. 2016, 178, 471–483. [Google Scholar] [CrossRef]
- Teng, J.; Potter, N.J.; Chiew, F.; Zhang, L.; Wang, B.; Vaze, J.; Evans, J.P. How does bias correction of regional climate model precipitation affect modelled runoff? Hydrol. Earth Syst. Sci. 2015, 19, 711–728. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Duan, Q.; Miao, C.; Ye, A.; Gong, W.; Di, Z. A review on statistical postprocessing methods for hydrometeorological ensemble forecasting. Wiley Interdiscip. Rev. Water 2017, 4, e1246. [Google Scholar] [CrossRef]
- Müller, M.F.; Thompson, S.E. Bias adjustment of satellite rainfall data through stochastic modeling: Methods development and application to Nepal. Adv. Water Resour. 2013, 60, 121–134. [Google Scholar] [CrossRef] [Green Version]
- Gumindoga, W.; Rientjes, T.; Haile, A.T.; Makurira, H.; Reggiani, P. Bias correction schemes for CMORPH satellite rainfall estimates in the Zambezi River Basin. Hydrol. Earth Syst. Sci. Discuss. 2016, 1–36. [Google Scholar] [CrossRef]
- Yang, Z.; Hsu, K.; Sorooshian, S.; Xu, X.; Braithwaite, D.; Verbist, K.M. Bias adjustment of satellite-based precipitation estimation using gauge observations: A case study in Chile. J. Geophys. Res. Atmos. 2016, 121, 3790–3806. [Google Scholar] [CrossRef]
- Smitha, P.S.; Narasimhan, B.; Sudheer, K.P.; Annamalai, H. An improved bias correction method of daily rainfall data using a sliding window technique for climate change impact assessment. J. Hydrol. 2018, 556, 100–118. [Google Scholar] [CrossRef]
- Dunn, P.K. Occurrence and quantity of precipitation can be modelled simultaneously. Int. J. Climatol. 2004, 24, 1231–1239. [Google Scholar] [CrossRef] [Green Version]
- Cannon, A.J. Probabilistic multisite precipitation downscaling by an expanded Bernoulli–Gamma density network. J. Hydrometeorol. 2008, 9, 1284–1300. [Google Scholar] [CrossRef]
- Scheuerer, M.; Hamill, T.M. Statistical postprocessing of ensemble precipitation forecasts by fitting censored, shifted gamma distributions. Mon. Weather Rev. 2015, 143, 4578–4596. [Google Scholar] [CrossRef]
- Baran, S.; Nemoda, D. Censored and shifted gamma distribution based EMOS model for probabilistic quantitative precipitation forecasting. Environmetrics 2016, 27, 280–292. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wu, L.; Scheuerer, M.; Schaake, J.; Kongoli, C. Comparison of Probabilistic Quantitative Precipitation Forecasts from Two Postprocessing Mechanisms. J. Hydrometeorol. 2017, 18, 2873–2891. [Google Scholar] [CrossRef]
- Schleiss, M.; Chamoun, S.; Berne, A. Nonstationarity in intermittent rainfall: The “dry drift”. J. Hydrometeorol. 2014, 15, 1189–1204. [Google Scholar] [CrossRef]
- Baxevani, A.; Lennartsson, J. A spatiotemporal precipitation generator based on a censored latent Gaussian field. Water Resour. Res. 2015, 51, 4338–4358. [Google Scholar] [CrossRef] [Green Version]
- Volosciuk, C.D.; Maraun, D.; Vrac, M.; Widmann, M. A combined statistical bias correction and stochastic downscaling method for precipitation. Hydrol. Earth Syst. Sci. 2017, 21, 1693–1719. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Wang, Z.; Guo, S.; Liao, W.; Zeng, Z.; Chen, X. Scenario-based projections of future urban inundation within a coupled hydrodynamic model framework: A case study in Dongguan City, China. J. Hydrol. 2017, 547, 428–442. [Google Scholar] [CrossRef]
- Frigessi, A.; Haug, O.; Rue, H. A dynamic mixture model for unsupervised tail estimation without threshold selection. Extremes 2002, 5, 219–235. [Google Scholar] [CrossRef]
- McInerney, D.; Thyer, M.; Kavetski, D.; Lerat, J.; Kuczera, G. Improving probabilistic prediction of daily streamflow by identifying Pareto optimal approaches for modeling heteroscedastic residual errors. Water Resour. Res. 2017, 53, 2199–2239. [Google Scholar] [CrossRef]
- Choulakian, V.; Stephens, M.A. Goodness-of-fit tests for the generalized Pareto distribution. Technometrics 2001, 43, 478–484. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: Bristol, UK, 2001. [Google Scholar]
- Zhang, Y.; Sun, A.; Sun, H.; Gui, D.; Xue, J.; Liao, W.; Yan, D.; Zhao, N.; Zeng, X. Error adjustment of TMPA satellite precipitation estimates and assessment of their hydrological utility in the middle and upper Yangtze River Basin, China. Atmos. Res. 2019, 216, 52–64. [Google Scholar] [CrossRef]
- Yihui, D.; Chan, J.C. The East Asian summer monsoon: An overview. Meteorol. Atmos. Phys. 2005, 89, 117–142. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Gemmer, M.; Jiang, T.; Su, B.; Kundzewicz, Z.W. Seasonal precipitation changes in the wet season and their influence on flood/drought hazards in the Yangtze River Basin, China. Quat. Int. 2008, 186, 12–21. [Google Scholar] [CrossRef]
- Jiang, T.; Kundzewicz, Z.W.; Su, B. Changes in monthly precipitation and flood hazard in the Yangtze River Basin, China. Int. J. Climatol. 2008, 28, 1471–1481. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Ziese, M. GPCC Monitoring Product: Near Real-Time Monthly Land-Surface Precipitation from Rain-Gauges Based on SYNOP and CLIMAT Data; Global Precipitation Climatology Centre: Deutscher Wetterdienst, Germany, 2011. [Google Scholar]
- Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG Early, Late, and Final rainfall estimates using WegenerNet gauge data in southeastern Austria. Hydrol. Earth Syst. Sci. 2017, 21, 6559–6572. [Google Scholar] [Green Version]
- Xie, P.; Xiong, A.Y. A conceptual model for constructing high-resolution gauge-satellite merged precipitation analyses. J. Geophys. Res. Atmos. 2011, 116, D21106. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, Y.; Shen, Y.; Zhang, S. Evaluation of global satellite mapping of precipitation project daily precipitation estimates over the Chinese mainland. Adv. Meteorol. 2016, 2016, 9365294. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115, D02114. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A. Validation and comparison of a new gauge-based precipitation analysis over mainland China. Int. J. Climatol. 2016, 36, 252–265. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, Z.; Shen, Y.; Zhang, S.; Shi, R. Evaluation of satellite rainfall estimates over the Chinese Mainland. Remote Sens. 2014, 6, 11649–11672. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Hu, J.; Yang, B.; Stepanian, P. Comprehensive evaluation of high-resolution satellite-based precipitation products over China. Atmosphere 2016, 7, 6. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48, RG3003. [Google Scholar] [CrossRef]
- Vrac, M.; Naveau, P. Stochastic downscaling of precipitation: From dry events to heavy rainfalls. Water Resour. Res. 2007, 43, W07402. [Google Scholar] [CrossRef]
- Albert, C.; Künsch, H.R.; Scheidegger, A. A simulated annealing approach to approximate Bayes computations. Stat. Comput. 2015, 25, 1217–1232. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Mathevet, T.; Andréassian, V. A downward structural sensitivity analysis of hydrological models to improve low-flow simulation. J. Hydrol. 2011, 411, 66–76. [Google Scholar] [CrossRef]
- Coron, L.; Thirel, G.; Delaigue, O.; Perrin, C.; Andréassian, V. The suite of lumped GR hydrological models in an R package. Environ. Model. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- Khan, S.I.; Adhikari, P.; Hong, Y.; Vergara, H.; F Adler, R.; Policelli, F.; Irwin, D.; Korme, T.; Okello, L. Hydroclimatology of Lake Victoria region using hydrologic model and satellite remote sensing data. Hydrol. Earth Syst. Sci. 2011, 15, 107–117. [Google Scholar] [CrossRef] [Green Version]
- Le Moine, N. Le Bassin Versant de Surface vu Par le Souterrain: Une Voie D’amélioration des Performances et du Réalisme des Modèles Pluie-Débit? Ph.D. Thesis, Universite Pierre et Marie Curie, Paris, France, 2008. [Google Scholar]
- Ren-Jun, Z. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based Multi-satellite Precipitation Analysis over the Wangchu Basin of Bhutan: Are the latest satellite precipitation products 3B42V7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Gao, B.; Jiao, Y.; Hong, Y.; Xu, T. Multiscale hydrologic applications of the latest satellite precipitation products in the Yangtze River Basin using a distributed hydrologic model. J. Hydrometeorol. 2015, 16, 407–426. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Hong, Y. Cross-evaluation of ground-based, multi-satellite and reanalysis precipitation products: Applicability of the Triple Collocation method across Mainland China. J. Hydrol. 2018, 562, 71–83. [Google Scholar] [CrossRef]
- Wang, L.N.; Shao, Q.X.; Chen, X.H.; Li, Y.; Wang, D.G. Flood changes during the past 50 years in Wujiang River, South China. Hydrol. Process. 2012, 26, 3561–3569. [Google Scholar] [CrossRef]
- Li, S.; Zhou, L.; Wang, H.; Xiong, M.; Yang, Z.; Hu, J.; Liang, Y.; Chang, J. Short-term impact of reservoir impoundment on the patterns of mercury distribution in a subtropical aquatic ecosystem, Wujiang River, southwest China. Environ. Sci. Pollut. Res. 2013, 20, 4396–4404. [Google Scholar] [CrossRef]
- Hongmei, J.; Xinbin, F.; Qianjin, D. Damming effect on the distribution of mercury in Wujiang River. Chin. J. Geochem. 2005, 24, 179–183. [Google Scholar] [CrossRef]



| Name | Description | Range | Unit | |
|---|---|---|---|---|
| GR6J | X1 | Production store capacity | 100–1400 | mm |
| X2 | Intercatchment exchange coefficient | −4–4 | mm/d | |
| X3 | Routing store capacity | 0–500 | mm | |
| X4 | Unit hydrograph time constant | 0–10 | d | |
| X5 | Intercatchment exchange threshold | −4–4 | – | |
| X6 | Coefficient for emptying exponential store | 0–20 | mm | |
| CREST | Ksat | Soil saturate hydraulic conductivity | 10–3000 | mm/d |
| WM | Mean water capacity | 80–200 | mm | |
| B | Exponent of the variable infiltration curve | 0.05–1.5 | – | |
| IM | Impervious area ratio | 0–0.2 | – | |
| KE | Factor to convert the potential evapotranspiration (ET) to local actual ET | 0.1–1.5 | – | |
| coeM | Overland runoff velocity coefficient | 1.0–150 | – | |
| expM | Overland flow speed exponent | 0.1–2.0 | – | |
| coeR | Multiplier used to convert overland flow speed to channel flow speed | 1.0–3.0 | – | |
| coeS | Multiplier used to convert overland flow speed to interflow speed | 0.001–1.0 | – | |
| KS | Overland reservoir discharge parameter | 0–1.0 | – | |
| KI | Interflow reservoir discharge parameter | 0–1.0 | – |
| Statistical Metric | Perfect Match | Equation | |
|---|---|---|---|
| Precipitation | Mean absolute error (MAE) a | 0 | |
| Modified index of agreement (MD) b | 1 | ||
| Modified Nash–Sutcliffe efficiency (mNSE) | 1 | ||
| Kling-Gupta efficiency (KGE) c | 1 | ||
| Correlation Coefficient (CC) | 1 | ||
| Streamflow | Nash–Sutcliffe efficiency (NSE) d | 1 | |
| Correlation Coefficient (r) | 1 | ||
| Relative deviation (RD) | 0 |
| GR6J | CREST | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | |||||||||
| NSE | r | RD (%) | NSE | r | RD (%) | NSE | r | RD (%) | NSE | r | RD (%) | |
| BerGam_whole | 0.62 | 0.79 | −0.70 | 0.30 | 0.66 | −17.30 | 0.62 | 0.79 | −4.22 | 0.68 | 0.86 | −9.83 |
| BerGam_mon | 0.49 | 0.70 | −1.70 | −0.15 | 0.05 | −20.10 | 0.57 | 0.76 | −4.42 | 0.66 | 0.83 | −9.06 |
| BerGam_MW | 0.47 | 0.69 | 0.30 | 0.40 | 0.63 | −0.50 | 0.58 | 0.77 | −4.26 | 0.67 | 0.83 | −6.54 |
| CSMD_whole | 0.51 | 0.72 | −0.50 | 0.51 | 0.74 | −5.80 | 0.45 | 0.73 | −10.86 | 0.62 | 0.86 | −20.11 |
| CSMD_mon | 0.56 | 0.75 | 0.10 | 0.35 | 0.68 | −16.60 | 0.58 | 0.78 | −6.38 | 0.69 | 0.86 | −12.74 |
| CSMD_MW | 0.56 | 0.75 | 0.40 | 0.44 | 0.71 | −11.30 | 0.59 | 0.77 | −3.39 | 0.74 | 0.87 | −10.08 |
| IMERG-E | 0.45 | 0.68 | 0.80 | 0.48 | 0.69 | 2.80 | 0.52 | 0.72 | −6.14 | 0.74 | 0.87 | −9.77 |
| IMERG-F | 0.56 | 0.75 | 0.01 | 0.54 | 0.74 | −4.40 | 0.58 | 0.78 | −5.81 | 0.70 | 0.87 | −12.40 |
| GDPA | 0.62 | 0.79 | −1.40 | 0.45 | 0.71 | −10.50 | 0.56 | 0.80 | −13.72 | 0.17 | 0.79 | −45.91 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Xiong, L.; Xia, J.; Xiong, B.; Yang, H.; Xu, C.-Y. A Censored Shifted Mixture Distribution Mapping Method to Correct the Bias of Daily IMERG Satellite Precipitation Estimates. Remote Sens. 2019, 11, 1345. https://doi.org/10.3390/rs11111345
Ma Q, Xiong L, Xia J, Xiong B, Yang H, Xu C-Y. A Censored Shifted Mixture Distribution Mapping Method to Correct the Bias of Daily IMERG Satellite Precipitation Estimates. Remote Sensing. 2019; 11(11):1345. https://doi.org/10.3390/rs11111345
Chicago/Turabian StyleMa, Qiumei, Lihua Xiong, Jun Xia, Bin Xiong, Han Yang, and Chong-Yu Xu. 2019. "A Censored Shifted Mixture Distribution Mapping Method to Correct the Bias of Daily IMERG Satellite Precipitation Estimates" Remote Sensing 11, no. 11: 1345. https://doi.org/10.3390/rs11111345
APA StyleMa, Q., Xiong, L., Xia, J., Xiong, B., Yang, H., & Xu, C.-Y. (2019). A Censored Shifted Mixture Distribution Mapping Method to Correct the Bias of Daily IMERG Satellite Precipitation Estimates. Remote Sensing, 11(11), 1345. https://doi.org/10.3390/rs11111345








