Automatic Extraction of Gravity Waves from All-Sky Airglow Image Based on Machine Learning

Abstract

With the development of ground-based all-sky airglow imager (ASAI) technology, a large amount of airglow image data needs to be processed for studying atmospheric gravity waves. We developed a program to automatically extract gravity wave patterns in the ASAI images. The auto-extraction program includes a classification model based on convolutional neural network (CNN) and an object detection model based on faster region-based convolutional neural network (Faster R-CNN). The classification model selects the images of clear nights from all ASAI raw images. The object detection model locates the region of wave patterns. Then, the wave parameters (horizontal wavelength, period, direction, etc.) can be calculated within the region of the wave patterns. Besides auto-extraction, we applied a wavelength check to remove the interference of wavelike mist near the imager. To validate the auto-extraction program, a case study was conducted on the images captured in 2014 at Linqu (36.2°N, 118.7°E), China. Compared to the result of the manual check, the auto-extraction recognized less (28.9% of manual result) wave-containing images due to the strict threshold, but the result shows the same seasonal variation as the references. The auto-extraction program applies a uniform criterion to avoid the accidental error in manual distinction of gravity waves and offers a reliable method to process large ASAI images for efficiently studying the climatology of atmospheric gravity waves.

1. Introduction

Gravity waves (GWs) are generated by the disturbance of the atmosphere parcel due to the unbalance between the gravity force and buoyancy force on the parcel. When GWs propagate away from their source region, they transport energy and momentum to the Mesosphere and Lower Thermosphere (MLT) [1] and even into the thermosphere [2]. Thus, its important roles in the atmospheric circulation have been recognized and reviewed [3,4,5].

When airglow is disturbed by GWs, its brightness changes due to the temperature fluctuations caused by GWs. Hence, airglow can act as a tracer for observing GWs. Since Peterson and Adams [6] captured the first airglow image of GWs with an all-sky airglow imager (ASAI) during the total lunar eclipse in 1982, ASAI has been widely applied to observe GWs [7,8,9,10]. Several years of ASAI GW observations have been analyzed, revealing the influence of the local environment on the occurrence frequency, propagating direction, horizontal wavelengths, and phase speeds of GWs [11,12,13,14]. To accumulate data, the Chinese Meridian Space Weather Monitoring Project [15] set up an airglow observation network of more than 10 sites since 2009 [10]. The identification of GWs from the massive ASAI images remains a challenging task for manual operations.

Automatic GW image detection has already been attempted with analysis in the frequency domain. Matsuda et al. [16] developed a statistical analysis method with three-dimensional (3D) Fourier transformation of GW images of time series. They used this method to extract the characteristics of the GW captured in a period of more than one month [17]. Hu et al. [18] applied a two-dimensional (2D) Stockwell transform to detect and characterize the GWs in satellite images. However, to obtain more information (e.g., wavelength, period, phase speed, and GW climatology) from the large ASAI images, the processing method requires the capacity of locating the wave pattern areas with high efficiency, and robustness.

Machine learning provides a route to automatically identify GW images. Inspired by the cat’s eye, Hubel and Wiesel [19] first proposed the convolutional neural network (CNN) for image processing in machine learning. LeCun et al. [20] designed a CNN using the backward propagation algorithm to apply CNN to computer vision. LeCun et al. [21] developed a LeNet-5 multi-layer neural network to classify handwritten digits, and established the modern structure of the CNN. Krizhevsky et al. [22] built a CNN called AlexNet, which further improved the ability of machine learning and won the ImageNet image recognition competition in 2012. To target the location of an object in an image, Ren et al. [23] proposed the faster regional convolutional neural network (Faster R-CNN). With the development of algorithms and computer capabilities, Clausen and Nickisch [24] trained a model based on the deep neural network and used the model as a classifier of six categories to distinguish whether auroras in images. However, there has no attempt to automatically detect or extract GW images with machine learning to the best of our knowledge.

We designed a two-step automatic extraction program to identify GW images and calculate their parameters automatically. First, the images of clear sky and unclear sky (e.g., with clouds or overexposed images) are classified. The images of the clear sky are selected and unwarped onto geographic maps. Second, the GW-containing images are extracted. The GW-containing images are selected and the regions of wave pattern are framed with rectangles. This program has two advantages: a unified criterion to avoid accidental errors caused by manual GW extraction, and high efficiency to process ASAI images for climatological studies of GWs.

This paper is organized as follows: Section 2 briefly introduces the ASAI data used in this study. Section 3 outlines the overall framework of our auto-extraction program. Section 4 describes the procedure for training and validating the classification model of CNN in detail. Section 5 presents the procedure for training the GW location model of Faster R-CNN. Section 6 describes the calculation of GW parameters. Section 7 compares the auto-extraction result with the manual result for validation, using the data from Linqu station (36.2°N, 118.7°E), China in 2014. Section 8 provides some discussion about our automatic GW detection program. Section 9

2. Instrument and Data Description

All data used in this paper were captured by the ASAI at Linqu station (36.2°N, 118.7°E), China. The ASAI uses a Nikkor 16 mm f/2.8D fish eye lens with a near-infrared (715–930 nm) filter to capture the OH emission at the height of 87 ± 5 km [12]. The raw data were stored in a 1024 × 1024 pixel CCD (charge-coupled device) detector in hexadecimal and are converted into decimals to illustrate the raw images. The interval between two adjacent photographs was 64 s, in which the exposure time was 60 s and the storage time was 4 s [10,14]. The raw image of ASAI has a warped round version with an 180° zenith angle due to the fish eye lens, and displays stars in the sky on clear nights. The spatial resolution has a highest value of 0.27 km at the zenith and decreases as the zenith angle increases. The OH airglow images from Linqu station are of medium observation quality compared with images from other stations in China. Hence, the trained models based on data from Linqu station can be adapted to other stations.

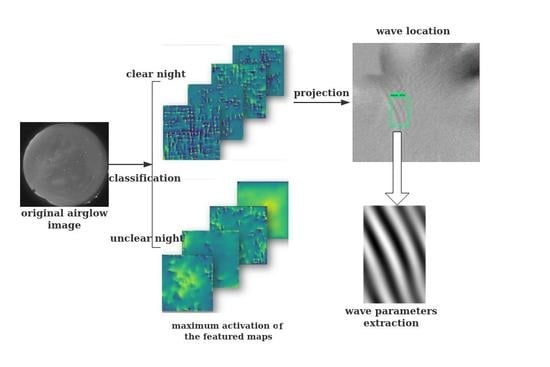
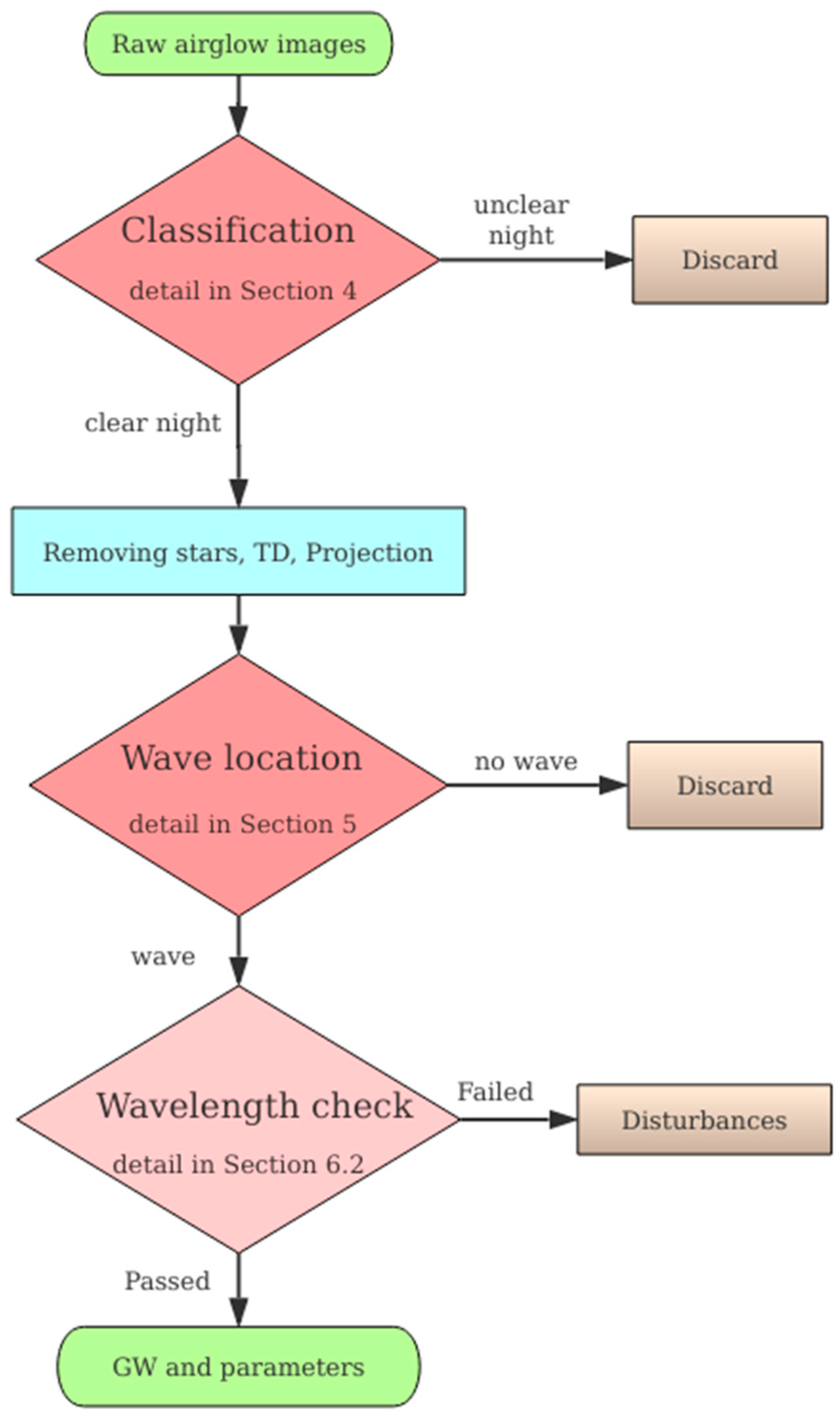
3. Frame of the Detection Program

The frame of the detection program is shown in Figure 1. Raw airglow images are classified by the classification model based on CNN to distinguish the ASAI raw images of clear and unclear nights. The raw images of clear nights are then processed with star-removing, time difference (TD), and are then unwarped by projecting to geographic coordinates [12]. The unwarped images are identified by the object detection model trained on Faster R-CNN to locate the wave patterns. The wavelengths of the wave patterns are then calculated and checked to determine if the wave patterns are GWs or other disturbances. Traditionally, the steps of classification and wave location are performed manually, which means a large amount of work and unavoidable accidental error. Replacing manual detection with automatic extraction based on machine learning can solve these problems.

4. Classification

In this step, we built a CNN to classify the warped raw images captured by ASAI and filtered out the images obtained on unclear nights, such as with cloudy sky or camera overexposure. The CNN performs the machine learning training process based on the prepared images in the dataset (including training set and validation set) to modify the trainable parameters of CNN to minimize the loss of classification. These parameters are stored in a generated model for being called during identification. The dataset is divided into a number of batches (groups). The number of images sampled for training in a single batch is called batch size. The process of a batch of data passing through the CNN is called an iteration. The trainable parameters are updated after each iteration. After the whole dataset is passed through the CNN, an epoch is finished. Usually, more than one epoch is required to complete the training.

We attempted to simplify the architecture of CNN and to reduce the computational cost to make the training and classification affordable for a personal computer. Based on Tensorflow (an open-source software library) and Keras (a high-level neural networks application programming interface; API) [25], the program was completed within 100 lines in Python.

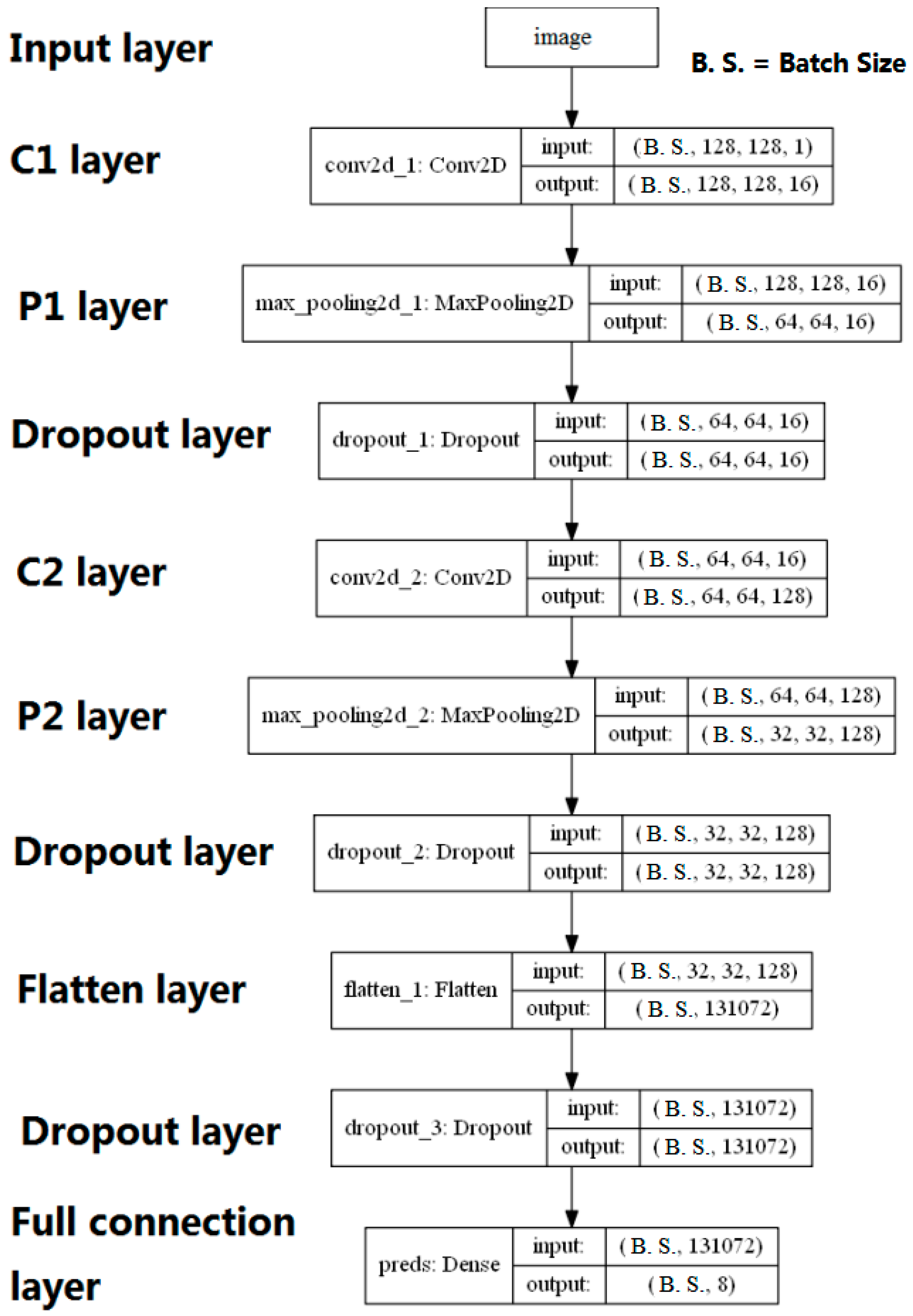
4.1. Architecture of CNN

The CNN is widely used for image recognition in machine learning because of its advantage in computation and extracting the features of images [21]. We built a CNN to classify the raw images of the ASAI into 8 categories. As shown in Figure 2, our CNN consists of an input layer, two convolutional layers, two pooling layers, three dropout layers, one flatten layer, and one full connect layer, with an 8-way Softmax [26] acting as the classifier. The layers are composed of neurons, which are the basic units of a neural network. A neuron includes a node to store and process data, and connections to the neurons in the previous layer and next layer.

The first layer is the input layer, where an input image is resized and transferred to a 128 × 128 × 1 tensor. Since images captured by the ASAI are grayscale images, the depth of the tensor in the input layer is 1 instead of 3 for colorful images in RGB form.

The C1 layer in Figure 2 is a convolutional layer, where the sub-structures of images are scanned and convoluted with filters. The filters are also called convolutional kernels, which are 3 × 3 matrixes here. For every 128 × 128 × 1 image input to the C1 layer, a corresponding 128 × 128 × 1 feature map is generated and stored in 128 × 128 × 1 neurons. Each neuron is connected to a 3 × 3 region in the input image. A neuron at (p,q) in the feature map f ^l output by filter l is:

$$f^l(p,q)=\mathrm{Re}\mathrm{LU}({\displaystyle \sum _{i=0}^2{\displaystyle \sum _{j=0}^{2}m(p+i,q+j)w_{i,j}^l}}+b^l) \forall p,q\in \left[1,130\right]$$

(1)

where m denotes the input image. To keep the image size unchanged, the input images are padded to 130 × 130 × 1 with pixels of 0 at four sides before convolution. The kernel elements $w_{i,j}^l$ (i, j = 0,1,2) indicate the 9 weights in filter l and b^l is the bias of filter l, both of which are trainable parameters. The destination of training in the machine learning is to find suitable value for such weights and biases to minimize the final loss. For one filter, all neurons in the feature map share the same weights and bias, which greatly reduces the number of weight parameters from 128 × 128 to 3 × 3. Besides reducing the computing burden, another advantage of using kernels is that the detection program can focus on the features of the local region of images while ignoring their relative positions. Both advantages improve the efficiency of the classification.

ReLU is the abbreviation of the activation function rectified linear unit, which is popularly used in constructing deep neural networks due to its efficiency in reducing the training error rate [22]. ReLU can be written as:

$$\mathrm{Re}\mathrm{LU}(x)=\max (x,0)$$

(2)

When an image is input to the C1 layer and zero-padded to a matrix of 130 × 130, the kernel slides on the matrix with the stride of 1, covering a 3 × 3 region (also called the local sensing field) in the zero-padded image at each step. It takes 128 × 128 steps for the kernel to go through every local sensing field of the padded image. In each single step, the dot production of the kernel and the local sensing field is added to the bias and then transferred to the neuron in the C1 layer through ReLU, as shown in Equation (1). Thus, each local sensing field is extracted by convolution and stored in the neuron connected to this region as a pixel in the feature map. In total, 16 kernels with different weights and biases are applied to every input image of C1 layer, so that the output data are a 128 × 128 × 16 tensor for one single input image.

The P1 layer is a pooling layer, and it functions to reduce the number of parameters and computation by progressively decreasing the size of the featured map. The max pooling method is used in the P1 layer: a 2 × 2 pooling window slides along the feature map with a stride of 2, and only outputs the maximum value of the covered 2 × 2 block in the feature map. Unlike the kernel, the pooling window does not have trainable parameters and the blocks do not overlap. After max pooling, the width and length of the feature map are reduced to half so that the size of the output of P1 layer is 64 × 64 × 16, while the size of the input to P1 layer is 128 × 128 × 16.

As shown in Figure 2, the P1 layer is followed by a dropout layer. Dropout works by randomly dropping a neuron from the network to prevent overfitting [27]. The dropout layer has 64 × 64 × 16 neurons, which connect with the neurons in the P1 layer one by one. Every neuron in the dropout layer has a separate random value between 0 and 1. The neuron outputs the data received from the previous layer if the random value is greater than p (p is 0.5 in our CNN). Otherwise, the neuron is temperately dropped out and outputs 0. The random value of every neuron will be regenerated at every iteration during the training. The following two dropout layers act similar to this one, having the same number of neurons as their previous layers.

In the next 3 steps, the network repeats the process of convolution, max pooling, and dropout in the C2 layer, P2 layer, and dropout layer. Note that there are 128 kernels with a dimension of 5 × 5 × 16 used in the C2 layer for convolution. So, every neuron in the P2 layer is connected to a region of 5 × 5 × 16 neurons in the C2 layer.

In the flatten layer, the input 32 × 32 × 128 tensor is flattened to a one-dimensional array of 131,072 elements. Through the following dropout layer, the array is output to the full connect layer.

There are 8 neurons in the full connect layer (FC layer), one for each category of the raw images. Every neuron in the FC layer is connected to all neurons in the previous dropout layer. The value C_u of uth neuron in the FC layer is the dot production of the array output from the previous dropout layer and its corresponding weights:

$$C_u={\displaystyle \sum _{v=1}^{131702}{w}_u{}_{,v}·n_v} u=1,2,\dots 8,$$

(3)

where w_u,v is the weight of the uth neuron in the FC layer for the vth input element and n_v indicates the vth element in the input array. For better expressing the classification results of sampled raw image m, the outputs are normalized by the Softmax function [26] to determine the probability p(m)_u of the uth category:

$$p{\left(m\right)}_u=\raisebox{1ex}{$e^{c_u}$}\!\left/ \!\raisebox{-1ex}{${\sum }_{k=1}^8{e}^{c_k}$}\right.$$

(4)

Now, the CNN has analyzed the loaded raw image and determined eight probabilities, the sum of which is 1. The image is classified according to the highest scores of the 8 probabilities. Being regarded as a function F, the whole process of CNN can be simply expressed as:

$$F\left(m\right)=u.$$

(5)

The input of CNN is an image m and the output is a prediction of the uth category of this image.

Loss is used to measure the degree of inconsistency between the predicted value and the real value of the object. The loss of CNN is calculated with a cross-entropy loss function [28]:

$$L_m=-\log p_g$$

(6)

where L_m is the loss of an input image m, and g indicates the ground true category for the input image, which is labeled to this image manually when the training dataset is created. In Equation (6), the higher the probability p_g, the lower the loss. p_g may not be the highest among the 8 category scores if the prediction of CNN is wrong. This situation normally leads to larger loss. In the ideal case, the probability of g is 1 (p_g = 1) while the other seven probabilities are all 0, so that the loss is 0.

4.2. Training and Validation with Datasets

The data used to train the classification model were obtained by the ASAI located at Linqu, from 1 October 2013 to 31 December 2013. Visible stars in the night sky were considered signs of clear nights. However, the artificial light at the edge of the round field of vision in the warped raw image is brighter than stars and is mis-identified as stars by the computer. To avoid the disturbance of artificial light and distortion at the edge, a 512 × 512 matrix at the center of the image was cropped for training and detection in the classification step (Figure 3). The range of the matrix is also close to the effective observation area of the ASAI [10].

To reduce the similarity of the images, we chose one image from every five consecutive images. In total, 1818 images were selected and divided into 8 categories according to the contents in their cropped region, as shown in Figure 4. The eight observed phenomena were denoted by category letters from a to h (Figure 4), which were one-to-one matched with the category number i ∈ [1, 2, … 8] output by Equation (5). There were eight categories instead of two coarse classification of star and starless, because the fine classification leads to a simpler architecture of CNN, less training time, and even higher accuracy. The images belonging to categories a, b, c and e (category numbers 1, 2, 3, and 5, respectively) were considered as clear night in which the GW patterns are visible.

About one-sixth of the images in each category were moved to the validation set while the other 1515 classified images were left in the training set to modify the trainable parameters. To expand the dataset, all images were quadrupled by being rotated 90°, 180°, and 270° [22,29]. Hence, there were a total of 7272 images: 6040 for training and 1212 for validation.

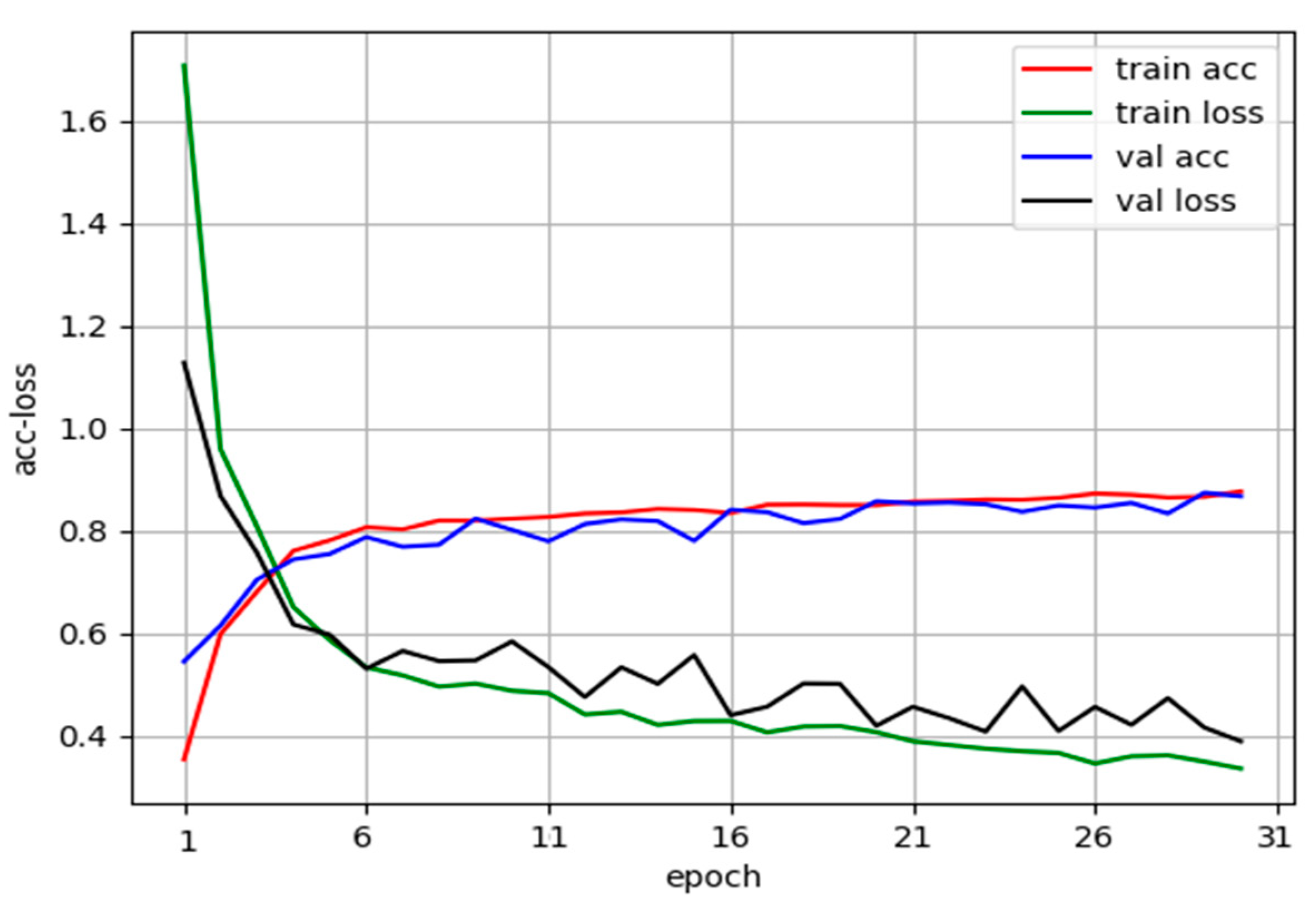
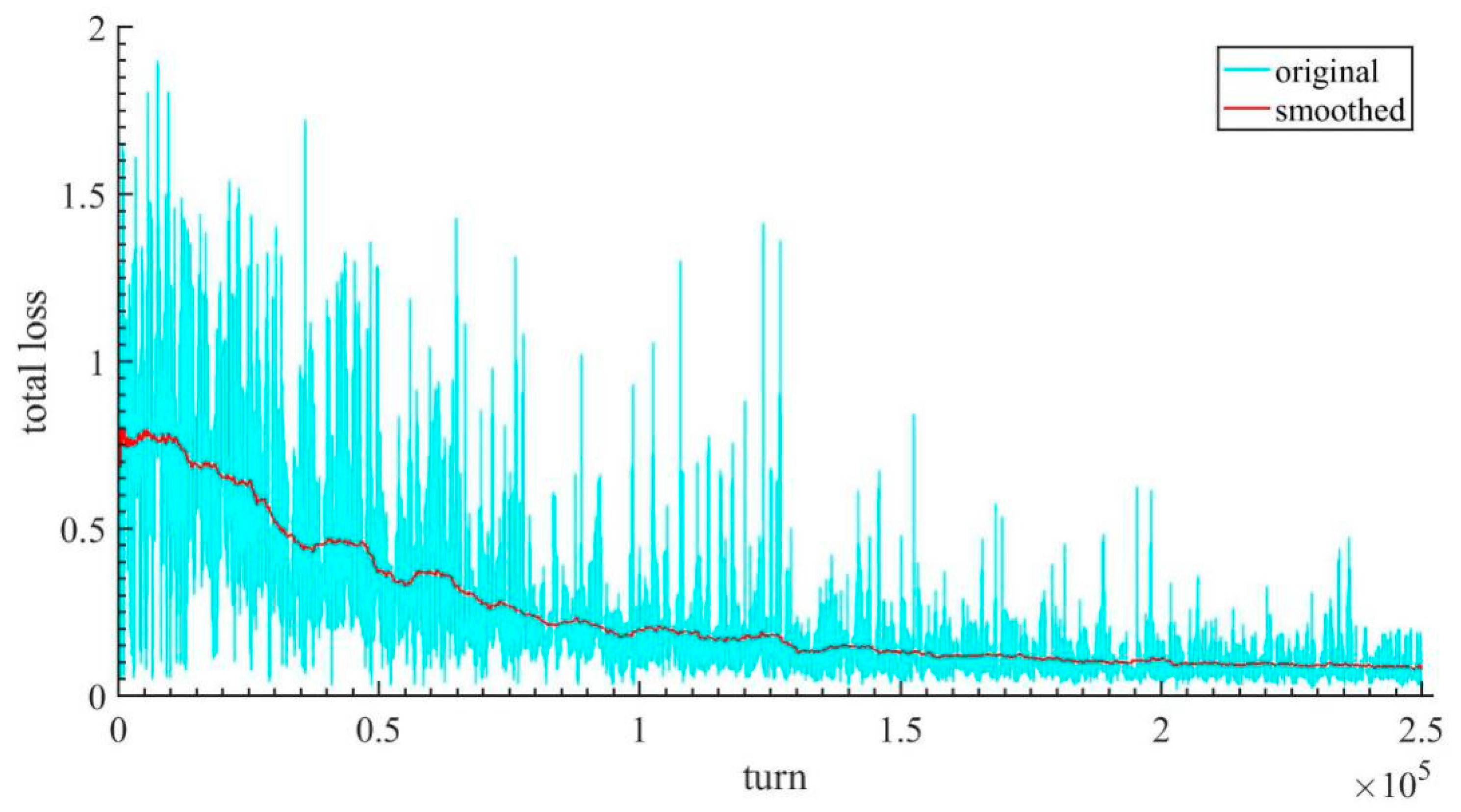
4.3. Training Process

In the training process, the trainable parameters are modified through iterations to minimize the loss of classification. In one epoch, all data in the training set are divided into 61 iterations to pass through the CNN. The trainable parameters are modified by the mini-batch gradient descent [30]:

$${\theta }^{\prime }=\theta -\eta ·{\nabla }_{\theta }L(\theta ;m_{t·z+1:t·z+z}), t=0,1,2,\dots 60,$$

(7)

where θ′ and θ denote the trainable parameters in the next and previous iteration step, respectively. θ′ and θ are vectors containing all trainable parameters (weights and biases). The initial parameters are evaluated randomly at the beginning of training. η is the learning rate, which is 0.001 by default in Keras API [25]; m_{t·z+1:t·z+z} is the mini-batch of images loaded in the tth iteration; and z is the batch size. The batch size for the first 60 iteration is 100, which means 100 samples of images are randomly loaded from training set in every iteration without repetition. The batch size for the last iteration is 40, since there are only 40 images left after 60 iterations. L is the average loss for parameters θ and image set x, ∇_θL indicates gradient of L with respect to θ, and the gradient is derived by the back-propagation algorithm [31,32] for its advantages in rapid learning speed and avoiding the local minimum trap.

The changes in accuracy and loss of both training and validation sets in multiple training epochs are shown in Figure 5. The accuracy is defined as the rate of correct predictions of classification over total number of predictions. The loss is the average loss of all predictions in one epoch. At the beginning of training, all loss and accuracy curves are very sharp because the randomly evaluated initial parameters are quickly corrected to a reasonable interval within several epochs. Due to the limitation of our computer memory, the batch size was small so that the random errors that occurred in the loading images were relatively big. The oscillations in both loss and accuracy curves of validation were caused by these random errors. After 30 epochs of training, although the losses of train and validation sets still continued converging, the accuracies of both datasets began to decrease, which indicates the model was overfitted. Hence the training process was stopped with an accuracy of 89.49%, as shown in Figure 5.

The 8 categories in Figure 4 are not absolutely distinguished, such as starring (a) and whitening and starring (b). Categories a and b have an overlapped area, where images do not have a clear distinction for classification, even for human eyes. For other categories, a similar situation occurred. The ambiguous images in these overlapped areas may lead to mis-classification, which results in high loss and low accuracy. However, these kinds of misjudgments are negligible because our goal was to distinguish images between 2 categories: clear night (starry) and unclear night (starless). The accuracy of separating starry and starless is much higher than 89.49% in practice.

4.4. Model Validation

Once the training is finished, the fitted parameters are stored in the model. Based on the trained model, the higher-layer features are visualized by the activation maximization method [33,34] to qualitatively analyze the basis of classification. The visualized higher-layer maximum activation images are shown in Figure 6. The brightness of pixels depends on the weights of the local region and shows the features of classification. Similar features can be found in the corresponding category image in Figure 4. Compared with the maximum activation image of a category, the more similar features a raw image has, the more likely the raw image will be classified to this category. The relative positions of the features in the image do not count much due to the convolution kernel mentioned in Section 4.1. The rotation of images in the dataset leads to the 90° symmetry in these maximum activation images. The symmetry is not strict due to the random process in the training, but can still be found in every maximum activation image. For example, in Figure 6c, there is a cross, which actually consists of the features of four light bands. In the training set, the light band appears from the left to the right in the raw images of category c, so that the light band feature appears in the middle, which is the average position. By comparing the corresponding sub-images in Figure 6 with Figure 4, we confirmed that the classification model can classify images based on the correct features.

5. GW Location

To locate and isolate the wave-containing local region for wavelength extraction, we generated a GW location model with the Object Detection API [35], which is an open source framework based on TensorFlow.

5.1. Datasets of GW Location

All 220,000 raw images captured in 2013 were classified by the model generated in Section 4 and 120,000 images were found to be of clear nights (being classified as a, b, c, or e). The raw images of clear nights were unwarped using following steps: removing stars with median filtering [8], minimizing the background noise using time difference [12,14,36], and then being projected to the 512 × 512 km geometric coordinate [37] as 512 × 512 matrixes. These unwarped images were manually identified and 1060 images containing representative wave patterns were selected for machine learning. After marking the rectangular local regions of wave structures, we divided these images into two parts: 795 for training and 265 for testing. The two data sets were compiled into two files for being used in the learning process.

5.2. Training of GW Location Model

To generate an accurate and fast model to address multiple objects in a single image, the training was operated under the Faster R-CNN framework [23] with the Tensorflow Object Detection API. Faster R-CNN is the combination of the Region Proposal Network (RPN) [23] and the Fast R-CNN [38]. The RPN predicts the object bounding boxes and tells the Fast R-CNN where to focus. The Fast R-CNN tells the RPN the object (wave structure in our research). The machine learning of the Faster R-CNN adopts the pragmatic four-step alternating training algorithm developed by Ren et al. [23] to train the GW location model. A model named faster_rcnn_resnet101_voc07, which is trained on the MS COCO (The Microsoft Common Objects in COntext) dataset [39] and accessible on Github [40], was chosen as the pre-trained model to initiate the training.

After 250,000 rounds of training, the total loss, including the classification loss of whether there is a wave and the localization loss of the rectangular object proposal around wave structures became stable and decreased to below 0.1 (Figure 7).

The GW location model is capable of locating the wave structure in a projected airglow image. As shown in Figure 8, the wave structures are marked with rectangles and the wave detection confidence is expressed as a percentage. If the confidence value is lower than 50% (default threshold of object detection API), the object will not be classified as a wave and the object box will not appear. The extraction program records the coordinates of diagonal vertexes of the rectangular object region and the confidence value.

6. Calculation of GW Parameters

We analyzed all data captured in 2014. In the first step, the raw images are classified by the classification model trained in Section 3. Then, the raw images of clear nights are unwarped following the steps in Section 4.1. In the second step, the unwarped images are processed by the GW location model trained in Section 5 to extract the wave patterns. In the third step, the wavelengths are measured by two-dimensional Fast Fourier Transform (2D FFT) and the GW events are counted with an additional wavelength check to remove the interference due to mist. We calculated the wavelength, lasting time, and number of events. Since the regions of GW are extracted, more parameters, such as horizontal wave speed and period, can be easily measured [41].

6.1. Calculation of Wavelength

Similar to Garcia’s approach [41] of measuring wavelength, we isolated the m × n submatrix I of wave structure in Figure 8a. I is subtracted from its average $\overline{I}$ to remove the background noise and then a band pass filter is applied to $I-\overline{I}$ to obtain clear peaks in the frequency domain. The pass window of the filter ranges from 10 km to 100 km, which is the effective wavelength range for gravity waves observed by a single ASAI [42]. After 2D FFT, we obtain the filtered 2D spectrum of the wave structure region (Figure 9). The two peaks located at (u_max, v_max) and (–u_max, –v_max) indicate the wave number of gravity waves in the frequency domain. The wavelength of the gravity wave can be derived by the wave equation of a monochromatic plane wave:

$$\lambda =\frac{{\lambda }_x\times {\lambda }_y}{\sqrt{{\lambda }_x^2+{\lambda }_y^2}},$$

(8)

where ${\lambda }_x=\frac{m}{\left|u_{\max }\right|}$ and ${\lambda }_y=\frac{n}{\left|v_{\max }\right|}$. m and n are the length and width of rectangles in Figure 8, respectively.

6.2. Removing the Interference of Mist

Although the cloudy images are removed in the classification step before projection, there are still some mist remains in the unwarped images. Some mist appears as band patterns, which leads to mis-identification by the GW location model. These thin fogs are below the tropopause and normally move faster than gravity waves. Therefore, we separated the mists from the gravity waves by comparing the wavelengths in the same region in the three images before and three images after the detected image. If the relative change in the wavelength in the object region is larger than 10%, the object will be classified as mist with band pattern instead of gravity waves. By this wavelength-change check, the interference of mist is removed.

Figure 10a,b compare the gravity wave extraction results before and after wavelength check, respectively. The x-axis denotes the ordinal of the captured images. In Figure 10, the actual observation lasted from 18:11 on 27 January 2014 to 6:14 on 28 January 2014 (local time) and captured 687 images. The absent images, due to time extension or deletion by classification, are filled with blank pictures. The left y-axis is the identification counter, which increase by one when an image-containing wave structure is detected and decreased by one on another occasion. A rising slope of the blue curve in Figure 10 implies a series of continuous images containing detected wave structures and a peak indicates the end of a series. The right y-axis is the wavelength of the detected wave structure. The wavelength in the image is represented by the red bar if a wave structure is detected. The wavelength of the region with the highest confidence value is adapted in this figure if there is more than one wave region detected in a single image.

We manually checked the 11 groups (A–K) of images corresponding to the ascending slopes in Figure 10a, and list the airglow images in Figure 11 to show the actual situation, one image for each group. Without any exceptions, all deleted series were composed of images containing mist or clouds of band structures (shown in Figure 11A–D,H–K). The sequences remaining in Figure 10b are indeed images containing GWs (shown in Figure 11 E–G).

From Figure 11b, we can find a series of wave-containing images indicating one gravity wave event and the peak approximately denotes the time of the GW event. For example, the series covering Figure 11E,F implies a long-lasting GW, whereas Figure 11H belongs to another shorter GW event.

7. Manual Validation

To verify the validity of the automatic extraction models, we compared the auto extracted and the manually detected results. Based on the classification model, GW location model, and wavelengths check, the GW statistics results were obtained.

For a case study, we automatically extracted the GW observations in January 2014 and compared the results with manually checked occurrences of GWs from the same period. The results are shown in Figure 12. Comparing the two panels in Figure 12, the auto-extraction models detected 570 GW images, which is 28.9% less than 802 GW images found by human eyes. This deviation is caused by the strict threshold and by ignoring the dim wave structures. With the strict threshold, there were only missed events. Lowering the threshold of the confidence value may reduce the deviation at the cost of confusing false and true GW events. The misidentification in events counting can be modified by adding a horizontal velocity test in our coming modification.

Both auto-extraction and manual check identify events based on the same criteria: If there are more than five images of 10 consecutive images are detected to contain gravity waves, an event is deemed to start. The event is considered to end if there are no eligible series that have more than five GW-containing images in ten consecutive images within 60 images. As shown in Figure 12b, the manual check finds two GW events on the night of 25 January which last from 20:32 to 21:18 (local time) and from 22:21 to 03:11 the next day, respectively. The auto-extraction missed the GW images captured from 00:27 to 02:10 on 26 January due to the dim wave pattern (Figure 13). Hence the event from 22:21 to 03:11 was regarded as two events by auto-extraction. In Figure 12a, the auto-extraction result shows three GW events on 25 January: 20:36–20:54 (blue bar), 22:27–00:26 (green bar), 02:11–03:05 (yellow bar).

We also performed automatic GW event detection using the observations during the entire year of 2014. The number of GW-containing images (containing at least one GW event in each image) is shown in Figure 14. The GW image number distribution in Figure 14 shows the same seasonal variations with the manually checked results at Linqu station for 2012–2013 [43].

8. Discussions

We developed an automatic extraction program based on machine learning to extract the characteristics of GWs from a tremendous amount of airglow images. The program mainly consists of a classification model trained by a CNN and a GW location model trained by Faster R-CNN. It uses two steps to perform the extraction automatically. Firstly, the raw images are classified by the classification model to select the images of clear nights. Then, the GW location model is applied on the unwarped images of clear nights to locate the GW patterns. Having located the wave patterns, the regions of wave patterns are isolated, which enables calculating the horizontal wavelengths, speeds, and directions of propagation with 2D FFT [41]. The two-step architecture allows the data processing to be undertaken by two models in turn, reducing the amount of data requiring processing by filtering out the images of unclear or cloudy nights. The wavelength check was added to eliminate the interference of mist and further improve the detection accuracy (Figure 10).

We completed a case study on the data captured by the ASAI at Linqu station. Compared with the manual detection of images observed in January 2014 (Figure 12), the auto-extraction found fewer GW images because of the strict threshold. Additionally, we processed the images captured in the whole year of 2014 (Figure 14) and found the same seasonal variations with Wang et al.’s manual result [43] at the same station in 2012–2013. In the GW auto-extraction, very few false positive judgements were provided from the disturbance of cloud or light bands, and the small amount of false negative (missing GW) judgements were mainly caused by dim waves.

The detection program is general for the automatically detection of GWs in OH airglow images. In preparing the dataset for training, we collected the GW patterns of variety forms with wavelength ranged from several kms to about 100 km, such as concentric waves triggered by thunderstorm, plane waves generated by jet, small ripples caused by wave breaking. Hence the trained models are able to recognize all kinds of wave structures in the OH airglow images, even GWs with wavelengths of hundreds of km in satellite images (not shown in this paper). For airglow from other sources (O, O₂, Na, etc.) at different heights, the program can identify wave structures in the airglow images as well if the wave patterns are clear enough. In our future study, we plan to modify the automatic extraction program with the fine tune technique of machine learning, so that the program can perform better in processing airglow images captured at other heights.

9. Conclusions

As far as we know, this is the first study to automatically extract GW patterns in the OH airglow images captured by ASAI using machine learning. The automatic extraction program offers a new approach to analyze the characteristics of GWs in the long term with more efficiency and uniform standards to avoid accidental error due to manual checks. With the development of ASAI observations around the world, our automatic extraction will play an increasingly important role in exploring atmospheric GWs.