Quantifying Leaf Phenology of Individual Trees and Species in a Tropical Forest Using Unmanned Aerial Vehicle (UAV) Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site and Ground-Based Forest Inventory Data
2.2. Overview of UAV Image Acquisition and Analysis
2.3. UAV Flights and Image Processing
2.4. Manual Tree Crown Delineation
2.5. Quality Assessment of Images
2.6. Statistical Analysis
2.6.1. Generating an Observation Dataset for the Machine Learning Algorithm
2.6.2. Feature Extraction from Images
2.6.3. Model Training and Evaluation
2.6.4. Evaluating Model Predictions of Intra-Annual Variation of Leaf Cover
2.6.5. Evaluating Model Predictions
3. Results
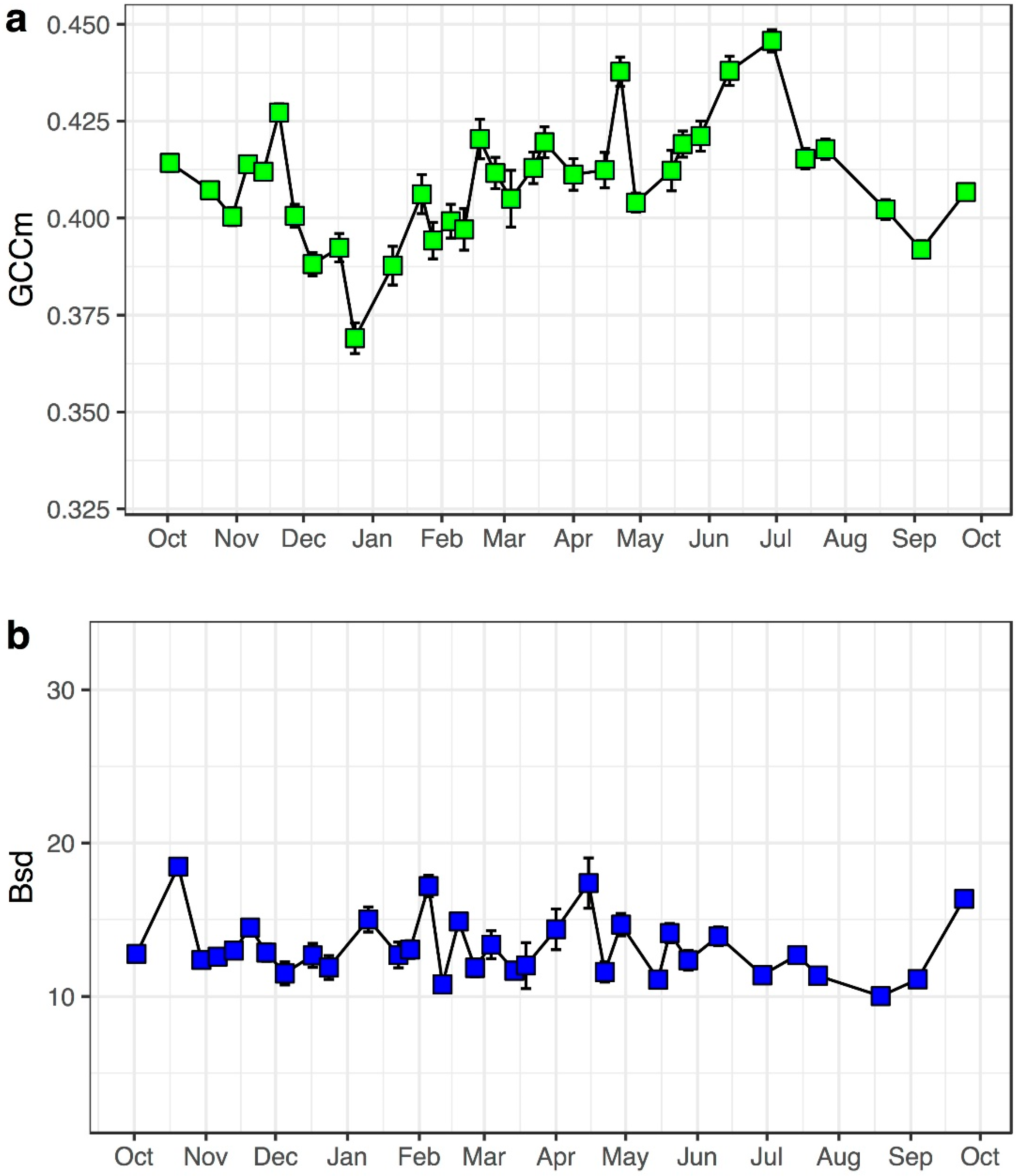
3.1. Comparing Models with Different Image Features
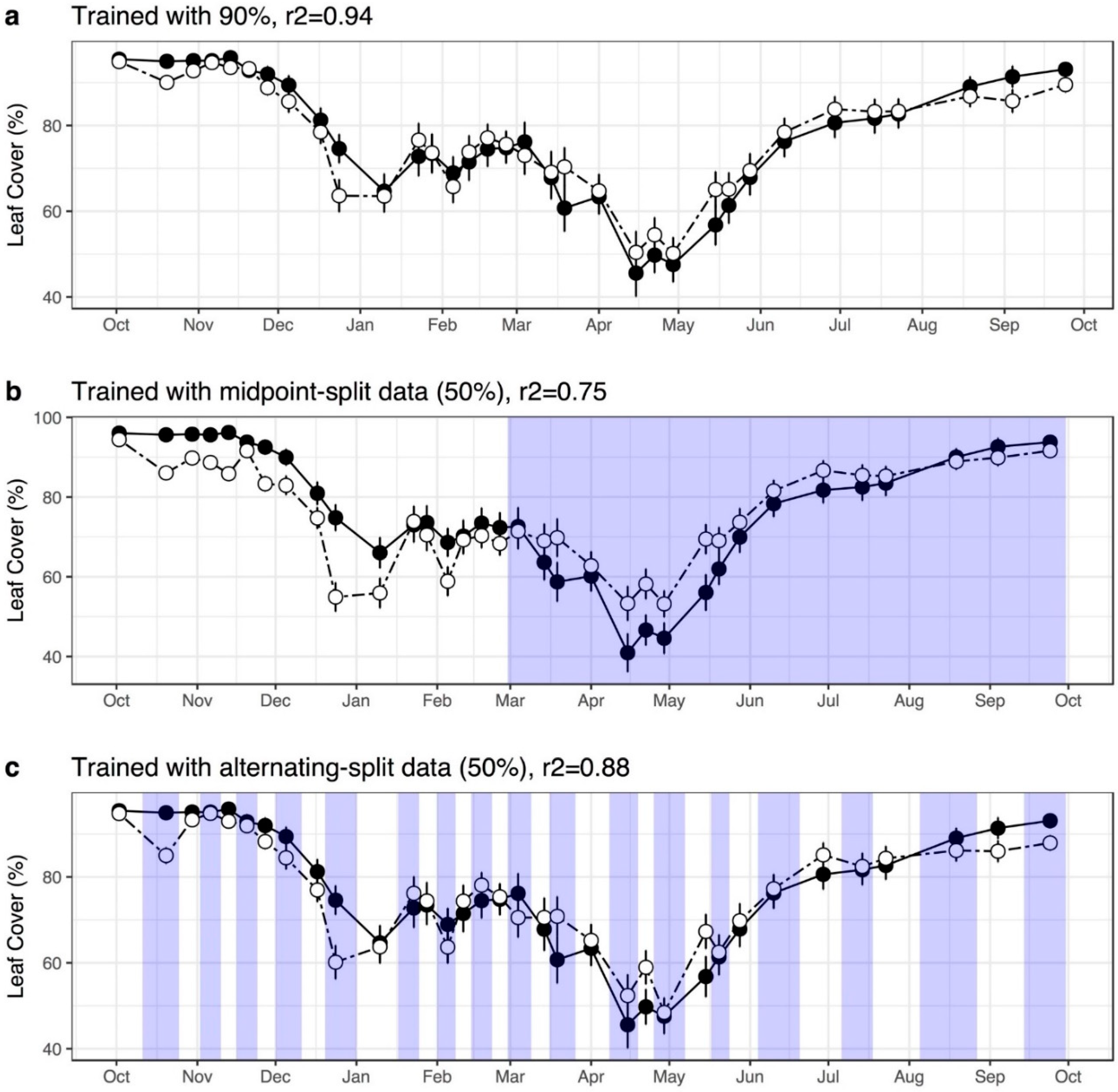
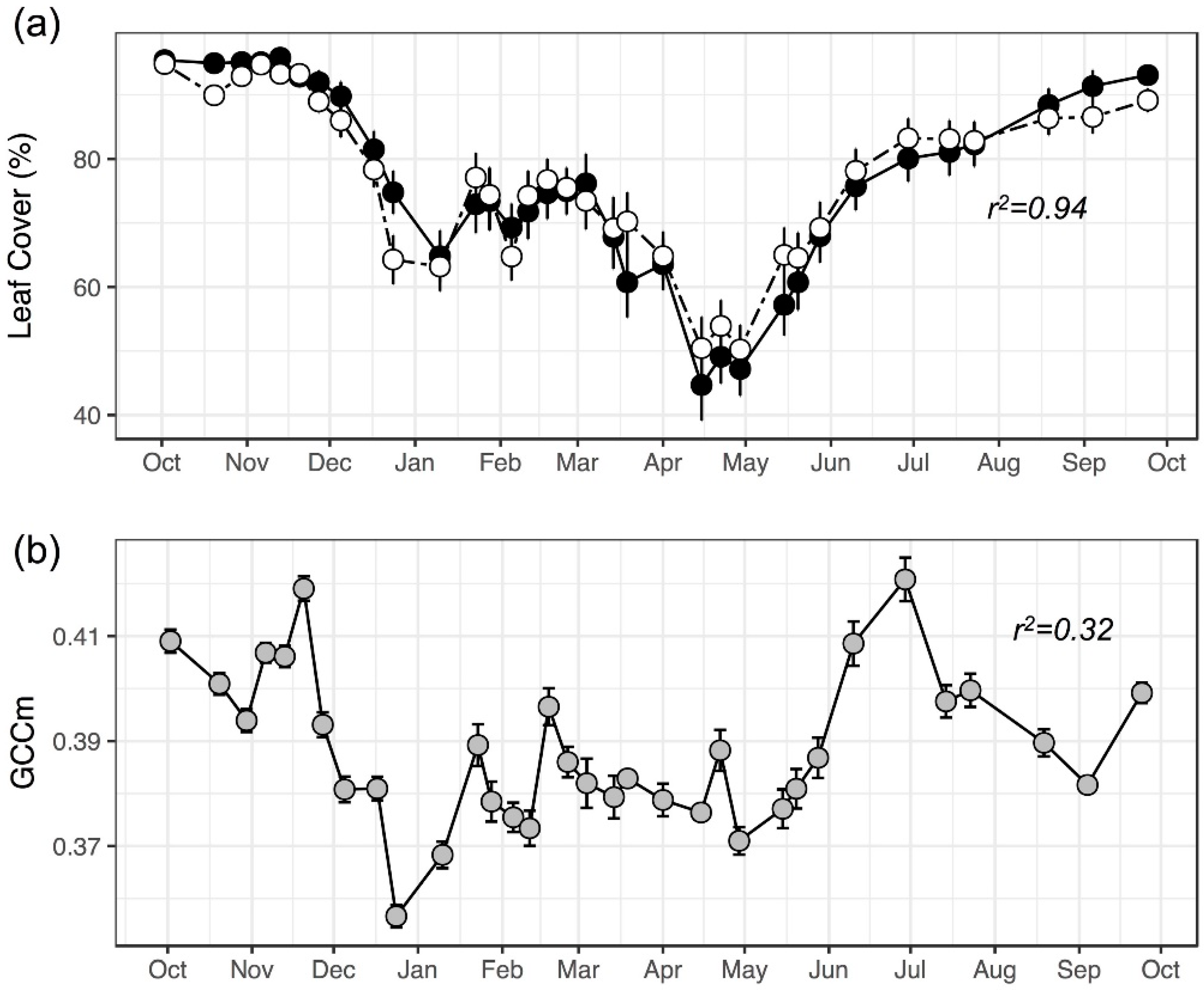
3.2. Model Performance in Capturing Intra-Annual Variation
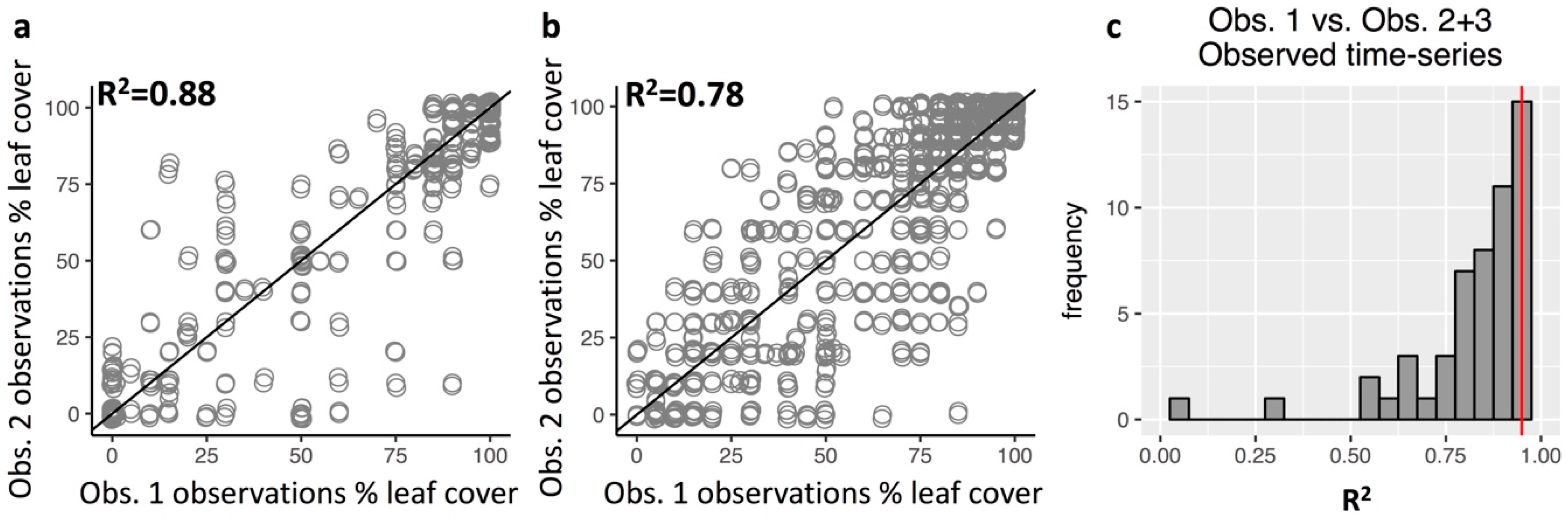
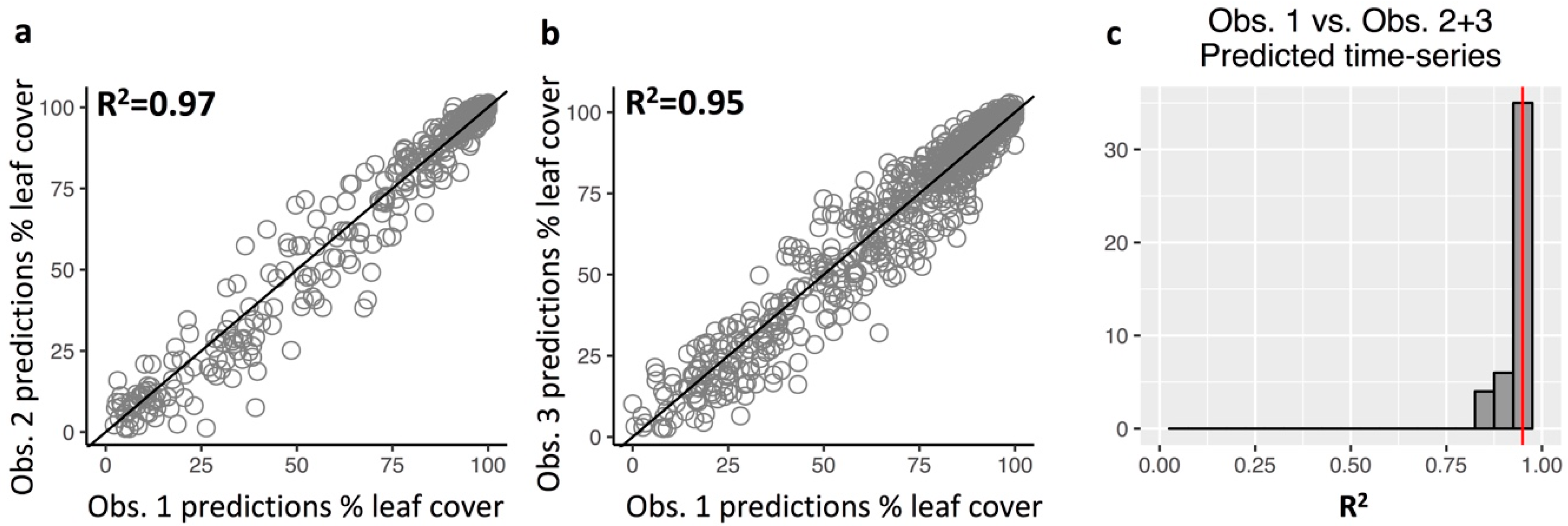
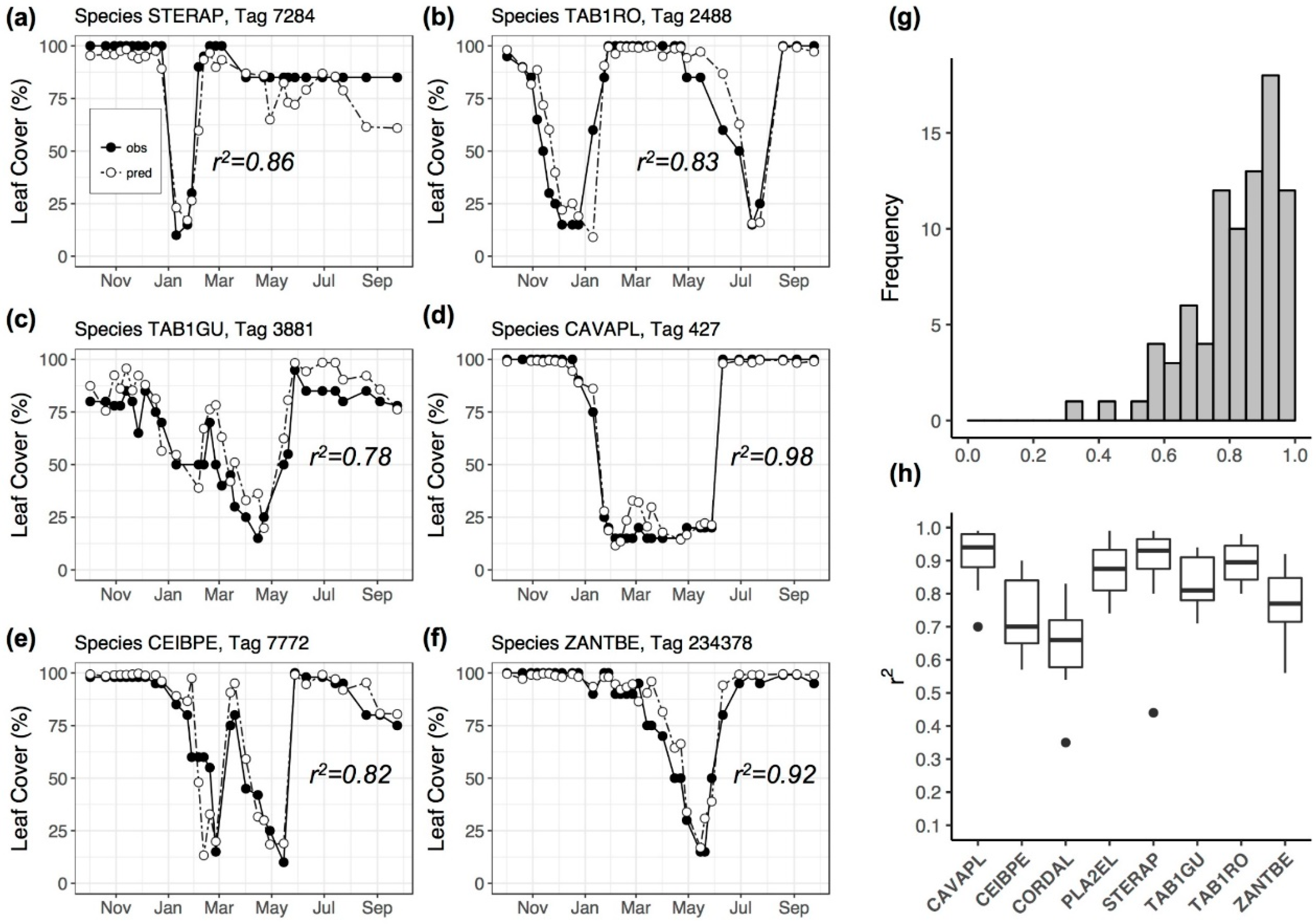
3.3. Repeatability of Visual Leaf-Cover Estimates and Model Predictions
4. Discussion
4.1. Image Features for Quantifying Phenology
4.2. Sources of Prediction Error
4.3. Advances in Phenological Observations of Tropical Forests
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Supplementary Methods and Results
Appendix A.1. Image Collection and Initial Image Processing
Appendix A.2. Radiometric Normalization
Appendix A.3. Orthomosaic Processing
Appendix A.4. Manual Tree Crown Delineation
Appendix A.5. Feature Extraction from Images
Appendix A.6. Model Training and Evaluation
Appendix A.7. Repeatability of Leaf Cover Observations and Predictions
| Features Included in Model | # of Features | r2 | MAE (%) | ME (%) |
|---|---|---|---|---|
| GCCm | 1 | 0.52 | 13.64 | 0.10 |
| BCCm | 1 | 0.16 | 21.08 | 0.09 |
| RCCm | 1 | 0.09 | 23.60 | 0.04 |
| ExGm | 1 | 0.28 | 18.72 | 0.01 |
| GVm | 1 | 0.44 | 15.97 | 0.03 |
| NPVm | 1 | 0.43 | 16.03 | 0.16 |
| GCCm, RCCm, BCCm | 3 | 0.62 | 11.90 | −0.07 |
| GVm, NPVm | 2 | 0.54 | 13.99 | 0.05 |
| GCCm, RCCm, BCCm, ExGm, Gvm, NPVm | 6 | 0.68 | 10.98 | 0.09 |
| GCCsd * | 1 | 0.001 | 27.01 | 0.07 |
| RCCsd * | 1 | 0.001 | 26.47 | 0.07 |
| BCCsd * | 1 | 0.01 | 26.50 | −0.04 |
| Gsd | 1 | 0.25 | 21.07 | 0.00 |
| Bsd | 1 | 0.63 | 12.87 | 0.02 |
| Rsd | 1 | 0.43 | 16.99 | −0.01 |
| ExGsd | 1 | 0.001 | 27.04 | −0.05 |
| GVsd | 1 | 0.0001 | 26.70 | 0.23 |
| NPVsd | 1 | 0.42 | 15.80 | 0.08 |
| Gcor_md | 1 | 0.19 | 21.25 | −0.05 |
| Gcor_sd | 1 | 0.37 | 17.19 | −0.13 |
| Gsd, Rsd, Bsd | 3 | 0.69 | 11.19 | −0.06 |
| Gsd, Rsd, Bsd, ExGsd, Gvsd, NPVsd | 6 | 0.71 | 10.81 | −0.03 |
| Gcor_md, Gcor_sd | 2 | 0.39 | 16.98 | −0.19 |
| Gsd, Rsd, Bsd, ExGsd, Gvsd, NPVsd, Gcor_md, Gcor_sd | 8 | 0.75 | 9.92 | −0.08 |
| GCCm, Gsd | 2 | 0.66 | 11.27 | 0.04 |
| GCCm, RCCm, BCCm, Gsd, Rsd, Bsd | 6 | 0.78 | 8.99 | −0.08 |
| FULL MODEL | 14 | 0.84 | 7.79 | −0.07 |
| LC% | GCCm | RCCm | BCCm | ExG m | NPVm | GV m | ExG sd | NPVsd | GV sd | G sd | R sd | B sd | Gcor_md | Gcor_sd | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LC% | - | 0.68 | −0.35 | −0.46 | 0.51 | −0.68 | 0.59 | −0.05 | −0.69 | −0.01 | −0.5 | −0.64 | −0.77 | −0.47 | −0.64 |
| GCCm | - | - | −0.28 | −0.83 | 0.79 | −0.61 | 0.81 | 0.25 | −0.61 | 0.24 | −0.26 | −0.42 | −0.53 | −0.34 | −0.46 |
| RCCm | - | - | - | -0.31 | −0.02 | 0.66 | −0.37 | 0.12 | 0.66 | −0.07 | 0.44 | 0.53 | 0.49 | 0.49 | 0.46 |
| BCCm | - | - | - | - | −0.77 | 0.22 | −0.58 | −0.32 | 0.22 | −0.2 | 0 | 0.1 | 0.25 | 0.05 | 0.19 |
| ExG m | - | - | - | - | - | −0.32 | 0.92 | 0.47 | −0.28 | 0.4 | 0.01 | −0.12 | −0.25 | 0.09 | −0.14 |
| NPVm | - | - | - | - | - | - | −0.55 | 0.1 | 0.77 | −0.03 | 0.5 | 0.64 | 0.7 | 0.78 | 0.73 |
| GV m | - | - | - | - | - | - | - | 0.38 | −0.49 | 0.39 | −0.14 | −0.3 | −0.4 | −0.11 | −0.3 |
| ExG sd | - | - | - | - | - | - | - | - | 0.29 | 0.92 | 0.59 | 0.46 | 0.35 | 0.34 | 0.32 |
| NPVsd | - | - | - | - | - | - | - | - | - | 0.22 | 0.67 | 0.83 | 0.83 | 0.63 | 0.76 |
| GV sd | - | - | - | - | - | - | - | - | - | - | 0.46 | 0.34 | 0.27 | 0.23 | 0.22 |
| G sd | - | - | - | - | - | - | - | - | - | - | - | 0.95 | 0.85 | 0.58 | 0.74 |
| R sd | - | - | - | - | - | - | - | - | - | - | - | - | 0.94 | 0.64 | 0.82 |
| B sd | - | - | - | - | - | - | - | - | - | - | - | - | - | 0.68 | 0.87 |
| Gcor_md | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0.82 |
| UAV Flight Date | Mean Observed Leaf Cover | Mean Predicted Leaf Cover | SD Observed Leaf Cover | SD Predicted Leaf Cover | Difference in Means (Observed–Predicted) |
|---|---|---|---|---|---|
| 10/02/14 | 95.52 | 94.78 | 12.23 | 9.33 | 0.74 |
| 10/20/14 | 95.05 | 90.21 | 9.39 | 13.48 | 4.84 |
| 10/30/14 | 95.22 | 92.83 | 8.88 | 12.44 | 2.39 |
| 11/06/14 | 95.14 | 94.96 | 9.56 | 8.20 | 0.18 |
| 11/13/14 | 95.84 | 93.61 | 9.51 | 9.49 | 2.23 |
| 11/20/14 | 93.04 | 93.43 | 14.52 | 11.72 | −0.39 |
| 11/27/14 | 92.06 | 89.31 | 16.50 | 15.66 | 2.75 |
| 12/05/14 | 89.95 | 85.90 | 19.94 | 22.77 | 4.05 |
| 12/17/14 | 81.49 | 78.54 | 25.73 | 24.53 | 2.95 |
| 12/24/14 | 74.73 | 63.60 | 29.68 | 34.10 | 11.13 |
| 01/10/15 | 64.88 | 63.50 | 34.81 | 32.75 | 1.38 |
| 01/23/15 | 73.00 | 77.17 | 34.34 | 29.50 | −4.17 |
| 01/28/15 | 73.75 | 74.40 | 34.07 | 31.87 | −0.65 |
| 02/05/15 | 69.53 | 64.60 | 33.41 | 33.93 | 4.93 |
| 02/11/15 | 72.00 | 74.03 | 34.68 | 30.97 | −2.03 |
| 02/18/15 | 74.73 | 76.72 | 32.19 | 25.97 | −1.99 |
| 02/25/15 | 75.03 | 75.98 | 29.50 | 25.26 | −0.95 |
| 03/04/15 | 75.16 | 72.59 | 31.21 | 29.65 | 2.57 |
| 03/14/15 | 67.84 | 68.40 | 32.93 | 32.49 | −0.56 |
| 03/19/15 | 60.61 | 71.10 | 35.01 | 28.58 | −10.49 |
| 04/01/15 | 64.11 | 65.53 | 32.57 | 30.48 | −1.42 |
| 04/15/15 | 44.69 | 50.64 | 37.19 | 33.69 | −5.95 |
| 04/22/15 | 49.23 | 54.28 | 36.60 | 35.00 | −5.05 |
| 04/29/15 | 47.85 | 50.40 | 37.28 | 34.23 | −2.55 |
| 05/15/15 | 57.29 | 65.90 | 38.68 | 33.88 | −8.61 |
| 05/20/15 | 61.34 | 65.07 | 37.64 | 34.35 | −3.73 |
| 05/28/15 | 68.35 | 69.76 | 36.65 | 35.50 | −1.41 |
| 06/10/15 | 75.98 | 78.50 | 34.13 | 31.19 | −2.52 |
| 06/29/15 | 80.28 | 83.85 | 33.25 | 27.83 | −3.57 |
| 07/14/15 | 81.31 | 83.61 | 33.49 | 26.57 | −2.30 |
| 07/23/15 | 82.42 | 83.32 | 30.90 | 27.10 | −0.90 |
| 08/19/15 | 88.58 | 86.60 | 23.08 | 23.64 | 1.98 |
| 09/04/15 | 91.47 | 86.08 | 19.24 | 20.60 | 5.39 |
| 09/24/15 | 93.28 | 89.63 | 13.31 | 16.17 | 3.65 |
| Species | r2 | MAE (%) | ME (%) |
|---|---|---|---|
| Cavanillesia platanifolia | 0.97 | 4.58 | −1.29 |
| Ceiba pentandra | 0.74 | 5.88 | −4.61 |
| Cordia alliodora | 0.81 | 7.27 | −1.77 |
| Platypodium elegans | 0.92 | 8.18 | 4.30 |
| Sterculia apetala | 0.93 | 4.22 | −2.31 |
| Handroanthus guayacan | 0.94 | 3.71 | 2.61 |
| Tabebuia rosea | 0.96 | 7.86 | 2.40 |
| Zanthoxylum ekmanii | 0.87 | 6.16 | 2.52 |
| Species | Mean r 2 (SD) | Mean MAE (SD) | Mean ME (SD) |
|---|---|---|---|
| Cavanillesia platanifolia | 0.92 (0.09) | 6.69 (2.47) | −1.86 (4.08) |
| Ceiba pentandra | 0.73 (0.12) | 9.24 (3.50) | −3.57 (4.33) |
| Cordia alliodora | 0.64 (0.15) | 11.95 (3.00) | −0.81 (6.77) |
| Platypodium elegans | 0.87 (0.08) | 8.09 (3.91) | 1.39 (6.28) |
| Sterculia apetala | 0.87 (0.17) | 4.36 (2.25) | −1.90 (1.97) |
| Handroanthus guayacan | 0.84 (0.08) | 7.83 (3.54) | 2.44 (5.58) |
| Tabebuia rosea | 0.89 (0.07) | 10.60 (2.64) | 2.11 (4.64) |
| Zanthoxylum ekmanii | 0.76 (0.12) | 7.70 (2.01) | 2.06 (3.61) |
| Model Description | # of Features | Obs. 1 Full | Obs. 1 Subset | Obs. 2+3 Subset |
|---|---|---|---|---|
| Mean Green Chromatic Coordinate | 1 | 0.52 | 0.43 | 0.38 |
| Means of Green, Blue, and Red Chromatic Coordinates | 3 | 0.62 | 0.55 | 0.49 |
| All mean color features | 6 | 0.68 | 0.64 | 0.55 |
| Standard deviation of green channel | 1 | 0.25 | 0.19 | 0.15 |
| Standard deviation of blue channel | 1 | 0.63 | 0.56 | 0.48 |
| Standard deviations of all color features | 6 | 0.71 | 0.64 | 0.54 |
| GLCM correlations | 2 | 0.39 | 0.31 | 0.25 |
| All texture measures including standard deviations of color features and GLCM correlation | 8 | 0.75 | 0.69 | 0.59 |
| Mean Green Chromatic Coordinate and standard deviation of green channel | 2 | 0.66 | 0.61 | 0.53 |
| Mean Chromatic Coordinates and standard deviations of color channels | 6 | 0.78 | 0.74 | 0.65 |
| Full model | 14 | 0.84 | 0.80 | 0.72 |




References
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P.; et al. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Pachauri, R.K., Meyer, L., Eds.; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Wolkovich, E.M.; Cook, B.I.; Davies, T.J. Progress towards an interdisciplinary science of plant phenology: Building predictions across space, time and species diversity. New Phytol. 2014, 201, 1156–1162. [Google Scholar] [CrossRef] [PubMed]
- Croat, T.B. Flora of Barro Colorado Island; Stanford University Press: Palo Alto, CA, USA, 1978; ISBN 978-0-8047-0950-7. [Google Scholar]
- Leigh, E.G. Tropical Forest Ecology: A View from Barro Colorado Island; Oxford University Press: Oxford, UK, 1999; ISBN 978-0-19-509603-3. [Google Scholar]
- Condit, R.; Watts, K.; Bohlman, S.A.; Pérez, R.; Foster, R.B.; Hubbell, S.P. Quantifying the deciduousness of tropical forest canopies under varying climates. J. Veg. Sci. 2000, 11, 649–658. [Google Scholar] [CrossRef] [Green Version]
- Reich, P.B.; Uhl, C.; Walters, M.B.; Prugh, L.; Ellsworth, D.S. Leaf demography and phenology in Amazonian rain forest: A census of 40,000 leaves of 23 tree species. Ecol. Monogr. 2004, 74, 3–23. [Google Scholar] [CrossRef]
- Elliott, S.; Baker, P.J.; Borchert, R. Leaf flushing during the dry season: The paradox of Asian monsoon forests. Glob. Ecol. Biogeogr. 2006, 15, 248–257. [Google Scholar] [CrossRef]
- Williams, L.J.; Bunyavejchewin, S.; Baker, P.J. Deciduousness in a seasonal tropical forest in western Thailand: Interannual and intraspecific variation in timing, duration and environmental cues. Oecologia 2008, 155, 571–582. [Google Scholar] [CrossRef] [PubMed]
- Wright, S.J.; Cornejo, F.H. Seasonal drought and leaf fall in a tropical forest. Ecology 1990, 71, 1165–1175. [Google Scholar] [CrossRef]
- Detto, M.; Wright, S.J.; Calderón, O.; Muller-Landau, H.C. Resource acquisition and reproductive strategies of tropical forest in response to the El Niño–Southern Oscillation. Nat. Commun. 2018, 9, 913. [Google Scholar] [CrossRef]
- Samanta, A.; Ganguly, S.; Vermote, E.; Nemani, R.R.; Myneni, R.B. Why is remote sensing of Amazon forest greenness so challenging? Earth Interact. 2012, 16, 1–14. [Google Scholar] [CrossRef]
- Morton, D.C.; Nagol, J.; Carabajal, C.C.; Rosette, J.; Palace, M.; Cook, B.D.; Vermote, E.F.; Harding, D.J.; North, P.R.J. Amazon forests maintain consistent canopy structure and greenness during the dry season. Nature 2014, 506, 221–224. [Google Scholar] [CrossRef]
- Wu, J.; Albert, L.P.; Lopes, A.P.; Restrepo-Coupe, N.; Hayek, M.; Wiedemann, K.T.; Guan, K.; Stark, S.C.; Christoffersen, B.; Prohaska, N.; et al. Leaf development and demography explain photosynthetic seasonality in Amazon evergreen forests. Science 2016, 351, 972–976. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopes, A.P.; Nelson, B.W.; Wu, J.; de Alencastro Graça, P.M.L.; Tavares, J.V.; Prohaska, N.; Martins, G.A.; Saleska, S.R. Leaf flush drives dry season green-up of the Central Amazon. Remote Sens. Environ. 2016, 182, 90–98. [Google Scholar] [CrossRef]
- Saleska, S.R.; Wu, J.; Guan, K.; Araujo, A.C.; Huete, A.; Nobre, A.D.; Restrepo-Coupe, N. Dry-season greening of Amazon forests. Nature 2016, 531, E4–E5. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Azofeifa, A.; Rivard, B.; Wright, J.; Feng, J.-L.; Li, P.; Chong, M.M.; Bohlman, S.A. Estimation of the distribution of Tabebuia guayacan (Bignoniaceae) using high-resolution remote sensing imagery. Sensors 2011, 11, 3831–3851. [Google Scholar] [CrossRef] [PubMed]
- Kellner, J.R.; Hubbell, S.P. Adult mortality in a low-density tree population using high-resolution remote sensing. Ecology 2017, 98, 1700–1709. [Google Scholar] [CrossRef] [PubMed]
- Alberton, B.; Almeida, J.; Helm, R.; Torres, R.D.S.; Menzel, A.; Morellato, L.P.C. Using phenological cameras to track the green up in a cerrado savanna and its on-the-ground validation. Ecol. Inform. 2014, 19, 62–70. [Google Scholar] [CrossRef]
- Klosterman, S.; Richardson, A.D. Observing spring and fall phenology in a deciduous forest with aerial drone imagery. Sensors 2017, 17, 2852. [Google Scholar] [CrossRef]
- Klosterman, S. Fine-scale perspectives on landscape phenology from unmanned aerial vehicle (UAV) photography. Agric. For. Meteorol. 2018, 248, 397–407. [Google Scholar] [CrossRef]
- Srinivasan, G.; Shobha, G. Statistical texture analysis. Proc. World Acad. Sci. Eng. Technol. 2008, 36, 1264–1269. [Google Scholar]
- Culbert, P.D.; Radeloff, V.C.; St-Louis, V.; Flather, C.H.; Rittenhouse, C.D.; Albright, T.P.; Pidgeon, A.M. Modeling broad-scale patterns of avian species richness across the Midwestern United States with measures of satellite image texture. Remote Sens. Environ. 2012, 118, 140–150. [Google Scholar] [CrossRef] [Green Version]
- Tuanmu, M.-N.; Jetz, W. A global, remote sensing-based characterization of terrestrial habitat heterogeneity for biodiversity and ecosystem modelling. Glob. Ecol. Biogeogr. 2015, 24, 1329–1339. [Google Scholar] [CrossRef]
- Hofmann, S.; Everaars, J.; Schweiger, O.; Frenzel, M.; Bannehr, L.; Cord, A.F. Modelling patterns of pollinator species richness and diversity using satellite image texture. PLoS ONE 2017, 12, e0185591. [Google Scholar] [CrossRef] [PubMed]
- Freeman, E.A.; Moisen, G.G.; Coulston, J.W.; Wilson, B.T. Random forests and stochastic gradient boosting for predicting tree canopy cover: Comparing tuning processes and model performance. Can. J. For. Res. 2015, 46, 323–339. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; White, J.C. Characterizing stand-level forest canopy cover and height using Landsat time series, samples of airborne LiDAR, and the Random Forest algorithm. ISPRS J. Photogramm. Remote Sens. 2015, 101, 89–101. [Google Scholar] [CrossRef]
- Hubbell, S.P.; Foster, R.B.; O’Brien, S.T.; Harms, K.E.; Condit, R.; Wechsler, B.; Wright, S.J.; De Lao, S.L. Light-gap disturbances, recruitment limitation, and tree diversity in a neotropical forest. Science 1999, 283, 554–557. [Google Scholar] [CrossRef] [PubMed]
- Paton, S. Meteorological and Hydrological Summary for Barro Colorado Island; Smithsonian Tropical Research Institute: Balboa, Panama, 2017. [Google Scholar]
- Dandois, J.P.; Olano, M.; Ellis, E.C. Optimal Altitude, overlap, and weather conditions for computer vision UAV estimates of forest structure. Remote Sens. 2015, 7, 13895–13920. [Google Scholar] [CrossRef]
- Zahawi, R.A.; Dandois, J.P.; Holl, K.D.; Nadwodny, D.; Reid, J.L.; Ellis, E.C. Using lightweight unmanned aerial vehicles to monitor tropical forest recovery. Biol. Conserv. 2015, 186, 287–295. [Google Scholar] [CrossRef] [Green Version]
- Lobo, E.; Dalling, J.W. Effects of topography, soil type and forest age on the frequency and size distribution of canopy gap disturbances in a tropical forest. Biogeosciences 2013, 10, 6769–6781. [Google Scholar] [CrossRef] [Green Version]
- Bohlman, S.; Pacala, S. A forest structure model that determines crown layers and partitions growth and mortality rates for landscape-scale applications of tropical forests. J. Ecol. 2012, 100, 508–518. [Google Scholar] [CrossRef]
- Graves, S.; Gearhart, J.; Caughlin, T.T.; Bohlman, S. A digital mapping method for linking high-resolution remote sensing images to individual tree crowns. PeerJ Prepr. 2018, 6, e27182v1. [Google Scholar]
- Richardson, A.D.; Braswell, B.H.; Hollinger, D.Y.; Jenkins, J.P.; Ollinger, S.V. Near-surface remote sensing of spatial and temporal variation in canopy phenology. Ecol. Appl. 2009, 19, 1417–1428. [Google Scholar] [CrossRef] [PubMed]
- Adams, J.B.; Sabol, D.E.; Kapos, V.; Almeida Filho, R.; Roberts, D.A.; Smith, M.O.; Gillespie, A.R. Classification of multispectral images based on fractions of endmembers: Application to land-cover change in the Brazilian Amazon. Remote Sens. Environ. 1995, 52, 137–154. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Frankie, G.W.; Baker, H.G.; Opler, P.A. Comparative phenological studies of trees in tropical wet and dry forests in the lowlands of Costa Rica. J. Ecol. 1974, 62, 881–919. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Wu, J.; Chavana-Bryant, C.; Prohaska, N.; Serbin, S.P.; Guan, K.; Albert, L.P.; Yang, X.; van Leeuwen, W.J.D.; Garnello, A.J.; Martins, G.; et al. Convergence in relationships between leaf traits, spectra and age across diverse canopy environments and two contrasting tropical forests. New Phytol. 2017, 214, 1033–1048. [Google Scholar] [CrossRef]
- Wieder, R.K.; Wright, S.J. Tropical forest litter dynamics and dry season irrigation on Barro Colorado Island, Panama. Ecology 1995, 76, 1971–1979. [Google Scholar] [CrossRef]
- Anderson-Teixeira, K.J.; Davies, S.J.; Bennett, A.C.; Gonzalez-Akre, E.B.; Muller-Landau, H.C.; Wright, S.J.; Abu Salim, K.; Almeyda Zambrano, A.M.; Alonso, A.; Baltzer, J.L.; et al. CTFS-ForestGEO: A worldwide network monitoring forests in an era of global change. Glob. Chang. Biol. 2015, 21, 528–549. [Google Scholar] [CrossRef]
- Xu, X.; Medvigy, D.; Powers, J.S.; Becknell, J.M.; Guan, K. Diversity in plant hydraulic traits explains seasonal and inter-annual variations of vegetation dynamics in seasonally dry tropical forests. New Phytol. 2016, 212, 80–95. [Google Scholar] [CrossRef]
- Du, Y.; Teillet, P.M.; Cihlar, J. Radiometric normalization of multitemporal high-resolution satellite images with quality control for land cover change detection. Remote Sens. Environ. 2002, 82, 123–134. [Google Scholar] [CrossRef]
- Adams, J.B.; Gillespie, A.R. Remote Sensing of Landscapes with Spectral Images; Cambridge University Press: Cambridge, UK, 2006; ISBN 978-0-521-66221-5. [Google Scholar]
- Grizonnet, M.; Michel, J.; Poughon, V.; Inglada, J.; Savinaud, M.; Cresson, R. Orfeo ToolBox: Open source processing of remote sensing images. Open Geospat. Data Softw. Stand. 2017, 2, 15. [Google Scholar] [CrossRef]
- Jordahl, K. GeoPandas: Python Tools for Geographic Data. Available online: https://github. com/geopandas/geopandas (accessed on 15 May 2019).
- Ridgeway, G. GBM: Generalized boosted regression models. R Package Version 2006, 1, 55. [Google Scholar]
- Ridgeway, G. Generalized Boosted Models: A guide to the gbm package. Update 2007, 1, 2007. [Google Scholar]




| Species Name | Abbreviation | N | Crown Area (m2) Mean (SD) | Min. Observed Leaf Cover (%) Mean (Range) | Mean Observed Leaf Cover (%) Mean (Range) | Max. Observed Leaf Cover (%) Mean (Range) |
|---|---|---|---|---|---|---|
| Cavanillesia platanifolia | CAVAPL | 14 | 274 (171) | 13 (5–30) | 69 (53–92) | 100 (100–100) |
| Ceiba pentandra | CIEBPE | 10 | 1180 (414) | 24 (10–52) | 81 (72–93) | 99 (95–100) |
| Cordia alliodora | CORDAL | 8 | 102 (43) | 20 (5–40) | 71 (64–86) | 99 (95–100) |
| Platypodium elegans | PLA2EL | 14 | 188 (51) | 12 (0–70) | 75 (53–96) | 100 (100–100) |
| Sterculia apetala | STERAP | 10 | 261 (116) | 14 (0–50) | 93 (85–98) | 100 (100–100) |
| Handroanthus guayacan | TAB1GU | 9 | 193 (40) | 18 (0–45) | 79 (63–92) | 99 (95–100) |
| Tabebuia rosea | TAB1RO | 10 | 146 (55) | 3 (0–15) | 65 (33–75) | 99 (85–100) |
| Zanthoxylum ekmanii | ZANTBE | 10 | 211 (38) | 16 (5–35) | 85 (79–93) | 100 (100–100) |
| Feature Type | Crown-Level Statistic | Feature Name | Abbreviation | Pixel-Scale Transformations | References |
|---|---|---|---|---|---|
| Mean Color Indices | Mean | RGB Chromatic Coordinates (RCC, GCC, BCC) | RCCm | RCC = red/(green + red + blue) | [35] |
| GCCm | GCC = green/(green + red + blue) | ||||
| BCCm | BCC = blue/(green + red + blue) | ||||
| Excess greenness | ExGm | ExG = 2*green − (red + blue) | [31] | ||
| Green vegetation | GVm | From linear mixture model, each endmember fractions were calculated (shade-normalized), for more details see methods | [36] | ||
| Non-photosynthetic vegetation | NPVm | ||||
| Texture Indices | Standard deviation | RGB color indices | Rsd | Red (no transformation) | NA |
| Gsd | Green (no transformation) | ||||
| Bsd | Blue (no transformation) | ||||
| Excess greenness | ExGsd | See above | Same as corresponding mean-based indices | ||
| Green vegetation | GVsd | ||||
| Non-photosynthetic vegetation | NPVsd | ||||
| Grey-Level Co-Occurrence Matrix (GLCM) correlation | Gcor_sd | Moving window (5 by 5 pixels) was used to calculate GLCM correlation of a target region within a crown image | [37] | ||
| Median | Gcor_md |
| Model Description | Features Included | # of Features | r2 | MAE | ME |
|---|---|---|---|---|---|
| Color Features | |||||
| Mean Green Chromatic Coordinate | GCCm | 1 | 0.52 | 13.6 | 0.10 |
| Means of Green, Blue, and Red Chromatic Coordinates | GCCm, RCCm, BCCm, | 3 | 0.62 | 11.9 | −0.07 |
| All mean color features | GCCm, RCCm, BCCm, ExGm, GVm, NPVm | 6 | 0.68 | 11.0 | 0.09 |
| Texture Features | |||||
| Standard deviation of green channel | Gsd | 1 | 0.25 | 22.0 | 0.00 |
| Standard deviation of blue channel | Bsd | 1 | 0.63 | 12.9 | 0.02 |
| Standard deviations of all color features | Gsd, Rsd, Bsd, ExGsd, GVsd, NPVsd | 6 | 0.71 | 10.8 | −0.03 |
| GLCM correlations | Gcor_md, Gcor_sd | 2 | 0.39 | 17.0 | −0.19 |
| All texture measures including standard deviations of color features and GLCM correlation | Gsd, Rsd, Bsd, ExGsd, Gvsd, NPVsd, Gcor_md, Gcor_sd | 8 | 0.75 | 9.9 | −0.08 |
| Color + Texture Features | |||||
| Mean Green Chromatic Coordinate and standard deviation of green channel | GCCm, Gsd | 2 | 0.66 | 11.5 | 0.04 |
| Mean Chromatic Coordinates and standard deviations of color channels | GCCm, Gsd, RCCm, Rsd, BCCm, Bsd | 6 | 0.78 | 9.0 | −0.08 |
| Full model | GCCm, RCCm, BCCm, ExGm, GVm, NPVm, Gsd, Rsd, Bsd, ExGsd, GVsd, NPVsd, Gcor_md, Gcor_sd | 14 | 0.84 | 7.8 | −0.07 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.Y.; Muller-Landau, H.C.; Lichstein, J.W.; Rifai, S.W.; Dandois, J.P.; Bohlman, S.A. Quantifying Leaf Phenology of Individual Trees and Species in a Tropical Forest Using Unmanned Aerial Vehicle (UAV) Images. Remote Sens. 2019, 11, 1534. https://doi.org/10.3390/rs11131534
Park JY, Muller-Landau HC, Lichstein JW, Rifai SW, Dandois JP, Bohlman SA. Quantifying Leaf Phenology of Individual Trees and Species in a Tropical Forest Using Unmanned Aerial Vehicle (UAV) Images. Remote Sensing. 2019; 11(13):1534. https://doi.org/10.3390/rs11131534
Chicago/Turabian StylePark, John Y., Helene C. Muller-Landau, Jeremy W. Lichstein, Sami W. Rifai, Jonathan P. Dandois, and Stephanie A. Bohlman. 2019. "Quantifying Leaf Phenology of Individual Trees and Species in a Tropical Forest Using Unmanned Aerial Vehicle (UAV) Images" Remote Sensing 11, no. 13: 1534. https://doi.org/10.3390/rs11131534
APA StylePark, J. Y., Muller-Landau, H. C., Lichstein, J. W., Rifai, S. W., Dandois, J. P., & Bohlman, S. A. (2019). Quantifying Leaf Phenology of Individual Trees and Species in a Tropical Forest Using Unmanned Aerial Vehicle (UAV) Images. Remote Sensing, 11(13), 1534. https://doi.org/10.3390/rs11131534






