A Multi-Scale Wavelet 3D-CNN for Hyperspectral Image Super-Resolution
Abstract
:1. Introduction
- In the predicting subnet, different branches corresponding to different wavelet sub-bands are trained jointly in a unified network, and the inter sub-band correlation can be utilized.
- The network is built based on 3D convolutional layers, which could exploit the correlation in both spectral and spatial domains of HSI.
- Instead of the conventional L2 norm, we propose to train the network with the L1 norm loss, which is fit for both low- and high- frequency wavelet sub-bands.
2. Related Works
2.1. CNN Based Single Image SR
2.2. Application of Wavelet in SR
3. Multi-Scale Wavelet 3D CNN For HSI SR
3.1. Wavelet Package Analysis
3.2. 3D CNN
3.3. Network Architecture of MW-3D-CNN
3.3.1. Embedding Subnet
3.3.2. Predicting Subnet
3.4. Training of MW-3D-CNN
4. Experimental Results
4.1. Experiment Setting
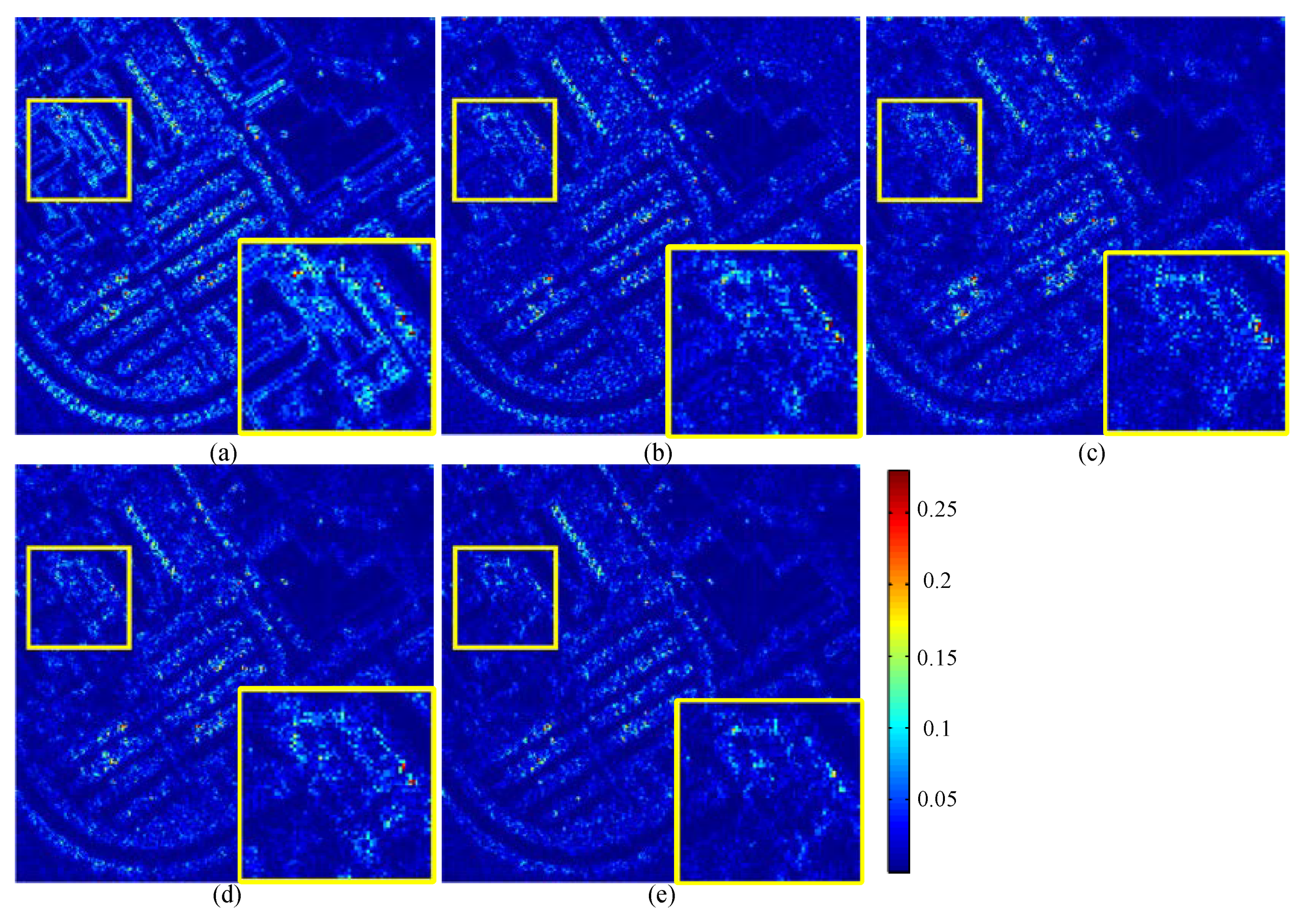
4.2. Comparison with State-of-the-Art SR Methods
4.3. Application on Real Spaceborne HSI
5. Analysis and Discussions
5.1. Sensitivity Analysis on Network Parameters
5.2. The Rationality Analysis of L1 Norm Loss
5.3. The Rationality Analysis of 3D Convolution
5.4. Robustness over Wavelet Functions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nasrabadi, N.M. Hyperspectral target detection: An overview of current and future challenges. IEEE Signal Process. Mag. 2014, 31, 34–44. [Google Scholar] [CrossRef]
- Clark, M.L.; Buck-Diaz, J.; Evens, J. Mapping of forest alliances with simulated multi-seasonal hyperspectral satellite imagery. Remote Sens. Environ. 2018, 210, 490–507. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Learning and transferring deep joint spectral–spatial features for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Chen, F.; Wang, K.; Van de Voorde, T.; Tang, T.F. Mapping urban land cover from high spatial resolution hyperspectral data: An approach based on simultaneously unmixing similar pixels with jointly sparse spectral mixture analysis. Remote Sens. Environ. 2017, 196, 324–342. [Google Scholar] [CrossRef]
- Yokoya, N.; Chan, J.C.W.; Segl, K. Potential of resolution-enhanced hyperspectral data for mineral mapping using simulated EnMAP and Sentinel-2 images. Remote Sens. 2016, 8, 172. [Google Scholar] [CrossRef]
- Loncan, L.; de Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simoes, M.; et al. Hyperspectral pansharpening: A review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Vivone, G.; Restaino, R.; Addesso, P.; Chanussot, J. Global and local Gram-Schmidt methods for hyperspectral pansharpening. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 37–40. [Google Scholar]
- Shahdoosti, H.R.; Ghassemian, H. Combining the spectral PCA and spatial PCA fusion methods by an optimal filter. Inf. Fusion 2016, 27, 150–160. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, K.; Wang, M. Learning low-rank decomposition for pan-sharpening with spatial- spectral offsets. IEEE Trans. Neural Netw. Learn. Syst. 2017, 20, 3647–3657. [Google Scholar]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Wei, Y.; Yuan, Q.; Shen, H.; Zhang, L. Boosting the Accuracy of multispectral image pansharpening by learning a deep residual network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1795–1799. [Google Scholar] [CrossRef]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5449–5457. [Google Scholar]
- Yuan, Q.; Wei, Y.; Meng, X.; Shen, H.; Zhang, L. A multiscale and multidepth convolutional neural network for remote sensing imagery pan-sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 978–989. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and multispectral data fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Zhu, X.X.; Grohnfeldt, C.; Bamler, R. Exploiting joint sparsity for pansharpening: The J-SparseFI algorithm. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2664–2681. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Sparse spatio-spectral representation for hyperspectral image super-resolution. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 63–78. [Google Scholar]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral and multispectral image fusion based on a sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef]
- Simões, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A convex formulation for hyperspectral image superresolution via subspace-based regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3373–3388. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, W.; Bai, C.; Gao, Y.; Zhang, Y. Exploiting clustering manifold structure for hyperspectral imagery super-resolution. IEEE Trans. Image Process. 2018, 27, 5969–5982. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Hyperspectral and Multispectral Image Fusion via Deep Two-Branches Convolutional Neural Network. Remote Sens. 2018, 10, 800. [Google Scholar] [CrossRef]
- Xie, Q.; Zhou, M.; Zhao, Q.; Meng, D.; Zuo, W.; Xu, Z. Multispectral and Hyperspectral Image Fusion by MS/HS Fusion Net. arXiv 2019, arXiv:1901.03281. [Google Scholar]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in hyperspectral image and signal processing: A comprehensive overview of the state of the art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Yang, J.; Chan, J.C.-W. Hyperspectral imagery super-resolution by spatial–spectral joint nonlocal similarity. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2671–2679. [Google Scholar] [CrossRef]
- Li, J.; Yuan, Q.; Shen, H.; Meng, X.; Zhang, L. Hyperspectral Image Super-Resolution by Spectral Mixture Analysis and Spatial-Spectral Group Sparsity. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1250–1254. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.A.; Han, Z.; He, S. Hyperspectral image super-resolution via nonlocal low-rank tensor approximation and total variation regularization. Remote Sens. 2017, 9, 1286. [Google Scholar] [CrossRef]
- Yuan, Y.; Zheng, X.; Lu, X. Hyperspectral image super-resolution by transfer learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1963–1974. [Google Scholar] [CrossRef]
- Li, Y.; Hu, J.; Zhao, X.; Xie, W.; Li, J.J. Hyperspectral image super-resolution using deep convolutional neural network. Neurocomputing 2017, 266, 29–41. [Google Scholar] [CrossRef]
- Hu, J.; Li, Y.; Xie, W. Hyperspectral image super-resolution by spectral difference learning and spatial error correction. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1825–1829. [Google Scholar] [CrossRef]
- Mei, S.; Yuan, X.; Ji, J.; Zhang, Y.; Wan, S.; Du, Q. Hyperspectral image spatial super-resolution via 3D full convolutional neural network. Remote Sens. 2017, 9, 1139. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, H.; Zhang, K.; Lin, L.; Zuo, W. Multi-level wavelet-CNN for image restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 773–782. [Google Scholar]
- Guo, T.; Mousavi, H.S.; Vu, T.H.; Monga, V. Deep wavelet prediction for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 104–113. [Google Scholar]
- Bae, W.; Yoo, J.J.; Ye, J.C. Beyond deep residual learning for image restoration: Persistent homology-guided manifold simplification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1141–1149. [Google Scholar]
- Huang, H.; He, R.; Sun, Z.; Tan, T. Wavelet-SRNet: A wavelet-based CNN for multi-scale face super resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1689–1697. [Google Scholar]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2017, 3, 47–57. [Google Scholar] [CrossRef]
- Cai, J.; Gu, S.; Zhang, L. Learning a deep single image contrast enhancer from multi-exposure images. IEEE Trans. Image Process. 2018, 27, 2049–2062. [Google Scholar] [CrossRef] [PubMed]
- Scarpa, G.; Vitale, S.; Cozzolino, D. Target-adaptive CNN-based pansharpening. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5443–5457. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1646–1654. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1637–1645. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. Memnet: A persistent memory network for image restoration. In Proceedings of the IEEE Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4539–4547. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Wang, Y.; Perazzi, F.; McWilliams, B. A Fully Progressive Approach to Single-Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshop, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep Laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 624–632. [Google Scholar]
- Anbarjafari, G.; Demirel, H. Image super resolution based on interpolation of wavelet domain high frequency subbands and the spatial domain input image. ETRI J. 2010, 32, 390–394. [Google Scholar] [CrossRef]
- Demirel, H.; Anbarjafari, G. Image resolution enhancement by using discrete and stationary wavelet decomposition. IEEE Trans. Image Process. 2011, 20, 1458–1460. [Google Scholar] [CrossRef]
- Chavez-Roman, H.; Ponomaryov, V. Super resolution image generation using wavelet domain interpolation with edge extraction via a sparse representation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1777–1781. [Google Scholar] [CrossRef]
- Demirel, H.; Anbarjafari, G. Discrete wavelet transform-based satellite image resolution enhancement. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1997–2004. [Google Scholar] [CrossRef]
- Ji, S.; Xu, W.; Yang, M.; Yu, K. 3D convolutional neural networks for human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 221–231. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Yang, J.; Zhao, Y.; Yi, C.; Chan, J.C.W. No-reference hyperspectral image quality assessment via quality-sensitive features learning. Remote Sens. 2017, 9, 305. [Google Scholar] [CrossRef]
- Yokoya, N.; Iwasaki, A. Airborne Hyperspectral Data over Chikusei; Technical Report; SAL-2016-05-27; Space Appl. Lab., University of Tokyo: Tokyo, Japan, 2016. [Google Scholar]
- 2018 IEEE GRSS Data Fusion Contest. Available online: http://www.grss-ieee.org/community/technical-committees/data-fusion (accessed on 10 June 2018).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.W. Nonlocal Low-Rank Regularized Tensor Decomposition for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5174–5189. [Google Scholar] [CrossRef]
- Yi, C.; Zhao, Y.Q.; Chan, J.C.-W. Spectral super-resolution for multispectral image based on spectral improvement strategy and spatial preservation strategy. IEEE Trans. Geosci. Remote Sens. 2019. [Google Scholar]
- Pan, L.; Hartley, R.; Liu, M.; Dai, Y. Phase-only Image Based Kernel Estimation for Single-image Blind Deblurring. arXiv 2018, arXiv:1811.10185. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]














| Data | Indices | Bicubic | SSG [27] | SRCNN [40] | 3D-CNN [32] | MW-3D-CNN |
|---|---|---|---|---|---|---|
| Pavia University | PSNR (dB) | 30.4032 | 31.7092 | 32.1961 | 33.1397 | 34.9394 |
| SSIM | 0.8867 | 0.9132 | 0.9234 | 0.9398 | 0.9537 | |
| FSIM | 0.9191 | 0.9460 | 0.9517 | 0.9643 | 0.9754 | |
| SAM | 4.0979° | 4.6845° | 3.7519° | 3.5470° | 3.3302° | |
| Chikusei | PSNR (dB) | 24.7892 | 26.7419 | 26.9271 | 28.0397 | 28.4288 |
| SSIM | 0.8596 | 0.9148 | 0.9301 | 0.9344 | 0.9396 | |
| FSIM | 0.8889 | 0.9313 | 0.9408 | 0.9483 | 0.9544 | |
| SAM | 4.2283° | 3.7700° | 3.0919° | 2.9650° | 2.9248° | |
| Houston University (grss_dfc_2018) | PSNR (dB) | 31.2005 | 32.5020 | 33.5990 | 34.9816 | 35.5552 |
| SSIM | 0.9280 | 0.9480 | 0.9596 | 0.9669 | 0.9710 | |
| FSIM | 0.9878 | 0.9953 | 0.9991 | 0.9993 | 0.9997 | |
| SAM | 2.5757° | 3.4858° | 2.4268° | 2.1029° | 1.9252° |
| Data | Indices | Bicubic | SSG [27] | SRCNN [40] | 3D-CNN [32] | MW-3D-CNN |
|---|---|---|---|---|---|---|
| Pavia University | PSNR (dB) | 27.5136 | 27.6828 | 27.8132 | 28.7122 | 29.1069 |
| SSIM | 0.7187 | 0.7328 | 0.7327 | 0.7745 | 0.7928 | |
| FSIM | 0.7905 | 0.8186 | 0.8058 | 0.8450 | 0.8620 | |
| SAM | 6.1537° | 7.7461° | 5.9707° | 5.6644° | 5.8828° | |
| Chikusei | PSNR (dB) | 19.8308 | 20.3108 | 21.0739 | 21.1284 | 20.6069 |
| SSIM | 0.5623 | 0.6280 | 0.6723 | 0.6741 | 0.6853 | |
| FSIM | 0.7039 | 0.7646 | 0.7985 | 0.7979 | 0.7934 | |
| SAM | 7.8073° | 7.9160° | 6.5647° | 6.5458° | 7.2638° | |
| Houston University (grss_dfc_2018) | PSNR (dB) | 25.3139 | 26.0628 | 26.7927 | 27.8006 | 28.4968 |
| SSIM | 0.7410 | 0.7703 | 0.7971 | 0.8259 | 0.8514 | |
| FSIM | 0.8988 | 0.9233 | 0.9372 | 0.9528 | 0.9653 | |
| SAM | 4.6611° | 6.9780° | 4.2034° | 4.0398° | 3.6881° |
| Data | Bicubic | SSG [27] | SRCNN [40] | 3D-CNN [32] | MW-3D-CNN |
|---|---|---|---|---|---|
| Pavia University | 0.42 s | 2.37 h | 233.45 s | 0.96 s | 1.18 s |
| Chikusei | 0.44 s | 2.86 h | 241.84 s | 1.14 s | 1.30 s |
| Houston University | 0.97 s | 4.33 h | 402.71 s | 1.76 s | 1.92 s |
| Data | Bicubic | SSG [27] | SRCNN [40] | 3D-CNN [32] | MW-3D-CNN |
|---|---|---|---|---|---|
| Pavia University | 0.24 s | 2.28 h | 237.58 s | 1.12 s | 1.16 s |
| Chikusei | 0.28 s | 2.77 h | 247.75 s | 1.20 s | 1.42 s |
| Houston University | 0.49 s | 4.21 h | 409.54 s | 1.76 s | 1.87 s |
| SR Methods | Bicubic | SSGS [27] | SRCNN [40] | 3D-CNN [32] | MW-3D-CNN |
|---|---|---|---|---|---|
| Scores | 31.3888 | 28.3041 | 26.9271 | 25.6205 | 25.4930 |
| Size of 3D Conv. Kernel | Pavia University | Chikusei | Houston University |
|---|---|---|---|
| 1 × 1 × 1 | 30.3859 | 23.3061 | 31.0492 |
| 3 × 3 × 3 | 34.9394 | 28.4288 | 35.5552 |
| 5 × 5 × 5 | 34.5399 | 27.9122 | 35.4294 |
| Number of 3D Conv. Kernels | Pavia University | Chikusei | Houston University |
|---|---|---|---|
| 16 (embedding subnet), 8 (predicting subnet) | 34.8725 | 28.3497 | 35.6839 |
| 32 (embedding subnet), 16 (predicting subnet) | 34.9394 | 28.4288 | 35.5552 |
| 64 (embedding subnet), 32 (predicting subnet) | 34.8568 | 28.2704 | 35.3547 |
| Number of 3D Conv. Layers | Pavia University | Chikusei | Houston University |
|---|---|---|---|
| 2 (embedding subnet), 3 (predicting subnet) | 34.9282 | 28.3663 | 35.4573 |
| 3 (embedding subnet), 4 (predicting subnet) | 34.9394 | 28.4288 | 35.5552 |
| 4 (embedding subnet), 5 (predicting subnet) | 35.1095 | 28.3744 | 35.4720 |
| Loss Functions | Pavia University | Chikusei | Houston University |
|---|---|---|---|
| L1 Norm Loss | 34.9394 | 28.4288 | 35.5552 |
| L2 Norm Loss | 34.6417 | 28.3176 | 35.2615 |
| Methods | Pavia University | Chikusei | Houston University |
|---|---|---|---|
| MW-3D-CNN | 34.9394 | 28.4288 | 35.5552 |
| Wavelet-SRNet-L2 | 32.2569 | 27.0149 | 34.1717 |
| Wavelet-SRNet-L1 | 32.3658 | 27.0903 | 34.1537 |
| Wavelets | Pavia University | Chikusei | Houston University |
|---|---|---|---|
| Haar wavelet | 34.9394 | 28.4288 | 35.5552 |
| Daubechies-2 wavelet | 35.0468 | 28.6751 | 35.5202 |
| Biorthogonal wavelet | 34.9695 | 28.4213 | 35.5594 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Zhao, Y.-Q.; Chan, J.C.-W.; Xiao, L. A Multi-Scale Wavelet 3D-CNN for Hyperspectral Image Super-Resolution. Remote Sens. 2019, 11, 1557. https://doi.org/10.3390/rs11131557
Yang J, Zhao Y-Q, Chan JC-W, Xiao L. A Multi-Scale Wavelet 3D-CNN for Hyperspectral Image Super-Resolution. Remote Sensing. 2019; 11(13):1557. https://doi.org/10.3390/rs11131557
Chicago/Turabian StyleYang, Jingxiang, Yong-Qiang Zhao, Jonathan Cheung-Wai Chan, and Liang Xiao. 2019. "A Multi-Scale Wavelet 3D-CNN for Hyperspectral Image Super-Resolution" Remote Sensing 11, no. 13: 1557. https://doi.org/10.3390/rs11131557
APA StyleYang, J., Zhao, Y.-Q., Chan, J. C.-W., & Xiao, L. (2019). A Multi-Scale Wavelet 3D-CNN for Hyperspectral Image Super-Resolution. Remote Sensing, 11(13), 1557. https://doi.org/10.3390/rs11131557







