GPU-Based Lossless Compression of Aurora Spectral Data using Online DPCM
Abstract
:1. Introduction
2. The Improved Online DPCM Method for Aurora Spectral Data Compression
2.1. Overview of the Online DPCM Method
- Compute the prediction coefficients for each pixel;
- Calculate the prediction image and its difference from the original image, i.e., the residual;
- Encode the residual.
2.2. Our Improvement to the Original Online DPCM Method
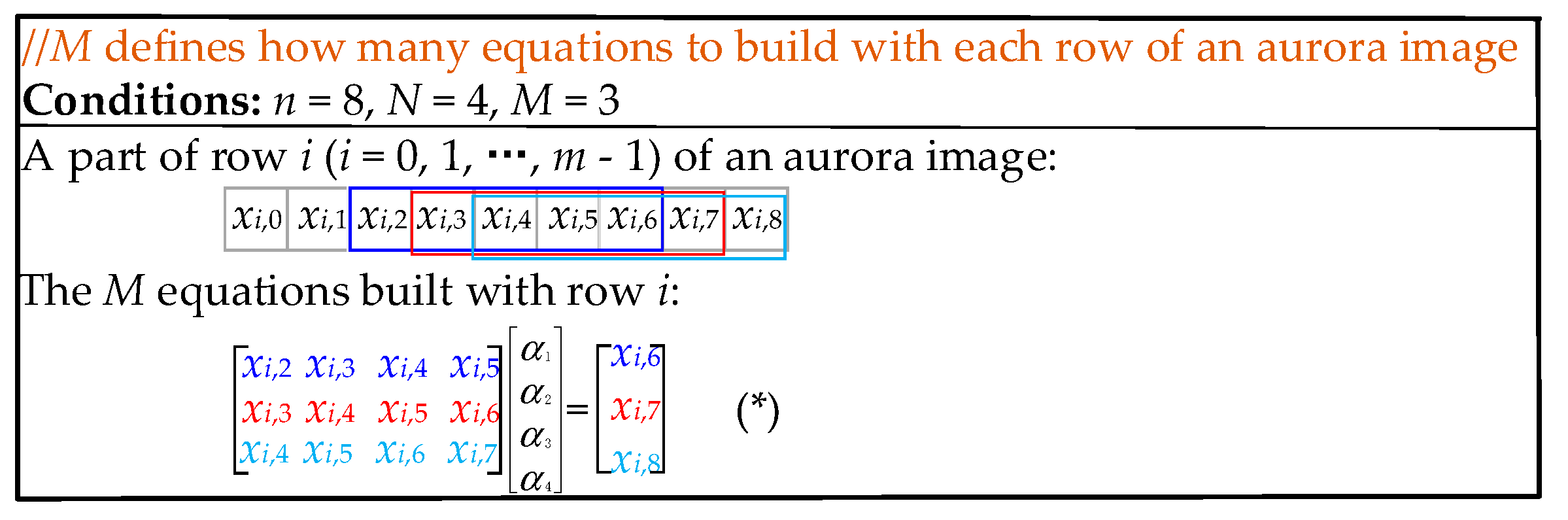
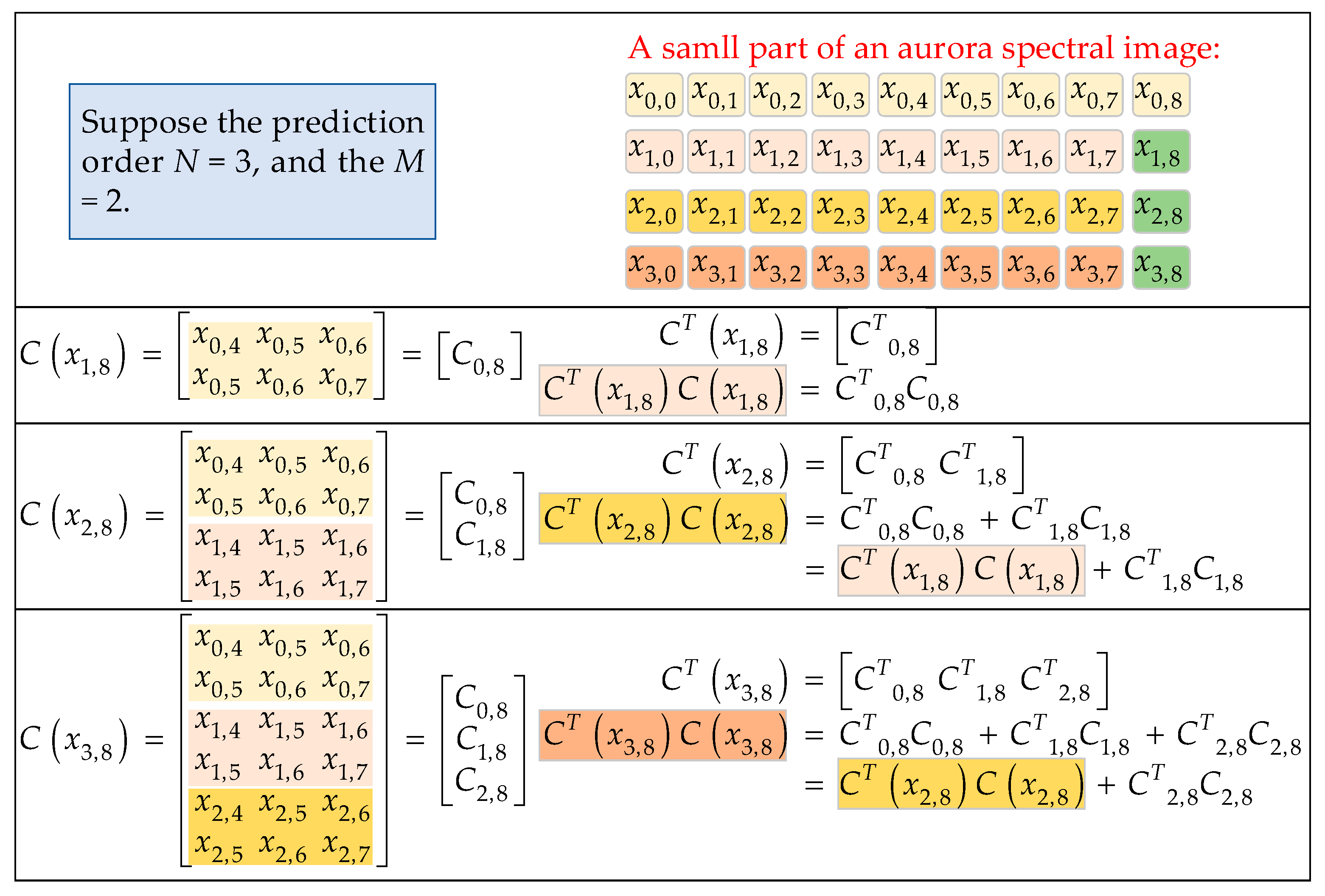
2.2.1. The Improvement on the Establishment of the Linear System of Equations

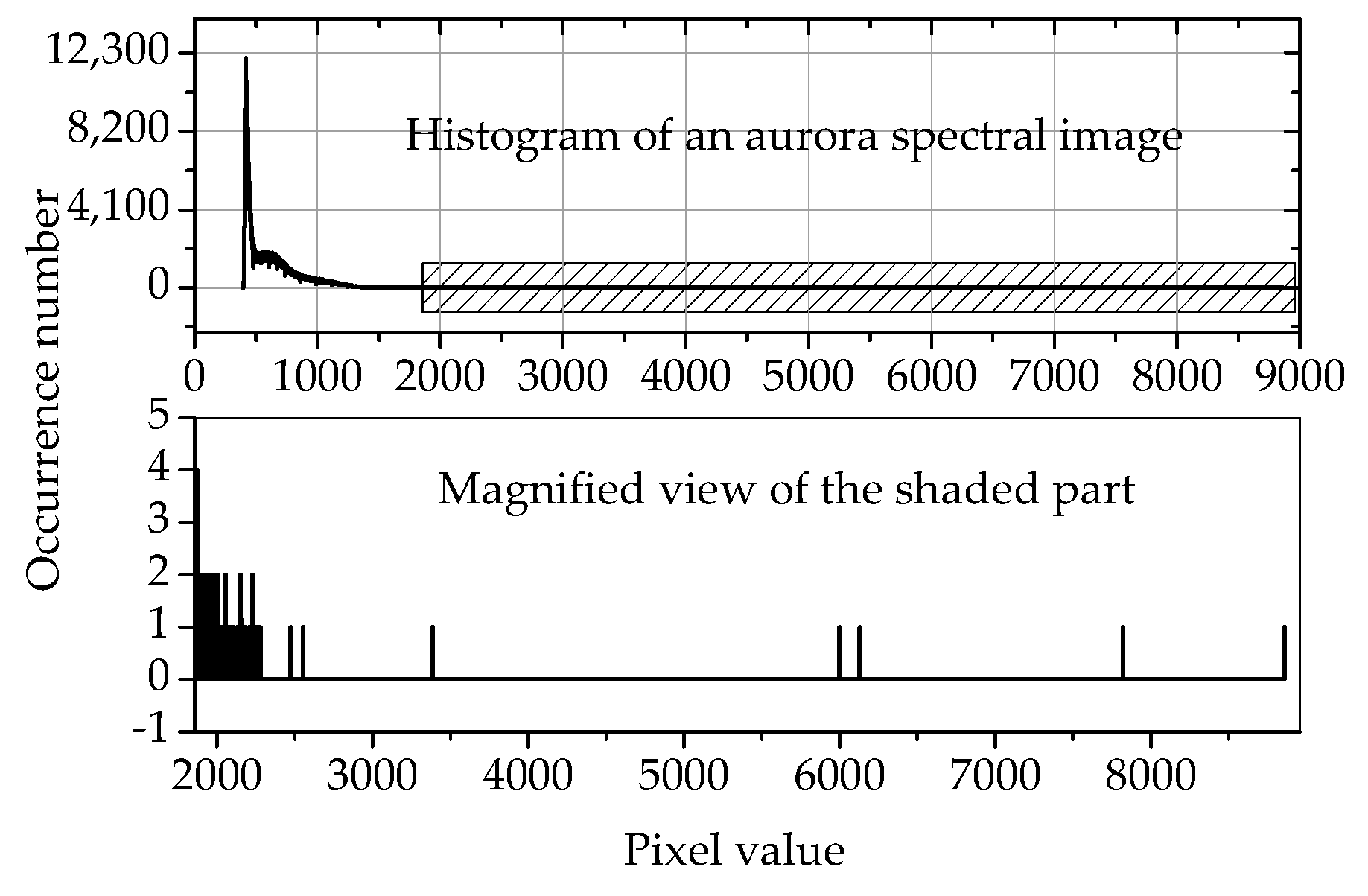
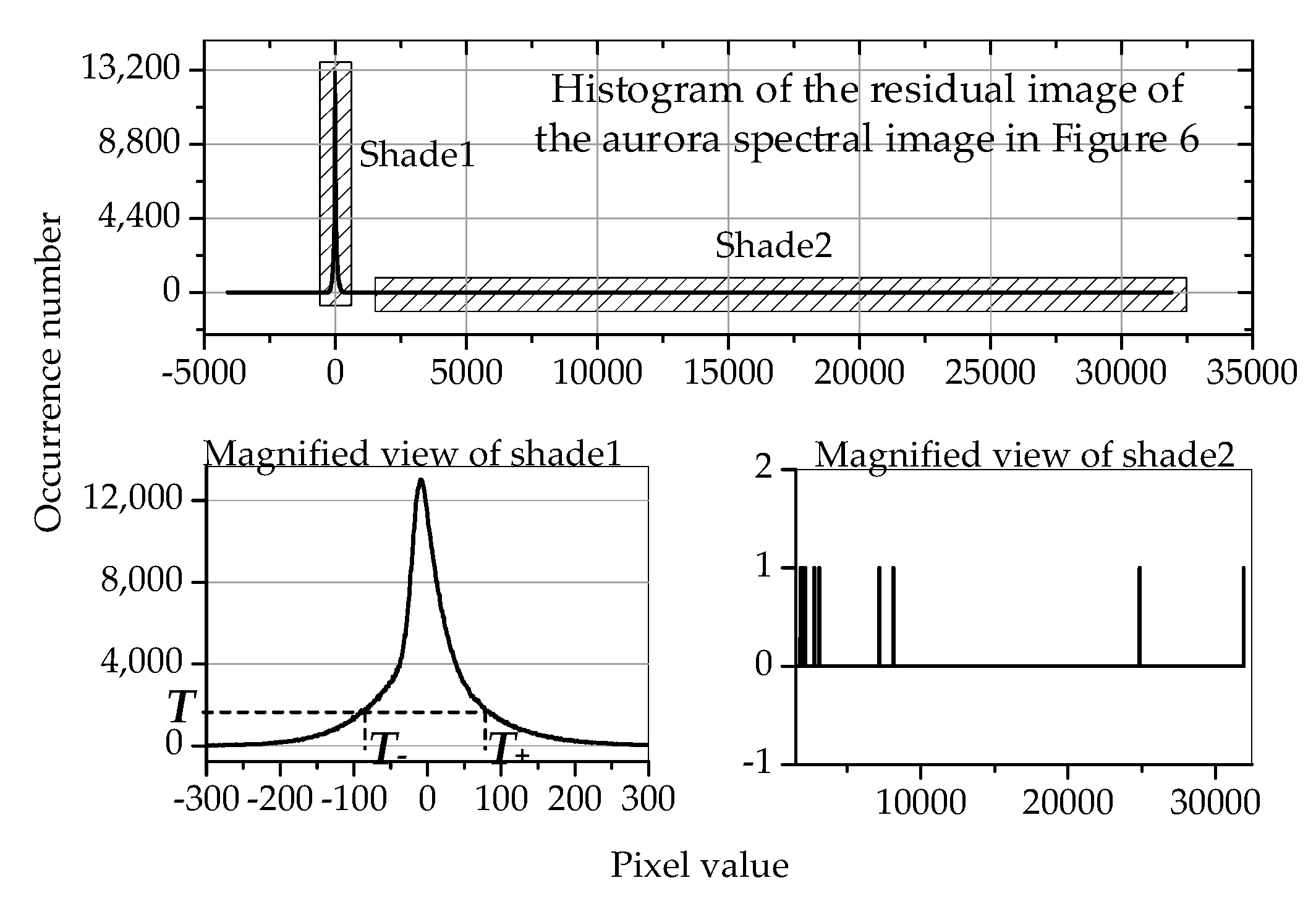
2.2.2. The Improvement on the Encoding of the Residual
2.3. Optimization of the Parameters N, M, and T
3. The GPU Implementation of the Calculation of the Prediction Coefficients using the Improved Online DPCM Algorithm
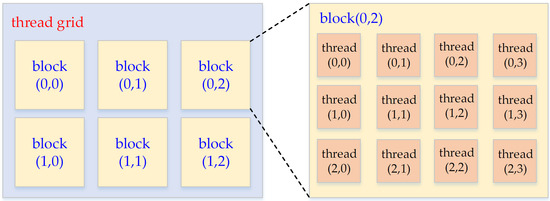
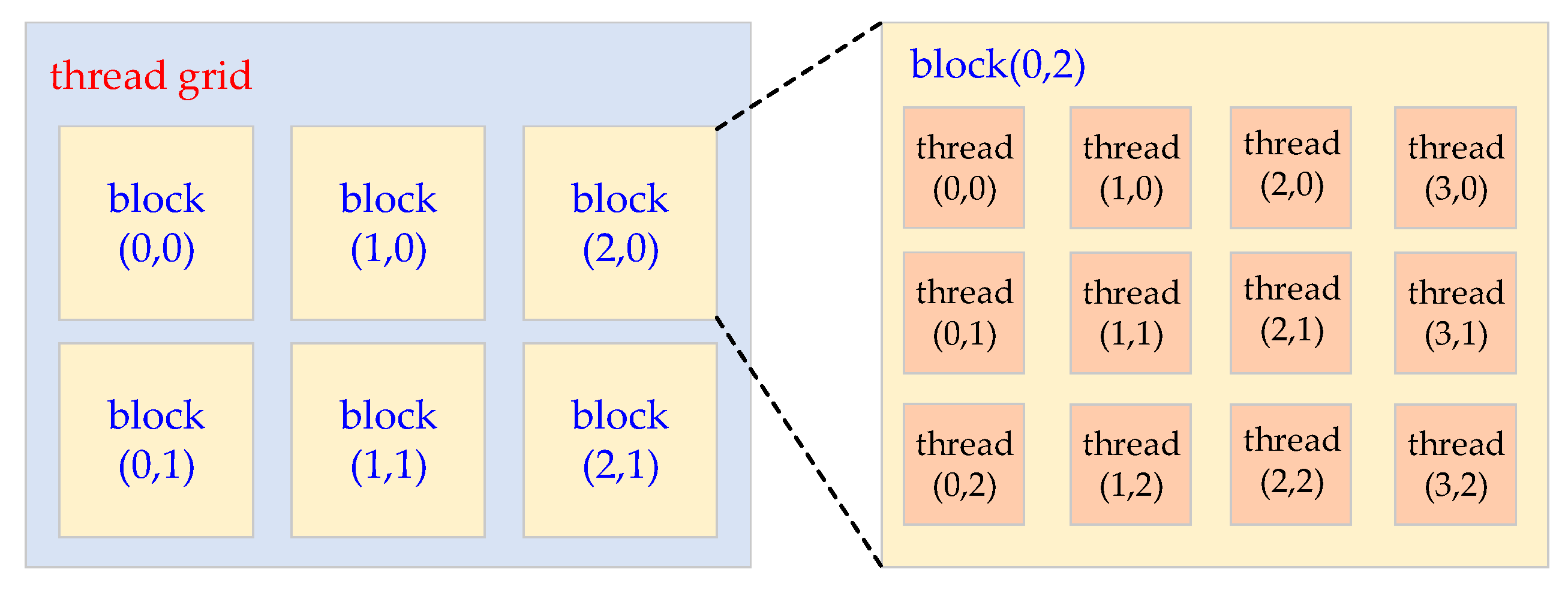
3.1. Some Basic Concepts of GPU Programming
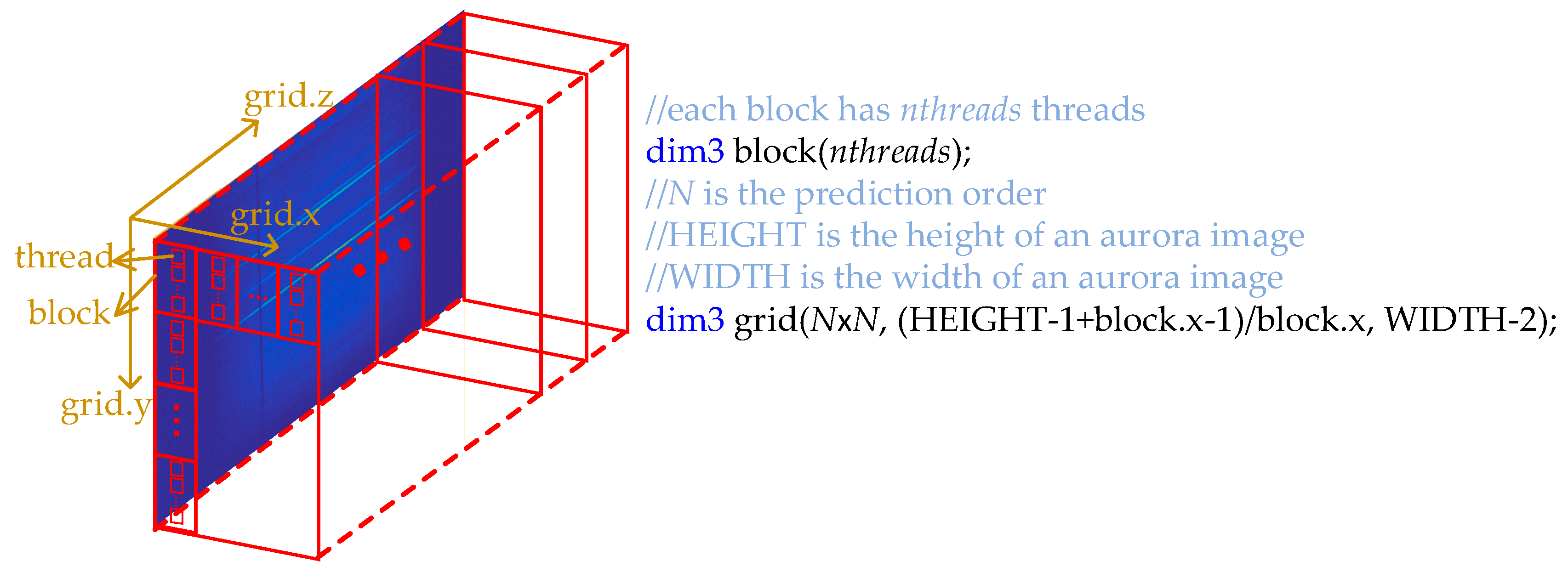
3.2. CUDA Implementation of the Multiplication of Matrices CT and C using a Decomposition Method
3.3. CUDA Implementation of the Inversion of Matrix CTC using the Gaussian Jordan Elimination Method
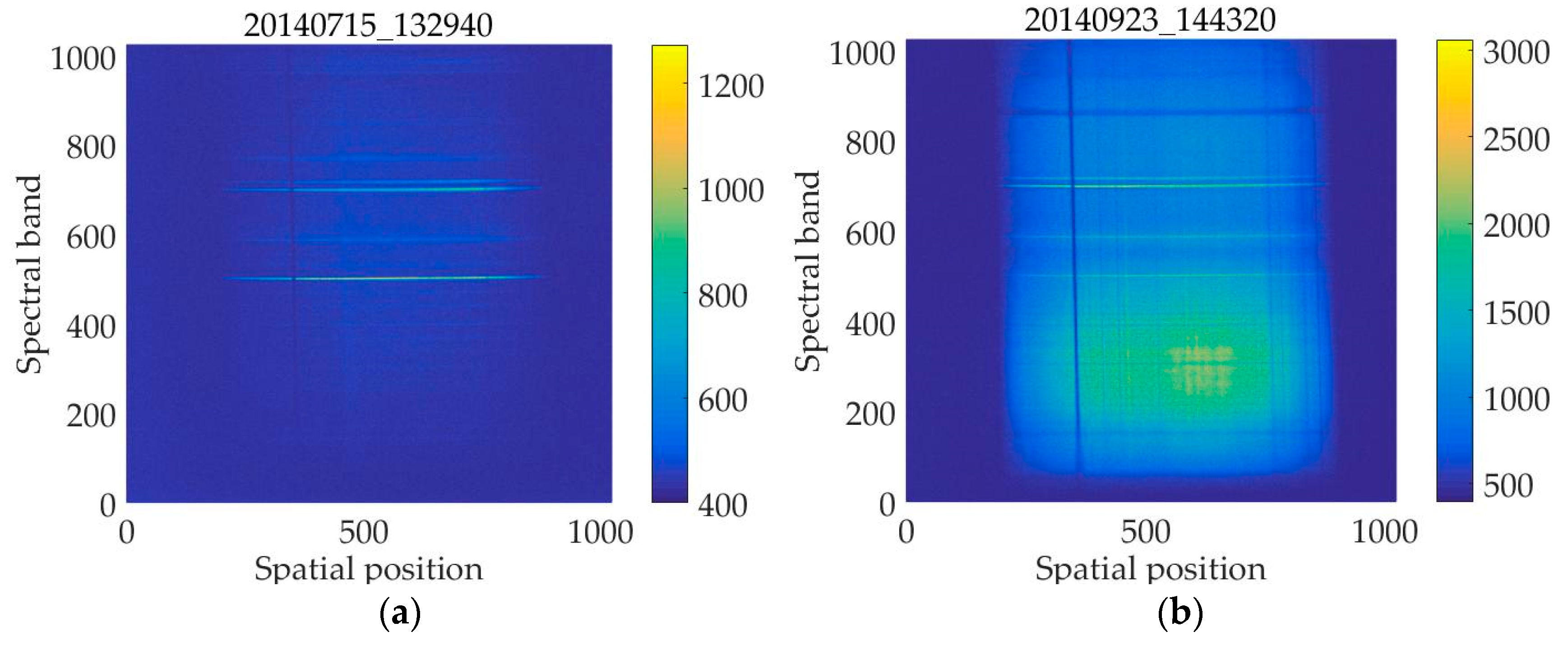
4. Experimental Results
4.1. The Compression Performance of the Improved online DPCM Algorithm Compared with Several Other Lossless Compression Algorithms
4.2. The Performance of the Parallel Implementation of the Online DPCM Algorithm
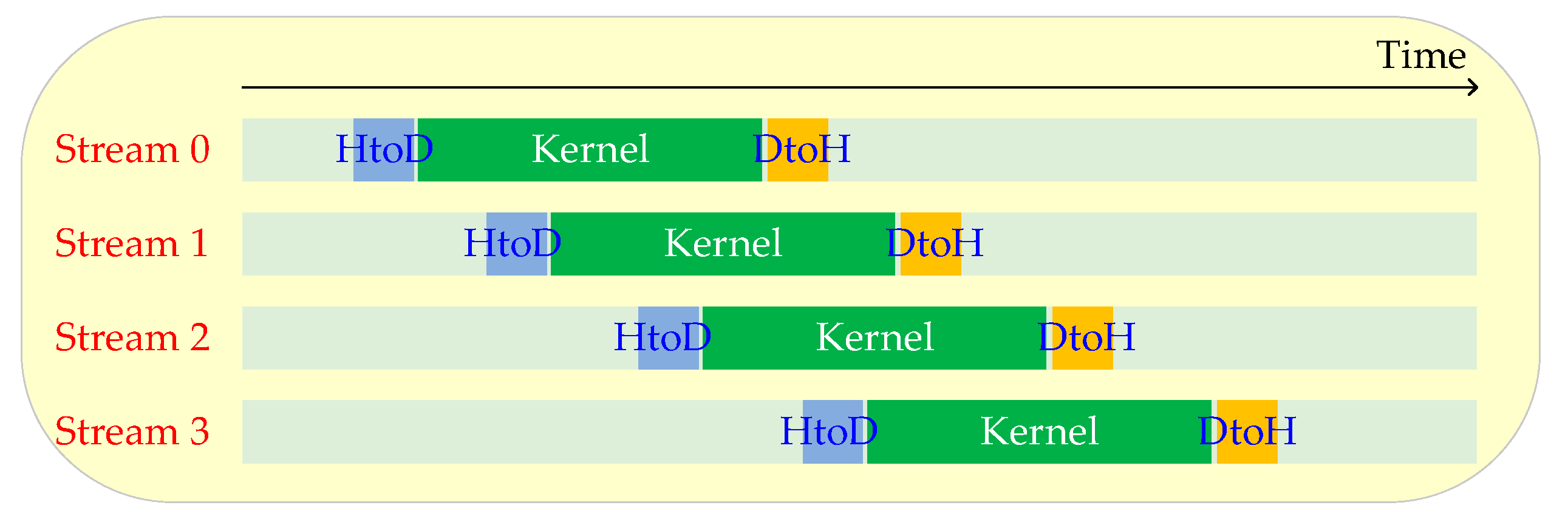
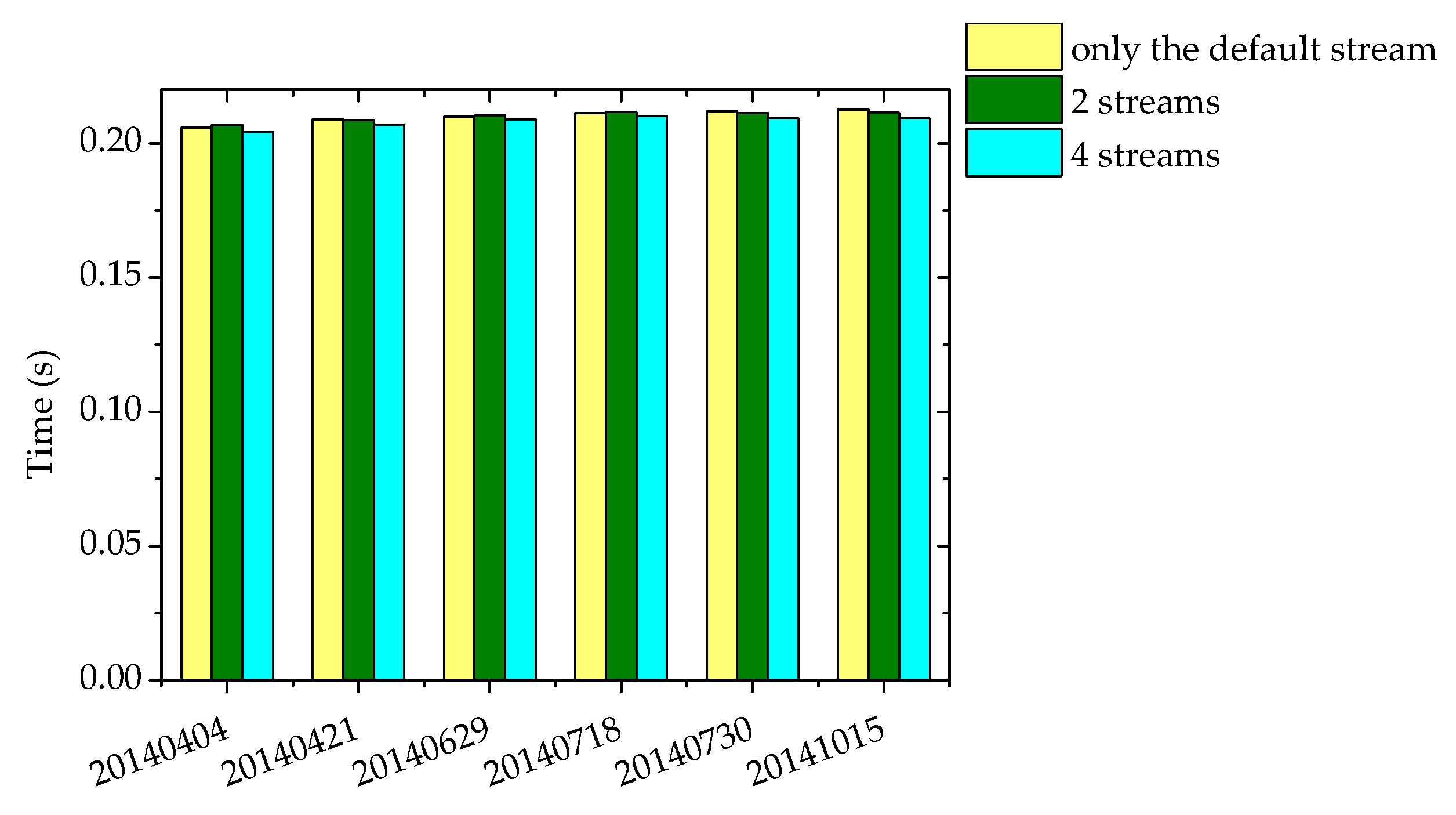
4.3. The Parallel Implementation of the Online DPCM Algorithm using the Multi-Stream Technique
4.4. The Parallel Implementation of the Online DPCM Algorithm using Multi-GPU Technique
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kong, W.; Wu, J. Fast DPCM scheme for lossless compression of aurora spectral images. In Proceedings of the High-Performance Computing in Geoscience and Remote Sensing VI, Edinburgh, UK, 26 September 2016; p. 100070M. [Google Scholar] [CrossRef]
- Kong, W.; Wu, J.; Hu, Z.; Anisetti, M.; Damiani, E.; Jeon, G. Lossless compression for aurora spectral images using fast online bi-dimensional decorrelation method. Inf. Sci. 2017, 381, 33–45. [Google Scholar] [CrossRef]
- Wells, D.C.; Greisen, E.W.; Harten, R.H. FITS—A flexible image transport system. Astron. Astrophys. Suppl. 1981, 44, 363. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S. Near-lossless image compression by relaxation-labelled prediction. Signal Process. 2002, 82, 1619–1631. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S. Fuzzy logic-based matching pursuits for lossless predictive coding of still images. IEEE Trans. Fuzzy Syst. 2002, 10, 473–483. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S. Context modeling for near-lossless image coding. IEEE Signal Process. Lett. 2002, 9, 77–80. [Google Scholar] [CrossRef]
- Mielikainen, J.; Toivanen, P. Clustered dpcm for the lossless compression of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2943–2946. [Google Scholar] [CrossRef]
- Martin, G. Range encoding: An algorithm for removing redundancy from a digitised message. In Proceedings of the Video and Data Recording Conference, Southampton, UK, 24–27 July 1979. [Google Scholar]
- Kong, W.; Wu, J. A lossless compression algorithm for aurora spectral data using online regression prediction. In Proceedings of the High-Performance Computing in Remote Sensing V, Toulouse, France, 21 September 2015; p. 964611. [Google Scholar] [CrossRef]
- Weinberger, M.J.; Seroussi, G.; Sapiro, G. LOCO-I: A low complexity, context-based, lossless image compression algorithm. In Proceedings of the Data Compression Conference-DCC 96, Snowbird, UT, USA, 31 March–3 April 1996; pp. 140–149. [Google Scholar] [CrossRef]
- Weinberger, M.J.; Seroussi, G.; Sapiro, G. The LOCO-I lossless image compression algorithm: Principles and standardization into JPEG-LS. IEEE Trans. Image Process. 2000, 9, 1309–1324. [Google Scholar] [CrossRef]
- Taubman, D.S.; Marcellin, M.W. JPEG2000: Standard for interactive imaging. Proc. IEEE 2002, 90, 1336–1357. [Google Scholar] [CrossRef]
- Wu, X.; Memon, N. Context-based, adaptive, lossless image coding. IEEE Trans. Commun. 1997, 45, 437–444. [Google Scholar] [CrossRef]
- Kim, B.J.; Pearlman, W.A. An Embedded Wavelet Video Coder Using Three-Dimensional Set Partitioning in Hierarchical Trees (SPIHT). In Proceedings of the Conference on Data Compression, Snowbird, UT, USA, 25–27 March 1997; p. 251. [Google Scholar] [CrossRef]
- Lucas, L.F.R.; Rodrigues, N.M.M.; Cruz, L.A.d.S.; Faria, S.M.M.d. Lossless Compression of Medical Images Using 3-D Predictors. IEEE Trans. Med Imaging 2017, 36, 2250–2260. [Google Scholar] [CrossRef]
- Xiaolin, W.; Memon, N. Context-based lossless interband compression-extending CALIC. IEEE Trans. Image Process. 2000, 9, 994–1001. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.; Pearlman, W.A. Three-dimensional wavelet-based compression of hyperspectral images. In Hyperspectral Data Compression; Springer: Boston, MA, USA, 2006; pp. 273–308. [Google Scholar] [CrossRef]
- Zhang, J.; Fowler, J.E.; Liu, G. Lossy-to-Lossless Compression of Hyperspectral Imagery Using Three-Dimensional TCE and an Integer KLT. IEEE Geosci. Remote Sens. Lett. 2008, 5, 814–818. [Google Scholar] [CrossRef] [Green Version]
- Karami, A.; Beheshti, S.; Yazdi, M. Hyperspectral image compression using 3D discrete cosine transform and support vector machine learning. In Proceedings of the 2012 11th International Conference on Information Science, Signal Processing and their Applications (ISSPA), Montreal, QC, Canada, 2–5 July 2012; pp. 809–812. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Lastri, C. Crisp and Fuzzy Adaptive Spectral Predictions for Lossless and Near-Lossless Compression of Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2007, 4, 532–536. [Google Scholar] [CrossRef]
- Simek, V.; Asn, R.R. GPU Acceleration of 2D-DWT Image Compression in MATLAB with CUDA. In Proceedings of the 2008 Second UKSIM European Symposium on Computer Modeling and Simulation, Liverpool, UK, 8–10 September 2008; pp. 274–277. [Google Scholar] [CrossRef]
- Tenllado, C.; Setoain, J.; Prieto, M.; Piñuel, L.; Tirado, F. Parallel Implementation of the 2D Discrete Wavelet Transform on Graphics Processing Units: Filter Bank versus Lifting. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 299–310. [Google Scholar] [CrossRef] [Green Version]
- Jozef, Z.; Matus, C.; Michal, H. Graphics processing unit implementation of JPEG2000 for hyperspectral image compression. J. Appl. Remote Sens. 2012, 6, 011507. [Google Scholar] [CrossRef]
- Santos, L.; Magli, E.; Vitulli, R.; López, J.F.; Sarmiento, R. Highly-Parallel GPU Architecture for Lossy Hyperspectral Image Compression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 670–681. [Google Scholar] [CrossRef]
- Keymeulen, D.; Aranki, N.; Hopson, B.; Kiely, A.; Klimesh, M.; Benkrid, K. GPU lossless hyperspectral data compression system for space applications. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–9. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, L.; Li, J.; Wang, Q.; Sun, L.; Wei, Z.; Plaza, J.; Plaza, A. GPU Parallel Implementation of Spatially Adaptive Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1131–1143. [Google Scholar] [CrossRef]
- CUBLAS_Library. Available online: https://docs.nvidia.com/cuda/cublas/#axzz4h7431Tsi (accessed on 22 May 2019).
- CUDA_C_Programming_Guide. Available online: https://docs.nvidia.com/cuda/cuda-c-programming-guide/#axzz4dQa7XYMd (accessed on 22 May 2019).
- Juanjuan, B.; Ling, G.; Lidong, H. Constructing windows+gcc+mpi+omp and performance testing with Gauss-Jordan elimination method in finding the inverse of a matrix. In Proceedings of the 2010 International Conference On Computer Design and Applications, Qinhuangdao, China, 25–27 June 2010. [Google Scholar] [CrossRef]
- Nyokabi, G.J.; Salleh, M.; Mohamad, I. NTRU inverse polynomial algorithm based on circulant matrices using gauss-jordan elimination. In Proceedings of the 2017 6th ICT International Student Project Conference (ICT-ISPC), Skudai, Malaysia, 23–24 May 2017; pp. 1–5. [Google Scholar] [CrossRef]
- 7-Zip. Available online: https://www.7-zip.org/ (accessed on 22 May 2019).
- Burrows, M.; Wheeler, D.J. A Block-Sorting Lossless Data Compression Algorithm. SRC Res. Rep. 1994. [Google Scholar]
- Shkarin, D. PPM: One step to practicality. In Proceedings of the DCC 2002, Data Compression Conference, Snowbird, UT, USA, 2–4 April 2002; pp. 202–211. [Google Scholar] [CrossRef]
- Cleary, J.; Witten, I. Data Compression Using Adaptive Coding and Partial String Matching. IEEE Trans. Commun. 1984, 32, 396–402. [Google Scholar] [CrossRef]














| Implementation | Serial Direct Time (s) | Serial Decomposed Time (s) | Parallel Time (s) | Speedup | |
|---|---|---|---|---|---|
| Data | |||||
| 20140328 | 869.16 | 3.75 | 0.19 | 19.7 | |
| 20140404 | 872.56 | 3.74 | 0.21 | 17.8 | |
| 20140425 | 872.28 | 3.74 | 0.21 | 17.8 | |
| 20140629 | 872.24 | 3.74 | 0.21 | 17.8 | |
| 20140705 | 872.12 | 3.74 | 0.21 | 17.8 | |
| 20140718 | 869.67 | 3.74 | 0.21 | 17.8 | |
| 20140730 | 870.48 | 3.73 | 0.21 | 17.8 | |
| 20140827 | 872.68 | 3.74 | 0.21 | 17.8 | |
| 20140514_133241 | 20140923_155500 | |||
|---|---|---|---|---|
| Time | Ratio (%) | Time | Ratio (%) | |
| CTCMulKernel | 10.820 ms | 5.71 | 10.759 ms | 5.71 |
| CTCBlockPrefixKernel | 11.920 ms | 6.29 | 11.857 ms | 6.29 |
| matrixInverseKernel | 137.29 ms | 72.41 | 136.42 ms | 72.36 |
| memcpyHtoD | 191.24 us | 0.10 | 194.25 us | 0.10 |
| memcpyDtoH | 161.32 us | 0.09 | 161.32 us | 0.09 |
| 20140514_133241 | 20140923_155500 | |||
|---|---|---|---|---|
| achieved_occupancy | gld_throughput | achieved_occupancy | gld_throughput | |
| CTCMulKernel | 87.06% | 5.43 GB/s | 87.24% | 4.61 GB/s |
| CTCBlockPrefixKernel | 94.88% | 321.91 GB/s | 94.88% | 310.63 GB/s |
| matrixInverseKernel | 99.63% | 183.53 GB/s | 99.63% | 183.21 GB/s |
| 20140514 | 20140705 | 20140827 | 20140916 | 20140930 | 20141017 | ||
|---|---|---|---|---|---|---|---|
| Serial time(s) | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 | |
| 2 GPUs | Time(s) | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 |
| Speedup | 31.2 | 31.2 | 31.2 | 31.2 | 31.2 | 31.2 | |
| 4 GPUs | Time(s) | 0.06 | 0.06 | 0.07 | 0.07 | 0.07 | 0.07 |
| Speedup | 62.3 | 62.3 | 53.4 | 53.4 | 53.4 | 53.4 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wu, J.; Jeon, G. GPU-Based Lossless Compression of Aurora Spectral Data using Online DPCM. Remote Sens. 2019, 11, 1635. https://doi.org/10.3390/rs11141635
Li J, Wu J, Jeon G. GPU-Based Lossless Compression of Aurora Spectral Data using Online DPCM. Remote Sensing. 2019; 11(14):1635. https://doi.org/10.3390/rs11141635
Chicago/Turabian StyleLi, Jiaojiao, Jiaji Wu, and Gwanggil Jeon. 2019. "GPU-Based Lossless Compression of Aurora Spectral Data using Online DPCM" Remote Sensing 11, no. 14: 1635. https://doi.org/10.3390/rs11141635
APA StyleLi, J., Wu, J., & Jeon, G. (2019). GPU-Based Lossless Compression of Aurora Spectral Data using Online DPCM. Remote Sensing, 11(14), 1635. https://doi.org/10.3390/rs11141635