A Hovercraft-Borne LiDAR and a Comprehensive Filtering Method for the Topographic Survey of Mudflats
Abstract
:1. Introduction
2. Hovercraft-Borne LiDAR System
3. Ground Points Acquisition
3.1. Data Synchronization
3.2. Coordinate Calculation of Laser Points
3.3. Comprehensive Filtering of the Point Cloud
3.3.1. Point Cloud Segmentation by Combining Normal Vector and Intensity
- For each point, its normal vector and curvature are estimated using the points within radius r to fit a local surface. The unitized normal vector and normalized intensity value are used to build a four-dimensional attribute vector A:where Nx, Ny, and Nz are the normal vector components in the directions of x, y, and z, and Nx2 + Ny2 + Nz2 = 1; I is the intensity value of the point within the range 0–1 after normalization.A = [ Nx Ny Nz I ],
- Among all points, the point with the minimum curvature is selected as a seed point P0, and a new segment O is generated. P0 is included in O and marked as a segmented point.
- The points around P0 within the radius R are searched as candidate points. For each candidate point Pi, the distance between the attribute vectors of Pi and P0 is calculated by Equation (5):where (//) and (//) represent the Nx(Ny/Nz/I) in the A of P0 and Pi, respectively.
- The threshold d is set in the region growing. Whether or not the candidate point is in O is judged based on the following principle:If Pi is included in O, it is marked as a segmented point and becomes a seed point.
- Repeating (4), all the seed points around P0 within the radius R are found and marked as segmented points.
- By region growing, the new seed points are further found by repeating (3)–(5) and are marked as segmented points until no new point is found and marked. These seed points are all included in O. Then the segment O is segmented completely.
- In the remaining unsegmented points, we can also find the point with the minimum curvature. By following (2)–(6), a new segment is generated. Similarly, we can obtain other segments by repeating (2)–(6) until all the points are segmented.
3.3.2. Fitting the Ground Surface and Calculating Its Normal Vector
3.3.3. Segmentation-Based Point Cloud Filtering
- For each segment, the points belonging to the segment are diagnosed as possible ground points by the following criteria:
- •
- The distance from a diagnosed point to the fitting surface is less than the given threshold h.
- •
- The angle between the normal vectors of the point and the fitting surface is less than the given threshold θ.
- For each segment, the proportion of the possible ground points in the total points of the segment is calculated. If the proportion is higher than the given threshold p, the segment is judged as a ground segment, and all the points belonging to the segment are judged as ground points; otherwise, they are judged as non-ground points.
3.3.4. The Comprehensive Point Cloud Filtering Process
3.4. Accuracy Assessment
4. Experiment and Analysis
4.1. Overview of the Experiment
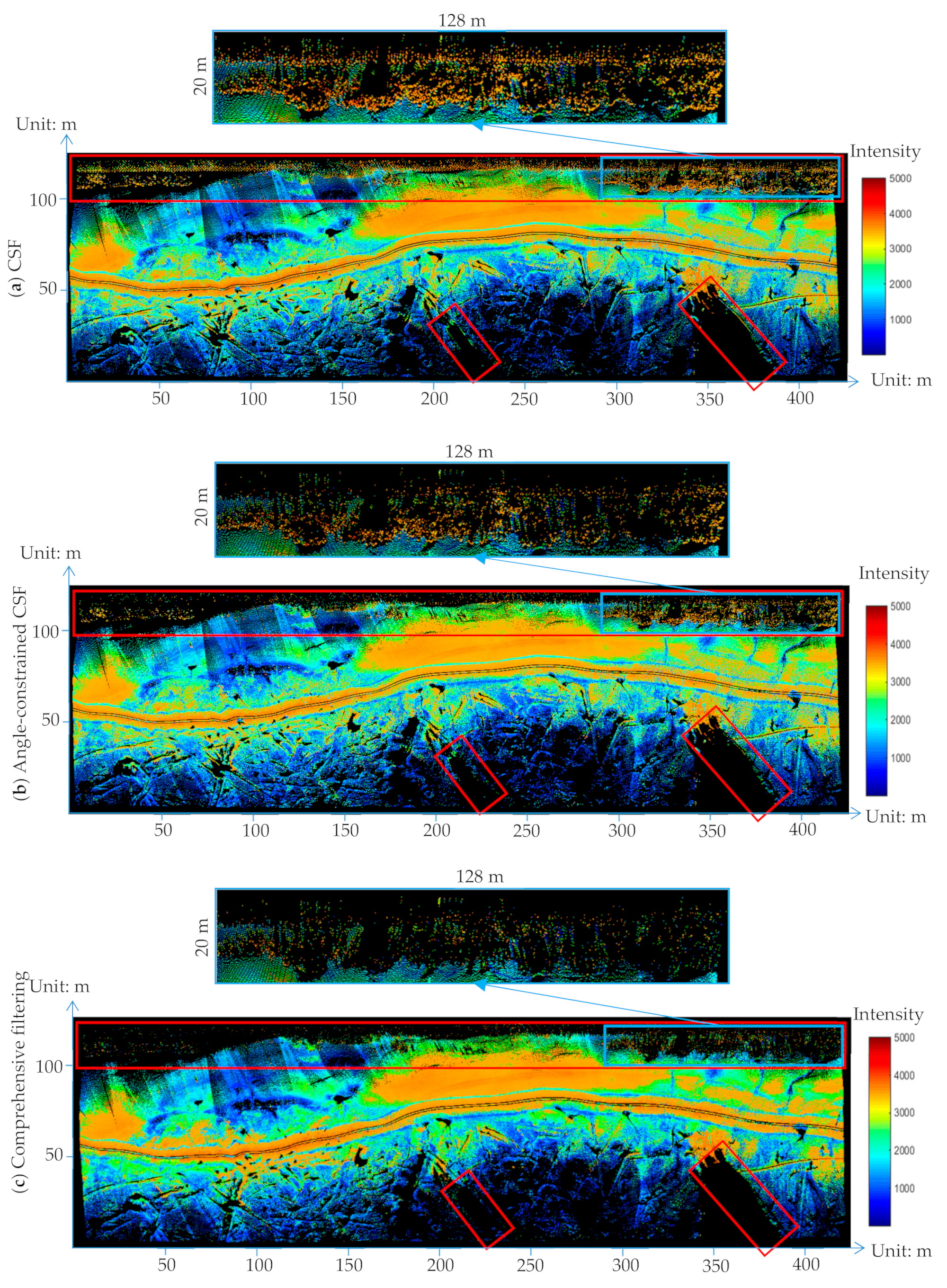
4.2. Data Processing and Analysis
5. Discussion
5.1. The Mobile Measuring System
5.2. Obtaining the Mudflat Topography
5.2.1. Removal of Outliers Lower than the Mudflat Surface before Filtering
5.2.2. Point Cloud Segmentation by Combining Normal Vector and Intensity
5.2.3. Filtering Parameter Setting
5.2.4. Interpolation in Blank Areas
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.G.; Guan, W.; Li, C.P.; Dong, L.J. A study on the exploitation and the sustainable utilization of marine resources in the Bohai Sea. J. Nat. Resour. 2002, 17, 768–775. [Google Scholar]
- Lai, Z.L.; Zhang, H.D.; Wan, Y.C.; Yue, Y.C. Applications of airborne LIDAR technology in topographic survey of tidal flat and coastal zone. Hydrogr. Surv. Charting 2008, 28, 37–39. [Google Scholar]
- Mason, D.C.; Kennett, C.G. Beach topography mapping: A comparison of techniques. J. Coast. Conserv. 2000, 6, 113–124. [Google Scholar] [CrossRef]
- Lee, J.M.; Park, J.Y.; Choi, J.Y. Evaluation of sub-aerial topographic surveying techniques using total station and RTK-GPS for applications in macrotidal sand beach environment. J. Coast. Res. 2013, 65, 535–540. [Google Scholar] [CrossRef]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. ISPRS J. Photogram. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Baltsavias, E.P. A comparison between photogrammetry and laser scanning. ISPRS J. Photogramm. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Irish, J.L.; White, T.E. Coastal engineering applications of high-resolution lidar bathymetry. Coast. Eng. 1998, 35, 47–71. [Google Scholar] [CrossRef]
- Dalloz, L.; Brand, A.; Chiniah, I.; Beaumale, D.; Commun, M. Autonomous area mapping with low cost hovercraft platform. Appl. Mech. Mater. 2015, 799–800, 1102–1106. [Google Scholar] [CrossRef]
- Kukko, A.; Kaartinen, H.; Hyyppä, J.; Chen, Y. Multiplatform mobile laser scanning: Usability and performance. Sensors 2012, 12, 11712–11733. [Google Scholar] [CrossRef]
- Vosselman, G. Slope based filtering of laser altimetry data. Int. Arch. Photogramm. Remote Sens. 2000, 33, 935–942. [Google Scholar]
- Sithole, G. Filtering of laser altimetry data using a slope adaptive filter. Int. Arch. Photogramm. Remote Sens. 2001, 34, 203–210. [Google Scholar]
- Kilian, J.; Haala, N.; Englich, M. Capture and evaluation of airborne laser scanner data. Int. Arch. Photogramm. Remote Sens. 1996, 31, 383–388. [Google Scholar]
- Zhang, K.; Chen, S.C.; Whitman, D.; Shyu, M.L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Gong, P.; Baldocchi, D.; Xie, G. Filtering airborne laser scanning data with morphological methods. Photogram. Eng. Remote Sens. 2007, 73, 175–185. [Google Scholar] [CrossRef]
- Li, Y.; Wu, H.; Xu, H.; An, R.; Xu, J.; He, Q. A gradient-constrained morphological filtering algorithm for airborne LiDAR. Opt. Laser Technol. 2013, 54, 288–296. [Google Scholar] [CrossRef]
- Pingel, T.J.; Clarke, K.C.; Mcbride, W.A. An improved simple morphological filter for the terrain classification of airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2013, 77, 21–30. [Google Scholar] [CrossRef]
- Mongus, D.; Lukač, N.; Žalik, B. Ground and building extraction from LiDAR data based on differential morphological profiles and locally fitted surfaces. ISPRS J. Photogramm. Remote Sens. 2014, 93, 145–156. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. Int. Arch. Photogramm. Remote Sens. 2000, 33, 111–118. [Google Scholar]
- Mongus, D.; Žalik, B. Parameter-free ground filtering of LiDAR data for automatic DTM generation. ISPRS J. Photogramm. Remote Sens. 2012, 67, 1–12. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Dong, Z.; Zang, Y.; Li, J. Two-step adaptive extraction method for ground points and breaklines from lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2016, 119, 373–389. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Tóvári, D.; Pfeifer, N. Segmentation Based Robust Interpolation—A New Approach to Laser Data Filtering. In Laser Scanning 2005; International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences: Enschede, The Netherlands, 2005; Volume 36, pp. 79–84. [Google Scholar]
- Sithole, G.; Vosselman, G. Filtering of Airborne Laser Scanner Data Based on Segmented Point Clouds. In Laser Scanning 2005; International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences: Enschede, The Netherlands, 2005; pp. 66–71. [Google Scholar]
- Yan, M.; Blaschke, T.; Liu, Y.; Wu, L. An object-based analysis filtering algorithm for airborne laser scanning. Int. J. Remote Sens. 2012, 33, 7099–7116. [Google Scholar] [CrossRef]
- Lin, X.G.; Zhang, J.X. Segmentation-based filtering of airborne LiDAR point clouds by progressive densification of terrain segments. Remote Sens. 2014, 6, 1294–1326. [Google Scholar] [CrossRef]
- Zhang, J.X.; Lin, X.G.; Liang, X.L. Advances and prospects of information extraction from point clouds. Acta Geod. et Cartogr. Sin. 2017, 46, 1460–1469. [Google Scholar]
- Liu, X. Airborne LiDAR for DEM generation: Some critical issues. Prog. Phys. Geogr. 2008, 32, 31–49. [Google Scholar]
- Chen, C.J. The Research on Key Technique of Mobile Mapping System Integration. Ph.D. Thesis, Wuhan University, Wuhan, China, 2013. [Google Scholar]
- Vaughn, C.R.; Bufton, J.L.; Krabill, W.B.; Rabine, D.L. Georeferencing of airborne laser altimeter measurements. Int. J. Remote Sens. 1996, 17, 2185–2200. [Google Scholar] [CrossRef]
- Besl, P.; Jain, R. Segmentation through variable-order surface fitting. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 167–192. [Google Scholar] [CrossRef]
- Zhan, Q.L. Segmentation of LiDAR point cloud based on similarity measures in multi-dimension Euclidean space. In Advances in Computer Science and Engineering; Zeng, D., Ed.; Springer: Berlin, Germany, 2012; Volume 141, pp. 349–357. [Google Scholar]












| Equipment | Specification | Accuracy/Range | Specification | Accuracy/Range |
|---|---|---|---|---|
| R-Angle 0300 Laser Scanner | Min. Range (m) | 1.5 | Field of View (°) | 360 |
| Max. Range (m) | 600 | Echoes | Multiple | |
| Max. Pulse Frequency (kHz) | 1000 | Wavelength (nm) | 1550 | |
| Scan Speed (Hz) | 10–200 | Scanner Weight (kg) | <5 | |
| Beam Divergence (mrad) | <0.35 | Power Supply (V DC) | 18–32 | |
| Angle Resolution (°) | 0.001 | Power Consumption (W) | <100 | |
| Angle Precision (°) | 0.005 | Storage Temperature (℃) | −35 to 70 | |
| Range Precision (mm @ 100 m) | 5–8 | Operation Temperature (℃) | −20 to 65 | |
| APPLANIX POS AV610 | GNSS Position (m) | 0.05–0.3 | Roll and Pitch (°) | 0.0025 |
| Velocity (m/s) | 0.005 | True Heading (°) | 0.005 | |
| CH-4 Hovercraft | Size (m) | 4.6 × 2.4 × 1.65 | Hover Height (mm) | ≤220 |
| Weight (kg) | 380 ± 50 | Speed (mud/sand) (km/h) | 30–45 |
| Method | Point Cloud Segmentation | Object-Based Filtering | ||||
|---|---|---|---|---|---|---|
| r (m) | R (m) | d | h (m) | θ (°) | p (%) | |
| Traditional CSF | - | - | - | 0.1 | - | - |
| Angle-constrained CSF | - | - | - | 0.1 | 30 | - |
| Comprehensive filtering | 0.5 | 0.5 | 0.6 | 0.1 | 30 | 75 |
| Method | E.I (%) | E.II (%) | E.T (%) |
|---|---|---|---|
| Traditional CSF | 0.2 | 20.1 | 1.9 |
| Angle-constrained CSF | 0.3 | 10.5 | 1.3 |
| Comprehensive filtering | 0.2 | 2.8 | 0.3 |
| Max. (cm) | Min. (cm) | Average (cm) | RMSE (cm) |
|---|---|---|---|
| 23.0 | −15.3 | −2.1 | 6.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Chen, M.; Zhang, H.; Zheng, G. A Hovercraft-Borne LiDAR and a Comprehensive Filtering Method for the Topographic Survey of Mudflats. Remote Sens. 2019, 11, 1646. https://doi.org/10.3390/rs11141646
Zhao J, Chen M, Zhang H, Zheng G. A Hovercraft-Borne LiDAR and a Comprehensive Filtering Method for the Topographic Survey of Mudflats. Remote Sensing. 2019; 11(14):1646. https://doi.org/10.3390/rs11141646
Chicago/Turabian StyleZhao, Jianhu, Mingyi Chen, Hongmei Zhang, and Gen Zheng. 2019. "A Hovercraft-Borne LiDAR and a Comprehensive Filtering Method for the Topographic Survey of Mudflats" Remote Sensing 11, no. 14: 1646. https://doi.org/10.3390/rs11141646
APA StyleZhao, J., Chen, M., Zhang, H., & Zheng, G. (2019). A Hovercraft-Borne LiDAR and a Comprehensive Filtering Method for the Topographic Survey of Mudflats. Remote Sensing, 11(14), 1646. https://doi.org/10.3390/rs11141646




