Next Article in Journal
LEO to GEO-SAR Interferences: Modelling and Performance Evaluation
Next Article in Special Issue
Field-Scale Crop Seeding Date Estimation from MODIS Data and Growing Degree Days in Manitoba, Canada
Previous Article in Journal
Canopy and Terrain Height Retrievals with ICESat-2: A First Look
Previous Article in Special Issue
Mapping Paddy Rice Planting Area in Northeastern China Using Spatiotemporal Data Fusion and Phenology-Based Method
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 11
Issue 14
10.3390/rs11141723
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Spatiotemporal Analysis of MODIS NDVI in the Semi-Arid Region of Kurdistan (Iran)

by
Mehdi Gholamnia
1,*,
Reza Khandan
2,
Stefania Bonafoni
3 and
Ali Sadeghi
4
1
Department of Civil Engineering, Islamic Azad University, Sanandaj Branch, Islamic Azad University, Sanandaj 6616935391, Iran
2
Department of GIS and Remote Sensing, Faculty of Geography, University of Tehran, Teheran 14155-6619, Iran
3
Department of Engineering, University of Perugia, via G. Duranti 93, 06125 Perugia, Italy
4
Department of GIS and Remote Sensing, Faculty of Geography, University of Isfahan, Isfahan 8415683111, Iran
*
Author to whom correspondence should be addressed.
Remote Sens. 2019, 11(14), 1723; https://doi.org/10.3390/rs11141723
Submission received: 28 May 2019 / Revised: 15 July 2019 / Accepted: 18 July 2019 / Published: 20 July 2019
(This article belongs to the Special Issue Advances of Multi-Temporal Remote Sensing in Vegetation and Agriculture Research)
Browse Figures
Versions Notes

Abstract

:
In this study, the spatiotemporal behavior of vegetation cover in the Kurdistan province of Iran was analyzed for the first time by TIMESAT and Breaks for Additive Season and Trend (BFAST) algorithms. They were applied on Normalized Vegetation Index (NDVI) time series from 2000 to 2016 derived from Moderate Resolution Imaging Spectroradiometer (MODIS) observations. The TIMESAT software package was used to estimate the seasonal parameters of NDVI and their relation to land covers. BFAST was applied for identifying abrupt changes (breakpoints) of NDVI and their magnitudes. The results from TIMESAT and BFAST were first reported separately, and then interpreted together. TMESAT outcomes showed that the lowest and highest amplitudes of NDVI during the whole time period happened in 2008 and 2010. The spatial distribution of the number of breakpoints showed different behaviors in the west and east of the study area, and the breakpoint frequency confirmed the extreme NDVI amplitudes in 2008 and 2010 found by TIMESAT. For the first time in Iran, a correlation analysis between accumulated precipitations and maximum NDVIs (from one to seven months before the NDVI maximum) was conducted. The results showed that precipitation one month before had a higher correlation with the maximum NDVIs in the region. Overall, the results describe the NDVI behavior in terms of greenness, lifetime, abrupt changes for the different land covers, and across the years, suggesting how the northwest and west of the study area can be more susceptible to drought conditions.

Graphical Abstract

1. Introduction

Vegetation cover has a crucial role in the climate and ecosystem of the Earth. It is an important factor in the surface energy budget and soil moisture variability [1]. Several climate research projects focused on the quantification of vegetation cover to study the emergence of drought [2,3,4,5]. Also, the relation of dust storms with vegetation cover has been the subject of several studies [4,6,7]. The emergence of drought and massive dust storms in the Middle East needs special attention, as does the study of vegetation cover. Longtime trends of vegetation variation measurements can yield suitable information regarding land surface cover changes. Satellite observations can provide long-term data on vegetation presence and temporal trends. The Normalized Vegetation Index (NDVI) derived from satellites has been used as an essential vegetation index for studying climate change since the early 1980s [4,8,9,10,11,12]. The time series of NDVI can be used for change detection in vegetation health and growth, especially in semi-arid regions [13,14,15,16]. The NDVI time series can be investigated from two perspectives: (1) annual or seasonal parameters and their longtime trends, and (2) abrupt changes between consecutive years.
Considering the seasonal parameters of NDVI and their longtime trends, some packages such as HANTS, TiSeG, TSPT, PPET, TIMESTATS, the software developed by the USGS Earth Resources Observation and Science Center, Enhanced TIMESAT, SPIRITS, and PhenoSat were proposed [17]. Among the proposed packages, only TIMESAT and PhenoSat are able to analyze double seasonality. The TIMESAT [18] software package has been broadly used to analyze the satellite time series data [18,19,20,21]. This software package is applied to parameterize the phenological and temporal behavior of NDVI on a seasonal scale [22].
According to [23], the methods for extracting abrupt changes can be divided into two groups: spectral frequency and statistical. Spectral-frequency approaches, Fourier transform [24], multi-resolution analysis wavelet transform (MRA-WT) [25], empirical mode decomposition [26], and singular spectrum analysis [27] emphasize the dominant frequency behaviors. Statistical approaches such as seasonal trend loess (STL) [28], seasonal auto-regressive integrated moving average [29], seasonal trend analysis of image time series [30], sub-annual change detection [30], breaks for additive season and trend (BFAST) [31], and detecting breakpoints and estimating segments in trend (DBEST) [32] concentrate on the vegetation dynamic parameters of seasonality, gradual trends, and abrupt changes. The BFAST has been introduced for estimating longtime trends and extracting breakpoints for each pixel. BFAST decomposes into the time series trend, seasonal, and remainder components. BFAST was widely used to study vegetation changes in different parts of the world for various applications [32,33,34,35,36,37,38,39]. The comparison of BFAST, MRA-WT, and STL by [23] showed that BFAST was the most accurate approach for their dataset. The results of Watts and Laffan [40] and Schultz et al. [41] showed that this algorithm had a satisfactory agreement with ground observations for fire and flood events.
The long time series data provided by satellite sensors could be a challenge for the detection of both seasonal details and their breakpoints. Although Aragones et al. [42] applied BFAST for noise removal and used trend and season components as input for TIMESAT, both methods have not yet been used together for NDVI time series analysis. It is essential that the seasonal parameters and trends are analyzed along with abrupt changes (hereafter referred to as breakpoints) for providing a more comprehensive investigation of NDVI time series. Therefore, the time series analysis of NDVI in any region can be done in two steps: (1) focusing on the temporal characteristics of the seasonal parameters and their relation to land covers, as well as investigating such parameters from a phenological perspective, and (2) detecting breakpoints for the entire time series and the time of their occurrences, analyzing their magnitude and their relation with the findings in (1).
In Iran, few research studies have investigated the time series of NDVI for drought monitoring and land-cover changes [43,44]. Examination of the vegetation cover changes as the primary precursors of drought and desertification in the Middle East, including Iran, is essential. Considering the emergence of drought and dust storms in the west of Iran during the last decade [45,46], the present study has chosen the Kurdistan province of Iran as a semi-arid region to quantify the trajectory of NDVI for different land covers and provide the status of the region. It aims to analyze, for the first time, the behavior of NDVI time series, derived from Moderate Resolution Imaging Spectroradiometer (MODIS) observation, using both TIMESAT (for the parameterization of seasonal changes and their relation to land cover) and BFAST (for the detection of breakpoints and their magnitude) from 2000 to 2016. This study focuses on the spatiotemporal NDVI behavior. Also, by considering precipitation as the primary climate factor on NDVI growth [47,48], an analysis of the relationship between the lag time of the NDVI maximum state and precipitation was performed in the study area.

2. Materials and Methods

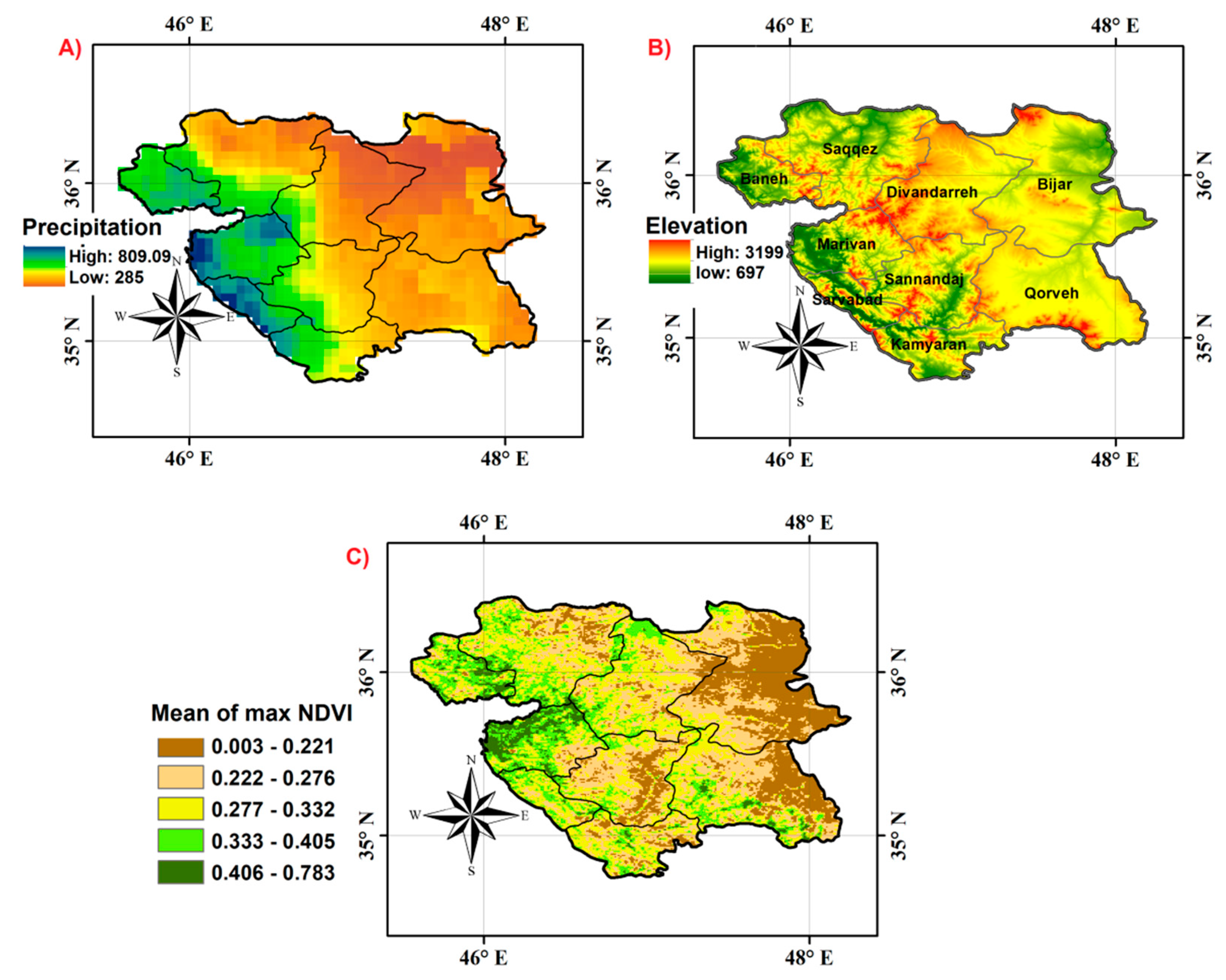
2.1. Study Area

The Kurdistan province of Iran is located in the west of Iran, and is divided in eight counties, as shown in Figure 1A. It is regarded as a mountainous and semi-arid region [49]. Rain gauge data showed that the maximum of annual precipitation happens in the western part of this province (706 mm), and the minimum of annual precipitation happens in the eastern parts (368.7 mm) [50]. Also, the mean of annual precipitation (from 2000 to 2016), which was extracted by monthly precipitation estimates of the Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS), showed higher accumulated precipitation in the western part in contrast with the eastern part (Figure 1A). Based on an ASTER Digital Elevation Model (DEM) with 30-m pixel size [51], the elevation of this region is between 697–3199 m (Figure 1B). The western part has higher elevation in comparison with the eastern part. Figure 1C shows the mean of the annual maximum NDVIs from 2000 to 2016. It indicates a similar pattern regarding precipitation; the western part of the study area is greener than the eastern part.

2.2. Dataset

2.2.1. MODIS NDVI

The Moderate Resolution Imaging Spectroradiometer (MODIS) NDVI 16-day level 3 product (MOD13Q1, collection-6) from the Terra platform with 1-km spatial resolution was downloaded from the MODIS website [52]. In this product, geometrical corrections were made, and the cloudy pixels were removed. The pixels flagged with high quality were used for the analysis [53]. A total of 388 products from 5 March 2000 to 18 December 2016 was used for time-series modeling in TIMESAT and BFAST. In 2000, 20 NDVI products were used, and for each of the other years, 23 NDVI maps were applied, covering all the months of a year.

2.2.2. Land Cover Map

European Space Agency Climate Change Initiative-Land Cover (ESA CCI-LC) products in 2015 with 300-m spatial resolution were utilized for this study. The typology of land covers is based on the United Nation Food and Agriculture Organization (FAO). The accuracy of these classes were reported in [54]: cropland—rainfed and herbaceous lands (92%), mosaic cropland (71%), mosaic natural vegetation (39%), shrubland (62%), grassland (46%), sparse vegetation (31%), bare area (88%), and water body (96%). The land cover was clipped based on the study area, which included eight types of land cover, excluding water types (Figure 2). The percent of different land covers is shown in the legend. Most of the study area is covered by the cropland (rainfed) and herbaceous categories. Comparing the annual ESA CCI-LC maps, the land cover areas from 2000 to 2015 changed less than 3%.

2.2.3. CHIRPS Data

Since dense rain gauge data were not available in the study area (nine weather stations), the monthly precipitation rates of CHIRPS (3B43) [55] from 2000 to 2016 were used to infer the correlation between the spatiotemporal NDVI behavior and precipitation. The monthly accumulated precipitation of CHIRPS integrates three data sources: the global precipitation climatology of the Climate Hazard group Precipitation climatology (CHPclim), precipitations estimated by the TIR bands of satellites, and ground stations. This product has a spatial resolution of 0.05°, and it covers latitudes of 50° S to 50°N. The results from some research studies such as [56,57,58,59,60] indicated that this product had good agreement with ground station data. Also, based on the results from [61], the average correlation with ground stations in Iran during the spring, summer, autumn, and winter were 0.61, 0.559, 0.585, and 0.453, respectively. The CHIRPS data were downloaded from ftp://ftp.chg.ucsb.edu/pub/org/chg/products/CHIRPS-2.0/global_monthly/tifs/.

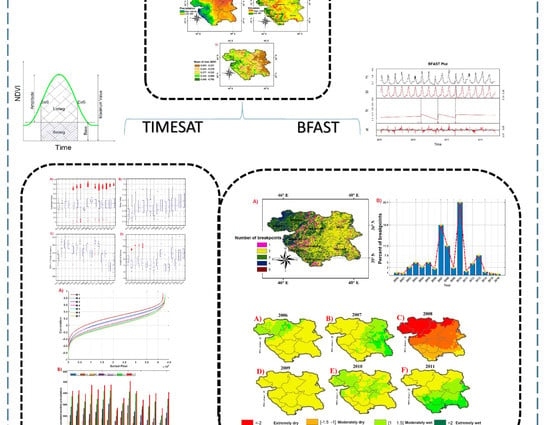
3. Methodology

To provide a comprehensive analysis of the vegetation dynamics in the Kurdistan province, the following investigations will be carried out:
  • TIMESAT [62] will be used to analyze the NDVI longtime trends, i.e., the temporal characteristics of the seasonal parameters and their relation to land covers.
  • The NDVI abrupt changes (breakpoints) across the years will be analyzed by BFAST [31] to find out their number and magnitude, and their relation with the findings of 1.
  • In order to investigate the influence of precipitation on NDVI dynamics, CHIRPS data will be related to the above NDVI results obtained by TIMESAT and BFAST. To this aim, a correlation study with monthly accumulated precipitation and maps reporting the Standardized Precipitation Index (SPI) [63] will be shown.
For the whole area, 46.673 NDVI pixels with 1-km spatial resolution were processed from 2000 to 2016; NDVI pixels with good quality (0 flag value) were chosen for analysis.

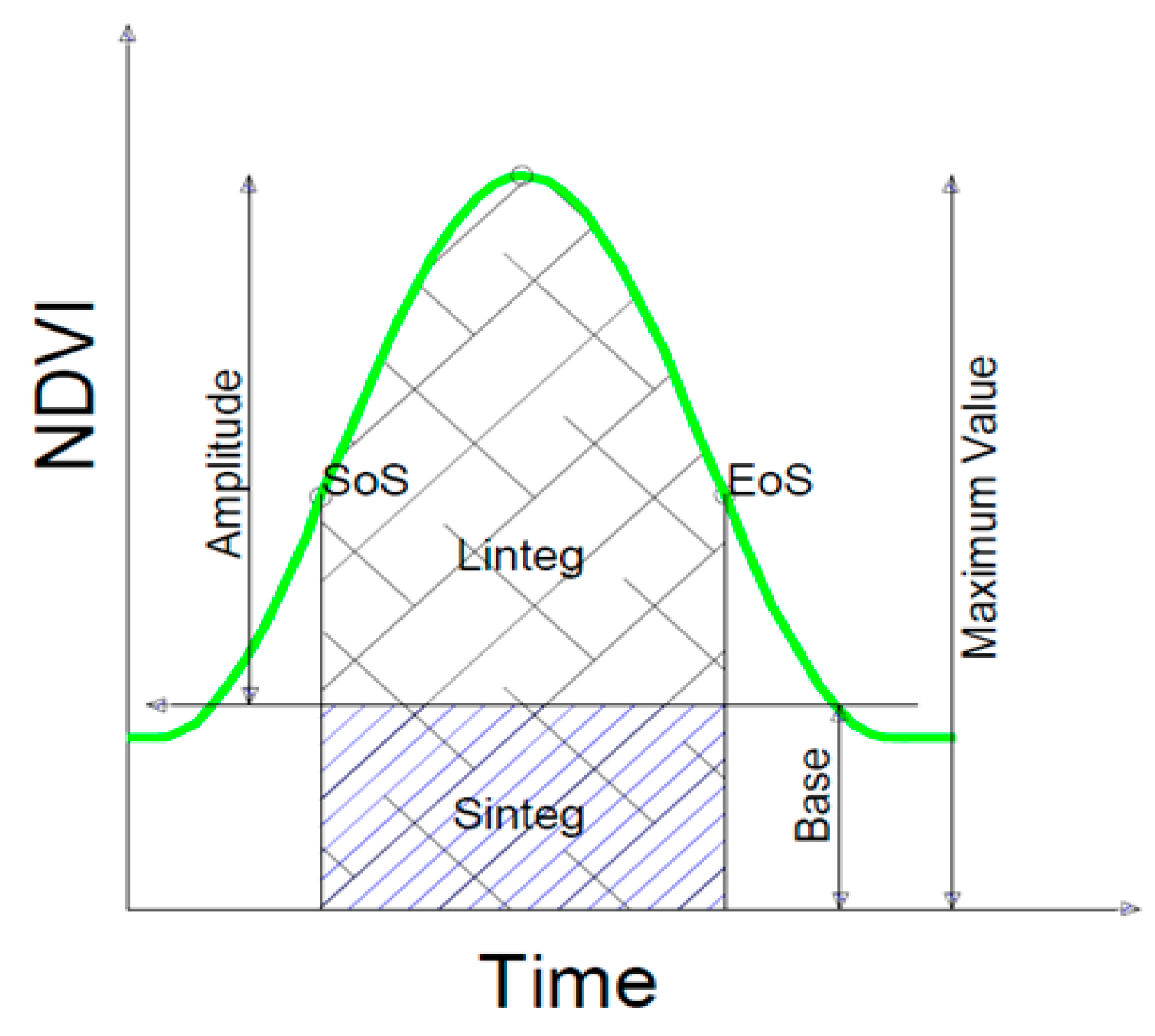
3.1. TIMESAT

TIMESAT is an algorithm that is used for analyzing and adapting mathematical modeling on satellite time series observations [22]. TIMESAT estimates the following seasonal parameters: the start of season, the end of season, the length of season, the base value, the middle of season, the maximum value, the amplitude, the small integrated, and the large integrated (Figure 3). Therefore, it provides an analysis of the global trend for all the seasonal parameters. The extraction of seasonal parameters has three steps. At first, the number of seasons and their approximate times were estimated; after that, a smoothing function was fitted, and then parameters were extracted. TIMESAT has three methods for smoothing: double logistic, asymmetric Gaussian, and Savitzky–Golay filtering. The Savitzky–Golay method was chosen since it can model local variations better; it tightens the search window iteratively for modeling rapid increases and decreases in the NDVI data, which makes it more useful for analysis in semi-arid areas [22]. Savitzky–Golay filters the noises through a quadratic polynomial. The coefficients of the equation are calculated by weighted least square.

3.2. BFAST

While TIMESAT focuses on the analysis of the NDVI global trend of the seasonal parameters, BFAST extracts the number of breakpoints and their magnitudes in the NDVI time series. Breakpoints can be detected in any part of the seasonal component, but BFAST can only detect a trend on a local scale. The BFAST algorithm estimates the breakpoint position on a time series by decomposing the data to three components (trend, seasonality, and remainder) [31]:
N D V I o b s = T i + S i + e i                                         i = 1 , 2 , 3 , … … ,   m
where T i is the local linear trend, S i the seasonality, e i the remainder, and “m” is the number of breakpoints. The trend component ( T i ) is defined by multiple linear functions between consequent times i − 1 and i.
T i = a i + b i t
where breakpoint “t” is time duration between two breakpoints. The coefficients of a i and b i are the slope and intercept. The magnitude of breakpoints is derived from the difference between T i − 1 and T i . One of the critical input parameters to run the algorithm is “h”, which defines the minimum period between breakpoints. Based on previous studies [35,40,63,64,65], the optimal “h” was considered 1/6, which means a minimum distance of two years between breakpoints (46 MODIS NDVI observations during two years).

4. Results

As highlighted previously, the result flow starts with the TIMESAT modeling outcomes in time and space (Section 4.1). Specifically, in Section 4.1.1, the annual behavior of the modeled amplitudes is analyzed. Then, greenness and seasonality (lifetime) of the different land covers (Section 4.1.2), as well as their variability across the years (Section 4.1.3), will be inferred from TIMESAT. However, NDVI abrupt changes related to the disruptions of biophysical and climatic factors [35,39] cannot be detected by the TIMESAT modeling of global trends, but can be extracted and analyzed by using BFAST (Section 4.2). Lastly, the outcomes of the NDVI modeling with both TIMESAT and BFAST will help to investigate the relation between precipitation and NDVI (Section 4.3).

4.1. TIMESAT Modeling Results

4.1.1. Analysis of NDVI Amplitudes Extracted from TIMESAT

TIMESAT was run to extract seasonal parameters, where the term “seasonal” refers to the annual cycle of NDVI. As an example of the outcomes of TIMESAT, Figure 4A reports the harmonic model fitted to the NDVI observations across 2000 to 2016 for a sample point (longitude: 46.2358°N, latitude: 35.8924°E, in Saqqez county). The values of NDVI in the start and end of the season extracted from TIMESAT are also shown.
In Figure 4B, the amplitudes of NDVI values for pixels were sorted for each year and shown. The range of amplitudes in the study area for the whole time series was between 0.0000–0.7357. The lowest amplitudes were in 2008, and the highest amplitudes were in 2010. In other years, the amplitudes had similar values, even though the curves are not always superimposed, suggesting different behaviors among years.
The analysis of NDVI amplitudes (Figure 4B) in the region showed that the highest and lowest amplitudes were in 2010 and 2008. Therefore, the years 2010 and 2008 were identified as two extreme cases of NDVI variations in the region for the whole period. To identify the range and spatial distribution of changes in these years, the maximum and base values of NDVI estimated from TIMESAT (cfr. Figure 3) were selected. Then, they were subtracted from their means computed for the whole time series (2000–2016). Figure 5A,B shows the difference of the maximum (in 2008 and 2010) and mean of maximum values (MMV, derived from the whole time series):
d i f f _ M a x k = m a x i m u m   v a l u e k − M M V   k = 2008   a n d   2010
In Figure 5A, the difference between maximum values and MMV varied between −0.296 and 0.126 in the study area. In the northwestern (Saqqez and Baneh) and western (west of Marivan) areas, the differences were lower in contrast with other parts; this shows that these areas had lower maximum values than the MMV. In other parts, the differences were almost near zero. In Figure 5B, the difference between the maximum values and MMV varied between −0.054 and 0.247 in the study area. Most of the study area experienced positive differences. Figure 5C,D show the difference of the base value (2008 and 2010) and mean of base values (MBV, derived from the whole time series).
d i f f _ b a s e k = b a s e   v a l u e k − M B V   k = 2008   a n d   2010
The differences between base values and MBV were almost zero for both years (Figure 5C,D). This indicates that the effects of the variations are mainly present in the maximum values.

4.1.2. TIMESAT Parameters and Land Covers

Figure 6 shows the sorted error bar plots (based on mean values) of maximum value, base value, day of year (DOY), middle of season, DOY start of season, DOY end of season, and length of season. In Figure 6A, mosaic cropland and bare land have the highest and the lowest mean of maximum values, respectively. The range of maximum values for all the land covers varies between 0.237–0.54. In Figure 6B, which shows base values, the order of land covers is as same as that in Figure 6A. The range of base values is between 0.114–0.223. In Figure 6C, the DOY of the middle of the season is shown. The mean DOY of the middle of the season is the latest in bare land and the earliest in mosaic cropland. The range for the DOY of the middle of the season varies between 147–194.5. In Figure 6D (DOY start of season), bare land has the latest DOY for the middle of the season, and mosaic cropland has the earliest. The order of land covers in this figure differs from DOY of the middle of the season. The range of the DOY for the start of the season is from 97 to 162.5. In Figure 6E, the DOY of the end of season is shown; bare land has the latest, and herbaceous has the earliest. The range of the DOY for the end of the season varies from 185.1 to 232.3. In Figure 6F, the length of season is shown for different land covers. Mosaic natural vegetation has the longest mean, and bare land has the shortest mean. The range of length of season for all the land covers is between 51.7–110.1.

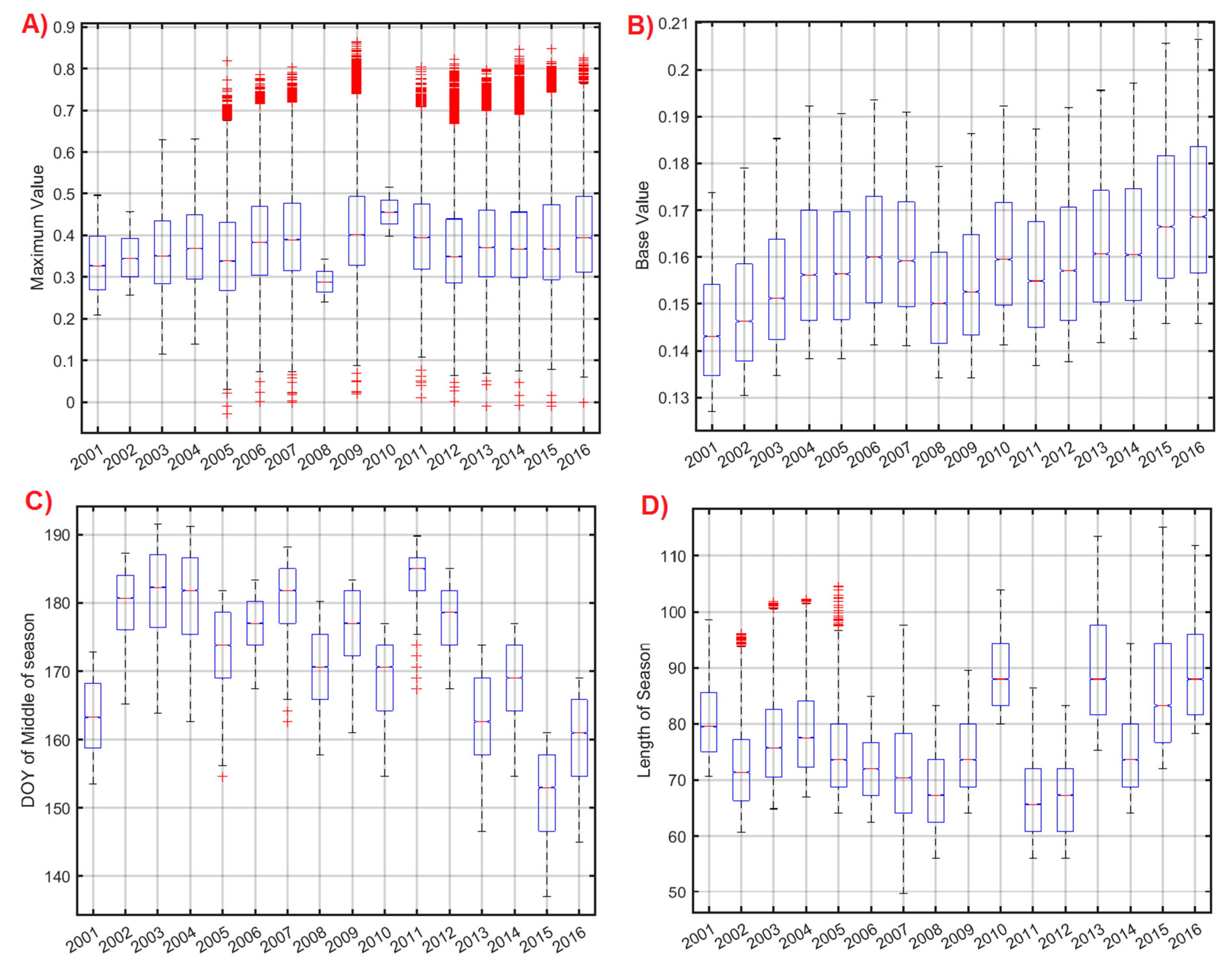
4.1.3. Annual Analysis of TIMESAT Parameters

The global trend of the NDVI seasonal parameters extracted from TIMESAT was also analyzed annually. Figure 7 shows the variations of maximum, base values, DOY of the middle of the season, and the length of the season in each year. Considering the boxplots and medians in Figure 7A, a gradual increase can be observed from 2001 to 2004. In 2005, they slightly decreased, and in 2006 they increased. In 2008, an evident minimum was detected, and afterwards, both parameters increased with a peak in 2010. The range of maximum values in 2008 and 2010 were the lowest; shows that most of the pixels in the study area experienced a decrease and an increase in maximum values in 2008 and 2010. After 2010, slight oscillations (decrease/increase) can be recognized. In Figure 7B, almost the same pattern can be observed. After 2011, despite the increase in the base values, there was no significant increase in the maximum values (Figure 7A). In Figure 7C, the DOY of the middle of the season had a large variation over the whole period of time (from 137 to 197). The length of season (DOY), as shown in Figure 7D, also exhibited large variations (49 to 115.2).

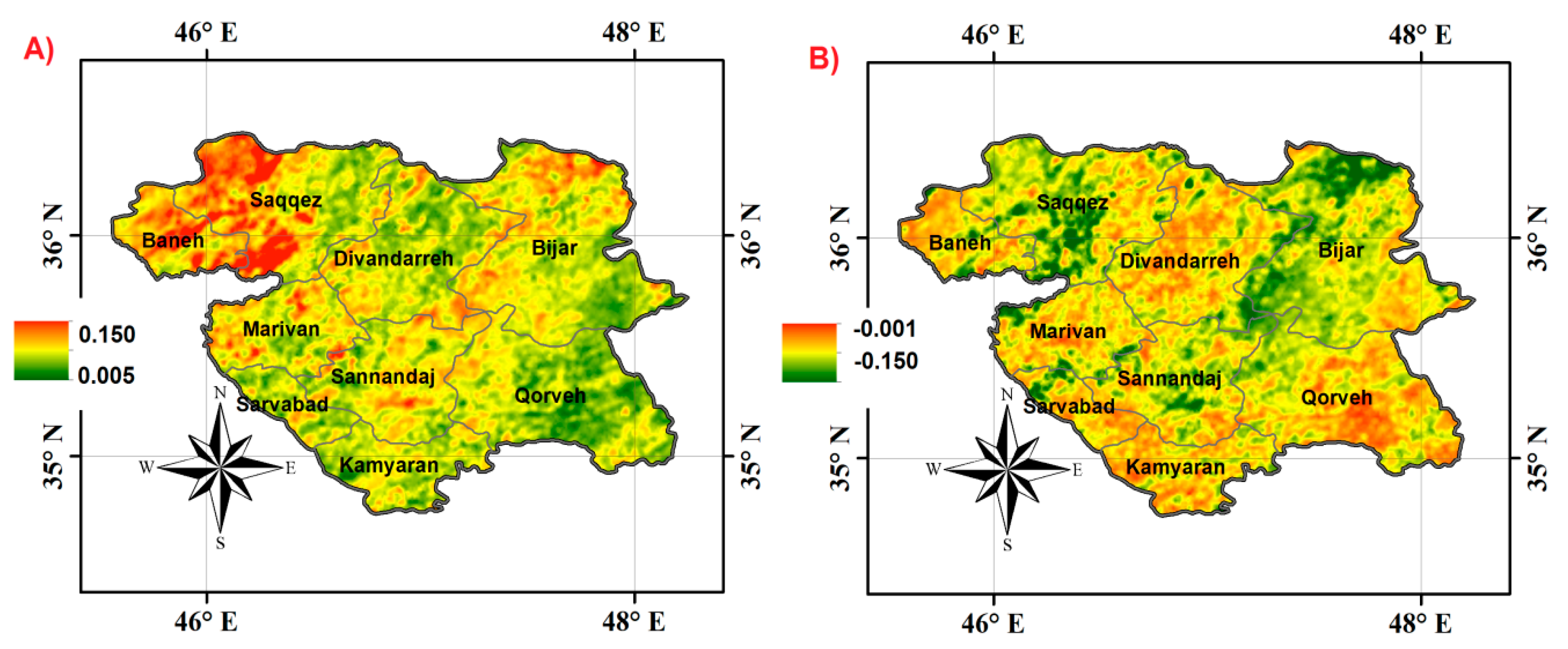
4.2. BFAST Modeling Results

From TIMESAT, describing the global trend of the NDVI seasonal parameters, it is not possible to extract the NDVI abrupt changes (breakpoints) related to climatic or biophysical disruptions. The number of breakpoints and their magnitudes in the NDVI time series can be extracted by BFAST. Therefore, the BFAST algorithm was run for the whole period and for all the NDVI pixels. In the first step, the number of breakpoints was extracted for each pixel across years, which was between 1–5 (Figure 8A). The spatial distribution of the number of breakpoints for each point was shown in Figure 8A: the figure highlights how the western region (Baneh, Saqqez, Sarvabad, Kamyaran, and the western part of Divandarreh) had more breakpoints in contrast with the eastern part (Bijar and Qhorveh). The percent of breakpoints in all the pixels, as extracted for each year, is reported in Figure 8B. The figure shows how the three highest percentages happened in 2010 (28.7%), 2007 (19.8%), and 2008 (11.5%). The lowest number of breakpoints happened in 2000 (seven breakpoints). In 2000, 2001, 2015, and 2016, the percent of breakpoints were lower than 1. The high frequency of breakpoints between 2–4 indicates that the selected “h” parameter was suitable for the study area.
The histogram of both positive and negative magnitudes (the value of increasing and decreasing NDVI local trends) of breakpoints for the entire period in all the sample points is shown in Figure 9A. The range of magnitude of breakpoints was between −0.14 and 0.12. The frequency of magnitudes near zero was the highest. In Figure 9B, the mean of number of breakpoints for each land cover is shown. The means are sorted from the highest to the lowest. The order of land covers from the highest to the lowest are mosaic natural vegetation, mosaic cropland, herbaceous, grassland, cropland (rainfed), shrubland, sparse vegetation, and bare land. The mean values vary between 2.5–3.
In Figure 10, the mean and standard deviation (STD) of positive and negative breakpoint magnitudes are shown. In both plots, the magnitudes are sorted based on means. In Figure 10A, the mean of positive magnitudes varies between 0.028–0.030. Grassland and shrubland had the lowest and highest means, respectively. The highest STD was in mosaic cropland (0.022), and the lowest STD was in grassland (0.018). In Figure 10B, the grassland again had the lowest mean (−0.029) as an absolute value, and sparse vegetation (−0.032) had the highest means. The highest STD was that of herbaceous (0.024) and the lowest was that of grassland (0.020).
Figure 11 shows the spatial distribution of the maximum of the breakpoint magnitudes that happened in the study area for the entire period. In Figure 11A, the maximum positive magnitudes have higher values in the northwest and northeast. In the eastern and southeastern zones, the values of magnitudes were lower. In Figure 11B, in the northwest (Saqqez) and northeast, the negative values were higher (north and west of Bijar).

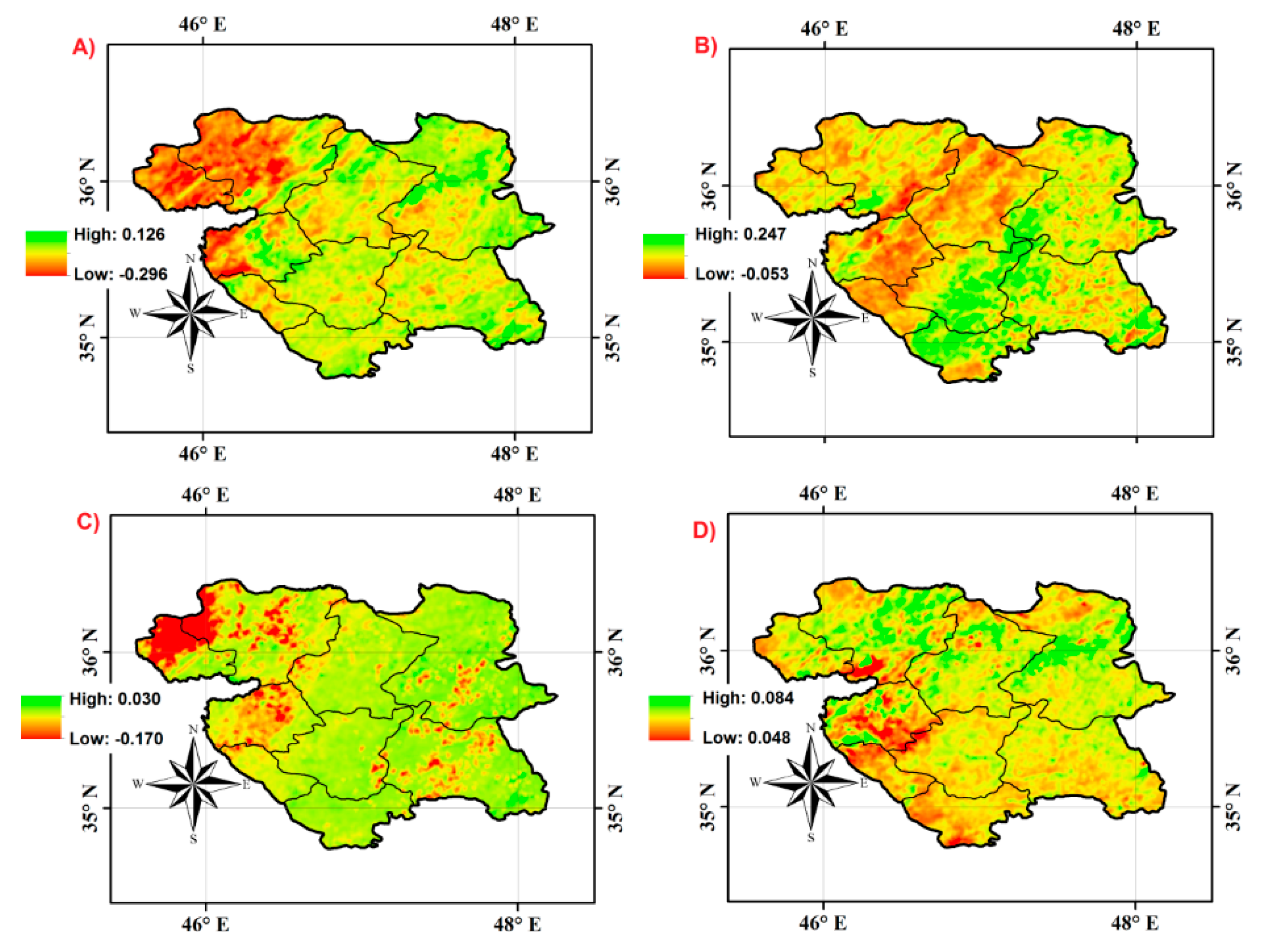
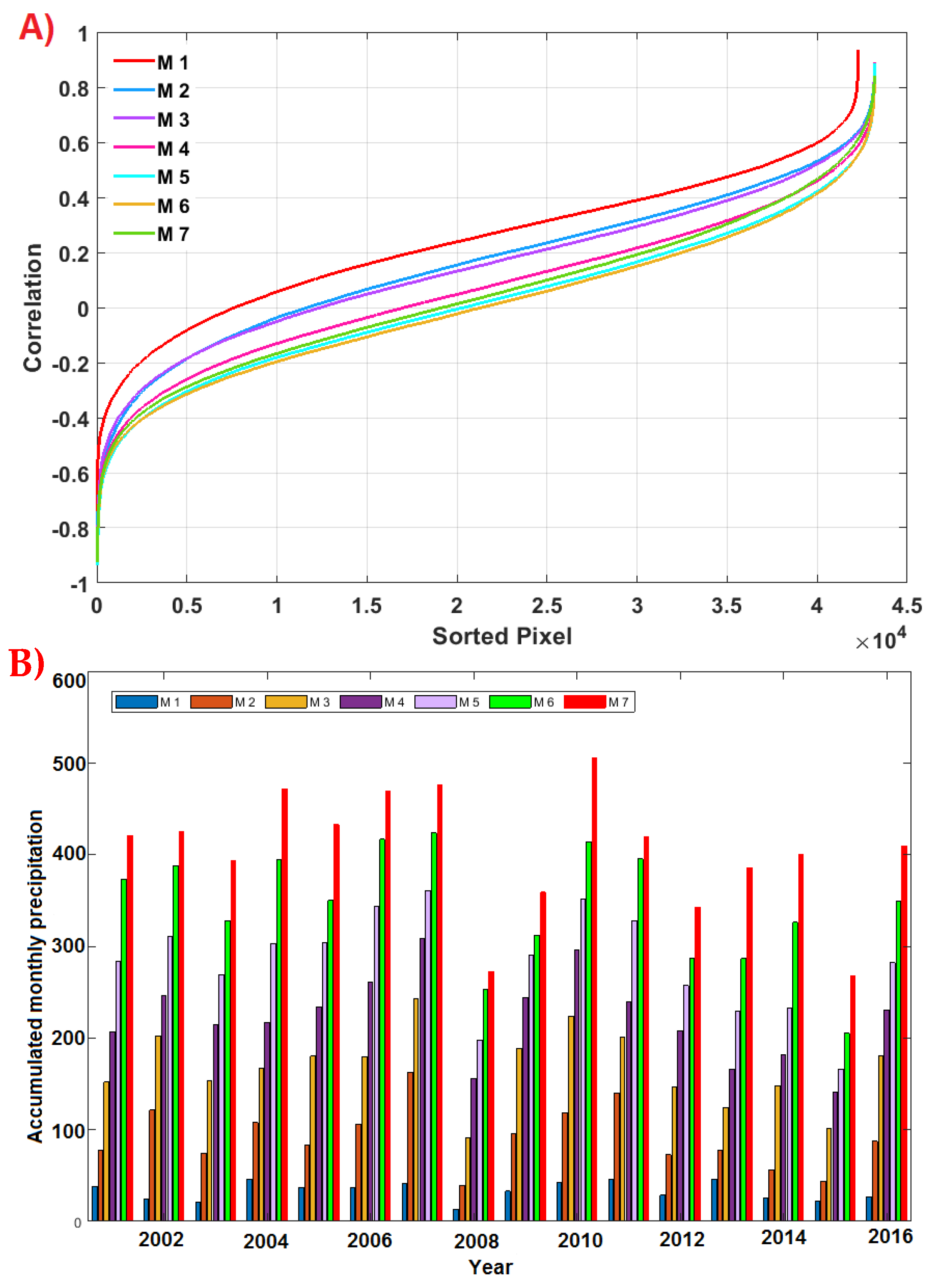
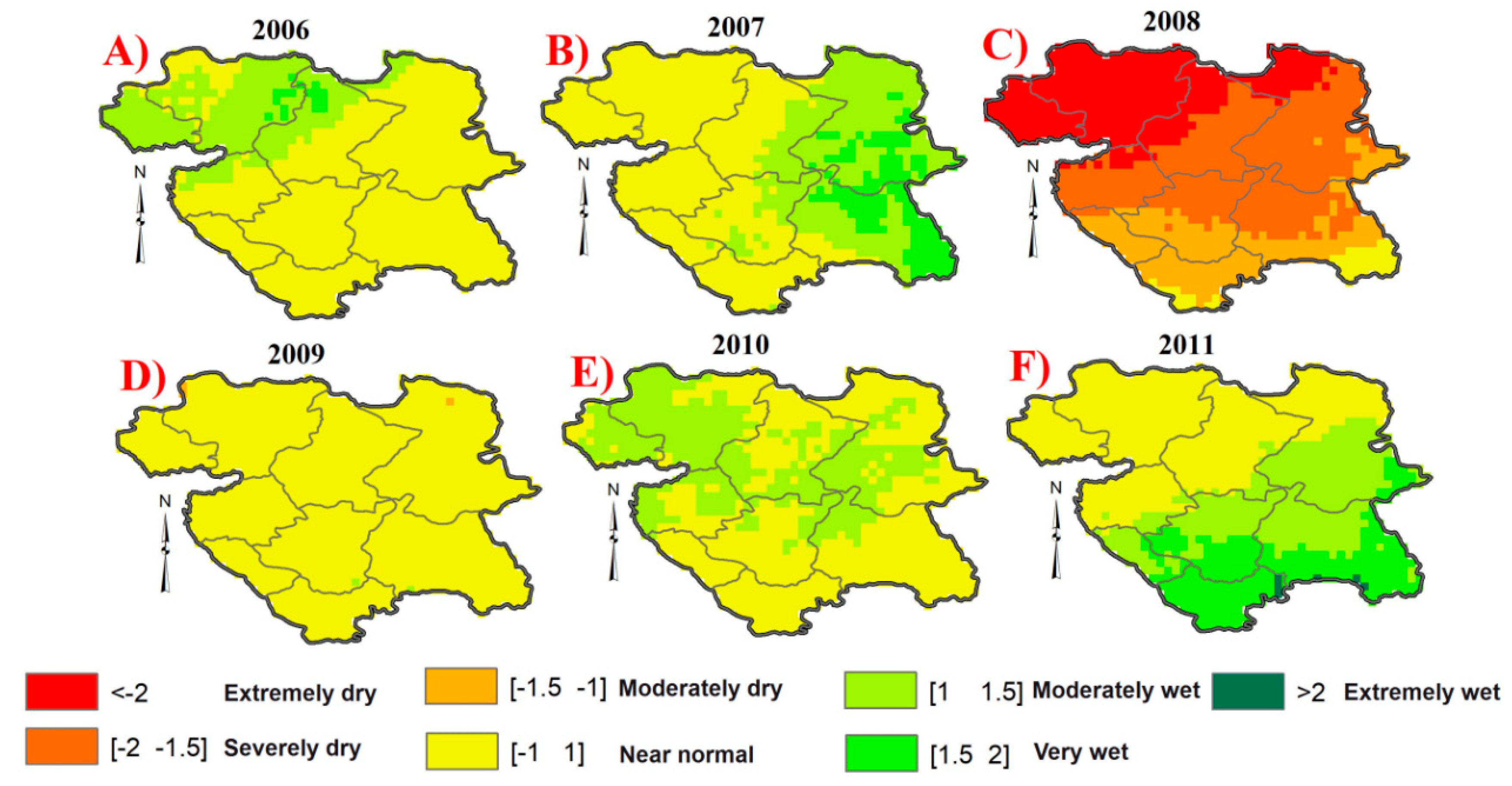
4.3. Relation between Precipitation and NDVI Changes

An investigation of the relation between precipitation and NDVI dynamics was performed, considering both maximum NDVI and NDVI breakpoints.
To investigate the influence of precipitation on maximum NDVI, the representative DOY of the maximum values of NDVI (i.e., DOY of middle of season, Figure 7C) estimated by TIMESAT for the whole time series was chosen. The results showed that 50.67% of DOYs were smaller or equal than 175. Therefore, 175 (24 June) was chosen as the DOY of maximum value of NDVI for all the land covers. The correlation between the NDVI maximum values and the accumulated precipitations in the first to the seventh month (M1 to M7) before DOY 175 was calculated. Since CHIRPS pixels have a coarser spatial resolution (0.05 × 0.05°) than MODIS NDVI (1 km), the CHIRPS pixels were resampled to 1-km resolution with a nearest neighbor interpolation. Then, the correlations were computed in each pixel of the study area over the 16 years. In Figure 12A, these correlations from the first to the seventh month of accumulated precipitations were sorted and superimposed. The results show that the first month had higher correlations for all pixels in comparison with other months. In Figure 12B, the mean of the CHIRPS accumulated precipitation for all the pixels in the study area, from the first to the seventh month before DOY 175, are shown for each year. Considering the first month as the most crucial precipitation on NDVI behavior, in 2008, the accumulated precipitation was 13.5 mm, i.e., the lowest value. After 2008, the precipitation increased up to 2011 (it was 42.5 mm). The highest value in the first month was in 2013 (46.5 mm).
To justify the frequency of breakpoints (Figure 8B) in relation to precipitation, the SPI [63] was computed for the whole period. The SPI is an index describing the spatiotemporal variation of dry/wet conditions, and it is comparable in different climates. The SPI maps from 2006 to 2011 are reported in Figure 13, where the color legend refers to the SPI values classified as dry/wet conditions based on [66]. While the percentage of breakpoints from 2002 to 2006 was low, in 2007 and 2008, the number of breakpoints increased significantly (Figure 8B). Figure 13A,B show wet and normal conditions in different parts of the region in 2006 and 2007, while in 2008, most of the region experienced drought status (Figure 13C). In 2008, the northwest part exhibited extremely dry conditions, i.e., the same region with the highest number of breakpoints (Figure 8A). In 2009, the whole region had near normal conditions, which turned into wet conditions for most of the northwest in 2010, and in the southeast for 2011 (Figure 13D–F). Therefore, 2009 was a transition year from extremely dry to wet conditions, resulting in the high number of breakpoints in 2010.

5. Discussion

In this study, the vegetation cover dynamics of the Kurdistan region of Iran were analyzed from 2000 to 2016. The NDVI trend of the seasonal parameters, the annual abrupt changes, and their relationship with precipitation were analyzed. The combined use of TIMESAT and BFAST for NDVI time series analyses provides a more comprehensive investigation of the NDVI behavior from a phenological perspective. Such investigation (global trends of seasonal parameters and local breakpoint extraction) cannot be conducted by a simple analysis of the maximum NDVI trend. Studies of the behavior and dynamics of vegetation covers as precursors of drought and desertification in Middle East is crucial. It provides an insight of the land-cover status of a region affected by climate hazards.

5.1. Seasonal Parameters: Greenness and Lifetime

From the TIMESAT seasonal parameters of amplitude, maximum NDVI, DOY of start of season, DOY of end of season, and length of season were extracted for the whole time series. Therefore, greenness and the lifetime of the different land covers and their variation across years were pointed out. The results show that two years, 2008 and 2010, were the two extreme cases of NDVI decrease and increase, respectively, in the whole time series. This result obtained from the global trend analysis by TIMESAT is confirmed at a local scale by BFAST. In fact, the high percent of number of breakpoints in 2007 and 2008 can be related to the NDVI decrease condition in 2008. Instead, the highest percent of number of breakpoints in 2010 is representative of the NDVI increase in 2010.
In Section 4.1.1, the maximum NDVI values in 2008 and 2010 were subtracted from the mean of the maximum NDVI values computed on the whole time series. The spatial distribution of the negative differences between maximum NDVI and MMV in 2008 showed that only northwestern and western parts of the region experienced a clear decrease in NDVI; this is in line with the spatial distribution of the number of breakpoints in these parts of the study area. In 2010, the negative values were very close to zero, proving that most of the parts of the study area had a seasonal increase, especially in Sanandaj and Kamyaran. However, such a seasonal increase did not have a dominant pattern in the northwest and west of the region. This can indicate that these areas are more susceptible to effects that cause the season to shorten. Also, the comparison of the difference range between maximum NDVI values and base values showed that maximum values had higher variations in these years, confirming the pronounced NDVI decrease and increase for these two years.
The analysis of the maximum NDVI values and base values in relation to land covers showed a similar order of greenness: mosaic cropland, mosaic natural vegetation, shrubland, sparse vegetation, herbaceous, cropland (rainfed), grass land, and bare land. These outcomes are related to those of the BFAST analysis, where the highest number of breakpoints was found for mosaic natural vegetation and mosaic cropland, while the lowest number was found for bare land.
From the lifetime standpoint, the order of the DOY of the middle of the season is: bare land, grass land, sparse vegetation, cropland (rainfed) shrubland, mosaic natural vegetation, herbaceous, and mosaic cropland. The comparison of the order of greenness with the DOY of the middle of the season and DOY of the start of the season indicates that the dryer land covers had later increase times than the greener ones. Along with lagged seasonal behavior in dryer vegetation covers, they also had shorter lifetimes (length of season).
The annual behavior of the maximum and base of NDVI values showed decreasing and increasing fluctuations, especially in the extreme cases in 2008 and 2010. Their same pattern indicates that the variation in maximum and base of NDVI values happened almost simultaneously. Instead, the annual analysis of the DOY in the middle of the season and length of the season proved that these parameters are dynamic and more influenced by the interannual changes of the environmental conditions. They can be affected by the near surface and atmospheric variables.

5.2. Abrupt Changes in Vegetation Cover

The number of breakpoints determines the occurrences of abrupt changes, i.e., anomalous perturbations in a time series for any pixel in the study area. The breakpoint presence assigns significance to NDVI changes, highlighting large variations that are not attributable to previous periodic or linear trends within statistical certainty. It may be related to disruptions of biophysical and meteorological factors [35,39]. For instance, in [39], the positive peaks in the breakpoint density corresponded to time periods associated with rainfall that was generally higher than average, suggesting that the correlation of NDVI positive breakpoint peaks with precipitation. The authors also suggested how drought, flood, and wildfires were plausible mechanisms for negative breakpoints [40,67,68].
The western and northwestern parts of the Kurdistan province exhibited the highest number (four and five) of breakpoints and the highest magnitudes during the whole time period: in other words, these areas are more prone to NDVI abrupt changes than other parts in the region. This can be related to the constituent land covers, precipitation accumulation, and probably to the occurrence of dust storms in the region [69]. Considering that cropland (rainfed) and herbaceous land covers as dominant land covers in the study area, the results suggest that herbaceous lands are slightly more susceptible to environmental changes than cropland (rainfed) land cover. The magnitudes of breakpoints varied between −0.14 and 0.12. The low variations of the magnitudes indicate zones and associated land covers that are less affected by biophysical and meteorological perturbations.

5.3. Vegetation Response to Precipitation

Concerning the spatial pattern of the precipitation, a clear similarity with the spatial distribution of the annual maximum NDVI is noticed (Figure 1), with the western zone greener than the eastern part.
The influence of the precipitation on the maximum NDVI and the NDVI abrupt variations can be analyzed from different standpoints. Firstly, the behavior of the accumulated precipitations in the first to the seventh month before the representative DOY of the maximum NDVI was presented. The first month exhibited higher correlations with maximum NDVIs. The results proved that the latest precipitations were more effective in the increase of all the land covers in the study area. Such outcomes were in line with [47,70,71], where it was found that the time lag was almost between 9–30 days for wet and dry conditions. The precipitation in the first month can be employed to justify the occurrence of frequent breakpoints. The monthly accumulated precipitations from 2007 to 2008 clearly decreased, whilst from 2008 to 2011, they increased. The SPI can also be used to justify the high number of breakpoints in 2007, 2008, and 2010. In particular, the year exhibiting a clear drought condition in terms of SPI (2008) is in line with the lowest amplitudes of NDVI found by TIMESAT and the high number of breakpoints extracted by BFAST.
It is important to note that the number of breakpoints extracted by BFAST depends on the input parameter “h” defining the minimum period between breakpoints. Therefore, it expected that the number of breakpoints can change before or after dry/wet conditions setting different “h” values. This point needs further investigations in future works.

5.4. Limitations and Future Works

The connection between the proposed statistical findings on NDVI time series with the changes of biophysical and meteorological factors should be deepened, especially with field studies. Air temperature, soil moisture, dust storm, topography, percentage of deciduous species, culture rotation, and irrigation practices are examples of further parameters to investigate and relate with breakpoints, greenness, and seasonality.
As a result, once the statistical results from satellite data and the physical meanings are better clarified and assessed by detailed field studies and extensive ground datasets, the proposed method will be a useful and practical tool to monitor the vegetation condition and land cover behavior, especially in regions with drought and desertification hazards.
Also, further research works with satellite data processed by BFAST and TIMESAT should be planned and carried out in the future over similar climate and land cover types. In recent studies [35], the number of NDVI breakpoints and magnitudes were investigated in relation to land covers. Due to the different climate and land cover characteristics, it is not possible to compare the results and provide a general interpretation. Few studies [72,73,74] have considered the land-cover phenological parameters derived by TIMESAT, but the land cover types, the environmental conditions, and the goal of these studies were different with respect to our analysis.

6. Conclusions

The NDVI time series of MODIS from 2000 to 2016 were analyzed. By using two modeling methods (TIMESAT and BFAST), the dynamics and seasonal behavior of NDVI was analyzed. In the first step, the TIMESAT was used to obtain the global trend of the seasonal parameters; then, the breakpoints and their magnitudes were extracted, and the results from both methods were interpreted. Both methods showed that two extreme senescence and growing seasons happened in 2008 and 2010. In 2008, the northwest and west of Kurdistan were affected by drought condition mostly. The spatiotemporal behavior of land covers, breakpoints, and precipitation showed that the northwest and west regions are generally greener, and therefore more susceptible to drought conditions. Although different land covers have different behaviors regarding greenness, lifetime, and number of breakpoints, they did not show significant differences in magnitudes of abrupt changes. Also, the results pointed out that the accumulated precipitation in the first month before the middle of season can better describe the NDVI increase or decrease with respect to the other months. Although the results prove that precipitation is an important factor also influencing the NDVI abrupt change occurrences, future research studies should investigate the relation between different environmental factors and breakpoint magnitude.

Author Contributions

M.G. performed computations and analyses. R.K. conceived the research plan and wrote the paper. S.B reviewed the research design and the text. A.S. gave recommendation regarding running the algorithms.

Funding

This research was funded by Islamic Azad University, Sanandaj branch, Iran by grant number 1.5758.

Acknowledgments

The authors acknowledge the Islamic Azad University, Sanandaj branch for supporting the research. Also, the authors acknowledge NASA’s MODIS Science Team and NASA/Goddard Space Flight Center’s and PPS for providing Terra MODIS-C6 VI and CHIRPS data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ahmed, M.; Else, B.; Eklundh, L.; Ardö, J.; Seaquist, J. Dynamic response of NDVI to soil moisture variations during different hydrological regimes in the Sahel region. Int. J. Remote Sens. 2017, 38, 5408–5429. [Google Scholar] [CrossRef]
  2. Mbatha, N.; Xulu, S. Time Series Analysis of MODIS-Derived NDVI for the Hluhluwe-Imfolozi Park, South Africa: Impact of Recent Intense Drought. Climate 2018, 6, 95. [Google Scholar] [CrossRef]
  3. Klisch, A.; Atzberger, C. Operational drought monitoring in Kenya using MODIS NDVI time series. Remote Sens. 2016, 8, 267. [Google Scholar] [CrossRef]
  4. An, L.; Che, H.; Xue, M.; Zhang, T.; Wang, H.; Wang, Y.; Zhou, C.; Zhao, H.; Gui, K.; Zheng, Y. Temporal and spatial variations in sand and dust storm events in East Asia from 2007 to 2016: Relationships with surface conditions and climate change. Sci. Total Environ. 2018, 633, 452–462. [Google Scholar] [CrossRef] [PubMed]
  5. Peters, A.J.; Walter-Shea, E.A.; Ji, L.; Vina, A.; Hayes, M.; Svoboda, M.D. Drought monitoring with NDVI-based standardized vegetation index. Photogramm. Eng. Remote Sens. 2002, 68, 71–75. [Google Scholar]
  6. Solomos, S.; Abuelgasim, A.; Spyrou, C.; Binietoglou, I.; Nickovic, S. Development of a dynamic dust source map for NMME-DREAM v1. 0 model based on MODIS Normalized Difference Vegetation Index (NDVI) over the Arabian Peninsula. Geosci. Model Dev. 2019, 12, 979–988. [Google Scholar] [CrossRef]
  7. Guan, Q.; Sun, X.; Yang, J.; Pan, B.; Zhao, S.; Wang, L. Dust storms in northern China: Long-term spatiotemporal characteristics and climate controls. J. Clim. 2017, 30, 6683–6700. [Google Scholar] [CrossRef]
  8. Fu, Y.H.; Zhao, H.; Piao, S.; Peaucelle, M.; Peng, S.; Zhou, G.; Ciais, P.; Huang, M.; Menzel, A.; Peñuelas, J. Declining global warming effects on the phenology of spring leaf unfolding. Nature 2015, 526, 104. [Google Scholar] [CrossRef]
  9. Bounoua, L.; Collatz, G.; Los, S.; Sellers, P.; Dazlich, D.; Tucker, C.; Randall, D. Sensitivity of climate to changes in NDVI. J. Clim. 2000, 13, 2277–2292. [Google Scholar] [CrossRef]
  10. Ichii, K.; Kawabata, A.; Yamaguchi, Y. Global correlation analysis for NDVI and climatic variables and NDVI trends: 1982–1990. Int. J. Remote Sens. 2002, 23, 3873–3878. [Google Scholar] [CrossRef]
  11. Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
  12. Lu, L.; Shuttleworth, W.J. Incorporating NDVI-derived LAI into the climate version of RAMS and its impact on regional climate. J. Hydrometeorol. 2002, 3, 347–362. [Google Scholar] [CrossRef]
  13. Measho, S.; Chen, B.; Trisurat, Y.; Pellikka, P.; Guo, L.; Arunyawat, S.; Tuankrua, V.; Ogbazghi, W.; Yemane, T. Spatio-Temporal Analysis of Vegetation Dynamics as a Response to Climate Variability and Drought Patterns in the Semiarid Region, Eritrea. Remote Sens. 2019, 11, 724. [Google Scholar] [CrossRef]
  14. Liu, S.; Li, W.; Qiao, W.; Wang, Q.; Hu, Y.; Wang, Z. Effect of natural conditions and mining activities on vegetation variations in arid and semiarid mining regions. Ecol. Indic. 2019, 103, 331–345. [Google Scholar] [CrossRef]
  15. Liu, S.; Huang, S.; Xie, Y.; Wang, H.; Huang, Q.; Leng, G.; Li, P.; Wang, L. Spatial-temporal changes in vegetation cover in a typical semi-humid and semi-arid region in China: Changing patterns, causes and implications. Ecol. Indic. 2019, 98, 462–475. [Google Scholar] [CrossRef]
  16. LeVine, D.; Crews, K. Time series harmonic regression analysis reveals seasonal vegetation productivity trends in semi-arid savannas. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 94–101. [Google Scholar] [CrossRef]
  17. Rodrigues, A.; Marcal, A.R.; Cunha, M. PhenoSat—A Tool for Remote Sensing Based Analysis of Vegetation Dynamics. In Multitemporal Remote Sensing; Springer: Berlin/Heidelberg, Germany, 2016; pp. 195–215. [Google Scholar]
  18. Udelhoven, T. TimeStats: A software tool for the retrieval of temporal patterns from global satellite archives. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 310–317. [Google Scholar] [CrossRef]
  19. McKellip, R.D.; Ross, K.W.; Spruce, J.P.; Smoot, J.C.; Ryan, R.E.; Gasser, G.E.; Prados, D.L.; Vaughan, R.D. Phenological Parameters Estimation Tool; NASA Tech: Briefs, NY, USA, 2010. [Google Scholar]
  20. McKellip, R.; Prados, D.; Ryan, R.; Ross, K.; Spruce, J.; Gasser, G.; Greer, R. Remote-Sensing Time Series Analysis, a Vegetation Monitoring Tool; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2008. [Google Scholar]
  21. Colditz, R.R.; Conrad, C.; Wehrmann, T.; Schmidt, M.; Dech, S. TiSeG: A flexible software tool for time-series generation of MODIS data utilizing the quality assessment science data set. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3296–3308. [Google Scholar] [CrossRef]
  22. Eklundh, L.; Jönsson, P. TIMESAT: A software package for time-series processing and assessment of vegetation dynamics. In Remote Sensing Time Series; Springer: Berlin/Heidelberg, Germany, 2015; pp. 141–158. [Google Scholar]
  23. Ben Abbes, A.; Bounouh, O.; Farah, I.R.; De Jong, R.; Martínez, B. Comparative study of three satellite image time-series decomposition methods for vegetation change detection. Eur. J. Remote Sens. 2018, 51, 607–615. [Google Scholar] [CrossRef] [Green Version]
  24. Azzali, S.; Menenti, M. Mapping vegetation-soil-climate complexes in southern Africa using temporal Fourier analysis of NOAA-AVHRR NDVI data. Int. J. Remote Sens. 2000, 21, 973–996. [Google Scholar] [CrossRef]
  25. Martínez, B.; Gilabert, M.A. Vegetation dynamics from NDVI time series analysis using the wavelet transform. Remote Sens. Environ. 2009, 113, 1823–1842. [Google Scholar] [CrossRef]
  26. Kong, Y.L.; Meng, Y.; Li, W.; Yue, A.Z.; Yuan, Y. Satellite image time series decomposition based on EEMD. Remote Sens. 2015, 7, 15583–15604. [Google Scholar] [CrossRef]
  27. Mahecha, M.D.; Fürst, L.M.; Gobron, N.; Lange, H. Identifying multiple spatiotemporal patterns: A refined view on terrestrial photosynthetic activity. Pattern Recognit. Lett. 2010, 31, 2309–2317. [Google Scholar] [CrossRef]
  28. Sanchez-Vazquez, M.J.; Nielen, M.; Gunn, G.J.; Lewis, F.I. Using seasonal-trend decomposition based on loess (STL) to explore temporal patterns of pneumonic lesions in finishing pigs slaughtered in England, 2005–2011. Prev. Vet. Med. 2012, 104, 65–73. [Google Scholar] [CrossRef] [PubMed]
  29. Jiang, B.; Liang, S.; Wang, J.; Xiao, Z. Modeling MODIS LAI time series using three statistical methods. Remote Sens. Environ. 2010, 114, 1432–1444. [Google Scholar] [CrossRef]
  30. Ronald Eastman, J.; Sangermano, F.; Ghimire, B.; Zhu, H.; Chen, H.; Neeti, N.; Cai, Y.; Machado, E.A.; Crema, S.C. Seasonal trend analysis of image time series. Int. J. Remote Sens. 2009, 30, 2721–2726. [Google Scholar] [CrossRef]
  31. Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
  32. Jamali, S.; Jönsson, P.; Eklundh, L.; Ardö, J.; Seaquist, J. Detecting changes in vegetation trends using time series segmentation. Remote Sens. Environ. 2015, 156, 182–195. [Google Scholar] [CrossRef]
  33. Lambert, J.; Denux, J.P.; Verbesselt, J.; Balent, G.; Cheret, V. Detecting clear-cuts and decreases in forest vitality using MODIS NDVI time series. Remote Sens. 2015, 7, 3588–3612. [Google Scholar] [CrossRef]
  34. Lambert, J.; Jacquin, A.; Denux, J.; Chéret, V. Comparison of two remote sensing time series analysis methods for monitoring forest decline. In Proceedings of the 2011 6th International Workshop on the Analysis of Multi-Temporal Remote Sensing Images (Multi-Temp), Trento, Italy, 12–14 July 2011; pp. 93–96. [Google Scholar]
  35. Fang, X.; Zhu, Q.; Ren, L.; Chen, H.; Wang, K.; Peng, C. Large-scale detection of vegetation dynamics and their potential drivers using MODIS images and BFAST: A case study in Quebec, Canada. Remote Sens. Environ. 2018, 206, 391–402. [Google Scholar] [CrossRef]
  36. Darmawan, Y.; Sofan, P. Comparison of the vegetation indices to detect the tropical rain forest changes using Breaks for Additive Seasonal and Trend (BFAST) Model. Int. J. Remote Sens. Earth Sci. (IJReSES) 2012, 9. [Google Scholar] [CrossRef]
  37. Tian, F.; Fensholt, R.; Verbesselt, J.; Grogan, K.; Horion, S.; Wang, Y. Evaluating temporal consistency of long-term global NDVI datasets for trend analysis. Remote Sens. Environ. 2015, 163, 326–340. [Google Scholar] [CrossRef]
  38. de Jong, R.; Verbesselt, J.; Schaepman, M.E.; De Bruin, S. Detection of Breakpoints in Global NDVI time series. In Proceedings of the 34th International Symposium on Remote Sensing of Environment (ISRSE), Sydney, Australia, 10–15 April 2011; pp. 10–15. [Google Scholar]
  39. Geng, L.; Che, T.; Wang, X.; Wang, H. Detecting Spatiotemporal Changes in Vegetation with the BFAST Model in the Qilian Mountain Region during 2000–2017. Remote Sens. 2019, 11, 103. [Google Scholar] [CrossRef]
  40. Watts, L.M.; Laffan, S.W. Effectiveness of the BFAST algorithm for detecting vegetation response patterns in a semi-arid region. Remote Sens. Environ. 2014, 154, 234–245. [Google Scholar] [CrossRef]
  41. Schultz, M.; Clevers, J.G.; Carter, S.; Verbesselt, J.; Avitabile, V.; Quang, H.V.; Herold, M. Performance of vegetation indices from Landsat time series in deforestation monitoring. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 318–327. [Google Scholar] [CrossRef]
  42. Aragones, D.; Rodriguez-Galiano, V.F.; Caparros-Santiago, J.A.; Navarro-Cerrillo, R.M. Could land surface phenology be used to discriminate Mediterranean pine species? Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 281–294. [Google Scholar] [CrossRef]
  43. BAJGIRAN, P.R.; Shimizu, Y.; Hosoi, F.; OMASA, K. MODIS vegetation and water indices for drought assessment in semi-arid ecosystems of Iran. J. Agric. Meteorol. 2009, 65, 349–355. [Google Scholar] [CrossRef] [Green Version]
  44. Kafaki, S.B.; Mataji, A.; Hashemi, S.A. Monitoring growing season length of deciduous broad leaf forest derived from satellite data in Iran. Am. J. Environ. Sci. 2009, 5, 647–652. [Google Scholar] [CrossRef]
  45. Amanollahi, J.; Kaboodvandpour, S.; Qhavami, S.; Mohammadi, B. Effect of the temperature variation between Mediterranean Sea and Syrian deserts on the dust storm occurrence in the western half of Iran. Atmos. Res. 2015, 154, 116–125. [Google Scholar] [CrossRef]
  46. Kaboodvandpour, S.; Amanollahi, J.; Qhavami, S.; Mohammadi, B. Assessing the accuracy of multiple regressions, ANFIS, and ANN models in predicting dust storm occurrences in Sanandaj, Iran. Nat. Hazards 2015, 78, 879–893. [Google Scholar] [CrossRef]
  47. Wang, J.; Rich, P.M.; Price, K.P. Temporal responses of NDVI to precipitation and temperature in the central Great Plains, USA. Int. J. Remote Sens. 2003, 24, 2345–2364. [Google Scholar] [CrossRef]
  48. Wang, J.; Price, K.; Rich, P. Spatial patterns of NDVI in response to precipitation and temperature in the central Great Plains. Int. J. Remote Sens. 2001, 22, 3827–3844. [Google Scholar] [CrossRef]
  49. Alijani, B.; Harman, J.R. Synoptic climatology of precipitation in Iran. Ann. Assoc. Am. Geogr. 1985, 75, 404–416. [Google Scholar] [CrossRef]
  50. Mahmoodi, P.; Alijani, B. Modeling the relationship between annual and seasonal precipitation and climatic factors in Kurdistan. J Appl. Geophys. Res 2013, 31, 93–112. [Google Scholar]
  51. NASA JPL. ASTER Global Digital Elevation Model [Data Set]; NASA JPL: Pasadena, CA, USA, 2009.
  52. Didan, K. MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid V006; NASA EOSDIS Land Processes Distributed Active Archive Center (LP DAAC): Sioux Falls, SD, USA, 2015. [CrossRef]
  53. Didan, K.; Munoz, A.B.; Solano, R.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series); Vegetation Index and Phenology Lab, The University of Arizona: Tucson, AZ, USA, 2015; pp. 1–38. [Google Scholar]
  54. Santoro, M.; Kirches, G.; Wevers, J.; Boettcher, M.; Brockmann, C.; Lamarche, C.; Defourny, P. Land Cover CCI: Product User Guide Version 2.0. Available online: https://maps.elie.ucl.ac.be/CCI/viewer/download/ESACCI-LC-Ph2-PUGv2_2.0.pdf (accessed on 1 February 2019).
  55. Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
  56. Kimani, M.; Hoedjes, J.; Su, Z. An assessment of satellite-derived rainfall products relative to ground observations over East Africa. Remote Sens. 2017, 9, 430. [Google Scholar] [CrossRef]
  57. Katsanos, D.; Retalis, A.; Michaelides, S. Validation of a high-resolution precipitation database (CHIRPS) over Cyprus for a 30-year period. Atmos. Res. 2016, 169, 459–464. [Google Scholar] [CrossRef]
  58. Rivera, J.A.; Marianetti, G.; Hinrichs, S. Validation of CHIRPS precipitation dataset along the Central Andes of Argentina. Atmos. Res. 2018, 213, 437–449. [Google Scholar] [CrossRef]
  59. Trejo, F.J.P.; Barbosa, H.A.; Peñaloza-Murillo, M.A.; Moreno, M.A.; Farías, A. Intercomparison of improved satellite rainfall estimation with CHIRPS gridded product and rain gauge data over Venezuela. Atmósfera 2016, 29, 323–342. [Google Scholar] [CrossRef] [Green Version]
  60. Paredes-Trejo, F.J.; Barbosa, H.; Kumar, T.L. Validating CHIRPS-based satellite precipitation estimates in Northeast Brazil. J. Arid Environ. 2017, 139, 26–40. [Google Scholar] [CrossRef]
  61. Saeidizand, R.; Sabetghadam, S.; Tarnavsky, E.; Pierleoni, A. Evaluation of CHIRPS rainfall estimates over Iran. Q. J. Royal Meteorol. Soc. 2018, 144, 282–291. [Google Scholar] [CrossRef] [Green Version]
  62. Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
  63. McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 12–22 January 1993; pp. 179–183. [Google Scholar]
  64. Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef]
  65. Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef] [Green Version]
  66. Svoboda, M.; Hayes, M.; Wood, D. Standardized Precipitation Index User Guide; World Meteorological Organization: Geneva, Switzerland, 2012. [Google Scholar]
  67. Verbesselt, J.; Zeileis, A.; Herold, M. Near real-time disturbance detection using satellite image time series. Remote Sens. Environ. 2012, 123, 98–108. [Google Scholar] [CrossRef]
  68. Chen, L.; Michishita, R.; Xu, B. Abrupt spatiotemporal land and water changes and their potential drivers in Poyang Lake, 2000–2012. ISPRS J. Photogramm. Remote Sens. 2014, 98, 85–93. [Google Scholar] [CrossRef]
  69. Nabavi, S.O.; Haimberger, L.; Samimi, C. Climatology of dust distribution over West Asia from homogenized remote sensing data. Aeolian Res. 2016, 21, 93–107. [Google Scholar] [CrossRef] [Green Version]
  70. Van Hoek, M.; Jia, L.; Zhou, J.; Zheng, C.; Menenti, M. Early drought detection by spectral analysis of satellite time series of precipitation and normalized difference vegetation index (NDVI). Remote Sens. 2016, 8, 422. [Google Scholar] [CrossRef]
  71. Fabricante, I.; Oesterheld, M.; Paruelo, J. Annual and seasonal variation of NDVI explained by current and previous precipitation across Northern Patagonia. J. Arid Environ. 2009, 73, 745–753. [Google Scholar] [CrossRef]
  72. Jones, M.O.; Kimball, J.S.; Small, E.E.; Larson, K.M. Comparing land surface phenology derived from satellite and GPS network microwave remote sensing. Int. J. Biometeorol. 2014, 58, 1305–1315. [Google Scholar] [CrossRef]
  73. Xue, Z.; Du, P.; Feng, L. Phenology-driven land cover classification and trend analysis based on long-term remote sensing image series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1142–1156. [Google Scholar] [CrossRef]
  74. Gessner, U.; Knauer, K.; Kuenzer, C.; Dech, S. Land surface phenology in a West African Savanna: Impact of land use, land cover and fire. In Remote Sensing Time Series; Springer: Berlin/Heidelberg, Germany, 2015; pp. 203–223. [Google Scholar]
Remotesensing 11 01723 g001 550
Figure 1. (A) Mean of annual precipitation from 2000 to 2016 in the Kurdistan province of Iran estimated by Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS), (B) elevation map from ASTER data, (C) mean of annual maximum Normalized Vegetation Index (NDVIs) from 2000 to 2016.
Figure 1. (A) Mean of annual precipitation from 2000 to 2016 in the Kurdistan province of Iran estimated by Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS), (B) elevation map from ASTER data, (C) mean of annual maximum Normalized Vegetation Index (NDVIs) from 2000 to 2016.
Remotesensing 11 01723 g001
Remotesensing 11 01723 g002 550
Figure 2. Land-cover map in 2015 with eight classes and their coverage percentage [54] in the Kurdistan province. Shrubland and grassland refer to “natural” classes.
Figure 2. Land-cover map in 2015 with eight classes and their coverage percentage [54] in the Kurdistan province. Shrubland and grassland refer to “natural” classes.
Remotesensing 11 01723 g002
Remotesensing 11 01723 g003 550
Figure 3. Normalized Vegetation Index (NDVI) parameters extracted from TIMESAT: amplitude, start of season (SoS), large integral (Linteg), small integral (Sinteg), base value, end of season (EOS), maximum value.
Figure 3. Normalized Vegetation Index (NDVI) parameters extracted from TIMESAT: amplitude, start of season (SoS), large integral (Linteg), small integral (Sinteg), base value, end of season (EOS), maximum value.
Remotesensing 11 01723 g003
Remotesensing 11 01723 g004 550
Figure 4. (A) TIMESAT modeling of the NDVI observations for a sample point in the study area, including the start and end of the season. (B) Sorted amplitudes of NDVI from TIMESAT, for each year, for all the pixels in the study area.
Figure 4. (A) TIMESAT modeling of the NDVI observations for a sample point in the study area, including the start and end of the season. (B) Sorted amplitudes of NDVI from TIMESAT, for each year, for all the pixels in the study area.
Remotesensing 11 01723 g004
Remotesensing 11 01723 g005 550
Figure 5. (A) Difference between the NDVI maximum values in 2008 and mean of maximum values (MMV) across 2000–2016, (B) Difference between the NDVI maximum values in 2010 and MMV across 2000–2016, (C) difference between the NDVI base values in 2008 and mean of base values (MBV) across 2000–2016, (D) difference between the NDVI base values in 2010 and MBV across 2000–2016.
Figure 5. (A) Difference between the NDVI maximum values in 2008 and mean of maximum values (MMV) across 2000–2016, (B) Difference between the NDVI maximum values in 2010 and MMV across 2000–2016, (C) difference between the NDVI base values in 2008 and mean of base values (MBV) across 2000–2016, (D) difference between the NDVI base values in 2010 and MBV across 2000–2016.
Remotesensing 11 01723 g005
Remotesensing 11 01723 g006 550
Figure 6. Error bar plot of TIMESAT seasonal parameters in relation to land covers for the whole time series: (A) maximum value of NDVI, (B) base value of NDVI, (C) day of year (DOY) of middle of season, (D) DOY of start of season, (E) DOY of end of season, and (F) length of season (the plots are sorted based on the mean values).
Figure 6. Error bar plot of TIMESAT seasonal parameters in relation to land covers for the whole time series: (A) maximum value of NDVI, (B) base value of NDVI, (C) day of year (DOY) of middle of season, (D) DOY of start of season, (E) DOY of end of season, and (F) length of season (the plots are sorted based on the mean values).
Remotesensing 11 01723 g006
Remotesensing 11 01723 g007 550
Figure 7. NDVI annual parameters from TIMESAT in the study area. (A) Maximum value, (B) base value, (C) DOY middle of season, and (D) length of season (DOY).
Figure 7. NDVI annual parameters from TIMESAT in the study area. (A) Maximum value, (B) base value, (C) DOY middle of season, and (D) length of season (DOY).
Remotesensing 11 01723 g007
Remotesensing 11 01723 g008 550
Figure 8. (A) Map of the number of breakpoints for the whole NDVI time series (2000–2016), and (B) frequency of the breakpoints for each year.
Figure 8. (A) Map of the number of breakpoints for the whole NDVI time series (2000–2016), and (B) frequency of the breakpoints for each year.
Remotesensing 11 01723 g008
Remotesensing 11 01723 g009 550
Figure 9. (A) Histograms of magnitudes of breakpoints for the whole NDVI time series, and (B) mean number of breakpoints for each land cover.
Figure 9. (A) Histograms of magnitudes of breakpoints for the whole NDVI time series, and (B) mean number of breakpoints for each land cover.
Remotesensing 11 01723 g009
Remotesensing 11 01723 g010 550
Figure 10. (A) The error bar plot of positive magnitudes, (B) the error bar plot of negative magnitudes in relation to land covers for the whole time series (the plots are sorted based on the mean of magnitudes).
Figure 10. (A) The error bar plot of positive magnitudes, (B) the error bar plot of negative magnitudes in relation to land covers for the whole time series (the plots are sorted based on the mean of magnitudes).
Remotesensing 11 01723 g010
Remotesensing 11 01723 g011 550
Figure 11. Spatial distribution of (A) maximum of breakpoint magnitudes with positive signs, (B) maximum of breakpoint magnitudes with negative signs for the whole time series 2000–2016.
Figure 11. Spatial distribution of (A) maximum of breakpoint magnitudes with positive signs, (B) maximum of breakpoint magnitudes with negative signs for the whole time series 2000–2016.
Remotesensing 11 01723 g011
Remotesensing 11 01723 g012 550
Figure 12. (A) Correlations between the maximum NDVI values and the accumulated precipitations from CHIRPS in the first (M1) to the seventh month (M7) before DOY 175, for all the pixels in the study area. (B) Accumulated monthly precipitations in the first to the seventh month before DOY 175 in each year for the whole area.
Figure 12. (A) Correlations between the maximum NDVI values and the accumulated precipitations from CHIRPS in the first (M1) to the seventh month (M7) before DOY 175, for all the pixels in the study area. (B) Accumulated monthly precipitations in the first to the seventh month before DOY 175 in each year for the whole area.
Remotesensing 11 01723 g012
Remotesensing 11 01723 g013 550
Figure 13. Standardized Precipitation IndexSPI) maps from 2006 (A) to 2011 (F) showing the wet and dry conditions in the study area.
Figure 13. Standardized Precipitation IndexSPI) maps from 2006 (A) to 2011 (F) showing the wet and dry conditions in the study area.
Remotesensing 11 01723 g013

Share and Cite

MDPI and ACS Style

Gholamnia, M.; Khandan, R.; Bonafoni, S.; Sadeghi, A. Spatiotemporal Analysis of MODIS NDVI in the Semi-Arid Region of Kurdistan (Iran). Remote Sens. 2019, 11, 1723. https://doi.org/10.3390/rs11141723

AMA Style

Gholamnia M, Khandan R, Bonafoni S, Sadeghi A. Spatiotemporal Analysis of MODIS NDVI in the Semi-Arid Region of Kurdistan (Iran). Remote Sensing. 2019; 11(14):1723. https://doi.org/10.3390/rs11141723

Chicago/Turabian Style

Gholamnia, Mehdi, Reza Khandan, Stefania Bonafoni, and Ali Sadeghi. 2019. "Spatiotemporal Analysis of MODIS NDVI in the Semi-Arid Region of Kurdistan (Iran)" Remote Sensing 11, no. 14: 1723. https://doi.org/10.3390/rs11141723

APA Style

Gholamnia, M., Khandan, R., Bonafoni, S., & Sadeghi, A. (2019). Spatiotemporal Analysis of MODIS NDVI in the Semi-Arid Region of Kurdistan (Iran). Remote Sensing, 11(14), 1723. https://doi.org/10.3390/rs11141723

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop