A New Approach to Earth’s Gravity Field Modeling Using GPS-Derived Kinematic Orbits and Baselines
Abstract
1. Introduction
2. Data and Methods
2.1. Data and Models
2.2. The Orbit and Baseline Approach
2.3. Data Weighting Scheme
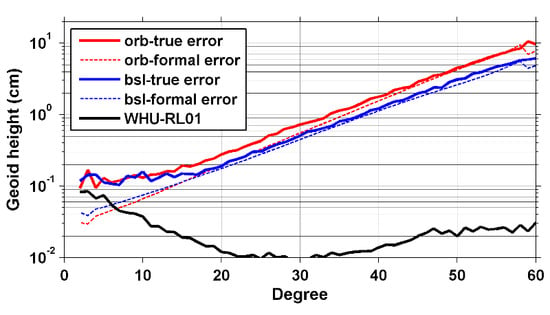
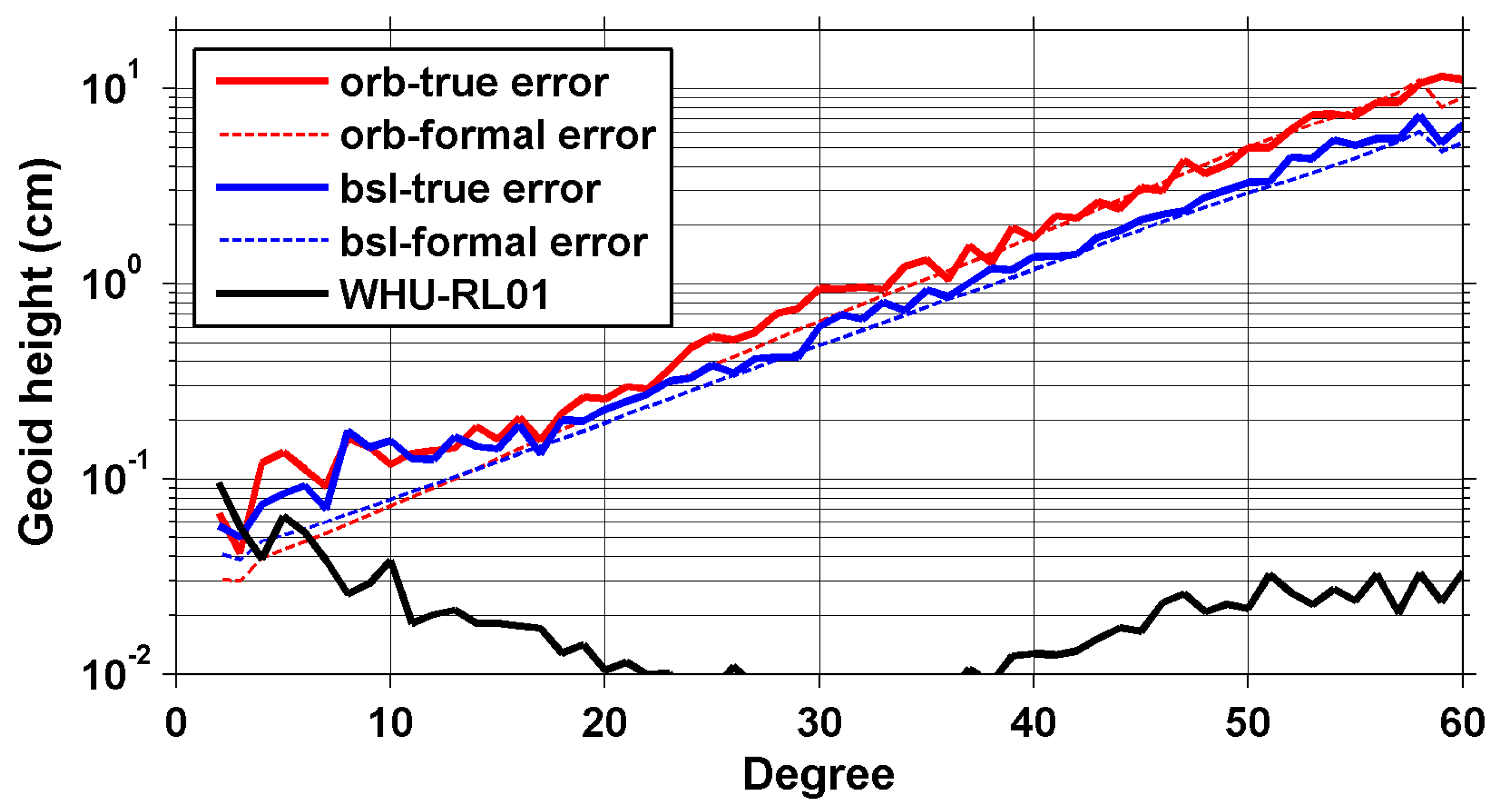
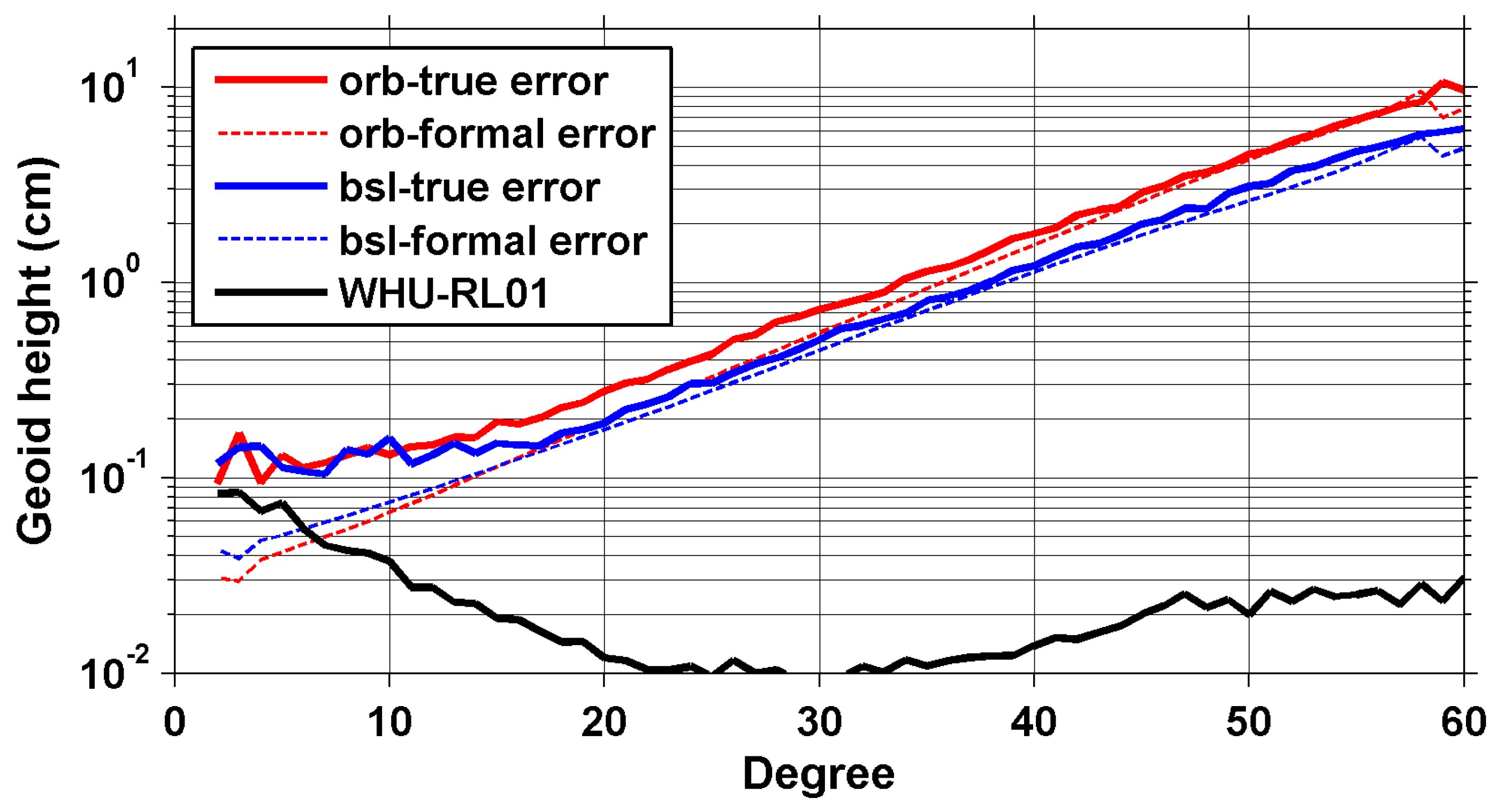
3. Results
3.1. Analysis in the Spectral Domain
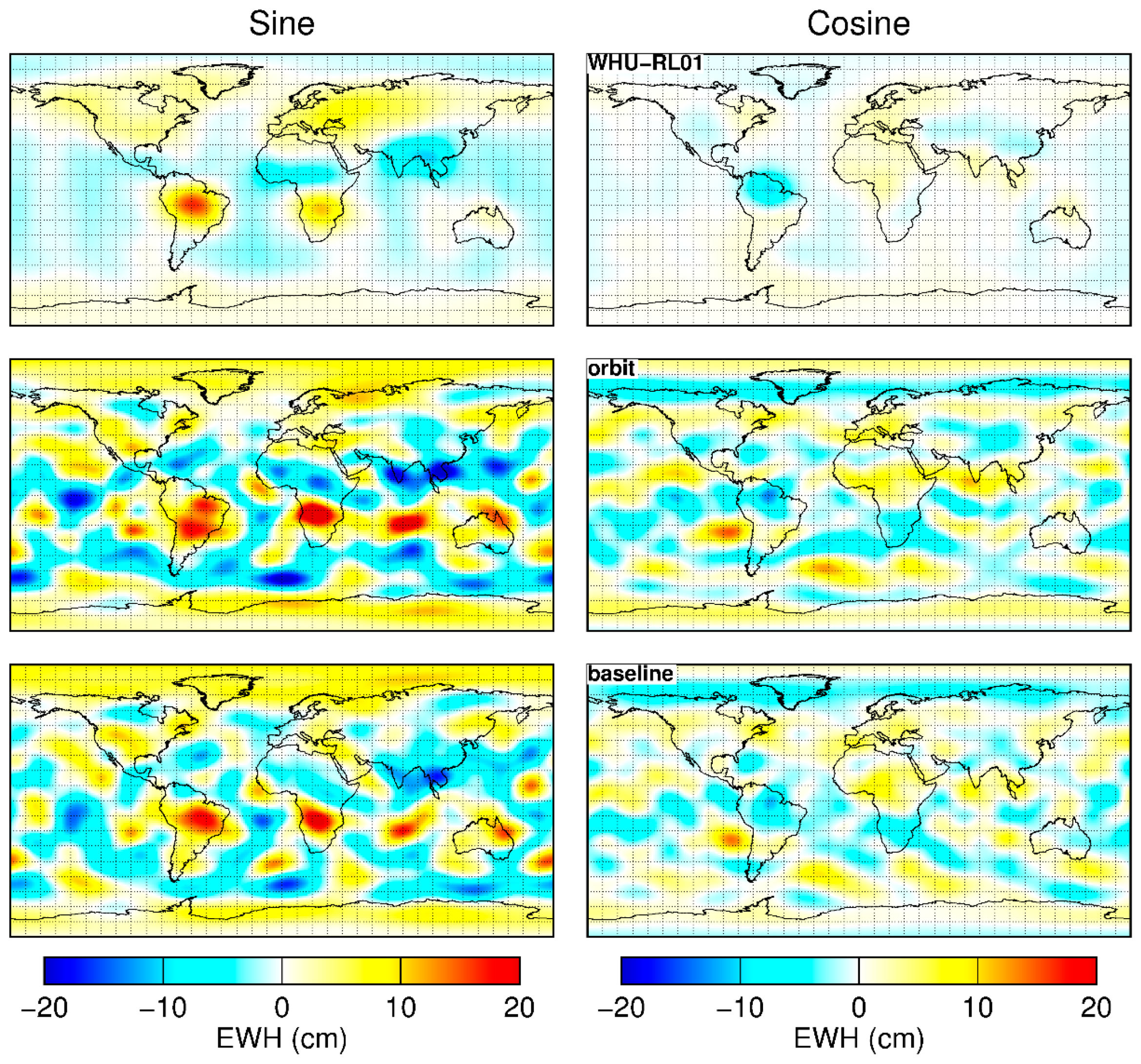
3.2. Analysis in the Spatial Domain
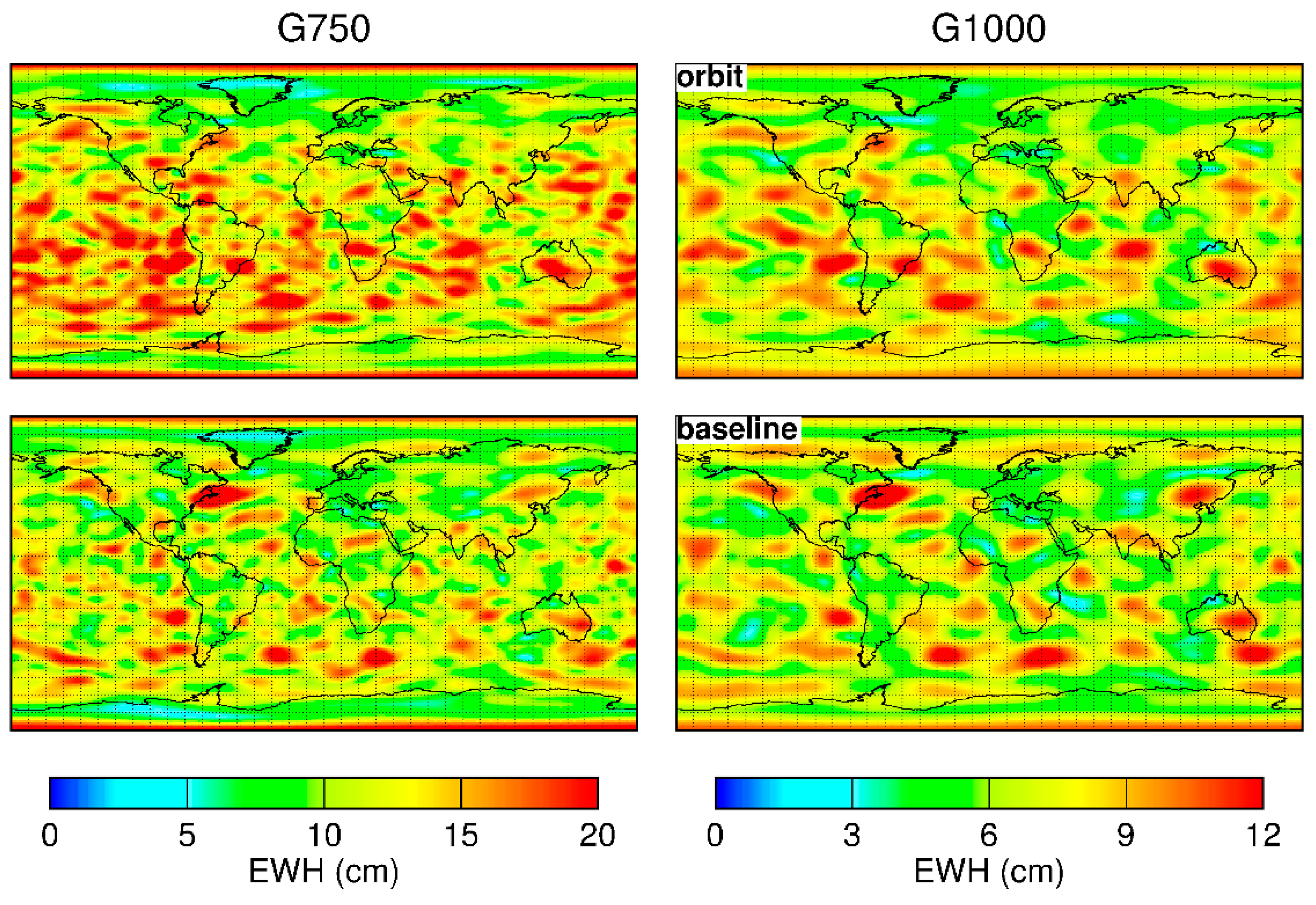
3.2.1. Gridded Mass Anomalies
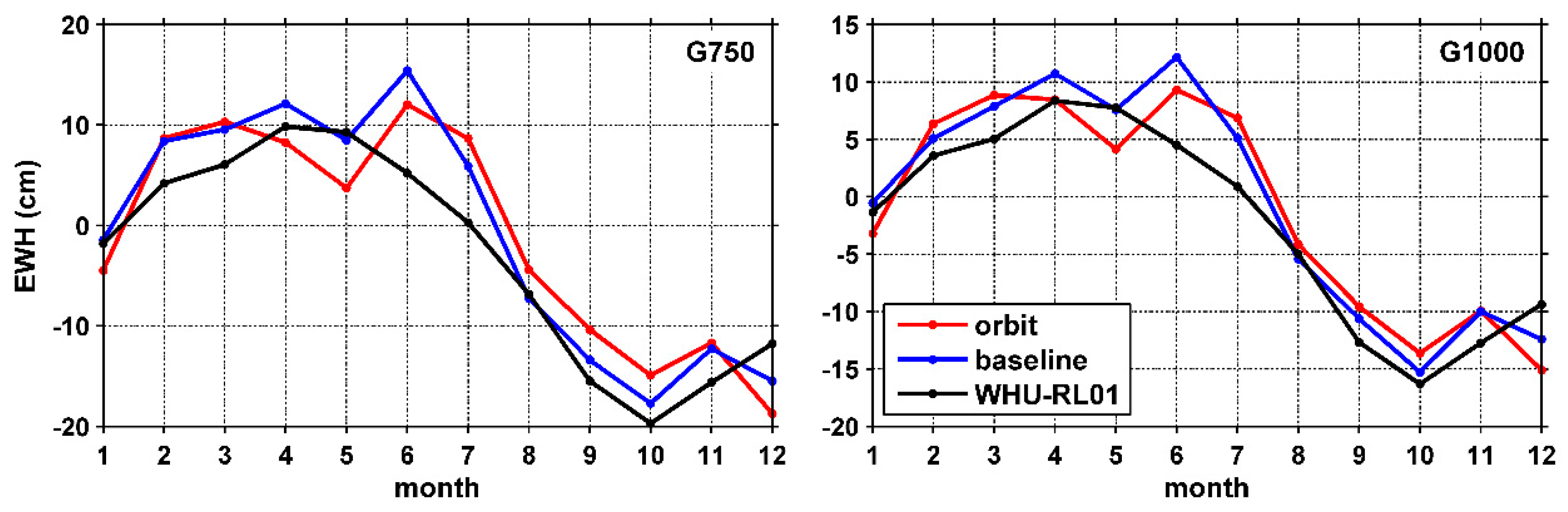
3.2.2. Regional Mass Anomalies
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Weigelt, M.; van Dam, T.; Jäggi, A.; Prange, L.; Tourian, M.J.; Keller, W.; Sneeuw, N. Time-variable gravity signal in Greenland revealed by high-low satellite-to-satellite tracking. J. Geophys. Res. Solid Earth 2013, 118, 3848–3859. [Google Scholar] [CrossRef]
- Bezděk, A.; Sebera, J.; Teixeira da Encarnação, J.; Klokočník, J. Time-variable gravity fields derived from GPS tracking of Swarm. Geophys. J. Int. 2016, 205, 1665–1669. [Google Scholar] [CrossRef]
- Jäggi, A.; Dahle, C.; Arnold, D.; Bock, H.; Meyer, U.; Beutler, G.; van den Ijssel, J. Swarm kinematic orbits and gravity fields from 18 months of GPS data. Adv. Space Res. 2016, 57, 218–233. [Google Scholar] [CrossRef]
- Visser, P.N.A.M.; van der Wal, W.; Schrama, E.J.O.; van den Ijssel, J.; Bouman, J. Assessment of observing time-variable gravity from GOCE GPS and accelerometer observations. J. Geod. 2014, 88, 1029–1046. [Google Scholar] [CrossRef]
- Guo, X.; Ditmar, P.; Zhao, Q.; Klees, R.; Farahani, H.H. Earth’s gravity field modelling based on satellite accelerations derived from onboard GPS phase measurements. J. Geod. 2017, 91, 1049–1068. [Google Scholar] [CrossRef]
- Jäggi, A.; Bock, H.; Meyer, U.; Beutler, G.; van den Ijssel, J. GOCE: Assessment of GPS-only gravity field determination. J. Geod. 2014, 89, 33–48. [Google Scholar] [CrossRef]
- Jäggi, A.; Dach, R.; Montenbruck, O.; Hugentobler, U.; Bock, H.; Beutler, G. Phase center modeling for LEO GPS receiver antennas and its impact on precise orbit determination. J. Geod. 2009, 83, 1145–1162. [Google Scholar] [CrossRef]
- Bock, H.; Jäggi, A.; Beutler, G.; Meyer, U. GOCE: Precise orbit determination for the entire mission. J. Geod. 2014, 88, 1047–1060. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; Jäggi, A. Precise orbit determination of the Sentinel-3A altimetry satellite using ambiguity-fixed GPS carrier phase observations. J. Geod. 2017, 92, 711–726. [Google Scholar] [CrossRef]
- Jäggi, A.; Bock, H.; Prange, L.; Meyer, U.; Beutler, G. GPS-only gravity field recovery with GOCE, CHAMP, and GRACE. Adv. Space Res. 2011, 47, 1020–1028. [Google Scholar] [CrossRef]
- Beutler, G.; Jäggi, A.; Mervart, L.; Meyer, U. The celestial mechanics approach: Theoretical foundations. J. Geod. 2010, 84, 605–624. [Google Scholar] [CrossRef]
- Jäggi, A.; Dahle, C.; Arnold, D.; Meyer, U.; Bock, H. Kinematic space-baselines and their use for gravity field recovery. In Proceedings of the 40th COSPAR Scientific Assembly, Moscow, Russia, 2–10 August 2014. [Google Scholar]
- Jäggi, A.; Beutler, G.; Prange, L.; Dach, R.; Mervart, L. Assessment of GPS-only Observables for Gravity Field Recovery from GRACE. In Observing Our Changing Earth; Sideris, M.G., Ed.; Springer: Berlin, Germany, 2009; pp. 113–123. [Google Scholar]
- Zehentner, N.; Mayer-Gürr, T.; Ellmer, M.; Teixeira da Encarnacao, J.; Visser, P.; Doornbos, E.; Van den IJssel, J.; Mao, X.; Iorfida, E.; Arnold, D. Investigations of GNSS-derived baselines for gravity field recovery. In Proceedings of the EGU General Assembly, Vienna, Austria, 4–13 April 2018; p. 11920. [Google Scholar]
- Guo, X.; Zhao, Q.; Ditmar, P.; Liu, J. A new time-series of GRACE monthly gravity field solutions obtained by accounting for the colored noise in the K-Band range-rate measurements. GFZ Data Serv. 2017. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, Q.; Ditmar, P.; Sun, Y.; Liu, J. Improvements in the monthly gravity field solutions through modeling the colored noise in the GRACE data. J. Geophys. Res. Solid Earth 2018, 123, 7040–7054. [Google Scholar] [CrossRef]
- Liu, J.; Ge, M. PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603–609. [Google Scholar]
- Shi, C.; Zhao, Q.; Geng, J.; Lou, Y.; Ge, M.; Liu, J. Recent development of PANDA software in GNSS data processing. Proceedings of the Society of Photographic Instrumentation Engineers. Li, D., Gong, J., Wu, H., Eds.; 2008, Volume 7285, p. 72851S. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/7285/72851S/Recent-development-of-PANDA-software-in-GNSS-data-processing/10.1117/12.816261.short?SSO=1 (accessed on 13 June 2019).
- Guo, X.; Zhao, Q. GRACE time-varying gravity field solutions based on PANDA software. Geod. Geodyn. 2018, 9, 162–168. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, J.; Hu, Z.; Shi, C.; Liu, J.; Cai, H.; Liu, X. GRACE gravity field modeling with an investigation on correlation between nuisance parameters and gravity field coefficients. Adv. Space Res. 2011, 47, 1833–1850. [Google Scholar] [CrossRef]
- Guo, X.; Geng, J.; Chen, X.; Zhao, Q. Enhanced Orbit Determination for Formation-Flying Satellites through Integrated Single- and Double-Difference GPS Ambiguity Resolution. under review.
- Kroes, R.; Montenbruck, O.; Bertiger, W.; Visser, P. Precise GRACE baseline determination using GPS. GPS Solut. 2005, 9, 21–31. [Google Scholar] [CrossRef]
- Kroes, R. Precise Relative Positioning of Formation Flying Spacecraft Using GPS. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Allende-Alba, G.; Montenbruck, O.; Jäggi, A.; Arnold, D.; Zangerl, F. Reduced-dynamic and kinematic baseline determination for the Swarm mission. GPS Solut. 2017, 21, 1275–1284. [Google Scholar] [CrossRef]
- Förste, C.; Bruinsma, S.L.; Abrikosov, O.; Lemoine, J.-M.; Marty, J.C.; Flechtner, F.; Balmino, G.; Barthelmes, F.; Biancale, R. EIGEN-6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. In Proceedings of the EGU General Assembly, Vienna, Austria, 27 April–2 May 2014. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions (2010); Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Rieser, D.; Mayer-Gürr, T.; Savcenko, R.; Bosch, W.; Wünsch, J.; Dahle, C.; Flechtner, F. The Ocean Tide Model EOT11a in Spherical Harmonics Representation; Institute of Theoretical Geodesy and Satellite Geodesy (ITSG): TU Graz, Austria; Deutsches Geodätisches Forschungsinstitut (DGFI): Munich, Germany; GFZ German Research Centre for Geosciences: Potsdam, Germany, 2012. [Google Scholar]
- Desai, S.D. Observing the pole tide with satellite altimetry. J. Geophys. Res. 2002, 107, 1–13. [Google Scholar] [CrossRef]
- Flechtner, F.; Dobslaw, H.; Fagiolini, E. AOD1B Product Description Document for Product Release 05; GFZ German Research Centre for Geosciences: Potsdam, Germany, 2015. [Google Scholar]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H. The Planetary and Lunar Ephemeris DE 421; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2009; pp. 1–34. [Google Scholar]
- Ditmar, P.; van Eck van der Sluijs, A.A. A technique for modeling the Earth’s gravity field on the basis of satellite accelerations. J. Geod. 2004, 78, 12–33. [Google Scholar] [CrossRef]
- Kaplan, M.H. Modern Spacecraft Dynamics and Control; John Wiley and Sons, Inc.: New York, NY, USA, 1976. [Google Scholar]
- Montenbruck, O.; Hackel, S.; van den Ijssel, J.; Arnold, D. Reduced dynamic and kinematic precise orbit determination for the Swarm mission from 4 years of GPS tracking. GPS Solut. 2018, 22, 79. [Google Scholar] [CrossRef]
- Ditmar, P.; Teixeira da Encarnação, J.; Hashemi Farahani, H. Understanding data noise in gravity field recovery on the basis of inter-satellite ranging measurements acquired by the satellite gravimetry mission GRACE. J. Geod. 2012, 86, 441–465. [Google Scholar] [CrossRef]
- Ditmar, P.; Klees, R.; Liu, X. Frequency-dependent data weighting in global gravity field modeling from satellite data contaminated by non-stationary noise. J. Geod. 2007, 81, 81–96. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J. The unexpected signal in GRACE estimates of C20. J. Geod. 2017, 91, 897–914. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Sun, Y.; Ditmar, P.; Riva, R. Statistically optimal estimation of degree-1 and C20 coefficients based on GRACE data and an ocean bottom pressure model. Geophys. J. Int. 2017, 210, 1305–1322. [Google Scholar] [CrossRef]
- Ditmar, P. Conversion of time-varying Stokes coefficients into mass anomalies at the Earth’s surface considering the Earth’s oblateness. J. Geod. 2018, 92, 1401–1412. [Google Scholar] [CrossRef]
- Xavier, L.; Becker, M.; Cazenave, A.; Longuevergne, L.; Llovel, W.; Filho, O.C.R. Interannual variability in water storage over 2003–2008 in the Amazon Basin from GRACE space gravimetry, in situ river level and precipitation data. Remote Sens. Environ. 2010, 114, 1629–1637. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]


| Background Force Models | Description |
|---|---|
| Mean gravity field model | EIGEN-6C4 [26] (120120) |
| Solid Earth and pole tides | IERS Conventions 2010 [27] |
| Ocean tides | EOT11a [28] (120120) |
| Ocean pole tides | Desai [29] (3030) |
| Atmosphere and ocean de-aliasing | AOD1B RL06 [30] |
| Third-body perturbations | DE421 [31] |
| General relativistic effects | IERS Conventions 2010 [27] |
| Reference frames | |
| Conventional inertial reference frame | IERS Conventions 2010 [27] |
| Precession/nutation | IAU 2006/2000A [27] |
| Earth orientation parameters | IERS EOP 08 C04 |
| Input data | |
| Kinematic orbits and baselines | 30 s sampling |
| GRACE attitudes | Level 1B RL03, 5 s sampling |
| Non-gravitational accelerations | Level 1B RL02, 5 s sampling |
| Estimated parameters | |
| Initial state vector | Position and velocity per satellite and per arc |
| Accelerometer bias | Three order polynomial for each component per arc |
| Accelerometer scale factor | One per month per component |
| Spherical harmonic coefficients | Between degrees 2 and 60 |
| Degree | True Error | ||
|---|---|---|---|
| Orbit | Baseline | ||
| 10 | 0.38 | 0.38 | 0% |
| 20 | 0.73 | 0.62 | −15% |
| 60 | 26.2 | 17.2 | −34% |
| Orbit | Baseline | ||
|---|---|---|---|
| G750 | 13.3 | 11.5 | −14% |
| G1000 | 7.2 | 6.8 | −6% |
| Correlation Coefficient | RMS Differences | |||||
|---|---|---|---|---|---|---|
| Orbit | Baseline | Orbit | Baseline | |||
| G750 | 0.90 | 0.96 | 7% | 5.1 | 4.1 | −20% |
| G1000 | 0.93 | 0.97 | 4% | 3.6 | 3.1 | −14% |
| Amplitude (cm) | Phase (Day) | |||||
|---|---|---|---|---|---|---|
| WHU RL01 | Orbit | Baseline | WHU RL01 | Orbit | Baseline | |
| G750 | 13.40.88 | 11.83.62 | 13.22.95 | −21.10.07 | −38.20.31 | −31.10.23 |
| G1000 | 11.20.82 | 10.52.76 | 10.92.05 | −21.40.07 | −34.70.27 | −32.30.19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Zhao, Q. A New Approach to Earth’s Gravity Field Modeling Using GPS-Derived Kinematic Orbits and Baselines. Remote Sens. 2019, 11, 1728. https://doi.org/10.3390/rs11141728
Guo X, Zhao Q. A New Approach to Earth’s Gravity Field Modeling Using GPS-Derived Kinematic Orbits and Baselines. Remote Sensing. 2019; 11(14):1728. https://doi.org/10.3390/rs11141728
Chicago/Turabian StyleGuo, Xiang, and Qile Zhao. 2019. "A New Approach to Earth’s Gravity Field Modeling Using GPS-Derived Kinematic Orbits and Baselines" Remote Sensing 11, no. 14: 1728. https://doi.org/10.3390/rs11141728
APA StyleGuo, X., & Zhao, Q. (2019). A New Approach to Earth’s Gravity Field Modeling Using GPS-Derived Kinematic Orbits and Baselines. Remote Sensing, 11(14), 1728. https://doi.org/10.3390/rs11141728