A Real-Time On-Orbit Signal Tracking Algorithm for GNSS Surface Observations

Abstract

This manuscript describes real-time on-orbit instrument compatible open loop signal tracking techniques for Global Navigation Satellite Systems (GNSS) reflection observations. All GNSS-reflection (GNSS-R) satellite instruments require algorithms which run in real-time on-board the satellite, that are capable of predicting the code phase time delay and Doppler frequency of surface reflected signals. The algorithms presented here are for open loop tracking techniques in reflected GNSS signals for the purposed of making surface remote sensing observations. Initially, the algorithms are demonstrated using high resolution sampled data from the NASA Cyclone GNSS (CYGNSS) mission over ocean and land surfaces. Subsequently. the algorithm performance over ocean regions is analyzed in detail using a larger data set. As part of the analysis, the algorithm is assessed for its speed of convergence, to demonstrate general compatibility with spacecraft instrument processing limitations. Results indicate that over ocean regions is it possible to robustly predict in real time the Doppler frequency and code phase time delay of multiple reflected signal to sufficient precision to make science observations of the scattering surface. These algorithms are intended to provide a baseline technique and variations from which the scientific community can design more specialized algorithms for individual applications.

1. Introduction

A significant challenge in all remote sensing with signals of opportunity, including transmissions from Global Navigation Satellite Systems (GNSS), such as the Global Positioning System (GPS) is the real-time determination of the time and frequency domain characteristics of these signals at the receiving instrument after they have traveled a large distances and been altered by the physical processes they are intending to observe in such a way that traditional signal tracking techniques are not sufficient. Where traditional techniques refers to the well known navigation tracking algorithms used in personal navigation devices (i.e., cell phones, etc.) [1]. For example, in a GNSS receiver radio occultation (RO) instrument, it is required to track GNSS signals as they pass through the lower atmosphere, which significantly alters their structure and prohibits traditional GNSS receivers from useing them for navigation. Hence, a customized open loop tracking algorithm is needed [2]. Similarly, for a GNSS surface reflected signal, the alterations the signal undergoes upon surface reflection, necessitate a customized open loop tracking algorithm which allows GNSS-reflection (GNSS-R) instruments to make real-time estimates of the delay and Doppler of GNSS signals after reflecting from the Earth’s surface.

This manuscript presents and validates a public domain GNSS-R open loop delay and Doppler tracking algorithm. The organization of this manuscript is as follows,

• Section 2 gives general background on the history of GNSS-R remote sensing and details the reasons why a custom GNSS-R open loop tracking algorithm is required. Additionally, this section also includes an outline of the presented GNSS-R open loop algorithm and how they are organized within the paper.
• Section 3 presents the algorithm for estimating the geographic location of the point of surface reflection, or specular point (SP), which represents the center of the surface scattering glistening zone. This point provides the center coordinated from which the GNSS-R open loop tracking delay and Doppler estimates are derived.
• Section 4 details how the open loop estimates of the reflected signal delay and Doppler are calculated using the estimated surface specular point from Section 3.
• Section 5 analyzes the performance of the algorithm derived in Section 3 and Section 4 using two example reflection tracks from the Cyclone GNSS (CYGNSS) GNSS-R receiver. Raw sampled data is analyzed for these tracks and used as a comparison reference for the algorithm performance.
• Section 6 then performs a statistical analysis, using a much larger set of CYGNSS data, which demonstrates the open loop algorithms performance globally. This section also includes discussion of the algorithms convergence speed and how this was optimized for the case of CYGNSS low Earth orbit GNSS-R reflections.
• Section 7 provides a discussion of additional algorithm modifications which would potentially further improve the performance (both in terms of accuracy and speed of convergence).

2. Background and Algorithm Overview

2.1. Brief History of GNSS-R Remote Sensing

Using GNSS signals in a bistatic scatterometer-like configuration was first proposed by Hall and Cordy in 1988 [3]. Subsequently, the PARIS altimetry concept was put forward by Martin-Neira in 1993 [4]. Several years later, the first demonstration of wind sensing using GPS reflections was carried out by Garrison, Katzberg and Hill in 1998 from an aircraft instrument [5]. Additionally, several other researchers have performed experiments from near Earth platforms performing wind or wave sensing: [6,7,8,9,10,11]. Together, this group of researchers established that GPS signals could be used to sense the near surface ocean wind conditions. In parallel, several researchers were performing GNSS altimetry studies. Importantly, Lowe et al. [12] detected a reflected signal from the SIR-C experiment carried on the Space Shuttle. This was followed by the GNSS experiment carried on the UK-DMC satellite which repeatedly detected signals from ocean, land and ice surfaces [13]. The UK-DMC experiment was used to demonstrate the feasibility of estimating ocean surface wind speed from space [14,15]. This was followed by the TechDemoSat (TDS) on-orbit demonstration [16] mission, and subsequently the NASA CYGNSS eight satellite constellation [17]. These results demonstrated that GNSS signals are easily detectable from a space platform, with the signals clearly responding to surface conditions. A summary of the GNSS-R technique and its applications can be found in [18,19,20].

2.2. GNSS-R Signal Tracking Overview

Navigation GNSS receivers in personal navigation devices (such as in cell phones) are efficient at acquiring and tracking direct GNSS signals (i.e., from a direct and unobstructed path between the transmitter and receiver) for use in determining the position, velocity and time at the receiver. Various GNSS signal tracking techniques exist and are described in detail in several GNSS specific books [1,21]. When tracking a direct signal, GNSS receivers are able to maintain a tight lock on the transmitted signal code phase and carrier phase for multiple parallel signals captured from a skyward oriented antenna. However, there are several complications to this standard receiver tracking technique that prevent or severely complicate the acquisition and tracking of an Earth reflected signal using existing tracking algorithms. These differences include,

• The delay and Doppler characteristics of a reflected signal vary significantly from surface to surface, causing significant variations in how the signal spreads in the delay and Doppler dimensions.
• The surface reflected signals are often very weak and can fluctuate wildly in magnitude (especially over land) due to the surface scattering conditions, often requiring extended non-coherent integration intervals for detection.
• Diffusely scattered signals often contain no information on the transmitted carrier phase, making traditional carrier phase tracking loops unreliable.

These characteristics of surface reflected signals require spaceborne (and aircraft) GNSS-R instruments to have an on-board real-time tracking algorithm capable of estimating the delay and Doppler reference centers at the reflection point for the generation of delay Doppler maps (DDM) of received signal power, which are used to estimate surface characteristics, such as near surface ocean wind speed [17].

By comparison, open loop tracking techniques for GNSS-RO receivers face a similar problem in that as the GNSS signals enter deep into the atmosphere, closed loop tracking techniques are not sufficient. In the case of RO receivers, it is often the case that on-board models are used to forward predict the signal path and open loop sample the received signal [2].

There exist, in the public literature, a number of algorithms which partially describe GNSS-R open loop tracking techniques, including [20,22,23,24]. These existing publications provide a starting point and a good overview of the basic concepts involved. However, the GNSS-R open loop tracking algorithm presented here expands on the existing state of the art in several important ways,

• This manuscript presents the first concise and self contained GNSS-R open loop tracking algorithm intended for general public use by the larger GNSS-R community world wide.
• The real time performance of this algorithm has been validated with a large set of on-orbit data and analyzed with respect to its feasibility for real-time implementation (i.e., speed of convergence and spacecraft processing resources).
• A land height correction technique is presented which will enable this algorithm to be run over low-lying land surfaces in addition to near ellipsoid ocean surfaces.

2.3. Applicability of Presented Open Loop Tracking Algorithm

The GNSS-R tracking algorithm presented here are valid for any remote sensing configuration involving a forward scattered transmission signal, such as all GNSS signals (GPS, Galileo, GLONASS, SBAS, etc.) as well as any other forward scattered signal of opportunity (SoOP) transmitter (such as communication satellites) or actively transmitting radar satellite instruments. These algorithms are applicable to aircraft observations but optimized for specific implementation on-board a GNSS-R satellite instrument.

Notably, the algorithm presented here is generally applicable to all GNSS transmitters, but has been validated only using signals from the GPS constellation received by the CYGNSS satellites. However, the general specular point derivation presented here is generic and will be valid for any transmitter-receiver combination, regardless of the specifics of the transmitted signal.

2.4. Overview of GNSS-R Open Loop Tracker Algorithm

The methodology of the GNSS-R open loop tracking algorithm presented here consists of two main parts: defining the reflection geometry and predicting the delay and Doppler of the reflected signal.

2.4.1. Defining Reflection Geometry

Initially, it is required to establish the reflection geometry as illustrated in Figure 1 and define unique path segments used in subsequent derivations. This includes estimating the positions of the transmitter and receiver and the location of the surface specular point. The algorithm for estimating the surface reflection point is derived in detail in Section 3. An alternative specular point estimation algorithm, developed for use with the CYGNSS end-to-end simulator was previously developed by O’Brien and can also be used with comparable performance [24].

Note that the specular point solver solution is iterative based on an initial (rough) guess of the specular point location. The convergence criteria for the solver is discussed in Section 3.1. Additionally, the speed of convergence of the specular point solver can be optimized by varying a linear scale factor. How this gain can be optimized is discussed in Section 6 for the case of CYGNSS GNSS-R observations.

2.4.2. Estimating Open Loop Delay and Doppler

When the best estimate of the surface specular point is obtained, the reflected signals delay code phase and Doppler frequency can be estimated as described in Section 4. The delay and Doppler of the reflected signal are estimated separately as described in Section 4.2 and Section 4.3, respectively. Importantly, the delay estimation calculation is relative to the tracked direct signal and requires a specific instrument hardware configuration with is described and illustrated in Section 4.1 (Figure 2). The reflected Doppler estimate is made using only the reflection geometry and a correction for the drift of the receiver clock.

3. Method, Part 1: Specular Reflection Point Calculation

The surface specular point for GNSS-R measurements from the ocean and low-lying land surfaces can be generally described as the point of specular reflection on the Earth surface between the transmitter and receiver. Additional information on GNSS-R specular point solvers can be found in [22,24,25]. All coordinates were in the WGS84 Earth center Earth fixed (ECEF) ellipsoid reference frame. Within this derivation, the surface point can be estimated using the following assumptions:

• The total path between the transmitter, surface specular point and the receiver will be the minimum of all possible paths across the Earth’s surface.
• The specular point must lie on the surface of the Earth. For reflections from the ocean the specular reflection point will lie close to the WGS84 ellipsoid. For reflections over land, local land height variations should be added to the local reference ellipsoid.
• The specular reflection will satisfy Snell’s Law, where the angle between the incoming wave and reflected waves with respect to the local surface ellipsoid normal are equal.
• For a real-time application, the specular reflection points need to be calculated slightly early and propagated forward, so that the open loop tracker predictions are available in real-time to the instrument observation processing hardware. Errors due to propagation inaccuracies are described in detail in [22].

Initially we represent the reflected signal path as a function of the transmitter, receiver and specular point locations. Refer to Figure 1 for illustration of signal paths. In the notation that follows, over-bar arrows indicate vectors, vertical lines indicate a magnitude operation.

$$P_{T2S2R}=P_{T2S}+P_{S2R}=\left|(\overrightarrow{T}-\overrightarrow{S})\right|+\left|(\overrightarrow{R}-\overrightarrow{S})\right|$$

(1)

where,

$\overrightarrow{T}$ = the ECEF vector to the GNSS transmitter.

$\overrightarrow{S}$ = the ECEF vector to the estimate of the specular point.

$\overrightarrow{R}$ = the ECEF vector to the GNSS-R receiver.

$P_{T2S}$ = the path magnitude from the GNSS transmitter to the specular point.

$P_{S2R}$ = the path magnitude from the specular point to the GNSS-R receiver.

$P_{T2S2R}$ = the total reflection path magnitude.

Using basic three dimensional geometry, the total path traveled can be expanded into its X,Y,Z components as follows,

$$P_{T2S2R}=\sqrt{{(T_x-S_x)}^2+{(T_y-S_y)}^2+{(T_z-S_z)}^2}+\sqrt{{(R_x-S_x)}^2+{(R_y-S_y)}^2+{(R_z-S_z)}^2}.$$

(2)

We can assume that $\overrightarrow{R}$ and $\overrightarrow{T}$ are known to a reasonable accuracy from the instrument GPS navigation solution. In this derivation these two variables are assumed known at the application time epoch, and the specular point $\overrightarrow{S}$ is the primary variable to be estimated. To solve for $\overrightarrow{S}$ we first take partial derivatives with respect to the specular point in the X, Y and Z dimensions. The partial derivatives with respect to all three dimensions of $\overrightarrow{S}$ are,

$${\partial }_{S_x}{P}_{T2S2R}(S_x)=\frac{(T_x-S_x)}{\sqrt{{(T_x-S_x)}^2+{(T_y-S_y)}^2+{(T_z-S_z)}^2}}+\frac{(R_x-S_x)}{\sqrt{{(R_x-S_x)}^2+{(R_y-S_y)}^2+{(R_z-S_z)}^2}}$$

(3)

$${\partial }_{S_y}{P}_{T2S2R}(S_y)=\frac{(T_y-S_y)}{\sqrt{{(T_x-S_x)}^2+{(T_y-S_y)}^2+{(T_z-S_z)}^2}}+\frac{(R_y-S_y)}{\sqrt{{(R_x-S_x)}^2+{(R_y-S_y)}^2+{(R_z-S_z)}^2}}$$

(4)

$${\partial }_{S_z}{P}_{T2S2R}(S_z)=\frac{(T_z-S_z)}{\sqrt{{(T_x-S_x)}^2+{(T_y-S_y)}^2+{(T_z-S_z)}^2}}+\frac{(R_z-S_z)}{\sqrt{{(R_x-S_x)}^2+{(R_y-S_y)}^2+{(R_z-S_z)}^2}}$$

(5)

Combining and simplifying these three equations gives us:

$$d{\overrightarrow{S}}_i={\partial }_{{\overrightarrow{S}}_i}{P}_{T2S2R}({\overrightarrow{S}}_i)=\frac{(\overrightarrow{T}-{\overrightarrow{S}}_i)}{P_{T2S}}+\frac{(\overrightarrow{R}-{\overrightarrow{S}}_i)}{P_{S2R}}.$$

(6)

where, $d\overrightarrow{S}$ represents the derivative component of the reflection path for the current estimate of ${\overrightarrow{S}}_i$ (where i is the iteration number). To quicken convergence, $d\overrightarrow{S}$ is multiplied by a scale factor and used directly to update the estimate of the specular point to be used as the input into the next iteration, such that,

$${\overrightarrow{S}}_{i+1}={\overrightarrow{S}}_i+Kd{\overrightarrow{S}}_i.$$

(7)

where K is a linear scale factor which can be used to optimize the speed of convergence, ${\overrightarrow{S}}_{i+1}$ and ${\overrightarrow{S}}_i$ are the updated and previous estimates of the specular point, respectively. How K is determined is discussed in more detail in Section 6.2.

An additional requirement on the specular point solution is that ${\overrightarrow{S}}_i$ must be constrained to the Earths surface. The estimated radius of the Earth surface can be calculated on the WGS84 ellipsoid plus a height correction above the reference ellipsoid, such that (from [26]).

$$r_i=a_{WGS84}\sqrt{\frac{1-e_{WGS84}^2}{1-(e_{WGS84}^2+cos(\lambda ))}}+h.$$

(8)

where,

$\lambda$ = the current estimate of the specular point latitude. This can be calculated directly from the Z component of the current specular point estimate, calculated as $\lambda =sin(\frac{S_z}{\left|\overrightarrow{S}\right|})$

$a_{WGS84}$ = the WGS84 ellipsoid semi-major axis, 6,378,137 m.

$e_{WGS84}$ = the WGS84 ellipsoid eccentricity, 0.08181919084262.

h = the height correction above the the WGS84 ellipsoid due to land surface topography (or ocean height variations).

The new estimate of the specular point, ${\overrightarrow{S}}_{i+1}$, is then corrected by scaling it by the estimated Earth radius, giving us the new corrected estimate of the specular point for the next iteration of the specular point solver,

$${\overrightarrow{S}}_i=r_i\frac{{\overrightarrow{S}}_{i+1}}{\left|{\overrightarrow{S}}_{i+1}\right|}.$$

(9)

This corrected specular point estimate is then used as the input into the subsequent iteration of the solver. After multiple iterations the specular point location will converge to within an acceptable accuracy and the iteration ends with a final best estimate of the specular point position. In summary, the iterative steps to estimate the surface specular point include,

• Determine an initial guess for the surface specular point location, ${\overrightarrow{S}}_1$. This could be either (a) an estimate based on previous, propagated or modeled initial specular point positions or (b) using the estimate of the receiver position $\overrightarrow{R}$, normalized to the Earth surface, calculated as,

  $${\overrightarrow{S}}_1={\overrightarrow{S}}_i=r_i\frac{\overrightarrow{R}}{\left|\overrightarrow{R}\right|}.$$

  (10)
• Solve for the correction derivative using Equation (6). Path magnitudes are calculated using best estimates of receiver and transmitter positions from GPS navigation solution, propagated ahead slightly to account for the non-zero computational time with respect to the application of the values in real-time on the instrument.
• Update estimated position of specular point from ${\overrightarrow{S}}_i$ to ${\overrightarrow{S}}_{i+1}$ using Equation (7).
• Calculate estimated Earth surface using Equation (8). Adjust WGS84 ellipsoid height (h) to account for height of surface topography over land or ocean height variations as needed.
• Project new corrected specular point estimate ${\overrightarrow{S}}_{i+1}$ to the Earth’s surface using Equation (9).
• Start next iteration (step 2) with updated value for specular point ${\overrightarrow{S}}_i$ calculated in Equation (9) until convergence criteria is met.

3.1. Successful Specular Reflection Point Convergence Criteria

A simple and accurate check on the specular point algorithm convergence is to test the Snell angle agreement at each iteration. Snell’s law states that the angle to the receiver and the GPS transmitter with respect to the local surface ellipsoid normal should be equal in the perfect case. As the estimated specular point converges on the final estimate, the Snell angle difference between the direct and reflected paths will approach zero. A reasonably accurate estimate can be obtained by setting a Snell success threshold at a low (but non-zero value). The Snell angle test is calculated as follows. Initially, calculate the unit vectors from the specular point to the transmitter and receiver, respectively, and the unit vector at the current estimate of the specular point,

$${\widehat{D}}_{RS}=\frac{\overrightarrow{R}-\overrightarrow{S}}{\left|\overrightarrow{R}-\overrightarrow{S}\right|}$$

(11)

$${\widehat{D}}_{TS}=\frac{\overrightarrow{T}-\overrightarrow{S}}{\left|\overrightarrow{T}-\overrightarrow{S}\right|}$$

(12)

$$\widehat{S}=\frac{\overrightarrow{S}}{\left|\overrightarrow{S}\right|}.$$

(13)

Using these values the difference magnitude between the two local surface Snell angles can be calculated in radians as (including vector dot product operations),

$$d\theta =\left|{cos}^{-1}({\widehat{D}}_{RS}·\widehat{S})-{cos}^{-1}({\widehat{D}}_{TS}·\widehat{S})\right|.$$

(14)

As the solution converges, $d\theta$ will approach zero. However, when $d\theta$ decreases below a given tolerance, the specular point solution iteration can be exited and the final estimate of ${\overrightarrow{S}}_i$ used as the final value for subsequent delay and Doppler calculations described in Section 4. Generally, a tolerance of 0.1 degrees is sufficient for open loop tracking reflection targeting as the analysis in Section 6 demonstrates.

4. Method, Part 2: Open Loop GNSS-R Delay and Doppler Tracking Algorithms

After the reflection geometry has been adequately defined (as per Figure 1) it is then possible to calculate the reflected signal code phase delay and Doppler frequency needed to initialize the DDM observation processing hardware. However, the delay estimation relies on a an important assumption of the instrument hardware configuration. This assumption allows for a much simpler calculation of relative code phase delay with respect to the directly tracked navigation signal from the same GPS transmitter.

4.1. Instrument Hardware Considerations

A key requirement in the tracking algorithm presented here is that signals from the two divergent paths from the transmitter to the receiver (Figure 1) must be clocked into the GNSS-R instrument with a common clock. If this is not the case, calculating the absolute code phase reference for both signals must consider the precise sub-millisecond timing and transmitter and receiver clock biases, as was outlined in [25]. However, if the zenith navigation and reflected nadir signals are both clocked into the digital signal processor with a common clock, then the sub-millisecond sampling reference is the same and the problem of predicting the reflected signals code phase time delay reduces to a relative calculation with respect to the code phase of the directly tracked signal from the same GPS transmitter, which is used by the navigation portion of the receiver for position and velocity estimation. A common clock configuration for a GNSS-R instrument is illustrated in Figure 2.

4.2. Estimating the Reflected Signal Code Phase Delay

With a common clock hardware configuration the predicted code phase of the reflected signal is a simple function of the path difference between the direct and reflected signals and the direct signal code phase. The path difference in meters ($dP$) can be calculated as,

$$dP=P_{T2S2R}-P_{T2R}=(P_{S2R}+P_{T2S})-P_{T2R}.$$

(15)

where ${\overline{P}}_{T2R}$ is the length of the path from the transmitter to the receiver, ${\overline{P}}_{T2S2R}$ is the combined path length of the reflected signal, which is the sum of the path from the transmitter to the specular point (${\overline{P}}_{T2R}$) plus the path from the specular point to the receiver (${\overline{P}}_{T2R}$). Equation (15) can also be expressed as a function of the transmitter, receiver, and estimated specular point location as,

$$dP=(\left|\overrightarrow{T}-\overrightarrow{S}\right|+\left|\overrightarrow{S}-\overrightarrow{R}\right|)-\left|\overrightarrow{T}-\overrightarrow{R}\right|.$$

(16)

Following, the code phase of the reflected signal can be calculated relative to the navigation tracked direct signal from the same transmitting satellite as,

$${\tau }_{ref}={\tau }_{dir}-d{P}_{chips}.$$

(17)

As the GPS signal code phase is a continually repeating length of psuedo-random sequence of transitions [1], a modulo of the code phase repeat period is needed to bring the absolute code phase within the range of the transmitted sequence. Therefore, ${\tau }_{ref}$ needs to be corrected based on the length of the specific code phase, for GPS L1 C/A code this can be expressed as,

$$if({\tau }_{ref}<0),{\tau }_{ref}={\tau }_{ref}+1023.$$

(18)

where ${\tau }_{ref}$ is the predicted code phase of the reflected signal, ${\tau }_{dir}$ is the code phase of the direct signal tracked from the zenith navigation channel for the same transmitter, and $d{P}_{chips}$ is the path difference converted from meters to code phase chips, such that $d{P}_{chips}=\frac{dP}{\alpha }$. Where $\alpha$ is the number of meters per code chip, in the case of the GPS L1 C/A signal, $\alpha =293.0522561$.

The estimated value of ${\tau }_{ref}$ can then be used to initialize the reflection channel correlators of the GNSS-R instrument as the reference code phase delay around which to produce a two dimensions map in delay and Doppler (DDM) suitable for surface observations.

4.3. Estimating the Reflected Signal Doppler Frequency

The Doppler frequency of a reflected signal can be calculated using the following terms,

$\overrightarrow{R}$ = The receiver position, ${\overrightarrow{R}}_v$ = the receiver velocity, $\overrightarrow{T}$ = the transmitter position, ${\overrightarrow{T}}_v$ = the transmitter velocity, $\overrightarrow{S}$ = the best estimate of the specular point position, $D_{clk}$ = the Doppler frequency contribution due to the GPS receiver clock, f = The GNSS signal transmit frequency, for GPS L1 = 1575.42 × ${10}^6$ Hz, and c is the speed of light, 299,792,458 m/s.

Using these parameters and estimates of the unit vectors from the specular point to the transmitter and receiver calculated using Equations (11) and (12), the individual Doppler components can be calculated as (from [27]),

$$D_R=-1({\overrightarrow{R}}_v·{\widehat{D}}_{RS})(\frac{f}{c})$$

(19)

$$D_T=-1({\overrightarrow{T}}_v·{\widehat{D}}_{TS})(\frac{f}{c}).$$

(20)

The open loop tracking reflected signal Doppler frequency is the sum of the two geometric components, and the contribution from the GPS receiver clock, expressed as follows,

$$D=D_R+D_T+D_{clk}.$$

(21)

The receiver clock error $D_{clk}$ is output regularly from the GPS navigation receiver position, velocity and timing estimation.

5. Results: Algorithm Verification Using On-Orbit Data

This section presents an initial validation of the algorithm using a 60 s capture of raw sampled GPS L1 data from the NASA CYGNSS satellite. Two parallel reflection tracks, one which traverses from ocean to land are processed independently and compared to the algorithm predictions. The raw sampled data (or high resolution data, logged at 16.0362 × ${10}^6$ samples per second) from CYGNSS does not undergo any digital signal processing by the CYGNSS GNSS-R instrument. This data is captured by the CYGNSS zenith and nadir instrument antennas with a common clock, amplified and down converted as described in [28] and then digitally sampled into a large memory buffer for downlink. This permits a comparison of the actual delay and Doppler characteristics of the real reflected signal and the predicted delay and Doppler from the algorithm presented here.

Section 6 presents a larger statistical validation of the algorithm performance as a function of geographic location and performs an analysis of the algorithm’s convergence speed.

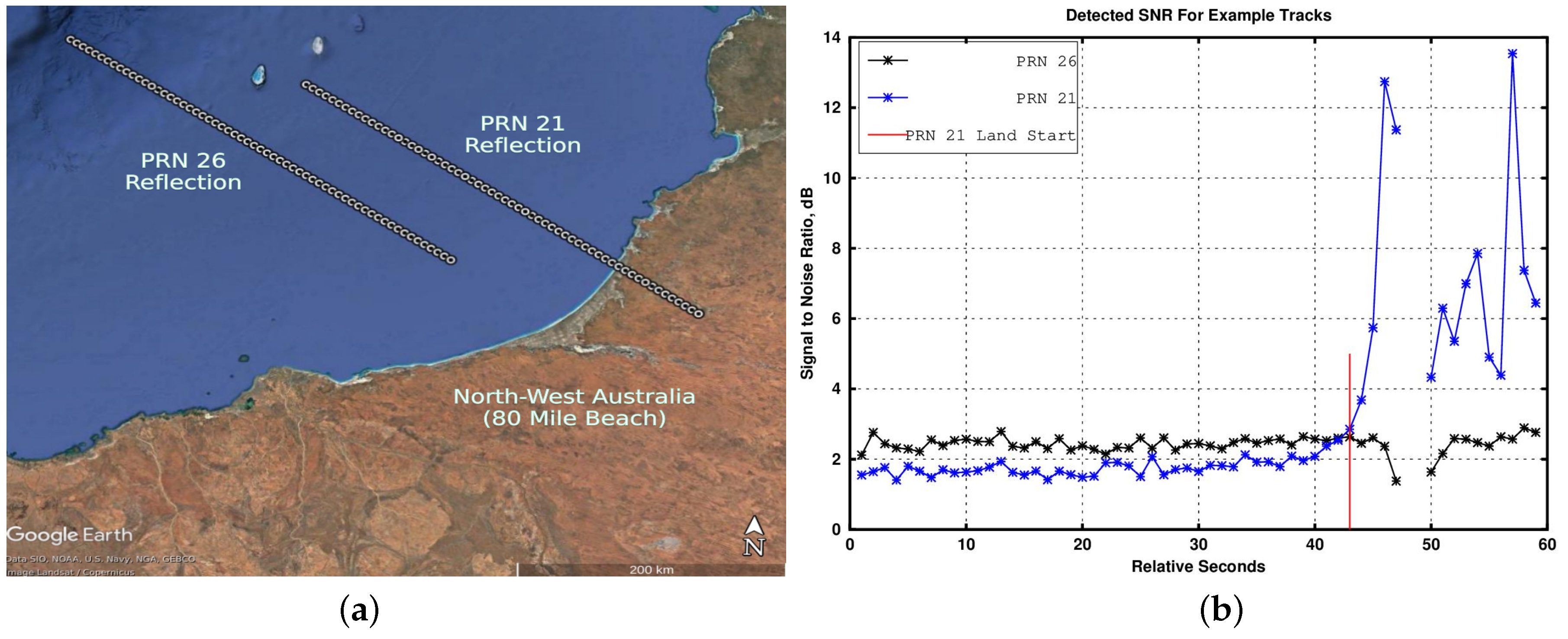
5.1. Geolocation of the Example Reflection Tracks

This CYGNSS data set was processed using a custom ground based software receiver, where the algorithms can be validated using a snap shot of real on-orbit signals. Two example signals were selected to demonstrate the proposed tracking algorithm. These reflection tracks are located off the north-west coast of Australia as indicated in Figure 3a. The reflection tracks for GPS transmitters were detected for pseudo random noise (PRN) codes 26 and 21. The reflection track for PRN 21 transitions from ocean to land at approximately second 43 of the raw data collection.

Figure 3b shows the signal to noise (SNR) values for each of the two example signals over the duration of the data set (calculated as described in [29]). The ocean reflection SNRs are both similar and relatively consistent (with slight fluctuation due to surface conditions and geometry) while the land reflections for PRN 21 clearly show a jump in the SNR as the signal is reflected from relatively flat dry land. The ground processed code phase delay and Doppler of the reflected signal maximum was logged over the duration of the track and was used as a truth reference for the reflected signal time and Doppler parameters versus time. Additionally, the direct signal for each track was tracked on the navigation channel over the 60 s interval using established GPS signal acquisition and tracking techniques.

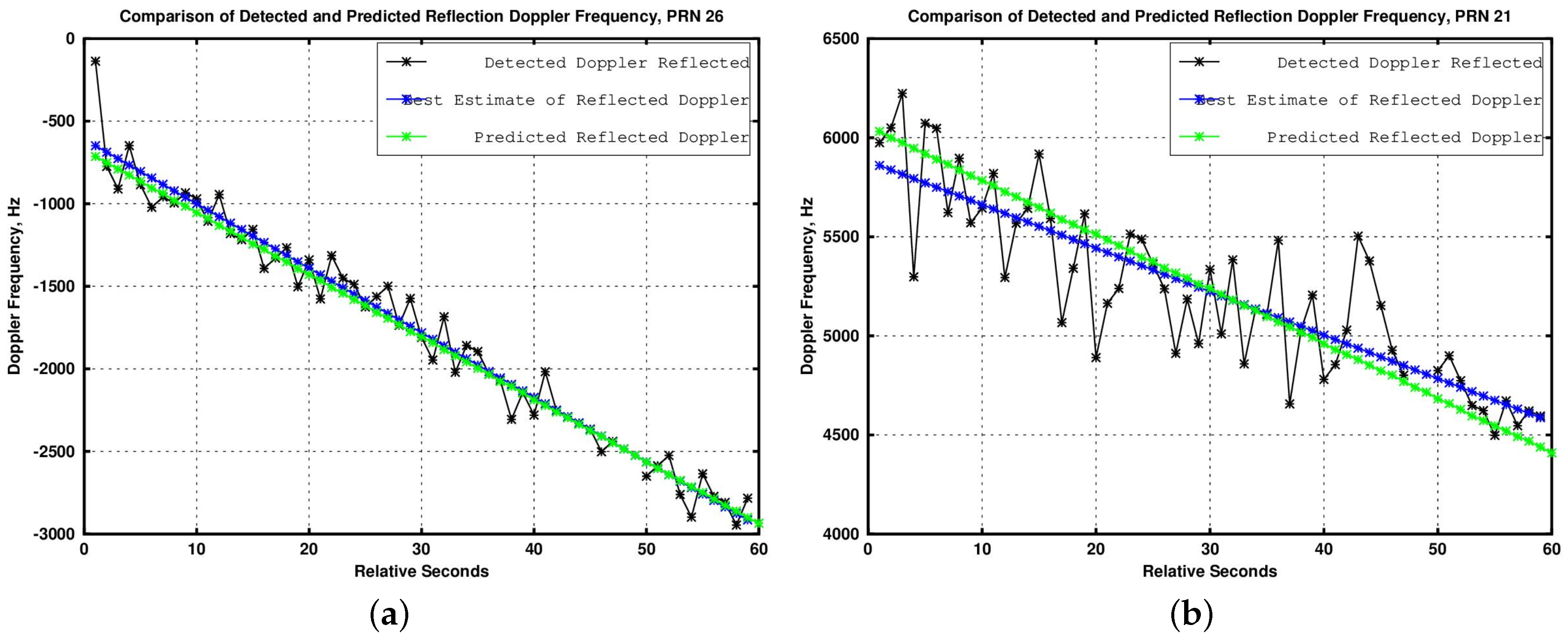
5.2. Open Loop Tracker Code Phase Predictions

The algorithm delay predictions were calculated for both tracks as follows: the GNSS-R receiver position and velocity was estimated using the direct navigation signals. The GNSS transmitter positions and velocities were obtained from the published GPS ephemeris over the collection interval. The surface specular reflection point was then estimated using the algorithm detailed in Section 3. Subsequently the reflected signal code phase delay and Doppler frequency were estimated along the length of both tracks as described in Section 4. The resulting truth reference values for the direct and reflected signal code phase delays, as well as the open loop predicted reflected code phase delays are shown in Figure 4. Importantly, the code delay rate is used to update the open-loop tracker at a rate that is less than the total measurement integration time in order to prevent smearing of the measurement. Measurement distortion will occur if the open loop tracker predictions lag behind the configuration of the hardware processing, causing the instrument processing to lag behind the real signal dynamics introducing distortions into the power detected across the processed DDM.

In Figure 4 the detected and predicted code phase delays align (and overlap) almost exactly. This figure is useful for observing how the difference in code phase delay due to the physical path difference changes as a function of time. The detected and predicted Doppler frequency across the example tracks are shown in Figure 5.

Finally, the errors in the predicted delay code phases and Doppler frequencies are plotted in Figure 6. The truth reference determination of the reflected signal represents only a rough estimate of the precise surface reflection location, due to integer processing bin uncertainties and other surface factors. However, the intent of this validation is to demonstrate that these tracking algorithm can successful predict the delay and Doppler to within the sub-bin level requirements of a typical GNSS-R delay Doppler map. These limits are generally; to within 0.25 chips accuracy in delay and within 500 Hz in Doppler, which is consistent with general GNSS-R observation requirements [28].

The errors in Figure 6 indicated that the duration along both tracks tested, the tracking accuracy is well within the requirements for DDM generation on-board the instrument. Notably, the transition from ocean to land for PRN 21, demonstrates the delay tracking performance with and without a land height correction. The reflection for PRN 21 passes onto land at approximately second 43 (while the PRN 26 reflection is over an ocean for the whole duration). At second 43, the PRN tracking error using the ocean WGS84 ellipsoid reference starts to increase. However, the red trace shows the improvement in delay tracking performance after the land transition when the land surface elevation is included in the estimate of the specular reflection point in Equation (8).

6. Results: Statistical Geographic Performance Validation and Analysis of Resource Requirements

This section first describes how the reflections from many transmitters are sorted and selected from amongst all the available surface reflections. From the potentially dozens of available surface reflections (all of which can be tracked using these algorithms), only some will produce good science observations. Subsequently, a large data set of GPS L1 data from the CYGNSS satellite mission is used to validate the performance of the presented open loop tracking algorithm.

6.1. On-Board Surface Reflection Prioritization

In theory, all of the signals tracked by the GNSS navigation receiver can be tracked and targeted for surface observations. However, only a smaller subset of reflections are usable due to the GNSS-R instrument’s antenna gain surface coverage. Only a subset of the total signals tracked will result in reflections that fall within viable regions of the ground projected antenna footprint(s). This requires an on-board reflection prioritization algorithm to determine the optimal surface reflections to open loop track. A basic prioritization algorithm consists of the following steps.

• Determine the surface specular points for a set of GNSS transmitters as described in Section 3. Generate a set of vectors from the GNSS-R satellite to the estimated specular reflection points.
• Map the vectors from the satellite receiver to the surface specular point into the satellite body frame, using a transformation derived using the satellite attitude matrix.
• Map the specular point direction in the body frame to an on board map of the GNSS-R instrument science antenna patterns figure of merit. The figure of merit can be simply the antenna gain, or a range corrected antenna gain [28].
• Rank the measurement points for all the GPS transmitters from highest to lowest figure of merit. Thus, sorting the surface reflections with high antenna gain to the highest ranking.
• Prioritize the reflections based on the highest figure of merit estimates and the available processing resources available within the GNSS-R receiver digital signal processing channels.

6.2. Performance Evaluation Using On-Orbit CYGNSS Data

The key evaluation parameters of the open loop tracker performance were the achieved accuracies of the predicted delay code phase and Doppler frequency. A total of 55 individual satellite days from the CYGNSS observatories was analyzed. For this statistical evaluation, the predicted code phase and Doppler from the tracking algorithms are compared with the precise estimates of delay and Doppler derived from the actual CYGNSS measurements. By processing a large set of CYGNSS data these errors can be mapped geographically to assess the algorithms performance as a function of location and geometry. The spatial distribution of the mean open loop tracking delay errors shown in Figure 7.

Additionally, we will analyze the processing required using the same CYGNSS data set. The dominant resource demand in the tracking algorithm is during the estimation of the surface specular point location. However, the speed of the specular point estimation algorithm can be controlled by adjusting the correction factor K in Equation (7). The second key parameter determining convergence is the tolerance applied to the solution accuracy. In order to assess the performance of the specular point estimator and the resulting open loop tracking errors, the algorithm was tested using 35 total satellite days worth of CYGNSS data, providing repeated measurements over the CYGNSS coverage extent. The spatial distribution of the mean number of iterations in the specular point solution are shown in Figure 8.

The optimal configuration of the specular point estimation was determined by gradually increasing the value of the feedback gain K with respect to a predetermined tolerance $tol$ value which resulted in acceptable delay tracking error (based on the maximum path variation over the ellipsoid for a given Snell angle error).

Table 1. Table summary of global performance of the specular point and delay tracking algorithms.

K	Snell Angle Tolerance	Mean Delay Error	Max Delay Error	Mean Iter.	Max Iter.
1.0 × ${10}^6$	0.1 degrees	0.13 chips	0.56 chips	8.6	29

shows the values of K and $tol$ and the resulting mean and max open loop tracking delay error and number of iterations. Notably, the specular point solution converged 100% of the time over the complete data set.

For the configuration listed in Table 1, convergence results in maximum delay tracking errors of less than 0.56 chips in all cases, with mean errors of 0.13 chip globally. The mean Doppler error globally was 78 Hz, with a maximum error of 376 Hz (within the 500 Hz Doppler bin limit as per CYGNSS requirement).

Essentially K acts as a linear feedback scale factor and the larger it is the faster the convergence of the solution, but with an important caveat: if the K is too large (with respect to the Snell angle tolerance), the solution will oscillate around the true specular point and not converge. Therefore, the tolerance must be small enough to represent a specular point region which results in low tracking errors, but not be too small as to require a small K factor to assure robust convergence.

The number of iterations acts as a proxy for estimating the required computer resources. However, the actual computation time will depend on the specific computer configuration and is not explored in detail here.

7. Discussion and Algorithm Variations

The algorithm presented here was designed to converge under all geometries for ocean reflections and low lying land reflections with mild topography with no specific tuning needed. However, there are a number of variations of the algorithm with potential advantages over the base line approach. It should be noted that because the delay and Doppler tracking values are normally fed into a real-time control loop, it is necessary to perform a linear or higher-order extrapolation of the transmitter and receiver positions based on simple dynamic models or more complex orbital predictions. Additional enhancements that could be made to improve the performance of the open loop tracking algorithms presented here are listed in the remainder of this section.

7.1. Inclusion of Ancillary Maps for Improved Specular Point Accuracy Over Ocean and Land

It is possible to further improve the accuracy of the specular point estimation with the inclusion of ancillary data maps of height variations with respect to the WGS84 ellipsoid reference. Over ocean the inclusion of a global mean sea surface map, such as those provides by the National Space Institute of Denmark [30], has been demonstrated to significantly improve the specular point estimation accuracy over ocean [31]. Additionally, land digital elevation maps are available such as the NASA Shuttle Radar Topography Mission (SRTM) data sets [32] which can greatly improve the accuracy of open loop tracking over land surfaces. It is recommended to apply a filter to the SRTM maps to create continuous and relatively smooth surfaces, which are more amenable to quick conversion of the specular point algorithm.

7.2. Propagated Specular Point Search Initialization

The default initialization of the specular point solution of the GNSS-R receiver sub-satellite point is not optimal. It was chosen for its simplicity and robustness. It is possible to provide a much more accurate initialization of the specular point for the calculation and greatly increase the speed of convergence (reduced iterations). This can be done simply by estimating the initialization of the specular point using the previous estimates of the specular point, where at the start of a track, the coarse initialization is used, while after the second point on an individual track is known, subsequent initialization points can be estimated much more accurately as follows,

$${\overrightarrow{S}}_{i+1}={\overrightarrow{S}}_i+({\overrightarrow{S}}_i-{\overrightarrow{S}}_{i-1})={\overrightarrow{S}}_i+{\overrightarrow{S}}_{vel}dt,$$

(22)

where i subscripts indicate relative time epochs, ${\overrightarrow{S}}_{vel}$ is the specular point velocity and $dt$ is the time step between consecutive measurements for a given reflection track.

7.3. Interpolated Prediction of Specular Point Parameters

Additional accuracy in the initialization of the specular point position can be achieved by estimating various parameters in the delay and Doppler open look tracking estimates using interpolated prediction techniques (such as polynomial fitting) for each parameter over short intervals (from 3 s to 1 min or more). This has the significant advantage of reducing the specular point calculation duty cycle which can result in significant on-board savings of available computational resources. Additionally, there are publically available orbit propagation tools which can be integrated into a forward orbit prediction module, including the SGP4 [33] or SPoCK [34] orbit propagation tool sets.

By using a general interpolation technique or propagated positions and velocities of the transmitter and receiver it is possible to forward-predict open loop tracking parameters such as the specular point $\overrightarrow{S}$, or the delay and Doppler estimates directly, D and $\tau$. Over ocean, this forward prediction can be very successful and greatly reduce the computational burdens. Over land with varying terrain, the specular point, delay and Doppler are less likely to change in a polynomial predictable fashion. For this reason it is recommended to constrain predictive algorithms to more uniform surface regions (such as ocean and sea ice). The general steps in the implementation of a forward propagated polynomial open loop tracking algorithm include,

• Depending on available computer resources, propagating forward the receiver satellite and transmitting satellite location using an existing orbit propagator, at 10 s intervals over a minute into the future for example.
• Estimate the surface specular points at each predicted future step.
• Use a standard polynomial fitting function to generate a function to forward predict the specular location, from which the delay and Doppler information can be quickly calculated. Or alternatively, perform a polynomial fit on the predicted delay and Doppler values directly.
• Use the generated polynomial function to calculate the open loop delay and Doppler over the entire measurement reflection track, while the reflection quality indicator indicates a viable measurement is possible.

7.4. Look Up Table Predictions

A technique which requires significant amounts of on-board memory, but results in potentially incredibly fast estimates of key tracking parameters (specular point, code phase delay difference and Doppler) is to include one or more of these parameters in an on-board look up table (LUT).

8. Conclusions

A stand-alone robust algorithm (and variations) for real-time open loop tracking of the code phase delay and Doppler of GNSS reflected signals has been proposed and validated. The algorithms were demonstrated on example tracks using CYGNSS raw sampled data as well as over a large CYGNSS data set. The demonstrated open loop tracking mean delay accuracy over ocean was found to be 0.13 L1 C/A code chips, with a mean Doppler error of 78Hz. The algorithm was found to converge 100% of the time with an average of 8.6 iterations of the specular point solver, which would allow implementation on an on-board satellite instrument. The paper provides a baseline publically available open loop GNSS-R tracking algorithm for use by the scientific community.