Feature Selection on Sentinel-2 Multispectral Imagery for Mapping a Landscape Infested by Parthenium Weed

Abstract

In the recent past, the volume of spatial datasets has significantly increased. This is attributed to, among other factors, higher sensor temporal resolutions of the recently launched satellites. The increased data, combined with the computation and possible derivation of a large number of indices, may lead to high multi-collinearity and redundant features that compromise the performance of classifiers. Using dimension reduction algorithms, a subset of these features can be selected, hence increasing their predictive potential. In this regard, an investigation into the application of feature selection techniques on multi-temporal multispectral datasets such as Sentinel-2 is valuable in vegetation mapping. In this study, ten feature selection methods belonging to five groups (Similarity-based, statistical-based, Sparse learning based, Information theoretical based, and wrappers methods) were compared based on f-score and data size for mapping a landscape infested by the Parthenium weed (Parthenium hysterophorus). Overall, results showed that ReliefF (a Similarity-based approach) was the best performing feature selection method as demonstrated by the high f-score values of Parthenium weed and a small size of optimal features selected. Although svm-b (a wrapper method) yielded the highest accuracies, the size of optimal subset of selected features was quite large. Results also showed that data size affects the performance of feature selection algorithms, except for statistically-based methods such as Gini-index and F-score and svm-b. Findings in this study provide a guidance on the application of feature selection methods for accurate mapping of invasive plant species in general and Parthenium weed, in particular, using new multispectral imagery with high temporal resolution.

1. Introduction

The dimension space of variables given as input to a classifier can be reduced without an important loss of information, while decreasing its processing time and improving the quality of its output [1]. To date, studies on dimension reduction in remote sensing have mostly focused on hyperspectral datasets [2,3,4] and high spatial resolution multispectral imagery using Object-Based Image Analysis (OBIA) [5,6,7]. Generally, multispectral images have received less attention comparatively, likely due to having a limited number of bands, which do not require dimension reduction. However, with the launch of high temporal resolution sensors such as Sentinel-2, the amount of image data that can be acquired within a short period has considerably increased [8]. This is due to the sensor’s improved spectral resolution (13 bands) and a five day temporal resolution [9].

Generally, high-dimensional remotely sensed datasets contain irrelevant information and highly redundant features. Such dimensionality deteriorates quantitative (e.g., leaf area index and biomass) and qualitative (e.g., land-cover) performance of statistical algorithms by overfitting data [10]. High dimensional data are often associated with the Hughes effects or the curse of dimensionality, a phenomenon that occurs when the number of features in a dataset is greater than the number of samples [11,12]. Hughes effects affects the performance of algorithms previously designed for low-dimensional data. Whereas high dimensionality can lead to poor generalization of learning algorithms during the classification process [12], it can also embed features that are crucial for classification enhancement. Hence, when using dimension reduction algorithms, a subset of those features can be selected from the high dimensional data, increasing their predictive potential [13].

There are two main components of dimension reduction strategies: feature extraction or construction and feature selection or feature ranking. Feature extraction (e.g., Principle Component Analysis (PCA)), constructs a new and low dimensional feature space using linear or non-linear combinations of the original high-dimensional feature space [14] while feature selection (e.g., Fisher Score and Information Gain) extracts subsets from existing features [10]. Although feature extraction methods produce higher classification accuracies, the interpretation of generated results is often challenging [2]. However, feature selection methods do not change the original information of features, thus giving models better interpretability and readability. Feature selection techniques have been applied in text mining and genetic analysis [14]. Hence, in this study, they were preferred over feature extraction methods.

Traditional feature selection techniques are typically grouped into three approaches namely; filter, embedded and wrapper methods [15]. In earth observation related studies, feature selection algorithms have generally been compared based on this grouping [5,16]. However, in the advent of big data, this grouping can be regarded to be very broad, necessitating development of new feature selections algorithms. For instance, within filter feature selection methods, there are some that evaluate the importance of features based on the ability to preserve data similarity (e.g., Fisher Score, ReliefF), while others use a heuristic filter criterion (e.g., Mutual Information Maximization). Therefore, it is crucial to re-evaluate the comparison of feature selection algorithms in a data specific perspective.

Li, et al. [17] reclassified traditional feature algorithms for generic data into five groups: similarity-based feature selection, information theoretical-based feature selection, statistical-based feature selection, sparse learning-based feature selection and wrappers. They devised an open-source feature selection repository, named scikit-feature that provides 40 feature selection algorithms (including unsupervised feature selection approaches). Some selections, such as Joint Mutual Information and decision tree forward, are relatively new in earth observation applications [18].

Over the last few decades, the number of vegetation indices has significantly increased. For instance, Henrich, et al. [19] gathered 250 vegetation indices derivable from Sentinel-2. Computation of vegetation indices from a higher temporal resolution imagery like Sentinel-2 would lead to data with very increased multi-collinearity, a higher number of derived variables, and increased dimensions. Hence, the need for accurate and efficient feature selection techniques when dealing with new generation multispectral imagers such as Sentinel-2 is becoming increasingly valuable in vegetation mapping [8]. To the best of our knowledge, no earth observation related study has endeavored to undertake empirical evaluation of feature selection methods as provided in the scikit-feature repository for generic data.

In this study, feature selection algorithms based on the Li, et al. [17]‘s classification were compared for mapping a landscape infested by Parthenium weed using Sentinel-2. The Parthenium weed is an alien invasive herb of tropical American origin that has infested over thirty countries. It has been identified as one of the seven most devastating and hazardous weeds worldwide [20]. A number of studies [21,22] have reported its adverse impacts on ecosystem functioning, biodiversity, agricultural productivity and human health. A detailed comparison of feature selection algorithms on Sentinel-2 spectral bands combined with vegetation indices and with respect to Li, et al. [17]’s classification, would therefore: (a) improve mapping accuracy, valuable for designing mitigation approaches; (b) shed light on the most valuable feature selection group and (c) identify the most suitable feature selection method for accurately mapping a Parthenium weed infested landscape. Unlike previous studies that evaluated features selection methods on the basis of overall classification accuracy [5,23,24], this study investigated their performance on a specific landscape phenomenon’s (Parthenium weed) mapping accuracy, as high overall classification accuracy does not always mean a reliable accuracy for a specific class [25]. In this study, we sought to provide a detailed comparison of feature selection algorithms on higher temporal resolution satellite images with high data volume. Specifically, we looked at (a) their performance on Parthenium weed using specific class-related accuracies as an evaluation criterion, and (b) the impact of data size on their accuracy.

2. Material and Method

2.1. Study Area

This study was conducted within the Mtubatuba municipality on the North-East Coast of the KwaZulu-Natal province, South Africa (Figure 1). The study area covers 129 km², and is characterized by heavy Parthenium infestation. The area is predominantly underlain by Basalt, Sand and Mudstone geological formations [26]. Annual average rainfall ranges from 600 mm to 1250 mm and temperatures vary around 21 °C, respectively. Summers are generally warm to hot, while winters are cool to mild [27]. The sampling area is characterized by a mosaic of several land use/land cover types that include commercial agriculture (e.g., forestry plantations and sugarcane farming), subsistence farming (beans, bananas, potatoes, and cattle), mining, and high and low density residential areas [27].

2.2. Reference Data

Using a high resolution (50 cm) color orthophotograph [28] of the study area, conspicuous patches of Parthenium weed infestations were randomly selected, stratified equally across different land cover/use types. The selected sites were then surveyed using a differentially corrected Trimble GeoXT handheld GPS receiver with about 50 cm accuracy. The ground truth campaign was conducted during summer, between the 12th of January and 2nd of February 2017. At each Parthenium weed site, at least 10 m × 10 m quadrats were demarcated. The quadrats were located mostly in the middle of a large patch (greater than 10 × 10 m) of Pathernium in order to cater for any possible mismatches with the sentinel pixels [29]. In total, 90 quadrats were randomly selected across different land-cover types to account for variability in different ecological conditions of the study area. GPS points of surrounding land cover types such as forest, grassland, built-up and water bodies were also collected. Supplementary X-Y coordinates of these land-cover types were also created from the color orthophotograph to increase the number of training samples. The aforementioned land-cover classes were the most predominant in the study area and were therefore used to evaluate the discriminatory power of different models developed in this study for mapping Parthenium weed infested areas. In total, 447 reference points for mapping Parthenium weed and its surrounding land cover classes were obtained. To determine the optimal feature selection methods, and to test the effect of data sizes, these ground reference data were randomly split into training and test sets in three different ratios: 1:3; 1:1; 3:1 as shown in

Table 1. Training and test dataset combinations for land cover classes.

Land-Cover Classes	Training Set 3 (70%)	Test Set 3 (30%)	Training Set 2 (50%)	Test Set 2 (50%)	Training Set 1 (30%)	Test Set 1 (70%)	Total
Forest	70	30	50	50	30	70	100
Water Body	49	21	35	35	21	49	70
Parthenium Weed	63	27	45	45	27	63	90
Grassland	64	28	46	46	28	64	92
Settlement	66	29	48	48	29	66	95

[30]. The random split was undertaken using the function “train_test_split” of the Sklearn python library. “Random-state” and “stratify” parameters were included in the function to respectively allow reproducibility and obtain the same proportions of class labels as the input dataset.

The data design also allowed evaluating the investigated feature selection methods with respect to Hughes effects.

2.3. Acquisition of Multi-Temporal Sentinel-2 Images and Pre-Processing

Three Level 1C Sentinel-2A images were acquired on 19 January of 2017 under cloudless conditions. The Semi-Automatic Classification Plugin [31] within the QGIS (version 2.14.11) software was used to correct the acquired images for atmospheric effects. The Semi-Automatic Classification Plugin uses the Dark Object Subtraction in order to convert Top Of Atmosphere reflectance (TOA) to Bottom Of Atmosphere reflectance (BOA). Bands (band 1, band 9 and band 10) with 60 m-resolution were omitted in this study. Moreover, bands with 20 m resolution were resampled to 10 m using ArcMap (version 10.3) to allow layer stacking with 10 m bands.

2.4. Data Analysis

2.4.1. Feature Section Methods

In this section, the five groups of feature selection methods are briefly discussed. Two representative methods were randomly chosen from each group to achieve the comparison.

(A) Similarity-Based Feature Selection Methods

Similarity-based feature selection methods evaluate the importance of features by determining their ability to preserve data similarity using some performance criterion. The two selected feature selection algorithms in this study were Trace ratio and Relief. Trace ratio [32] maximizes data similarity for samples of the same class or those that are close to each other while minimizing data similarity for the sample of different classes or those that are far away from each other. More important features also have a larger score. ReliefF [33] assigns a weight to each feature of a dataset and feature values which are above a predefined threshold are then selected. The rationale behind ReliefF is to select features randomly, and based on nearest neighbors, the quality of features is estimated according to how well their values distinguish among the instances of the same and different classes nearing each other. The larger the weight value of a feature, the higher the relevance [34].

(B) Statistical-Based Feature Selection Methods

Statistical-based feature selection methods rely on statistical measures in order to the estimate relevance of features. Some examples of statistical-based feature selection methods include the Gini index and the F-score. The Gini index [35] is a statistical measure that quantitatively evaluates the ability of a feature to separate instances from different classes [14]. It was earlier used in decision tree for splitting attributes. The rationale behind Gini index is as follows: Suppose S is the set of s samples with m different classes $\left(C_i,i=1,\dots ,\mathrm{m}\right).$ According to the differences of classes, S can be divided into m subset $\left(S_i,i=1,\dots ,\mathrm{m}\right).$ Given $S_i$ is the sample set which belongs to class $C_i$, $s_i$ is the sample number of set Si, Gini index of set S can be computed according to the equation below [36]:

$$Gini\left(S\right)=1-{\displaystyle \sum }_{i =1}^m{P}_i^2$$

(1)

where $P_i$ denotes the probability for any sample to belong to $C_i$ and to estimate with $s_i/s$.

The F-score [37] is calculated as follows: Given feature $f_i$, $n_j$, µ, $u_j$, ${\sigma }_j$ represent the number of instances from class j, the mean feature value, the mean feature value on class j, the standard deviation of feature value on class j, respectively, the F-score of a feature fi can be determined as follows:

$$F{\_}_{score}\left(f_i\right)=\frac{{\sum }_j\frac{n_j}{c-1}{\left(u_j-u\right)}^2}{\frac{1}{n-c}{\sum }_j\left(n_j-1\right){\sigma }_j^2}$$

(2)

(C) Sparse Learning Based Methods

Sparse learning based methods is a group of embedded approaches. They aim at reducing the fitting errors along with some sparse regularization terms, which make feature coefficients small or equal to zero. To make a selection, corresponding features are discarded [14]. Feature selection algorithms belonging to this group have been recognized to produce good performance and interpretability. In this study, sparse learning based methods with the following sparse regularization terms: ℓ1-norm Regularizer (LS-121) [38] and ℓ2,1-norm Regularizer (LL-121) [39] were implemented.

(D) Information Theoretical Based Methods

Information theoretical-based methods apply some heuristic filter criteria in order to estimate the relevance of features. Some feature selection algorithms that belong to this family include Joint Mutual Information (JMI) and Mutual Information Maximization (MIM) or Information Gain. The JMI seeks to incorporate new unselected features that are complementary to existing features given the class labels in the feature selection process [14] while the MIM measures the importance of a feature by its correlation with the class labels. MIM assumes that features with strong correlations would achieve a good classification performance [14].

(E) Wrapper

Wrapper methods use a predefined learning algorithm, which acts like a black box to assess the importance measures of selected features based on their predictive performance. Two steps are involved in selecting features. First, a subset of features is searched and then selected features are evaluated repeatedly until the highest learning performance is reached. Features regarded as being relevant are the ones that yield the highest learning performance [14]. These two steps are implemented using the forward or backward selection strategies. In forward selection strategy, the search of relevant features starts with an empty set of features, then features are progressively added into larger subsets, whereas in backward elimination, it starts with the full set of features and then progressively eliminates the least relevant ones [40].

However, the implementation of wrapper methods is limited in practice for high-dimensional dataset due to the large size of the search space. Some examples of wrapper methods that were used in this study include decision tree forward (dt-f) [41] and Support vector machine backward (svm-b) [41].

2.4.2. Vegetation Indices Computation

In total, 75 vegetation indices (VI) derived from Sentinel-2 wavebands were computed using the online indices-database (IDB) developed by Henrich, et al. [19]. The IDB provides over 261 parametric and non-parametric indices that can be used for over 99 sensors and allows the viewing of all available VI for specific sensors and applications [19]. VI in this study were selected because of their usefulness for vegetation mapping and in order to increase the dimensionality of Sentinel-2 data.

2.4.3. Classification Algorithm: Random Forest (RF)

RF classifier was used to infer models from different selected features using the investigated feature selection methods. Random forest (RF) is a combination of decision tree classifiers where each classifier casts a single vote for the most frequent class to classify an input vector [42]. RF grows trees from random subsets drawn from the input dataset using methods such as bagging or bootstrap aggregation. Split of input dataset is typically performed using attribute selection measures (Information Gain, Gini-Index). Attribute selection measures are useful in maximizing dissimilarity between classes and therefore determine the best split selection in creating subsets [43]. In the process of a RF model training, the user defines the number of features at each node in order to generate a tree and the number of trees to be grown. The classification of a new dataset is done by passing down each case of the datasets to each of the grown trees, then the forest chooses a class having the most votes of the trees for that case [44]. More details on RF can be found in Breiman [45]. RF was chosen in this study, as it can efficiently handle large and highly dimensional datasets [46,47].

2.4.4. Model Assessment

To assess the classification accuracy of models on test datasets, estimated classes in different models developed in this study were cross-tabulated against the ground-sampled classes for corresponding pixels in a confusion matrix. The performance of developed models was assessed on test data sets using performance measures such as user’s (UA), and producer’s accuracies (PA) and f-score of Parthenium weed class. Supplementary information including PA, UA of other classes, and Kappa coefficient was added. The UA refers to the probability that a pixel labeled as a certain class on the map represents that class on the ground. PA represents pixels that belong to a ground-sampled class but fail to be classified into the correct class. F-score is the harmonic mean of UA and PA. F-score is typically used to assess accuracy per-class as it represents a true outcome for specific classes [23,25]. Kappa coefficient represents the extent to which classes on the ground are correct representations of classes on the map. Their formulae are as follows:

$$PA=\frac{TP}{TP+FN}$$

(3)

$$UA=\frac{TP}{TP+FP}$$

(4)

$$F=\frac{2\times PA\times UA}{PA+UA}$$

(5)

$$Kappacoefficient=\frac{P_o-P_e}{1-P_e}$$

(6)

where:

TP (true positive) represents the number of correctly labeled positive samples;

FP (false positive) represents to the number of negative samples that were incorrectly labeled as positive samples;

FN (false negative) represents the number of positive samples that were incorrectly labeled as negative samples;

P_o: relative observed agreement among classes;

P_e: hypothetical probability of chance agreement.

2.4.5. Software and Feature Selection

All investigated feature selection methods were applied on the three training datasets aforementioned using Scikit-feature library, a package of the Python (version 3.6) programming language. This library was developed by Li, et al. [14] and provides more than 40 feature selection algorithms. To obtain the f-score accuracy of selected features for each feature selection method, we first created a range of numbers that started from 1 to 85 (which is the total of variables) instead of specifying the number of selected features as prescribed by Li, et al. [14]. Each number in the range corresponded to the size of selected feature subsets. Then, for each dataset, a RF model was trained and evaluated on test dataset using selected feature subset through a loop iteration. RF was run in python (version 3.6) using the Sklearn library [48]. As RF was only used in this study for evaluating the performance of optimal variables selected by different feature selection methods, its hyperparameters were kept in default (e.g., number of trees in the forest equals to 10; criterion sets to “gini”). Default hyperparameters often yield excellent results [49]. Additionally, according to Du, et al. [50], larger number of trees do not influence classification results. This procedure was repeated ten times by reshuffling samples of training and test sets and the mean of f-score was computed for each select feature subset. This was to ensure the reliability of the results of investigated feature selection methods. The feature subset with the highest mean f-score was considered the most optimal. A code that automates the whole procedure including deriving VI, was written in Python (version 3.6).

3. Results

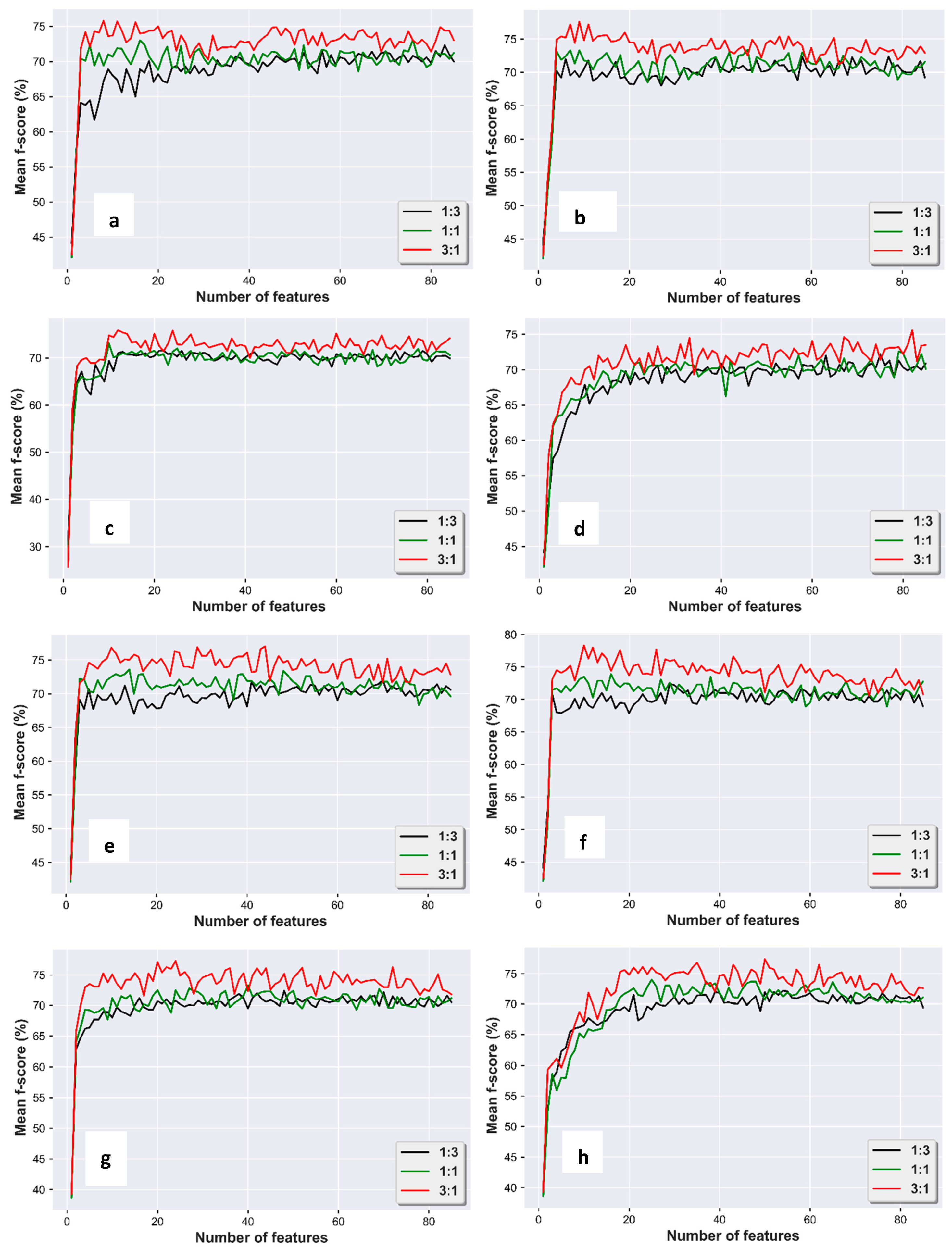
3.1. Comparison Among Investigated Features Algorithms

Figure 2 shows that the size of the feature subset and training and test sets determine the f-score accuracy of Parthenium weed using RF. In general, f-score increases with an increase in the size of feature subset until it reaches a plateau around 10 features, showing the insensitivity of RF in face of the noisy or redundant variables. However, it is noticeable that f-score accuracy of some feature selection methods such as Gini-index and ReliefF, which belong to the statistical-based feature selection methods, and LL-121 were found at smaller feature subsets. With respect to the size of the training set, f-score of Parthenium weed increased as the ratio between training and test got larger. As rule of thumb, this shows that when the ratio between training and test dataset is large (for example 3:1), a learning curve of higher F-score would be produced. Nevertheless, some feature selection methods such as svm-b, Gini-index and F-score seemed to yield similar f-score accuracies, regardless of the size of the dataset.

3.2. Comparison of Performance Between Peak Accuracy and Accuracy Derived From Full Feature Subsets

3.2.1. 1st Training Set

As per

Table 2. F-score, PA and UA of Parthenium weed using optimal feature subsets yielded by investigated feature selection methods for first training set.

Feature Selection Method	Peak Accuracy
	PA (%)	UA (%)	F-score (%)	Number of Features	*Comput. Time
Trace Ratio	74	69.8	71.6	56	0.58
ReliefF	74.5	70.1	72	6	1.05
Gini-Index	74.2	69.3	71.3	13	18.54
F-Score	74.9	69.5	72	63	0.25
LS_121	73.4	71.2	71.8	41	20.01
LL_121	75.2	70.2	72.4	29	0.37
JMI	74.8	69.6	71.9	38	38.58
MIM	74.4	70.1	72.0	39	39.45
SVM-B	74.7	71.1	72.5	26	0.50
DT-F	73.2	68.5	70.3	38	573.44
None	72.7	69.1	70.4	85	-

*Comput. Time (s): Computational time in seconds.

, all the investigated feature selection methods yielded similar f-score of Parthenium weed for optimal feature subset. F-score accuracies varied from 71% to 72%. Svm-b produced the highest f-score accuracy (72.5%). However, in terms of the size of optimal feature subset, Relief and Gini-index were the best in reducing dimensionality of full-dataset. The size of feature subsets was 6 and 13 respectively. F-score method was the lowest at this point of view. For this dataset, the ReliefF method can be recommended as its f-score is among the highest and the size of optimal feature subset among the smallest. Computational time and accuracies of other classes were also low and high, respectively, for ReliefF method (

Table 3. Classification accuracies of other classes using optimal feature subsets yielded by investigated feature selection methods for first training set.

	Forest		Water Body		Grassland		Settlements
*F.S.M	PA (%)	UA (%)	PA (%)	UA (%)	PA (%)	UA (%)	PA (%)	UA (%)	**Kappa Coef.
Trace Ratio	89.4	88.8	99	97	58.2	64.5	85.8	81.3	0.78
ReliefF	91.1	90	100	97.6	58.5	67.6	85.6	79	0.75
Gini-Index	90.8	90.4	99.2	95.4	57.9	64.5	85.4	82.4	0.74
F-Score LS_121	90.3	88.5	100	96.8	58.6	66.6	85.9	82.5	0.76
	91.8	88.8	100	96	55.8	62.8	85	81.7	0.75
LL_121	90.7	90.8	100	97.8	58.3	64.2	83.8	80.3	0.76
JMI	91.8	90.7	99.4	96.8	59.5	67.2	85.6	81.9	0.77
MIM	93.3	90.8	99.2	95	59.7	66.6	84.6	83.1	0.78
SVM-b	90.4	90.3	97.4	100	60	64.4	84.4	82.3	0.75
DT-F	91.8	89.1	100	96.8	58.7	64.8	83.3	80.8	0.73
None	91.4	89.7	100	97.4	58.8	66.2	87.1	81.8	0.78

*F.S.M.: Feature selection method; **Kappa Coef.: Kappa coefficient.

).

3.2.2. 2nd Training Set

As shown in

Table 4. F-score, PA and UA of Parthenium weed using optimal feature subsets yielded by investigated feature selection methods for the second training set.

Feature Selection Method	Peak Accuracy
	PA (%)	UA (%)	F-score (%)	Number of Features	Comput. Time (s)
Trace Ratio	77	70.3	73	16	0.60
ReliefF	77.1	69.6	73.1	4	2.14
Gini-Index	75.6	71.1	73.1	10	31.29
F-score	75.7	68.6	72	57	0.26
LS_121	76	68.7	71.9	41	20.12
LL_121	76.6	70	73.1	9	0.43
JMI	75.5	71.5	73.3	40	59.46
MIM	75.3	72.7	74.0	25	61.07
SVM-b	77.1	72	74.1	41	0.54
DT-F	78.3	69.6	73.3	39	934.08
None	75.9	69.7	72.6	85	-

, apart from LS_121 and F-score, all feature selection methods could reduce the number of features with higher f-score accuracy than the full dataset. As for the first dataset, Svm-b was the best performing feature selection method. Its PA, UA and f-score of Parthenium weed and Kappa coefficient (

Table 5. Classification accuracies of other classes using optimal feature subsets yielded by investigated feature selection methods for the second training set.

	Forest		Water Body		Grassland		Settlements
F.S.M	PA (%)	UA (%)	PA (%)	UA (%)	PA (%)	UA (%)	PA (%)	UA (%)	Kappa Coef.
Trace Ratio	91.6	90.2	99.2	95.2	61.3	72.8	86.7	81	0.76
ReliefF	89	91.2	98.5	97.6	61.6	68.9	85.6	81.4	0.78
Gini-Index	91.5	91.6	98.9	95.5	60.3	66.8	86.8	83.1	0.79
F-Score	90.4	92.2	100	96.4	63.5	71.8	87.7	84.1	0.79
LS_121	90.7	91.4	98.8	95	59.9	69	86.5	81.7	0.78
LL_121	90.2	91.4	98.8	96.7	60.6	68.8	85.1	80.7	0.80
JMI	91.9	91	98.8	96.1	62.3	70.3	88	82.1	0.77
MIM	90	91.8	98.9	95.5	64.8	69.1	86.6	82.9	0.82
SVM-b	91.4	92.8	100	97	64	70.7	86.9	82.7	0.83
DT-F	91.0	86.0	100	96	60	68	83.3	80.8	78.1
None	87.2	82.5	99.7	97.3	62.2	68.6	87.2	82.5	0.79

) were the highest. ReliefF selected the least number (4) of optimal features and was among the highest top performing feature selection methods after svm_b in terms of f-score and PA of Parthenium weed. It was followed by Gini-index, LL_121 with respect to f-score and size of feature subsets. Once more, F-score method turned out to perform poorly because of a large number of selected features and no improvement of f-score accuracy of the Parthenium weed.

3.2.3. Third Training Set

Table 6. F-score, PA and UA of Parthenium weed using optimal feature subsets yielded by investigated feature selection methods for third training set.

Feature Selection Method	Peak Accuracy
	PA (%)	UA (%)	F-score (%)	Number of Features	Comput. Time (s)
Trace Ratio	77.2	74.5	75.7	11	0.70
Relief	80	75	77.2	7	3.56
Gini-Index	78.5	74.2	75.9	12	43.97
F-Score	78.5	73.6	75.6	82	0.30
LS_121	78.6	76.1	76.8	10	20.64
LL_12 1	79.2	78.2	78.3	10	2.20
MIM	76.9	72.6	74.1	50	87.71
SVM-b	82.3	75	78.1	33	0.54
DT-F	76.6	72.4	74.1	26	1346.43
None	75.2	71.4	72.6	85	-

shows that LL_121 and ReliefF, respectively were among the feature selection methods that selected a small subset of features with high f-score of Parthenium weed, with PA and UA accuracies above 3% difference from the full dataset. ReliefF, for example, yielded 77.2% of f-score, 80% of PA and 75% of UA with only 7 optimal features. Full dataset yielded 72.6% of f-score, 75.2% of PA and 71.4% of UA without any feature selection method applied. Svm_b outperformed all the feature selection methods with the highest PA (82.3%) and f-score of Parthenium weed (78.1%), and kappa coefficient (0.83) (

Table 7. Classification accuracies of other classes using optimal feature subsets yielded by investigated feature selection methods for third training set.

	Forest		Water Body		Grassland		Settlements
F.S.M	PA (%)	UA (%)	PA (%)	UA (%)	PA (%)	UA (%)	PA (%)	UA (%)	Kappa Coef.
Trace Ratio	93.5	81	98.5	81	61.8	81	88.3	81	0.75
ReliefF	92	81.4	100	81.4	66.2	81.4	89.9	81.4	0.77
Gini-Index	92.1	83.1	99.5	83.1	64	83.1	86.3	83.1	0.78
F-Score	92.2	95.2	99.5	98	64.4	71.2	91.4	84.4	0.79
LS_121	92.5	81.7	99.5	81.7	62.9	81.7	89	81.7	0.82
LL_121	92.3	68.8	98.5	68.8	63.4	68.8	90	68.8	0.77
JMI	90.6	82.1	99.5	82.1	68.4	82.1	90.9	82.1	0.80
MIM	76.9	72.6	99	82.9	63.7	82.9	84.8	82.9	0.75
SVM-b	91.6	82.7	99.5	82.7	67.2	82.7	89.7	82.7	0.83
DT-F	93.1	73	100	73	63.7	73	87.9	73	0.82
None	90.8	82.5	100	82.5	64.3	82.5	89.1	82.5	0.74

). However, the number of optimal features selected was quite large (33). As for previous datasets, the performance of F-score method was the worst with the lowest PA (78.5%), UA (73.6%) and f-score (75.6%) of Parthenium weed and largest feature subset (82).

Figure 3 illustrates the spatial distribution of Parthenium weed and surrounding land-cover using full dataset and optimal features from ReliefF.

4. Discussion

This study sought to compare ten feature selection algorithms with two of those belonging to the following feature selection method groups: Similarity based feature selection methods, Statistical-based feature selection methods, sparse learning based methods, Information theoretical based methods and Wrapper methods. These feature selection algorithms were applied on Sentinel-2 spectral bands combined with 75 vegetation indices for mapping a landscape infested by Parthenium weed. The comparison was based on the f-score of Parthenium weed using Random forest (RF). We also tested the effect of training and test sets sizes on the performance of the investigated feature selection algorithm.

4.1. Comparison of Feature Selection Methods

The results showed that feature selection algorithms could reduce the dimensionality of Sentinel-2 spectral bands combined with vegetation indices. The algorithms could increase classification accuracies of Parthenium weed using the random forest classifier by up to 4%, depending on the adopted feature selection method and size of the dataset. Previous studies found similar results [34,51]. For example, Colkesen and Kavzoglu [34] who applied filter-based feature selection algorithms and three machine learning techniques on WorldView-2 image for determining the most effective object features in object-based image analysis achieved a significant improvement (about 4%) by applying feature selection methods. Overall, ReliefF was the best performing feature selection method because it could bring down the number of features from 85 to 6, 4 and 7 on the first, second and third dataset respectively. Its f-score, PA and UA accuracies for Parthenium weed were also among the highest (Table 2, for example). According to Vergara and Estévez [52], the purpose of feature selection is to determine the smallest feature subset that can produce the minimum classification error. This finding concurs with studies that endeavored to compare ReliefF with other feature selection methods. For example, Kira and Rendell [53] found that subset of features selected by ReliefF tend to be small compared to other feature selection methods as only statistically relevant features are retained during the selection process. Studies that compared ReliefF with other feature selection methods reported that mapping accuracy with selected features from ReliefF was similar to the best feature selection methods [34,54]. However, our findings are opposed to [34] who found that ReliefF selected the highest number of features in comparison with Chi -square and information gain algorithms, but slightly lower classification accuracies than information gain using random forest, support vector machines and neural network. We suggest that repeated classifications on reshuffled training and test data should be investigated to confirm their findings. In terms of f-score, PA and UA of Parthenium weed, svm-b, which belongs to the wrapper group outperformed all the feature selection methods for the three datasets (Table 2, Table 4 and Table 6). Although computationally expensive, several authors have noted that wrappers outperform filter methods [55,56,57]. However, in this study svm-b was found to be less computational intense than some of filter methods (Table 2, Table 4 and Table 6). F-score method did not perform well for mapping Parthenium weed because of low accuracies and large subset of selected features. To the best of our knowledge, its use is very limited in earth observation related studies. Further investigations are therefore necessary. Concerning investigated feature selection groups, not a single group performed well on all the datasets. This supports the recommendation that there is no universal ‘best’ method for all the learning tasks [58].

4.2. Impact of Training Sizes on Feature Selection Performance

The results show that the performance of feature selection algorithm depends on the ratio between the training and test dataset. It can be noticed that smaller difference of f-score accuracies of Parthenium weed between optimal features and full dataset were obtained when the ratio between training and test was 1:3 or 1:1 (Table 2 and Table 3). In consistency with Jain and Zongker [59], a small sample size and a large number of features impair the performance of feature selection methods due to the curse of dimensionality. All the investigated feature selection algorithms positively influenced f-score accuracies of dataset when the ratio between training and test was large (1:3 or 70% training and 30% test) (Table 6). This concurs with reference [51], who demonstrated that the higher the training size was, the better the classification accuracy. They also highlighted the necessity of selecting the appropriate feature selection for improving classification accuracies. In this study, we found that some feature selection algorithms such as Gini-index and F-score, which belong to the Statistical-based Feature selection methods, and svm-b did not seem to be affected by the curse of dimensionality (Figure 2). We did not come across studies showing this finding, hence further investigations should be carried out for corroboration.

4.3. Implications of Findings in Parthenium Weed Management

On invaded landscapes, Parthenium weed expands more rapidly than native plants [60]. Spectral bands alone are not enough to achieve reliable mapping accuracies [61]. Increasing data dimensionality by combining, among others, Sentinel-2 image bands, vegetation indices and other variable types and applying an appropriate feature selection approach, higher Pathenium mapping accuracy can be achieved. This study provides a guidance on how newly developed feature selection methods based on Li, et al. [17]‘s classification should be used to reduce the dimension of high temporal resolution imagery such as Sentinel-2 in mapping Parthenium weed. Accurate spatial distribution of Pathenium weed would enhance the decision-making for appropriate mitigation measures.

5. Conclusions

The following conclusions can be drawn from the findings:

(1)

Wrappers methods such as svm-b yield higher accuracies on classifying Parthenium weed using the Random forest classifier;

(2)

ReliefF was the best performing feature selection method in terms of f-score and the size of optimal features selected;

(3)

To achieve better performance with feature selection methods, the ratio of 3:1 between the training and test set size turned out to be better than ratios of 1.1 and 1:3;

(4)

Gini-index, F-score and svm-b, were slightly affected by the curse of dimensionality;

(5)

None of feature selection method groups seemed to perform the best for all the datasets.

The findings of this study are critical for reducing the computational complexity of processing large volume of Sentinel-2 image data. With the advent of Sentienl-2A and B, an increased volume of data is available, necessitating feature selection. This offers possibilities to derive useful information from them, hence accurate classification maps of Parthenium weed. Further research should look at comparing other feature selection methods with different classifiers. Moreover, a combination of feature selection methods such ReliefF and svm-b should be considered, as they select a small number of features and yield a high f-score accuracy, respectively.