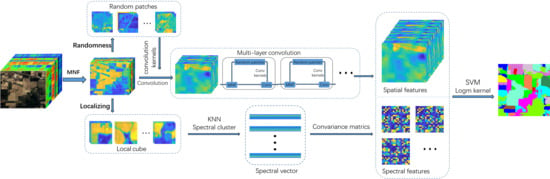
1. Introduction
There are more and more remote sensing applications based on hyperspectral images (HSIs). The latest hyperspectral sensors can obtain hundreds of spectral channel data points in high spatial resolution [
1]. Rich spectral‒spatial information is widely used in HSIs for scene recognition [
2], regional variation of urban areas [
3], and classification of features [
4,
5,
6]. Classification of HSIs for ground objects can be widely used in precision agriculture [
7], urban mapping [
8], and environmental monitoring [
9]. As such, classification has attracted much attention, and a wide variety of methods have been developed. HSI classification uses a small number of manual tags to indicate the category label of each pixel [
10]. Like other classification applications, there are significant challenges involved in HSIs classification tasks, such as the well-known Hough phenomenon [
11]. If the label data are very limited, more spectral data will reduce the accuracy of classification [
12].
In order to overcome this problem, a large number of studies [
13,
14] have proposed many effective methods. These methods include dimensionality reduction (DR) [
15,
16] and band selection [
17,
18]. Hyperspectral dimensionality reduction has both supervised and unsupervised methods [
19]. The difference is in whether the two use annotation information—for example, locally linear embedding [
20], principal component analysis (PCA), and the maximum noise fraction (MNF) [
21]. Jiang et al. [
22] proposed a multi-scale PCA method based on superpixel segmentation, called superPCA, which uses principal component analysis in different regions. The supervised approach uses sample categories to achieve data dimensionality reduction through learning metrics that are closer to the same category of data [
23,
24]: for example, linear discriminant analysis and local discriminant embedding (LDE) [
25]. Unlike PCA, which maximizes the variation in the projected sample, MNF can reduce the dimensionality and noise of image data more efficiently by maximizing the signal-to-noise ratio of the sample. Simultaneously, in many fields, such as image classification [
26], face recognition [
27], HSI scene classification [
28], and pixel classification [
29], these applications obtain features between samples by calculating a covariance matrix (CM) method. This is because the covariance matrix can effectively express the correlation between hyperspectral bands. Using the concept of CM, these methods [
28,
29] have achieved good results.
With the development of computer vision, spatial features are playing an increasingly pivotal role in HSI classification [
30]. Many classic feature extraction methods have been developed, such as the gray level co-occurrence matrix [
31], wavelet texture [
32], and Gabor texture features [
33]. To extract the spatial information from HSIs for their classification, Benediktsson et al. [
34] uses morphological opening and closing to extract the spatial features of HSIs. In reference [
35], there is a more efficient and automated approach based on this. Afterwards, references [
36,
37] and many other scholars have conducted relevant research on the same topics. However, the above features are traditional handcrafted features that are generally applicable to specific scenarios; the algorithm is not robust enough when the task environment that needs to be processed is complex. This means that the algorithm parameters can only be targeted to specific scenes and only shallow features are obtained, such as shapes and textures. When the terrain of the study area changes drastically, it is difficult to apply them to the entire scene [
38].
Recently, in order to improve classification performance, many HIS classification methods based on spectral-spatial features have been proposed. There are several ways to apply spatial information, such as joint sparse models [
39] and Markov random fields (MRF) [
40]. In reference [
39], a spectral–spatial feature learning method based on the group sparse coding (GSC) for the HSI classification is proposed, which incorporates spatial neighborhood correlations information via clusters, each of which is an adaptive spatial partition of pixels. In addition, they also develop kernel GSC to capture nonlinear relationships that can achieve a group sparse representation in the kernel space where data become more separate. Zhang et al. [
40] propose a novel method that could obtain the semantic representation of each pixel with more detailed information and less noise for HSI classification. First, different types of features on different feature spaces are mapped to the same semantic space via a probabilistic support vector machine (SVM) classifier. Then, various semantic representations and local spatial information are integrated into the MRF model. Both of these methods achieve efficient fusion of spectral spatial features, learn a representative subspace from the spectral and spatial domains, and produce good classification performance.
However, most of the traditional spectral and spectral–spatial classifiers do not classify the hyperspectral data in a deep manner [
41]. Artificial intelligence technology has led to the development of new deep neural networks [
42,
43] and has been widely used in the field of image processing, with the performance greatly exceeding that of traditional methods. Compared with handcrafted features, deep neural networks can obtain deeper features and are robust for classification or segmentation tasks. Unlike shallow handcrafted features, deep learning features are derived from the intrinsic, more abstract information of the image, which can well represent local variation in the image. Long et al. [
44] proposes FCN, which is the first pixel-by-pixel prediction segmentation framework for end-to-end training. Badrinarayanan et al. [
45] proposed the earliest semantic segmentation framework for encoding and decoding modes, called SegNet. Both promoted the application of deep learning in image classification and semantic segmentation.
In the field of HSIs classification, Chen et al. [
46] constructed a stacked autoencoder (SAE) deep learning framework for HSIs classification. The SAE can extract the depth features, but the input data must be one-dimensional and the spatial information is lost. Chen et al. [
47] used a 2D convolutional neural network (CNN) to identify vehicles in high-resolution remote sensing images. Unlike Chen et al. [
46], Zhao and Du [
48] first performed data dimensionality reduction based on balanced local discriminant, and then classified HSIs using pixel-level CNN via spectral-spatial features. Considering the limited hyperspectral image training data, it may not be appropriate to directly apply the image segmentation or classification framework based on deep learning in the field of computer vision. Zhu et al. [
41] proposed two generative adversarial network (GAN) frameworks for HSI classification. The first one, called the 1D-GAN, is based on spectral vectors and the second one, called the 3D-GAN, combines the spectral and spatial features. These two architectures demonstrated excellent abilities in feature extraction and the classification results showed that the GANs are superior to traditional CNNs even under the condition of limited training samples. In [
49], Xu et al. proposed RPNet, which does not require training and backward propagation, and used a multi-layer convolution feature to achieve good results for HSI classification. It can be seen that there are some flaws in these works. First, it is very time consuming to apply deep learning directly [
46,
47,
48] in the field of computer vision. The authors of references [
46,
47,
48], only use the deepest features. Third, some abovementioned works overlooked or did not make full use of the band information of hyperspectral images, which is the most valuable information that can be obtained from hyperspectral images.
Therefore, to tackle the above problems faced during hyperspectral images classification, inspired by reference [
29] and reference [
49], we tested a novel hyperspectral image classification model using random patches convolution and local covariance (RPCC). Our proposed method combines all spectral correlation information and multi-scale convolution features, which makes it highly discriminative for HSIs classification. In our RPCC, first, spectral features are extracted based on the maximum noise fraction method [
21] and covariance matrix (CM) representation [
29]. However, CM is on the Manifold space and does not apply to the calculation of Euclidean space. So the CMs are converted to Euclidean space for the next step. Second, we randomly generate image patches from the original hyperspectral image as a convolution kernel by random projection. This uses each convolution kernel to perform multi-layer convolution on the image. Then the obtained multi-scale spatial information and spectral covariance matrix are merged into spectral-spatial features. Finally, we use the SVM classifier and fused spectral–spatial features to identify the class label.
Our work makes the following three contributions:
For the first time, we introduce a RPCC method combining random patches convolution and covariance matrix representation into hyperspectral image classification. RPCC has a simple structure, and the experiments show that its performance can match the state of the art.
Our RPCC is able to extract highly discriminative features, and combines both multi-scale multi-layer convolution information and the correlation between different spectral bands without any training.
We verified that the applicability of the randomness and localizing in our method is a kind of regularization pattern that has great potential to overcome the salt-and-pepper noise and over-smoothing phenomena in HSIs processing.
Our article is organized as follows. In
Section 2, we introduce the proposed method RPCC in detail.
Section 3 introduces the relevant experiments, and the results show the excellent performance of RPCC in three experiments.
Section 4 and
Section 5 provide a discussion and conclusions, respectively.
4. Discussion
In
Figure 11,
Figure 12 and
Figure 13 and
Table 5,
Table 6 and
Table 7, a comparison with the other seven methods of the Indian Pine, Pavia University, and the KSC data-set shows that the proposed RPCC method can obtain better visual effects and higher accuracy. This proves the validity of the spectral spatial‒feature extraction pattern in our method. There are three reasons for this. First, we perform spectral clustering on each pixel neighborhood region and then calculate the spectral covariance matrix of the extracted pixels, so that we obtain spectral correlation information for all regions of the entire image. Second, the random-patch convolution can extract shallow and deep features, allowing both multi-scale and multi-layer spatial features to be combined. Third, the randomness and localization in RPCC are a kind of regularization pattern that has great potential to overcome the pepper noise and over-smoothing phenomena in HSIs processing. Through the above classification results and quantitative evaluation, our method can be a novel and effective spectral‒spatial classification framework.
In the field of machine learning, it is difficult to achieve the desired performance with single features and single models. An important method is to integrate. Typical fusion methods are early fusion and late fusion. Early fusion is a feature-level fusion that concatenates different features and puts them into a model for training. For example, these spectral-spatial classification methods in [
39,
40] and our RPCC are early fusion methods. Late fusion refers to the fusion of the score level. The practice is to train multiple models. Each model will have a prediction score, and the results of all models will be fused to obtain the final prediction results. Here, we have designed two late fusion methods as variants of RPCC. One is RPCC-LPR, which shares the same process as RPCC except that it uses SVM with linear, polynomial, and radial basis functions. Another is S-LPR-S-LPR, which uses SVM with linear, polynomial and radial basis functions to classify spatial and spectral features. Both methods use the majority vote method to obtain the final classification result with default parameters.
Table 8 shows the classification accuracy of the three methods. It can be seen that the two simple fusion strategies do not improve the classification accuracy. On the one hand, it may be that the two methods require more complicated parameter adjustments to achieve the best results. On the other hand, since the most suitable kernel functions may be different for different features, perhaps the multiple kernel learning (MKL) method is more suitable for spectral‒spatial feature fusion. By adopting different kernels for different features, multiple kernels are formed for different parameters. Then we can train the weight of each kernel and learn the best combination of kernel functions for classification. In short, our method is very suitable as a simple baseline method based on spectral‒spatial feature classification, but there is still much room for improvement.
The computation time of the algorithm has a significant impact on various remote sensing applications.
Table 9 summarizes the computational time required by the SMLR-SpTV, Gabor-based, EMAP, LCMR, RPNet, and RPCC methods. Based on the overall performance of each method in the three experiments, the SMLR-SpTV and Gabor-based methods are the slowest. This is due to the fact that the SMLR-SpTV method trained samples in 10 Monte Carlo runs and the high-dimensional features of each pixel extracted by Gabor-based methods reduce its efficiency; both of these are very time-consuming processes. The RPNet method is clearly the fastest. Compared with the CMR and EMAP methods, our proposed RPCC runs faster for two data-sets, since the efficient random convolution and simplified covariance representation operations are adopted when extracting spatial–spectral features. Our RPCC method is more time-consuming than the RPNet method for all three data sets, this is because the RPCC is subject to the construction of covariance features. This process takes up two-thirds of the total runtime of the method. Since our algorithm is a two-branch structure, spectral and spatial features can be calculated in parallel. Therefore, we can further improve the efficiency of our algorithm.
To summarize, by comparing the above algorithms on three experiments, it was shown that the RPCC method is able to extract highly discriminative features by combining both multi-scale, multi-layer convolution information and correlations between different spectral bands in the classification. The RPCC can be a competitive and robust approach for hyperspectral image classification. Specifically, our experiments show that randomness and local clustering are reliable techniques and have great potential to overcome the pepper noise and over-smoothing phenomena in HSI classification.