Relative Importance of Binocular Disparity and Motion Parallax for Depth Estimation: A Computer Vision Approach
Abstract
:1. Introduction
2. Methods
2.1. Depth Estimation Using Stereo Cameras
- Undistortion: In this first step, radial and tangential lens distortions are removed mathematically. The outputs of this step are undistorted images.
- Rectification: This is the process of adjusting the angles and the distances between cameras to get a frontal parallel arrangement. This process is a crucial step in any stereo imaging algorithm. The outputs of this step are rectified and row-aligned images.
- Correspondence: This is the process of finding common features in the left and right camera views. The output of this process is a disparity map, where the disparities are the differences in x-coordinates on the image plane.
- Triangulation: In this process, the disparity map is converted to distances using the known geometric arrangement of the cameras. The output of this process is a depth map.
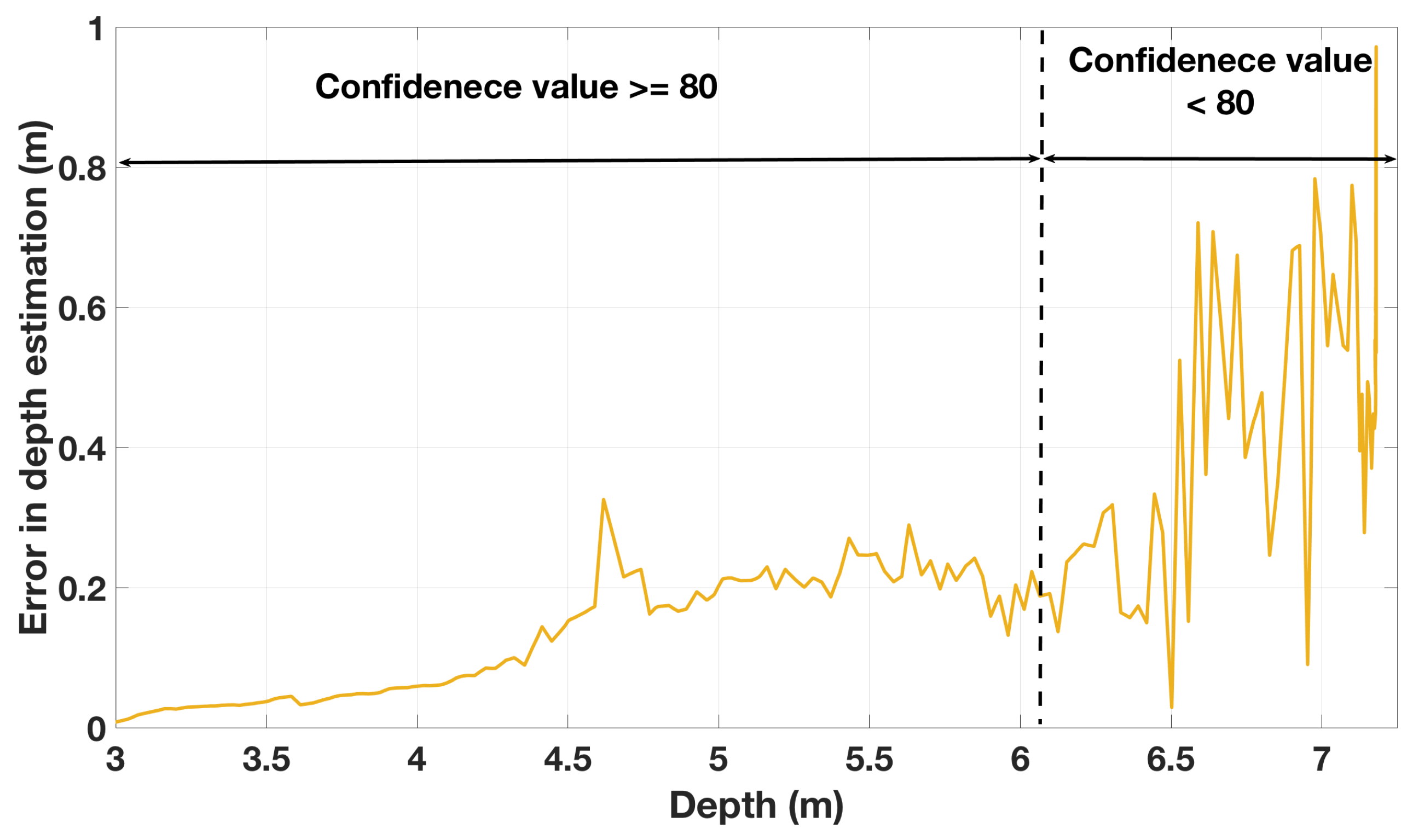
The Accuracy of the Estimated Depth Using a Stereo Camera
- The error of the estimated depth is proportional to the error of the computed disparity.
- The error of the estimated depth is proportional to the depth squared.
- The accuracy can be improved if the baseline is increased. However, in this case, the overlapping between cameras decreases, affecting the field of view at short distances.
2.2. Depth Estimation Using a Monocular Camera
Problem Formulation
2.3. Hardware Description
2.3.1. Hokuyo UTM-30LX
2.3.2. NVIDIA Jetson TX2 Development Kit
2.3.3. ZED Stereo Camera
2.4. Data Processing
- Angular and linear velocities measured by the IMU and odometer.
- Distance values from the Hokuyo LiDAR.
- Rectified RGB images from the left ZED camera.
- The depth map computed with respect to the center of the left camera using ZED SDK and CUDA toolkit.
2.4.1. Feature Point Ranging
2.4.2. Object Detection and Tracking
2.4.3. Stereo Computation
2.4.4. Monocular Computation
3. Results
4. Discussion
5. Conclusions
- The image points in successive frames are tracked as a part of the state vector and camera noises will be presented by a measurement error. By doing so, we have the ability to estimate them more accurately and decrease the error in the disparity between the image points recursively in the successive frames.
- It is a multiview-based approach. It means that the baseline is increased from frame to frame in a dynamic way due to the camera motion. It leads to increasing the baseline–depth ratio, making depth estimation more accurate.
- The proposed approach does not depend, as in plain stereo vision, on how far the object is. Instead, it depends on how wider the triangulation angle between the first view and the last view is.
Author Contributions
Funding
Conflicts of Interest
References
- Landy, M.S.; Maloney, L.T.; Johnston, E.B.; Young, M. Measurement and modeling of depth cue combination: In defense of weak fusion. Vis. Res. 1995, 35, 389–412. [Google Scholar] [CrossRef]
- Smolyanskiy, N.; Kamenev, A.; Birchfield, S. On the importance of stereo for accurate depth estimation: An efficient semi-supervised deep neural network approach. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1007–1015. [Google Scholar]
- Saxena, A.; Schulte, J.; Ng, A.Y. Depth Estimation Using Monocular and Stereo Cues. In Proceedings of the 20th International Joint Conference on Artificial Intelligence, Hyderabad, India, 6–12 January 2007; Volume 7, pp. 2197–2203. [Google Scholar]
- Bradshaw, M.F.; Rogers, B.J. The interaction of binocular disparity and motion parallax in the computation of depth. Vis. Res. 1996, 36, 3457–3468. [Google Scholar] [CrossRef]
- Durgin, F.H.; Proffitt, D.R.; Olson, T.J.; Reinke, K.S. Comparing depth from motion with depth from binocular disparity. J. Exp. Psychol. Hum. Percept. Perform. 1995, 21, 679. [Google Scholar] [CrossRef] [PubMed]
- Ono, H.; Wade, N.J. Depth and motion perceptions produced by motion parallax. Teach. Psychol. 2006, 33, 199–202. [Google Scholar]
- McKee, S.P.; Taylor, D.G. The precision of binocular and monocular depth judgments in natural settings. J. Vis. 2010, 10, 5. [Google Scholar] [CrossRef] [PubMed]
- Sousa, R.; Brenner, E.; Smeets, J. A new binocular cue for absolute distance: Disparity relative to the most distant structure. Vis. Res. 2010, 50, 1786–1792. [Google Scholar] [CrossRef] [Green Version]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Lazaros, N.; Sirakoulis, G.C.; Gasteratos, A. Review of stereo vision algorithms: From software to hardware. Int. J. Optomechatron. 2008, 2, 435–462. [Google Scholar] [CrossRef]
- Hamzah, R.A.; Ibrahim, H. Literature survey on stereo vision disparity map algorithms. J. Sens. 2016, 2016, 8742920. [Google Scholar] [CrossRef]
- Vishnyakov, B.V.; Vizilter, Y.V.; Knyaz, V.A.; Malin, I.K.; Vygolov, O.V.; Zheltov, S.Y. Stereo sequences analysis for dynamic scene understanding in a driver assistance system. In Proceedings of the Automated Visual Inspection and Machine Vision, Munich, Germany, 21–25 June 2015; Volume 9530. [Google Scholar]
- Wu, B.; Zhang, Y.; Zhu, Q. A triangulation-based hierarchical image matching method for wide-baseline images. Photogramm. Eng. Remote Sens. 2011, 77, 695–708. [Google Scholar] [CrossRef]
- Milella, A.; Reina, G. 3D reconstruction and classification of natural environments by an autonomous vehicle using multi-baseline stereo. Intell. Serv. Robot. 2014, 7, 79–92. [Google Scholar] [CrossRef]
- Tippetts, B.; Lee, D.J.; Lillywhite, K.; Archibald, J. Review of stereo vision algorithms and their suitability for resource-limited systems. J. Real-Time Image Process. 2016, 11, 5–25. [Google Scholar] [CrossRef]
- Kytö, M.; Nuutinen, M.; Oittinen, P. Method for measuring stereo camera depth accuracy based on stereoscopic vision. In Proceedings of the SPIE Three-Dimensional Imaging, Interaction, and Measurement Conference, San-Francisco, CA, USA, 24–27 January 2011; p. 7864. [Google Scholar]
- Sabattini, L.; Levratti, A.; Venturi, F.; Amplo, E.; Fantuzzi, C.; Secchi, C. Experimental comparison of 3D vision sensors for mobile robot localization for industrial application: Stereo-camera and RGB-D sensor. In Proceedings of the 2012 12th International Conference on Control Automation Robotics & Vision (ICARCV), Guangzhou, China, 5–7 December 2012; pp. 823–828. [Google Scholar]
- Ortiz, L.E.; Cabrera, E.V.; Gonçalves, L.M. Depth Data Error Modeling of the ZED 3D Vision Sensor from Stereolabs. Electron. Lett. Comput. Vis. Image Anal. 2018, 17, 1–15. [Google Scholar] [CrossRef]
- Hanes, D.A.; Keller, J.; McCollum, G. Motion parallax contribution to perception of self-motion and depth. Biol. Cybern. 2008, 98, 273–293. [Google Scholar] [CrossRef] [PubMed]
- Holmin, J.; Nawrot, M. Motion parallax thresholds for unambiguous depth perception. Vis. Res. 2015, 115, 40–47. [Google Scholar] [CrossRef] [PubMed]
- Regan, D.; Beverley, K.; Cynader, M. The visual perception of motion in depth. Sci. Am. 1979, 241, 136–151. [Google Scholar] [CrossRef] [PubMed]
- Gordon, D.A. Static and dynamic visual fields in human space perception. J. Opt. Soc. Am. 1965, 55, 1296–1303. [Google Scholar] [CrossRef] [PubMed]
- Gibson, J.J. The Ecological Approach to Visual Perception: Classic Edition; Psychology Press: Abingdon, UK, 2014. [Google Scholar]
- Gibson, J.J. The Perception of the Visual World; Houghton Mifflin: Boston, MA, USA, 1950. [Google Scholar]
- Grabe, V.; Bulthoff, H.H.; Giordano, P.R. A comparison of scale estimation schemes for a quadrotor UAV based on optical flow and IMU measurements. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 5193–5200. [Google Scholar]
- Schmid, S.; Fritsch, D. Precision analysis of triangulations using forward-facing vehicle-mounted cameras for augmented reality applications. In Proceedings of the Videometrics, Range Imaging, and Applications XIV, Munich, Germany, 26–27 June 2017; Volume 10332. [Google Scholar]
- Davidson, P.; Raunio, J.P.; Piché, R. Monocular vision-based range estimation supported by proprioceptive motion. Gyroscopy Navig. 2017, 8, 150–158. [Google Scholar] [CrossRef]
- Mansour, M.; Davidson, P.; Stepanov, O.; Aref, M.; Raunio, J.P.; Piché, R. Depth estimation with egomotion assisted monocular camera. Gyroscopy Navig. 2019, 10, 111–123. [Google Scholar]
- Oshman, Y.; Davidson, P. Optimal observer trajectories for passive target localization using bearing-only measurements. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San-Diego, CA, USA, 29–31 July 1996; p. 3740. [Google Scholar]
- Oshman, Y.; Davidson, P. Optimization of observer trajectories for bearings-only target localization. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 892–902. [Google Scholar] [CrossRef]
- Kaehler, A.; Bradski, G. Learning OpenCV 3: Computer Vision in C++ with the OpenCV Library; O’Reilly Media Inc.: Sebastopol, CA, USA, 2016. [Google Scholar]
- Corke, P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB®; Springer-Verlag: Berlin/Heidelberg, Germany, 2011; Volume 73, pp. 329–340. [Google Scholar]
- Longuet-Higgins, H.C.; Prazdny, K. The interpretation of a moving retinal image. Proc. R. Soc. Lond. B 1980, 208, 385–397. [Google Scholar]
- Davidson, P.; Mansour, M.; Stepanov, O.; Piché, R. Depth estimation from motion parallax: Experimental evaluation. In Proceedings of the 2019 26th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), St. Petersburg, Russia, 27–29 May 2019. [Google Scholar]
- Cooper, M.A.; Raquet, J.F.; Patton, R. Range Information Characterization of the Hokuyo UST-20LX LiDAR Sensor. Photonics 2018, 5, 12. [Google Scholar] [CrossRef]












© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mansour, M.; Davidson, P.; Stepanov, O.; Piché, R. Relative Importance of Binocular Disparity and Motion Parallax for Depth Estimation: A Computer Vision Approach. Remote Sens. 2019, 11, 1990. https://doi.org/10.3390/rs11171990
Mansour M, Davidson P, Stepanov O, Piché R. Relative Importance of Binocular Disparity and Motion Parallax for Depth Estimation: A Computer Vision Approach. Remote Sensing. 2019; 11(17):1990. https://doi.org/10.3390/rs11171990
Chicago/Turabian StyleMansour, Mostafa, Pavel Davidson, Oleg Stepanov, and Robert Piché. 2019. "Relative Importance of Binocular Disparity and Motion Parallax for Depth Estimation: A Computer Vision Approach" Remote Sensing 11, no. 17: 1990. https://doi.org/10.3390/rs11171990
APA StyleMansour, M., Davidson, P., Stepanov, O., & Piché, R. (2019). Relative Importance of Binocular Disparity and Motion Parallax for Depth Estimation: A Computer Vision Approach. Remote Sensing, 11(17), 1990. https://doi.org/10.3390/rs11171990







