Evaluating the Drought-Monitoring Utility of Four Satellite-Based Quantitative Precipitation Estimation Products at Global Scale
Abstract
1. Introduction
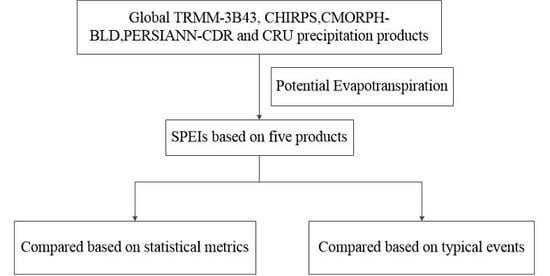
2. Materials and Methods
2.1. Data Used in This Study
2.1.1. Reference Data
2.1.2. Satellite-Based Data
2.1.3. Potential Evapotranspiration Data
2.2. The Standardized Precipitation Evapotranspiration Index (SPEI)
2.3. Statistical Metrics
3. Results
3.1. Comparison of the Accuracy of the Precipitation of Quantitative Precipitation Estimation (QPE) Products Versus Reference Data
3.2. Comparison of the Grid SPEI Estimates from the QPE Products and References
3.3. Analysis of SPEI-Based Drought Events
3.4. Studies of Several Specific Drought Events
4. Discussion
4.1. Precipitation Accuracy Comparison of the Four QPE Products
4.2. Drought Monitoring Utility of the Four QPE Products
5. Conclusions
- (1)
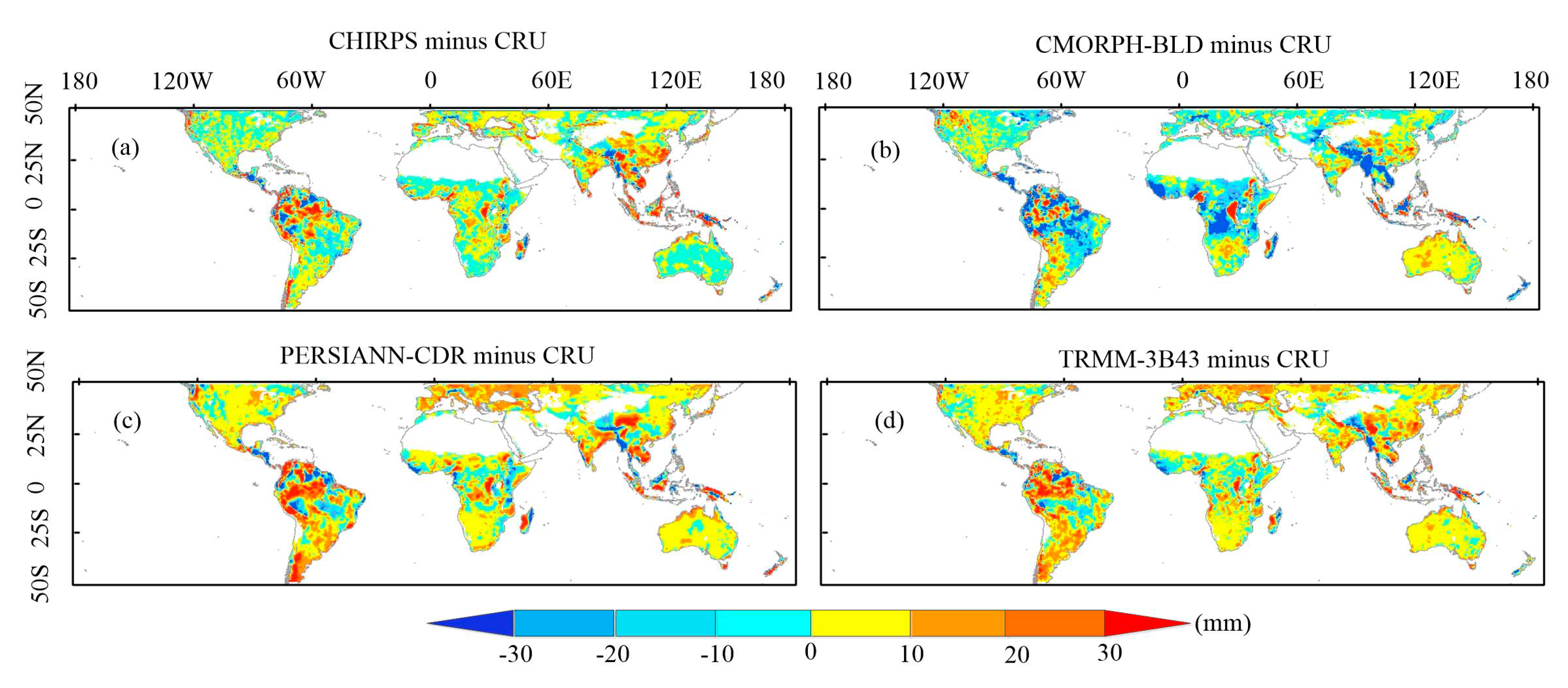
- PERSIANN-CDR and TRMM-3B43 overestimated precipitation more and CHIRPS underestimated precipitation more for most regions. Severe discrepancies for the above three QPE products against CRU gauge observations are clearly distributed in Southeast Asia, Central Africa, and Amazonia; however, the CMORPH-BLD product had the opposite performance. On the basis of the CC and RMSE, the worst CC and RMSE occurred in the regions above; generally, CHIRPS had the best performance in Europe, Oceania and Africa; the PERSIANN-CDR had the best performance in North America, South America and Asia; the CMORPH-BLD had the worst statistical indices in all continents.
- (2)
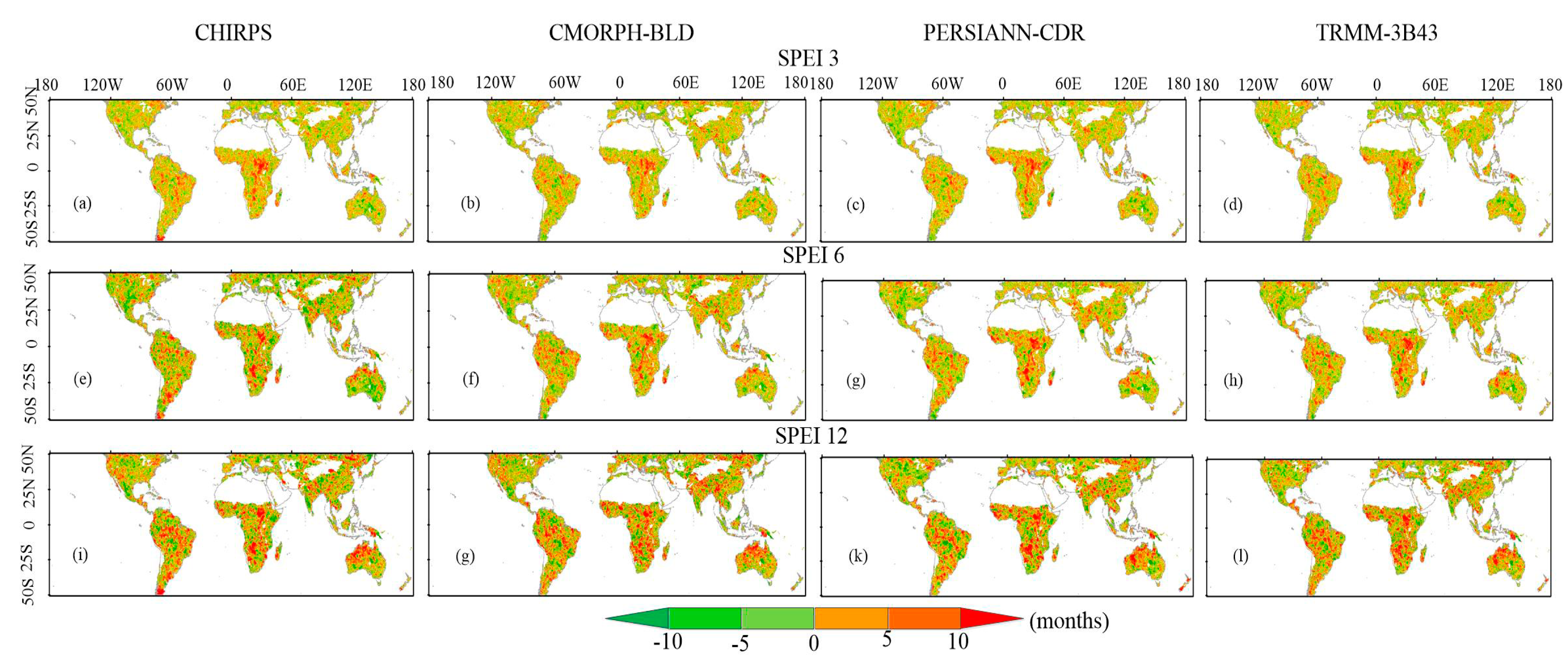
- On the basis of the SPEI statistics, the four SPEIs performed worse in Central Africa, Amazonia, the Tibetan plateau, the Himalayas, and Southeast Asia; Central Africa had the worst CC (<0.5) and RMSE (>0.8) performances for the four QPE products. In contrast, the southeastern United States, the southeast of South America, the south of Africa, most areas of India, Australia, and eastern China have higher CC values (>0.8) and low RMSE values (<0.4) for the four QPE products. The PERSIANN-CDR generally had higher CC in most regions in the world (except for Africa) and the CMORPH-BLD had lower CC in the world; CHIRPS and TRMM-3B43 had comparable performances.
- (3)
- According to POD and FAR for the SPEI, more than 50% of the drought events cannot be accurately identified by the QPE products in Central Africa, Amazonia, the Tibetan plateau, the Himalayas, and parts of Southeast Asia and Australia. In other regions, e.g., the southeastern United States, southeastern China, and South Africa, the QPE product can capture more than 75% of drought events.
- (4)
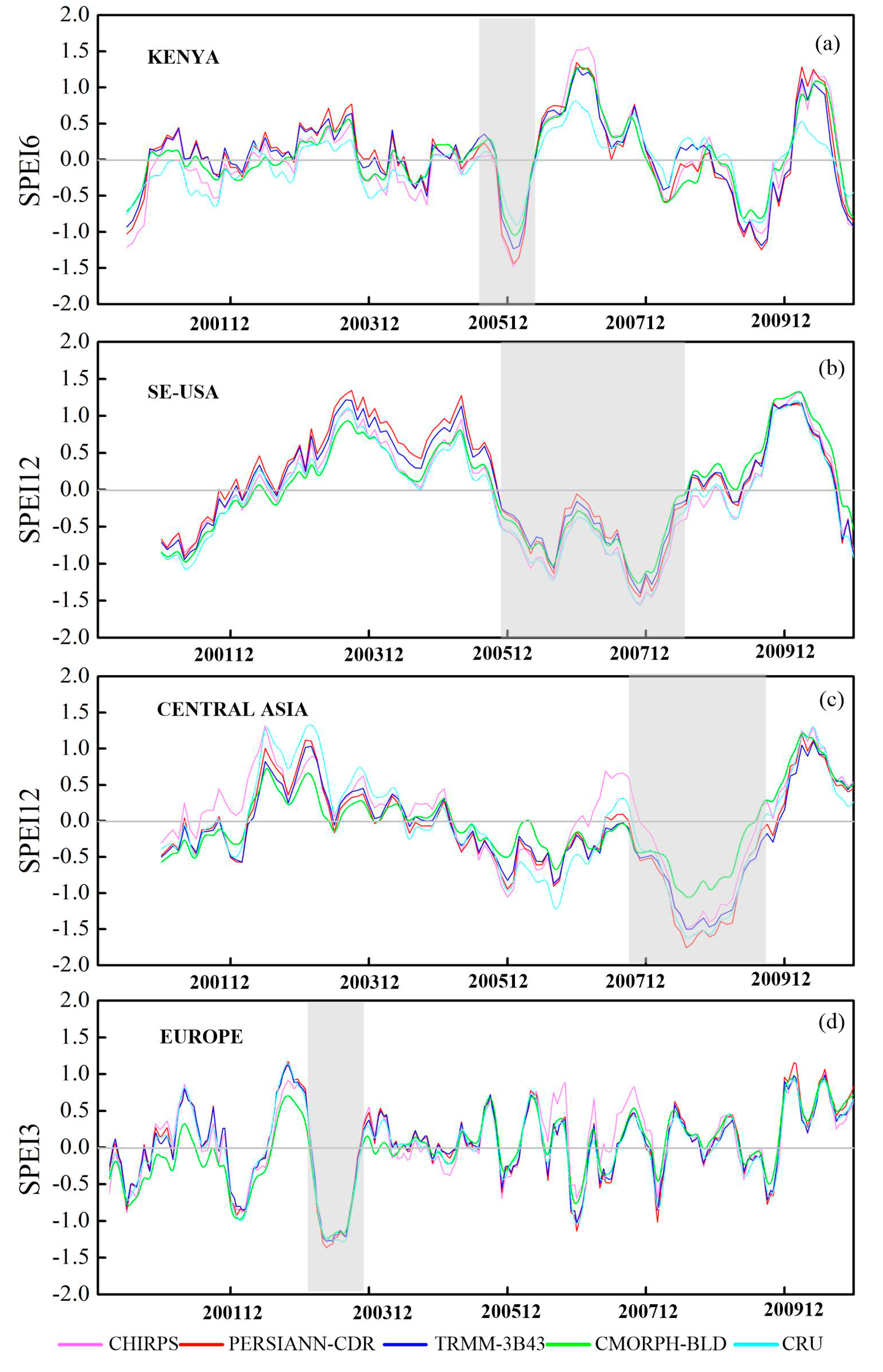
- All datasets (except for CMORPH-BLD) could detect all four typical drought events in Table 5 using the domain-averaged SPEIs of less than −1. The CMORPH-BLD was not able to effectively detect the 2007 central Asian drought and the 2006 Kenyan drought. The spatial SPEI patterns of the four QPE products agreed very well with that of the CRU precipitation for the 2007 southeastern USA drought and the 2003 western European drought. CHIRPS had a distinct over-recognition of drought severity for the 2006 Kenyan drought. In addition, CMORPH-BLD had obvious spatial discrepancies in comparison with other precipitation products for the 2008 central Asian drought.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Lai, C.; Zhong, R.; Wang, Z.; Wu, X.; Chen, X.; Wang, P.; Lian, Y. Monitoring hydrological drought using long-term satellite-based precipitation data. Sci. Total Environ. 2019, 649, 1198–1208. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Heim, R.R. A review of twentieth-century drought indices used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1165. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A. The quantification of drought: An evaluation of drought indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Boston, CA, USA, 17–22 January 1993. [Google Scholar]
- Palmer, W.C. Meteorological Drought. Research Paper No. 45, US Dept. of Commerce 58. 1965. Available online: http://www.ncdc.noaa.gov/oa/climate/research/drought/palmer.pdf (accessed on 25 August 2019).
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Bayissa, Y.; Tadesse, T.; Demisse, G.; Shiferaw, A. Evaluation of Satellite-Based Rainfall Estimates and Application to Monitor Meteorological Drought for the Upper Blue Nile Basin, Ethiopia. Remote Sens. 2017, 9, 669. [Google Scholar] [CrossRef]
- Frank, A.; Armenski, T.; Gocic, M.; Popov, S.; Popovic, L.; Trajkovic, S. Influence of mathematical and physical background of drought indices on their complementarity and drought recognition ability. Atmos. Res. 2017, 194, 268–280. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.M.; Liu, T.; Jiapaer, G.; Ndayisaba, F.; Jiang, L.L.; Kurban, A.; De Maeyer, P. Spatial and temporal characteristics of droughts in Central Asia during 1966–2015. Sci. Total Environ. 2018, 624, 1523–1538. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Yuan, S.S.; Quiring, S.M. Evaluation of six indices for monitoring agricultural drought in the south central United States. Agric. For. Meteorol. 2018, 249, 107–119. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Lai, C.; Zeng, Z.; Zhong, R.; Chen, X.; Zhou, X.; Wang, M. Does drought in China show a significant decreasing trend from 1961 to 2009? Sci. Total Environ. 2017, 579, 314–324. [Google Scholar] [CrossRef] [PubMed]
- Zambrano, F.; Wardlow, B.; Tadesse, T.; Lillo-Saavedra, M.; Lagos, O. Evaluating satellite-derived long–term historical precipitation datasets for drought monitoring in Chile. Atmos. Res. 2016, 186, 26–42. [Google Scholar] [CrossRef]
- Yoon, J.H.; Mo, K.; Wood, E.F. Dynamic–Model–Based Seasonal Prediction of Meteorological Drought over the Contiguous United States. J. Hydrometeorol. 2012, 13, 463–482. [Google Scholar] [CrossRef]
- Zhong, R.D.; Chen, X.H.; Lai, C.G.; Wang, Z.L.; Lian, Y.Q.; Yu, H.J.; Wu, X.Q. Drought monitoring utility of satellite–based precipitation products across mainland China. J. Hydrol. 2019, 568, 343–359. [Google Scholar] [CrossRef]
- Alley, W.M. The palmer drought severity index—Limitations and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.M.; Liu, T.; Chen, S.; Felix Ndayisaba, F. Evaluation of PERSIANN–CDR for Meteorological Drought Monitoring over China. Remote Sens. 2016, 8, 379. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Ren, L.L.; Singh, V.P.; Yang, X.L.; Yuan, F. A multiscalar Palmer drought severity index. Geophys. Res. Lett. 2017, 44, 6850–6858. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A self–calibrating palmer drought severity index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Begueria, S.; Lorenzo-Lacruz, J.; Camarero, J.J.; Lopez-Moreno, J.I.; Azorin-Molina, C.; Revuelto, J.; Moran-Tejeda, E.; Sanchez-Lorenzo, A. Performance of Drought Indices for Ecological, Agricultural, and Hydrological Applications. Earth Interact. 2012, 16, 10. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and Hydrological Comparisons between TRMM and GPM Level-3 Products over a Midlatitude Basin: Is Day-1 IMERG a Good Successor for TMPA 3B42V7? J. Hydrometeorol. 2015, 17, 121–131. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C. Evaluation and Hydrologic Validation of TMPA Satellite Precipitation Product Downstream of the Pearl River Basin, China. Hydrol. Process 2017, 31, 4169–4182. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Schrier, G.V.D.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Chang. 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Chen, S.; Hu, J.J.; Zhang, Z.X.; Behrangi, A.; Hong, Y.; Gebregiorgis, A.S.; Cao, J.R.; Hu, B.Q.; Xue, X.W.; Zhang, X.H. Hydrologic Evaluation of the TRMM Multisatellite Precipitation Analysis Over Ganjiang Basin in Humid Southeastern China. IEEE J. STARS 2015, 8, 4568–4580. [Google Scholar] [CrossRef]
- Zhao, H.G.; Yang, S.T.; Wang, Z.W.; Zhou, X.; Luo, Y.; Wu, L.N. Evaluating the suitability of TRMM satellite rainfall data for hydrological simulation using a distributed hydrological model in the Weihe River catchment in China. J. Geogr. Sci. 2015, 25, 177–195. [Google Scholar] [CrossRef]
- Yang, B.G.; Zhao, Y.J.; Zhao, H.G.; Li, B.B.; Huang, Y.C. Assessment of the Two Successive GPM–Based V3 and V4 GSMaP Precipitation Products at Multiple Temporal and Spatial Scales Over China. IEEE J. STARS 2019, 12, 577–588. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Sheffield, J.; Pan, M.; Wood, E.F. Evaluation of the Tropical Rainfall Measuring Mission Multi-Satellite Precipitation Analysis (TMPA) for assessment of large–scale meteorological drought. Remote Sens. Environ. 2015, 159, 181–193. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM multisatellite precipitation analysis (TMPA): Quasi–global, multiyear, combined–sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of persiann system satellite-based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN–CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2014, 96, 197–210. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Bo, E.R.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A Quasi-Global Precipitation Time Series for Drought Monitoring. US Geol. Surv. 2014, 832, 1–12. [Google Scholar]
- Lu, J.; Jia, L.; Menenti, M.; Yan, Y.P.; Zheng, C.L.; Zhou, J. Performance of the Standardized Precipitation Index Based on the TMPA and CMORPH Precipitation Products for Drought Monitoring in China. IEEE J. STARS 2018, 11, 1387–1396. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Alizadeh, M.R.; Nikoo, M.R. A fusion-based methodology for meteorological drought estimation using remote sensing data. Remote Sens. Environ. 2018, 211, 229–247. [Google Scholar] [CrossRef]
- Wang, F.; Yang, H.B.; Wang, Z.M.; Zhang, Z.Z.; Li, Z.H. Drought Evaluation with CMORPH Satellite Precipitation Data in the Yellow River Basin by Using Gridded Standardized Precipitation Evapotranspiration Index. Remote Sens. 2019, 11, 485. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high–resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Mitchell, T.D.; Jones, P.D. An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int. J. Climatol. 2005, 25, 693–712. [Google Scholar] [CrossRef]
- Pan, M.; Sahoo, A.K.; Troy, T.J.; Vinukollu, R.K.; Sheffield, J.; Wood, E.F. Multisource estimation of long–term terrestrial water budget for major global river basins. J. Clim. 2012, 25, 3191–3206. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-Satellite Precipitation Analysis (TMPA) Satellite Rainfall Applications for Surface Hydrology; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar]
- Faridzad, M.; Yang, T.T.; Hsu, K.; Sorooshian, S.; Xiao, C. Rainfall frequency analysis for ungauged regions using remotely sensed precipitation information. J. Hydrol. 2018, 563, 123–142. [Google Scholar] [CrossRef]
- Channan, S.; Collins, K.; Emanuel, W.R. Global Mosaics of the Standard MODIS Land Cover Type Data; University of Maryland and the Pacific Northwest National Laboratory: College Park, MD, USA, 2014. [Google Scholar]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernandez-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Peng, J.; Dadsona, S.; Leng, G.Y.; Duan, Z.; Jagdhuber, T.; Guo, W.D.; Ludwig, R. The impact of the Madden-Julian Oscillation on hydrological extremes. J. Hydrol. 2019, 571, 142–149. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Miralles, D.G.; Domínguez-Castro, D.; Azorin-Molina, C.; Eenawy, A.E.; Mcvicar, T.R.; Tomás-Burguera, M.; Beguería, S.; Maneta, M.; Peña-Gallardo, M. Global Assessment of the Standardized Evapotranspiration Deficit Index (SEDI) for Drought Analysis and Monitoring. J. Clim. 2018, 31, 5371–5393. [Google Scholar] [CrossRef]
- Liu, W.B.; Sun, F.B.; Sun, S.B.; Guo, L.M.; Wang, H.; Cui, H.J. Multi-scale assessment of eco-hydrological resilience to drought in China over the last three decades. Sci. Total Environ. 2019, 672, 201–211. [Google Scholar] [CrossRef]
- Wang, Q.F.; Wu, J.J.; Li, X.H.; Zhou, H.K.; Yang, J.H.; Geng, G.P.; An, X.L.; Liu, L.Z.; Tang, Z.H. A comprehensively quantitative method of evaluating the impact of drought on crop yield using daily multi-scale SPEI and crop growth process model. Int. J. Biometeorol. 2017, 61, 685–699. [Google Scholar] [CrossRef]
- Xie, P.; Joyce, R.; Wu, S.R.; Yoo, S.Y.; Yarosh, Y.; Sun, F.Y.; Lin, R. Reprocessed, Bias-Corrected CMORPH Global High-Resolution Precipitation Estimates from 1998. J. Hydrometeorol. 2017, 8, 1617–1640. [Google Scholar] [CrossRef]
- Rivera, J.A.; Marianetti, G.; Hinrichs, S. Validation of CHIRPS precipitation dataset along the Central Andes of Argentina. Atmos. Res. 2018, 213, 437–449. [Google Scholar] [CrossRef]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.-P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 Global Precipitation Climatology Project (GPCP) monthly precipitation analysis (1979–present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Xie, P.; Chen, M.; Shi, W. 2010: CPC Unified Gauge-Based Analysis of Global Daily Precipitation. Available online: https://ams.confex.com/ams/90annual/webprogram/Paper163676.html (accessed on 25 August 2019).
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Yong, B.; Liu, D.; Gourley, J.J.; Tian, Y.; Huffman, G.J.; Ren, L.; Hong, Y. Global View of Real-Time Trmm Multisatellite Precipitation Analysis: Implications for Its Successor Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2015, 96, 283–296. [Google Scholar] [CrossRef]
- Dembele, M.; Zwart, S.J. Evaluation and comparison of satellite-based rainfall products in Burkina Faso, West Africa. Int. J. Remote. Sens. 2017, 37, 3995–4014. [Google Scholar] [CrossRef]
- Bookhagen, B.; Burbank, D.W. Topography, relief, and TRMM–derived rainfall variations along the Himalaya. Geophys. Res. Lett. 2006, 33, L08405. [Google Scholar] [CrossRef]
- Awange, J.L.; Forootan, E. An evaluation of high–resolution gridded precipitation products over Bhutan (1998–2012). Int. J. Climatol. 2016, 36, 1067–1087. [Google Scholar]
- Shrestha, N.K.; Qamer, F.M.; Pedreros, D.; Murthy, M.S.R.; Wahid, S.M.; Shrestha, M. Evaluating the accuracy of Climate Hazard Group (CHG) satellite rainfall estimates for precipitation based drought monitoring in Koshi basin, Nepal. J. Hydrol. Reg. Stud. 2017, 13, 138–151. [Google Scholar] [CrossRef]
- Vernimmen, R.R.; Hooijer, A.; Aldrian, E.; Van Dijk, A.I. Evaluation and bias correction of satellite rainfall data for drought monitoring in Indonesia. Hydrol. Earth Syst. Sci. 2012, 16, 133–146. [Google Scholar] [CrossRef]
- Aadhar, S.; Mishra, V. High-resolution near real-time drought monitoring in South Asia. Sci. Data 2017, 4, 170145. [Google Scholar] [CrossRef]





| Products | Temporal Resolution | Spatial Resolution (°) | Coverage | Period | Data Source |
|---|---|---|---|---|---|
| CMORPH-BLD | daily | 0.25 × 0.25 | 60N–60S | 1998 to present | ftp://ftp.cpc.ncep.noaa.gov/precip/CMORPH_V1.0/ |
| CHIRPS | daily | 0.05 × 0.05 | 60N–60S | 1981 to present | ftp://ftp.chg.ucsb.edu/pub/org/chg/products/CHIRPS-2.0/ |
| PERSIANN-CDR | daily | 0.25 × 0.25 | 60N–60S | 1983 to present | http://chrsdata.eng.uci.edu/ |
| TRMM-3B43 | monthly | 0.25 × 0.25 | 50N–50S | 1998 to present | https://pmm.nasa.gov/data-access/downloads/trmm |
| Drought Class | SPEI Values |
|---|---|
| Extreme wet | SPEI ≥ 2.0 |
| Severe wet | 1.5 < SPEI < 2.0 |
| Moderate wet | 1 < SPEI ≤ 1.5 |
| Mild wet | 0.5 < SPEI ≤ 1.0 |
| Normal | −0.5 ≤ SPEI ≤ 0.5 |
| Mild dry | −1 < SPEI < −0.5 |
| Moderate dry | −1.5 < SPEI ≤ −1.0 |
| Severe dry | −2 < SPEI ≤ −1.5 |
| Extreme dry | SPEI ≤ −2.0 |
| Continents | Quantile | CHIRPS | CMORPH-BLD | PERSIANN-CDR | TRMM-3B43 | ||||
|---|---|---|---|---|---|---|---|---|---|
| CC | RMSE | CC | RMSE | CC | RMSE | CC | RMSE | ||
| North America | 5% | 0.82 | 19.38 | 0.74 | 23.48 | 0.82 | 20.78 | 0.84 | 20.58 |
| 50% | 0.88 | 33.08 | 0.83 | 39.93 | 0.89 | 31.07 | 0.90 | 32.92 | |
| 95% | 0.92 | 45.92 | 0.89 | 52.45 | 0.93 | 41.34 | 0.94 | 42.69 | |
| South America | 5% | 0.78 | 44.30 | 0.67 | 51.95 | 0.78 | 41.86 | 0.78 | 45.36 |
| 50% | 0.85 | 62.78 | 0.79 | 74.59 | 0.86 | 60.67 | 0.85 | 64.28 | |
| 95% | 0.91 | 81.09 | 0.88 | 93.03 | 0.91 | 79.76 | 0.91 | 84.08 | |
| Asia | 5% | 0.82 | 31.94 | 0.68 | 41.43 | 0.81 | 29.95 | 0.82 | 34.20 |
| 50% | 0.89 | 51.15 | 0.82 | 59.31 | 0.90 | 43.59 | 0.89 | 47.92 | |
| 95% | 0.94 | 95.92 | 0.89 | 108.03 | 0.94 | 82.77 | 0.93 | 89.01 | |
| Europe | 5% | 0.74 | 17.14 | 0.58 | 21.61 | 0.74 | 17.11 | 0.76 | 18.15 |
| 50% | 0.82 | 23.65 | 0.76 | 28.64 | 0.84 | 25.03 | 0.85 | 26.50 | |
| 95% | 0.91 | 33.81 | 0.86 | 37.22 | 0.91 | 36.44 | 0.92 | 40.68 | |
| Oceania | 5% | 0.74 | 15.76 | 0.63 | 18.62 | 0.69 | 17.25 | 0.71 | 16.25 |
| 50% | 0.86 | 24.04 | 0.80 | 28.89 | 0.84 | 25.77 | 0.85 | 24.91 | |
| 95% | 0.93 | 57.63 | 0.90 | 70.14 | 0.93 | 60.36 | 0.94 | 67.52 | |
| Africa | 5% | 0.81 | 32.98 | 0.58 | 58.82 | 0.79 | 37.35 | 0.73 | 44.45 |
| 50% | 0.89 | 42.59 | 0.70 | 71.55 | 0.86 | 46.50 | 0.82 | 54.62 | |
| 95% | 0.93 | 57.05 | 0.78 | 87.44 | 0.91 | 61.68 | 0.89 | 67.08 | |
| Regions | Quantile | CHIRPS | CMORPH-BLD | PERSIANN-CDR | TRMM-3B43 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SPEI3 | SPEI6 | SPEI12 | SPEI3 | SPEI6 | SPEI12 | SPEI3 | SPEI6 | SPEI12 | SPEI3 | SPEI6 | SPEI12 | ||
| North America | 5% | 0.63 | 0.60 | 0.61 | 0.58 | 0.52 | 0.52 | 0.67 | 0.65 | 0.64 | 065 | 0.60 | 0.58 |
| 50% | 0.81 | 0.81 | 0.79 | 0.75 | 0.73 | 0.70 | 0.83 | 0.82 | 0.80 | 0.81 | 0.80 | 0.78 | |
| 95% | 0.89 | 0.89 | 0.87 | 0.83 | 0.83 | 0.80 | 0.90 | 0.90 | 0.90 | 0.88 | 0.88 | 0.88 | |
| South America | 5% | 0.47 | 0.44 | 0.40 | 0.34 | 0.32 | 0.30 | 0.50 | 0.49 | 0.47 | 0.49 | 0.47 | 0.46 |
| 50% | 0.61 | 0.59 | 0.56 | 0.51 | 0.50 | 0.46 | 0.64 | 0.65 | 0.63 | 0.62 | 0.62 | 0.60 | |
| 95% | 0.76 | 0.78 | 0.78 | 0.68 | 0.71 | 0.69 | 0.80 | 0.81 | 0.81 | 0.75 | 0.77 | 0.78 | |
| Asia | 5% | 0.60 | 0.61 | 0.59 | 0.51 | 0.49 | 0.46 | 0.62 | 0.64 | 0.66 | 0.61 | 0.61 | 0.64 |
| 50% | 0.75 | 0.74 | 0.74 | 0.64 | 0.63 | 0.62 | 0.74 | 0.75 | 0.75 | 0.73 | 0.73 | 0.73 | |
| 95% | 0.83 | 0.83 | 0.81 | 0.74 | 0.73 | 0.70 | 0.84 | 0.83 | 0.83 | 0.82 | 0.82 | 0.80 | |
| Europe | 5% | 0.66 | 0.66 | 0.65 | 0.57 | 0.54 | 0.51 | 0.71 | 0.72 | 0.71 | 0.71 | 0.72 | 0.70 |
| 50% | 0.82 | 0.81 | 0.81 | 0.75 | 0.73 | 0.72 | 0.85 | 0.85 | 0.84 | 0.84 | 0.83 | 0.83 | |
| 95% | 0.91 | 0.90 | 0.89 | 0.5 | 0.83 | 0.82 | 0.92 | 0.93 | 0.93 | 0.91 | 0.91 | 0.91 | |
| Oceania | 5% | 0.50 | 0.40 | 0.26 | 0.39 | 0.31 | 0.30 | 0.45 | 0.39 | 031 | 0.47 | 0.40 | 0.35 |
| 50% | 0.70 | 0.68 | 0.64 | 0.65 | 0.61 | 0.55 | 0.70 | 0.69 | 0.64 | 0.71 | 0.68 | 0.63 | |
| 95% | 0.86 | 0.86 | 0.87 | 0.83 | 0.83 | 0.84 | 0.87 | 0.87 | 0.88 | 0.86 | 0.86 | 0.86 | |
| Africa | 5% | 0.42 | 0.40 | 0.36 | 0.29 | 0.28 | 0.23 | 0.36 | 0.37 | 0.37 | 0.37 | 0.36 | 0.36 |
| 50% | 0.57 | 0.52 | 0.51 | 0.44 | 0.39 | 0.37 | 0.53 | 0.51 | 0.49 | 0.51 | 0.47 | 0.45 | |
| 95% | 0.72 | 0.66 | 0.61 | 0.63 | 0.54 | 0.52 | 0.72 | 0.67 | 0.66 | 0.69 | 0.64 | 0.63 | |
| Events Location | Event Extents | Drought Duration | Index Time Scale |
|---|---|---|---|
| 2007 southeastern US | 31°N to 40°N; 92°W to 80°W | Winter June 2005 to winter August 2007 | 12 |
| 2003 western European | 40°N to 50°N; 0° to 30°E | June 2003 to August 2003 | 3 |
| 2006 Kenyan | 5°S to 10°N; 35°E to 45°E | End of 2005 and beginning of 2006 | 6 |
| 2008 Central Asia | 45°N to 50°N;64.5°E to 87.5°E | December 2007 and July 2009 | 12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Ma, Y. Evaluating the Drought-Monitoring Utility of Four Satellite-Based Quantitative Precipitation Estimation Products at Global Scale. Remote Sens. 2019, 11, 2010. https://doi.org/10.3390/rs11172010
Zhao H, Ma Y. Evaluating the Drought-Monitoring Utility of Four Satellite-Based Quantitative Precipitation Estimation Products at Global Scale. Remote Sensing. 2019; 11(17):2010. https://doi.org/10.3390/rs11172010
Chicago/Turabian StyleZhao, Haigen, and Yanfei Ma. 2019. "Evaluating the Drought-Monitoring Utility of Four Satellite-Based Quantitative Precipitation Estimation Products at Global Scale" Remote Sensing 11, no. 17: 2010. https://doi.org/10.3390/rs11172010
APA StyleZhao, H., & Ma, Y. (2019). Evaluating the Drought-Monitoring Utility of Four Satellite-Based Quantitative Precipitation Estimation Products at Global Scale. Remote Sensing, 11(17), 2010. https://doi.org/10.3390/rs11172010