1. Introduction
Retreat of coastal forests with rising sea levels has been documented [
1,
2,
3,
4]; however, this forest response can be influenced by a variety of circumstances. Storm surges, saltwater intrusion, flooding, and drought can also have a significant effect on these regions [
5,
6]. Even if these events do not kill trees outright, they can affect saplings that tend to be more sensitive to environmental stressors, thus reducing rates of overall forest regeneration.
In fact, salt and flooding can suppress tree regeneration before the death of mature trees [
1,
7], so that at lower elevations only mature trees are present. Critical factors controlling soil and groundwater salinity are the height and frequency of storm surges compared to the elevation of the forest soil [
8]. Groundwater also plays a critical role, reducing salinity in areas where underground freshwater fluxes are high [
9,
10]. Marsh species cannot fully develop under the shade of trees [
11], so that tree dieback is necessary to allow a complete transition from forest to salt marsh. Often trees are killed during intense storms, when temporary soil salinity is very high and soil saturation caused by rainfall and ocean waters increase the likelihood of windthrow [
12]. As the magnitude of these events increases with changing climate, one would expect increased stress on these coastal ecosystems as well.
The low lying forests in the Delmarva Peninsula are often flooded. Vanderhoof et al. [
13] used Radarsat-2 and Worldview-3 imagery integrated with LiDAR data to map flooding extent in wetland forests in Maryland and Delaware. Their analysis indicates that the hydrological connections between streams and low lying areas control flooding extent. Jin et al. [
14] used Landsat time-series imagery to monitor inundation patterns in two watersheds of the Delmarva Peninsula. They found that tidal wetlands are, on average, more inundated than forest and scrub-shrub wetlands, with the latter prone to flooding due to rainfall. Huang et al. [
15] used Landsat and airborne LiDAR data to measure inundation in a coastal forest in Maryland. Their analysis shows that the inundated area increases five times during wet years with respect to dry ones. Flooding regime and topographic elevation also affect forest structure in low lying areas. la Cecilia et al. [
16] studied the forested floodplains of the Apalachicola River in Florida with Normalized Difference Vegetation Index (NDVI) data derived from Landsat images. They discovered that hardwood swamp has been partly replaced by bottomland hardwood forest in the last 30 years, predominantly near river banks, where the bottom elevations are higher.
The normalized difference water index (NDWI) has also been used to retrieve vegetation water content, and therefore, can monitor plant water stress [
17,
18,
19]. Hamzeh et al. [
20] compared NDVI and NDWI values derived from a Hyperion level 1B1 image to soil salinity levels measured in sugarcane fields. The good agreement of their results indicates that both NDVI and NDWI can be used to map salinity stress of crops. Similarly, Penuelas et al. [
21] studied the effects of a soil salinity gradient on the spectral reflectance of barley measured in the field. Both NDVI and NDWI were found to be useful indexes to detect the response of barley to salinity. Justin George and Kumar [
22] used NDWI to characterize soil salinity in an alluvial floodplain. Their analysis showed that areas with high soil salinity had very negative NDWI values, whereas normal soils had higher values, although negative, possibly due to presence of denser vegetation.
NDWI has already been used with success to classify and monitor wetland vegetation [
23]. However, the link between NDWI, vegetation stress, and soil salinity might be more elusive than in carefully managed crop agriculture. This is because wetland soils may be an overwhelming source of moisture, especially when there are gaps in wetland vegetation. Here we will use NDWI to determine variations in forest characteristics driven by sea level rise and storms. The results will be discussed, taking in account both vegetation stress and canopy gaps.
2. Ecological Ratchet Model of Marsh Transgression in a Forest
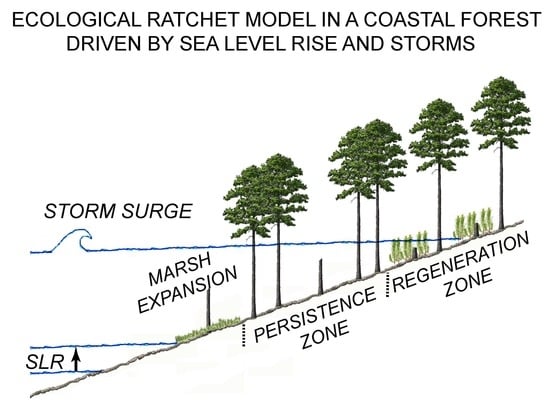
A recent field study in the coastal pine forest on the Delmarva Peninsula, Virginia, USA, has proposed that the forest in this region can be divided into two distinctive zones [
24]. The first zone, referred to as the persistence zone, is characterized by lower elevations, mature trees, but no new saplings. The size of this zone is related to the amount sea level rose since forest establishment [
24]. The second zone, the regenerative zone, is characterized by higher elevations, mature trees, as well as saplings, indicating that the forest here is regenerating.
The ecological ratchet model of Kearney et al. [
24] starts with the establishment of a forest stand, as it happened in the Delmarva Peninsula after the peak in deforestation at the beginning of the 20th century [
25] (
Figure 1A). As sea level rises and forest matures, the salinity of the soil increases, thus hindering forest regeneration at lower elevations (
Figure 1B). Infrequent storms kill trees in the forest (
Figure 1C), but only in the regeneration zone, the dead trees are replaced by saplings, so that the forest can fully recover (
Figure 1D). By killing trees at the marsh boundary, storms also enable salt marsh plants to move into the dead forests, taking advantage of light availability. As a result the lower boundary of the persistence zone moves upland. On the other hand, sea level rise is responsible for the transgression of the upper boundary of the persistence zone in the regenerative zone, because edaphic conditions become less and less favorable to forest regeneration. Thus, in this model of marsh transgression, storms intermittently move the lower boundary of the regenerative zone (move the round gear of the ratchet), while sea level rise prevents forest recovery in the persistence zone (sea level is the ratchet pawl that blocks the wheel, not allowing the reverse movement). Note that in this model the upper elevation of the persistence zone is determined, as a first approximation, by how much sea level rose since the establishment of the forest, so that in theory it could be possible to delineate the persistence zone on a topographic map, if the elevation of the landscape beneath the forest is known [
24]. Moreover, since the persistence zone is characterized by a sparse tree canopy and the absence of saplings, which are typically very green, it should appear in remote sensing images, using for example the NDVI index.
These proposed zones are based on field data at two sites on the southeastern coast of the Delmarva Peninsula in the Eastern Shore of Virginia National Wildlife Refuge [
24] (
Figure 2). Field surveys found saplings only at elevations above 0.92 m with respect to NAVD88 at one site and above 1.37 m at the other site, suggesting that the boundary between these two zones varies slightly along the coast. The area between 0.92 and 1.37 m will be referred to as the transition zone. Forest below 0.92 m will be referred to as persistence zone and forest above 1.37 m will be referred to as regenerative zone. Note that current mean sea level is 0.146 m below NAVD88.
Since the defining characteristics of these zones are primarily demographic and not visually distinct in high resolution aerial imagery, with a typical resolution of 1–5 m per pixel, an attempt will be made to find corresponding physiological characteristics that will allow for the differentiation of these zones using remote sensing spectral data. Therefore, the primary purpose of this study is to determine if these proposed persistence and regenerative zones can be differentiated with remote sensing data, and if years with large storm events are distinguishable based on the spectral characteristics.
5. Results
The average NDVI as a function of day of the year displays the typical seasonal variability, with higher values in summer (around 0.8 and higher) and lower values in winter (around 0.6–0.75) (
Figure 4).
More importantly, the NDVI in the persistence zone below 0.92 m is lower than the value in the regenerative zone above 1.37 m. To determine whether this difference is significant, and whether this difference varies if we change the elevation of the boundaries, we plotted the mean NDVI plus two standard deviations for different zones for four images taken in June, August, November and December of 2017 (
Figure 5B). We focused on few selected images to account for the seasonal variability in NDVI within each zone, considering all pixels. Furthermore, we chose the images of 2017 because it was temporally distant from major storms, so the NDVI and NDWI values better represent the long-term forest conditions. We divided the forest based on the three boundary elevations of Kearney et al. [
24]: Below and above the maximum sapling elevation of 1.37 m (
Figure 5A), below and above the average sapling elevation of 1.24 m (
Figure 5B), below and above the lower sapling elevation of 0.92 m (
Figure 5C), along with the average NDVI for the zone below 0.92 meters, and the zone above 1.37 m (
Figure 5D). The Cohen’s
d effect size was computed to determine whether the difference in mean NDVI between these zones was large enough (
Table 5).
Figure 5A–C and
Figure 6A–C represent a sensitivity analysis of the regenerative and persistence zone with respect to elevation.
The average NDVI of the area above each elevation boundary is consistently higher than below the boundary, at all three elevations. The zones based on the 0.92 m boundary show a larger difference between average NDVI values, and the upper zone shows a larger drop moving from June to the end of August (
Figure 5C). The zones based on the average sapling elevation of 1.24 m show a smaller difference throughout the year, with the exception of a large drop in NDVI in the persistence zone in the fall (
Figure 5B). The zones based on the 1.37 m upper boundary show a more consistent difference throughout the year (
Figure 5A). The last plot, showing the difference between the average NDVI below 0.92 m (persistence zone) and above 1.37 m (regenerative zone), also appears to have a more consistent difference and steady decline throughout the year. However, in this plot, the NDVI of the persistence zone is larger than that of the regenerative zone in June (
Figure 5D).
A similar analysis was carried out for the average NDWI and pairs of zones delineated by four possible boundaries: Below and above 1.37 m (
Figure 6A), below and above 1.24 m (
Figure 6B), below and above 0.92 m (
Figure 6C), and below 0.92 m and above 1.37 m (
Figure 6D). The Cohen’s
d effect size was also high between zones (
Table 6). Overall, NDWI shows similar trends to NDVI. The NDWI in the upper zone is consistently higher than in the lower zone for all boundaries based on minimum, mean, and maximum sapling elevation. The difference between NDWI in each zone does not vary much, and the overall pattern throughout the year is pretty consistent for each elevation boundary (relatively similar throughout the summer and declining in the fall and winter).
For NDVI, the Cohen’s
d values are all positive and above 0.5 (medium effect size) in the June and August Landsat images, above 0.8 (large effect size) in November, and between 0.2 and 0.5 in December (small effect size) (
Table 5). The difference is larger if we compare the zone below 0.92 m and the zone above 1.37 m, excluding the image of June, where the average NDVI above 1.37 is lower than the average NDVI below 0.92 m. For NDWI the effect size is always medium (above 0.5) or large (above 0.8) in June August and November, while it is small (between 0.2 and 0.5) in December (
Table 6). Therefore the two zones seem better separated in summer and fall than in winter, when the NDVI and NDWI values decrease. The Cohen’s
d effect size is always higher if we compare the zone below 0.92 m to the zone above 1.37 m, excluding the NDVI values in June. The choice of the boundary elevation thus slightly affects the difference in average NDVI and NDWI values. Based on those results in the remaining analyses we separated the dataset in below 0.92 m (persistence zone) and above 1.37 m (regenerative zone). Those two zones yield the highest effect size. Forest with elevation between 0.92 m and 1.37 m (transition zone in
Figure 2) was not assigned to either persistence or regenerative zone. In this way, we controlled for possible errors in LiDAR elevations that were around 20 cm.
The seasonal variability in NDVI during the study period is reported in
Figure 7. We also indicate in the figure the ten storms that generated the highest storm surges since 2000 (
Table 4). For each storm we report on the right y-axis the elevation of the storm surge. As expected, the NDVI values are higher in summer months for both zones (right-tailed
t-test,
p < 0.05) and lower in winter (left-tailed
t-test,
p < 0.05). Moreover, the moving average of the NDVI in the regenerative zone is always higher than the moving average in the persistence zone. In some winters, the NDVI values are reduced after a major storm (2004); in other years the reduction does not occur the year after a storm (2009). Summer peaks are also lower in some years (2004, 2011, and 2012) and they seem related to intense storms occurring in the fall of the year before. Additionally, the summer of 2003 displays a strong decrease in NDVI; this could be partly caused by hurricane Isabel, that struck on September 18. Note that in September the NDVI values are still very high (
Figure 4) and they start declining in November.
The NDVI moving average, drawn as a thick line in
Figure 7, represents more clearly the trend during the analyzed period. The detrended average NDVI in the regenerative zone is lower (negative) between July 2002 and June 2006, and between January 2010 and May 2015 (left-tailed
t-test,
p < 0.05,
Figure 8), while it is higher (positive) between July 2006 and December 2009, and between June 2015 and December 2018 (right-tailed
t-test,
p < 0.05,
Figure 8). The overall trend of NDVI is increasing from 2000 to 2019 in the regenerative zone (
r = 0.68,
p < 0.05, black dotted line in
Figure 7A). The persistence forest moving average has a trend similar to the regenerative forest moving average—lower between June 2002 and August 2005, and between January 2009 and June 2015 (left-tailed
t-test,
p < 0.05,
Figure 8); and higher in the periods September 2007 to December 2008 and July 2015 to December 2018 (right-tailed
t-test,
p < 0.05). The overall trend of NDVI in the persistence zone is a slightly decreasing one between 2000 and 2019 (
r = −0.16,
p < 0.05, red dotted line in
Figure 7A). Inter-annual NDVI variations are larger for the persistence forest (
σ2 = 0.010) than for the regenerative one (
σ2 = 0.005).
Figure 7B suggests that NDWI values for the regenerative and persistence forests are different. The regenerative forest achieves much higher NDWI values in summer (right-tailed
t-test,
p < 0.05). The NDWI moving average for this area, represented as a thick black line in
Figure 7B, shows a quite small reduction during the August 2003 to July 2005 period, and a very large decrease during the September 2010 to July 2015 period (left-tailed
t-test,
p < 0.05,
Figure 8). On the contrary, the August 2005 to October 2010 and August 2015 to December 2018 periods are characterized by a high detrended average NDWI (right-tailed
t-test,
p < 0.05). The overall NDWI trend for the regenerative forest displays a small decrease over the 2000 to 2019 period (
r = −0.22
p < 0.05, black dotted line in
Figure 7B). The persistence forest achieves a maximum NDWI value of about 0.35–0.4 in the 2000 to 2002 period, while in the following years the NDWI is lower, varying between 0.1 and 0.3 (left-tailed
t-test,
p < 0.05). Minimum NDWI values decrease too, varying from 0.25 during 2000 to 2003 period to −0.1 during 2016–2018 period. The NDWI moving average is decreasing, although it shows a limited recovery in the periods from 2004 to 2010 and from 2016 to 2018. The overall decrease in NDWI in the persistence zone is confirmed by the regression line ((
r = −0.97
p < 0.05, red dotted line in
Figure 7B). Inter-annual NDWI variations are larger for the regenerative zone (
σ2 = 0.041) than for the persistence zone (
σ2 = 0.005).
Figure 9A suggests that the difference between NDVI in the regenerative and persistence forest increases over the 2000 to 2019 period; and linear regressions of the yearly averaged values confirm this trend (
r = 0.73,
p < 0.05). Overall, the NDVI difference almost doubles during the 2000 to 2019 period. Moreover, the difference between NDWI in the regenerative and persistence zones increases over the 2000 to 2019 period, as a linear regression of the yearly average values clearly indicates (
r = 0.62,
p < 0.05). The maximum differences in NDWI occur in 2010, when NDWI in the persistence zone is quite low in comparison to the NDWI in regenerative zone (
Figure 7B), and in 2012, when NDWI in regenerative zone achieves its minimum value over the 2000 to 2019 period (
Figure 7B). Overall, the NDWI difference increases more than twice during the 2000 to 2019 period.
The NDWI resistance index for hurricane Isabel in 2003 is similar in the persistence and regenerative zones (
Figure 10A). The NDWI then recovers in the regenerative zone in the following three years but not in the persistence zone (
Figure 10B), so that the resilience index is higher in the regenerative zone and equal to one (full recovery
Figure 10C). In terms of NDVI, the resistance is slightly higher in the persistence zone (
Figure 10D), but the recovery is much higher in the regenerative zone, although it displays a larger yearly variability (
Figure 10E). As a result, the resilience index is slightly higher in the regenerative zone (
Figure 10F).
NDWI resistance against the combined storms Nor’Ida, Irene, and Sandy is higher in the persistence zone (
Figure 11A), while the recovery is much higher in the regenerative zone (
Figure 11B), although with a larger temporal variability. As a result, the resilience is higher in the regenerative zone, and again, close to one (
Figure 11C). In terms of NDVI, the resistance is higher in the regenerative zone (
Figure 11D), while the recovery is higher in the persistence zone (
Figure 11E). This results in a similar resilience index in the two zones (
Figure 11F).
6. Discussion
Both NDVI and NDWI indexes are consistently higher in the proposed regenerative zone than in the persistence zone, throughout the year. NDVI does show some more variation in how much it differs and when; however, this could be a result of the index capturing some of the broadleaf vegetation in the understory. This supports the idea that these two zones are distinctly different, both demographically and physiologically. Due to the scale of the area and the challenge of retrieving ground elevation below a forest canopy, the results of this analysis do not allow for clearer distinction between zones along the coast. In fact the margin of error of the LiDAR data is 20 cm, so it would be challenging to attribute the transition area between 0.92 and 1.37 m above NAVD88 to either the regenerative or persistence zone. Moving forward, this analysis should be expanded to see if this difference in average NDVI and NDWI can be used to more accurately represent this persistence–regenerative boundary at different points along the coast, instead of using a single elevation for the whole area.
The forest seems responsive to storms, particularly to those having a surge above 1.3 m with respect to NAVD88 (
Figure 7). Four of such events occurred in the period 2000 to 2019. Both NDVI and NDWI decreased after the storms (
Figure 8); pronounced more so for NDWI (
Figure 7). This index might be, therefore, more suited to study the effect of hurricanes on coastal forests.
One very interesting result is that the difference in NDVI and NDWI between the persistence and regenerative zones grows in time, possibly indicating the slow effect of sea level rise on the lower zone. An increase in salinity (in both soil and groundwater) would prevent the growth of very green saplings and understory vegetation, leading to a difference in NDVI. NDVI in the upper zone could also increase due to forest succession, with a canopy becoming denser and greener as the forest matures. However, forest succession would not explain the decrease in NDVI in the persistence zone or the decrease in NDWI in both zones. In fact, succession should also occur in the lower zone and NDWI should increase as the forest matures [
41]. The increasing difference in NDVI and NDWI could also be driven by the transient response to the 2009–2012 storms, without representing a long term trend. This could be particularly true for the NDWI in the regenerative zone, which displays large oscillations. However, the increase is NDWI difference is mostly driven by a steady decrease in NDWI in the persistence zone, which is only slightly affected by the transient response (
Figure 7).
In our study area, sea level rose only 7 cm from 2000 to 2019, but it rose 25 cm since some of these forests were established at the beginning of the 20th century [
24]. Following the conceptual model of Kearney et al. [
24], it is the overall increase in sea level since forest establishment that prevents the recruitment of new saplings. A 25 cm increase in sea level, likely accompanied by higher water tables and soil salinity, is therefore responsible for forest changes in the persistence zone. The decrease in NDVI and NDWI values in the persistence zone do not directly measure a rise in sea level, but forest mortality and the failure to recruit new saplings.
The NDWI index proposed by Gao [
19] is affected by soil moisture only when the leaf area index is low [
42]. So it is plausible that a large increase in canopy gaps would expose more soil, thus affecting the NDWI value. Four different processes triggered by sea level rise could lead to a change in the NDWI index: (i) Higher groundwater levels that increase soil moisture; (ii) more frequent flooding by storm surges; (iii) an increase in soil salinity, that stresses mature trees; and (iv) an increase in canopy gaps due to forest dieback, which exposes moist soils. All these processes lead to either vegetation water stress or a change in soil moisture, which are both potentially captured by the NDWI index. Therefore, NDWI seems very well suited to monitor the overall effect of sea level rise and storms on coastal forests.
An increase in soil moisture would increase NDWI values, whereas we detected a decrease in our study area. The NDWI values measured at our site are positive, ranging between 0.1 and 0.3 (
Figure 7B). Areas with sparse vegetation and wet soils are characterized by negative NDWI values [
22]. We, therefore, deduce that the vegetation canopy has a strong effect on the index, and that NDWI is not merely measuring soil wetness. This is further corroborated by high resolution aerial images, showing a dense tree canopy covering most of the persistence and regenerative areas. Flooding by storms increases soil wetness, but for few hours only. Since we do not detect negative spikes in NDWI after hurricanes, we conclude that storm flooding does not affect the NDWI index. Similarly, an increase in soil moisture due to higher groundwater levels does not seem to be captured by the NDWI index.
Instead, after large storm surges, we measured a decrease in NDWI that lasted 3–4 years. This long-term effect is likely linked to damage to the trees, with a subsequent slow-recovery. Moreover a decrease in NDWI values is also followed by a slight decrease in NDVI values (
Figure 7). Because the NDVI index is mildly affected by soil moisture, we conclude that vegetation stress or damage is captured by NDWI. Note that both vegetation stress due to soil salinity, and tree damage that augment canopy gaps, can decrease NDWI after a storm. Both processes are reducing the health of the forest and can be ascribed to the combined effect of sea level rise and storm surges. More research is clearly needed to separate the effect of vegetation stress from the effect of canopy gaps on the NDWI index.
The NDWI and NDVI values almost fully recover in the regenerative zone after a storm, while the indexes do not recover in the persistence zone, permanently decreasing. This indicates that the ecological ratchet model might be valid. In the ratchet model an extreme event reduces the NDWI values in both the persistence and regenerative zones (the gear of the ratchet), which cannot then allow a return to the original condition in the persistence zone because of sea level rise (the pawl of the ratchet, which is present only in the persistence zone).
When Hurricane Isabel hit in September 2003 the average NDVI and NDWI in both regenerative and persistence zones were relatively low, and they stayed low even in the following year (
Figure 7 and
Figure 8). While the timing of hurricane Isabel does not correspond with the beginning of the lower NDVI and NDWI period, the hurricane may have contributed to keeping these values low in subsequent years. After hurricane Isabel, the vegetation indexes remained low for a period between 2 years (NDVI in persistence zone) and 4 years (NDWI in persistence zone). We notice a negative spike in NDVI in both the regenerative and persistence zones in the winter following the hurricane, and a reduction in NDWI in October 2003.
After Nor’Ida in 2009, the NDWI in the regenerative zone started decreasing and kept decreasing when Irene hit in 2011 and Sandy in 2012. After that, the NDWI grew for a period of 4–5 years. A similar trend, although more subtle, is also present in the NDWI of the persistence zone and the NDVI of both persistence and regenerative zones. We, therefore, suggest that forest trees in the regenerative zone were affected by the combination of the three storms, and recovered only 3–4 years after Sandy. In fact, periods of lower NDVI and NDWI ended between summer 2015 and summer 2016 (
Figure 8). Periods of lower NDWI in the persistence zone are shifted with respect to period of lower NDVI and NDWI in the regenerative zone (
Figure 8). This is probably due to the steep overall decrease in NDWI in the persistence zone, which affects the beginning of the low NDWI periods. These results are in agreement with the tree cores analyzed by Fernandes et al. [
31] at a location within our study area. Fernandes et al. [
31] discovered that radial growth of loblolly pines is suppressed in the three years after a flooding event triggered by a storm surge. This supports the hypothesis that NDWI is linked to vegetation stress in coastal pine forests, as was already proven in agricultural fields [
20,
21].
The regenerative zone of the forest has lower resistance in terms of NDWI, but a higher recovery and resilience. This likely indicates that trees in this area are affected by the flooding and the increase in soil salinity following a storm, but they are able to fully recover afterward, when edaphic conditions return to normal due to rainfalls. Saplings in this area can be killed by the storm, leading to a sharp reduction in NDVI and NDWI. This area is therefore affected by the pulse effect of storms. This is in agreement with the data collected by Kearney et al. [
24] at a site within the study area. They measured a sharp increase in groundwater salinity after storm surges in the persistence zone; and a gradual decrease in salinity after rainfalls. On the contrary, surviving trees in the persistence zone seem to have a higher resistance in terms of NDWI, possibly because they are somehow accustomed to higher soil salinities. The lack of saplings also minimizes the consequences of a storm. However, both the recovery and overall resilience of the persistence zone is low, indicating that the vegetation here is slowly deteriorating. This is probably due to the press disturbance of sea level rise.
The NDVI resistance, recovery, and resilience indexes display a similar behavior for hurricane Isabel, with higher resistance in the persistence zone, and a higher recovery and resilience in the regenerative zone (
Figure 10D–F). However, they are different from the combined Nor’Ida, Irene, and Sandy storms. For that ‘event’ the resistance of the regenerative zone is higher; therefore, reducing the recovery also. This is because NDVI was slowly increasing in the regenerative zone (
Figure 7A), and that long-term trend mitigates the effect of the storms, particularly when considering a 5 year window.
The decrease in NDVI and NDWI starts one year before hurricane Isabel in 2003 (
Figure 7), but it is magnified after the hurricanes. Other processes might, therefore, affect the forest canopy in this area; for instance, rainfall patterns, draughts, and temperature. However, as also discussed by Fernandes et al. [
31], those effects are weaker compared to hurricanes.
The timing of hurricane arrival may also plays a role in forest disturbance, as corroborated by the dendroclimatic study of Fernandes et al. [
31]. The growing season for these coastal forests extends from May to October, as indicated by the high NDVI values in
Figure 4. If a large storm strikes during these months, the forest could be is instantly affected. The NDWI value of the regenerative zone dropped in the month following hurricanes Isabel and Irene, which hit in September and August respectively, becoming significantly lower than the monthly average for the period 2000 to 2012. Hurricane Sandy, which occurred at the end of October, and the Nor’Ida storm, which occurred in November, did not trigger a sudden decrease in NDWI in the regenerative zone. However, the forest seems affected by those storms in the following years.
The difference in NDVI between persistence and regenerative zones might not be due only to absence of saplings. Seasonal NDVI data collected in stands of evergreen loblolly pines do not show a significant difference between winter and summer months [
16], while our data indicate a strong seasonal variation (
Figure 7). Different species of deciduous oaks can be found within the pine forests of the Delmarva Peninsula [
28], lowering the NDVI values in winter. We also ascribe this strong NDVI seasonality to other understory vegetation species, and not only to pine saplings. Understory vegetation is particularly common in low lying coastal forests, where storm surges and wind kills trees, creating gaps in the canopy [
28].