Combining Deep Learning and Prior Knowledge for Crop Mapping in Tropical Regions from Multitemporal SAR Image Sequences
Abstract
:1. Introduction
1.1. Crop Mapping from Remote Sensing Data
1.2. Related Works
1.3. Goals and Contributions
- We propose a prior knowledge-based method to model complex crop dynamics in tropical regions, which enforces crop type classification to be consistent in both the spatial and temporal domains.
- We evaluate and compare three different approaches for crop type classification, namely: Autoencoders (AEs), Convolutional Neural Networks (CNNs), and Fully Convolutional Networks (FCNs), upon a SAR multitemporal image sequence.
2. Materials and Methods
2.1. Crop Classification Approaches Considered in This Study
2.1.1. Random Forest/pixel-wise (RFpixel)
2.1.2. Autoencoder/patch-wise (AEpatch)
2.1.3. Convolutional Neural Network/patch-wise (CNNpatch)
2.1.4. Fully Convolutional Network/pixel-wise (FCNpixel)
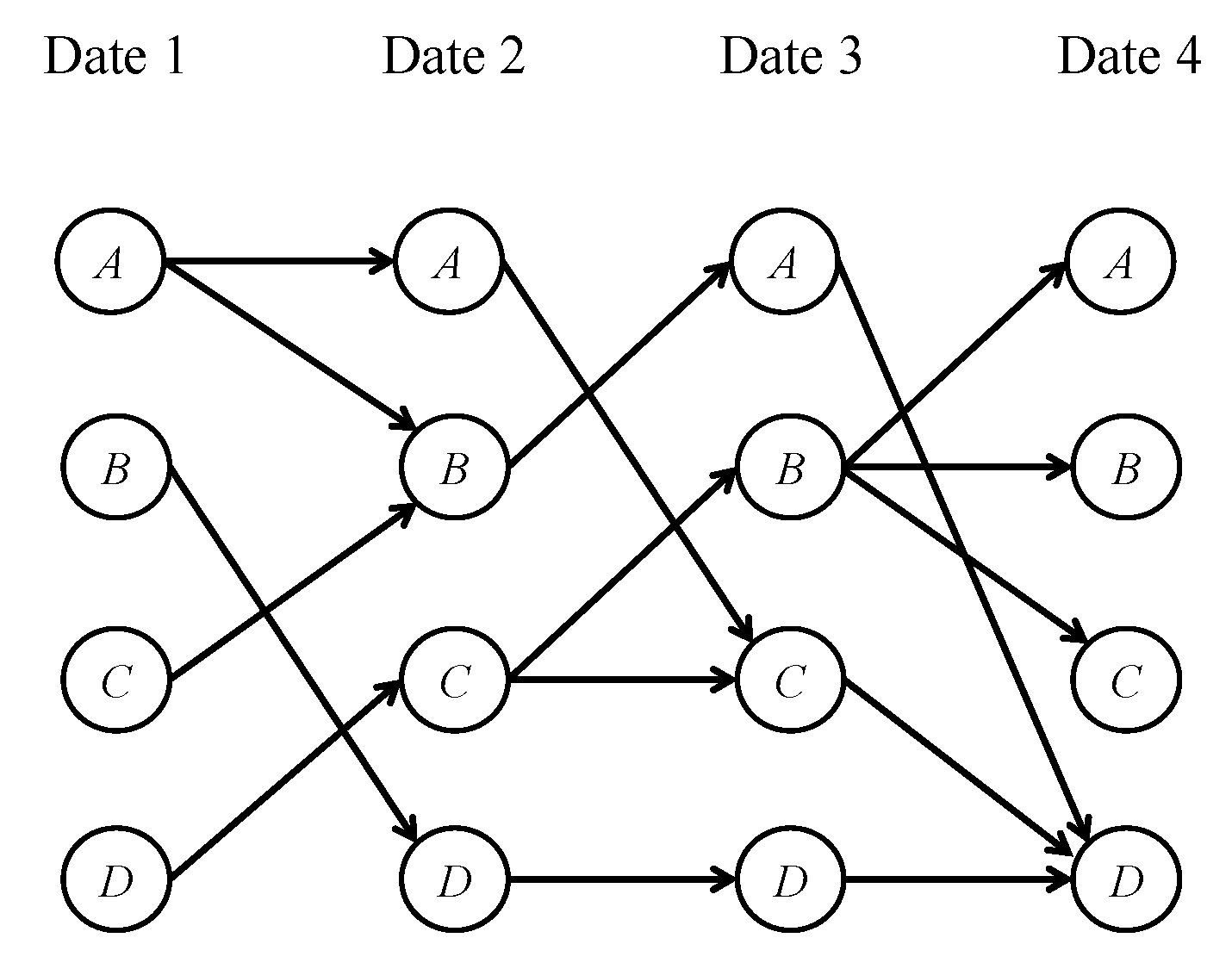
2.2. Modelling Crop Dynamics
2.3. Dataset and Study Site
2.4. Implementation of Classification Approaches
2.4.1. RFpixel
2.4.2. AEpatch
2.4.3. CNNpatch
2.4.4. FCNpixel
2.5. Training and Validation Sample Sets
2.6. Accuracy Assessment
3. Results and Discussion
3.1. Results for Protocol I
3.2. Results for Protocol II
3.3. Assessment of the crop dynamics model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Food and Agriculture Organiztaion of the United Nations. The State of Food Insecurity in the World Meeting the 2015 International Hunger Targets: Taking Stock of Uneven Progress; Working Papers, eSocialSciences; FAO: Rome, Italy, 2015. [Google Scholar]
- Tulchinsky, T.H. Micronutrient deficiency conditions: Global health issues. Public Health Rev. 2010, 32, 243. [Google Scholar] [CrossRef]
- Nations, U. World Population Prospects: The 2017 Revision, Key Findings and Advance Tables; Working Paper No. ESA/P/WP/248; Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2017. [Google Scholar]
- Ramankutty, N.; Mehrabi, Z.; Waha, K.; Jarvis, L.; Kremen, C.; Herrero, M.; Rieseberg, L.H. Trends in global agricultural land use: Implications for environmental health and food security. Ann. Rev. Plant Biol. 2018, 69, 789–815. [Google Scholar] [CrossRef] [PubMed]
- Sanches, I.D.; Feitosa, R.Q.; Diaz, P.M.A.; Soares, M.D.; Luiz, A.J.B.; Schultz, B.; Maurano, L.E.P. Campo Verde Database: Seeking to Improve Agricultural Remote Sensing of Tropical Areas. IEEE Geosci. Remote Sens. Lett. 2018, 15, 369–373. [Google Scholar] [CrossRef]
- Anderson, J.R. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; US Government Printing Office: Washington, DC, USA, 1976; Volume 964.
- Moran, M.S.; Inoue, Y.; Barnes, E. Opportunities and limitations for image-based remote sensing in precision crop management. Remote Sens. Environ. 1997, 61, 319–346. [Google Scholar] [CrossRef]
- Panigrahy, S.; Sharma, S. Mapping of crop rotation using multidate Indian Remote Sensing Satellite digital data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 85–91. [Google Scholar] [CrossRef]
- Wardlow, B.D.; Egbert, S.L. Large-area crop mapping using time-series MODIS 250 m NDVI data: An assessment for the U.S. Central Great Plains. Remote Sens. Environ. 2008, 112, 1096–1116. [Google Scholar] [CrossRef]
- Immitzer, M.; Vuolo, F.; Atzberger, C. First experience with Sentinel-2 data for crop and tree species classifications in central Europe. Remote Sens. 2016, 8, 166. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Belgiu, M.; Csillik, O. Sentinel-2 cropland mapping using pixel-based and object-based time-weighted dynamic time warping analysis. Remote Sens. Environ. 2018, 204, 509–523. [Google Scholar] [CrossRef]
- Skakun, S.; Kussul, N.; Shelestov, A.Y.; Lavreniuk, M.; Kussul, O. Efficiency Assessment of Multitemporal C-Band Radarsat-2 Intensity and Landsat-8 Surface Reflectance Satellite Imagery for Crop Classification in Ukraine. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3712–3719. [Google Scholar] [CrossRef]
- Inglada, J.; Arias, M.; Tardy, B.; Morin, D.; Valero, S.; Hagolle, O.; Dedieu, G.; Sepulcre, G.; Bontemps, S.; Defourny, P. Benchmarking of algorithms for crop type land-cover maps using Sentinel-2 image time series. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3993–3996. [Google Scholar] [CrossRef]
- Eberhardt, I.; Schultz, B.; Rizzi, R.; Sanches, I.; Formaggio, A.; Atzberger, C.; Mello, M.; Immitzer, M.; Trabaquini, K.; Foschiera, W.; et al. Cloud cover assessment for operational crop monitoring systems in tropical areas. Remote Sens. 2016, 8, 219. [Google Scholar] [CrossRef]
- Henderson, F.M.; Chasan, R.; Portolese, J.; Hart, T., Jr. Evaluation of SAR-optical imagery synthesis techniques in a complex coastal ecosystem. Photogramm. Eng. Remote Sens. 2002, 68, 839–846. [Google Scholar]
- Forkuor, G.; Conrad, C.; Thiel, M.; Ullmann, T.; Zoungrana, E. Integration of Optical and Synthetic Aperture Radar Imagery for Improving Crop Mapping in Northwestern Benin, West Africa. Remote Sens. 2014, 6, 6472–6499. [Google Scholar] [CrossRef] [Green Version]
- Haack, B. A comparison of land use/cover mapping with varied radar incident angles and seasons. GISci. Remote Sens. 2007, 44, 305–319. [Google Scholar] [CrossRef]
- Soria-Ruiz, J.; Fernandez-Ordonez, Y.; McNairn, H. Corn monitoring and crop yield using optical and microwave remote sensing. In Geoscience and Remote Sensing; IntechOpen: London, UK, 2009. [Google Scholar]
- Jia, K.; Li, Q.; Tian, Y.; Wu, B.; Zhang, F.; Meng, J. Crop classification using multi-configuration SAR data in the North China Plain. Int. J. Remote Sens. 2012, 33, 170–183. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A. Introduction neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Nitze, I.; Schulthess, U.; Asche, H. Comparison of machine learning algorithms random forest, artificial neural network and support vector machine to maximum likelihood for supervised crop type classification. In Proceedings of the 4th GEOBIA, Rio de Janeiro, Brazil, 7–9 May 2012; pp. 7–9. [Google Scholar]
- Lucieer, A.; Stein, A.; Fisher, P. Multivariate texture-based segmentation of remotely sensed imagery for extraction of objects and their uncertainty. Int. J. Remote Sens. 2005, 26, 2917–2936. [Google Scholar] [CrossRef]
- Ruiz, L.; Fdez-Sarría, A.; Recio, J. Texture feature extraction for classification of remote sensing data using wavelet decomposition: A comparative study. In Proceedings of the 20th ISPRS Congress, Istanbul, Turkey, 12–23 July 2004; Volume 35, pp. 1109–1114. [Google Scholar]
- He, D.C.; Wang, L. Texture unit, texture spectrum, and texture analysis. IEEE Trans. Geosci. Remote Sens. 1990, 28, 509–512. [Google Scholar]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote Sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Melgani, F.; Serpico, S.B. A Markov random field approach to spatio-temporal contextual image classification. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2478–2487. [Google Scholar] [CrossRef]
- Achanccaray, P.; Feitosa, R.Q.; Rottensteiner, F.; Sanches, I.; Heipke, C. Spatial-temporal conditional random field based model for crop recognition in tropical regions. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3007–3010. [Google Scholar]
- Leite, P.B.C.; Feitosa, R.Q.; Formaggio, A.R.; da Costa, G.A.O.P.; Pakzad, K.; Sanches, I.D.A. Hidden Markov Models for crop recognition in remote sensing image sequences. Pattern Recognit. Lett. 2011, 32, 19–26. [Google Scholar] [CrossRef]
- Siachalou, S.; Mallinis, G.; Tsakiri-Strati, M. A hidden Markov models approach for crop classification: Linking crop phenology to time series of multi-sensor remote sensing data. Remote Sens. 2015, 7, 3633–3650. [Google Scholar] [CrossRef]
- Firat, O.; Can, G.; Vural, F.T.Y. Representation learning for contextual object and region detection in remote sensing. In Proceedings of the 2014 22nd International Conference on Pattern Recognition (ICPR), Stockholm, Sweden, 24–28 August 2014; pp. 3708–3713. [Google Scholar]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised deep feature extraction for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1349–1362. [Google Scholar] [CrossRef]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep Learning Classification of Land Cover and Crop Types Using Remote Sensing Data. IEEE Geosc. Remote Sens. Lett. 2017, 14, 778–782. [Google Scholar] [CrossRef]
- Rußwurm, M.; Körner, M. Multi-temporal land cover classification with sequential recurrent encoders. ISPRS Int. J. Geo-Inf. 2018, 7, 129. [Google Scholar] [CrossRef]
- Ndikumana, E.; Ho Tong Minh, D.; Baghdadi, N.; Courault, D.; Hossard, L. Deep recurrent neural network for agricultural classification using multitemporal SAR Sentinel-1 for Camargue, France. Remote Sens. 2018, 10, 1217. [Google Scholar] [CrossRef]
- Zhong, L.; Hu, L.; Zhou, H. Deep learning based multi-temporal crop classification. Remote Sens. Environ. 2019, 221, 430–443. [Google Scholar] [CrossRef]
- Hinton, G.E.; Zemel, R.S. Autoencoders, Minimum Description Length and Helmholtz Free Energy. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 28 November–1 December 1994; pp. 3–10. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Castro, J.D.B.; Feitoza, R.Q.; Rosa, L.C.L.; Diaz, P.M.A.; Sanches, I.D.A. A Comparative Analysis of Deep Learning Techniques for Sub-Tropical Crop Types Recognition from Multitemporal Optical/SAR Image Sequences. In Proceedings of the 2017 30th SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Niteroi, Brazil, 17–20 October 2017; pp. 382–389. [Google Scholar] [CrossRef]
- Tuia, D.; Volpi, M.; Moser, G. Decision Fusion With Multiple Spatial Supports by Conditional Random Fields. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3277–3289. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Volpi, M.; Tuia, D. Dense semantic labeling of subdecimeter resolution images with convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 881–893. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional neural networks for large-scale remote-sensing image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 645–657. [Google Scholar] [CrossRef]
- La Rosa, L.E.C.; Happ, P.N.; Feitosa, R.Q. Dense Fully Convolutional Networks for Crop Recognition from Multitemporal SAR Image Sequences. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 7460–7463. [Google Scholar]
- Waldhoff, G.; Curdt, C.; Hoffmeister, D.; Bareth, G. Analysis of Multitemporal and Multisensor Remote Sens. Data for Crop Rotation Mapping. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-7, 177–185. [Google Scholar] [CrossRef]
- Kussul, N.; Skakun, S.; Shelestov, A.; Kussul, O. The Use of Satellite Sar Imagery to Crop Classification in Ukraine Within Jecam Project Space Research Institute NAS Ukraine and SSA Ukraine; National Technical University of Ukraine “Kyiv Polytechnic Institute”; National University of Life and Environ. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 1497–1500. [Google Scholar] [CrossRef]
- Kenduiywo, B.K.; Bargiel, D.; Soergel, U. Crop Type Mapping From A Sequence Of Terrasar-X Images with Dynamic Conditional Random Fields. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 59. [Google Scholar] [CrossRef]
- Inglada, J.; Vincent, A.; Arias, M.; Marais-Sicre, C. Improved early crop type identification by joint use of high temporal resolution SAR and optical image time series. Remote Sens. 2016, 8, 362. [Google Scholar] [CrossRef]
- Kenduiywo, B.K.; Bargiel, D.; Soergel, U. Higher Order Dynamic Conditional Random Fields Ensemble for Crop Type Classification in Radar Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4638–4654. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef] [Green Version]
- Bargiel, D. Capabilities of high resolution satellite radar for the detection of semi-natural habitat structures and grasslands in agricultural landscapes. Ecol. Inform. 2013, 13, 9–16. [Google Scholar] [CrossRef]
- Sonobe, R.; Tani, H.; Wang, X.; Kobayashi, N.; Shimamura, H. Random forest classification of crop type using multi-temporal TerraSAR-X dual-polarimetric data. Remote Sens. Lett. 2014, 5, 157–164. [Google Scholar] [CrossRef] [Green Version]
- Larrañaga, A.; Álvarez-Mozos, J. On the added value of Quad-Pol Data in a multi-temporal crop classification framework based on RADARSAT-2 imagery. Remote Sens. 2016, 8, 335. [Google Scholar] [CrossRef]
- Jegou, S.; Drozdzal, M.; Vazquez, D.; Romero, A.; Bengio, Y. The One Hundred Layers Tiramisu: Fully Convolutional DenseNets for Semantic Segmentation. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1175–1183. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC press: Boca Raton, FL, USA, 2008. [Google Scholar]

















| Year | Month | Date |
|---|---|---|
| October | 29 | |
| 2015 | November | 10, 22 |
| December | 04, 16 | |
| January | 21 | |
| February | 14 | |
| 2016 | March | 09, 21 |
| May | 08, 20 | |
| June | 13 | |
| July | 07, 21 |
| Type | Output Size | Params |
|---|---|---|
| Input | - | |
| Conv | 70,100 | |
| Pool | - | |
| FC | 200 | 180,200 |
| Drop | 200 | - |
| Softmax | 1809 | |
| Total | - | 252,109 |
| Type | Output Size | Params |
|---|---|---|
| Input | - | |
| Conv-1 | 12,096 | |
| DB-1 | 16,576 | |
| DS-1 | 6720 | |
| DB-2 | 26,048 | |
| DS-2 | 12,992 | |
| DB-3 | 35,520 | |
| TConv-1 | 9248 | |
| DB-4 | 44,992 | |
| TConv-2 | 9248 | |
| Conv-2 | 1120 | |
| Total params | - | 174,560 |
| Trainable params | - | 172,512 |
| ... | ||||
|---|---|---|---|---|
| ... | ||||
| ... | ||||
| ... | ... | ... | ... | ... |
| ... |
| RFpixel | AEpatch | CNNpatch | FCNpixel | |
|---|---|---|---|---|
| Before MLCS | 15,609 | 17,532 | 34,591 | 16,478 |
| After MLCS | 183 | 173 | 238 | 252 |
| Reference | Total of 71 sequences | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cué La Rosa, L.E.; Queiroz Feitosa, R.; Nigri Happ, P.; Del’Arco Sanches, I.; Ostwald Pedro da Costa, G.A. Combining Deep Learning and Prior Knowledge for Crop Mapping in Tropical Regions from Multitemporal SAR Image Sequences. Remote Sens. 2019, 11, 2029. https://doi.org/10.3390/rs11172029
Cué La Rosa LE, Queiroz Feitosa R, Nigri Happ P, Del’Arco Sanches I, Ostwald Pedro da Costa GA. Combining Deep Learning and Prior Knowledge for Crop Mapping in Tropical Regions from Multitemporal SAR Image Sequences. Remote Sensing. 2019; 11(17):2029. https://doi.org/10.3390/rs11172029
Chicago/Turabian StyleCué La Rosa, Laura Elena, Raul Queiroz Feitosa, Patrick Nigri Happ, Ieda Del’Arco Sanches, and Gilson Alexandre Ostwald Pedro da Costa. 2019. "Combining Deep Learning and Prior Knowledge for Crop Mapping in Tropical Regions from Multitemporal SAR Image Sequences" Remote Sensing 11, no. 17: 2029. https://doi.org/10.3390/rs11172029
APA StyleCué La Rosa, L. E., Queiroz Feitosa, R., Nigri Happ, P., Del’Arco Sanches, I., & Ostwald Pedro da Costa, G. A. (2019). Combining Deep Learning and Prior Knowledge for Crop Mapping in Tropical Regions from Multitemporal SAR Image Sequences. Remote Sensing, 11(17), 2029. https://doi.org/10.3390/rs11172029








