Estimating Peanut Leaf Chlorophyll Content with Dorsiventral Leaf Adjusted Indices: Minimizing the Impact of Spectral Differences between Adaxial and Abaxial Leaf Surfaces
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Data Analysis
2.2.1. Construction of a Dorsiventral Leaf Adjusted Ratio Index
2.2.2. Published Vegetation Indices
2.2.3. Model Calibration and Validation
3. Results
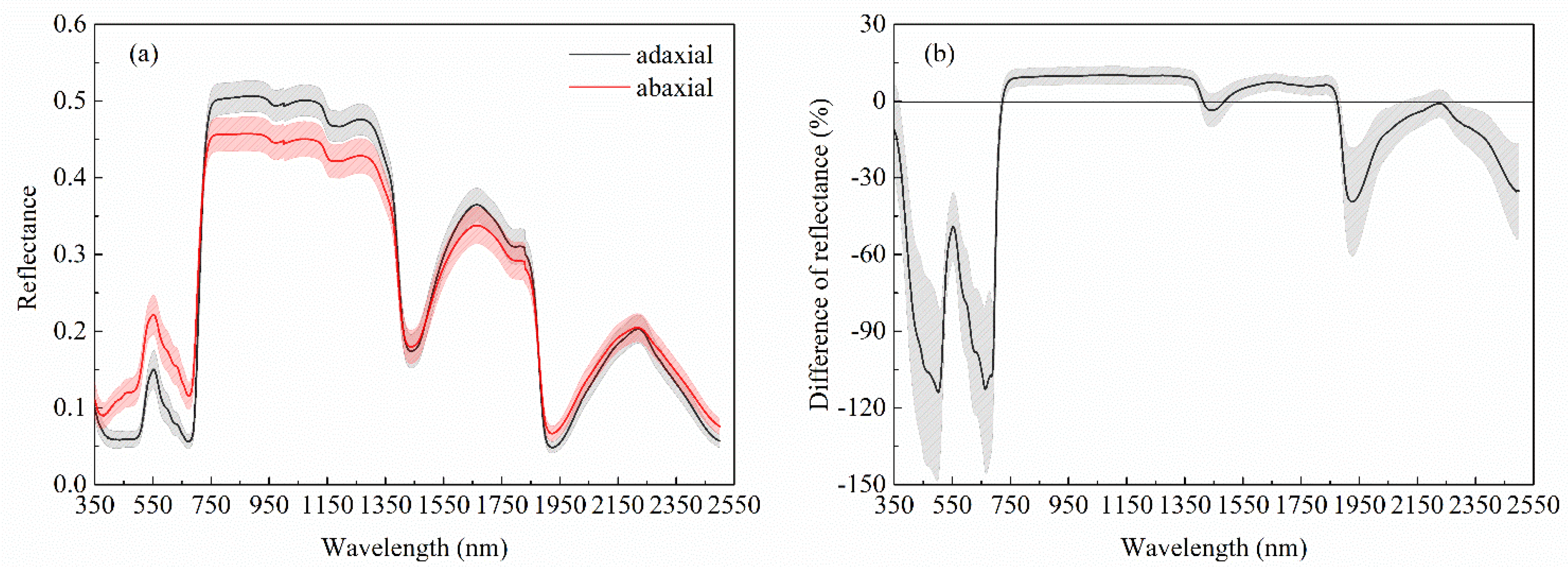
3.1. Spectral Differences Between Adaxial and Abaxial Surfaces
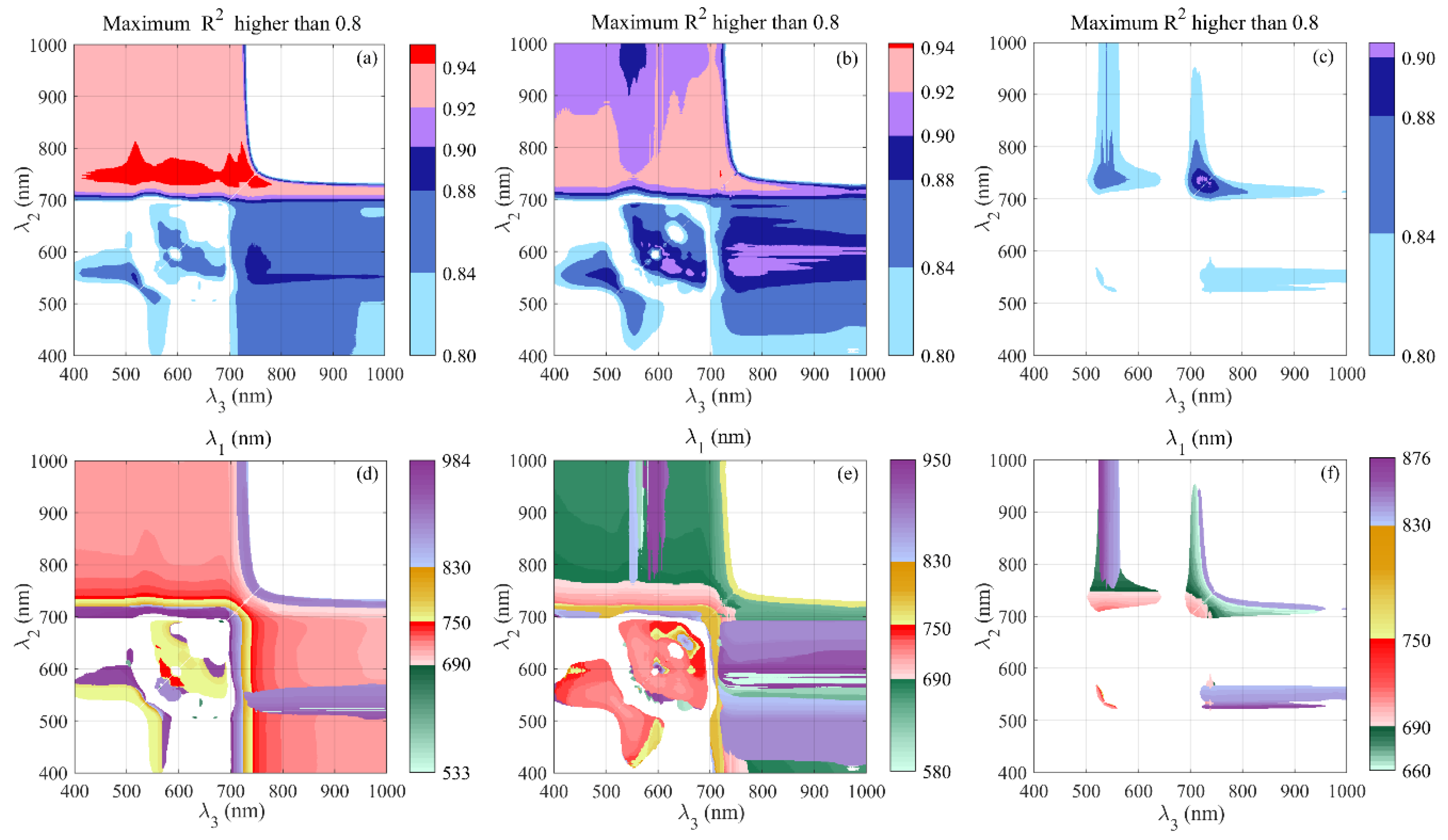
3.2. Relationships Between Optimal MDATT Indices and Peanut LCC
3.3. Relationships Between DLARI and Peanut LCC
3.3.1. Performance of DLARIs Incorporating Wavelengths Between 660 and 750 nm
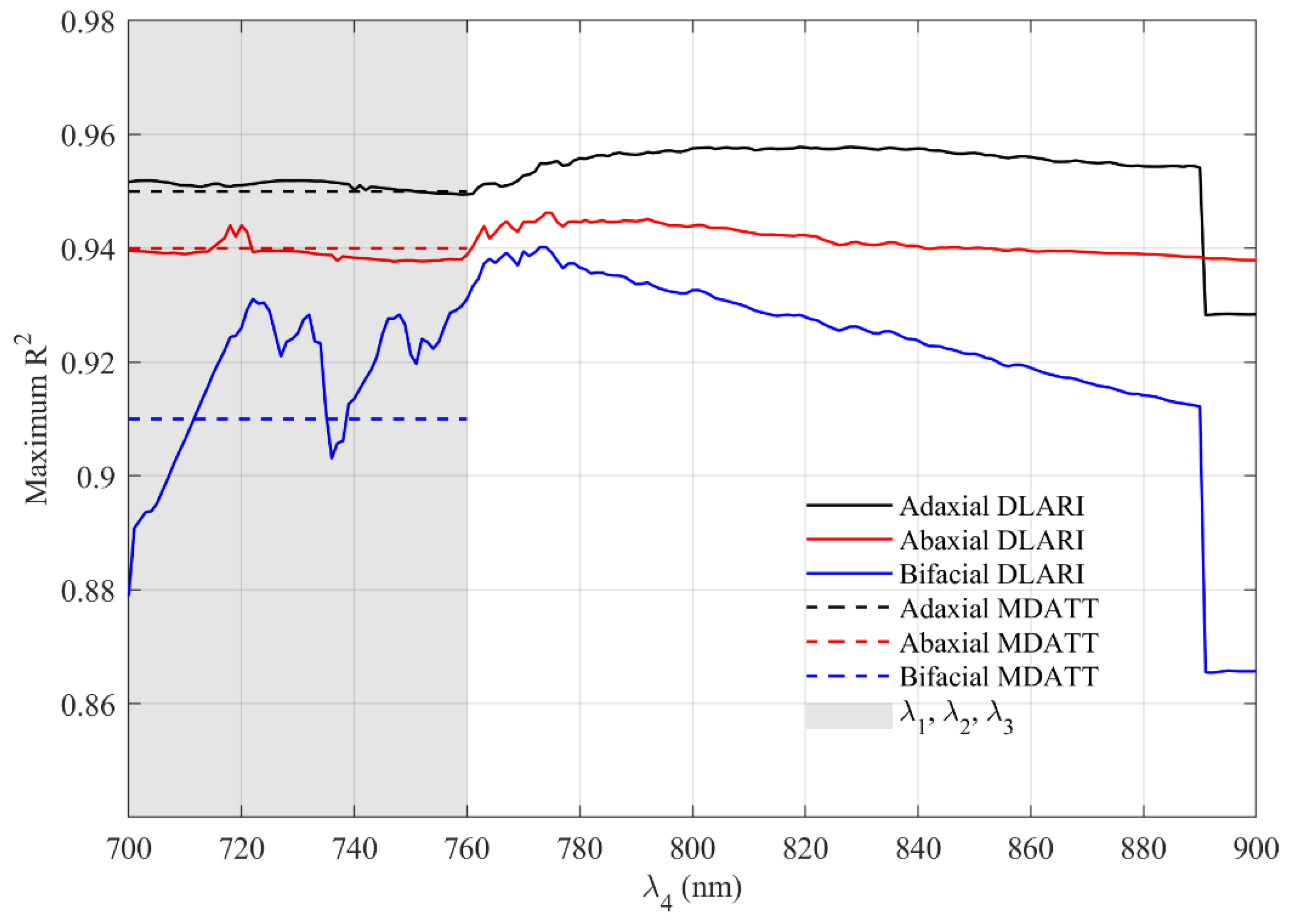
3.3.2. Performance of DLARIs Incorporating Wavelengths Over 750 nm
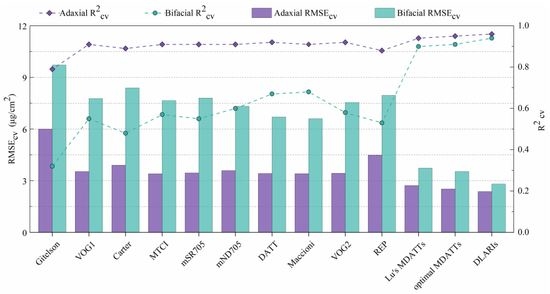
3.4. Comparing Developed Indices with Those of Previous Studies
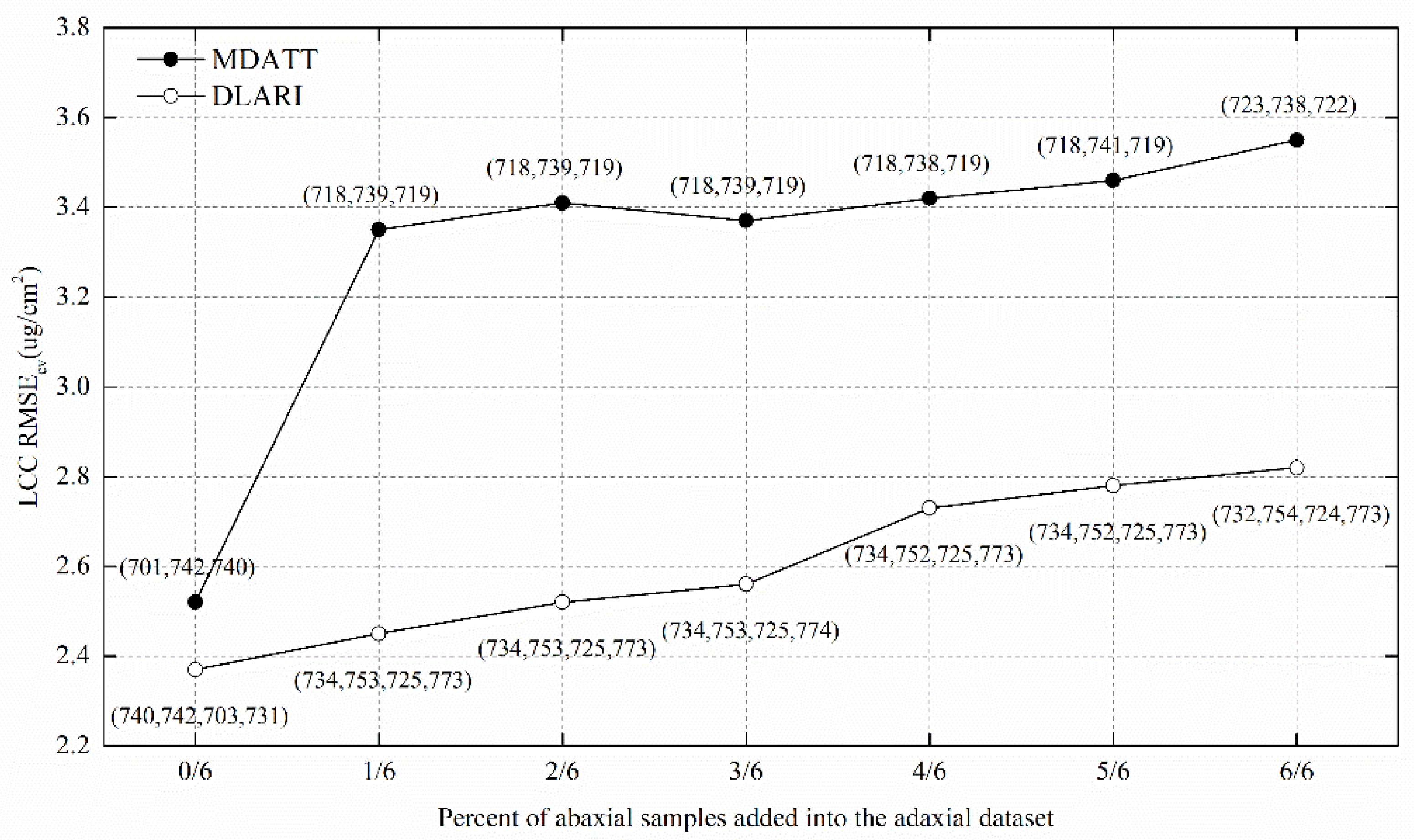
3.5. Comparison of the DLARI and MDATT
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FAOSTAT. 2017. Available online: http://www.fao.org (accessed on 21 May 2019).
- Akram, N.A.; Shafiq, F.; Ashraf, M. Peanut (Arachis hypogaea L.): A prospective legume crop to offer multiple health benefits under changing climate. Compr. Rev. Food Sci. Food Saf. 2018, 17, 1325–1338. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Anjum, S.A.; Xie, X.Y.; Wang, L.C.; Saleem, M.F.; Man, C.; Lei, W. Morphological, physiological and biochemical responses of plants to drought stress. Afr. J. Agric. Res. 2011, 6, 2026–2032. [Google Scholar]
- Mulla, D.J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Hunt, E.R.; Doraiswamy, P.C.; McMurtrey, J.E.; Daughtry, C.S.T.; Perry, E.M.; Akhmedov, B. A visible band index for remote sensing leaf chlorophyll content at the canopy scale. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 103–112. [Google Scholar] [CrossRef] [Green Version]
- Verrelst, J.; Malenovský, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.-P.; Lewis, P.; North, P.; Moreno, J. Quantifying vegetation biophysical variables from imaging spectroscopy data: A review on retrieval methods. Surv. Geophys. 2019, 40, 589–629. [Google Scholar] [CrossRef]
- Féret, J.-B.; François, C.; Gitelson, A.; Asner, G.P.; Barry, K.M.; Panigada, C.; Richardson, A.D.; Jacquemoud, S. Optimizing spectral indices and chemometric analysis of leaf chemical properties using radiative transfer modeling. Remote Sens. Environ. 2011, 115, 2742–2750. [Google Scholar] [CrossRef] [Green Version]
- Malenovský, Z.; Homolová, L.; Zurita-Milla, R.; Lukeš, P.; Kaplan, V.; Hanuš, J.; Gastellu-Etchegorry, J.-P.; Schaepman, M.E. Retrieval of spruce leaf chlorophyll content from airborne image data using continuum removal and radiative transfer. Remote Sens. Environ. 2013, 131, 85–102. [Google Scholar] [CrossRef] [Green Version]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P. Retrieval of foliar information about plant pigment systems from high resolution spectroscopy. Remote Sens. Environ. 2009, 113, S67–S77. [Google Scholar] [CrossRef] [Green Version]
- Datt, B. A new reflectance index for remote sensing of chlorophyll content in higher plants: Tests using eucalyptus leaves. J. Plant Physiol. 1999, 154, 30–36. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz †, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Kalariya, K.A.; Singh, A.L.; Goswami, N.; Mehta, D.; Mahatma, M.K.; Ajay, B.C.; Chakraborty, K.; Zala, P.V.; Chaudhary, V.; Patel, C.B. Photosynthetic characteristics of peanut genotypes under excess and deficit irrigation during summer. Physiol. Mol. Biol. Plants 2015, 21, 317–327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hlavinka, J.; Nauš, J.; Špundová, M. Anthocyanin contribution to chlorophyll meter readings and its correction. Photosynth. Res. 2013, 118, 277–295. [Google Scholar] [CrossRef] [PubMed]
- Stuckens, J.; Verstraeten, W.W.; Delalieux, S.; Swennen, R.; Coppin, P. A dorsiventral leaf radiative transfer model: Development, validation and improved model inversion techniques. Remote Sens. Environ. 2009, 113, 2560–2573. [Google Scholar] [CrossRef]
- Baránková, B.; Lazár, D.; Nauš, J. Analysis of the effect of chloroplast arrangement on optical properties of green tobacco leaves. Remote Sens. Environ. 2016, 174, 181–196. [Google Scholar] [CrossRef]
- Lu, X.; Lu, S. Effects of adaxial and abaxial surface on the estimation of leaf chlorophyll content using hyperspectral vegetation indices. Int. J. Remote Sens. 2015, 36, 1447–1469. [Google Scholar] [CrossRef]
- Lu, S.; Lu, X.; Zhao, W.; Liu, Y.; Wang, Z.; Omasa, K. Comparing vegetation indices for remote chlorophyll measurement of white poplar and Chinese elm leaves with different adaxial and abaxial surfaces. J. Exp. Bot. 2015, 66, 5625–5637. [Google Scholar] [CrossRef] [Green Version]
- Lu, S.; Lu, F.; You, W.; Wang, Z.; Liu, Y.; Omasa, K. A robust vegetation index for remotely assessing chlorophyll content of dorsiventral leaves across several species in different seasons. Plant Methods 2018, 14, 15. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.P.W.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods—A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Wang, W.; Yao, X.; Yao, X.; Tian, Y.; Liu, X.; Ni, J.; Cao, W.; Zhu, Y. Estimating leaf nitrogen concentration with three-band vegetation indices in rice and wheat. Field Crop. Res. 2012, 129, 90–98. [Google Scholar] [CrossRef]
- Xie, Q.; Dash, J.; Huang, W.; Peng, D.; Qin, Q.; Mortimer, H.; Casa, R.; Pignatti, S.; Laneve, G.; Pascucci, S.; et al. Vegetation indices combining the red and red-edge spectral information for leaf area index retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1482–1493. [Google Scholar] [CrossRef]
- Brown, L.A.; Dash, J.; Lidón, A.L.; Lopez-Baeza, E.; Dransfeld, S. Synergetic exploitation of the Sentinel-2 missions for validating the Sentinel-3 ocean and land color instrument terrestrial chlorophyll index over a vineyard dominated mediterranean environment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2244–2251. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J.; Tallis, M.J.; Llewellyn, G.M.; Taylor, G.; Snoeij, P. Validating the MERIS Terrestrial Chlorophyll Index (MTCI) with ground chlorophyll content data at MERIS spatial resolution. Int. J. Remote Sens. 2010, 31, 5513–5532. [Google Scholar] [CrossRef] [Green Version]
- Vuolo, F.; Dash, J.; Curran, P.J.; Lajas, D.; Kwiatkowska, E. Methodologies and uncertainties in the use of the terrestrial chlorophyll index for the Sentinel-3 mission. Remote Sens. 2012, 4, 1112–1133. [Google Scholar] [CrossRef]
- Kong, W.; Huang, W.; Liu, J.; Chen, P.; Qin, Q.; Ye, H.; Peng, D.; Dong, Y.; Mortimer, A.H. Estimation of canopy carotenoid content of winter wheat using multi-angle hyperspectral data. Adv. Space Res. 2017, 60, 1988–2000. [Google Scholar] [CrossRef]
- Sartory, D.P.; Grobbelaar, J.U. Extraction of chlorophyll a from freshwater phytoplankton for spectrophotometric analysis. Hydrobiologia 1984, 114, 177–187. [Google Scholar] [CrossRef]
- Arnon, D.I. Copper enzymes in isolated chloroplasts. polyphenol oxidase in beta vulgaris. Plant Physiol. 1949, 24, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Baret, F.; Andrieu, B.; Guyot, G. A simple model for leaf optical properties in visible and near-infrared: Application to the analysis of spectral shifts determinism. In Applications of Chlorophyll Fluorescence in Photosynthesis Research, Stress Physiology, Hydrobiology and Remote Sensing; Springer: Dordrecht, The Netherlands, 1988; pp. 345–351. [Google Scholar]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red edge spectral measurements from sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Carter, G.A. Ratios of leaf reflectances in narrow wavebands as indicators of plant stress. Int. J. Remote Sens. 1994, 15, 697–703. [Google Scholar] [CrossRef]
- Maccioni, A.; Agati, G.; Mazzinghi, P. New vegetation indices for remote measurement of chlorophylls based on leaf directional reflectance spectra. J. Photochem. Photobiol. B Biol. 2001, 61, 52–61. [Google Scholar] [CrossRef]
- Guyot, G.; Baret, F. Utilisation de la haute resolution spectrale pour suivre l’etat des couverts vegetaux. In Proceedings of the Spectral Signatures of Objects in Remote Sensing, Modane, France, 18–22 January 1988; p. 279. [Google Scholar]
- Meyer, H.; Lehnert, L.W.; Wang, Y.; Reudenbach, C.; Nauss, T.; Bendix, J. From local spectral measurements to maps of vegetation cover and biomass on the Qinghai-Tibet-Plateau: Do we need hyperspectral information? Int. J. Appl. Earth Obs. Geoinf. 2017, 55, 21–31. [Google Scholar] [CrossRef]
- Reicosky, D.A.; Hanover, J.W. Physiological effects of surface waxes. Plant Physiol. 1978, 62, 101–104. [Google Scholar] [CrossRef]
- McClendon, J.H.; Fukshansky, L. On the interpretation of absorption spectra of leaves–I. Introduction and the correction of leaf spectra for surface reflection. Photochem. Photobiol. 1990, 51, 203–210. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.M.; Zhang, Y. The applicability of empirical vegetation indices for determining leaf chlorophyll content over different leaf and canopy structures. Ecol. Complex. 2014, 17, 119–130. [Google Scholar] [CrossRef]
- Kross, A.; McNairn, H.; Lapen, D.; Sunohara, M.; Champagne, C. Assessment of RapidEye vegetation indices for estimation of leaf area index and biomass in corn and soybean crops. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 235–248. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Dash, J.; Huete, A.; Jiang, A.; Yin, G.; Ding, Y.; Peng, D.; Hall, C.C.; Brown, L.; Shi, Y.; et al. Retrieval of crop biophysical parameters from Sentinel-2 remote sensing imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 187–195. [Google Scholar] [CrossRef]
- Delloye, C.; Weiss, M.; Defourny, P. Retrieval of the canopy chlorophyll content from Sentinel-2 spectral bands to estimate nitrogen uptake in intensive winter wheat cropping systems. Remote Sens. Environ. 2018, 216, 245–261. [Google Scholar] [CrossRef]
- Kanning, M.; Kühling, I.; Trautz, D.; Jarmer, T. High-Resolution UAV-Based Hyperspectral Imagery for LAI and Chlorophyll Estimations from Wheat for Yield Prediction. Remote Sens. 2018, 10, 2000. [Google Scholar] [CrossRef]
- Tahir, N.; Naqvi, S.M.; Lan, Y.; Zhang, Y.; Wang, Y.; Afzal, M.; Cheema, M.J. Real time monitoring chlorophyll content based on vegetation indices derived from multispectral UAVs in the kinnow orchard. Int. J. Precis. Agric. Aviat. 2018, 1, 24–31. [Google Scholar] [CrossRef]






| Index | Abbreviation | Formula | Scale | Reference |
|---|---|---|---|---|
| Gitelson’s index | Gitelson | 1/R700 | Leaf | [35] |
| Vogelmann’s first Index | VOG1 | R740/R720 | Leaf | [36] |
| Carter’ Index | Carter | R710/R760 | Leaf | [37] |
| MERIS Terrestrial Chlorophyll Index | MTCI | (R740 − R705)/(R705 − R665) | Canopy | [22] |
| Modified Simple Ratio | mSR705 | (R750 − R445)/(R705 − R445) | Leaf | [13] |
| Modified Normalized Difference Vegetation Index | mND705 | (R750 − R705)/(R750 + R705 − 2 × R445) | Leaf | [13] |
| Datt’ Index | DATT | (R850 − R710)/(R850 − R680) | Leaf | [12] |
| Maccioni’ Index | Maccioni | (R780 − R710)/(R780 − R680) | Leaf | [38] |
| Vogelmann’s second Index | VOG2 | (R734 − R747)/(R715 + R720) | Leaf | [36] |
| Red-Edge Position Index | REP | 700 + 40 × (((R670 + R780)/2 − R700)/(R740 − R700)) | Leaf | [39] |
| Modified Datt Index | Lu′s MDATT | (R691 − R7745)/(R7691 − R745) | Leaf | [21] |
| Modified Datt Index | Lu′s MDATT | (R721 − R744)/(R721 − R714) | Leaf | [21] |
| Index | Dataset | Wavelength Region Considered (nm) | Optimal Wavelengths (nm) | R2 | R2cv | RMSEcv (μg/cm2) |
|---|---|---|---|---|---|---|
| MDATT | Adaxial reflectance | 400–1000 | λ1: 701; λ2: 742; λ3: 740 | 0.95 | 0.95 | 2.52 |
| Abaxial reflectance | 400–1000 | λ1: 718; λ2: 747; λ3: 720 | 0.94 | 0.94 | 2.69 | |
| Bifacial reflectance | 400–1000 | λ1: 723; λ2: 738; λ3: 722 | 0.91 | 0.91 | 3.53 |
| Dataset | Adaxial MDATT | Bifacial MDATT | ||
|---|---|---|---|---|
| R2cv | RMSEcv (μg/cm2) | R2cv | RMSEcv (μg/cm2) | |
| Bifacial reflectance | 0.87 | 4.14 | 0.91 | 3.53 |
| Index | Dataset | Wavelength Region Considered (nm) | Optimal Wavelengths (nm) | R2 | R2cv | RMSEcv (μg/cm2) |
|---|---|---|---|---|---|---|
| DLARI | Adaxial reflectance | 660–750 | λ1: 740; λ2: 742; λ3: 703; λ4: 731 | 0.95 | 0.95 | 2.53 |
| Abaxial reflectance | 660–750 | λ1: 714; λ2: 746; λ3: 718; λ4: 720 | 0.94 | 0.94 | 2.62 | |
| Bifacial reflectance | 660–750 | λ1: 731; λ2: 741; λ3: 722; λ4: 750 | 0.91 | 0.92 | 3.34 |
| Index | Dataset | Wavelength Region Considered (nm) | Optimal Wavelengths (nm) | R2 | R2cv | RMSEcv (μg/cm2) |
|---|---|---|---|---|---|---|
| DLARI | Adaxial reflectance | 660–820 | λ1: 735; λ2: 753; λ3: 715; λ4: 819 | 0.96 | 0.96 | 2.37 |
| Abaxial reflectance | 660–820 | λ1: 731; λ2: 755; λ3: 722; λ4: 774 | 0.95 | 0.95 | 2.58 | |
| Bifacial reflectance | 660–820 | λ1: 732; λ2: 754; λ3: 724; λ4: 773 | 0.94 | 0.94 | 2.81 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, M.; Wang, Z.; Huete, A.; Brown, L.A.; Wang, H.; Xie, Q.; Xu, X.; Ding, Y. Estimating Peanut Leaf Chlorophyll Content with Dorsiventral Leaf Adjusted Indices: Minimizing the Impact of Spectral Differences between Adaxial and Abaxial Leaf Surfaces. Remote Sens. 2019, 11, 2148. https://doi.org/10.3390/rs11182148
Xie M, Wang Z, Huete A, Brown LA, Wang H, Xie Q, Xu X, Ding Y. Estimating Peanut Leaf Chlorophyll Content with Dorsiventral Leaf Adjusted Indices: Minimizing the Impact of Spectral Differences between Adaxial and Abaxial Leaf Surfaces. Remote Sensing. 2019; 11(18):2148. https://doi.org/10.3390/rs11182148
Chicago/Turabian StyleXie, Mengmeng, Zhongqiang Wang, Alfredo Huete, Luke A. Brown, Heyu Wang, Qiaoyun Xie, Xinpeng Xu, and Yanling Ding. 2019. "Estimating Peanut Leaf Chlorophyll Content with Dorsiventral Leaf Adjusted Indices: Minimizing the Impact of Spectral Differences between Adaxial and Abaxial Leaf Surfaces" Remote Sensing 11, no. 18: 2148. https://doi.org/10.3390/rs11182148
APA StyleXie, M., Wang, Z., Huete, A., Brown, L. A., Wang, H., Xie, Q., Xu, X., & Ding, Y. (2019). Estimating Peanut Leaf Chlorophyll Content with Dorsiventral Leaf Adjusted Indices: Minimizing the Impact of Spectral Differences between Adaxial and Abaxial Leaf Surfaces. Remote Sensing, 11(18), 2148. https://doi.org/10.3390/rs11182148