Rain Monitoring with Polarimetric GNSS Signals: Ground-Based Experimental Research
Abstract
:1. Introduction
2. Experiments and Data
2.1. Mechanism of Detection
2.2. Experiments
2.3. Data Processing Algorithm
2.3.1. Observation Equation
2.3.2. Method to Solve Hardware Effect and Phase Ambiguity
2.3.3. Method to Deal with Multipath Effect
2.3.4. Method to Identify Phase Shift Induced by Raindrops
2.3.5. Comparison with Multi-Source Data
3. Results and Discussion
3.1. Statistical Results of G27 Satellite in 2015
3.1.1. Phase Shift in No-Rain and Rainy Days
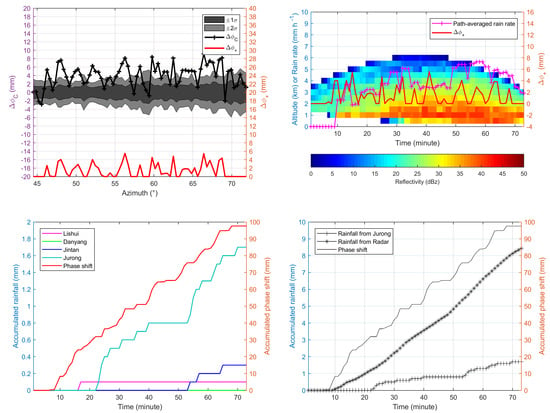
3.1.2. Comparison with Weather Radar
3.1.3. Comparison with Weather Station
3.2. Statistical Results of G22 Satellite in 2015
3.2.1. Phase Shift in No-Rain and Rainy Days
3.2.2. Comparison with Weather Radar
3.2.3. Comparison with Weather Station
3.3. Statistical Results in 2016
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science: An Introductory Survey; Academic Press: Burlington, MA, USA, 2006; pp. 1–10. [Google Scholar]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Ribbe, L.; Nauditt, A.; Giraldo-Osorio, J.D.; Thinh, N.X. Temporal and spatial evaluation of satellite rainfall estimates over different regions in Latin-America. Atmos. Res. 2018, 213, 34–50. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Andsager, K.; Easterling, D.R. Long-Term Trends in Extreme Precipitation Events over the Conterminous United States and Canada. J. Clim. 1999, 12, 2515–2527. [Google Scholar] [CrossRef] [Green Version]
- Ricciardelli, E.; Di Paola, F.; Gentile, S.; Cersosimo, A.; Cimini, D.; Gallucci, D.; Geraldi, E.; Larosa, S.; Nilo, S.T.; Ripepi, E.; et al. Analysis of Livorno Heavy Rainfall Event: Examples of Satellite-Based Observation Techniques in Support of Numerical Weather Prediction. Remote Sens. 2018, 10, 1549. [Google Scholar] [CrossRef]
- Gabella, M.; Speirs, P.; Hamann, U.; Germann, U.; Berne, A. Measurement of Precipitation in the Alps Using Dual-Polarization C-Band Ground-Based Radars, the GPM Spaceborne Ku-Band Radar, and Rain Gauges. Remote Sens. 2017, 9, 1147. [Google Scholar] [CrossRef]
- Woldemeskel, F.M.; Sivakumar, B.; Sharma, A. Merging gauge and satellite rainfall with specification of associated uncertainty across Australia. J. Hydrol. 2013, 499, 167–176. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Bringi, V.N.; Balakrishnan, N.; Zrnic, D.S. Error structure of multiparameter radar and surface measurements of rainfall. Part III: Specific differential phase. J. Atoms. Ocean. Tech. 1990, 7, 621–629. [Google Scholar] [CrossRef]
- English, M.; Kochtubajda, B.; Barlow, F.D.; Holt, A.R.; McGuinness, R. Radar measurement of rainfall by differential propagation phase: A pilot experiment. Atmos. Ocean 1991, 29, 357–380. [Google Scholar] [CrossRef] [Green Version]
- Notaroš, B.M.; Bringi, V.N.; Kleinkort, C.; Kennedy, P.; Huang, G.-J.; Thurai, M.; Newman, A.J.; Bang, W.; Lee, G. Accurate Characterization of Winter Precipitation Using Multi-Angle Snowflake Camera, Visual Hull, Advanced Scattering Methods and Polarimetric Radar. Atmosphere 2016, 7, 81. [Google Scholar] [CrossRef]
- Jameson, A.R. The meteorological parameterization of specific attenuation and polarization differential phase shift in rain. J. Appl. Meteorol. 1993, 32, 1741–1750. [Google Scholar] [CrossRef]
- Yan, W.; An, H.; Fu, Y.; Han, Y.; Wang, X.; Ai, W. A method for estimating rain rate from polarimetric GNSS measurements: Preliminary analysis. Atmos. Res. 2014, 149, 70–76. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Iwanami, K. Global precipitation map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Atlas, D.; Ulbrich, C.W. Path-and area-integrated rainfall measurement by microwave attenuation in the 1–3 cm band. J. Appl. Meteorol. 1977, 16, 1322–1331. [Google Scholar] [CrossRef]
- Taur, R.R. Rain Depolarization Measurements on a Satellite-Earth Propagation Path at 4 GHz. IEEE Trans. Antennas Propag. 1975, 23, 854–858. [Google Scholar] [CrossRef]
- Messer, H.; Zinevich, A.; Alpert, P. Environmental Monitoring by Wireless Communication Networks. Science 2006, 312, 713. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Country-wide rainfall maps from cellular communication networks. Proc. Natl. Acad. Sci. USA 2013, 110, 2741–2745. [Google Scholar] [CrossRef] [Green Version]
- Van Leth, T.C.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. A measurement campaign to assess sources of error in microwave link rainfall estimation. Atmos. Meas. Tech. 2018, 11, 4645–4669. [Google Scholar] [CrossRef] [Green Version]
- Asgarimehr, M.; Zavorotny, V.; Wickert, J.; Reich, S. Can GNSS Reflectometry Detect Precipitation Over Oceans? Geophys. Res. Lett. 2018, 45, 12–585. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Cerezo, F. Polarimetric GNSS Radio-Occultations for Heavy Rain Detection. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3841–3844. [Google Scholar]
- Cardellach, E.; Tomás, S.; Oliveras, S.; Padullés, R.; Rius, A.; de la Torre-Juarez, M.; Joseph Turk, F.; Ao, C.O.; Kursinski, E.R.; Schreiner, B.; et al. Sensitivity of PAZ LEO Polarimetric GNSS Radio-Occultation Experiment to Precipitation Events. IEEE Trans. Geosci. Remote Sens. 2015, 53, 190–206. [Google Scholar] [CrossRef]
- Padullés, R.; Cardellach, E.; de la Torre Juárez, M.; Tomás, S.; Turk, F.J.; Oliveras, S.; Rius, A. Atmospheric polarimetric effects on GNSS radio occultations: The ROHP-PAZ field campaign. Atmos. Chem. Phys. 2016, 16, 635–649. [Google Scholar] [CrossRef]
- An, H.; Yan, W.; Huang, Y.; Ai, W.; Wang, Y.; Zhao, X.; Huang, X. GNSS Measurement of Rain Rate by Polarimetric Phase Shift: Theoretical Analysis. Atmosphere 2016, 7, 101. [Google Scholar] [CrossRef]
- Cardellach, E.; Oliveras, S.; Rius, A.; Tomás, S.; Ao, C.O.; Franklin, G.W.; de la Torre Juárez, M. Sensing heavy precipitation with GNSS polarimetric radio occultations. Geophys. Res. Lett. 2019, 46, 1024–1031. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Bai, W.H.; Liu, C.L.; Liu, Y.; Du, Q.F.; Wang, X.Y.; Yang, G.L.; Liao, M.; Yang, Z.D.; Zhang, X.X.; et al. The FengYun-3C radio occultation sounder GNOS: A review of the mission and its early results and science applications. Atmos. Meas. Tech. 2018, 11, 5797–5811. [Google Scholar] [CrossRef]
- Blewitt, G. Carrier phase ambiguity resolution for the Global Positioning System applied to geodetic baselines up to 2000 km. J. Geophys. Res. 1989, 94, 10187–10203. [Google Scholar] [CrossRef] [Green Version]
- Bilich, A.; Larson, K.M. Mapping the GPS multipath environment using the signal-to-noise ratio (SNR). Radio Sci. 2007, 42, RS6003. [Google Scholar] [CrossRef]
- Yedukondalu, K.; Sarma, A.D.; Srinivas, V.S. Estimation and mitigation of GPS multipath interference using adaptive filtering. Progr. Electromagn. Res. M 2011, 21, 133–148. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Smith, J.A. On the estimation of climatological Z–R relationships. J. Appl. Meteor. 1991, 30, 1436–1445. [Google Scholar] [CrossRef]

















| Satellite | Minimum Elevation (°) | Maximum Elevation (°) | Maximum Standard Deviation (mm) | Minimum Standard Deviation (mm) | Mean Standard Deviation (mm) | Number of Rainfall Cases |
|---|---|---|---|---|---|---|
| G1 | 2 | 22.4 | 3.28 | 1.24 | 1.98 | 4 |
| G3 | 2 | 26.5 | 2.40 | 1.01 | 1.55 | 3 |
| G7 | 2 | 11.2 | 3.63 | 1.08 | 2.0 | 2 |
| G9 | 2 | 24.3 | 2.57 | 1.13 | 1.62 | 3 |
| G12 | 2 | 26 | 2.87 | 1.15 | 1.73 | 3 |
| G13 | 2 | 20.8 | 2.75 | 1.34 | 1.96 | 4 |
| G22 | 2 | 25 | 2.77 | 1.03 | 1.63 | 1 |
| G23 | 2 | 18.4 | 2.48 | 0.69 | 1.59 | 1 |
| G24 | 2 | 23.2 | 2.82 | 1.19 | 1.81 | 1 |
| G25 | 2 | 26.7 | 2.57 | 1.03 | 1.63 | 1 |
| G27 | 2 | 20.7 | 2.81 | 1.49 | 2.17 | 2 |
| G30 | 2 | 17.2 | 2.54 | 0.94 | 1.67 | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, H.; Yan, W.; Bian, S.; Ma, S. Rain Monitoring with Polarimetric GNSS Signals: Ground-Based Experimental Research. Remote Sens. 2019, 11, 2293. https://doi.org/10.3390/rs11192293
An H, Yan W, Bian S, Ma S. Rain Monitoring with Polarimetric GNSS Signals: Ground-Based Experimental Research. Remote Sensing. 2019; 11(19):2293. https://doi.org/10.3390/rs11192293
Chicago/Turabian StyleAn, Hao, Wei Yan, Shuangshuang Bian, and Shuo Ma. 2019. "Rain Monitoring with Polarimetric GNSS Signals: Ground-Based Experimental Research" Remote Sensing 11, no. 19: 2293. https://doi.org/10.3390/rs11192293
APA StyleAn, H., Yan, W., Bian, S., & Ma, S. (2019). Rain Monitoring with Polarimetric GNSS Signals: Ground-Based Experimental Research. Remote Sensing, 11(19), 2293. https://doi.org/10.3390/rs11192293