A Structural Classification of Australian Vegetation Using ICESat/GLAS, ALOS PALSAR, and Landsat Sensor Data
Abstract
:1. Introduction
2. The Australian Landscape and Vegetation
3. Methods
3.1. Remote Sensing Data
3.2. Analysis
3.2.1. Segmentation of ALOS PALSAR and Landsat Data
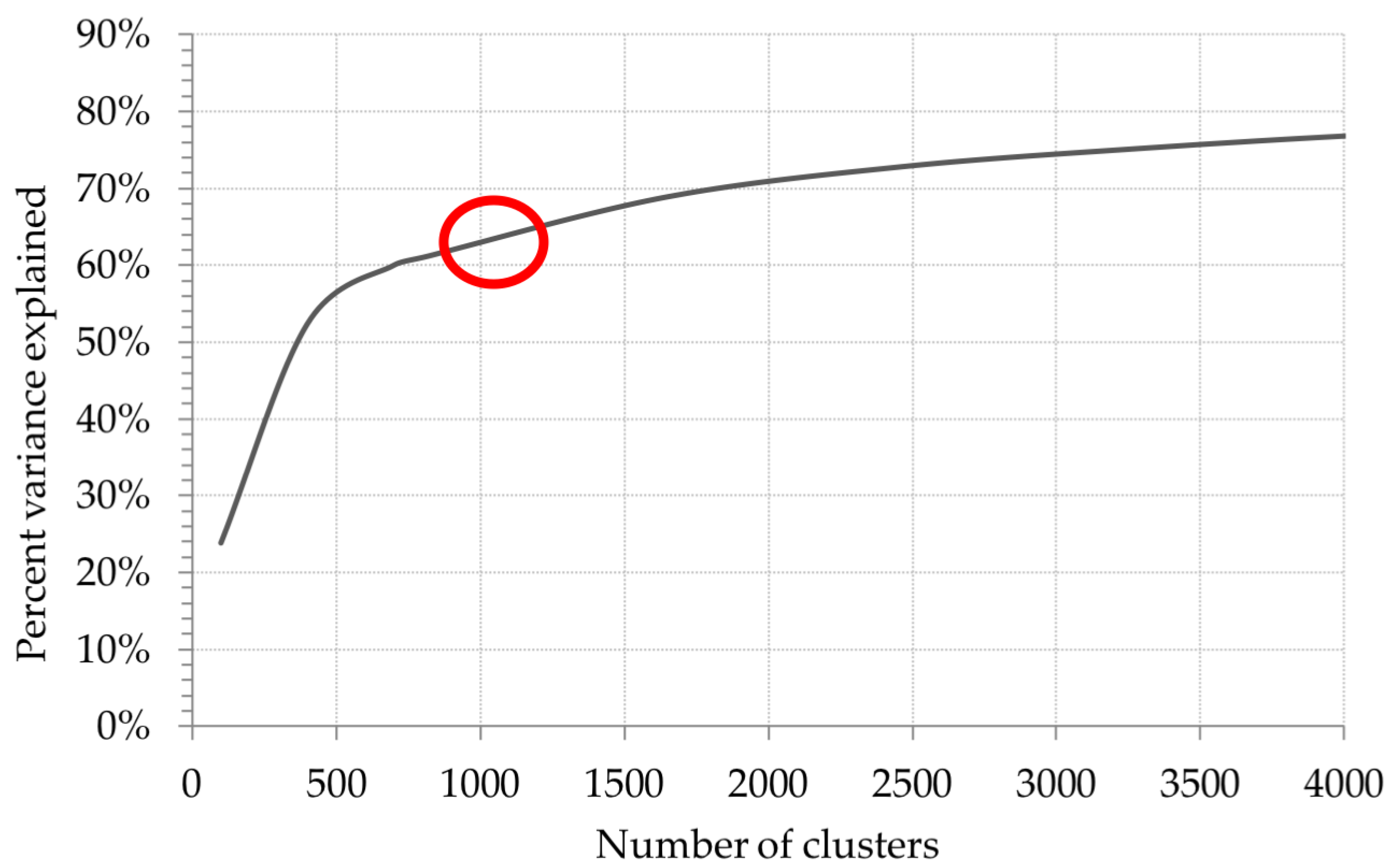
3.2.2. Clustering of Segments
3.2.3. ICESat/GLAS Processing
3.3. Vertical Cover Profile Derivation
3.4. Height Metric Bias Correction
3.5. Imputation of Metrics
3.6. Validation
4. Results
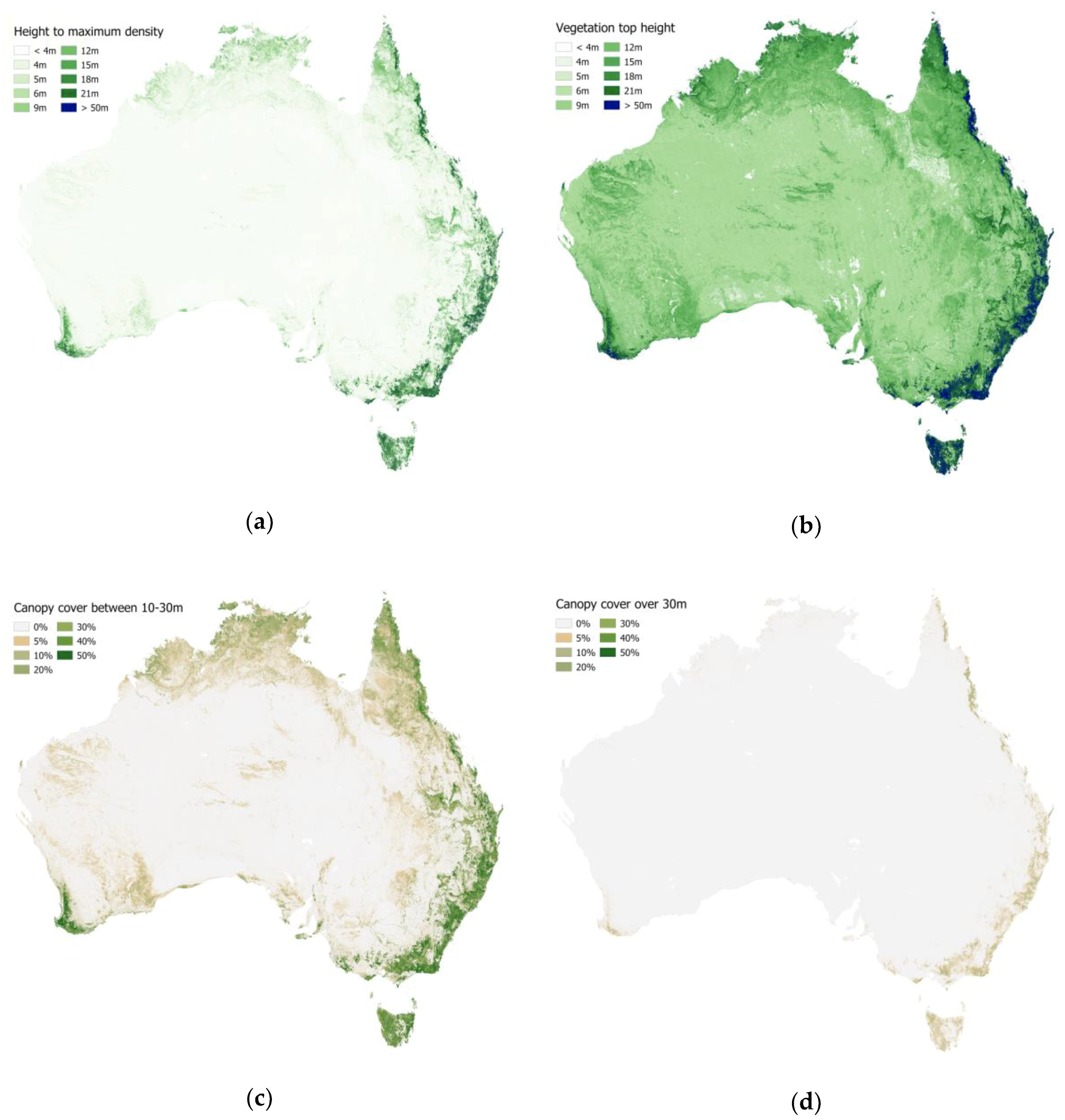
4.1. Height and Cover Maps
4.2. Comparison with Airborne LiDAR Products
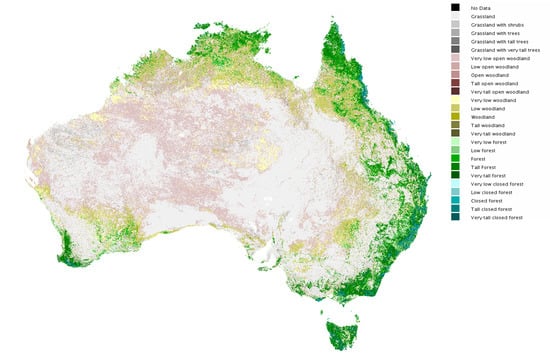
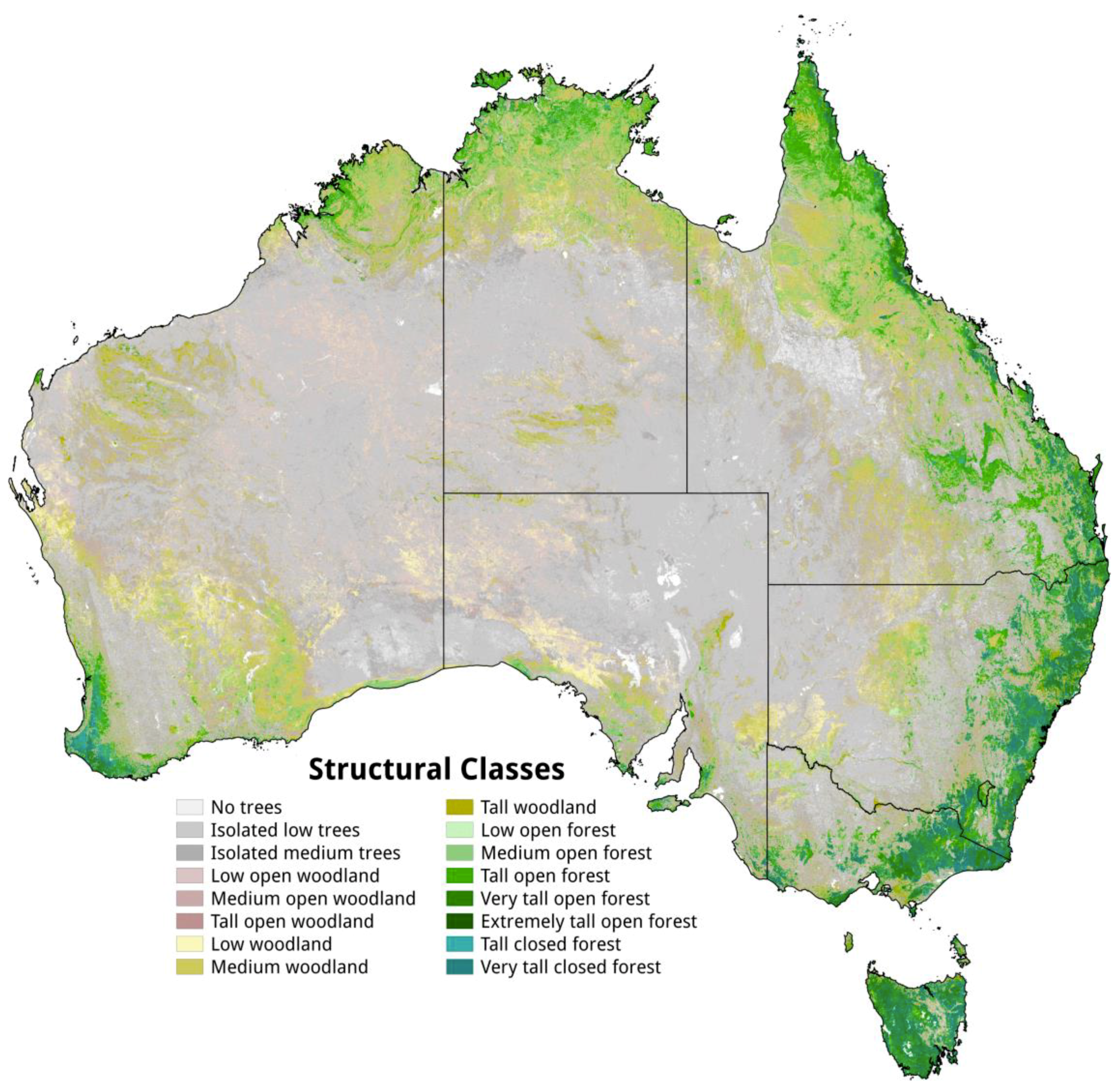
4.3. Structural Formation Map
- The height and cover of dryland woody vegetation (woodland and isolated trees classes) are better represented in the products generated in this study, which was supported by the validation of ALS products (e.g. detection of low trees at the Alice Mulga TERN Auscover site; see Figure 10). This translates into greater extent in the structural formation map, which is also consistent with the findings of Bastin et al. [35].
- This study has used SAR and vegetation cover datasets that were only recently available at the national level, and were resampled to 30 m resolution for segmentation in this study. The resulting fine scale of this data product, compared to Spectht [15], Carnahan [16], and the NVIS [17], will also contribute to the difference in areal extents, particularly for forest classes which are often small and patchy across the landscape and may include riparian areas.
- There is considerable uncertainty introduced by thresholding, since a small change in a height and cover threshold may lead to a large change in areal extent for a given class. The use of ICESat data, while leading to an improved product, is not optimized for vegetation and may limit the detection of low vegetation (<5 m) and differentiation between classes. The smaller footprint of the upcoming NASA GEDI instrument (~25 m) will reduce this uncertainty.
5. Discussion
5.1. Segmentation and Classification of the Landscape
5.2. Vertical Profiles as a Function of Forest Type
5.3. Comparison with Other Studies
5.4. Wider Applications
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fatoyinbo, T.E.; Simard, M. Height and biomass of mangroves in Africa from ICESat/GLAS and SRTM. Int. J. Remote Sens. 2013, 34, 668–681. [Google Scholar] [CrossRef]
- Walker, W.S.; Kellndorfer, J.M.; Pierce, L.E. Quality assessment of SRTM C- and X-band interferometric data: Implications for the retrieval of vegetation canopy height. Remote Sens. Environ. 2007, 106, 428–448. [Google Scholar] [CrossRef]
- Boudreau, J.; Nelson, R.; Margolis, H.; Beaudoin, A.; Guindon, L.; Kimes, D. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Nelson, R.; Boudreau, J.; Gregoire, T.G.; Margolis, H.; Næsset, E.; Gobakken, T.; Ståhl, G. Estimating Quebec provincial forest resources using ICESat/GLAS. Can. J. For. Res. 2009, 39, 862–881. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef] [Green Version]
- Nelson, R.; Ranson, K.J.; Sun, G.; Kimes, D.S.; Kharuk, V.; Montesano, P. Estimating Siberian timber volume using MODIS and ICESat/GLAS. Remote Sens. Environ. 2009, 113, 691–701. [Google Scholar] [CrossRef]
- Kellndorfer, J.M.; Walker, W.S.; LaPoint, E.; Kirsch, K.; Bishop, J.; Fiske, G. Statistical fusion of lidar, InSAR, and optical remote sensing data for forest stand height characterization: A regional-scale method based on LVIS, SRTM, Landsat ETM+, and ancillary data sets. J. Geophys. Res. Biogeosci. 2010. [Google Scholar] [CrossRef]
- Ørka, H.O.; Wulder, M.A.; Gobakken, T.; Næsset, E. Integrating airborne laser scanner data and ancillary information for delineating the boreal–alpine transition zone in Hedmark County, Norway. In Proceedings of the Proceedings of SilviLaser, Freiburg, Germany, 14–17 September 2010. [Google Scholar]
- Los, S.O.; Rosette, J.A.B.; Kljun, N.; North, P.R.J.; Chasmer, L.; Suárez, J.C.; Hopkinson, C.; Hill, R.A.; van Gorsel, E.; Mahoney, C.; et al. Vegetation height and cover fraction between 60° S and 60° N from ICESat GLAS data. Geosci. Model Dev. 2012, 5, 413–432. [Google Scholar] [CrossRef] [Green Version]
- Lefsky, M.A. A global forest canopy height map from the Moderate Resolution Imaging Spectroradiometer and the Geoscience Laser Altimeter System. Geophys. Res. Lett. 2010. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. 2011. [Google Scholar] [CrossRef]
- Chi, H.; Sun, G.; Huang, J.; Guo, Z.; Ni, W.; Fu, A. National Forest Aboveground Biomass Mapping from ICESat/GLAS Data and MODIS Imagery in China. Remote Sens. 2015, 7, 5534–5564. [Google Scholar] [CrossRef] [Green Version]
- Gill, T.; Johansen, K.; Phinn, S.; Trevithick, R.; Scarth, P.; Armston, J. A method for mapping Australian woody vegetation cover by linking continental-scale field data and long-term Landsat time series. Int. J. Remote Sens. 2017, 38, 679–705. [Google Scholar] [CrossRef]
- An Interim Biogeographic Regionalisation for Australia: A Framework for Setting Priorities in the National Reserves System Cooperative Program; Thackway, R.; Cresswell, I.; Australian Nature Conservation Agency (Eds.) Version 4.0; Australian Nature Conservation Agency, Reserve Systems Unit: Canberra, Australia, 1995; ISBN 978-0-642-21371-6. [Google Scholar]
- Specht, R.L. Vegetation. In Leeper, G.W. (ed.), “Australian Environment”; Melbourne University Press: Melbourne, Australia, 1970; pp. 44–67. [Google Scholar]
- Carnahan, J.A. Natural Vegetation. In Atlas of Australian Resources; Second Series; Department of Natural Resources: Canberra, Australia, 1976. [Google Scholar]
- Department of the Environment and Water Resources. Australia’s Native Vegetation: A Summary of Australia’s Major Vegetation Groups; Australian Government: Canberra, Australia, 2007. [Google Scholar]
- Specht, R.L.; Specht, A. Australian plant communities: dynamics of structure, growth and biodiversity; Oxford University Press: Melbourne, Australia, 2000. [Google Scholar]
- Walker, J.; Hopkins, M.S. Vegetation. In Australian Soil and Land Survey: Field Handbook; Inkata Press: Melbourne, Australia, 1990. [Google Scholar]
- Shimada, M.; Ohtaki, T. Generating Large-Scale High-Quality SAR Mosaic Datasets: Application to PALSAR Data for Global Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 637–656. [Google Scholar] [CrossRef]
- Lucas, R.; Armston, J.; Fairfax, R.; Fensham, R.; Accad, A.; Carreiras, J.; Kelley, J.; Bunting, P.; Clewley, D.; Bray, S. An evaluation of the ALOS PALSAR L-band backscatter—Above ground biomass relationship Queensland, Australia: Impacts of surface moisture condition and vegetation structure. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 576–593. [Google Scholar] [CrossRef]
- Clewley, D.; Bunting, P.; Shepherd, J.; Gillingham, S.; Flood, N.; Dymond, J.; Lucas, R.; Armston, J.; Moghaddam, M. A python-based open source system for geographic object-based image analysis (GEOBIA) utilizing raster attribute tables. Remote Sensss. 2014, 6, 6111–6135. [Google Scholar] [CrossRef]
- Shephard, J.; Bunting, P.; Dymond, J. Operational large-scale segmentation of imagery based on iterative elimination. Remote Sens. Submitted.
- Lucas, R.M.; Moghaddam, M.; Cronin, N. Microwave scattering from mixed-species forests, Queensland, Australia. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2142–2159. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Ketchen, D.J.; Shook, C.L. The application of cluster analysis in strategic management research: An analysis and critique. Strateg. Manag. J. 1996, 17, 441–458. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Bom, F.D.; Hunter, M.O.; Oliveira, R.J. de Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Lee, S.; Ni-Meister, W.; Yang, W.; Chen, Q. Physically based vertical vegetation structure retrieval from ICESat data: Validation using LVIS in White Mountain National Forest, New Hampshire, USA. Remote Sens. Environ. 2011, 115, 2776–2785. [Google Scholar] [CrossRef]
- Nelson, R. Model effects on GLAS-based regional estimates of forest biomass and carbon. Int. J. Remote Sens. 2010, 31, 1359–1372. [Google Scholar] [CrossRef] [Green Version]
- Rosette, J.A.B.; North, P.R.J.; Suárez, J.C.; Los, S.O. Uncertainty within satellite LiDAR estimations of vegetation and topography. Int. J. Remote Sens. 2010, 31, 1325–1342. [Google Scholar] [CrossRef]
- Johansen, K.; Trevithick, R.; Bradford, M.; Hacker, J.; McGrath, A.; Lieff, W. Australian examples of field and airborne TERN Landscape Assessment campaigns. In Effective Field Calibration and Nalidation Practices: A Practical Handbook for Calibration and Validation of Satellite and Model-Derived Terrestrial Environmental Variables for Research and Management; Held, A., Phinn, S., Soto-Berrelov, M., Jones, S., Eds.; TERN Auscover: Canberra, Australia, 2018; ISBN 978-0-646-94137-0. [Google Scholar]
- Armston, J.; Disney, M.; Lewis, P.; Scarth, P.; Phinn, S.; Lucas, R.; Bunting, P.; Goodwin, N. Direct retrieval of canopy gap probability using airborne waveform lidar. Remote Sens. Environ. 2013, 134, 24–38. [Google Scholar] [CrossRef]
- Garcia, D. Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef] [Green Version]
- Fisher, A.; Scarth, P.; Armston, J.; Danaher, T. Relating foliage and crown projective cover in Australian tree stands. Agric. For. Meteorol. 2018, 259, 39–47. [Google Scholar] [CrossRef]
- Bastin, J.-F.; Berrahmouni, N.; Grainger, A.; Maniatis, D.; Mollicone, D.; Moore, R.; Patriarca, C.; Picard, N.; Sparrow, B.; Abraham, E.M.; et al. The extent of forest in dryland biomes. Science 2017, 356, 635. [Google Scholar] [CrossRef] [PubMed]
- Dolan, K.; Masek, J.G.; Huang, C.; Sun, G. Regional forest growth rates measured by combining ICESat GLAS and Landsat data. J. Geophys. Res. Biogeosci. 2009. [Google Scholar] [CrossRef]
- Mitchell, A.L.; Tapley, I.; Milne, A.K.; Williams, M.L.; Zhou, Z.-S.; Lehmann, E.; Caccetta, P.; Lowell, K.; Held, A. C- and L-band SAR interoperability: Filling the gaps in continuous forest cover mapping in Tasmania. Remote Sens. Environ. 2014, 155, 58–68. [Google Scholar] [CrossRef]
- Lucas, R.M.; Clewley, D.; Accad, A.; Butler, D.; Armston, J.; Bowen, M.; Bunting, P.; Carreiras, J.; Dwyer, J.; Eyre, T. Mapping forest growth and degradation stage in the Brigalow Belt Bioregion of Australia through integration of ALOS PALSAR and Landsat-derived foliage projective cover data. Remote Sens. Environ. 2014, 155, 42–57. [Google Scholar] [CrossRef] [Green Version]
- Regional Ecosystems Descriptions—Methodology for Survey and Mapping of Regional Ecosystems and Vegetation Communities—Publications | Queensland Government Available online:. Available online: https://publications.qld.gov.au/dataset/redd/resource/6dee78ab-c12c-4692-9842-b7257c2511e4 (accessed on 5 August 2018).
- Scarth, P.; Armston, J.; Goodwin, N. If You Climb Up A Tree, You Must Climb Down The Same Tree. But How High Was It? Available online: https://search.datacite.org/works/10.6084/m9.figshare.94251.v1 (accessed on 5 August 2018).
- Bowen, M.E.; McAlpine, C.A.; House, A.P.N.; Smith, G.C. Agricultural landscape modification increases the abundance of an important food resource: Mistletoes, birds and brigalow. Biol. Conserv. 2009, 142, 122–133. [Google Scholar] [CrossRef]
- Pereira, H.M.; Ferrier, S.; Walters, M.; Geller, G.N.; Jongman, R.H.G.; Scholes, R.J.; Bruford, M.W.; Brummitt, N.; Butchart, S.H.M.; Cardoso, A.C.; et al. Essential Biodiversity Variables. Science 2013, 339, 277–278. [Google Scholar] [CrossRef] [PubMed] [Green Version]










| Lifeform and Height of the Tallest Stratum | Foliage Projective Cover (FPC) or Crown Cover (CC) of the Tallest Plant Layer | |||
|---|---|---|---|---|
| Dense 70–100% FPC >80% CC | Mid-dense 30–70% FPC 50–80% CC | Sparse 10–30% FPC 20–50% CC | Very Sparse/Isolated <10% FPC 0.25–20% CC | |
| Trees > 30 m | tall closed forest | tall open forest | tall woodland | tall open woodland |
| Trees 10–30 m | closed forest | open forest | woodland | open woodland |
| Trees 5–10 m | low closed forest | low open forest | low woodland | low open woodland |
| Shrubs 2–8 m | closed scrub | open scrub | tall shrubland | tall open shrubland |
| Shrubs 0–2 m | closed heath | open heath | low shrubland | low open shrubland |
| Site Name | Longitude | Latitude | Environment |
|---|---|---|---|
| Chowilla (Calperum Mallee) | 140.59 | −34.00 | Semi-arid mallee ecosystem in dune and swale system covered with an open mallee woodland upper story with a chenopod and native grass understory. |
| Watts Creek | 145.68 | −37.69 | Open forest with a eucalypt overstorey greater than 40 m in height consisting mainly of mountain ash. |
| Rushworth Forest | 144.96 | −36.76 | Open forest of red iron bark, red stringybark, red box, long leaf box, and grey box. |
| Zig Zag Creek | 148.28 | −37.48 | Dominated by shrubby dry forest and damp forest on the upland slopes, wet forest ecosystems which are restricted to the higher altitudes and grassy woodlands, grassy dry forest and valley grassy forest ecosystems are associated with major river valleys. |
| Credo (Great Western Woodlands) | 120.64 | −30.19 | Open woodland inter-dispersed with open, treeless areas. Main vegetation species are Salmon Gums up to 20 m and Gimlet between 5–10 m, both with little understory. Salt bush and similar shrubs are also prevalent. |
| South East Queensland | 153.09 | −27.63 | Karawatha Forest: bushland with tall eucalypt species and patches of heatlands and Melaleuca swamps. |
| Litchfield | 130.79 | −13.18 | Savanna, eucalypt open forests, dominated by Eucalyptus miniata and Eucalyptus tetrodonta. |
| Alice Mulga | 133.25 | −22.28 | Mulga (Acacia aneura) canopy, which is 6.5 m tall on average. |
| Warra | 146.66 | −43.09 | Homogenous tall, wet Eucalyptus obliqua forest with wet sclerophyll/rainforest understorey. |
| Structural Formation | Percentage of Total Area | Area ('000s km2) |
|---|---|---|
| no trees | 3.8% | 290 |
| low isolated trees | 16.6% | 1274 |
| isolated trees | 4.9% | 379 |
| low open woodland | 32.6% | 2510 |
| open woodland | 20.2% | 1552 |
| tall open woodland | 0.0% | 2 |
| low woodland | 0.4% | 27 |
| woodland | 14.3% | 1102 |
| tall woodland | 0.1% | 5 |
| open forest | 4.7% | 362 |
| tall open forest | 2.3% | 179 |
| closed forest | 0.1% | 10 |
| tall closed forest | 0.0% | 0 |
| Total: 7692 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scarth, P.; Armston, J.; Lucas, R.; Bunting, P. A Structural Classification of Australian Vegetation Using ICESat/GLAS, ALOS PALSAR, and Landsat Sensor Data. Remote Sens. 2019, 11, 147. https://doi.org/10.3390/rs11020147
Scarth P, Armston J, Lucas R, Bunting P. A Structural Classification of Australian Vegetation Using ICESat/GLAS, ALOS PALSAR, and Landsat Sensor Data. Remote Sensing. 2019; 11(2):147. https://doi.org/10.3390/rs11020147
Chicago/Turabian StyleScarth, Peter, John Armston, Richard Lucas, and Peter Bunting. 2019. "A Structural Classification of Australian Vegetation Using ICESat/GLAS, ALOS PALSAR, and Landsat Sensor Data" Remote Sensing 11, no. 2: 147. https://doi.org/10.3390/rs11020147
APA StyleScarth, P., Armston, J., Lucas, R., & Bunting, P. (2019). A Structural Classification of Australian Vegetation Using ICESat/GLAS, ALOS PALSAR, and Landsat Sensor Data. Remote Sensing, 11(2), 147. https://doi.org/10.3390/rs11020147