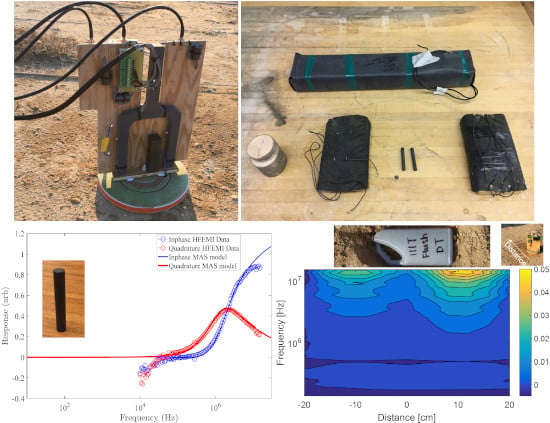
High-Frequency Electromagnetic Induction (HFEMI) Sensor Results from IED Constituent Parts
Abstract
1. Introduction
2. EMI Phenomenology
3. Materials and Methods
4. Results
- Isolate the HFEMI instrument from known targets except for the ground (for field results)
- Set LabVIEW program to program VirtualBench to cycle through n log-spaced frequencies (often from 50 kHz to 15 MHz)
- With these parameters, acquire 100 waveforms of data with sampling frequency at least 100*frequency as a background
- Place a piece of ferrite near the sensor, acquire data again. Remove ferrite.
- Place a target near the sensor (or move sensor over a subsurface target), acquire data again
- Use the method described in [13] to extract the I and Q of the target
- Repeat steps 5 and 6 for next target
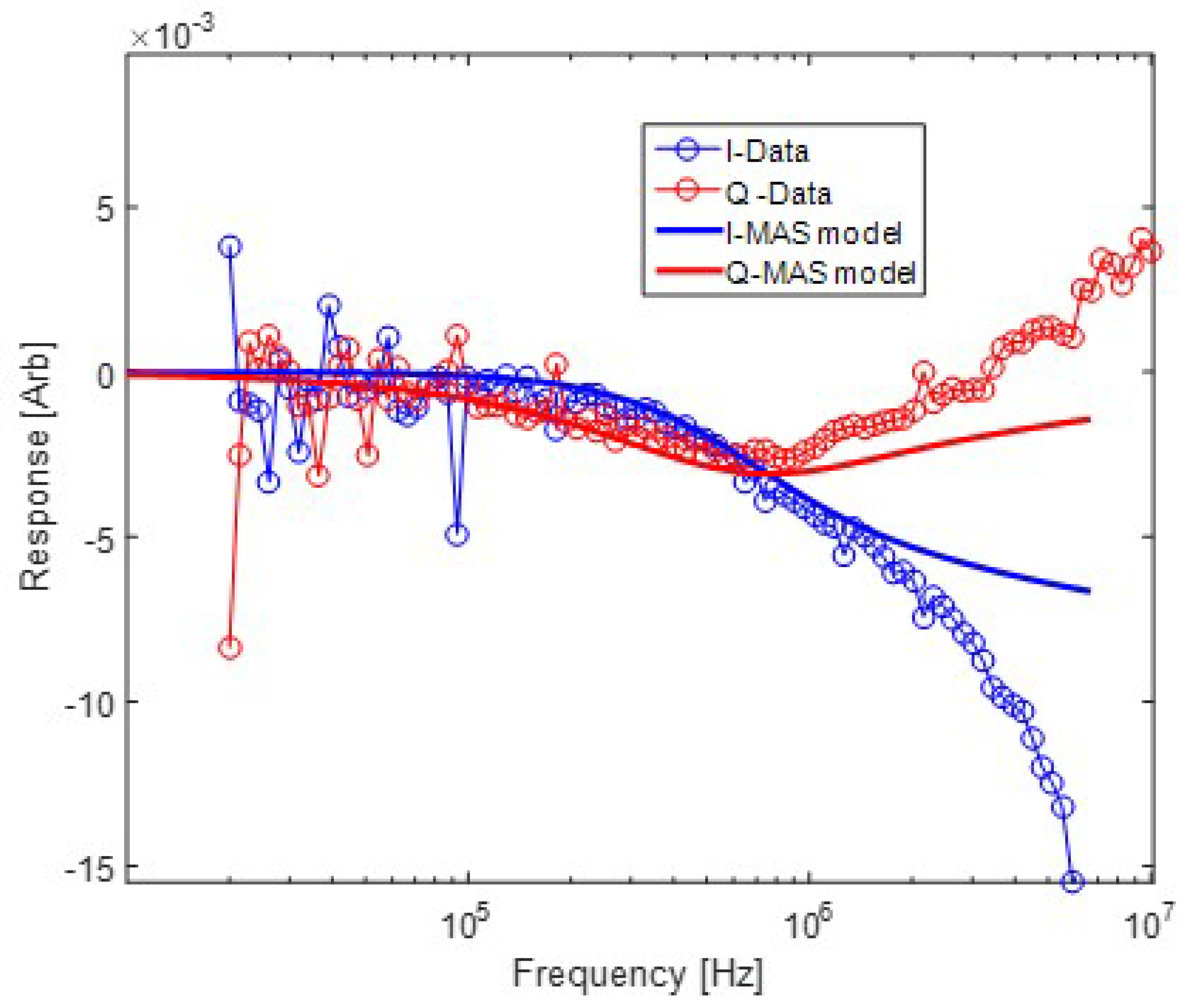
4.1. Laboratory Results
4.2. Fort AP Hill Data
4.3. Wire Detection at HFEMI Frequencies
5. Discussion
6. Conclusions
7. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- O’Neill, K. Discrimination of Subsurface Unexploded Ordnance; SPIE Press: Bellingham WA, USA, 2016. [Google Scholar]
- Ratto, C.R.; Torrione, P.A.; Collins, L.M. Exploiting ground-penetrating radar phenomenology in a context-dependent framework for landmine detection and discrimination. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1689–1700. [Google Scholar] [CrossRef]
- Shamatava, I.; Shubitidze, F.; Chen, C.; Youn, H.; O’Neill, K.; Sun, K. Potential benefits of combining EMI and GPR for enhanced UXO discrimination at highly contaminated sites. Proc. SPIE Int. Soc. Opt. Eng. 2004, 5415, 1201–1210. [Google Scholar]
- O’Neill, K.; Sun, K.; Chen, C.; Shubitidze, F.; Paulsen, K. Combining GPR and EMI Data for Discrimination of Multiple Subsurface Metallic Objects. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 4157–4159. [Google Scholar]
- Barrowes, B.; Glaser, D.; Prishvin, M.; Coleman, M.; Shubitidze, F. Assessing the Frozen State of Soils Using iFrost: An Electromagnetic Induction Sensor on a UAS Platform. In Proceedings of the 18th International Conference on Cold Regions Engineering and the 8th Canadian Permafrost Conference, Quebec City, QC, Canada, 19–21 August 2019. [Google Scholar]
- Barrowes, B.E.; Sigman, J.B.; O’Neill, K.; Simms, J.E.; Bennett, H.J.; Yule, D.E.; Shubitidze, F. Detection of conductivity voids and landmines using high frequency electromagnetic induction. In Proceedings of the 2016 XXIst International Seminar/Workshop on Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED), Tbilisi, Georgia, 26–29 September 2016; pp. 118–122. [Google Scholar]
- Hendrickx, J.; Borchers, B.; Corwin, D.; Lesch, S.; Hilgendorf, A.; Schlue, J. Inversion of soil conductivity profiles from electromagnetic induction measurements. Soil Sci. Soc. Am. J. 2002, 66, 673–685. [Google Scholar] [CrossRef]
- Shubitidze, F.; Fernández, J.P.; Barrowes, B.; Shamatava, I.; O’Neill, K. Rapid and Accurate Estimate of the Effect of Magnetically Susceptible Soil on MPV-TD Sensor Data Using the Method of Images. In Proceedings of the XIIIth International Seminar/Workshop on Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED), Tbilisi, Georgia, 22–25 September 2008. [Google Scholar]
- Glaser, D.R.; Barrowes, B.E.; Prishvin, M.; O’Neill, K.; Shubitidze, F. Bench Scale Measurement of Unsaturated Soils Using EMI, IP, TDR, and GPR. In Proceedings of the Symposium on the Application of Geophysics to Environmental and Engineering Problems, Portland, OR, USA, 17–21 March 2019. [Google Scholar]
- Barrowes, B.E.; Fernandez, J.P.; O’Neill, K.; Shamatava, I.; Shubitidze, F. Electromagnetic Induction Tools for Discrimination of Unexploded Ordnance: From Basic Physics to Blind Tests. FastTIMES 2015, 20, 13–30. [Google Scholar]
- SERDP. Classification Applied to Munitions Response. Available online: https://www.serdp-estcp.org/Featured-Initiatives/Munitions-Response-Initiatives/Classification-Applied-to-Munitions-Response (accessed on 27 September 2019).
- Shubitidze, F.; Barrowes, B.; Sigman, J.; Wang, Y.; Shamatava, I.; O’Neill, K. Detecting and classifying small and deep targets using improved EMI hardware and data processing approach. Proc. SPIE 2014, 9072. [Google Scholar] [CrossRef]
- Sigman, J.B.; Barrowes, B.; O’Neill, K.; Simms, J.; Bennett, J.; Yule, D.; Shubitidze, F. High-frequency electromagnetic induction sensing of non-metallic materials. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5254–5263. [Google Scholar] [CrossRef]
- Ao, C.O.; Braunisch, H.; O’Neill, K.; Kong, J.A. Quasi-Magnetostatic Solution for a Conducting and Permeable Spheroid With Arbitrary Excitation. IEEE Trans. Geosci. Remote Sens. 2002, 40, 887–897. [Google Scholar] [CrossRef]
- Barrowes, B.E.; O’Neill, K.; Grzegorczyk, T.M.; Chen, X.; Kong, J.A. Broadband Analytical Magnetoquasistatic Electromagnetic Induction Solution for a Conducting and Permeable Spheroid. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2479–2489. [Google Scholar] [CrossRef]
- Braunisch, H.; Ao, C.O.; O’Neill, K.; Kong, J.A. Magnetoquasistatic Response of Conducting and Permeable Prolate Spheroid Under Axial Excitation. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2689–2701. [Google Scholar] [CrossRef]
- Bossavit, A. Computational Electromagnetism: Variational Formulations, Complementarity, Edge Elements; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Schmidt, K.; Sterz, O.; Hiptmair, R. Estimating the eddy-current modeling error. IEEE Trans. Magn. 2008, 44, 686–689. [Google Scholar] [CrossRef]
- Ledger, P.; Lionheart, W. The Spectral Properties of the Magnetic Polarizability Tensor for Metallic Object Characterisation. arXiv 2019, arXiv:1906.00382. [Google Scholar] [CrossRef]
- Buffa, A.; Ammari, H.; Nédélec, J.C. A justification of eddy currents model for the Maxwell equations. SIAM J. Appl. Math. 2000, 60, 1805–1823. [Google Scholar] [CrossRef]
- Abraham, J.D.; Smith, D.; Wright, D.L. Final Report VETEM (Very Early Time Electromagnetic) System Survey of Pit 4 and Pit 10 Subsurface Disposal Area, Radioactive Waste Management Complex, Idaho National Engineering and Environmental Laboratory, Idaho Falls, ID; Technical Report Open-File Report 03-140; U.S. Department of Energy: Washington, DC, USA, 2003.
- Aydaner, A.A.; Chew, W.C.; Cui, T.J.; Wright, D.L.; Smith, D.V.; Abraham, J.D. 3-D Imaging of Large Scale Buried Structure by 1-D Inversion of Very Early Time Electromagnetic (VETEM) Data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1307–1315. [Google Scholar] [CrossRef]
- Stewart, D.C.; Anderson, W.L.; Grover, T.P.; Labson, V.F. Shallow subsurface mapping by electromagnetic sounding in the 300 kHz to 30 MHz range: Model studies and prototype system assessment. Geophysics 1994, 59, 1201–1210. [Google Scholar] [CrossRef]
- Stewart, D.; Anderson, W.; Grover, T.; Labson, V. A new instrument and inversion program for near-surface mapping—High frequency EM sounding in the frequency range of 300 kHz–30 MHz. Soc. Explor. Geophys. 1990, 60, 130. [Google Scholar]
- Sternberg, B. A new method of subsurface imaging- the LASI high frequency ellipticity system: Part 1. System design and development. J. Environ. Eng. Geophys. 1999, 4, 197–214. [Google Scholar] [CrossRef]
- Simms, J.E.; Sigman, J.B.; Barrowes, B.E.; Bennett Jr, H.H.; Yule, D.E.; O’Neill, K.; Shubitidze, F. Initial development of a high-frequency EMI sensor for detection of subsurface intermediate electrically conductive (IEC) targets. J. Environ. Eng. Geophys. 2017, 22, 111–120. [Google Scholar] [CrossRef]
- Barrowes, B.E. High Frequency Electromagnetic Induction. U.S. Patent 14661779, 19 June 2018. [Google Scholar]
- Sigman, J.B.; Barrowes, B.E.; Wang, Y.; Bennett, H.J.; Simms, J.E.; Yule, D.E.; O’Neill, K.; Shubitidze, F. Coil design considerations for a high-frequency electromagnetic induction sensing instrument. Proc. SPIE 2016, 9823, 982302. [Google Scholar] [CrossRef]
- Shubitidze, F.; Barrowes, B.E.; Ballard, J.; Unz, R.; Randle, A.; Larson, S.L.; O’Neill, K.A. High frequency EMI sensing for estimating depleted uranium radiation levels in soil. Proc. SPIE 2018, 10628. [Google Scholar] [CrossRef]
- Shubitidze, F.; Barrowes, B.E.; Sigman, J.B.; O’Neill, K. Ultra-wide-band EMI sensing for subsurface depleted uranium detection. Proc. SPIE 2017, 10182, 1018216. [Google Scholar] [CrossRef]
- Barrowes, B.E.; Shubitidze, F.; Sigman, J.B.; Bennett, J.; Simms, J.E.; Yule, D.; O’Neill, K. Void and landmine detection using the HFEMI sensor. Proc. SPIE 2017, 10182, 1018210. [Google Scholar] [CrossRef]
- Barrowes, B.E.; O’Neill, K.; Shubitidze, F. High Frequency Electromagnetic Response from Short and Long Wires for IED and Tunnel Detection. In Proceedings of the 31st Symposium on the Application of Geophysics to Engineering and Environmental Problems (SAGEEP), Nashville, TN, USA, 25–29 March 2018. [Google Scholar]
- Barrowes, B.; Glaser, D.R.; Prishvin, M.; O’Neill, K.; Shubitidze, F. Short and long wire detection using high-frequency electromagnetic induction techniques. Proc. SPIE 2018, 10628, 106280K. [Google Scholar] [CrossRef]
- Shubitidze, F.; Sigman, J.; O’Neill, K.; Shamatava, I.; Barrowes, B. High frequency electromagnetic induction sensing for non-metallic ordnances detection. In Proceedings of the 2014 XIXth International Seminar/Workshop on Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED), Tbilisi, Georgia, 22–25 September 2014; pp. 180–182. [Google Scholar]
- Michael Yon, O.M. Low Metal Content 2019. Available online: https://www.michaelyon-online.com/low-metal-content.htm (accessed on 26 September 2019).
- Won, I.J.; Keiswetter, D.A.; Bell, T.H. Electromagnetic induction spectroscopy for clearing landmines. IEEE Trans. Geosci. Remote Sens. 2001, 39, 703–709. [Google Scholar] [CrossRef]
- Gasperikova, E.; Smith, J.T.; Morrison, H.F.; Becker, A.; Kappler, K. UXO detection and identification based on intrinsic target polarizabilities—A case history. Geophysics 2009, 74, B1–B8. [Google Scholar] [CrossRef][Green Version]
- Nelson, H.; McDonald, J. Multisensor towed array detection system for UXO detection. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1139–1146. [Google Scholar] [CrossRef]
- Barrowes, B.E.; Sigman, J.B.; Wang, Y.; O’Neill, K.A.; Shubitidze, F.; Simms, J.; Bennett, H.J.; Yule, D.E. Carbon fiber and void detection using high-frequency electromagnetic induction techniques. Proc. SPIE 2016, 9823, 98230D. [Google Scholar] [CrossRef]
- Ward, S.H.; Hohmann, G.W. Electromagnetic theory for geophysical applications. In Electromagnetic Methods in Applied Geophysics; Nabighian, M.N., Ed.; Investigations in Geophysics; Society of Exploration Geophysicists: Tulsa, OK, USA, 1988; Volume 1, pp. 131–311. [Google Scholar]
- George, D.C.; Kingdon, J.B.; Furuya, T.; Keiswetter, D.A.; Bell, T.H.; Harbaugh, G.R.; Steinhurst, D.A. EMI Array for Cued UXO Discrimination, ESTCP MM-0601, Final Report; NRL Memorandum Report NRL/MR/6110–10-9289; Naval Research Laboratory: Washington, DC, USA, 2010. [Google Scholar]
- Fernández, J.P.; Barrowes, B.E.; Grzegorczyk, T.M.; Lhomme, N.; O’Neill, K.; Shubitidze, F. A Man-Portable Vector Sensor for Identification of Unexploded Ordnance. IEEE Sens. J. 2011, 11, 2542–2555. [Google Scholar] [CrossRef]
- Barrowes, B.E.; Shubitidze, F.; Fernández, J.P.; Grzegorczyk, T.M.; O’Neill, K. Pedemis: A portable electromagnetic induction sensor with integrated positioning. Proc. SPIE 2012, 8357, 835702. [Google Scholar] [CrossRef]
- Barrowes, B.E.; Shubitidze, F.; Grzegorczyk, T.M.; Fernandez, P.; ONeill, K. Electromagnetic Induction Sensing of UneXploded Ordnance with Pedemis. In Proceedings of the MSS BAMS Conference, Washington, DC, USA, 22 October 2012. [Google Scholar]
- Nelson, C.; Cooperman, C.; Schneider, W.; Wenstrand, D.; Smith, D. Wide bandwidth time-domain electromagnetic sensor for metal target classification. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1129–1138. [Google Scholar] [CrossRef]
- Olhoeft, G.; Strangway, D. Magnetic relaxation and the electromagnetic response parameter. Geophysics 1974, 39, 302–311. [Google Scholar] [CrossRef]
- Cheng, D.K. Field and Wave Electromagnetics; Addison-Wesley: New York, NY, USA, 1989; Volume 2. [Google Scholar]
- Grant, F.S.; West, G.F. Interpretation Theory in Applied Geophysics; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Wait, J.R. Geo-Electromagnetism; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Sigman, J.B. Ultra-Wideband EMI Sensing: Non-Metallic Target Detection and Automatic Classification of Unexploded Ordnance; Dartmouth College: Hanover, NH, USA, 2017. [Google Scholar]
- Bogdanov, F.G.; Karkashadze, D.D.; Zaridze, R.S. The method of auxiliary sources in electromagnetic scattering problems. Gen. Multipole Tech. Electromagn. Light Scatt. 1999, 4, 143–172. [Google Scholar]
- Shubitidze, F.; Fernández, J.P.; Barrowes, B.E.; Shamatava, I.; O’Neill, K. The Method of Auxiliary Sources for Solving Low-Frequency Electromagnetic Induction Problems in Underwater Environments. In Proceedings of the Applied Computational Electromagnetics Symposium (ACES), Williamsburg, VA, USA, 27–31 March 2011. [Google Scholar]
- Shubitidze, F.; O’Neill, K.; Haider, S.A.; Sun, K.; Paulsen, K.D. Application of the Method of Auxiliary Sources to the Wide-Band Electromagnetic Induction Problem. IEEE Trans. Geosci. Remote Sens. 2002, 40, 928–942. [Google Scholar] [CrossRef]
- Shubitidze, F.; O’Neill, K.; Shamatava, I.; Sun, K.; Paulsen, K. Analysis of geological soil effects on EMI responses relevant to UXO discrimination. Proc. SPIE Int. Soc. Opt. Eng. 2005, 5794, 296–307. [Google Scholar]
- Shubitidze, F.; O’Neill, K.; Haider, S.; Sun, K.; Paulsen, K. Analysis of induction responses from metal objects using the method of auxiliary sources. In Proceedings of the 2000 International Conference on Mathematical Methods in Electromagnetic Theory, Kharkov, Ukraine, 12–15 September 2000; pp. 468–470. [Google Scholar]
- Lindon, J.C.; Tranter, G.E.; Koppenaal, D. Encyclopedia of Spectroscopy and Spectrometry; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Web Soil Survey. 2019. Available online: https://websoilsurvey.nrcs.usda.gov/app/WebSoilSurvey.aspx (accessed on 23 September 2019).
- Shubitidze, F.; Barrowes, B.E.; Prishvin, M.; O’Neill, K.; Shamatava, I. Investigating EMI responses for buried wires to enahnce utility mapping. In Proceedings of the Symposium on the Application of Geophysics to Environmental and Engineering Problems, Portland, OR, USA, 17–21 March 2019. [Google Scholar]
- McKenna, S.P.; Parkman, K.B.; Perren, L.J.; McKenna, J.R. Automatic detection of a subsurface wire using an electromagnetic gradiometer. IEEE Trans. Geosci. Remote Sens. 2012, 51, 132–139. [Google Scholar] [CrossRef]










© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrowes, B.; Prishvin, M.; Jutras, G.; Shubitidze, F. High-Frequency Electromagnetic Induction (HFEMI) Sensor Results from IED Constituent Parts. Remote Sens. 2019, 11, 2355. https://doi.org/10.3390/rs11202355
Barrowes B, Prishvin M, Jutras G, Shubitidze F. High-Frequency Electromagnetic Induction (HFEMI) Sensor Results from IED Constituent Parts. Remote Sensing. 2019; 11(20):2355. https://doi.org/10.3390/rs11202355
Chicago/Turabian StyleBarrowes, Benjamin, Mikheil Prishvin, Guy Jutras, and Fridon Shubitidze. 2019. "High-Frequency Electromagnetic Induction (HFEMI) Sensor Results from IED Constituent Parts" Remote Sensing 11, no. 20: 2355. https://doi.org/10.3390/rs11202355
APA StyleBarrowes, B., Prishvin, M., Jutras, G., & Shubitidze, F. (2019). High-Frequency Electromagnetic Induction (HFEMI) Sensor Results from IED Constituent Parts. Remote Sensing, 11(20), 2355. https://doi.org/10.3390/rs11202355