Spatial Resolution Matching of Microwave Radiometer Data with Convolutional Neural Network
Abstract
:1. Introduction
2. Instrument and Imaging Process
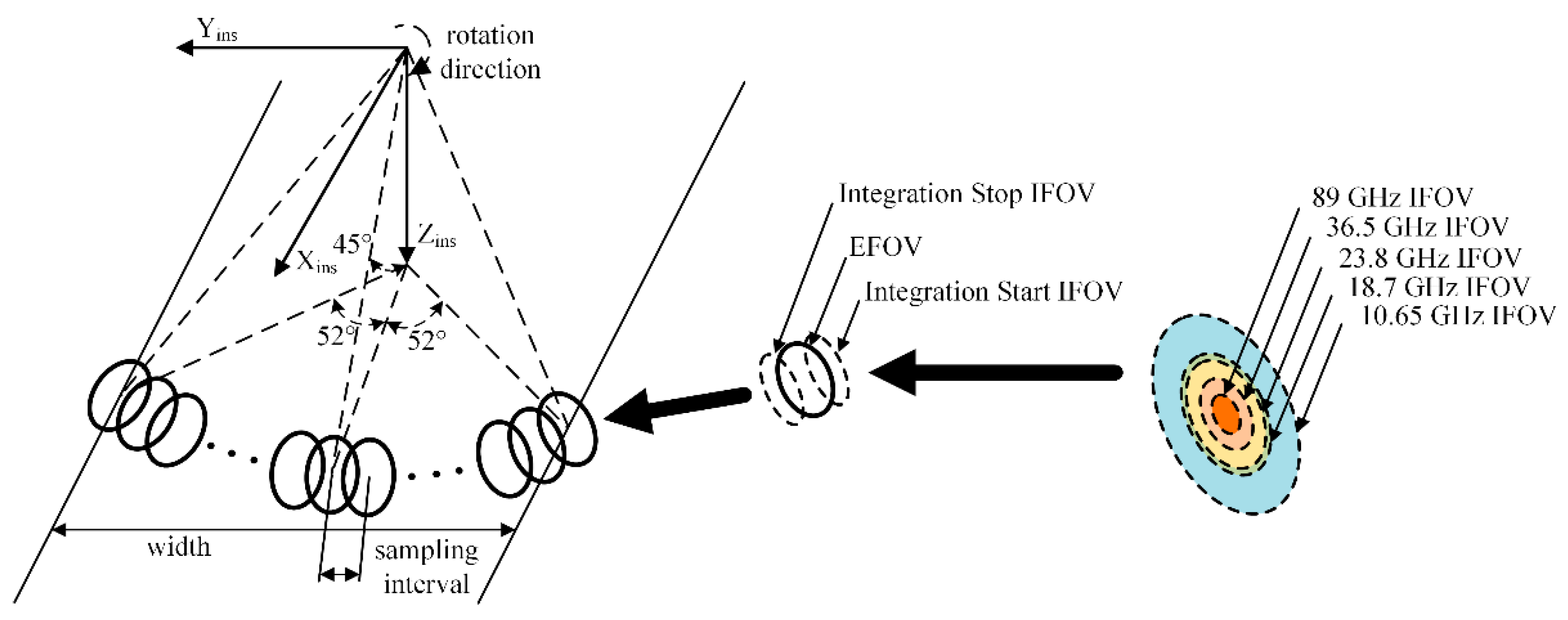
2.1. MWRI Instrument
2.2. Imaging Process
3. Spatial Resolution Match Method
3.1. Flexible Degradation Model
3.2. Network Architecture
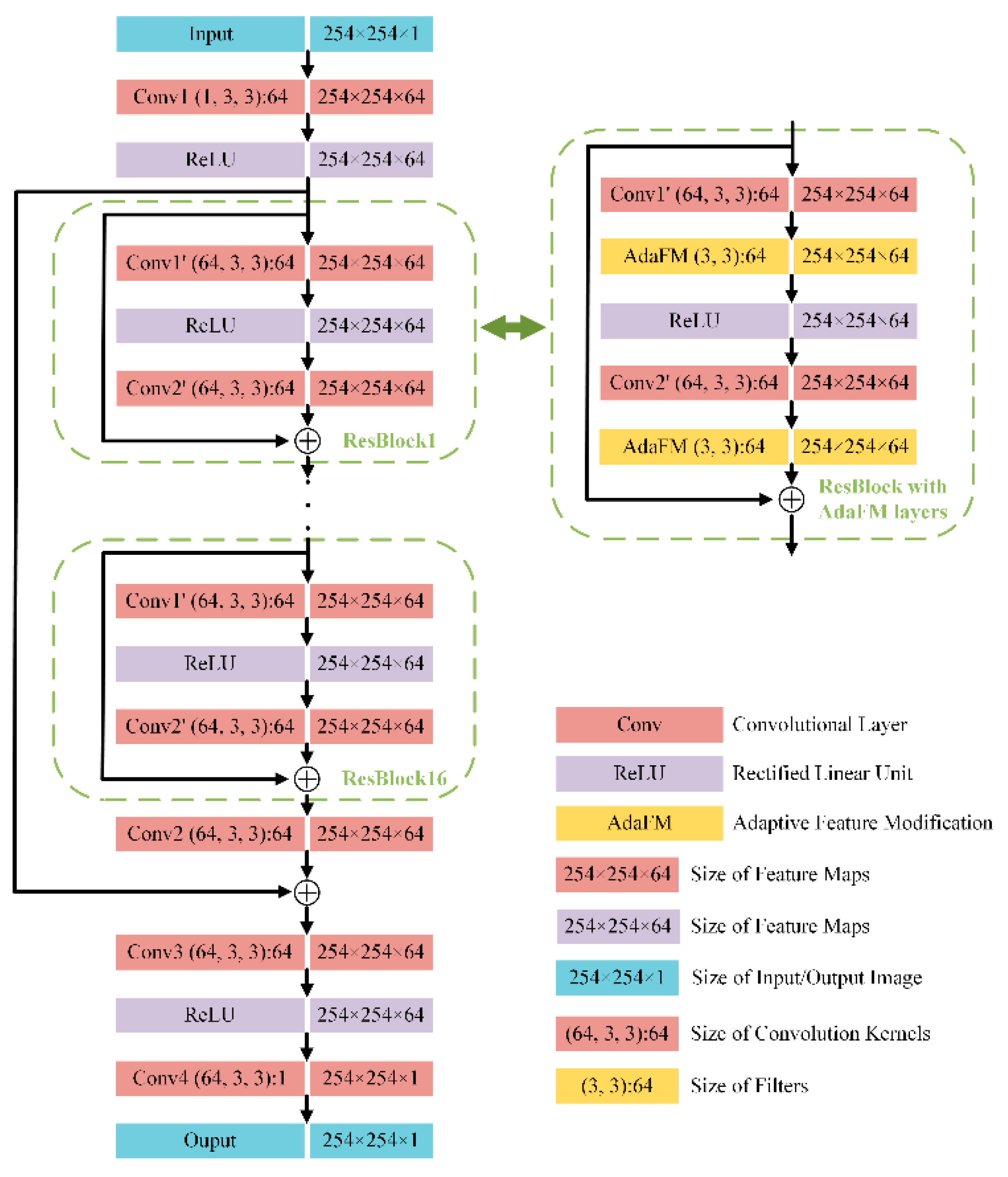
3.2.1. Basic Network
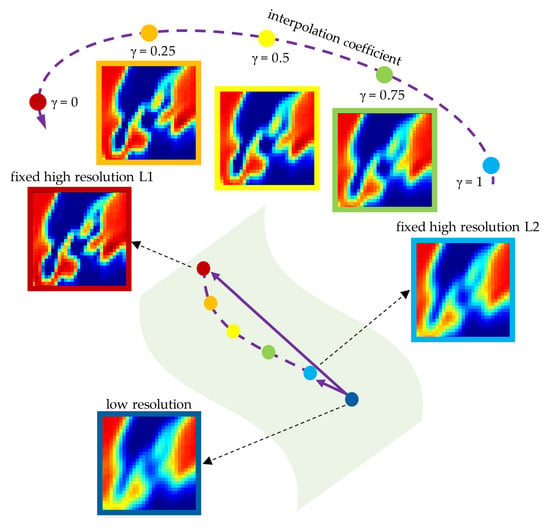
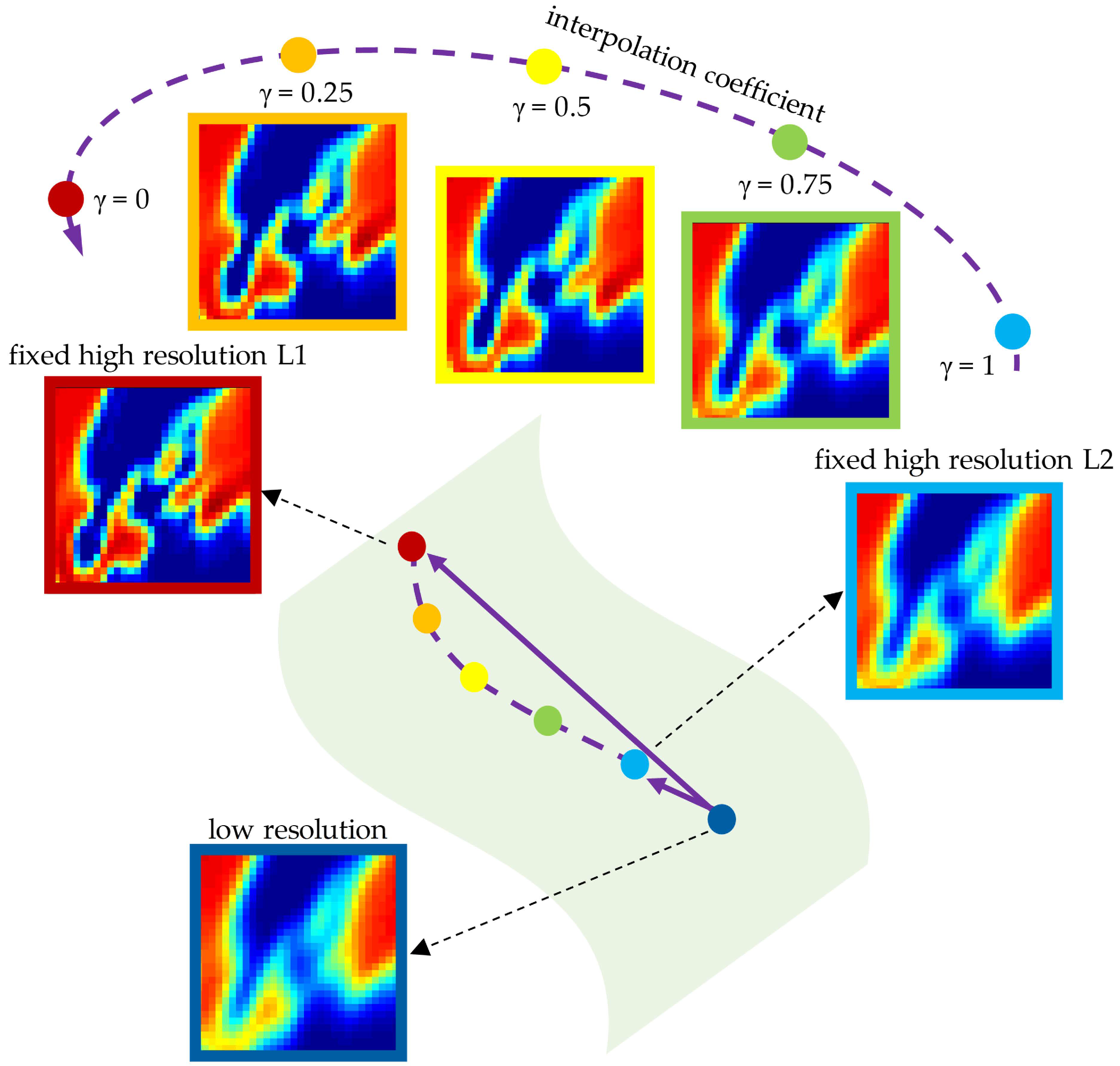
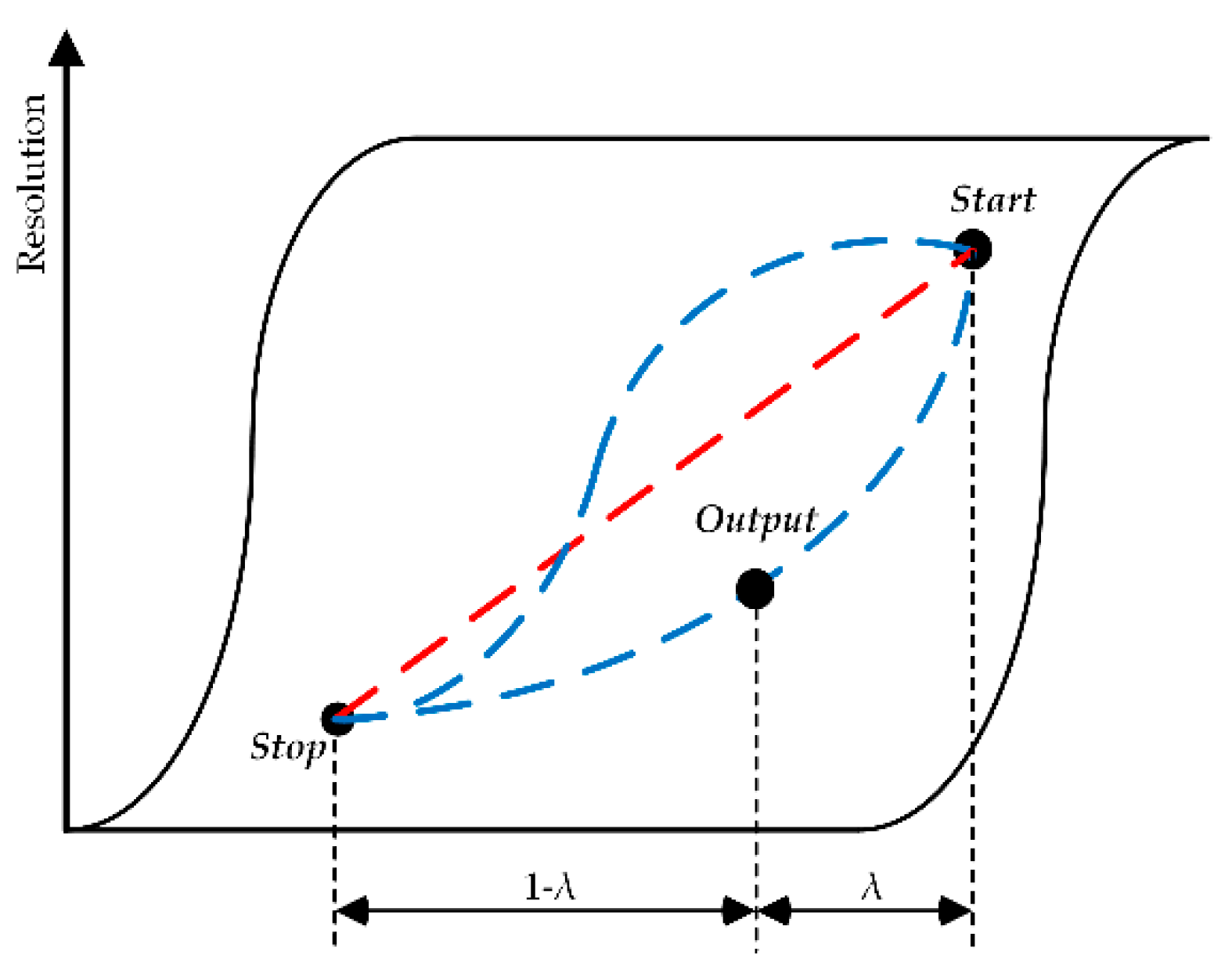
3.2.2. Adjustable Network
3.3. ASRM for the FY-3C MWRI
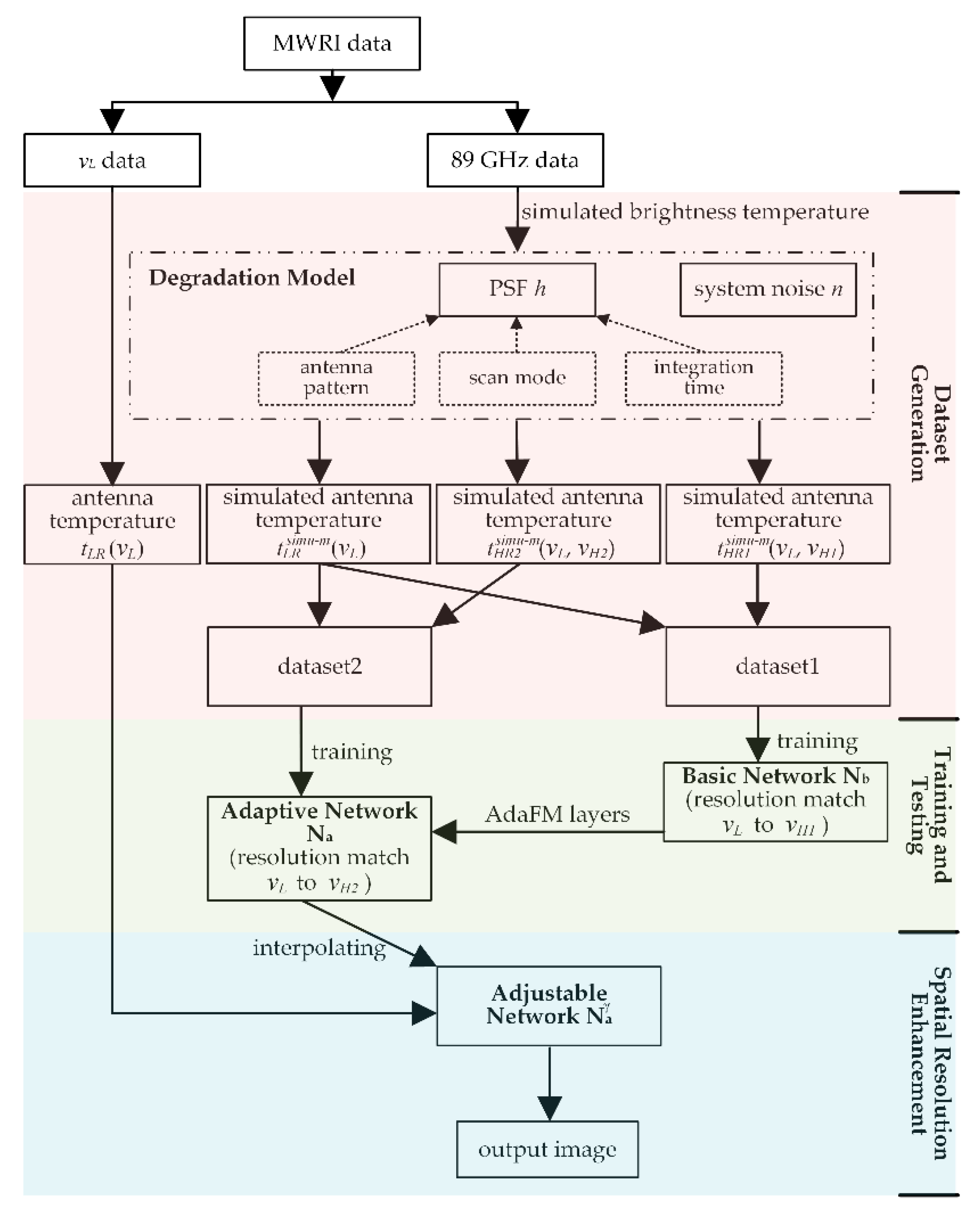
3.3.1. ASRM Framework Flowchart
3.3.2. Training Details
4. Experiment Results
4.1. Quantitative and Qualitative Evaluation of Fixed Level Resolution Match
4.1.1. Synthetic Scenario Evaluation
4.1.2. Test Set Evaluation
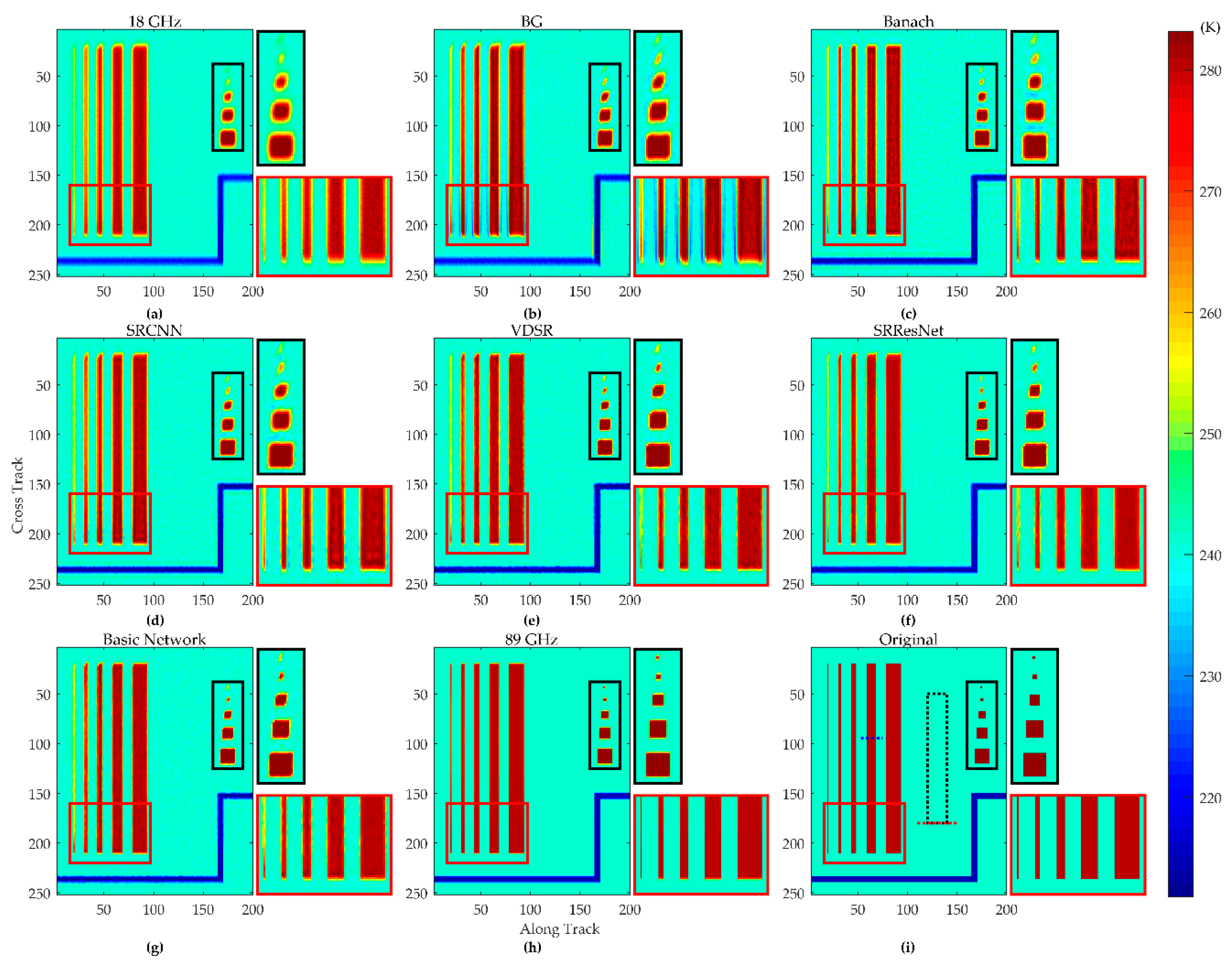
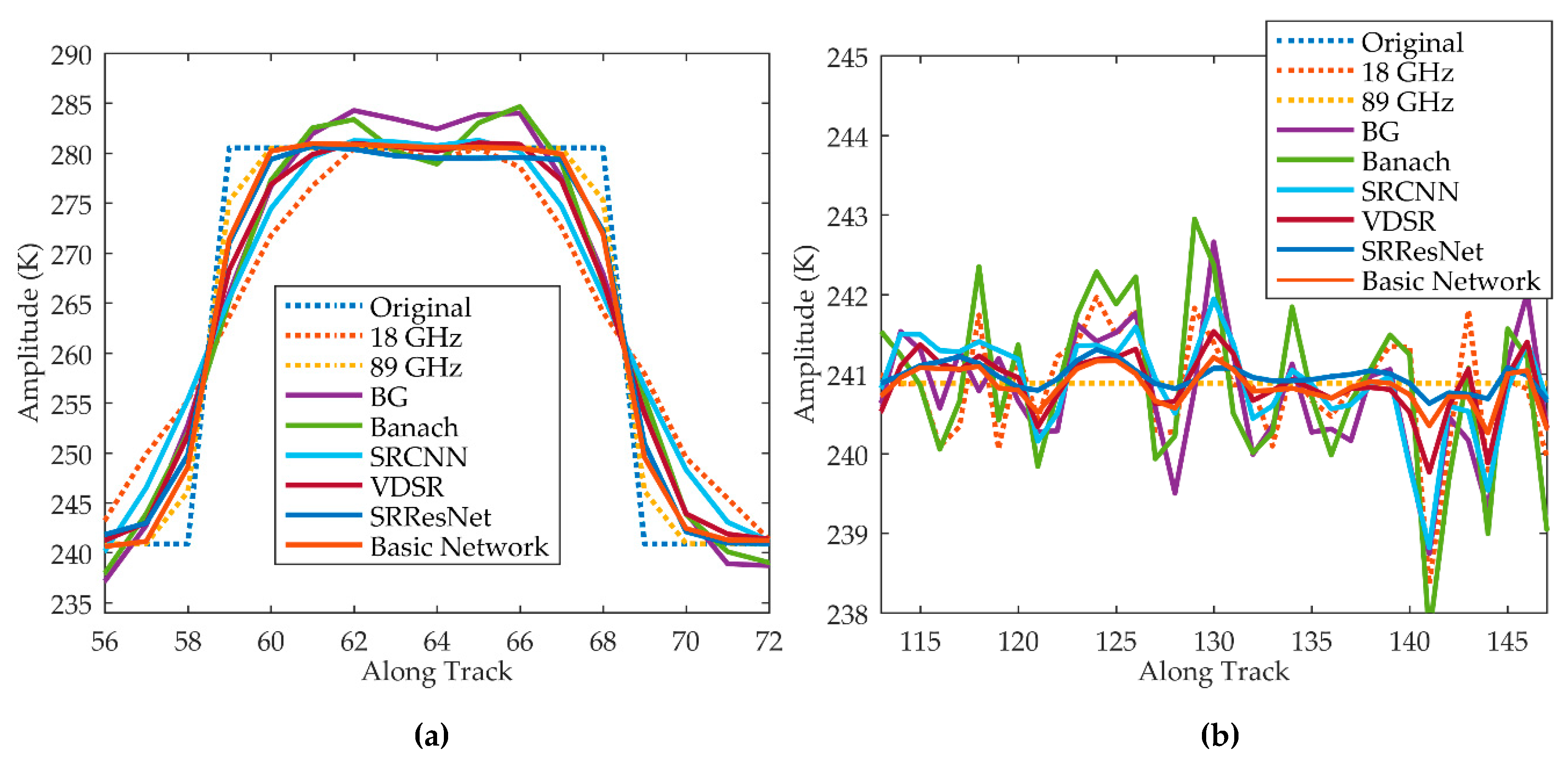
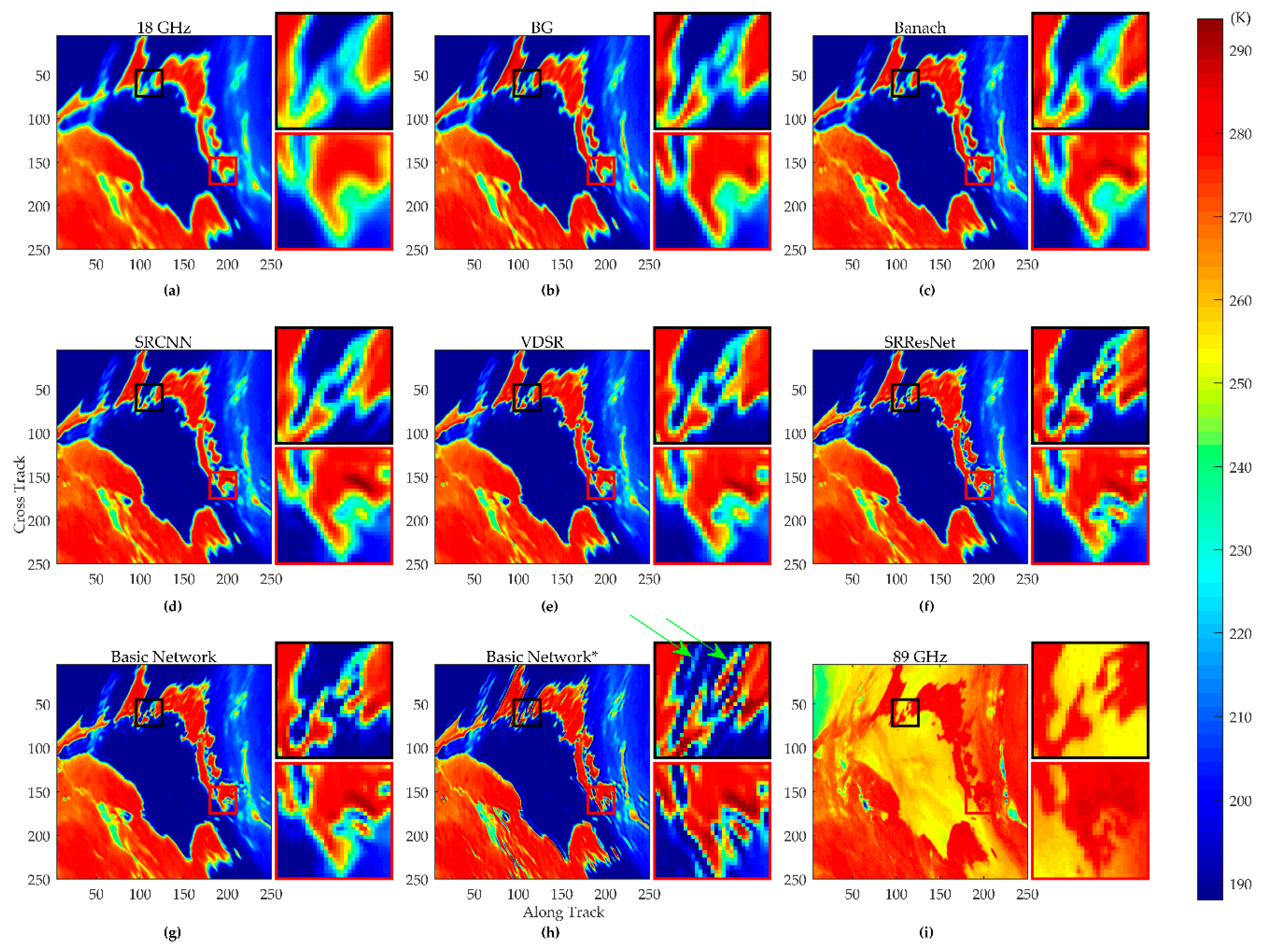
4.1.3. Real Data Testing
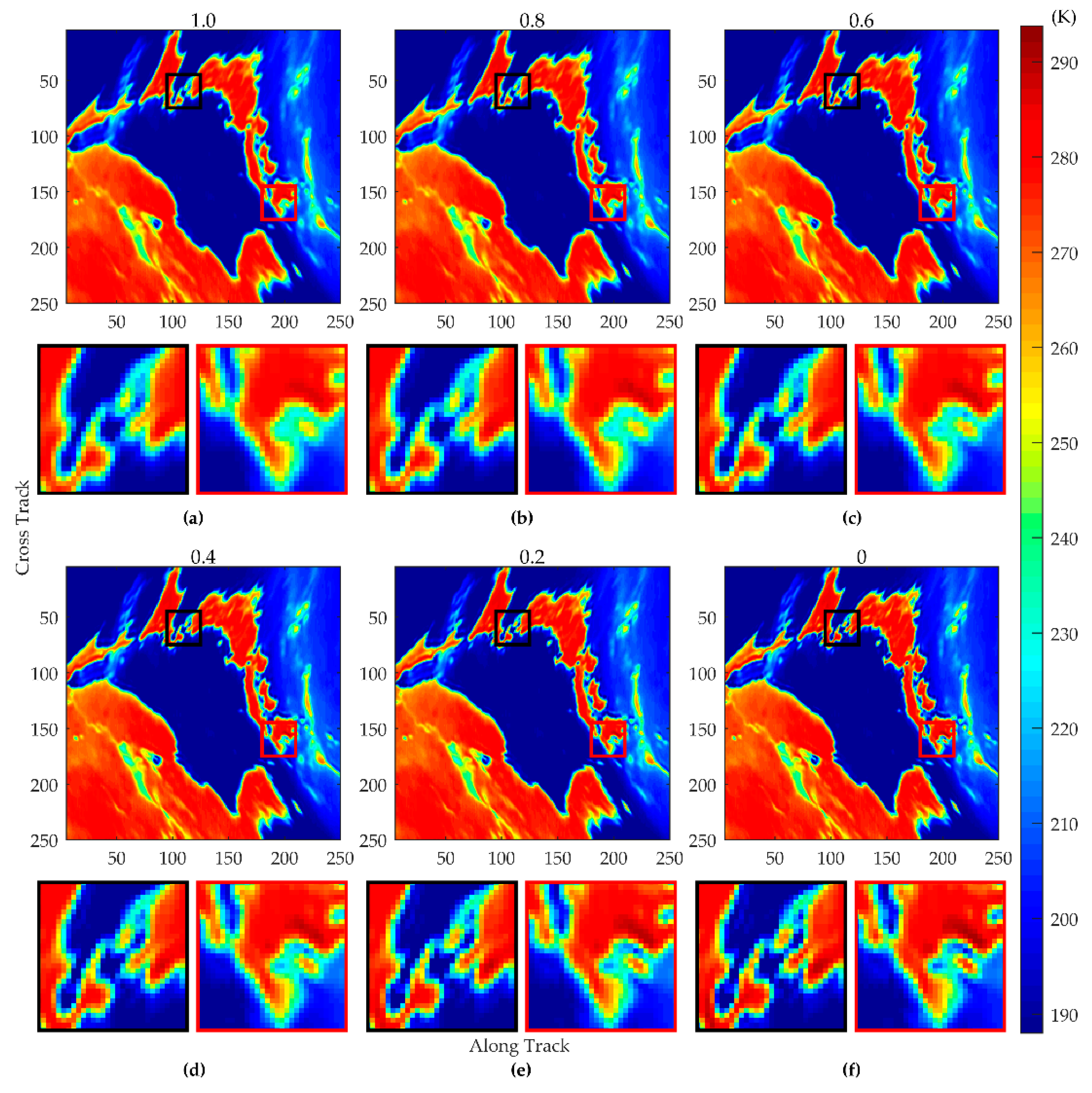
4.2. Resolution Match with Adjustable Network
4.2.1. Case 1 When vH1 = 89 GHz and vH2 = 36.5 GHz
4.2.2. Case 2 When vH1 = 89 GHz and vH2 = 23.8 GHz
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive, Volume I: Microwave Remote Sensing Fundamentals and Radiometry; Artech House: Norwood, MA, USA, 1981. [Google Scholar]
- Yang, Z.; Lu, N.; Shi, J.; Zhang, P.; Dong, C.; Yang, J. Overview of FY-3 payload and ground application system. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4846–4853. [Google Scholar] [CrossRef]
- Yang, H.; Weng, F.; Lv, L.; Lu, N.; Liu, G.; Bai, M.; Qian, Q.; He, J.; Xu, H. The FengYun-3 microwave radiation imager on-orbit verification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4552–4560. [Google Scholar] [CrossRef]
- Yang, H.; Zou, X.; Li, X.; You, R. Environmental data records from FengYun-3B microwave radiation imager. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4986–4993. [Google Scholar] [CrossRef]
- Robinson, W.D.; Kummerow, C.; Olson, W.S. A technique for enhancing and matching the resolution of microwave measurements from the SSM/I instrument. IEEE Trans. Geosci. Remote Sens. 1992, 30, 419–429. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, J.; Jiang, L.; Du, J.; Tian, B. The development of an algorithm to enhance and match the resolution of satellite measurements from AMSR-E. Sci. China Earth Sci. 2011, 54, 410–419. [Google Scholar] [CrossRef]
- Drusch, M.; Wood, E.F.; Lindau, R. The impact of the SSM/I antenna gain function on land surface parameter retrieval. Geophys. Res. Lett. 1999, 26, 3481–3484. [Google Scholar] [CrossRef]
- Tang, F.; Zou, X.; Yang, H.; Weng, F. Estimation and correction of geolocation errors in FengYun-3C Microwave Radiation Imager Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 407–420. [Google Scholar] [CrossRef]
- Sethmann, R.; Burns, B.A.; Heygster, G.C. Spatial resolution improvement of SSM/I data with image restoration techniques. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1144–1151. [Google Scholar] [CrossRef]
- Long, D.G.; Daum, D.L. Spatial resolution enhancement of SSM/I data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 407–417. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Li, Y.; Zhang, W.; Chen, S.; Lv, X.; Ligthart, L. Spatial resolution enhancement of satellite microwave radiometer data with deep residual convolutional neural network. Remote Sens. 2019, 11, 771. [Google Scholar] [CrossRef]
- Stogryn, A. Estimates of brightness temperatures from scanning radiometer data. IEEE Trans. Antennas Propag. 1978, 26, 720–726. [Google Scholar] [CrossRef]
- Migliaccio, M.; Gambardella, A. Microwave radiometer spatial resolution enhancement. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1159–1169. [Google Scholar] [CrossRef]
- Liu, D.; Liu, K.; Lv, C.; Miao, J. Resolution enhancement of passive microwave images from geostationary Earth orbit via a projective sphere coordinate system. J. Appl. Remote Sens. 2014, 8, 083656. [Google Scholar] [CrossRef] [Green Version]
- Lenti, F.; Nunziata, F.; Estatico, C.; Migliaccio, M. On the spatial resolution enhancement of microwave radiometer data in Banach spaces. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1834–1842. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, W.; Chen, S.; Lv, X.; An, D.; Ligthart, L. A deconvolution technology of microwave radiometer data using convolutional neural networks. Remote Sens. 2018, 10, 275. [Google Scholar] [CrossRef]
- Hu, T.; Zhang, F.; Li, W.; Hu, W.; Tao, R. Microwave Radiometer Data Superresolution Using Image Degradation and Residual Network. IEEE Trans. Geosci. Remote Sens. 2019, 1–14. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Gu, S.; Zhang, L. Learning deep CNN denoiser prior for image restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2808–2817. [Google Scholar]
- Liu, X.; Jiang, L.; Wu, S.; Hao, S.; Wang, G.; Yang, J. Assessment of methods for passive microwave snow cover mapping using FY-3C/MWRI data in China. Remote Sens. 2018, 10, 524. [Google Scholar] [CrossRef]
- Yang, S.; Weng, F.; Yan, B.; Sun, N.; Goldberg, M. Special Sensor Microwave Imager (SSM/I) intersensor calibration using a simultaneous conical overpass technique. J. Appl. Meteorol. Climatol. 2011, 50, 77–95. [Google Scholar] [CrossRef]
- Wu, S.; Chen, J. Instrument performance and cross calibration of FY-3C MWRI. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 388–391. [Google Scholar]
- Piepmeier, J.R.; Long, D.G.; Njoku, E.G. Stokes antenna temperatures. IEEE Trans. Geosci. Remote Sens. 2008, 46, 516–527. [Google Scholar] [CrossRef]
- Di Paola, F.; Dietrich, S. Resolution enhancement for microwave-based atmospheric sounding from geostationary orbits. Radio Sci. 2008, 43, 1–14. [Google Scholar] [CrossRef]
- Gong, R.; Li, W.; Chen, Y.; Van Gool, L. DLOW: Domain flow for adaptation and generalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 2477–2486. [Google Scholar]
- He, J.; Dong, C.; Qiao, Y. Modulating image restoration with continual levels via adaptive feature modification layers. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11056–11064. [Google Scholar]
- Efrat, N.; Glasner, D.; Apartsin, A.; Nadler, B.; Levin, A. Accurate blur models vs. image priors in single image super-resolution. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 2832–2839. [Google Scholar]
- Kim, J.; Kwon Lee, J.; Mu Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Damera-Venkata, N.; Kite, T.D.; Geisler, W.S.; Evans, B.L.; Bovik, A.C. Image quality assessment based on a degradation model. IEEE Trans. Image Process. 2000, 9, 636–650. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2017, 3, 47–57. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.P.; Tejani, A.; Totz, J.; Wang, Z. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]





| Frequency (GHz) | Polarization | IFOV (km) | Sensitivity NEΔT (K) | Integration Time (ms) |
|---|---|---|---|---|
| 10.65 | V/H | 51 × 85 | 0.5 | 15.0 |
| 18.7 | V/H | 30 × 50 | 0.5 | 10.0 |
| 23.8 | V/H | 27 × 45 | 0.5 | 7.5 |
| 36.5 | V/H | 18 × 30 | 0.5 | 5.0 |
| 89.0 | V/H | 9 × 15 | 0.8 | 2.5 |
| Methods | PSNR (dB) | SSIM | IFOV’ (km) | Noise |
|---|---|---|---|---|
| 18 GHz | 37.601 | 0.945 | 40.00 | 0.501 |
| BG | 38.962 | 0.960 | 26.85 | 0.535 |
| Banach | 40.776 | 0.966 | 23.73 | 0.700 |
| 3-layer CNN | 39.612 | 0.962 | 28.25 | 0.401 |
| VDSR | 42.501 | 0.980 | 21.63 | 0.284 |
| SRResNet | 43.077 | 0.983 | 21.35 | 0.140 |
| Basic Network | 43.134 | 0.983 | 20.76 | 0.200 |
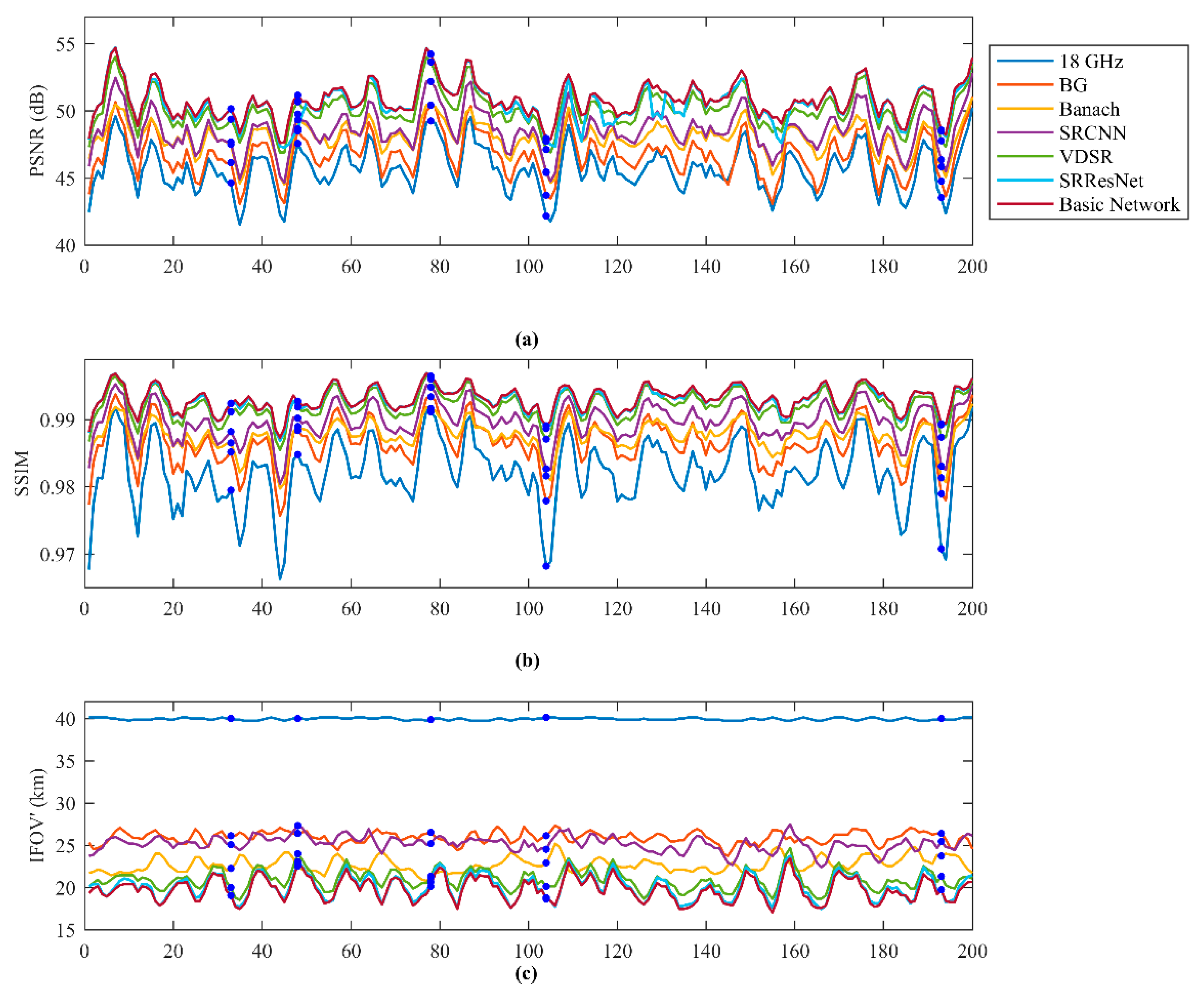
| Test Scenes | Indexes | 18 GHz | BG | Banach | SRCNN | VDSR | SRRestNet | Basic Network |
|---|---|---|---|---|---|---|---|---|
| Scene 33 | PSNR (dB) | 44.459 | 46.400 | 47.619 | 47.888 | 49.619 | 50.433 | 50.617 |
| SSIM | 0.980 | 0.986 | 0.987 | 0.989 | 0.992 | 0.993 | 0.993 | |
| IFOV’ (km) | 39.73 | 25.73 | 21.73 | 24.93 | 19.33 | 18.13 | 18.13 | |
| Scene 48 | PSNR (dB) | 47.104 | 47.883 | 49.151 | 49.238 | 50.185 | 48.070 | 50.716 |
| SSIM | 0.983 | 0.987 | 0.988 | 0.989 | 0.991 | 0.991 | 0.992 | |
| IFOV’ (km) | 40.13 | 26.13 | 23.53 | 27.33 | 24.13 | 22.93 | 22.93 | |
| Scene 78 | PSNR (dB) | 48.550 | 49.748 | 50.248 | 51.986 | 53.884 | 54.544 | 54.544 |
| SSIM | 0.991 | 0.993 | 0.992 | 0.995 | 0.996 | 0.997 | 0.997 | |
| IFOV’ (km) | 39.73 | 26.13 | 20.93 | 23.73 | 19.33 | 18.93 | 18.13 | |
| Scene 104 | PSNR (dB) | 41.459 | 43.018 | 44.953 | 44.624 | 46.141 | 46.882 | 47.037 |
| SSIM | 0.960 | 0.973 | 0.978 | 0.978 | 0.983 | 0.986 | 0.986 | |
| IFOV’ (km) | 40.13 | 26.13 | 22.53 | 24.53 | 20.93 | 19.33 | 19.33 | |
| Scene 193 | PSNR (dB) | 41.129 | 42.684 | 43.782 | 44.523 | 46.501 | 47.010 | 47.390 |
| SSIM | 0.964 | 0.974 | 0.978 | 0.981 | 0.986 | 0.988 | 0.989 | |
| IFOV’ (km) | 39.73 | 27.73 | 24.93 | 24.53 | 19.73 | 17.73 | 17.73 | |
| 200 Scenes Average | PSNR (dB) | 45.646 | 46.692 | 47.983 | 48.588 | 50.132 | 50.538 | 50.816 |
| SSIM | 0.982 | 0.987 | 0.988 | 0.990 | 0.992 | 0.993 | 0.993 | |
| IFOV’ (km) | 39.94 | 25.94 | 22.70 | 25.20 | 20.99 | 20.12 | 19.82 |
| Case | Network | PSNR (dB) | SSIM | IFOV’ (km) |
|---|---|---|---|---|
| 1: vH2 = 36.5 GHz | Na (trained from Nb) | 57.78 | 0.9986 | 26.16 |
| Na (trained from scratch) | 57.83 | 0.9986 | 26.23 | |
| 2: vH2 = 23.8 GHz | Na (trained from Nb) | 65.66 | 0.9997 | 35.83 |
| Na (trained from scratch) | 65.48 | 0.9998 | 35.76 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Hu, W.; Chen, S.; Zhang, W.; Guo, R.; He, J.; Ligthart, L. Spatial Resolution Matching of Microwave Radiometer Data with Convolutional Neural Network. Remote Sens. 2019, 11, 2432. https://doi.org/10.3390/rs11202432
Li Y, Hu W, Chen S, Zhang W, Guo R, He J, Ligthart L. Spatial Resolution Matching of Microwave Radiometer Data with Convolutional Neural Network. Remote Sensing. 2019; 11(20):2432. https://doi.org/10.3390/rs11202432
Chicago/Turabian StyleLi, Yade, Weidong Hu, Shi Chen, Wenlong Zhang, Rui Guo, Jingwen He, and Leo Ligthart. 2019. "Spatial Resolution Matching of Microwave Radiometer Data with Convolutional Neural Network" Remote Sensing 11, no. 20: 2432. https://doi.org/10.3390/rs11202432
APA StyleLi, Y., Hu, W., Chen, S., Zhang, W., Guo, R., He, J., & Ligthart, L. (2019). Spatial Resolution Matching of Microwave Radiometer Data with Convolutional Neural Network. Remote Sensing, 11(20), 2432. https://doi.org/10.3390/rs11202432