An Integrated GIS and Remote Sensing Approach for Monitoring Harvested Areas from Very High-Resolution, Low-Cost Satellite Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Characterization of the Study Area
2.2. Terrestrial Data Acquisition and Processing
2.3. Acquisition and Pre-Processing of Satellite Images
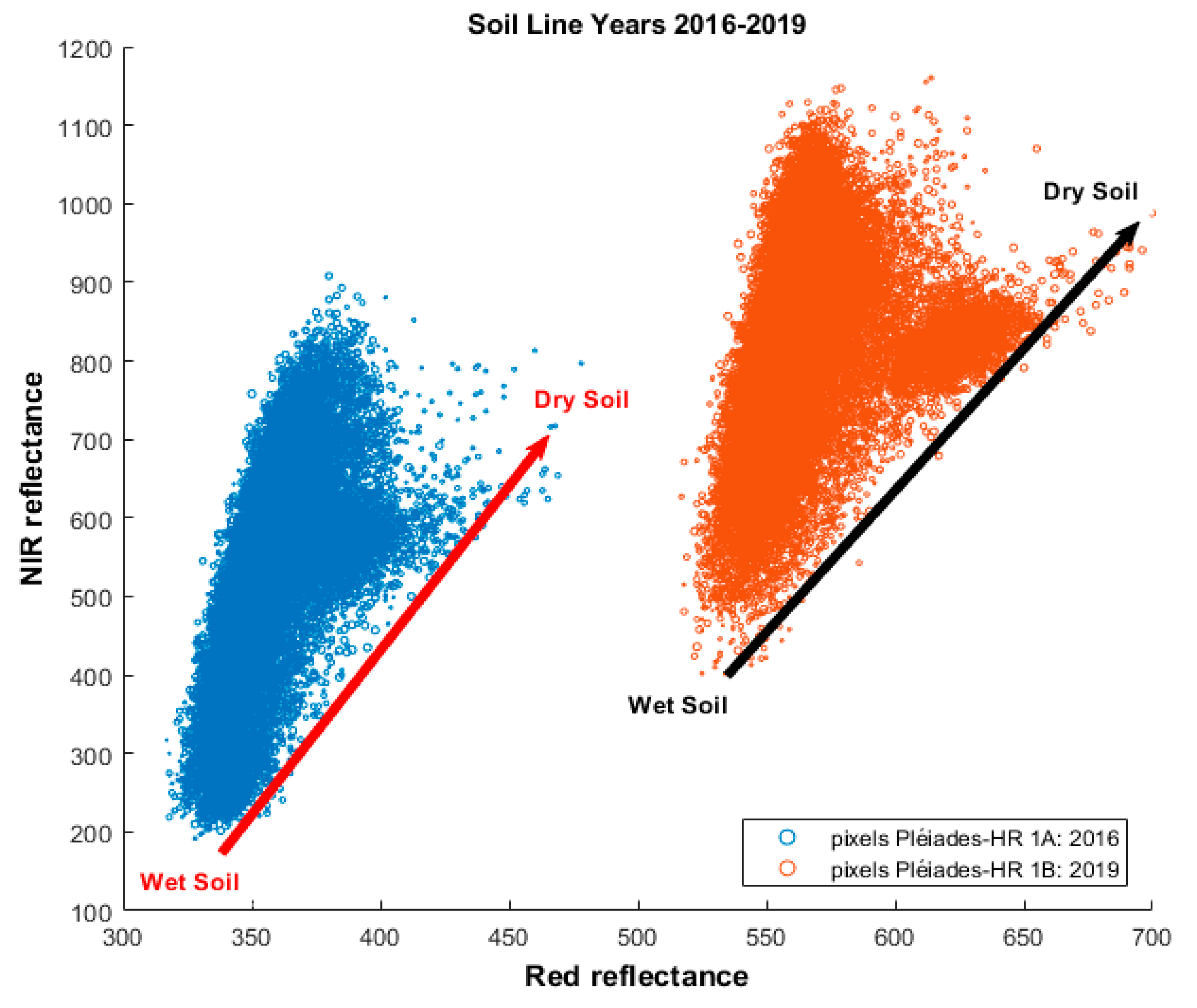
2.4. Satellite Image Processing
2.5. Modeling and Extrapolation of Harvested Parameters
3. Results
3.1. Vegetation Indices
3.2. Texture Analysis
3.3. Modeling and Extrapolation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gillis, M.D.; Leckie, D.G. Forest Inventory Mapping Procedures Across Canada; Information Report PI-X-114; Forestry Canada, Petawawa National Forestry Institute: Chalk River, ON, Canada, 1993.
- Wulder, M.A.; White, J.C.; Fournier, R.A.; Luther, J.E.; Magnussen, S. Spatially explicit large area biomass estimation: Three approaches using forest inventory and remotely sensed imagery in a GIS. Sensors 2008, 8, 529–560. [Google Scholar] [CrossRef] [PubMed]
- Hanewinkel, M.; Cullmann, D.A.; Schelhaas, M.J.; Nabuurs, G.J.; Zimmermann, N.E. Climate change may cause severe loss in the economic value of European forest land. Nat. Clim. Chang. 2012, 3, 203–207. [Google Scholar] [CrossRef]
- Nabuurs, G.J.; Lindner, M.; Verkerk, P.J.; Gunia, K.; Deda, P.; Michalak, R.; Grassi, G. First signs of carbon sink saturation in European forest biomass. Nat. Clim. Chang. 2013, 3, 792–796. [Google Scholar] [CrossRef]
- He, H.S.; Mladenoff, D.J.; Crow, T.R. Linking an ecosystem model and alandscape model to study forest species response to climate warming. Ecol. Model. 1999, 114, 213–233. [Google Scholar] [CrossRef]
- Dixon, R.K.; Brown, S.; Houghton, R.A.; Solomon, A.M.; Trexler, M.C.; Wisniewski, J. Carbon pools and flux of global forest ecosystem. Science 1994, 263, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Kašpar, J.; Hlavatý, R.; Kuželka, K.; Marušák, R. The Impact of Assumed Uncertainty on Long-Term Decisions in Forest Spatial Harvest Scheduling as a Part of Sustainable Development. Forests 2017, 8, 335. [Google Scholar] [CrossRef]
- Asner, G.P.; Rudel, T.K.; Aide, T.M.; Defries, R.; Emerson, R. A contemporary assessment of change in humid tropical forests. Conserv. Biol. 2009, 23, 1386–1395. [Google Scholar] [CrossRef]
- Oliver, C.D.; Larson, B.C. Forest Stand Dynamics; John Wiley and Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Cannon, C.H.; Peart, D.R.; Leighton, M.; Keratinase, K. The structure of lowland rain-forest after selective logging in West Kalimantan, Indonesia. For. Ecol. Manag. 1994, 67, 49–68. [Google Scholar] [CrossRef]
- Perrotta, J.A.; Francis, J.K.; Knowles, O.H. Harvesting intensity affects forest structure and composition in an upland Amazonian forest. For. Ecol. Manag. 2002, 169, 243–255. [Google Scholar] [CrossRef]
- Jackson, S.M.; Frederiksen, T.S.; Malcolm, J.R. Area disturbed and residual stand damage following logging in a Bolivian tropical forest. For. Ecol. Manag. 2002, 166, 271–283. [Google Scholar] [CrossRef]
- Asner, G.P.; Keller, M.; Pereira, R.; Weeded, J.C. Remote sensing of selective logging in Amazonia. Remote Sens. Environ. 2002, 80, 483–496. [Google Scholar] [CrossRef]
- Laporte, N.T.; Staubach, J.A.; Grosch, R.; Lin, T.S.; Goetz, S.J. Expansion of industrial logging in Central Africa. Science 2007, 316, 1451. [Google Scholar] [CrossRef] [PubMed]
- Keller, M.; Palace, M.; Asner, G.P.; Pereira, R.; Silva, J.N.M. Coarse woody debris in undisturbed and logged forests in the eastern Brazilian Amazon. Glob. Chang. Biol. 2004, 10, 784–795. [Google Scholar] [CrossRef]
- Shimabukuro, Y.E.; Beachie, R.; Gracchi, R.C.; Achard, F. Assessment of forest degradation in Brazilian Amazon due to selective logging and fires using time series of fraction images derived from Landsat ETM+ images. Remote Sens. Lett. 2014, 5, 773–782. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Ediriwickrema, J.; Johnson, D.M.; Lyon, J.G.; McKerrow, A. Impacts of vegetation dynamics on the identification of land-cover change in a biologically complex community in North Carolina, USA. Remote Sens. Environ. 2002, 82, 258–270. [Google Scholar] [CrossRef]
- Chiteculo, V.; Abdollahnejad, A.; Panagiotidis, D.; Surový, P.; Sharma, R.P. Defining Deforestation Patterns Using Satellite Images from 2000 and 2017: Assessment of Forest Management in Miombo Forests—A Case Study of Huambo Province in Angola. Sustainability 2019, 11, 98. [Google Scholar] [CrossRef]
- Kayitakire, F.; Hamel, C.; Defourny, P. Retrieving forest structure variables based on image texture analysis and IKONOS-2 imagery. Remote Sens. Environ. 2006, 102, 390–401. [Google Scholar] [CrossRef]
- St-Onge, B.; Hu, Y.; Vega, C. Mapping the height and above-ground biomass of a mixed forest using LiDAR and stereo Ikonos images. Int. J. Remote Sens. 2008, 29, 1277–1294. [Google Scholar] [CrossRef]
- Ozdemir, I.; Karnieli, A. Predicting forest structural parameters using the image texture derived from WorldView-2 multi-spectral imagery in a dryland forest, Israel. Int. J. Appl. Earth Obs. Geoinform. 2011, 13, 701–710. [Google Scholar] [CrossRef]
- Stibig, H.; Achard, F.; Carboni, S.; Raši, R.; Miettinen, J. Change in tropical forest cover of Southeast Asia from 1990 to 2010. Biogeosciences 2014, 11, 247–258. [Google Scholar] [CrossRef] [Green Version]
- Abdollahnejad, A.; Panagiotidis, D.; Shataee Joybari, S.; Surový, P. Prediction of Dominant Forest Tree Species Using QuickBird and Environmental Data. Forests 2017, 8, 42. [Google Scholar] [CrossRef]
- Abdollahnejad, A.; Panagiotidis, D.; Surový, P. Estimation and Extrapolation of Tree Parameters Using Spectral Correlation between UAV and Pléiades Data. Forests 2018, 9, 85. [Google Scholar] [CrossRef]
- Souza, C.M., Jr.; Siqueira, J.V.; Sales, M.H.; Fonseca, A.V.; Ribeiro, J.G.; Numata, I.; Cochrane, M.A.; Barber, C.P.; Roberts, D.A.; Barlow, J. Ten-year Landsat classification of deforestation and forest degradation in the Brazilian Amazon. Remote Sens. 2013, 5, 5493–5513. [Google Scholar] [CrossRef]
- Melaas, E.; Friedl, M.A.; Zhu, Z. Detecting interannual variation in deciduous broadleaf forest phenology using Landsat TM/ETM+ data. Remote Sens. Environ. 2013, 132, 176–185. [Google Scholar] [CrossRef]
- Souza, C., Jr.; Firestone, L.; Silva, L.M.; Roberts, D. Mapping forest degradation in the Eastern Amazon from SPOT4 through spectral mixture models. Remote Sens Environ. 2003, 87, 494–506. [Google Scholar] [CrossRef]
- Mitchell, A.L.; Rosenqvist, A.; Mora, B. Current remote sensing approaches to monitoring forest degradation in support of countries measurement, reporting and verification (MRV) systems for REDD+. Carbon Balance Manag. 2017, 12, 9. [Google Scholar] [CrossRef]
- Kennedy, C.; Cuddihy, J.; Engel-Yan, J. The changing metabolism of cities. J. Ind. Ecol. 2007, 11, 43–59. [Google Scholar] [CrossRef]
- Thompson, I.D.; Guariguata, M.R.; Okabe, k.; Bahamondez, C.; Nasi, R.; Heymell, V. An operational framework for defining and monitoring forest degradation. Ecol. Soc. 2013, 18, 20. [Google Scholar] [CrossRef]
- Turubanova, S.; Potapov, P.; Krylov, A.; Tyukavina, A.; McCarty, J.L.; Radeloff, V.C.; Hansen, M.C. Using the landsat data archive to assess long-term regional forest dynamics assessment in Eastern Europe, 1985–2012. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 531–537. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Williams, L.E.; Suárez, L.; Berni, J.A.J.; Goldhamer, D.; Fereres, E. A PRI-based water stress index combining structural and chlorophyll effects: Assessment using diurnal narrow-band airborne imagery and the CWSI thermal index. Remote Sens. Environ. 2013, 138, 38–50. [Google Scholar] [CrossRef]
- Glenn, E.; Nagler, P.; Huete, A. Vegetation index methods for estimating evapotranspiration by remote sensing. Surv. Geophys. 2010, 31, 531–555. [Google Scholar] [CrossRef]
- Tucker, C.J.; Townshend, J.R.G.; Goff, T.E. African land-cover classification using satellite data. Science 1985, 227, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Eastman, J.R. IDRISI Kilimanjaro: Guide to GIS and Image Processing; Clark University: Worcester, MA, USA, 2003. [Google Scholar]
- Blackard, J.A.; Finco, M.V.; Helmer, E.H.; Holden, G.R.; Hoppus, M.L.; Jacobs, D.M.; Lister, A.J.; Moisen, G.G.; Nelson, M.D.; Riemann, R.; et al. Mapping U.S. forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
- Hansen, J.; Makiko, S.; Pushker, K.; David, B.; Robert, B.; Valerie, M.D.; Mark, P.; Maureen, R.; Dana, L.R.; James, C.Z. Target atmosphere CO2: Where should humanity aim. Open Atmos. Sci. J. 2008, 2, 217–231. [Google Scholar] [CrossRef]
- Romero-Sanchez, M.E.; Ponce-Hernandez, R. Assessing and Monitoring Forest Degradation in a Deciduous Tropical Forest in Mexico via Remote Sensing Indicators. Forests 2017, 8, 302. [Google Scholar] [CrossRef]
- Soil Map. Available online: http://www.geology.cz/extranet-eng/services/web-applications/ (accessed on 19 August 2019).
- Tolasz, R. Atlas podnebí Česka (Climate atlas of Czechia), 1st ed.; Český hydrometeorologický ústav, Univerzita Palackého v Olomouci: Praha, Czech Republic, 2007; p. 255. [Google Scholar]
- Petráš, R.; Pajtík, J. Sústava česko-slovenských objemových tabuliek drevín. Lesnický Časopis 1991, 1, 49–56. [Google Scholar]
- Purevdorj, T.S.; Tateishi, R.; Ishiyama, T.; Honda, Y. Relationships between percent vegetation cover and vegetation indices. Int. J. Remote Sens. 1998, 19, 3519–3535. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation system in the great plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Greenbelt, MD, USA, 10–14 December 1974. pp. 309–3017. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19740022614.pdf (accessed on 19 August 2019).
- Perry, C.R., Jr.; Lautenschlager, L.F. Functional equivalence of spectral vegetation indices. Remote Sens. Environ. 1984, 14, 169–182. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Birth, G.S.; McVey, G.R. Measuring the color of growing turf with a reflectance spectrophotometer. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogram. Eng. Remote Sens. 1977, 43, 15–41. [Google Scholar]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H. Modified Soil Adjusted Vegetation Index (MSAVI). Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Sader, S.A.; Bertran, M.; Wilson, E.H. Satellite change detection of forest harvest patterns on an industrial forest landscape. For. Sci. 2003, 49, 341–353. [Google Scholar]
- Masiliūnas, D. Evaluating the Potential of Sentinel-2 and Landsat Image Time Series for Detecting Selective Logging in the Amazon; Wageningen University and Research Centre: Wageningen, The Netherlands, 2014; p. 54. [Google Scholar]
- Shchur, A.; Bragina, E.; Sieber, A.; Pidgeon, A.M.; Radelof, V.C. Monitoring selective logging with Landsat satellite imagery reveals that protected forests in Western Siberia experience greater harvest than non-protected forests. Environ. Conserv. 2017, 44, 191–199. [Google Scholar] [CrossRef] [Green Version]
- Read, J.M. Spatial analyses of logging impacts in Amazonia using remotely sensed data. Photogramm. Eng. Remote Sens. 2003, 69, 275–282. [Google Scholar] [CrossRef]










| Estimated Parameter | Tree Species | Number of Trees | Trendline | Equation | R2 |
|---|---|---|---|---|---|
| Height | Scots pine | 25 | linear | y = 0.1581x + 21.141 | 0.48 |
| Norway spruce | 25 | linear | y = 0.2354x + 17.145 | 0.58 | |
| Scots pine | 40 | linear | y = 1.0601x + 5.7583 | 0.92 | |
| Norway spruce | 40 | linear | y = 1.29x - 0.165 | 0.96 |
| Scots Pine | A | B | C | E | |||
|---|---|---|---|---|---|---|---|
| Coefficients | 3.03E-05 | 2.075238 | 0.012492 | 0.961028 | 0.071975 | −2.12449 | 1.372591 |
| Norway spruce | A | B | C | E | F | G | |
| Coefficients | 4.01E-05 | 1.821816 | 1.132062 | 9.29E-03 | −1.02037 | 0.896101 |
| Pléiades HR 1A-1B | |
|---|---|
| Imagery products | 2 m multi-spectral resolution |
| Bundle: 50 cm panchromatic—2 m multi-spectral | |
| Panchromatic resolution 50 cm | |
| Spectral bands | Red: 600–720 nm |
| Green: 490–610 nm | |
| Blue: 430–550 nm | |
| Near Infrared: 750–950 nm | |
| Panchromatic: 480–830 nm | |
| Image location accuracy | With * GCPs is 1 m |
| Without GCPs is 3 m (CE90) | |
| VIs | References | Explanation of Symbols | |
|---|---|---|---|
| Slope-based | Rouse et al. [45] | R = red band B = blue band L = soil NIR = near infrared band | |
| × | Perry and Lautenschlager [46] | ||
| Baret and Guyot [47] | |||
| Birth and McVey [48] | |||
| Richardson and Wiegand [49] | |||
| Huete [35] | |||
| Distance-based | Qi et al. [39] | Qi et al. [50] | R = reflectance in the visible red L = 1 − (2 × NDVI × WDVI) WDVI = NIR − (slope × R) |
| Qi et al. [50] | pR = reflectance of the red pNIR = reflectance of the near infrared |
| * VIs | S ource | *SS | * df | * MS | F-Statistic | * Prob>F | |
|---|---|---|---|---|---|---|---|
| Slope-based | CTVI | * Groups | 0.02 | 1 | 0.02 | 120.57 | 0.00 |
| * Error | 0.02 | 94 | 0.00 | ||||
| * Total | 0.04 | 95 | |||||
| NDVI | Groups | 0.06 | 1 | 0.06 | 132.78 | 0.00 | |
| Error | 0.04 | 94 | 0.00 | ||||
| Total | 0.10 | 95 | |||||
| NRVI | Groups | 0.06 | 1 | 0.06 | 132.78 | 0.00 | |
| Error | 0.04 | 94 | 0.00 | ||||
| Total | 0.10 | 95 | |||||
| RATIO | Groups | 0.61 | 1 | 0.61 | 169.74 | 0.00 | |
| Error | 0.34 | 94 | 0.00 | ||||
| Total | 0.95 | 95 | |||||
| RVI | Groups | 0.11 | 1 | 0.11 | 105.84 | 0.00 | |
| Error | 0.10 | 94 | 0.00 | ||||
| Total | 0.21 | 95 | |||||
| SAVI | Groups | 0.01 | 1 | 0.01 | 16.60 | 0.00 | |
| Error | 0.08 | 94 | 0.00 | ||||
| Total | 0.09 | 95 | |||||
| Distance-based | MSAVI1 | Groups | 0.23 | 1 | 0.23 | 132.42 | 0.00 |
| Error | 0.17 | 94 | 0.00 | ||||
| Total | 0.40 | 95 | |||||
| MSAVI2 | Groups | 0.11 | 1 | 0.11 | 105.7 | 0.00 | |
| Error | 0.10 | 94 | 0.00 | ||||
| Total | 0.21 | 95 |
| Dependent Variables | Variable Category | Variable | Loading |
|---|---|---|---|
| -Total Harvested Volume -Average Volume -Changes in Openness Based on Volume -Changes in Openness Based on Basal Area -Changes in Openness Based on Tree Density | * TA | GLDVContrast-NIR band | 0.927 |
| TA | Contrast-NIR band | 0.927 | |
| TA | GLDVContrast-NIR band | 0.927 | |
| TA | Dissimilarity-blue band | 0.924 | |
| TA | GLDVMean-blue band | 0.924 | |
| TA | Entropy-NIR band | 0.92 | |
| TA | STANDDEV-blue band | 0.918 | |
| * VI | NDVI | 0.975 | |
| VI | NRVI | −0.975 | |
| VI | MSAVI1 | 0.975 | |
| VI | CTVI | 0.975 | |
| VI | MSAVI2 | 0.972 | |
| VI | RVI | −0.972 | |
| VI | SAVI | 0.971 | |
| VI | RATIO | 0.965 |
| Parameters (Per Plot) | Independent Variables | RMSE | RMSE Reduction | Bias | Bias% | |
|---|---|---|---|---|---|---|
| 2016 | Total volume (m3) | * VIs | 4.49 | 16.98 | 0.66 | 2.43 |
| * TA | 5.4 | 19.37 | −1.63 | −6.24 | ||
| Total | 4.51 | 16.53 | −0.27 | −1.01 | ||
| Average volume (m3) | VIs | 4.52 | 17.11 | 0.73 | 2.71 | |
| TA | 0.24 | 17.06 | −0.002 | −0.13 | ||
| Total | 0.23 | 16.04 | −0.01 | −0.68 | ||
| 2019 | Total volume (m3) | VIs | 3.53 | 27.24 | −1.62 | −14.3 |
| TA | 3.43 | 28.87 | −0.05 | −0.47 | ||
| Total | 2.58 | 25.59 | 1.88 | 15.74 | ||
| Average volume (m3) | VIs | 0.22 | 17.47 | −0.036 | 2.89 | |
| TA | 0.2 | 15.74 | −0.02 | −2.25 | ||
| Total | 0.21 | 16.97 | 0.03 | 2.67 | ||
| Harvested or changes | Total volume (m3) | VIs | 6.88 | 53.42 | 3.38 | 20.78 |
| TA | 8.16 | 52.63 | −0.63 | −4.23 | ||
| Total | 5.18 | 33.57 | −0.53 | −3.57 | ||
| Average volume (m3) | VIs | 0.45 | 26.74 | −0.15 | −9.7 | |
| TA | 0.4 | 24.84 | −0.023 | −1.46 | ||
| Total | 0.35 | 23.52 | 0.15 | 9.5 | ||
| * COV% | VIs | 20.65 | 43.13 | 8.85 | 15.6 | |
| TA | 18.49 | 34.66 | 0.24 | 0.45 | ||
| Total | 11.48 | 20.97 | 0.48 | 0.88 | ||
| * COB% | VIs | 20.03 | 42.29 | 8.73 | 15.56 | |
| TA | 18.12 | 34.29 | −0.04 | −0.08 | ||
| Total | 11.15 | 20.54 | −0.09 | −0.18 | ||
| * COD% | VIs | 21.55 | 51.87 | 11.29 | 21.37 | |
| TA | 16.47 | 32.9 | −1.68 | −3.47 | ||
| Total | 9.07 | 17.79 | −1.91 | −3.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdollahnejad, A.; Panagiotidis, D.; Bílek, L. An Integrated GIS and Remote Sensing Approach for Monitoring Harvested Areas from Very High-Resolution, Low-Cost Satellite Images. Remote Sens. 2019, 11, 2539. https://doi.org/10.3390/rs11212539
Abdollahnejad A, Panagiotidis D, Bílek L. An Integrated GIS and Remote Sensing Approach for Monitoring Harvested Areas from Very High-Resolution, Low-Cost Satellite Images. Remote Sensing. 2019; 11(21):2539. https://doi.org/10.3390/rs11212539
Chicago/Turabian StyleAbdollahnejad, Azadeh, Dimitrios Panagiotidis, and Lukáš Bílek. 2019. "An Integrated GIS and Remote Sensing Approach for Monitoring Harvested Areas from Very High-Resolution, Low-Cost Satellite Images" Remote Sensing 11, no. 21: 2539. https://doi.org/10.3390/rs11212539
APA StyleAbdollahnejad, A., Panagiotidis, D., & Bílek, L. (2019). An Integrated GIS and Remote Sensing Approach for Monitoring Harvested Areas from Very High-Resolution, Low-Cost Satellite Images. Remote Sensing, 11(21), 2539. https://doi.org/10.3390/rs11212539








