Using Tree Detection Based on Airborne Laser Scanning to Improve Forest Inventory Considering Edge Effects and the Co-Registration Factor

Abstract

The estimation of forest biophysical attributes improves when airborne laser scanning (ALS) is integrated. Individual tree detection methods (ITD) and traditional area-based approaches (ABA) are the two main alternatives in ALS-based forest inventory. This study evaluated the performance of the enhanced area-based approach (EABA), an edge-correction method based on ALS data that combines ITD and ABA, at improving the estimation of forest biophysical attributes, while testing its efficiency when considering co-registration errors that bias remotely sensed predictor variables. The study was developed based on a stone pine forest (Pinus pinea L.) in Central Spain, in which tree spacing and scanning conditions were optimal for the ITD approach. Regression modeling was used to select the optimal predictor variables to estimate forest biophysical attributes. The accuracy of the models improved when using EABA, despite the low-density of the ALS data. The relative mean improvement of EABA in terms of root mean squared error was 15.2%, 17.3%, and 7.2% for growing stock volume, stand basal area, and dominant height, respectively. The impact of co-registration errors in the models was clear in the ABA, while the effect was minor and mitigated under EABA. The implementation of EABA can highly contribute to improve modern forest inventory applications.

1. Introduction

The use of active remote sensing in forest inventories is a clear trend due to the capability of lasers to precisely describe the three dimensional (3D) structure of trees and stands [1]. Researchers have been focused on two main approaches, two scales, when it comes to estimating forest attributes by relying on airborne laser scanning (ALS): individual tree detection (ITD) and area-based approach (ABA) methods. Methods under the ITD approach are based on the capability of algorithms to derive the position and the height of detected trees [2], while in ABA approaches the statistics computed for a given area are used to estimate forest biophysical attributes at plot- or stand-level, such as stand basal area or dominant height, for instance [3].

In operational forestry, the simplicity of ABA methods is preferred as the position of the measured trees is not required to compute statistics from the ALS echoes [2]. The co-registration between ground measurements and ALS data is straightforwardly done based on plot center coordinates recorded with positioning systems during field operations. The implementation of the ITD approach typically requires the use of local maxima algorithms to detect tree top coordinates to be used for canopy segmentation [4]. The goodness of tree detection is usually validated using more extensive and time-consuming field work involving tree-level measurements and the positioning of all trees within the sample plots. Consequently, the application of ITD has been restricted and not as commonly implemented as ABA approaches. It is important to recognize that some factors, such as the complexity of the forest structure, tree spacing, and point cloud density, can determine the applicability and efficiency of ITD methods in dense forest ecosystems [1]. In addition, the complexity and steepness of the terrain can challenge the assignment of ground coordinates to measured trees as the discrepancy between the stems’ base position and the center point of the canopies can progressively increase with the slope. However, the performance of the ITD method can be optimal in sparse, relatively flat and open forest ecosystems, in which tree positions can be accurately detected using recent developments in both airborne laser scanning, even with less densified ALS point clouds, and more advanced photogrammetry methods, such as Structure-from-Motion (SfM), combining Digital Aerial Photogrammetry (DAP) and image-matching algorithms, which is a promising approach to deriving canopy height models (CHM) using drone-based sensors [5,6].

The development of ITD methods is important to boost the implementation of tree-level forest planning [7], but also to enhance forest inventory methods. The standard ABA method is straightforward and easy to implement, but it ignores the impact of edges (discontinuities) when computing ALS statistics, leading to the introduction of bias in the estimation models, as previous studies showed [8]. To account for the distribution of trees within, and in the proximity of, sample edges, it is necessary to combine the ABA and ITD methods. The detection of tree canopies under the ITD approach can be used to adjust the edge of the sample plots to the distribution of trees, using both detected trees inside and outside of the sampling areas [9]. The purpose is to identify measured trees whose canopies are partially contained in the sample plots and non-measured trees whose canopies overlap the sample edge. As a result, the computed ALS statistics truly correspond to the measured trees. The method, referred to as the enhanced area-based approach (EABA) method in the literature, has been previously applied in boreal forests with high-density ALS data [8] and also with less densified ALS point clouds, with the purpose of estimating carbon stocking [10]. The implementation rate of the EABA is still low in operational forest inventory despite its good performance, which could be even better when considering the occurrence of co-registration errors between ground observations and statistics computed from the ALS data.

In ALS-based forest inventory, the statistics computed from a three-dimensional (3D) point cloud are related to measured data collected in sampling designs, as the x, y, and z coordinates (easting, northing, and elevation) of all ALS echoes are recorded. Therefore, the geographical co-registration between ALS data and ground-measured data is essential to properly estimate forest biophysical attributes [2,11]. Co-registration errors can occur due to GPS positioning errors in the field due to signal losses below forest canopies, for instance, and this can worsen the relationship between ground measurements and the ALS statistics computed for the given area of interest. The occurrence of positioning errors in ground operations can be costly when estimating forest biophysical attributes [12,13,14] and, as a result, the error further impacts harvest-scheduling solutions in forest planning [15]. Therefore, there is a need to integrate new solutions that can potentially correct, or at least mitigate, the impact of frequently ignored co-registration errors in modern forest inventory. There is a real need to account for data uncertainty when using modern forest inventory methods [1,16] in which (i) the relevance of edge tree errors is frequently ignored and (ii) the traditional ABA approach is being challenged by novel methods and remote sensing possibilities in the field [17,18].

The EABA method could be effective at mitigating the effect of positioning errors during the modeling stage as sample plot edges are adjusted to the distribution of trees and this novel feature of the EABA can help to correct the mismatch between ground data and ALS statistics when altering plot coordinates, as already observed for the traditional ABA. Based on an adequate methodological framework, combining ALS data and tree-level measurements, the expected improvement in the predictive capability of the models under the EABA method was firstly benchmarked against the standard ABA approach in the context of co-registration errors. The EABA-versus-ABA assessment was conducted in Central Spain on a stone pine forest (Pinus pinea L.), in which the spatial distribution and the size of the trees are aligned with the optimal conditions for the full and successful implementation of the ITD approach.

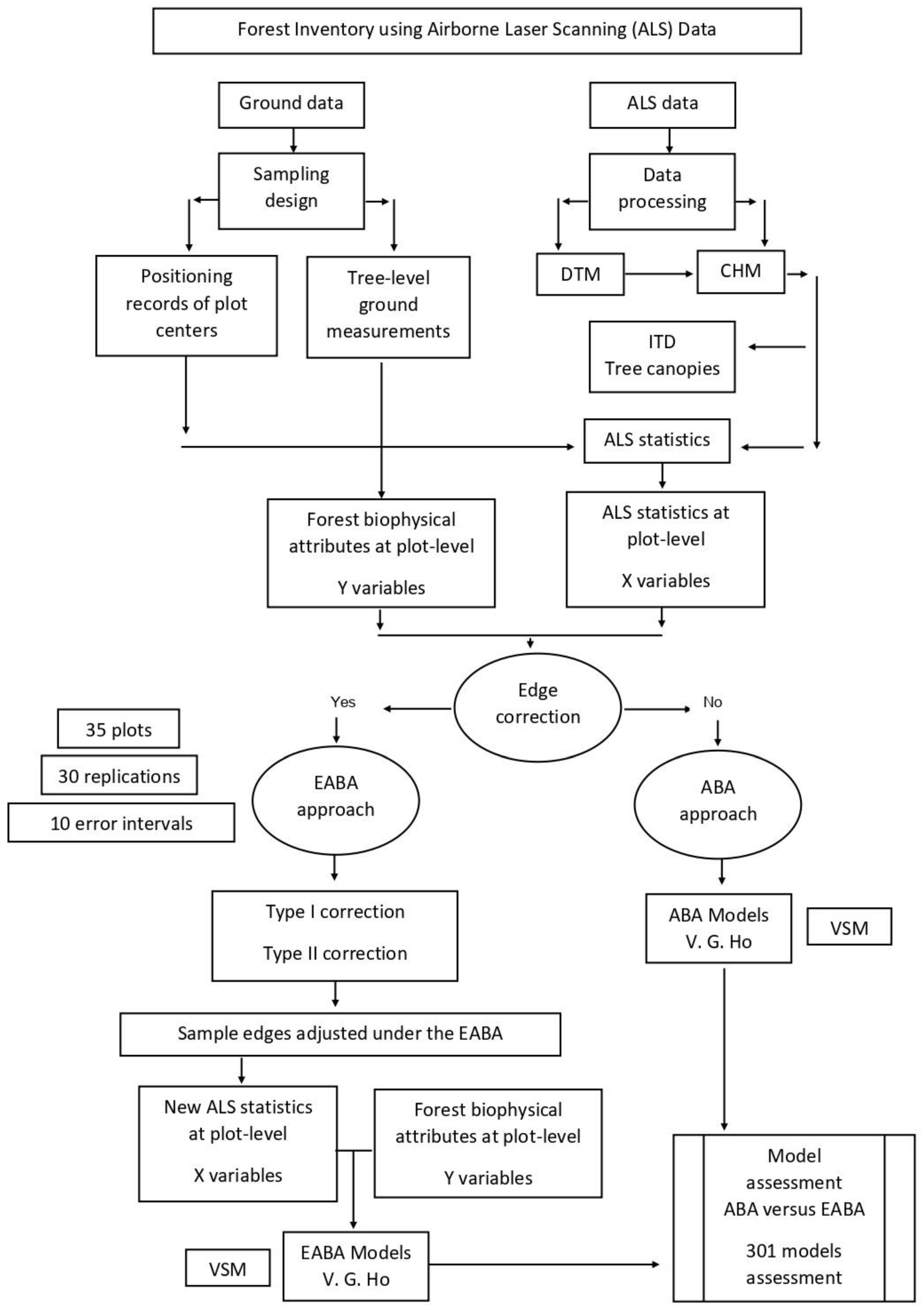
2. Materials and Methods

2.1. Study Area

The study area was the public forest MUP50 (1100 ha), owned by the municipality of Portillo in the province of Valladolid (Figure 1), located in Castilla y León (Central Spain). The study area consisted of a mosaic of stone pine (Pinus pinea L.) stands, on which even-aged forestry using long rotation ages (>100 years) has been prescribed for decades. The study area consisted of pure stone pine stands at different stages of development. The production of pine seeds is especially relevant for the local economies, which explains the long rotation ages used in the area. The species naturally regenerates in stands after harvests due to its tolerance of sandy soils, continental climates, and drought episodes. The area is part of the Northern Plateu [19], in which the role of stone pine forests has been essential in economic development (production of firewood and non-wood forest products), while providing important ecosystem services such as erosion control and wildlife conservation. The integration of modern forest inventory methods using ITD is being regarded as the optimal guideline to improve forest management planning in the area. The relationship between the size of tree canopies and the production of cones (pine seeds) is clear for the species [20], as the large canopies of the stone pine trees are prone to be optimally detected, even when using low-density ALS data, as recently documented [5]. The conditions of the forest area selected to test the research hypothesis were optimal due to the sparse distribution of mature trees, the presence of advanced natural regeneration, and the lack of steep areas for which tree positions can differ depending on whether the ground measurement refers to the base of the stem or to the center point of the canopy.

2.2. Data

2.2.1. Ground Tree-Level Measurements

Systematic sampling was used to establish a network of 35 circular sample plots of 15 m radius. A set of positioning records were measured in each plot using submeter precision GNSS equipment (Garmin International Inc., Olathe, Kansas, USA). The sparse conditions of the area and the equipment used during fieldwork operations set the basis for an optimal recording of the sample plots’ coordinates during fieldwork operations, which eased the co-registration in the ALS-based forest inventory. On each plot, all trees with a diameter at breast height (DBH) >7.5 cm were callipered and their height was measured using a Vertex IV hypsometer (Haglöf, Långsele, Sweden). The ground data corresponding to the 2014 campaign contained 344 tree measurements (

Table 1. Summary information of the tree- and plot-level ground data.

Variable	Min	Mean	Max
DBH (cm)	9.0	33.0	68.0
h (m)	3.5	9.7	13.8
N (trees ha−1)	64.0	129.2	292.0
G (m2 ha−1)	5.2	11.9	18.4
H0 (m)	8.9	11.2	13.8

¹DBH: tree diameter measured at breast height (1.3 m); h: tree height (m); N: number of trees per hectare; G: stand basal area; H₀: dominant height.

). Dominant height was computed as the arithmetic mean of the 100 largest trees in diameter, which corresponded to 7 trees for the 15 m radius sample plots. The volume of the individual trees was calculated using the taper functions developed for the stone pine forests of the Northern Plateau, which are being used in operational forestry in the area [19].

2.2.2. Data—ALS-Derived Metrics Assessment

The ALS data were collected in 2010 using an ALS60 laser scanning system. The dataset is part of the first round of scanning carried out by the Spanish National Program of Aerial Orthophotography (PNOA). The nominal average density of first echoes per square meter was 0.5 at national level, although in the study area the value reached 0.7. The area was scanned from 2000 m altitude using a scan angle of ±10 degrees. The extension of the ALS data was 24 km² and it was divided into a manageable set of tiles. An interpolated digital terrain model (DTM) of 1 m² cell size was constructed for each tile, before aggregating all to form a single DTM covering the whole area of interest. The DTMs were derived by classifying echoes as ground and non-ground hits according to the approach described by [21]. The rescaling of non-ground ALS echoes from height above the ellipsoid GRS80 to above ground level was calculated by subtracting bare land elevation (DTM) from the elevation of ALS echoes. The 1 m² canopy height model (CHM) was interpolated by searching the highest ALS echo from the center of each cell. The above-ground height values ranged from 0 to 29.6 m. The software LasTools [22] and FUSION [23] were used to visualize, to derive both the DTM and CHM, and finally to compute the ALS statistics for each sample plot. The above-ground height of ALS echoes was used to distinguish between tree canopies (echoes above 2 m) and the shrub layer (echoes below 2 m) when computing ALS statistics.

2.3. Individual Tree Detection (ITD) and DBH Prediction

The implementation of the ITD approach followed two steps: (i) detection of local maxima candidates and (ii) segmentation of the tree canopies using the detected trees and the CHM [4]. First, a local maxima algorithm implemented in the SAGA watershed segmentation module [24] was used to derive tree positions and the height of trees from the 1 m² CHM raster. These tree positions were used as seeds from which to apply the region growing algorithm using the CHM for the delineation of the canopies. The goodness of the tree canopies segmentation was evaluated based on visual inspection, comparing the perimeter boundaries of the delineated tree canopies with ground measurements and the spatial layout of the CHM in the transition boundary between two canopies was carefully inspected. Ground measurements, the CHM, and the distribution of trees within the 35 sample plots were used to validate the accuracy of the algorithms in the first step (Figure 2). Measured and detected data were associated using a maximum of 3 m in the Euclidean space [2]. Ground tree-level attributes were joined to the corresponding detected positions to model the nonlinear relationship between tree height and diameter [25]. The following one-predictor model Equation (1) was fitted to the data:

$$DBH=a\ast \ln {\left(h\right)}^{ b},$$

(1)

where DBH is the measured diameter at breast height and h is tree height derived with ALS data. The model was used to predict DBH for all detected trees. At this stage, forest inventory was completed: the location, height, and canopy area of all detected trees in the study forest were captured from the ALS data, while DBH was predicted for all detected trees.

2.4. The Edge-Correction Method

In field operations, the distance from the stem base of a tree to the center of the sample plot determines the number of trees included in the sampling for a given plot radius. In the standard ABA approach, plot radius and the center point coordinates recorded with the positioning equipment are used to extract the ALS echoes registered within a circular sample plot (Figure 3a). As already highlighted in the previous sections, the spatial distribution of trees within and outside the sample edges cannot be recognized using the traditional ABA. Under the EABA approach, the edges of the sample plots are adjusted to the distribution of tree canopies to avoid two types of errors commonly ignored when processing ALS data for forest inventory applications:

• Type I. Inclusion error that refers to the situation in which the canopies of the measured trees are partially contained within the sample edge. The edge of the sample plot is corrected to follow the irregular pattern of the tree canopies included in the sampling. The sampled area increased compared to the ABA (Figure 3b).
• Type II. Exclusion error that refers to the case in which trees outside the sample edge are not measured but the canopy is partially contained within the sample plot. The edge of the sample is adjusted again from Type I correction by removing the canopy area that belongs to the trees located outside of the sample plot. In this way, ALS echoes corresponding to non-measured are remove for the computation of ALS statistics (Figure 3c).

The area of sample plots using the measured ground coordinates increased 8%, on average, when implementing Type I correction, but the increment was mitigated when implementing Type II correction to fully apply the EABA approach. The area for an average sample plot under Type II correction was 2% higher than in the ABA approach. In the next sections of the research article, the term EABA will denote the presented Type II correction (Figure 3c). The complete workflow of the research, including the implementation of the EABA method, is presented in Figure A1 (Annex I).

The final sample edges under the EABA were derived using a Python script within the ArcGIS environment [26], which involved the following steps:

• Coordinates and radius were used to create a buffer for each of the 301 plots.
• Detected trees corresponding to a ground measured tree were selected and their detected canopies were used to clip (area increment) the sample edge for ABA.
• Feature Type I was created.
• Non-measured trees whose centroid was located outside of Feature Type I were selected and their canopy area was removed from Feature Type I.
• Feature Type II was created.

2.5. Computation of Point Cloud Statistics

Sample edges for both ABA and EABA methods were used to compute a long array of elevation and density statistics from the ALS point clouds [23]. The set of ALS statistics were computed using the FUSION software. The whole set of ALS statistics was shortlisted to 24 possibilities (including a balanced proportion of elevation and density metrics) to be used as candidate predictor variables to estimate forest biophysical attributes. The mean (H_mean), minimum (H_min), and maximum height (H_max) of the ALS echoes and their standard elevation (H_std) were computed, as were percentiles (10th, 20th, …, 99th), for the canopy height. The density metrics were also calculated and separately computed, considering only first and all echoes, respectively. For example, H₂₀ for a plot is the 20th height percentile of the ALS echoes distributed within the plot. The proportion of ALS echoes above 2 m (FC_2m), above the mean height (FC_mean), and above the elevation mode (FC_mode) were computed for first and all echoes, respectively.

2.6. Simulation of Co-Registration Mismatch

The statistics were computed for ABA and EABA using the ground truth coordinates of the sample plots (Ref). In line with previous studies on the topic [14], ground truth coordinates were altered to simulate positioning errors and bias the co-registration factor. The simulation was as follows: errors in the easting and northing values of all plot center coordinates were randomly simulated to mimic the occurrence of GPS errors in ground operations (Figure 4). The scale of these errors reached a maximum of 5 m, and those were computed along 10 intervals using breaks of 0.5 m. The magnitude of the simulated GPS errors was fixed, but the angle was randomly selected between 0° and 360°, both for every plot and for each of the 30 replications tested on each interval as presented in [15]. Overall, plot-level statistics from ALS echoes were computed 301 times for each plot, and for both ABA and EABA: 300 cases containing simulated GPS errors and one using the ground truth coordinates (Ref). The EABA method presented in Section 2.4 was applied 301 times for each of the 35 sample plots used for in the study. The resulting sample edges were used to extract the ALS statistics for each case using the PolyClipData command with the FUSION software [23].

2.7. Modelling

The estimation of forest biophysical attributes using statistics derived from 3D point clouds has been widely studied in the sciences [27]. The set of possible modeling techniques to be applied for this purpose is rich and of different complexity due to the increasingly applied methods based on machine-learning algorithms [14,16,26]. For simplicity and due to the straightforward interpretation of the results, parametric regression was preferred for the modeling analyses [3,14]. Multiple linear regression was used to estimate three forest biophysical attributes: growing stock volume (V, m³ ha⁻¹), stand basal area (G, m² ha⁻¹), and dominant height (H₀, m). The three forest biophysical attributes were expected to be accurately estimated using ALS statistics, as previously documented in the field [27] and despite the less densified ALS data used in the research. Therefore, the effect of co-registration errors in the performance of the models (goodness of fit) can be measured under the ABA and later compared to the gained benefit from implementing EABA. The pool of possibilities to combine the 24 candidate predictors usually requires the use of variable selection methods (VSM) to reduce the complexity of the models by selecting an optimal set, in terms of number and predictive capability. For this study, the number of predictor variables in the models was forced to be three or less to reduce the level of overfitting and for an easy interpretation of the results, following guidelines of recent studies [14,28]. The use of automatic VSM, such as the stepwise approach [14], was replaced by a combinatorial search that evaluated all possible combinations of one, two, and three predictors from the list of 24 possible predictor candidates. The set of models in both ABA and EABA comprised 24,276 and 2024 models for the one-, two-, and three-predictor case, respectively, and for each of the tested forest biophysical attributes. The computational effort to fit all the models in the R statistical software [29] under the proposed combinatorial search to select predictor variables was feasible and the performance was similar to available code implementations [30]. The smallest root mean squared error (RMSE) was used as the criterion for the selection of models, in line with recent studies in the field [15,31,32]. The best model in each case was selected when using ground truth data (Ref). The selected models were then fitted using the 300 datasets containing simulated GPS errors to evaluate the expected impact of co-registration errors on the accuracy of the models [11,14]. The RMSE was computed as follows:

$$\mathrm{RMSE}=\sqrt{\frac{{\sum }_{i = 1}^n{\left(H_0 - \widehat{H_0} \right)}^2}{n}}$$

(2)

where H_o is the ground dominant height, ($\widehat{H_0}$) is the predicted dominant height of plot i, and n is the number of sample plots (n = 35). The relative RMSE% values were calculated as the percentage of the average ground value of the given forest biophysical attribute. The benefit of EABA was expressed as the relative decrement of the RMSE percentage compared to the values for ABA.

3. Results

3.1. Performance of ITD and DBH Prediction

Tree-level ground measurements comprised 344 observations, while the number of detected trees within the sample edges was 357. The 0.97 kappa coefficient pointed out the high efficiency of local maxima algorithms under the ITD approach for the species and study area conditions. The average height difference between each tree-level ground observation and its corresponding detected tree was 0.37 m (measured tree height less detected height using ALS). The observed nonlinear relationship between measured tree diameter and detected tree height values was explained by the selected model form (

Table 2. Summary information of the tree- and plot-level ground data.

Parameters	Estimate	Std. Error	t Value
a	4.9098	0.3922	<2 × 10−16
b	2.3281	0.0959	<2 × 10−16

). The degree of significance of both model parameters was high (less than 0.001), resulting in a 6.41 percentage value of root mean squared error (RMSE, %) and a 0.76 value for the total explained variance of the model (R²) for the tree-level model.

3.2. EABA Versus ABA Using Ground Truth Coordinates

The distribution of ALS statistics using ground truth coordinates showed how edge effects partially biased the distribution of ALS echoes within the samples. The implemented edge-correction method shrank the distribution of plot-level statistics for density statistics, while the distribution of height-based information was similar in both methods (Figure 5). The results in the modeling part showed how EABA improved the performance of the models in all cases (

Table 3. Selection of predictors and computed RMSE (expressed as the percentage value over the mean value of the ground measurements) for the one-, two-, and three-parameter models fitted with OLS regression. The results are presented for the standard ABA approach (left) and the improved EABA method (right).

RMSE (%)	ABA			EABA
Models	1-pred	2-pred	3-pred	1-pred	2-pred	3-pred
V	Hmax	Hmax	Hmax	FCmean_1	FCmean_1	FCmean_1
	23.1	H95	H95	19.4	Hmean	FCmean_All
		18.2	Hmode		16.5	Hmode
			17.0			13.9
G	Hmax	Hmax	Hmax	FCmean_1	FCmean_1	FCmean_1
	22.7	H95	H95	18.8	Hmean	Hmean
		18.2	Hmean		15.8	FCmean_All
			16.5			13.0
Ho	Hmax	Hmax	Hmax	H80	FCmean_1	H80
	5.0	H10	H10	4.6	H90	H60
		4.1	FCmode_All		3.9	H10
			3.8			3.5

). The RMSE values for EABA were, on average, 15.5% less than for ABA when estimating growing stock volume, 17.3% less for stand basal area, and 7.2% less for dominant height. In absolute terms, EABA reduced RMSE between two and four points for growing stock volume and stand basal area, while the difference barely reached 0.5% for dominant height. Increasing the number of predictors in the models from one to two reduced the error. The improvement was less in models with three predictors. The composition of the models (selection of predictors) was different between ABA and EABA. The results showed how edge tree correction moved the selection of the best predictor from height predictors in ABA to density predictors in EABA for the case of volume and stand basal area.

3.3. Influence of Co-Registration Errors

The selected models in the absence of co-registration errors showed a worse performance when predictor variables were computed, altering the positioning mismatch. The trend was different between ABA and EABA (Figure 6). While in the ABA method, an increasing error in the computed RMSE was observed (the more error, the larger the increment in the RMSE), the pattern became flattened under the EABA approach. The progressively increasing pattern was observed in all estimated forest attributes under the ABA. The largest impacts of co-registration when compared to the Ref case were 7.2, 6.5, and 1.3 points in the RMSE percentage for growing stock volume, stand basal area, and dominant height, respectively. However, the pattern was different for EABA, as models for both growing stock volume and stand basal area showed an increment for a 0.5 m error that remained steady along the simulated error range, before reaching the maximum RMSE value for the 5 m error. The pattern in the models looked similar for one, two, and three predictors. For the latter, and for the case of dominant height and EABA, an increasing positioning error had no effect on model performance.

4. Discussion

The integration of remote sensing methods in forest inventory has steadily contributed to improving traditional forest inventory methods based on extensive ground campaigns. The enhanced description of the 3D structure of the forests using ALS data needs to properly co-register with ground measurements in order to gain accuracy in the estimation models. The development and implementation of forest inventory based on ALS data is already solid and established in the community, both by researchers and practitioners [28]. Area-based methods, such as the ABA evaluated in this research, have been used worldwide to estimate and predict forest biophysical attributes [1]. The method is scientifically and operationally established, but there are factors that can substantially affect the performance of the approach. Two of the most important and frequent sources of uncertainty are simultaneously evaluated in this research: the impact of edge-effects and the influence of co-registration errors.

Edge effects can play a significant role in the estimation of forest attributes by creating uncertainty when collecting present-state information during the inventory [33], and their recognition requires efficient solutions to implement the ITD approach, in which the centroid of the trees are first detected and the canopy is latter delineated [4,8]. The conditions of the study area and the quality of the data should go together, as in the sparse study forest area used for this research. The results underlined that just 3% of all the detected data did not correspond to a measured tree, which can be regarded as an outstanding performance of the ITD implementation in the area, as previous research recently pointed out [5], and considering the low density of the ALS data [2,34]. The singularity of the study area eased the detection of the large canopies of stone pine trees, as well as the implementation of the EABA method, which is not such a straightforward step in other forest ecosystems [35,36,37,38]. On the other side, the circular shape and large size of stone pines challenged field work operations when it came to determining the height of measured trees. Arguably, the scale of the tree height underestimation from using the ALS data compared to ground truth observations may be minor, as in the presented study (only 37 cm on average). The number of trees close to the edge in sampling designs might be greater in dense boreal areas or in tropical ecosystems, for instance, but the total canopy area affected might be smaller than that for the stone pine trees evaluated in this study. Another factor to consider is the steepness of the terrain [39], which can highly challenge and increase the resources devoted to ground operations as the centroid of the tree canopy progressively differs from the stem base position as the slope increases. The mismatch between stem base positions measured in the field and canopy centroids detected with ALS data needs to be carefully considered in mountainous and dense forest ecosystems [40,41]. Therefore, the response of the models to edge tree correction methods might be different depending on the type and the structure of forests. The influence of resolution when building DTMs and CHMs can also play an important role [42]. The 1 m resolution of the CHM used in this research might be rather low, considering the size of stone pine trees, and decreasing the resolution to 2 m might provide similar results. A forthcoming paper on the influence of EABA under alternative resolutions will help to better understand the results presented in this study.

Another important factor is the ability to optimally parametrize algorithms in order to detect tree locations and to derive tree canopies [8]. The latter is the cornerstone of the EABA approach as tree canopies are used to correct sample edges [9]. The use of a more densified ALS point cloud might improve the performance of EABA, although the reported level of improvement in [9] was very similar to these results despite using low-density ALS data. In this study, the EABA approach considerably improved the estimation of the three forest biophysical attributes tested. The RMSE values decreased between two and four points when estimating volume and stand basal area using simple one-predictor models. For the case of dominant height, the improvement was less relevant, as expected due to the lack of pronounced height differences in the even-aged stands and the already good predictive capability of ABA models to estimate dominant height [43,44]. The performance of the EABA method could be even better if the sampling design had included more observations in forest areas of different structures and management, allowing the testing of more advanced modeling techniques [9] or the use of hierarchical approaches to mitigate the spatial correlation factor [45], which can be a problem in the small fitting dataset. The presented results based on the computed RMSE percentage were compared to those obtained when the selection was based on total explained variance (R²) and the outcomes were very similar in terms of the selected predictors and equal when the RMSE percentage was computed afterwards. The EABA method was also effective at controlling the impact of co-registration errors, which is a novel finding in the context of ALS-based forest inventory.

The occurrence of co-registration errors is always a source of uncertainty in remote sensing studies and it can substantially bias the estimation of forest attributes as the computed ALS statistics were calculated from the area actually covered by the field sampling plots [12,14]. Consequently, the predictive capability of the models is usually affected, although variable selection methods, model structure, and the given response variable can determine the severity of the bias [11,14,15]. In this study, the maximum impact of co-registration errors in the models when using ABA were 7.2, 6.8, and 1.4 points in the RMSE percentage for growing stock volume, stand basal area, and dominant height, respectively. In other studies, a maximum error of 8% for stand basal area and 1% for dominant height were reported [14], which is in line with the presented results. The impact could be more severe in spatially heterogeneous stands [13], but the sampling design [45,46] could determine the level of bias in the ABA approach [11]. For instance, the impact in [15] only reached 0.3 points in the RMSE percentage for dominant height models simulating positioning errors up to five meters, but the value jumped to 2.3 points when increasing the error up to 10 m. The relationship between canopy cover conditions in each of the samples and the magnitude of plot positioning errors could be tested in further ground campaigns in order to better understand co-registration errors in forest ecosystems. In this way, the simulated plot positioning error for each sample plot could be plot-specific and determined by both the ALS statistics at plot-level and the forest biophysical attributes measured in the field.

The ratio between the simulated mismatch and the size of stone pines canopies was low in this study area, and maybe that factor can partially explain the outstanding performance of EABA at mitigating the severity of co-registration errors. The simulated errors could have been greater but then they would not have been realistically adjusted to the operational and technical conditions of current survey projects in the region. The presence of gaps and the proximity of dominant trees close to the sample edge can also determine the severity of co-registration errors. For instance, excluding ALS echoes of measured dominant trees can highly bias the computation of height percentiles, while the presence of discontinuities in the surroundings of the sampling plots can result in a severe impact when computing density metrics. The implications of the sampling design, the size of the sample plots, and the inclusion of more spatially heterogeneous forest ecosystems could be further tested when implementing ITD under the EABA method [11,44].

Unfortunately, there is a lack of studies regarding the efficiency of edge correction methods in the context of co-registration uncertainty, so the validation and the comparison of the presented results remains as a matter of future studies. Arguably, the importance of the traditional ABA is expected to decrease, or at least be substantially enforced, in the light of (i) how different laser-based methods are evolving to favor the use of tree-level solutions [1] and (ii) due to the fact that EABA is not only restricted to active laser scanning under optimal conditions as presented in this study. For instance, tree positions and canopies can be derived at a feasible operational cost when drone-based mapping and photogrammetry methods are integrated in ground operations [6,47,48]. The scope of the EABA approach is at plot-level, with the idea of building robust inference in the samples before predicting forest biophysical attributes wall-to-wall over a large-scale forest area. The technical limitations of using SfM in large-scale applications to derive fine-grained CHMs were not applied in this EABA context, for which only 3D data at plot-level were required. Therefore, tree canopies derived with SfM can be used to correct sample edges, same as presented in Type I and Type II corrections, and to correct sample boundaries before computing the true ALS statistics for each given plot.

The transferability of models when using ALS-based predictors is being regarded as a feasible approach to overcome 3D data limitations between forest ecosystems of similar structural complexity [49,50]. Further research can target the response of EABA methods to transfer EABA models to other areas, for which tree density, ground data, and ALS surveys might not be as suitable as in the presented case. For instance, the small crown plasticity and the response to light from the stone pines in the area could differ compared to more heterogeneous stands, and EABA can be used to monitor growth patterns and crown development when performing the method over the same sample area multiple times [51]. The more reliable use of ITD than the EABA method can be especially relevant when using structural indictors to evaluate, classify, and manage forest ecosystems [52,53,54]. Tree-level data for ecological purposes are gaining popularity within research, which can also be substantially enriched within the context of modern forest inventory approaches—terrestrial laser scanning (TLS). The integration of TLS when building EABA models at plot level could be used to validate the canopy positions detected from the ALS source when either the density of the ALS point cloud or the complexity of the forest ecosystem represents a challenge. The operability of TLS within complex environments is being steadily improved [55] by the development of more sophisticated scanning equipment.

5. Conclusions

This study showed how the combined used of ITD and ABA can be jointly applied to evaluate a promising methodology, the EABA approach, which reduces model error when estimating forest biophysical attributes, while also reducing the impact of co-registration errors. This is the first study that documents the benefit of EABA in mitigating the co-registration factor. Although the goal of this paper was to benchmark ABA to EABA when estimating forest structural attributes on a species-specific forest ecosystem, the conclusions on the presented work are of global importance due to the increasing availability of high-quality scanning data worldwide and the important task of updating forest inventories over the years using scares resources. The tested EABA approach has the potential to become a reference method in modern and remote-based forest inventory between practitioners while transforming standard, and biased, procedures used in operational forestry that ignore the relevance of edge effects when modeling forest attributes. Based on the enhanced performance of EABA compared to ABA and the multiple possibilities to derive tree canopies using several sources of remotely sensed dates, one can forecast a great potential of the presented EABA to update forest inventory estimates.