Aircraft Target Classification for Conventional Narrow-Band Radar with Multi-Wave Gates Sparse Echo Data
Abstract
1. Introduction
2. Reconstruction Algorithm of Sparse Echo Data
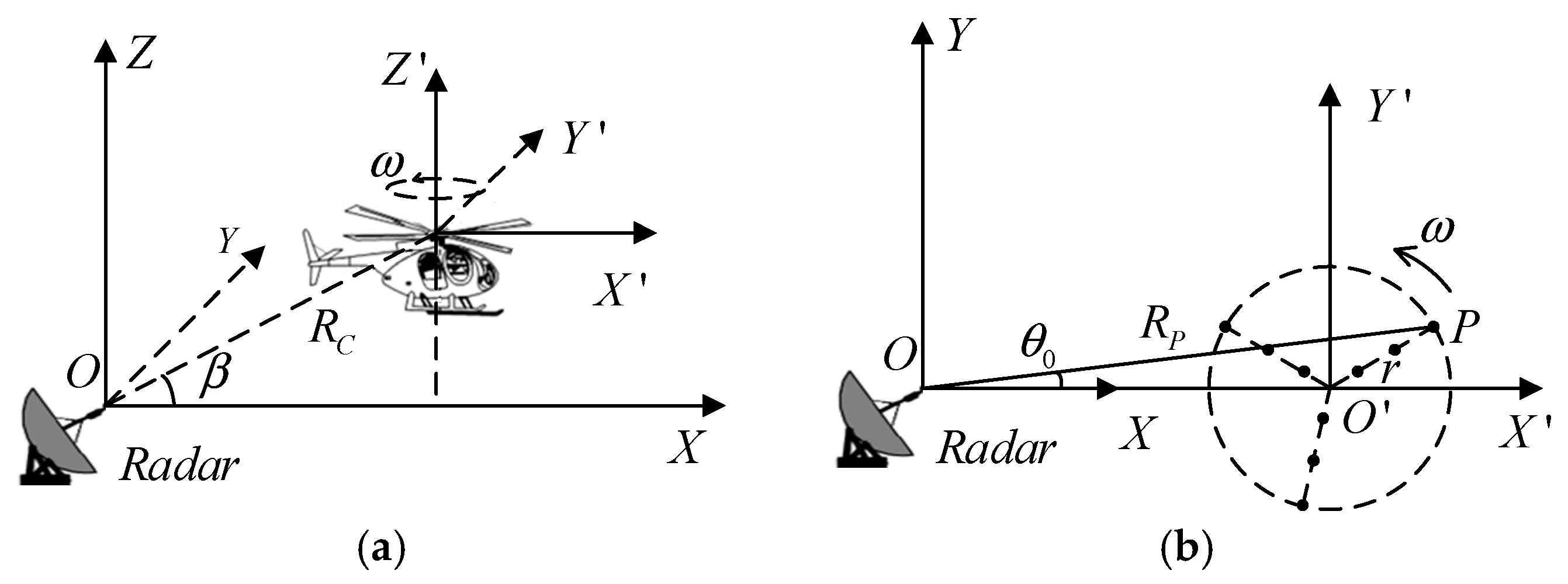
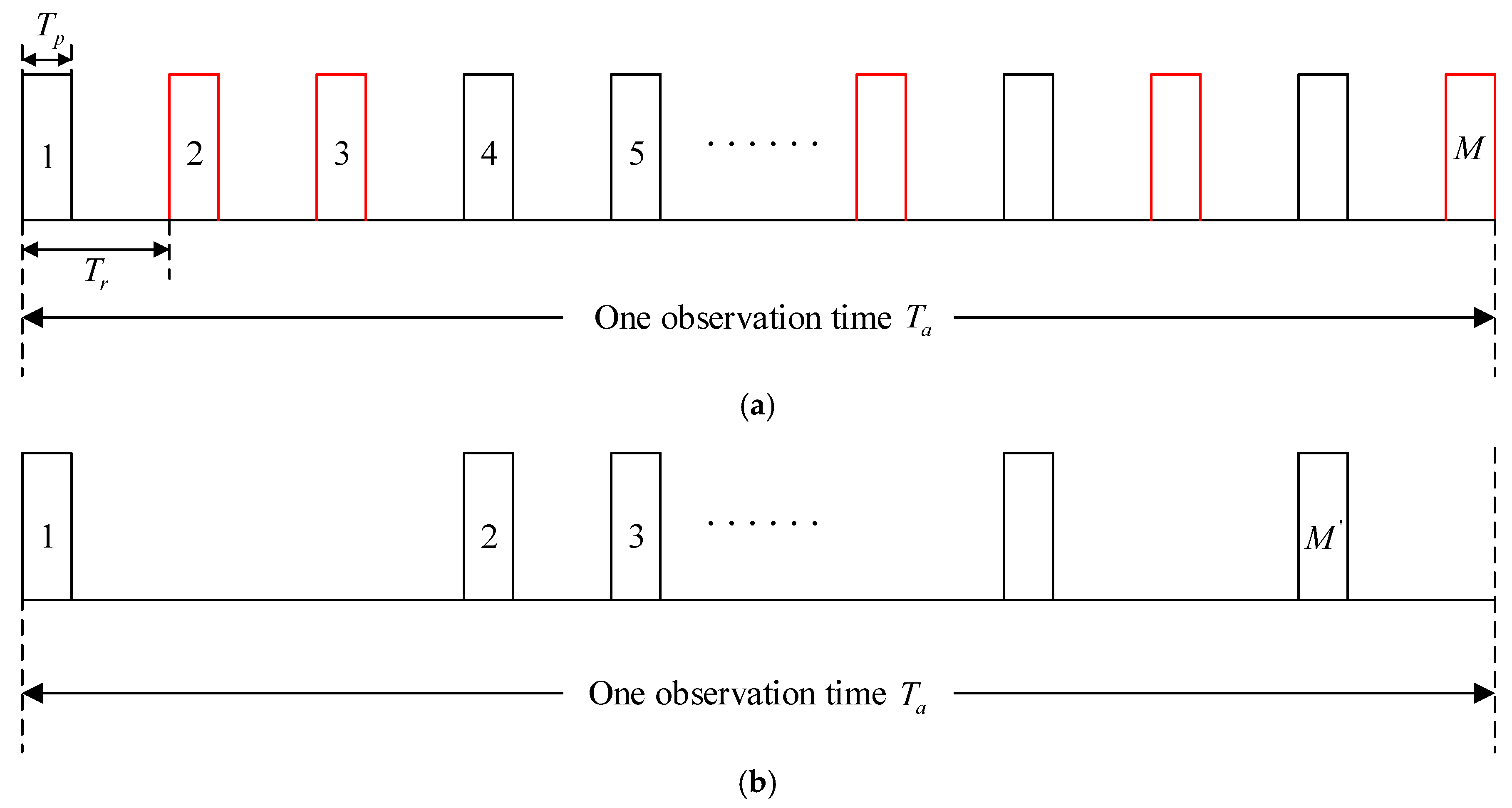
2.1. Echo Model
2.2. Reconstruction Algorithm
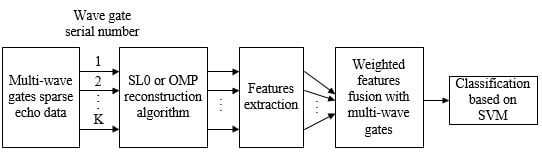
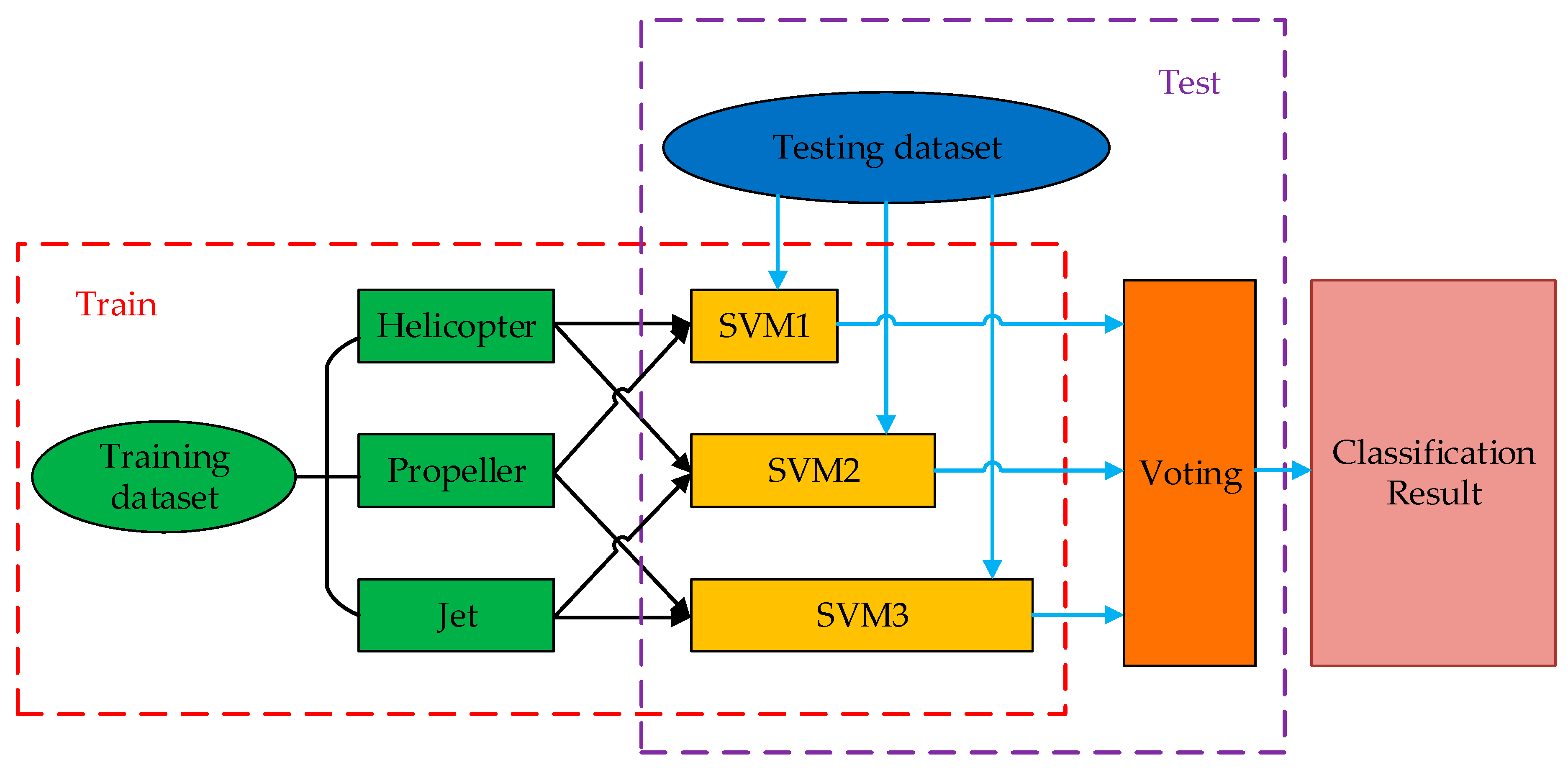
3. Classification Algorithm Based on the Weighted Features Fusion of Multi-Wave Gates
3.1. Features Extraction
3.2. Weighted Features Fusion
3.3. Classification Algorithm
4. Experimental Results
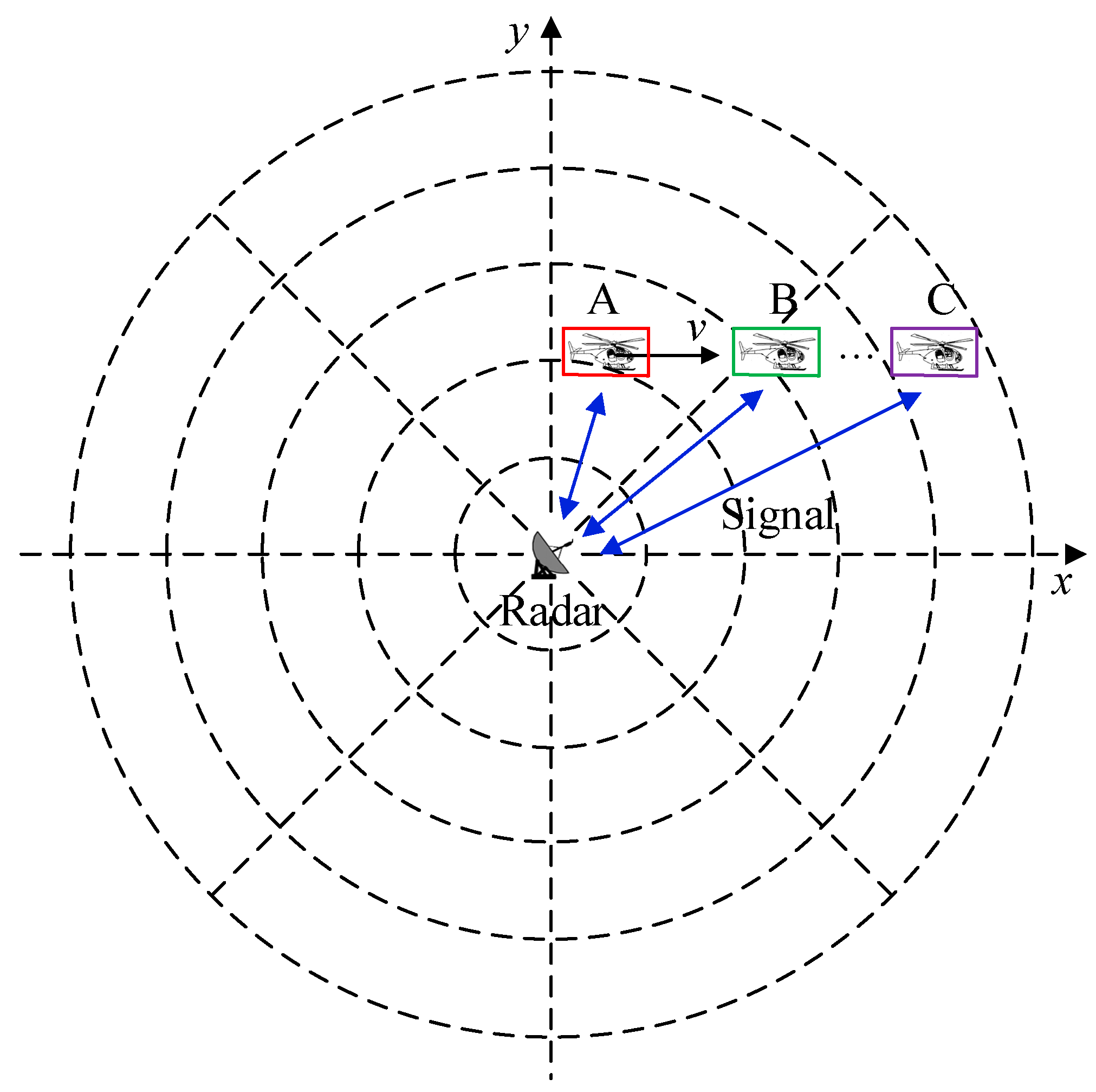
4.1. Dataset Details
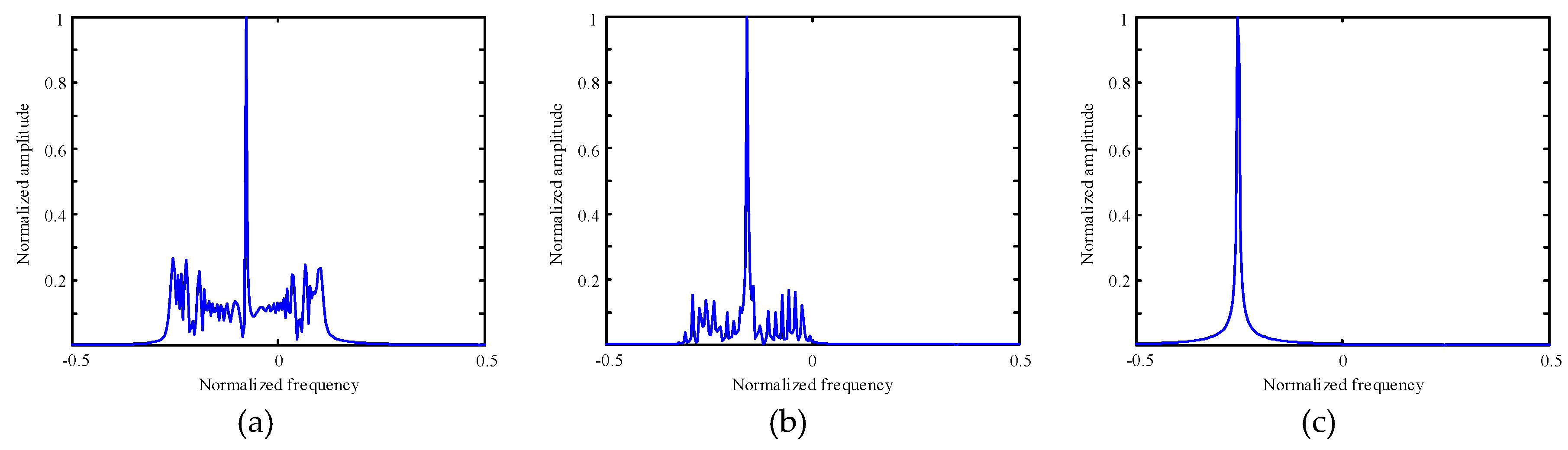
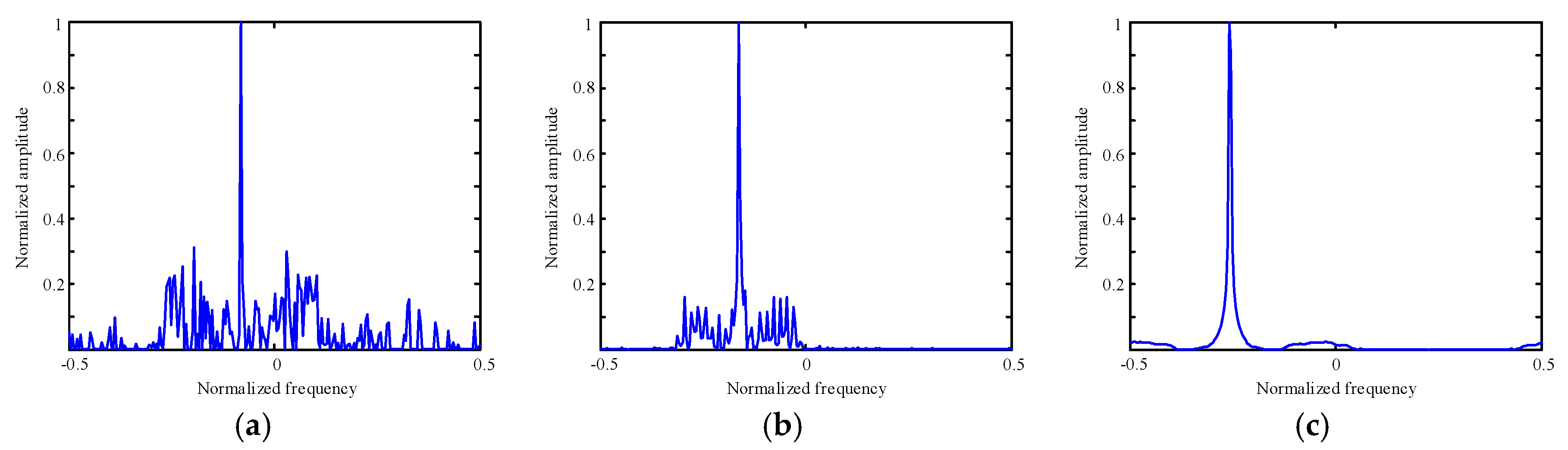
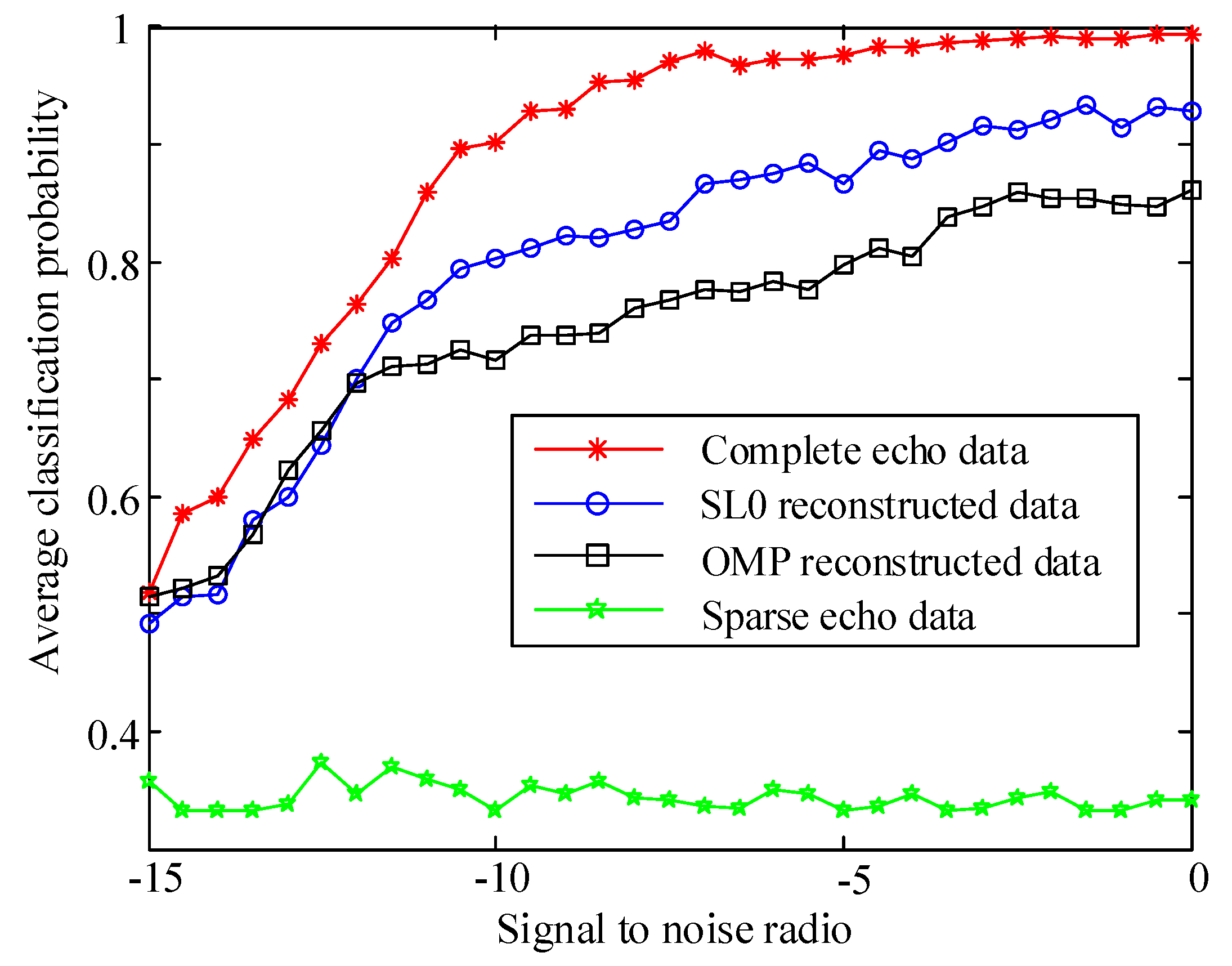
4.2. Validity Experiment of Reconstruction Algorithm
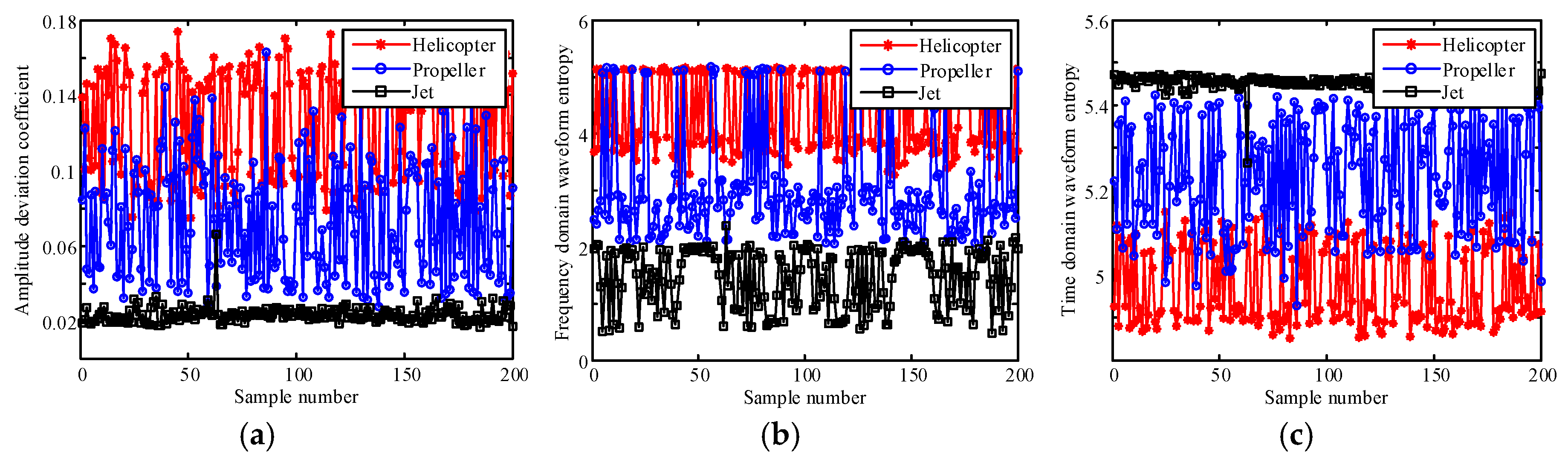
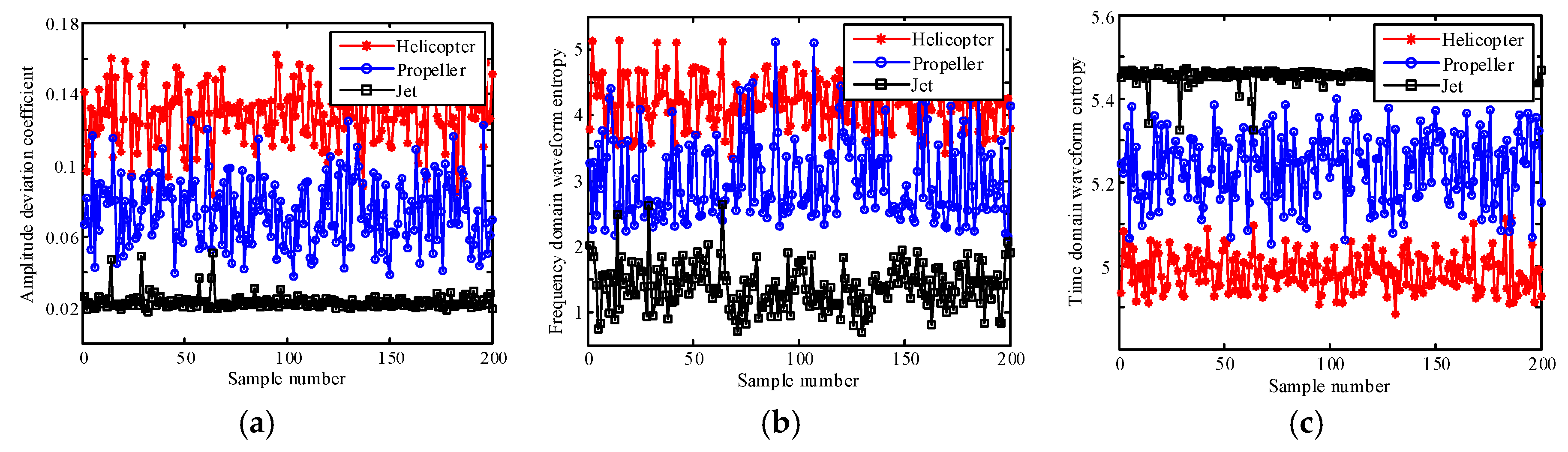
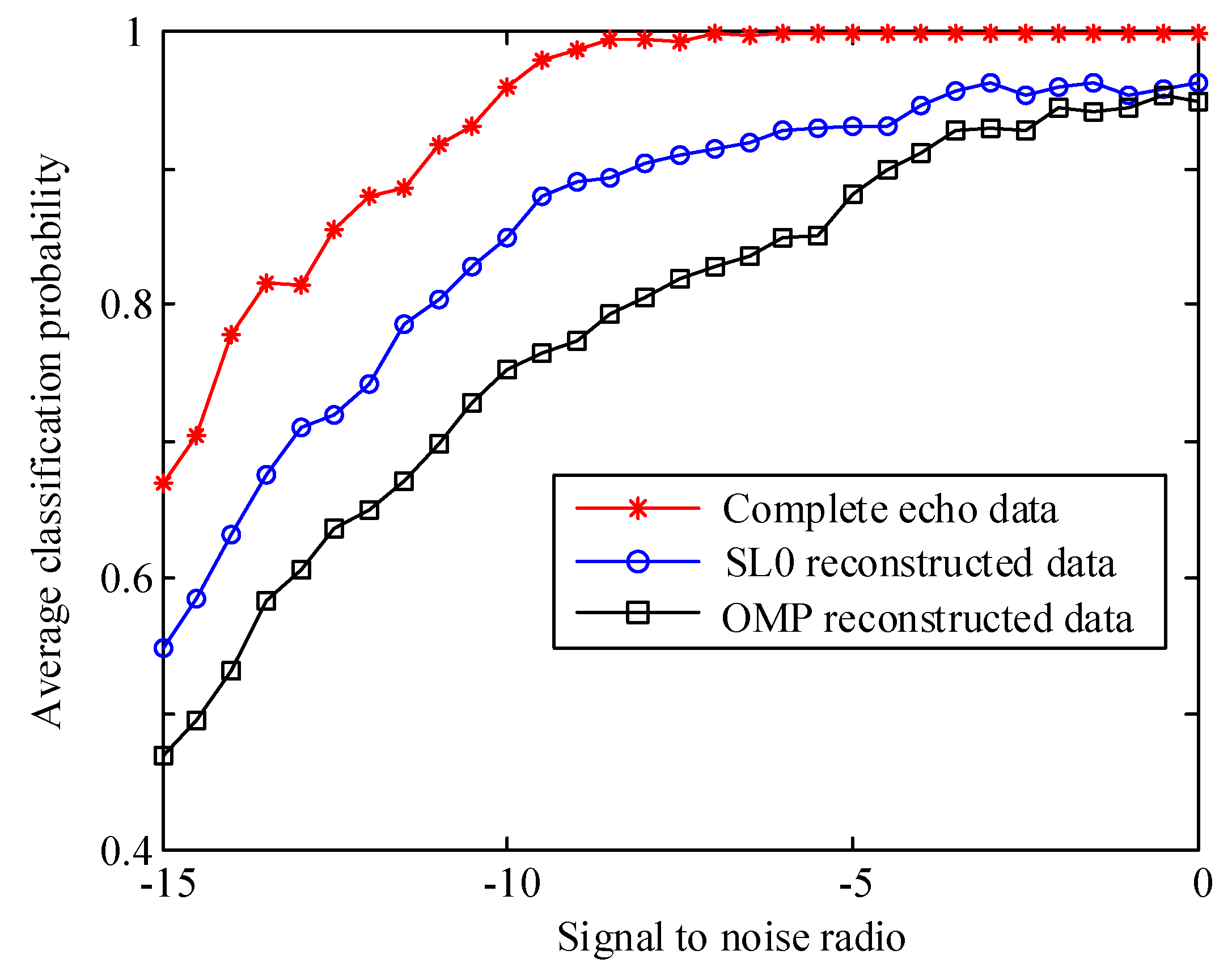
4.3. Selection of Wave Gate Number in Weighted Features Fusion
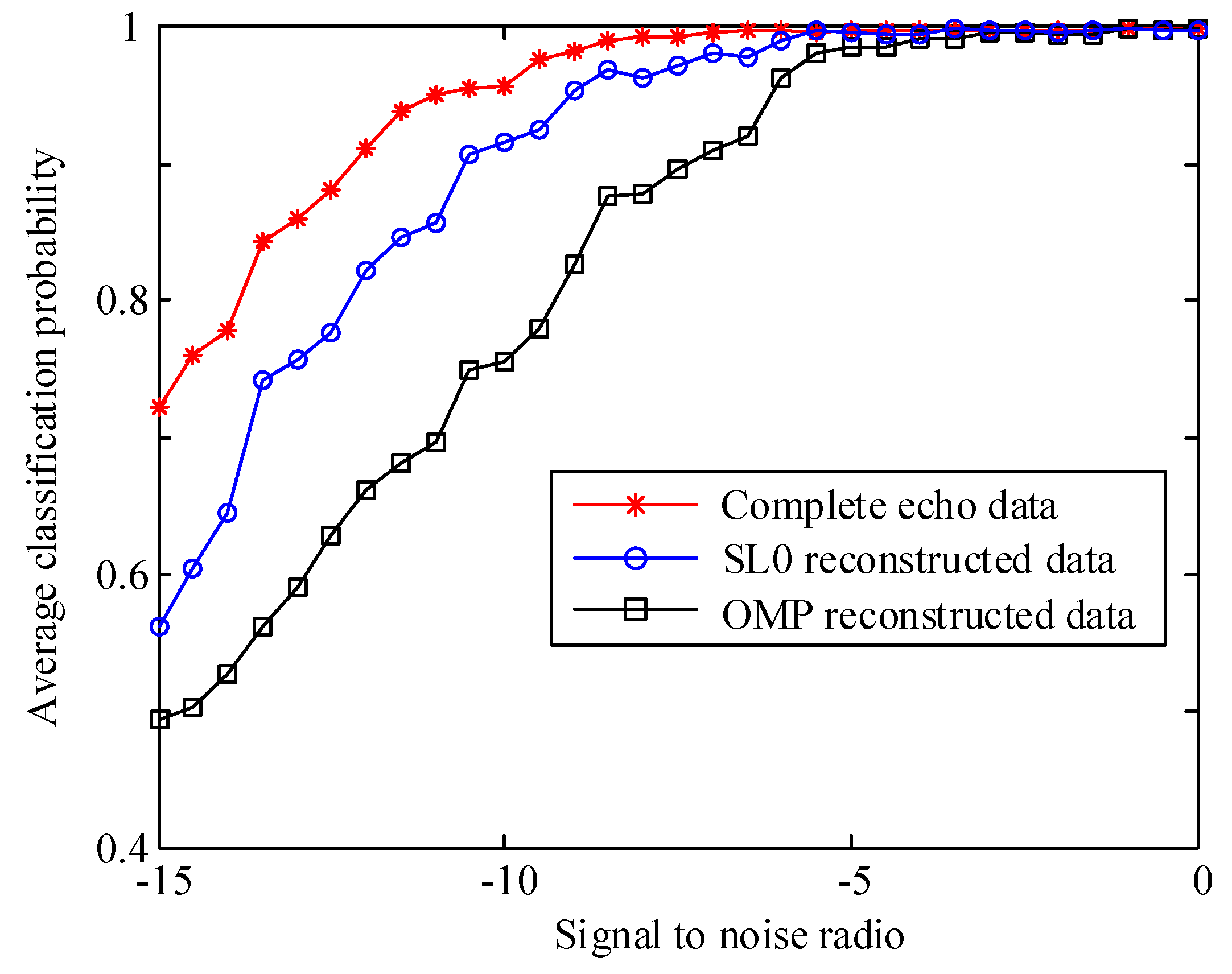
4.4. Classification Experiment Based on Weighted Features Fusion with Four Wave Gates Sparse Echo Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pan, X.R.; Yang, F.; Gao, L.R.; Chen, Z.C.; Zhang, B.; Fan, H.R.; Ren, J.C. Building extraction from high-resolution aerial imagery using a generative adversarial network with spatial and channel attention mechanisms. Remote Sens. 2019, 11, 917. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Denis, L.; Poggi, G.; Tupin, F.; Verdoliva, L. Exploiting patch similarity for SAR image processing: The nonlocal paradigm. IEEE Signal Process. Mag. 2014, 31, 69–78. [Google Scholar] [CrossRef]
- Zhao, C.H.; Wang, Y.; Masahide, K. An optimized method for image classification based on bag of words model. J. Electron. Inf. Technol. 2013, 34, 2064–2070. [Google Scholar] [CrossRef]
- Wang, Y.P.; Hu, Y.H.; Lei, W.H. Aircraft target classification method based on texture feature of laser echo time-frequency image. Acta Optica Sin. 2017, 37, 1128004. [Google Scholar] [CrossRef]
- Fu, K.; Dai, W.; Zhang, Y.; Wang, Z.R.; Yan, M.L.; Sun, X. Multiple class activation mapping for aircraft recognition in remote sensing images. Remote Sens. 2019, 11, 544. [Google Scholar] [CrossRef]
- Karacor, A.G.; Torun, E.; Abay, R. Aircraft classification using image processing and artificial neural networks. Int. J. Patt. Recogn. Artif. Intell. 2011, 25, 1321–1335. [Google Scholar] [CrossRef]
- Hwang, J.; Lin, K.; Chiu, Y. Automatic target recognition based on high-resolution range profiles with unknown circular range shift. In Proceedings of the IEEE International Symposium on Signal Processing & Informational Technology, Bilbao, Spain, 18–20 December 2017. [Google Scholar]
- Jiang, Y.; Li, Y.; Cai, J.J.; Wang, Y.H.; Xu, J. Robust automatic target recognition via HRRP sequence based on scatter matching. Sensors 2018, 18, 593. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.X.; Liu, Y.X.; Huo, K.; Zhang, S.H.; Zhang, Z.S. Radar HRRP target recognition based on stacked autoencoder and extreme learning machine. Sensors 2018, 18, 173. [Google Scholar] [CrossRef]
- Suresh, P.; Thayaparan, T.; Obulesu, T. Extracting micro-Doppler radar signatures from signatures from rotating targets using Fourier-Bessel transform and time-frequency analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3204–3210. [Google Scholar] [CrossRef]
- Smith, G.E.; Mobasseri, B.G. Robust through-the-wall radar image classification using a target-model alignment procedure. IEEE Trans. Image Process. 2012, 21, 754–767. [Google Scholar] [CrossRef]
- Liu, J.; Fang, N.; Wang, B.F.; Xie, Y.J. Scale-space theory-based multi-scale features for aircraft classification using HRRP. Electron. Lett. 2016, 52, 475–477. [Google Scholar] [CrossRef]
- Tang, N.; Gao, X.Z.; Li, X. Target classification of ISAR images based on feature space optimization of local non-negative matrix factorization. IET Signal Process. 2012, 6, 494–502. [Google Scholar] [CrossRef]
- Lopez-Rodriguez, P.; Fernandez-Recio, R.; Bravo, I.; Gardel, A.; Lazaro, J.L.; Rufo, E. Computational burden resulting from image recognition of high resolution radar sensors. Sensors 2013, 13, 5381–5402. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, P.K. Novel and comprehensive approach for the feature extraction and recognition method based on ISAR images of ship target. J. Harbin Inst. Technol. 2017, 5, 12–19. [Google Scholar]
- Karine, A.; Toumi, A.; Khenchaf, A.; EI Hassouni, M. Radar target recognition using salient keypoint descriptors and multitask sparse representation. Remote Sens. 2018, 10, 843. [Google Scholar] [CrossRef]
- Wang, F.; Sheng, W.X.; Ma, X.F.; Wang, H. ISAR image recognition with fusion of Gabor magnitude and phase feature. J. Electron. Inf. Technol. 2013, 35, 1813–1818. [Google Scholar] [CrossRef]
- Saidi, M.N.; Daoudi, K.; Khenchaf, A.; Hoeltzener, B.; Aboutajdine, D. Automatic target recognition of aircraft models based on ISAR images. In Proceedings of the Geoscience & Remote Sensing Symposium IEEE, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Biondi, F.; Addabbo, P.; Orlando, D.; Clemente, C. Micro-motion estimation of maritime targets using pixel tracking in Cosmo-Skymed Synthetic Aperture Radar data-An operative assessment. Remote Sens. 2019, 11, 1637. [Google Scholar] [CrossRef]
- Ji, J.Z.; Jiang, J.X.; Al-Armaghany, A.; Shu, C.Y.; Huang, P.L. Nutation and geometrical parameters estimation of cone-shaped target based on micro-Doppler effect. Optik Int. J. Light Electron Opt. 2017, 150, 1–10. [Google Scholar] [CrossRef]
- Abdullah, R.S.A.R.; Alnaeb, A.; Salah, A.A.; Rashid, N.E.A.; Sali, A.; Pasya, I. Micro-Doppler estimation and analysis of slow moving objects in forward scattering radar system. Remote Sens. 2017, 9, 699. [Google Scholar] [CrossRef]
- Thayaparan, T.; Stanković, L.J.; Daković, M.; Popović, V. Micro-Doppler parameter estimation from a fraction of the period. IET Signal Process. 2010, 4, 201–212. [Google Scholar] [CrossRef]
- Zuo, L.; Li, M.; Zhang, X.W. Micro-Doppler parameter estimation from a fraction of the period data with the MMSE criterion. J. Xidian Univ. 2013, 40, 123–129. [Google Scholar]
- Li, G.; Varshney, P.K. Micro-Doppler parameter estimation via parametric sparse representation and pruned orthogonal matching pursuit. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 4937–4948. [Google Scholar] [CrossRef]
- Liu, Y.X.; Li, X.; Zhuang, Z.W. Estimation of micro-motion parameters based on micro-Doppler. IET Signal Process. 2010, 4, 213–217. [Google Scholar] [CrossRef]
- Song, C.; Wu, Y.R.; Zhou, L.J.; Li, R.M.; Yang, J.F.; Liang, W.; Ding, C.B. A multicomponent micro-Doppler signal decomposition and parameter estimation method for target recognition. Sci. China Inf. Sci. 2019, 62, 029304. [Google Scholar] [CrossRef]
- Mujica, F.A.; Leduc, J.P.; Murenzi, R.; Smith, M.J.T. A new motion parameter estimation algorithm based on the continuous wavelet transform. IEEE Trans. Image Process. 2000, 9, 873–888. [Google Scholar] [CrossRef]
- Wang, B.S.; Du, L.; He, H.; Liu, H.W. Reconstruction method for narrow-band radar returns with missing samples based on complex Gaussian model. J. Electron. Inf. Technol. 2015, 37, 1065–1070. [Google Scholar]
- Yang, J.B.; Liao, X.J.; Yuan, X.; Llull, P.; Brady, D.J.; Sapiro, G.; Carin, L. Compressive sensing by learning a Gaussian mixture model from measurements. IEEE Trans. Image Process. 2015, 24, 106–119. [Google Scholar] [CrossRef]
- Xue, H.; Zhang, S.J.; Su, Y.K.; Wu, Z.Z. Capital cost optimization for prefabrication: A factor analysis evaluation model. Sustainability 2018, 10, 159. [Google Scholar] [CrossRef]
- Shi, H.R. Research on Feature Extraction of Micro Motion Target and Reconstruction of Incomplete Signal. Master’ Thesis, XiDian University, Xi’an, China, May 2017. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Li, Y.; Fu, K.; Sun, H.; Sun, X.W. An aircraft detection framework based on reinforcement learning and convolutional neural networks in remote sensing images. Remote Sens. 2018, 10, 243. [Google Scholar] [CrossRef]
- Rikhtegar, A.; Pooyan, M.; Manzuri-Shalmani, M.T. Ga-optimized structure of CNN for face recognition applications. IET Comput. Vis. 2016, 10. [Google Scholar] [CrossRef]
- Zhao, A.; Fu, K.; Wang, S.Y.; Zuo, J.W. Aircraft recognition based on landmark detection in remote sensing images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1413–1417. [Google Scholar] [CrossRef]
- Zuo, J.W.; Xu, G.L.; Fu, K.; Sun, X.W. Aircraft type recognition based on segmentation with deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 282–286. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet classification with deep convolutional neural networks. In Proceedings of the 26th Annual Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Zhang, Y.H.; Sun, H.; Zuo, J.W.; Wang, H.Q.; Xu, G.L.; Sun, X. Aircraft type recognition in remote sensing images based on feature learning with conditional generative adversarial networks. Remote Sens. 2018, 10, 1123. [Google Scholar] [CrossRef]
- Wang, D.; He, X.; Yu, H. A method of aircraft image target recognition based on modified PCA features and SVM. In Proceedings of the 9th International Conference on Electronic Measurement & Instruments, Beijing, China, 16–19 August 2009. [Google Scholar]
- Diao, W.; Sun, X.; Dou, F.; Yan, M.; Wang, H.; Fu, K. Object recognition in remote sensing images using sparse deep belief networks. Remote Sens. Lett. 2015, 6, 745–754. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Li, S.D.; Pei, W.J.; Yang, J.; Hu, G.Q. OMP reconstruction algorithm via Bayesian model and its application. Syst. Eng. Electron. 2015, 37, 246–251. [Google Scholar]
- Li, M.; Wu, J.J.; Zuo, L.; Song, W.J.; Liu, H.M. Aircraft target classification and recognition algorithm based on measured data. J. Electron. Inf. Technol. 2018, 40, 2606–2612. [Google Scholar]
- Mario, G.; Thorsten, R.; Christoph, E.; Thomas, U. Remote sensing based binary classification of maize. Dealing with residual autocorrelation in sparse sample situations. Remote Sens. 2019, 11, 2172. [Google Scholar]
- Man, Q.X.; Dong, P.L. Extraction of urban objects in cloud shadows on the basis of fusion of airborne LiDAR and hyperspectral data. Remote Sens. 2019, 11, 713. [Google Scholar] [CrossRef]
- Gapper, J.J.; EI-Askary, H.; Linstead, E.; Piechota, T. Coral Reef change Detection in Remote Pacific islands using support vector machine classifiers. Remote Sens. 2019, 11, 1525. [Google Scholar] [CrossRef]
- Kutyniok, G. Compressed Sensing: Theory and Applications; Cambridge University Press,: Cambridge, UK, 2012; pp. 1–20. [Google Scholar]
- Rauhut, H.; Schnass, K.; Vandergheynst, P. Compressed sensing and redundant dictionaries. IEEE Trans. Inf. Theory 2008, 54, 2210–2219. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]



| Target Type | Rotor Length (m) | Blade Number | Rotation Velocity (rad/s) | Translational Velocity (km/h) |
|---|---|---|---|---|
| Helicopter | 8 | 4 | 20 | 250 |
| Propeller | 2 | 4 | 130 | 500 |
| Jet | 1 | 27 | 380 | 800 |
| Input: estimated signal , dictionary matrix , error threshold . |
| Initialization: let the iterative counter , residual matrix , the index set . |
| Iteration: at the -th iteration |
| (1) Update the index set , where , is the i-th column of . |
| (2) Update the support set , and calculate the signal . |
| (3) Update the residual matrix . |
| (4) Increment , and return to Step (1) until the stopping criterion is met. The selection of the error threshold is related to the precision requirement. |
| Output: Reconstructed signal . |
| Input: estimated signal , dictionary matrix , the search step length . |
| Initialization: Choose an appropriate standard deviation parameter decrement sequence , the outer loop number is , the inner loop number is . The initial solution is the minimum L2 norm of , that is . |
| Iteration: |
| (1) The -th outer iteration, , at this time , . |
| (2) The -th inner iteration, |
| 1. Update the signal with , where . |
| 2. Project onto the feasible domain, that is . |
| (3) Update the reconstructed signal . |
| Output: Reconstructed signal . |
| Target Type | Amplitude Deviation Coefficient | Frequency Domain Waveform Entropy | Time Domain Waveform Entropy | |||
|---|---|---|---|---|---|---|
| No Fusion | Fusion | No Fusion | Fusion | No Fusion | Fusion | |
| Helicopter | 8.60 | 2.19 | 0.45 | 0.13 | 8.50 | 1.60 |
| Propeller | 11.00 | 2.70 | 0.98 | 0.31 | 18.60 | 4.80 |
| Jet | 0.21 | 0.14 | 0.27 | 0.09 | 0.31 | 0.27 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Tang, Z.; Chen, Y.; Zhang, Y.; Sun, Y. Aircraft Target Classification for Conventional Narrow-Band Radar with Multi-Wave Gates Sparse Echo Data. Remote Sens. 2019, 11, 2700. https://doi.org/10.3390/rs11222700
Wang W, Tang Z, Chen Y, Zhang Y, Sun Y. Aircraft Target Classification for Conventional Narrow-Band Radar with Multi-Wave Gates Sparse Echo Data. Remote Sensing. 2019; 11(22):2700. https://doi.org/10.3390/rs11222700
Chicago/Turabian StyleWang, Wantian, Ziyue Tang, Yichang Chen, Yuanpeng Zhang, and Yongjian Sun. 2019. "Aircraft Target Classification for Conventional Narrow-Band Radar with Multi-Wave Gates Sparse Echo Data" Remote Sensing 11, no. 22: 2700. https://doi.org/10.3390/rs11222700
APA StyleWang, W., Tang, Z., Chen, Y., Zhang, Y., & Sun, Y. (2019). Aircraft Target Classification for Conventional Narrow-Band Radar with Multi-Wave Gates Sparse Echo Data. Remote Sensing, 11(22), 2700. https://doi.org/10.3390/rs11222700