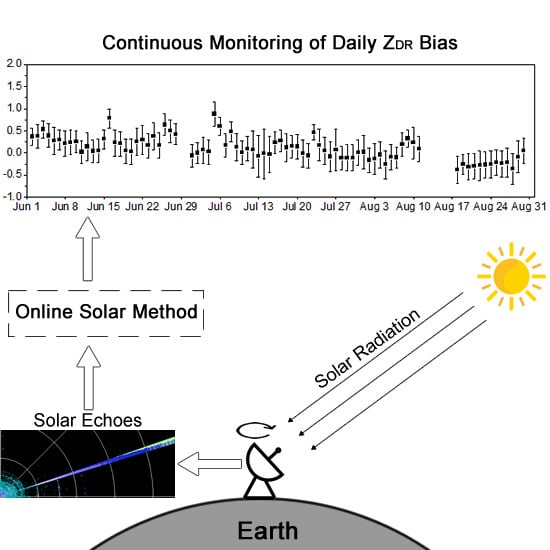
Continuous Monitoring of Differential Reflectivity Bias for C-Band Polarimetric Radar Using Online Solar Echoes in Volume Scans
Abstract
:1. Introduction
2. Radar and Methodology
2.1. C-Band Polarimetric Radar
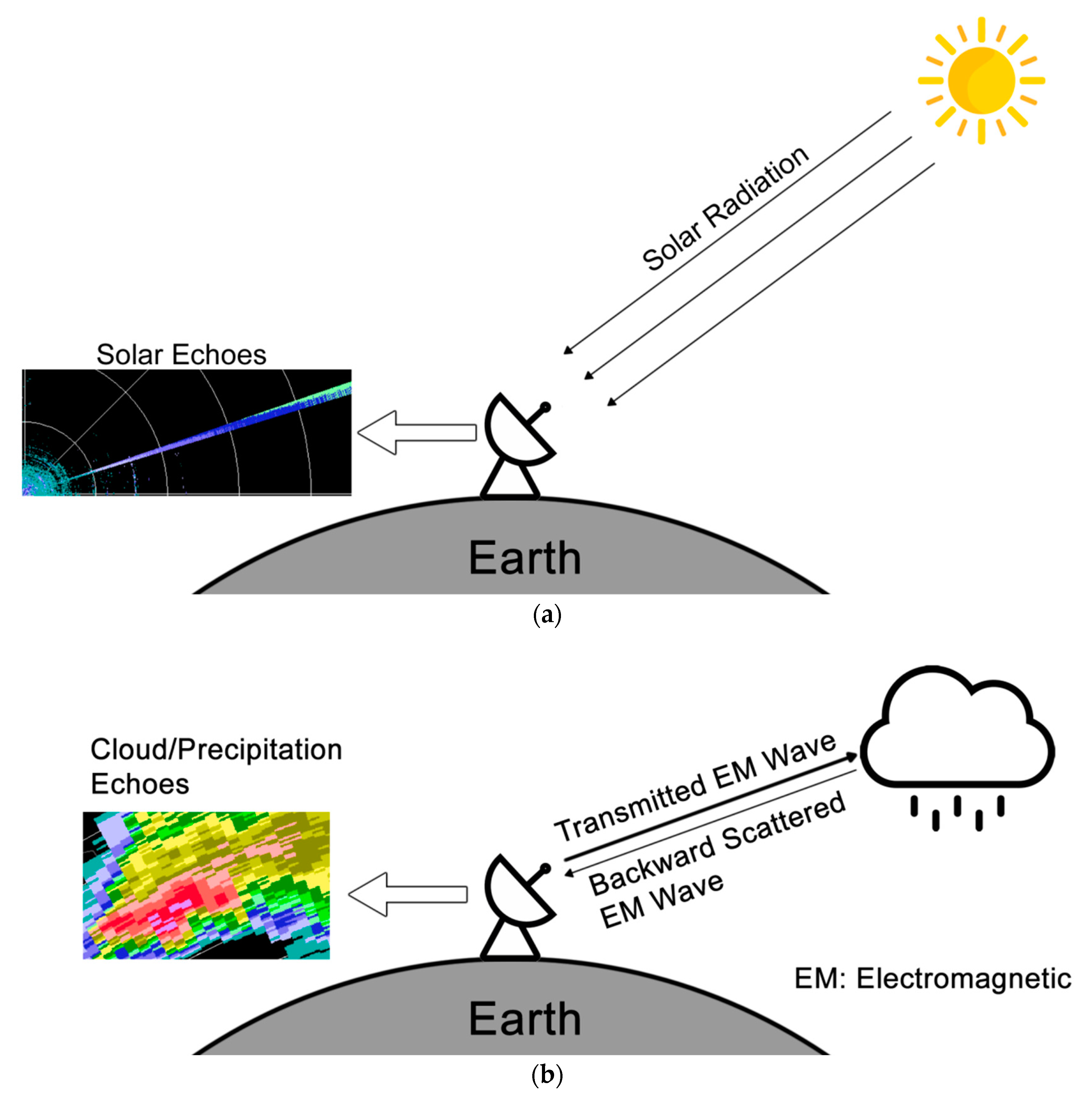
2.2. Automatic Online Solar Method
2.2.1. Extracting Online Solar Radials
2.2.2. One-Way Differential Attenuation Correction of Online Solar Data
2.2.3. Estimation of Daily ZDR from Online Solar Echoes
2.3. Processing of Vertical Pointing Data
3. Results
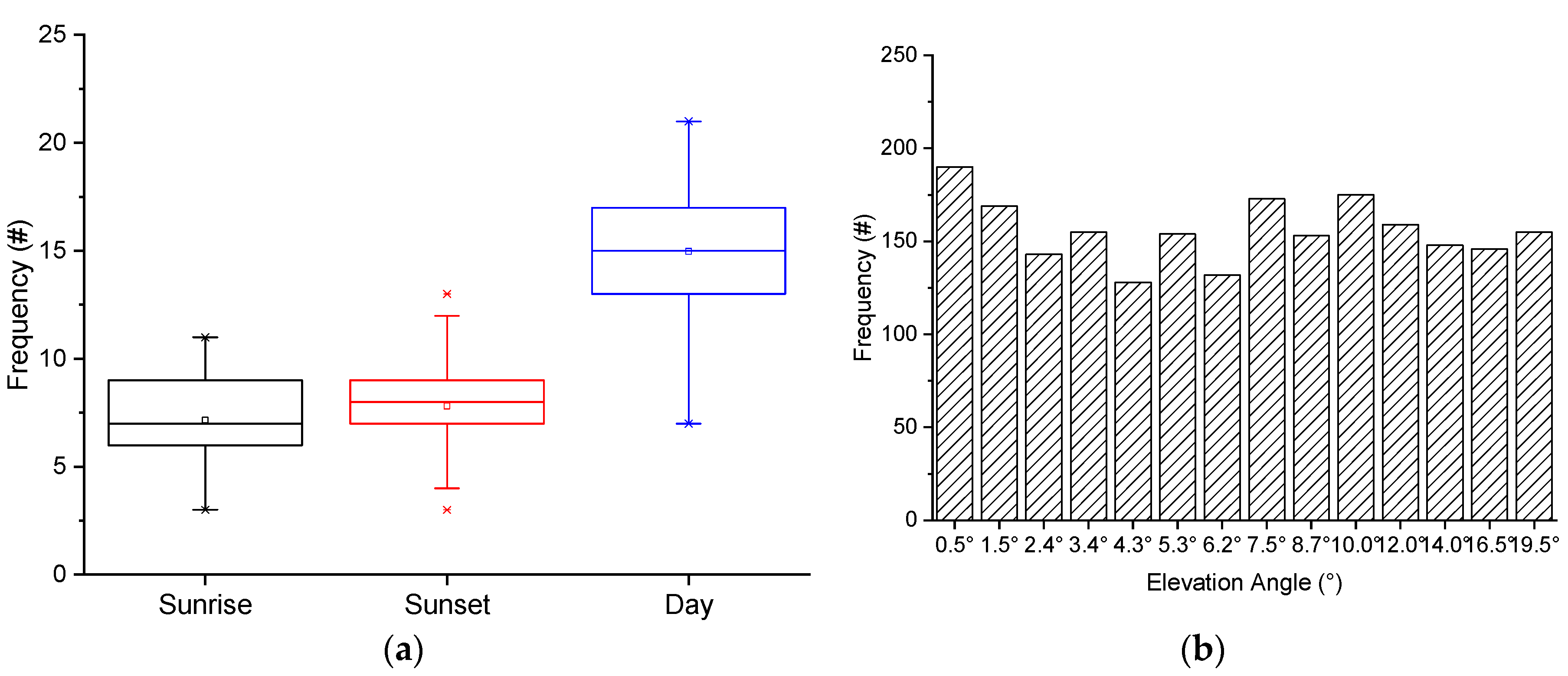
3.1. Occurrence Frequency of Online Solar Radials
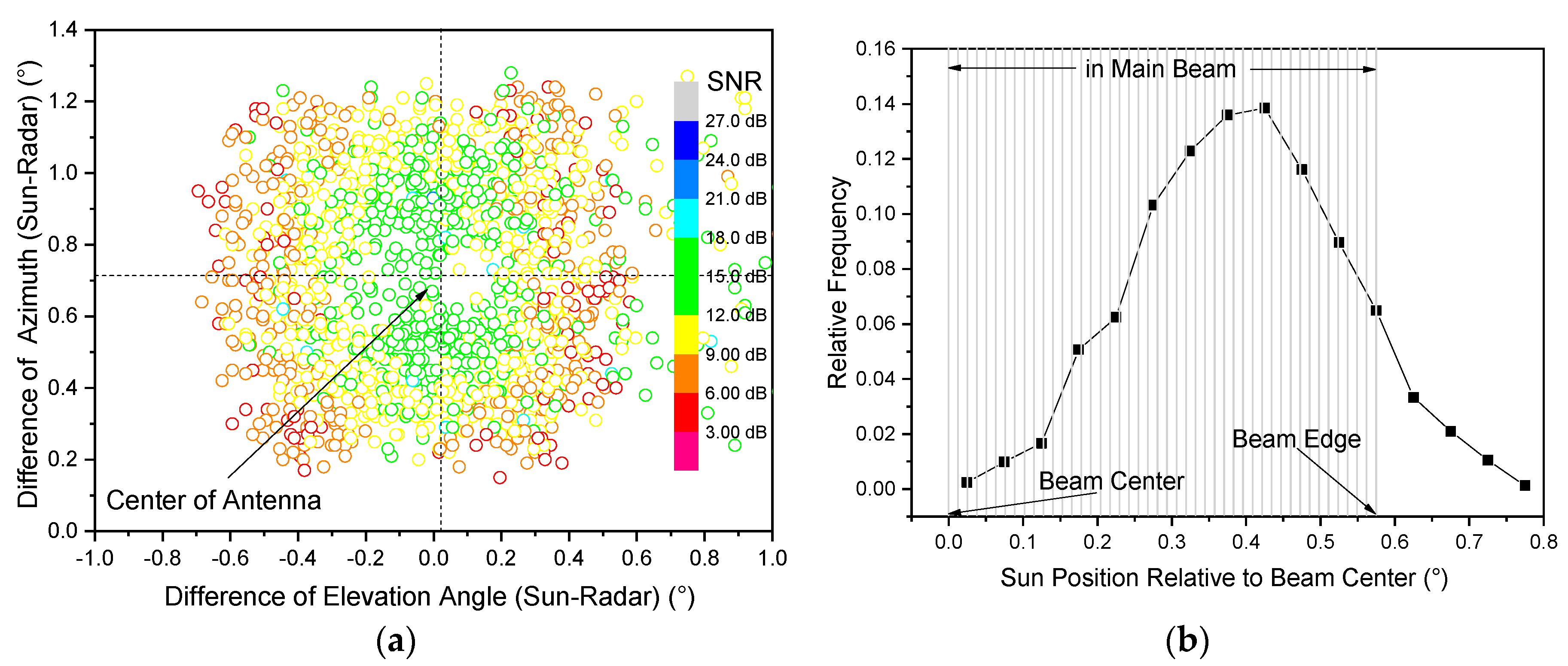
3.2. Characteristics of Online Solar Echoes along the Radial
3.3. Distribution within the Main Beam
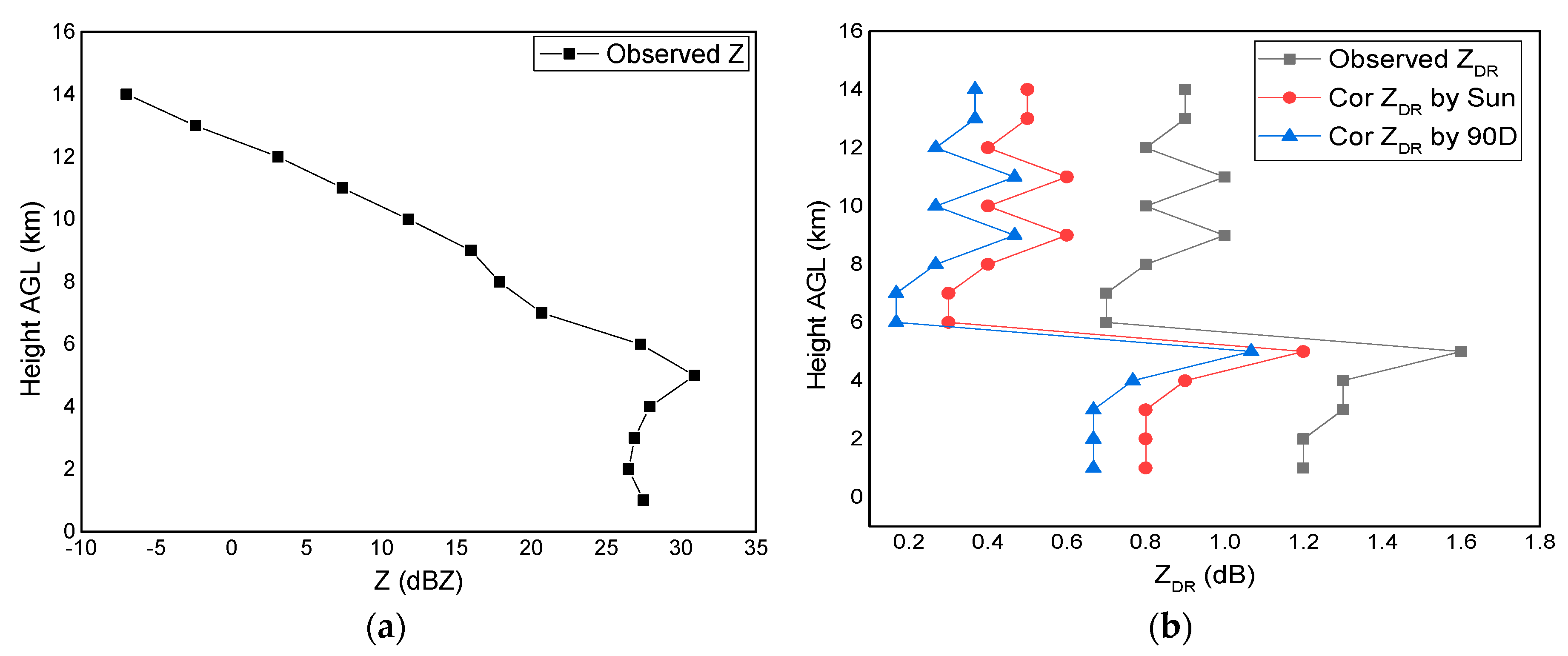
3.4. Comparison with the Vertical Pointing Method
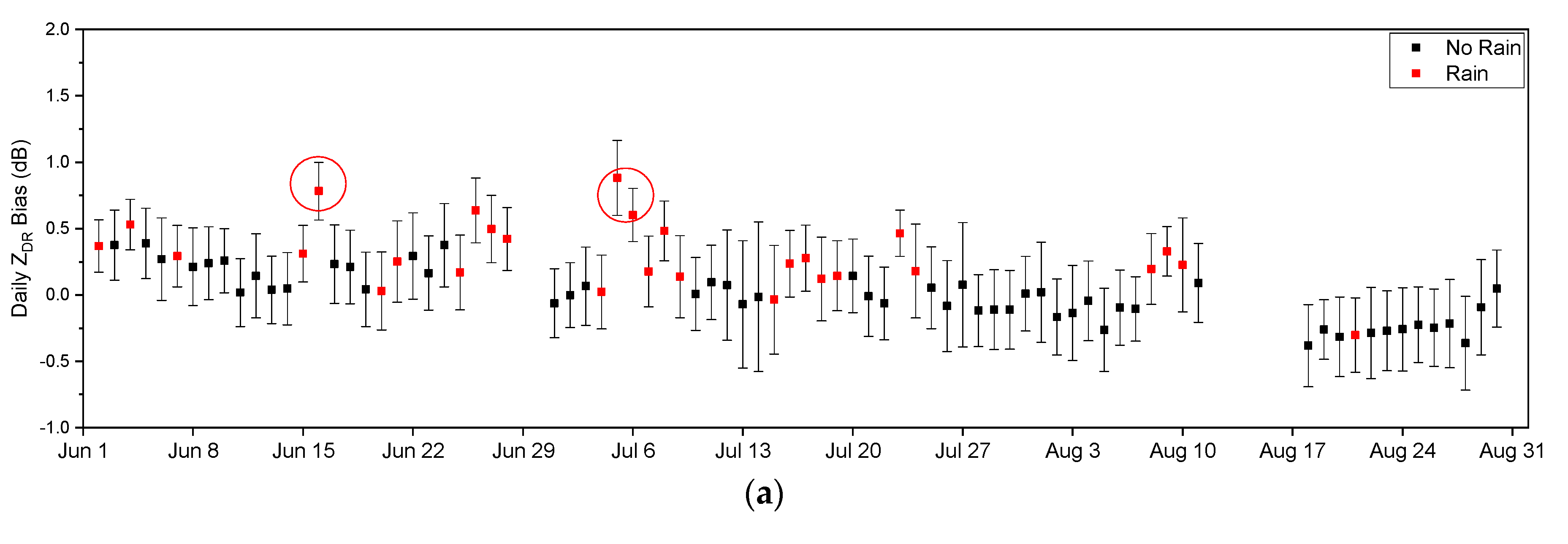
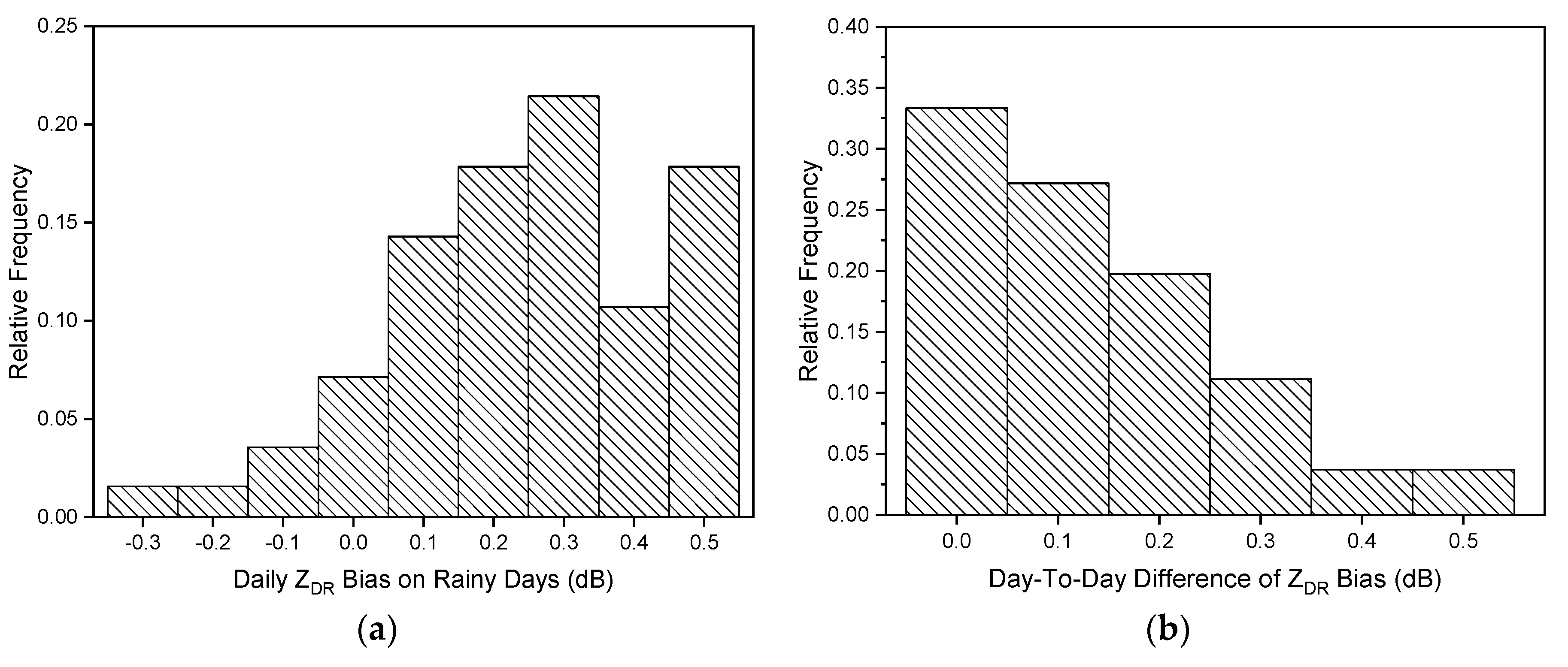
3.5. Variation in Daily ZDR Bias
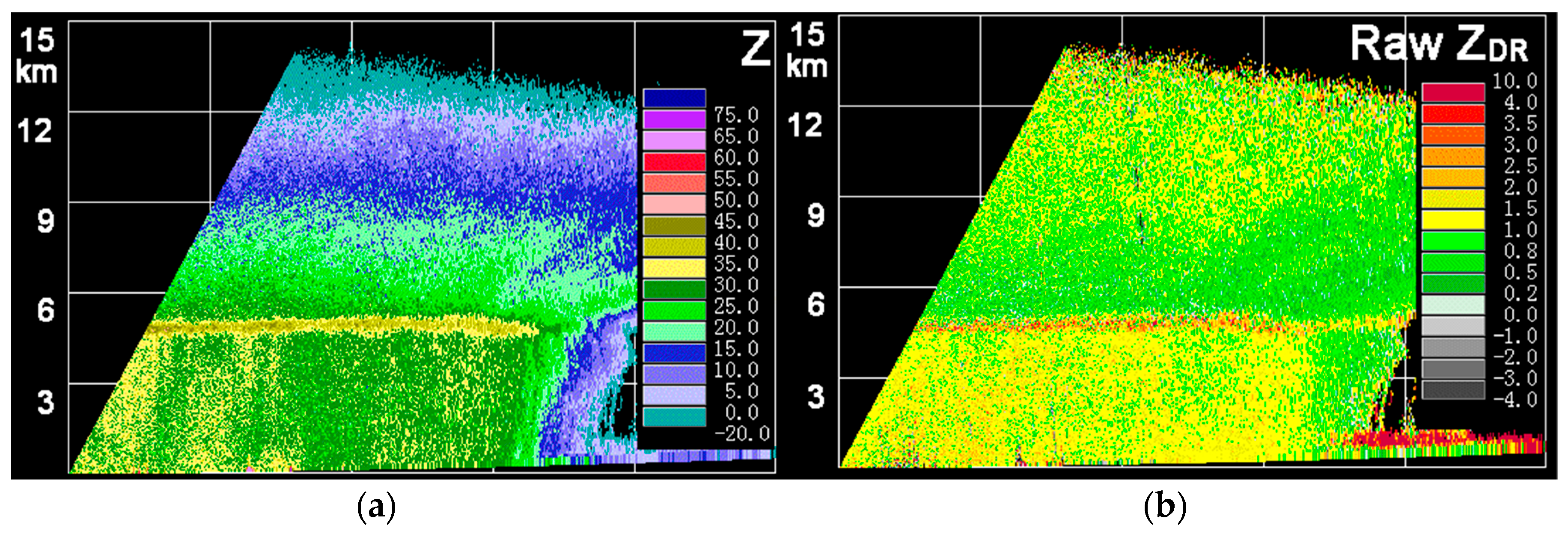
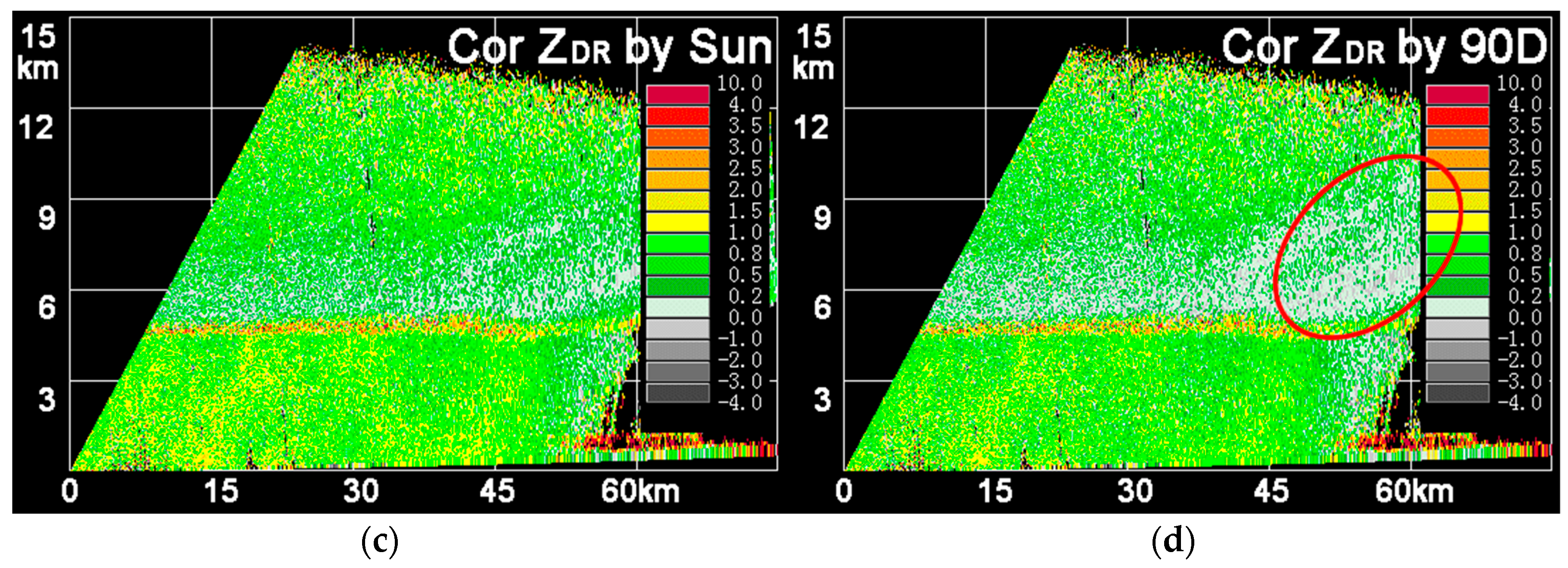
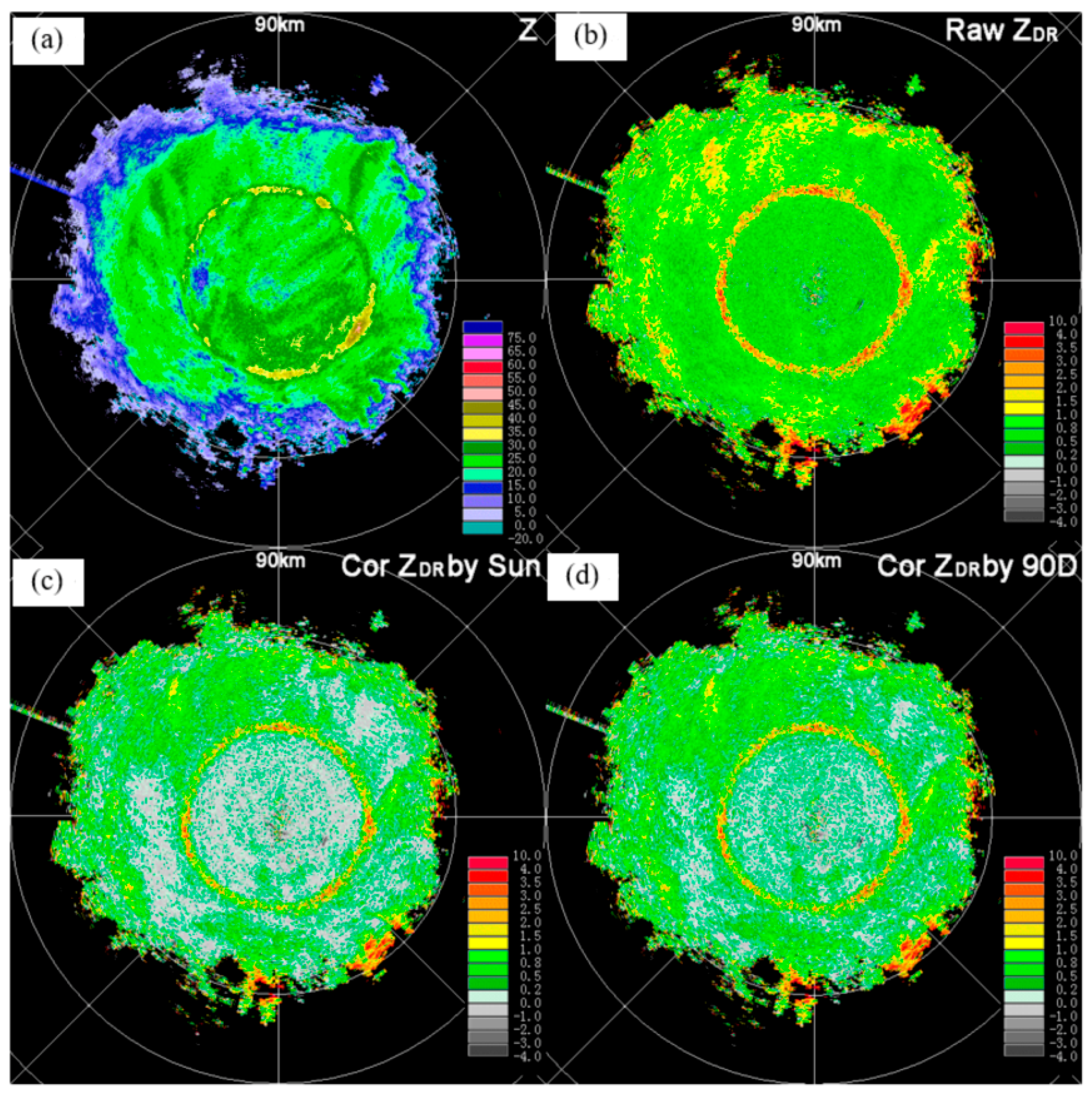
3.6. ZDR Correction Cases
4. Discussion
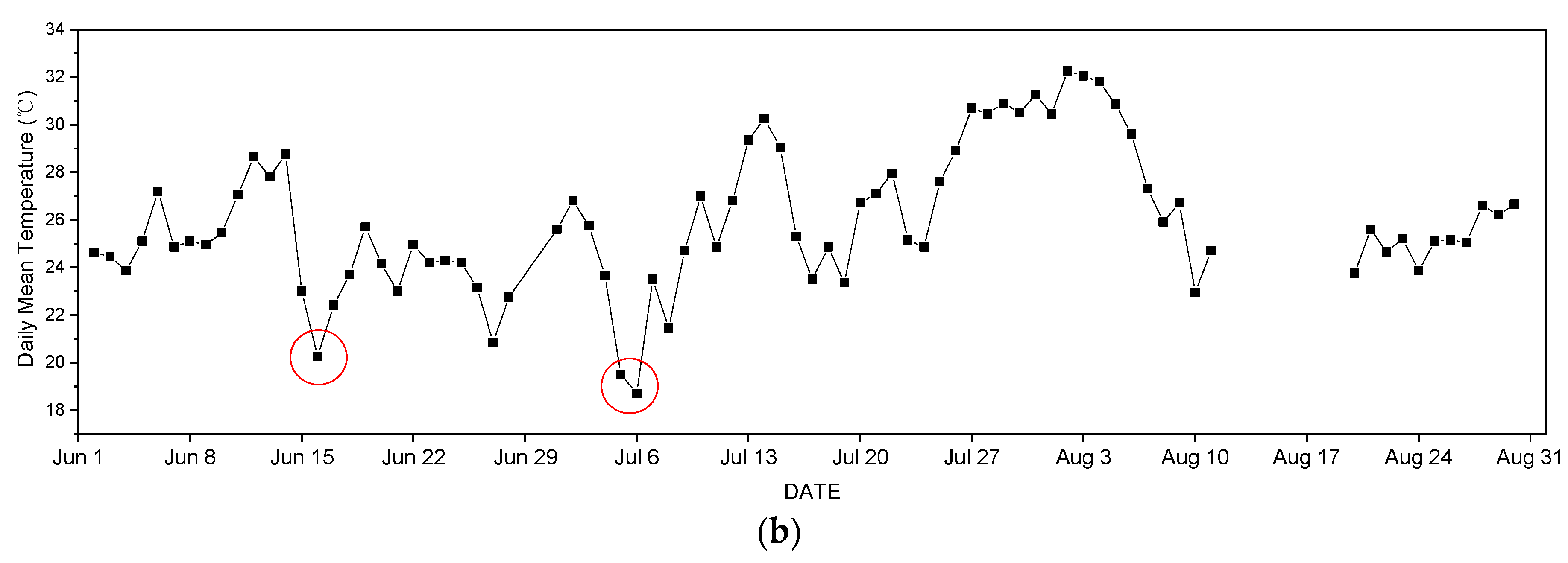
4.1. ZDR Bias and Ambient Temperature
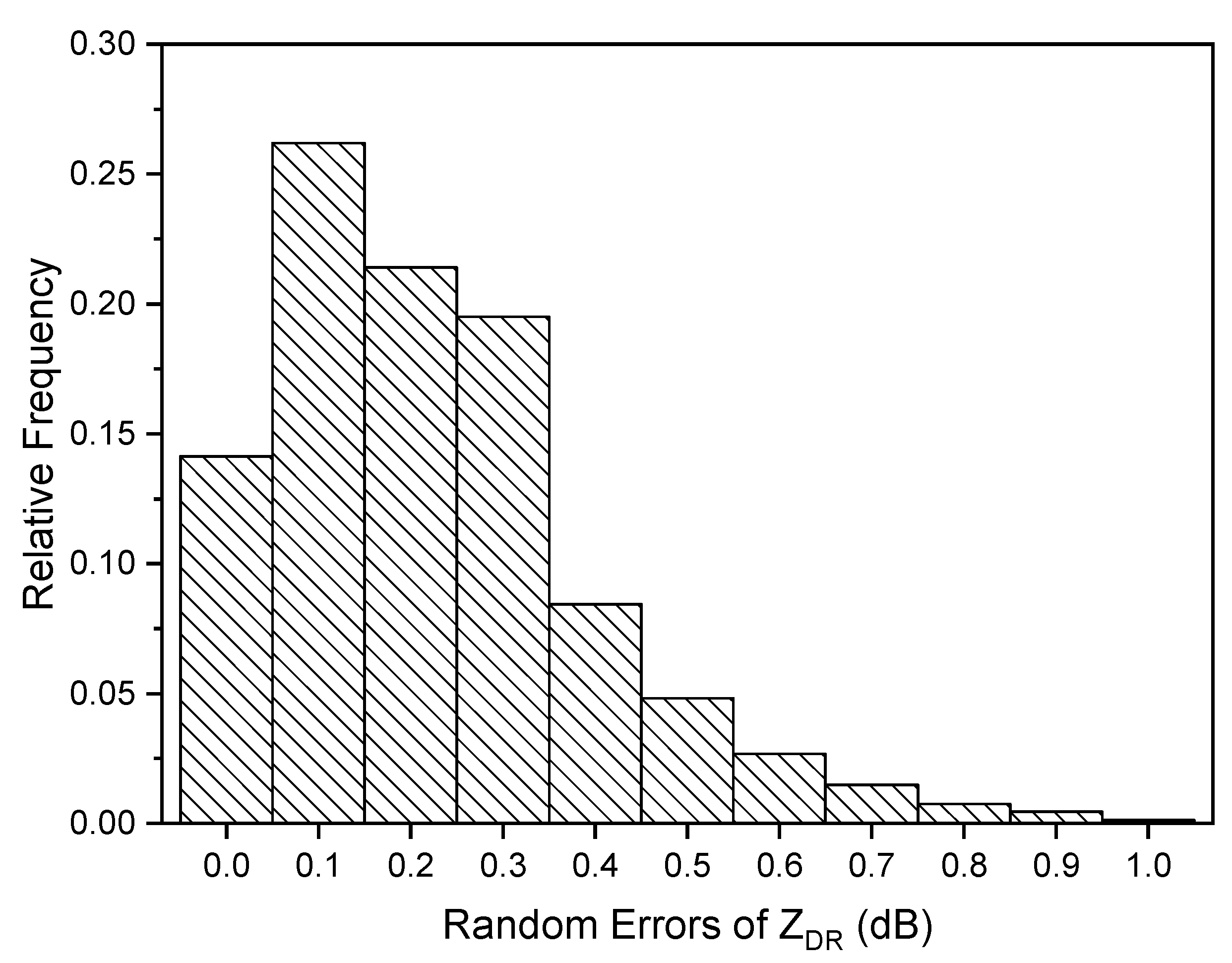
4.2. Random Error and Systematic Bias of ZDR
4.3. Uncertainty of the Proposed Online Solar Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Seliga, T.A.; Bringi, V.N. Potential Use Of Radar Differential Reflectivity Measurements at Orthogonal Polarizations for Measuring Precipitation. J. Appl. Meteorol. 1976, 15, 69–76. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Zrnic, D.S.; Ellis, S.M.; Oye, R.; Ryzhkov, A.V.; Straka, J. Cloud Microphysics Retrieval Using S-Band Dual-Polarization Radar Measurements. Bull. Am. Meteorol. Soc. 1999, 80, 381–388. [Google Scholar] [CrossRef]
- Lim, S.; Chandrasekar, V.; Bringi, V.N. Hydrometeor Classification System using Dual-polarization Radar Measurements: Model Improvements and in situ Verification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 792–801. [Google Scholar] [CrossRef]
- Park, H.S.; Ryzhkov, A.V.; Zrnić, D.S.; Kim, K.-E. The Hydrometeor Classification Algorithm for the Polarimetric WSR-88D: Description -and Application to an MCS. Weather Forecast. 2009, 24, 730–748. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Giangrande, S.E.; Schuur, T.J. Rainfall Estimation with a Polarimetric Prototype of WSR-88D. J. Appl. Meteorol. 2005, 44, 502–515. [Google Scholar] [CrossRef]
- Chen, H.; Chandrasekar, V. The Quantitative Precipitation Estimation System for Dallas–Fort Worth (DFW) Urban Remote Sensing Network. J. Hydrol. 2015, 531, 259–271. [Google Scholar] [CrossRef]
- Bringi, V.N.; Seliga, T.A.; Aydin, K. Hail detection with a differential reflectivity radar. Science 1984, 225, 1145–1147. [Google Scholar] [CrossRef] [PubMed]
- Ryzhkov, A.V.; Schuur, T.J.; Burgess, D.W.; Zrnic, D.S. Polarimetric Tornado Detection. J. Appl. Meteorol. 2005, 44, 557–570. [Google Scholar] [CrossRef]
- Zhang, G.; Vivekanandan, J.; Brandes, E. A Method for Estimating Rain Rate and Drop Size Distribution from Polarimetric Radar Measurements. IEEE Trans. Geosci. Remote Sens. 2001, 39, 830–841. [Google Scholar] [CrossRef]
- Wen, G.; Chen, H.N.; Zhang, G.F.; Sun, J.M. An Inverse Model for Raindrop Size Distribution Retrieval with Polarimetric Variables. Remote Sens. 2018, 10, 1179. [Google Scholar] [CrossRef]
- Jung, Y.; Zhang, G.; Xue, M. Assimilation of Simulated Polarimetric Radar Data for a Convective Storm Using the Ensemble Kalman Filter. Part I: Observation Operators for Reflectivity and Polarimetric Variables. Mon. Weather Rev. 2008, 136, 2228–2245. [Google Scholar] [CrossRef]
- Kumjian, M. Principles and Applications of Dual-polarization Weather Radar. Part I: Description of the Polarimetric Radar Variables. J. Oper. Meteorol. 2013, 1, 226–242. [Google Scholar] [CrossRef]
- Gabella, M. On the Use of Bright Scatterers for Monitoring Doppler, Dual-Polarization Weather Radars. Remote Sens. 2018, 10, 1007. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Giangrande, S.E.; Melnikov, V.M.; Schuur, T.J. Calibration Issues of Dual-Polarization Radar Measurements. J. Atmos. Ocean. Technol. 2005, 22, 1138–1155. [Google Scholar] [CrossRef]
- Zrnic, D.S.; Melnikov, V.M.; Carter, J.K. Calibrating Differential Reflectivity on the WSR-88D. J. Atmos. Ocean. Technol. 2006, 23, 944–951. [Google Scholar] [CrossRef]
- Gorgucci, E.; Scarchilli, G.; Chandrasekar, V. Calibration of Radars using Polarimetric Techniques. IEEE Trans. Geosci. Remote Sens. 1992, 30, 853–858. [Google Scholar] [CrossRef]
- Bechini, R.; Baldini, L.; Cremonini, R.; Gorgucci, E. Differential Reflectivity Calibration for Operational Radars. J. Atmos. Ocean. Technol. 2008, 25, 1542–1555. [Google Scholar] [CrossRef]
- Gorgucci, E.; Scarchilli, G.; Chandrasekar, V. A Procedure to Calibrate Multiparameter Weather Radar using Properties of the Rain Medium. IEEE Trans. Geosci. Remote Sens. 1999, 37, 269–276. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: New York, NY, USA, 2001; p. 636. [Google Scholar]
- Hubbert, J.C.; Bringi, V.N.; Brunkow, D. Studies of the Polarimetric Covariance Matrix. Part I: Calibration Methodology. J. Atmos. Ocean. Technol. 2003, 20, 696–706. [Google Scholar] [CrossRef]
- Melnikov, V.M.; Doviak, R.J.; Zrnić, D.S.; Stensrud, D.J. Mapping Bragg Scatter with a Polarimetric WSR-88D. J. Atmos. Ocean. Technol. 2011, 28, 1273–1285. [Google Scholar] [CrossRef]
- Richardson, L.M.; Zittel, W.D.; Lee, R.R.; Melnikov, V.M.; Ice, R.L.; Cunningham, J.G. Bragg Scatter Detection by the WSR-88D. Part II: Assessment of ZDR Bias Estimation. J. Atmos. Ocean. Technol. 2017, 34, 479–493. [Google Scholar] [CrossRef]
- Huuskonen, A.; Holleman, I. Determining Weather Radar Antenna Pointing Using Signals Detected from the Sun at Low Antenna Elevations. J. Atmos. Ocean. Technol. 2007, 24, 476–483. [Google Scholar] [CrossRef]
- Henson, R.; Ahrens, C. Meteorology Today: An Introduction to Weather, Climate, and the Environment, 12th ed.; Cengage Learning: Boston, MA, USA, 2018; p. 656. [Google Scholar]
- Holleman, I.; Huuskonen, A.; Gill, R.; Tabary, P. Operational Monitoring of Radar Differential Reflectivity Using the Sun. J. Atmos. Ocean. Technol. 2010, 27, 881–887. [Google Scholar] [CrossRef]
- Holleman, I.; Huuskonen, A.; Kurri, M.; Beekhuis, H. Operational Monitoring of Weather Radar Receiving Chain Using the Sun. J. Atmos. Ocean. Technol. 2010, 27, 159–166. [Google Scholar] [CrossRef]
- Hubbert, J.C. Differential Reflectivity Calibration and Antenna Temperature. J. Atmos. Ocean. Technol. 2017, 34, 1885–1906. [Google Scholar] [CrossRef]
- Chu, Z.; Hu, H.; Huang, X.; Wei, M. The Narrow Beam C-band Dual-polarization Doppler Weather Radar of NUIST and Its Performance Analysis (In Chinese). Plateau Meteorol. 2017, 36, 1072–1082. [Google Scholar] [CrossRef]
- Michalsky, J.J. The Astronomical Almanac’s Algorithm for Approximate Solar Position (1950–2050). Sol. Energy 1988, 40, 227–235. [Google Scholar] [CrossRef]
- Testud, J.; Bouar, E.L.; Obligis, E.; Ali-Mehenni, M. The Rain Profiling Algorithm Applied to Polarimetric Weather Radar. J. Atmos. Ocean. Technol. 2000, 17, 332–356. [Google Scholar] [CrossRef]
- Lim, S.; Chandrasekar, V. A Dual-Polarization Rain Profiling Algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1011–1021. [Google Scholar] [CrossRef]
- Zhang, G. Weather Radar Polarimetry; CRC Press Publications: Boca Raton, FL, USA, 2016; p. 304. [Google Scholar]
- Zhang, J.; Howard, K.; Langston, C.; Vasiloff, S.; Kaney, B.; Arthur, A.; Van Cooten, S.; Kelleher, K.; Kitzmiller, D.; Ding, F.; et al. National Mosaic and Multi-Sensor QPE (NMQ) System: Description, Results, and Future Plans. Bull. Am. Meteorol. Soc. 2011, 92, 1321–1338. [Google Scholar] [CrossRef]
- Gorgucci, E.; Bechini, R.; Baldini, L.; Cremonini, R.; Chandrasekar, V. The Influence of Antenna Radome on Weather Radar Calibration and Its Real-Time Assessment. J. Atmos. Ocean. Technol. 2013, 30, 676–689. [Google Scholar] [CrossRef]







| Parameters | Values |
|---|---|
| Pulse width | 0.5 μs |
| Main beamwidth | 0.54° |
| Range resolution | 75 m |
| Azimuthal resolution | ~0.6° |
| Pulse repetition frequency | 1000 Hz |
| Samples | 43 |
| Antenna rotation rate (rpm) | ~2 |
| Elevation Angles | 0.5, 1.5, 2.4, 3.4, 4.3, 5.3, 6.2, 7.5, 8.7, 10.0, 12.0, 14.0, 16.7, 19.5, 90.0° |
| Polarization mode | Simultaneous transmission and simultaneous reception |
| Radar variables | Reflectivity factor (Z), Radial velocity (V), Velocity spectrum (W), Differential reflectivity (ZDR), Differential phase (ϕDP), Co-polar correlation coefficient (ρhv), Signal to noise ratio (SNR) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, Z.; Liu, W.; Zhang, G.; Kou, L.; Li, N. Continuous Monitoring of Differential Reflectivity Bias for C-Band Polarimetric Radar Using Online Solar Echoes in Volume Scans. Remote Sens. 2019, 11, 2714. https://doi.org/10.3390/rs11222714
Chu Z, Liu W, Zhang G, Kou L, Li N. Continuous Monitoring of Differential Reflectivity Bias for C-Band Polarimetric Radar Using Online Solar Echoes in Volume Scans. Remote Sensing. 2019; 11(22):2714. https://doi.org/10.3390/rs11222714
Chicago/Turabian StyleChu, Zhigang, Wei Liu, Guifu Zhang, Leilei Kou, and Nan Li. 2019. "Continuous Monitoring of Differential Reflectivity Bias for C-Band Polarimetric Radar Using Online Solar Echoes in Volume Scans" Remote Sensing 11, no. 22: 2714. https://doi.org/10.3390/rs11222714
APA StyleChu, Z., Liu, W., Zhang, G., Kou, L., & Li, N. (2019). Continuous Monitoring of Differential Reflectivity Bias for C-Band Polarimetric Radar Using Online Solar Echoes in Volume Scans. Remote Sensing, 11(22), 2714. https://doi.org/10.3390/rs11222714