High-Rate Monitoring of Satellite Clocks Using Two Methods of Averaging Time
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Discussion
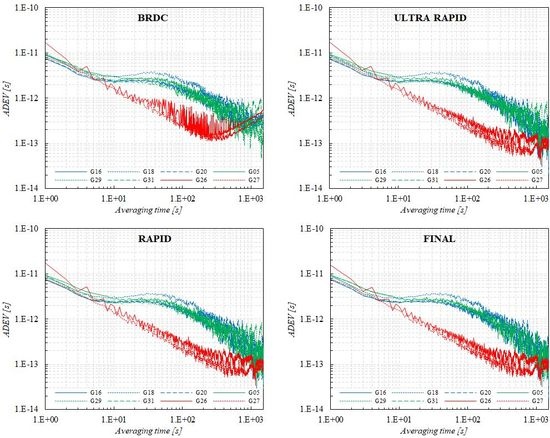
4.1. Allan Deviation: τ = 2n
4.2. Allan Deviation: All τ Method
4.3. Time Deviation: τ = 2n
4.4. Time Deviation: All τ Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hordyniec, P.; Kapłon, J.; Rohm, W.; Kryza, M. Residuals of Tropospheric Delays from GNSS Data and Ray-Tracing as a Potential Indicator of Rain and Clouds. Remote Sens. 2018, 10, 1917. [Google Scholar] [CrossRef]
- Wielgosz, P.; Paziewski, J.; Baryła, R. On Constraining Zenith Tropospheric Delays in Processing of Local GPS Networks with Bernese Software. Surv. Rev. 2011, 43, 472–483. [Google Scholar] [CrossRef]
- Xie, X.; Geng, T.; Zhao, Q.; Liu, J.; Wang, B. Performance of BDS-3: Measurement Quality Analysis, Precise Orbit and Clock Determination. Sensors 2017, 17, 1233. [Google Scholar] [CrossRef]
- Yu, X.; Gao, J. Kinematic Precise Point Positioning Using Multi-Constellation Global Navigation Satellite System (GNSS) Observations. ISPRS Int. J. Geo-Inf. 2017, 6, 6. [Google Scholar] [CrossRef]
- Kaloop, M.; Elbeltagi, E.; Hu, J.; Elrefai, A. Recent Advances of Structures Monitoring and Evaluation Using GPS-Time Series Monitoring Systems: A Review. ISPRS Int. J. Geo-Inf. 2017, 6, 382. [Google Scholar] [CrossRef]
- Lv, Y.; Dai, Z.; Zhao, Q.; Yang, S.; Zhou, J.; Liu, J. Improved Short-Term Clock Prediction Method for Real-Time Positioning. Sensors 2017, 17, 1308. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Wang, G.; Han, X.; Guo, J. Impacts of satellite orbit and clock on real-time GPS point and relative positioning. Sensors 2017, 17, 1363. [Google Scholar] [CrossRef] [PubMed]
- Gruszczynski, W. Influence of model parameter uncerainties on forecasted subsidence. Acta Geodyn. Geomater. 2018, 15, 211–228. [Google Scholar] [CrossRef]
- Niedojadło, Z.; Gruszczyński, W. The Impact of the Estimation of the Parameters Values on the Accuracy of Predicting the Impacts of Mining Exploitation/Wpływ Oszacowania Wartości Parametrów Modelu Na Dokładność Prognozowania Wpływów Eksploatacji Górniczej. Arch. Min. Sci. 2015, 60, 173–193. [Google Scholar] [CrossRef]
- Malinowska, A.A.; Hejmanowski, R.; Witkowski, W.T.; Guzy, A. Mapping of slow vertical ground movement caused by salt cavern convergence with sentinel-1 tops data. Arch. Min. Sci. 2018, 63, 383–396. [Google Scholar]
- Kampczyk, A. Geodäsie im Investitionsbauprozess auf den Bahngebieten in Polen. Bautechnik 2014, 91, 409–413. [Google Scholar] [CrossRef]
- Kampczyk, A. Technische Spezifikationen für die Interoperabilität und die polnischen Vorschriften in der Projektierung von der Geometrie der Eisenbahnstrecken/Technical specifications for interoperability and Polish regulations in the design of the geometry of railway lines. Bauingenieur 2015, 90, 229–234. [Google Scholar]
- Borowski, L.; Pienko, M.; Wielgos, P. Evaluation of Inventory Surveying of Façade Scaffolding Conducted during ORKWIZ Project. In Proceedings of the 2017 Baltic Geodetic Congress (BGC Geomatics), Gdansk, Poland, 22–25 June 2017; pp. 189–192. [Google Scholar]
- Chrobak, T.; Lupa, M.; Szombara, S.; Dejniak, D. The use of cartographic control points in the harmonization and revision of MRDBs. GEOCARTO Int. 2019, 34, 260–275. [Google Scholar] [CrossRef]
- Ligas, M.; Szombara, S. Geostatistical prediction of a local geometric geoid-kriging and cokriging with the use of EGM2008 geopotential model. Stud. Geophys. Geod. 2018, 62, 187–205. [Google Scholar] [CrossRef]
- Grešlová, P.; Štych, P.; Salata, T.; Hernik, J.; Knížková, I.; Bičík, I.; Jeleček, L.; Prus, B.; Noszczyk, T. Agroecosystem energy metabolism in Czechia and Poland in the two decades after the fall of communism: From a centrally planned system to market oriented mode of production. Land Use Policy 2019, 82, 807–820. [Google Scholar] [CrossRef]
- Bieda, A.; Bieda, A. Renewable energy in the system of spatial planning in Poland. In Proceedings of the Geographic Information Systems Conference and Exhibition (GIS ODYSSEY 2017), Trento, Italy, 4–8 September 2017; pp. 28–42. [Google Scholar]
- Bieda, A.; Adamczyk, T.; Bieda, A. The energy performance of buildings directive as one of the solutions for smart cities. In Proceedings of the Geographic Information Systems Conference and Exhibition—GIS ODYSSEY 2016, Perugia, Italy, 5–9 September 2016; pp. 44–49. [Google Scholar]
- Kukulska-Kozieł, A.; Szylar, M.; Cegielska, K.; Noszczyk, T.; Hernik, J.; Gawroński, K.; Dixon-Gough, R.; Jombach, S.; Valánszki, I.; Kovács, K.F. Towards three decades of spatial development transformation in two contrasting post-Soviet cities—Kraków and Budapest. Land Use Policy 2019, 85, 328–339. [Google Scholar] [CrossRef]
- Hanus, P.; Pęska-Siwik, A.; Szewczyk, R. Spatial analysis of the accuracy of the cadastral parcel boundaries. Comput. Electron. Agric. 2018, 144, 9–15. [Google Scholar] [CrossRef]
- Benduch, P.; Pęska-Siwik, A. Assessing the usefulness of the photogrammetric method in the process of capturing data on parcel boundaries. Geod. Cartogr. 2017, 66, 3–22. [Google Scholar] [CrossRef]
- Busko, M.; Szafranska, B. Analysis of Changes in Land Use Patterns Pursuant to the Conversion of Agricultural Land to Non-Agricultural Use in the Context of the Sustainable Development of the Malopolska Region. Sustainability 2018, 10, 136. [Google Scholar] [CrossRef]
- Busko, M.; Meusz, A. Current status of real estate cadastre in Poland with reference to historical conditions of different regions of the country. In Proceedings of the 9th International Conference Environmental Engineering (9th ICEE)—Selected Papers, Vilnius, Lithuania, 22–23 May 2014. [Google Scholar]
- Noszczyk, T. Land Use Change Monitoring as a Task of Local Government Administration in Poland. J. Ecol. Eng. 2018, 19, 170–176. [Google Scholar] [CrossRef]
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.M.; Webb, F. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Choy, S.; Bisnath, S.; Rizos, C. Uncovering common misconceptions in GNSS Precise Point Positioning and its future prospect. GPS Solut. 2016, 21, 1–10. [Google Scholar] [CrossRef]
- Chan, F.C.; Joerger, M.; Pervan, B. Stochastic modeling of atomic receiver clock for high integrity GPS navigation. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1749–1764. [Google Scholar] [CrossRef]
- Wang, D.; Guo, R.; Xiao, S.; Xin, J.; Tang, T.; Yuan, Y. Atomic clock performance and combined clock error prediction for the new generation of BeiDou navigation satellites. Adv. Space Res. 2018, 63, 2889–2898. [Google Scholar] [CrossRef]
- Bock, H.; Dach, R.; Jäggi, A.; Beutler, G. High-rate GPS clock corrections from CODE: Support of 1 Hz applications. J. Geod. 2009, 83, 1083–1094. [Google Scholar] [CrossRef]
- Dach, R.; Walser, P. Bernese GNSS Software Version 5.2; Astronomical Institute, University of Bern: Bern, Switzerland, 2013. [Google Scholar]
- Cernigliaro, A.; Valloreia, S.; Fantino, G.; Galleani, L.; Tavella, P. Analysis on GNSS space clocks performances. In Proceedings of the 2013 Joint European Frequency and Time Forum & International Frequency Control Symposium (EFTF/IFC), Prague, Czech Republic, 21–25 July 2013; pp. 835–837. [Google Scholar]
- Zhang, B.; Ou, J.; Yuan, Y.; Zhong, S. Yaw attitude of eclipsing GPS satellites and its impact on solutions from precise point positioning. Chin. Sci. Bull. 2010, 55, 3687–3693. [Google Scholar] [CrossRef]
- Daly, P.; Kitching, I.D.; Allan, D.W.; Peppler, T.K. Frequency and time stability of GPS and GLONASS clocks. In Proceedings of the 44th Annual Symposium on Frequency Control, Baltimore, MD, USA, 23–25 May 1990; Volume 9, pp. 127–139. [Google Scholar]
- Delporte, J.; Boulanger, C.; Mercier, F. Short-term stability of GNSS on-board clocks using the polynomial method. In Proceedings of the 2012 European Frequency and Time Forum, Gothenburg, Sweden, 23–27 April 2012; pp. 117–121. [Google Scholar]
- Delporte, J.; Boulanger, C.; Mercier, F. Straightforward estimations of GNSS on-board clocks. In Proceedings of the 2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum (FCS) Proceedings, San Francisco, CA, USA, 2–5 May 2011; pp. 1–4. [Google Scholar]
- Qing, Y.; Lou, Y.; Dai, X.; Liu, Y. Benefits of satellite clock modeling in BDS and Galileo orbit determination. Adv. Space Res. 2017, 60, 2550–2560. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, J.; Lee, Y.J. Protecting signal integrity against atomic clock anomalies on board GNSS satellites. IEEE Trans. Instrum. Meas. 2011, 60, 2738–2745. [Google Scholar] [CrossRef]
- Maciuk, K. Satellite clock stability analysis depending on the reference clock type. Arab. J. Geosci. 2019, 12, 28. [Google Scholar] [CrossRef]
- Maciuk, K. Monitoring of Galileo on-board oscillators variations, disturbances & noises. Measurement 2019, 147, 106843. [Google Scholar]
- Wang, S.; Yang, F.; Gao, W.; Yan, L.; Ge, Y. A new stochastic model considering satellite clock interpolation errors in precise point positioning. Adv. Space Res. 2018, 61, 1332–1341. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, X.; Li, X.; Cai, S. Impact of sampling rate of IGS satellite clock on precise point positioning. Geo-Spat. Inf. Sci. 2010, 13, 150–156. [Google Scholar] [CrossRef]
- Yeh, T.-K.; Hwang, C.; Xu, G.; Wang, C.-S.; Lee, C.-C. Determination of global positioning system (GPS) receiver clock errors: Impact on positioning accuracy. Meas. Sci. Technol. 2009, 20, 075105. [Google Scholar] [CrossRef]
- Elsobeiey, M.; Al-Harbi, S. Performance of real-time Precise Point Positioning using IGS real-time service. GPS Solut. 2016, 20, 565–571. [Google Scholar] [CrossRef]
- Lutz, S.; Beutler, G.; Schaer, S.; Dach, R.; Jäggi, A. CODE’s new ultra-rapid orbit and ERP products for the IGS. GPS Solut. 2016, 20, 239–250. [Google Scholar] [CrossRef] [Green Version]
- Luo, X. Mathematical Models for GPS Positioning. In GPS Stochastic Modelling; Springer: Berlin/Heidelberg, Germany, 2013; pp. 55–116. [Google Scholar]
- Fu, W.; Huang, G.; Liu, Y.; Zhang, Q.; Yu, H. The analysis of the characterization for GLONASS and GPS on-board satellite clocks. Lect. Notes Electr. Eng. 2013, 244, 549–566. [Google Scholar]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- ICD-GPS-870. NAVSTAR GPS Interface Control Document. 2017. Available online: https://www.gps.gov/technical/icwg/ (accessed on 25 October 2019).
- Petovello, M.G.; Lachapelle, G. Estimation of Clock Stability Using GPS. GPS Solut. 2000, 4, 21–33. [Google Scholar] [CrossRef]
- Allan, D.W. Clock characterization tutorial. In Proceedings of the 15th Annual Precise Time and Time Interval (PTTI) Applications and Planning Meeting, Washington, DC, USA, 6–8 December 1983; pp. 459–475. [Google Scholar]
- Allan, D.W. Time and Frequency (Time-Domain) Characterization, Estimation, and Prediction of Precision Clocks and Oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 647–654. Available online: https://tf.nist.gov/general/pdf/2082.pdf (accessed on 25 October 2019). [CrossRef]
- Riley, W.J. Handbook of Frequency Stability Analysis; National Institute of Standards and Technology: Washington, DC, USA, 2008. [Google Scholar]
- Allan, D.W.; Weiss, M.A.; Jespersen, J.L. A frequency-domain view of time-domain characterization of clocks and time and frequency distribution systems. In Proceedings of the 45th Annual Symposium on Frequency Control 1991, Los Angeles, CA, USA, 29–31 May 1991; pp. 667–678. [Google Scholar]
- Zhang, X.; Li, X.; Guo, F. Satellite clock estimation at 1 Hz for realtime kinematic PPP applications. GPS Solut. 2011, 15, 315–324. [Google Scholar] [CrossRef]
- Han, S.-C.; Kwon, J.H.; Jekeli, C. Accurate absolute GPS positioning through satellite clock error estimation. J. Geod. 2001, 75, 33–43. [Google Scholar] [CrossRef]
- Delporte, J. Simple methods for the estimation of the short-term stability of GNSS on-board clocks. In Proceedings of the 42nd Annual Precise Time and Time Interval Applications Planning Meeting, Reston, VA, USA, 15–18 November 2010; pp. 215–223. [Google Scholar]










| Type | Accuracy | Latency | Updates (Per Day) |
|---|---|---|---|
| Broadcast | ~100 cm | real time | 12 |
| ~5 ns | |||
| Ultra-Rapid (predicted half) | ~5 cm | real time | 4 |
| ~3 ns | |||
| Ultra-Rapid (observed half) | ~3 cm | 3–9 h | 4 |
| ~150 ps | |||
| Rapid | ~2.5 cm | 17–41 h | 1 |
| ~75 ps | |||
| Final | ~2.5 cm | 12–18 days | 1 week |
| Satellite Category | Launches During | SVN a | Atomic Clock | Design Life (Years) |
|---|---|---|---|---|
| Block I | 1978–1985 | 01–11 (07) b | 1 Cs + 2 Rb | 4.5 |
| Block II | 1989–1990 | 13–21 | 2 Cs + 2 Rb | 7.5 |
| Block IIA | 1990–1997 | 22–40 | 2 Cs + 2 Rb | 7.5 |
| Block IIR | 1997–2004 | 41–61 (42) | 3 Rb | 10 |
| Block IIR-M | 2005–2009 | 48–58 | 3 Rb | 10 |
| Block IIF | 2010–2012 | 62–73 | 1 Cs + 2 Rb | 12.7 |
| Station | Country | City | Clock |
|---|---|---|---|
| DLF1 | Netherlands | Delft | External Caesium |
| GOP6 | Czech Republic | Ondrejov | External Caesium |
| GOP7 | Czech Republic | Ondrejov | External Caesium |
| JOZ2 | Poland | Jozefoslaw | Internal |
| KIR8 | Sweden | Kiruna | External Rubidium |
| M0SE | Italy | Rome | External Rubidium |
| MATE | Italy | Matera | External H_Maser |
| NICO | Cyprus | Nicosia | Internal |
| ONS1 | Sweden | Onsala | External H-Maser |
| PDEL | Portugal | Ponta Delgada | External Quartz |
| REYK | Iceland | Reykjavik | Internal |
| WTZR | Germany | Bad Koetzting | External H-Maser |
| YEBE | Spain | Yebes | External H-Maser |
| ZIM2 | Switzerland | Zimmerwald | Internal |
| PRN a | SVN | Orbit Plane | Block | Freq. Standard | Launch Date | Available (UT) |
|---|---|---|---|---|---|---|
| G20 | 51 | E4 | IIR-4 | Rb1 | 2000-05-11 | 2000-06-01 16:09 |
| G18 | 34 | D6 | IIR-7 | Rb1 | 2001-01-30 | 2001-02-15 15:51 |
| G16 | 56 | B1 | IIR-8 | Rb3 | 2003-01-29 | 2003-02-18 15:53 |
| G31 | 52 | A2 | IIR-M-2 | Rb3 | 2006-09-25 | 2006-10-12 22:53 |
| G29 | 57 | C1 | IIR-M-5 | Rb3 | 2007-12-20 | 2008-01-02 20:41 |
| G05 | 50 | E3 | IIR-M-8 | Rb1 | 2009-08-17 | 2009-08-27 14:40 |
| G27 | 66 | C2 | IIF-4 | Rb2 | 2013-05-15 | 2013-06-21 19:58 |
| G26 | 71 | B5 | IIF-9 | Rb1 | 2015-03-25 | 2015-04-20 22:22 |
| Orbit Type | PRN | τ [s] | |||||
|---|---|---|---|---|---|---|---|
| 1 | 4 | 16 | 64 | 256 | 1024 | ||
| Broadcast | G16 | 7.42 × 10−12 | 2.95 × 10−12 | 2.44 × 10−12 | 1.98 × 10−12 | 6.08 × 10−13 | 2.85 × 10−13 |
| G20 | 7.77 × 10−12 | 3.15 × 10−12 | 2.61 × 10−12 | 2.07 × 10−12 | 8.89 × 10−13 | 4.16 × 10−13 | |
| G27 | 8.12 × 10−12 | 3.40 × 10−12 | 9.82 × 10−13 | 3.83 × 10−13 | 1.39 × 10−13 | 2.67 × 10−13 | |
| G18 | 9.02 × 10−12 | 3.68 × 10−12 | 3.18 × 10−12 | 3.46 × 10−12 | 1.18 × 10−12 | 3.27 × 10−13 | |
| G26 | 1.70 × 10−12 | 5.08 × 10−12 | 9.83 × 10−13 | 4.55 × 10-13 | 1.57 × 10−13 | 3.75 × 10−13 | |
| G29 | 9.90 × 10−12 | 3.58 × 10−12 | 2.61 × 10−12 | 2.24 × 10−12 | 6.45 × 10−13 | 2.05 × 10−13 | |
| G31 | 8.90 × 10−12 | 3.75 × 10−12 | 2.27 × 10−12 | 1.60 × 10−12 | 6.91 × 10−13 | 5.07 × 10−13 | |
| G05 | 9.24 × 10−12 | 3.86 × 10−12 | 2.76 × 10−12 | 2.20 × 10−12 | 9.91 × 10−13 | 3.92 × 10−13 | |
| Ultra-Rapid | G16 | 7.36 × 10−12 | 2.94 × 10−12 | 2.43 × 10−12 | 1.99 × 10−12 | 6.04 × 10−13 | 1.93 × 10−13 |
| G20 | 7.52 × 10−12 | 3.01 × 10−12 | 2.59 × 10−12 | 2.07 × 10−12 | 8.84 × 10−13 | 2.95 × 10−13 | |
| G27 | 7.67 × 10−12 | 3.17 × 10−12 | 8.34 × 10−13 | 3.07 × 10−13 | 1.18 × 10−13 | 8.05 × 10−13 | |
| G18 | 8.76 × 10−12 | 3.51 × 10−12 | 3.12 × 10−12 | 3.41 × 10−12 | 1.03 × 10−12 | 1.88 × 10−13 | |
| G26 | 1.73 × 10−11 | 5.01 × 10−12 | 9.71 × 10−13 | 4.43 × 10-13 | 1.82 × 10−13 | 1.42 × 10−13 | |
| G29 | 8.31 × 10−12 | 3.32 × 10−12 | 2.31 × 10−12 | 1.75 × 10−12 | 7.33 × 10−13 | 7.28 × 10−13 | |
| G31 | 9.05 × 10−12 | 3.61 × 10−12 | 2.50 × 10−12 | 1.88 × 10−12 | 7.56 × 10−13 | 2.63 × 10−13 | |
| G05 | 9.49 × 10−12 | 4.04 × 10−12 | 2.76 × 10−12 | 2.03 × 10−12 | 9.72 × 10−13 | 4.22 × 10−13 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maciuk, K.; Lewińska, P. High-Rate Monitoring of Satellite Clocks Using Two Methods of Averaging Time. Remote Sens. 2019, 11, 2754. https://doi.org/10.3390/rs11232754
Maciuk K, Lewińska P. High-Rate Monitoring of Satellite Clocks Using Two Methods of Averaging Time. Remote Sensing. 2019; 11(23):2754. https://doi.org/10.3390/rs11232754
Chicago/Turabian StyleMaciuk, Kamil, and Paulina Lewińska. 2019. "High-Rate Monitoring of Satellite Clocks Using Two Methods of Averaging Time" Remote Sensing 11, no. 23: 2754. https://doi.org/10.3390/rs11232754
APA StyleMaciuk, K., & Lewińska, P. (2019). High-Rate Monitoring of Satellite Clocks Using Two Methods of Averaging Time. Remote Sensing, 11(23), 2754. https://doi.org/10.3390/rs11232754