Modified Search Strategies Assisted Crossover Whale Optimization Algorithm with Selection Operator for Parameter Extraction of Solar Photovoltaic Models
Abstract
:1. Introduction
- (1)
- An improved variant of WOA, i.e., MCSWOA, is presented to parameter extraction of PV models. In MCSWOA, three improved components, including two modified search strategies, a crossover operator, and a selection operator are developed and integrated well to enhance its performance.
- (2)
- MCSWOA is applied to five PV types, including RTC France cell, Photowatt-PWP201 module, STM6-40/36 module, STP6-120/36 module, and Sharp ND-R250A5 module. Both SDM and DDM are used to model these five PV types.
- (3)
- The good performance of MCSWOA in extracting accurate parameters of PV models is fully verified through comparison with other 31 algorithms in terms of the parameter accuracy, convergence speed, robustness, and statistics.
2. Problem Formulation
2.1. Single Diode Model (SDM)
2.2. Double Diode Model (DDM)
2.3. PV Module Model
2.4. Objective Function
3. Whale Optimization Algorithm
4. The Proposed MCSWOA
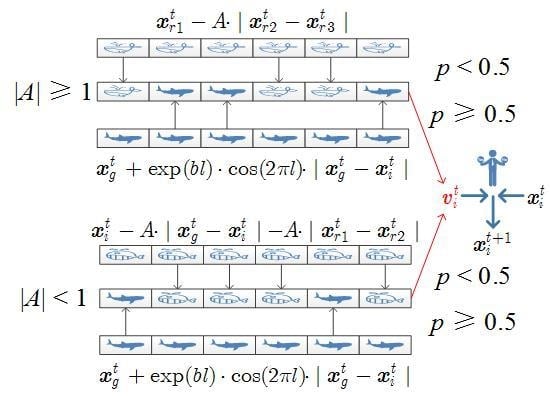
4.1. Modified Search Strategies
4.2. Modified Search Strategies Assisted Crossover Operator
4.3. Selection Operator
4.4. The Main Procedure of MCSWOA
| Algorithm 1: The main procedure of MCSWOA | |
| 1: | Generate a random initial population |
| 2: | Evaluate the fitness for each individual |
| 3: | Select the best individual and set it as |
| 4: | Initialize the iteration counter |
| 5: | While the stopping condition is not satisfied do |
| 6: | for to do |
| 7: | Update , , and |
| 8: | for to do |
| 9: | Update |
| 10: | if then |
| 11: | Select three random individuals |
| 12: | if then |
| 13: | |
| 14: | else |
| 15: | |
| 16: | end if |
| 17: | else |
| 18: | |
| 19: | end if |
| 20: | end for |
| 21: | end for |
| 22: | Evaluate the fitness for each donor individual |
| 23: | for to do |
| 24: | if then |
| 25: | |
| 26: | else |
| 27: | |
| 28: | end if |
| 29: | end for |
| 30: | Select the best individual of the updated population |
| 31: | if then |
| 32: | |
| 33: | else |
| 34: | |
| 35: | end if |
| 36: | |
| 37: | End while |
5. Experimental Results
5.1. Test Cases
5.2. Experimental Settings
5.3. Experimental Results
5.3.1. Comparison of MCSWOA with WOA
5.3.2. The Benefit of MCSWOA Components
5.3.3. Comparison with Advanced WOA Variants
5.3.4. Comparison with Advanced Non−WOA Variants
6. Discussions
- (1)
- MCSWOA obtains better results on most of the cases except Case 4, which can be explained by the no free lunch theorem [52]. According to the theorem, there is no “one size fits all” method that always wins all cases.
- (2)
- The convergence curves show that MCSWOA converges the fastest overall throughout the whole evolutionary process, which indicates that it achieves an excellent balance between exploration and exploitation.
- (3)
- The crossover operator contributes the most to MCSWOA, followed by the selection operator and modified search strategies. Nevertheless, each component is indispensable, and missing anyone will deteriorate the performance MCSWOA significantly.
- (4)
- Comparing the results of SDM and DDM, it concludes that not every equivalent circuit model is suitable for every PV type. Notwithstanding, the differences are very small. In addition, the DDM is harder to optimize under the same stopping condition (i.e., the same value of Max_FEs) because it has seven unknown parameters whereas the SDM has only five.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hayat, M.B.; Ali, D.; Monyake, K.C.; Alagha, L.; Ahmed, N. Solar energy—A look into power generation, challenges, and a solar-powered future. Int. J. Energy Res. 2019, 43, 1049–1067. [Google Scholar] [CrossRef]
- Islam, M.R.; Mahfuz-Ur-Rahman, A.M.; Muttaqi, K.M.; Sutanto, D. State-of-the-Art of the Medium-Voltage Power Converter Technologies for Grid Integration of Solar Photovoltaic Power Plants. IEEE Trans. Energy Conver. 2019, 34, 372–384. [Google Scholar] [CrossRef]
- National Energy Administration. Introduction to the Operation of Grid Connected Renewable Energy in the First Quarter of 2019. Available online: http://www.nea.gov.cn/2019-04/29/c_138021561.htm (accessed on 25 May 2019). (In Chinese)
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H.; Shamsudin, A. A critical evaluation of EA computational methods for Photovoltaic cell parameter extraction based on two diode model. Sol. Energy 2011, 85, 1768–1779. [Google Scholar] [CrossRef]
- Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Wang, Z.; Qu, J.; Wang, H. Parameter extraction of solar cell models using improved shuffled complex evolution algorithm. Energy Convers. Manag. 2018, 157, 460–479. [Google Scholar] [CrossRef]
- Gomes, R.C.M.; Vitorino, M.A.; Fernandes, D.A.; Wang, R. Shuffled Complex Evolution on Photovoltaic Parameter Extraction: A Comparative Analysis. IEEE Trans. Sustain Energy 2016, 8, 805–815. [Google Scholar] [CrossRef]
- Yeh, W.C.; Huang, C.L.; Lin, P.; Chen, Z.; Jiang, Y.; Sun, B. Simplex Simplified Swarm Optimization for the Efficient Optimization of Parameter Identification for Solar Cell Models. IET Renew. Power Gen. 2018, 12, 45–51. [Google Scholar] [CrossRef]
- Rezaee Jordehi, A. Enhanced leader particle swarm optimisation (ELPSO): An efficient algorithm for parameter estimation of photovoltaic (PV) cells and modules. Sol. Energy 2018, 159, 78–87. [Google Scholar] [CrossRef]
- Nunes, H.G.G.; Pombo, J.A.N.; Mariano, S.J.P.S.; Calado, M.R.A.; Souza, J.A.M.F. A new high performance method for determining the parameters of PV cells and modules based on guaranteed convergence particle swarm optimization. Appl. Energy 2018, 211, 774–791. [Google Scholar] [CrossRef]
- Ma, J.; Man, K.L.; Guan, S.U.; Ting, T.O.; Wong, P.W.H. Parameter estimation of photovoltaic model via parallel particle swarm optimization algorithm. Int. J. Energy Res. 2016, 40, 343–352. [Google Scholar] [CrossRef]
- Muangkote, N.; Sunat, K.; Chiewchanwattana, S.; Kaiwinit, S. An advanced onlooker-ranking-based adaptive differential evolution to extract the parameters of solar cell models. Renew. Energy 2019, 134, 1129–1147. [Google Scholar] [CrossRef]
- Chen, X.; Yu, K.; Du, W.; Zhao, W.; Liu, G. Parameters identification of solar cell models using generalized oppositional teaching learning based optimization. Energy 2016, 99, 170–180. [Google Scholar] [CrossRef]
- Yu, K.; Chen, X.; Wang, X.; Wang, Z. Parameters identification of photovoltaic models using self-adaptive teaching-learning-based optimization. Energy Convers. Manag. 2017, 145, 233–246. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Shi, D.; Yuan, X. Application of Supply-Demand-Based Optimization for Parameter Extraction of Solar Photovoltaic Models. Complexity 2019, 2019, 3923691. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Yuan, X.; Shi, D.; He, Y. Application of Symbiotic Organisms Search Algorithm for Parameter Extraction of Solar Cell Models. Appl. Sci. 2018, 8, 2155. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.J.; Qu, B.Y.; Chen, X.; Wang, H. Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Convers. Manag. 2017, 150, 742–753. [Google Scholar] [CrossRef]
- Oliva, D.; Ewees, A.A.; Aziz, M.A.E.; Hassanien, A.E.; Cisneros, M.P. A Chaotic Improved Artificial Bee Colony for Parameter Estimation of Photovoltaic Cells. Energies 2017, 10, 865. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. Parameter estimation of photovoltaic system using imperialist competitive algorithm. Renew. Energy 2017, 111, 307–320. [Google Scholar] [CrossRef]
- Benkercha, R.; Moulahoum, S.; Taghezouit, B. Extraction of the PV modules parameters with MPP estimation using the modified flower algorithm. Renew. Energy 2019, 143, 1698–1709. [Google Scholar] [CrossRef]
- Ram, J.P.; Babu, T.S.; Dragicevic, T.; Rajasekar, N. A new hybrid bee pollinator flower pollination algorithm for solar PV parameter estimation. Energy Convers. Manag. 2017, 135, 463–476. [Google Scholar] [CrossRef]
- Mughal, M.A.; Ma, Q.; Xiao, C. Photovoltaic Cell Parameter Estimation Using Hybrid Particle Swarm Optimization and Simulated Annealing. Energies 2017, 10, 1213. [Google Scholar] [CrossRef]
- Muhsen, D.H.; Ghazali, A.B.; Khatib, T.; Abed, I.A. Extraction of photovoltaic module model’s parameters using an improved hybrid differential evolution/electromagnetism−like algorithm. Sol. Energy 2015, 119, 286–297. [Google Scholar] [CrossRef]
- Chen, X.; Xu, B.; Mei, C.; Ding, Y.; Li, K. Teaching–learning–based artificial bee colony for solar photovoltaic parameter estimation. Appl. Energy 2018, 212, 1578–1588. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Oliva, D.; Aziz, M.A.E.; Hassanien, A.E. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 2017, 200, 141–154. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Oliva, D. Parameter estimation of solar cells diode models by an improved opposition-based whale optimization algorithm. Energy Convers. Manag. 2018, 171, 1843–1859. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Shi, D.; He, Y. Parameter extraction of solar photovoltaic models using an improved whale optimization algorithm. Energy Convers. Manag. 2018, 174, 388–405. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Yuan, X.; Shi, D.; He, Y.; Yao, G. Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm. Sol. Energy 2018, 176, 742–761. [Google Scholar] [CrossRef]
- Muhsen, D.H.; Ghazali, A.B.; Khatib, T.; Abed, I.A. A comparative study of evolutionary algorithms and adapting control parameters for estimating the parameters of a single-diode photovoltaic module’s model. Renew. Energy 2016, 96, 377–389. [Google Scholar] [CrossRef]
- Kichou, S.; Silvestre, S.; Guglielminotti, L.; Mora-López, L.; Muñoz-Cerón, E. Comparison of two PV array models for the simulation of PV systems using five different algorithms for the parameters identification. Renew. Energy 2016, 99, 270–279. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yu, K.; Qu, B.; Yue, C.; Ge, S.; Chen, X.; Liang, J. A performance-guided JAYA algorithm for parameters identification of photovoltaic cell and module. Appl. Energy 2019, 237, 241–257. [Google Scholar] [CrossRef]
- Prasad, D.; Mukherjee, A.; Shankar, G.; Mukherjee, V. Application of chaotic whale optimization algorithm for transient stability constrained optimal power flow. IET Sci. Meas. Technol. 2017, 11, 1002–1013. [Google Scholar] [CrossRef]
- Venkata Krishna, J.; Apparao Naidu, G.; Upadhayaya, N. A Lion-Whale optimization-based migration of virtual machines for data centers in cloud computing. Int. J. Commun. Syst. 2018, 31, e3539. [Google Scholar] [CrossRef]
- Ling, Y.; Zhou, Y.; Luo, Q. Lévy flight trajectory-based whale optimization algorithm for global optimization. IEEE Access 2017, 5, 6168–6186. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, X.; Chen, Y.; Liu, Z. A modified whale optimization algorithm for large-scale global optimization problems. Expert Syst. Appl. 2018, 114, 563–577. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Jangir, P.; Kumar, A.; Jangir, N.; Totlani, R. A novel hybrid PSO-WOA algorithm for global numerical functions optimization. In Advances in Computer and Computational Sciences; Bhatia, S., Mishra, K., Tiwari, S., Singh, V., Eds.; Springer: Singapore, 2018; Volume 554. [Google Scholar]
- El-Amary, N.H.; Balbaa, A.; Swief, R.; Abdel-Salam, T. A reconfigured whale optimization technique (RWOT) for renewable electrical energy optimal scheduling impact on sustainable development applied to Damietta seaport, Egypt. Energies 2018, 11, 535. [Google Scholar] [CrossRef] [Green Version]
- Reddy, M.P.K.; Babu, M.R. Implementing self adaptiveness in whale optimization for cluster head section in Internet of Things. Clust. Comput. 2017, 22, 1–12. [Google Scholar] [CrossRef]
- Mafarja, M.; Mirjalili, S. Whale optimization approaches for wrapper feature selection. Appl. Soft Comput. 2018, 62, 441–453. [Google Scholar] [CrossRef]
- Abed-alguni, B.H.; Klaib, A.F. Hybrid Whale Optimization and β-hill Climbing Algorithm for Continuous Optimization Problems. Int. J. Comput. Sci. Math. 2019, in press. [Google Scholar]
- Chen, X.; Tianfield, H.; Mei, C.; Du, W.; Liu, G. Biogeography-based learning particle swarm optimization. Soft Comput. 2017, 21, 7519–7541. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A competitive swarm optimizer for large scale optimization. IEEE Trans. Cybern. 2015, 42, 191–204. [Google Scholar] [CrossRef]
- Boussaïd, I.; Chatterjee, A.; Siarry, P.; Ahmed-Nacer, M. Two-stage update biogeography-based optimization using differential evolution algorithm (DBBO). Comput. Oper. Res. 2011, 38, 1188–1198. [Google Scholar] [CrossRef]
- Gong, W.; Cai, Z.; Ling, C. DE/BBO: A hybrid differential evolution with biogeography-based optimization for global numerical optimization. Soft Comput. 2010, 15, 645–665. [Google Scholar] [CrossRef] [Green Version]
- Zou, F.; Wang, L.; Hei, X.; Chen, D. Teaching-learning-based optimization with learning experience of other learners and its application. Appl. Soft Comput. 2015, 37, 725–736. [Google Scholar] [CrossRef]
- Gao, W.; Liu, S. A modified artificial bee colony algorithm. Comput. Oper. Res. 2012, 39, 687–697. [Google Scholar] [CrossRef]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M. Opposition-based differential evolution. IEEE Trans. Evol. Comput. 2008, 12, 64–79. [Google Scholar] [CrossRef] [Green Version]
- Cheng, R.; Jin, Y. A social learning particle swarm optimization algorithm for scalable optimization. Inf. Sci. 2015, 291, 43–60. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]








| Case | PV Type | Number of Cells (Ns × Np) | Irradiance (W/m2) | Temperature (°C) | PV model |
|---|---|---|---|---|---|
| 1/2 | RTC France cell | 1 × 1 | 1000 | 33 | SDM/DDM |
| 3/4 | Photowatt-PWP201 module | 36 × 1 | 1000 | 45 | SDM/DDM |
| 5/6 | STM6-40/36 module | 36 × 1 | NA | 51 | SDM/DDM |
| 7/8 | STP6-120/36 module | 36 × 1 | NA | 55 | SDM/DDM |
| 9/10 | Sharp ND-R250A5 module | 60 × 1 | 1040 | 59 | SDM/DDM |
| Parameter | RTC France Cell | Photowatt-PWP201 Module | STM6-40/36 Module | STP6-120/36 Module | Sharp ND-R250A5 Module | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| LB | UB | LB | UB | LB | UB | LB | UB | LB | UB | |
| Iph (A) | 0 | 1 | 0 | 2 | 0 | 2 | 0 | 8 | 0 | 10 |
| Isd (µA) | 0 | 1 | 0 | 50 | 0 | 50 | 0 | 50 | 0 | 10 |
| Rs (Ω) | 0 | 0.5 | 0 | 2 | 0 | 0.36 | 0 | 0.36 | 0 | 2 |
| Rsh (Ω) | 0 | 100 | 0 | 2000 | 0 | 1000 | 0 | 1500 | 0 | 5000 |
| n, n1, n2 | 1 | 2 | 1 | 50 | 1 | 60 | 1 | 50 | 1 | 50 |
| Case | Algorithm | Min | Max | Mean | Std. Dev. |
|---|---|---|---|---|---|
| 1 | WOA | 1.0395 × 10−3 | 1.1528 × 10−2 | 3.3118 × 10−3 | 2.5700 × 10−3 |
| MCSWOA | 9.8602 × 10−4 | 9.8603 × 10−4 | 9.8602 × 10−4 | 4.8373 × 10−10 | |
| 2 | WOA | 1.0381 × 10−3 | 1.3797 × 10−2 | 3.6217 × 10−3 | 2.7791 × 10−3 |
| MCSWOA | 9.8250 × 10−4 | 1.1903 × 10−3 | 1.0078 × 10−3 | 3.7264 × 10−5 | |
| 3 | WOA | 2.4991 × 10−3 | 4.9837 × 10−2 | 9.6733 × 10−3 | 1.1794 × 10−2 |
| MCSWOA | 2.4251 × 10−3 | 2.4270 × 10−3 | 2.4252 × 10−3 | 3.2927 × 10−7 | |
| 4 | WOA | 2.4270 × 10−3 | 7.5526 × 10−2 | 2.4505 × 10−2 | 2.2337 × 10−2 |
| MCSWOA | 2.4251 × 10−3 | 2.4881 × 10−3 | 2.4377 × 10−3 | 1.3424 × 10−5 | |
| 5 | WOA | 2.9904 × 10−3 | 3.1090 × 10−1 | 2.8343 × 10−2 | 6.0554 × 10−2 |
| MCSWOA | 1.7298 × 10−3 | 1.7364 × 10−3 | 1.7311 × 10−3 | 1.0774 × 10−6 | |
| 6 | WOA | 3.3265 × 10−3 | 4.8619 × 10−2 | 1.2171 × 10−2 | 8.5449 × 10−3 |
| MCSWOA | 1.7061 × 10−3 | 1.7358 × 10−3 | 1.7296 × 10−3 | 5.4724 × 10−6 | |
| 7 | WOA | 1.6759 × 10−2 | 1.4164 | 1.3390 × 10−1 | 3.3374 × 10−1 |
| MCSWOA | 1.6601 × 10−2 | 1.6741 × 10−2 | 1.6632 × 10−2 | 2.6486 × 10−5 | |
| 8 | WOA | 1.7345 × 10−2 | 5.6762 × 10−2 | 3.8581 × 10−2 | 1.1413 × 10−2 |
| MCSWOA | 1.6601 × 10−2 | 1.6732 × 10−2 | 1.6640 × 10−2 | 2.8956 × 10−5 | |
| 9 | WOA | 1.1206 × 10−2 | 2.1439 | 1.9117 × 10−1 | 5.2271 × 10−1 |
| MCSWOA | 1.1183 × 10−2 | 1.1244 × 10−2 | 1.1187 × 10−2 | 9.1358 × 10−6 | |
| 10 | WOA | 1.1233 × 10−2 | 5.1709 × 10−2 | 3.4638 × 10−2 | 1.2972 × 10−2 |
| MCSWOA | 1.1183 × 10−2 | 1.1220 × 10−2 | 1.1190 × 10−2 | 8.4623 × 10−6 |
| Case | Iph (A) | Isd1 (µA) | Rs (Ω) | Rsh (Ω) | n1 | Isd2 (µA) | n2 | RMSE |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.7608 | 0.3230 | 0.0364 | 53.7185 | 1.4812 | — | — | 9.8602 × 10−4 |
| 2 | 0.7608 | 0.2206 | 0.0368 | 53.6255 | 1.4490 | 0.7974 | 2.0000 | 9.8250 × 10−4 |
| 3 | 1.0305 | 3.4822 | 1.2013 | 981.9585 | 48.6428 | — | — | 2.4251 × 10−3 |
| 4 | 1.0305 | 0.3648 | 1.2017 | 976.2658 | 48.6426 | 3.1036 | 48.6377 | 2.4251 × 10−3 |
| 5 | 1.6639 | 1.7390 | 0.0043 | 15.9294 | 1.5203 | — | — | 1.7298 × 10−3 |
| 6 | 1.6639 | 0.6103 | 0.0054 | 16.9519 | 1.4224 | 11.7629 | 2.1992 | 1.7061 × 10−3 |
| 7 | 7.4727 | 2.3300 | 0.0046 | 21.9831 | 1.2599 | — | — | 1.6601 × 10−2 |
| 8 | 7.4722 | 2.3466 | 0.0046 | 22.9095 | 1.2605 | 4.8598 | 49.5302 | 1.6601 × 10−2 |
| 9 | 9.1431 | 1.1142 | 0.0098 | 5000 | 1.2150 | — | — | 1.1183 × 10−2 |
| 10 | 9.1431 | 1.1142 | 0.0098 | 5000 | 1.2150 | 5.3615 × 10−9 | 45.2483 | 1.1183 × 10−2 |
| Item | VL (V) | IL Measured (A) | SDM (Case 1) | DDM (Case 2) | ||
|---|---|---|---|---|---|---|
| IL Calculated (A) | IAE (A) | IL Calculated (A) | IAE (A) | |||
| 1 | −0.2057 | 0.7640 | 0.76408765 | 0.00008765 | 0.76397504 | 0.00002496 |
| 2 | −0.1291 | 0.7620 | 0.76266264 | 0.00066264 | 0.76259878 | 0.00059878 |
| 3 | −0.0588 | 0.7605 | 0.76135473 | 0.00085473 | 0.76133540 | 0.00083540 |
| 4 | 0.0057 | 0.7605 | 0.76015424 | 0.00034576 | 0.76017516 | 0.00032484 |
| 5 | 0.0646 | 0.7600 | 0.75905594 | 0.00094406 | 0.75911205 | 0.00088795 |
| 6 | 0.1185 | 0.7590 | 0.75804334 | 0.00095666 | 0.75812819 | 0.00087181 |
| 7 | 0.1678 | 0.7570 | 0.75709159 | 0.00009159 | 0.75719567 | 0.00019567 |
| 8 | 0.2132 | 0.7570 | 0.75614207 | 0.00085793 | 0.75625201 | 0.00074799 |
| 9 | 0.2545 | 0.7555 | 0.75508732 | 0.00041268 | 0.75518481 | 0.00031519 |
| 10 | 0.2924 | 0.7540 | 0.75366447 | 0.00033553 | 0.75372792 | 0.00027208 |
| 11 | 0.3269 | 0.7505 | 0.75138806 | 0.00088806 | 0.75139769 | 0.00089769 |
| 12 | 0.3585 | 0.7465 | 0.74734834 | 0.00084834 | 0.74729341 | 0.00079341 |
| 13 | 0.3873 | 0.7385 | 0.74009688 | 0.00159688 | 0.73998455 | 0.00148455 |
| 14 | 0.4137 | 0.7280 | 0.72739678 | 0.00060322 | 0.72725566 | 0.00074434 |
| 15 | 0.4373 | 0.7065 | 0.70695328 | 0.00045328 | 0.70682698 | 0.00032698 |
| 16 | 0.4590 | 0.6755 | 0.67529492 | 0.00020508 | 0.67522445 | 0.00027555 |
| 17 | 0.4784 | 0.6320 | 0.63088433 | 0.00111567 | 0.63088651 | 0.00111349 |
| 18 | 0.4960 | 0.5730 | 0.57208208 | 0.00091792 | 0.57214313 | 0.00085687 |
| 19 | 0.5119 | 0.4990 | 0.49949167 | 0.00049167 | 0.49957540 | 0.00057540 |
| 20 | 0.5265 | 0.4130 | 0.41349364 | 0.00049364 | 0.41356073 | 0.00056073 |
| 21 | 0.5398 | 0.3165 | 0.31721950 | 0.00071950 | 0.31724418 | 0.00074418 |
| 22 | 0.5521 | 0.2120 | 0.21210317 | 0.00010317 | 0.21208087 | 0.00008087 |
| 23 | 0.5633 | 0.1035 | 0.10272136 | 0.00077864 | 0.10266905 | 0.00083095 |
| 24 | 0.5736 | −0.0100 | −0.00924878 | 0.00075122 | −0.00929990 | 0.00070010 |
| 25 | 0.5833 | −0.1230 | −0.12438136 | 0.00138136 | −0.12439111 | 0.00139111 |
| 26 | 0.5900 | −0.2100 | −0.20919308 | 0.00080692 | −0.20914456 | 0.00085544 |
| SIAE of MCSWOA | 0.01770381 | 0.01730633 | ||||
| SIAE of WOA | 0.01928659 | 0.01876701 | ||||
| Item | VL (V) | IL Measured (A) | SDM (Case 3) | DDM (Case 4) | ||
|---|---|---|---|---|---|---|
| IL Calculated (A) | IAE (A) | IL Calculated (A) | IAE (A) | |||
| 1 | 0.1248 | 1.0315 | 1.02912301 | 0.00237699 | 1.02914976 | 0.00235024 |
| 2 | 1.8093 | 1.0300 | 1.02738443 | 0.00261557 | 1.02740128 | 0.00259872 |
| 3 | 3.3511 | 1.0260 | 1.02574218 | 0.00025782 | 1.02575007 | 0.00024993 |
| 4 | 4.7622 | 1.0220 | 1.02410400 | 0.00210400 | 1.02410397 | 0.00210397 |
| 5 | 6.0538 | 1.0180 | 1.02228339 | 0.00428339 | 1.02227663 | 0.00427663 |
| 6 | 7.2364 | 1.0155 | 1.01991736 | 0.00441736 | 1.01990537 | 0.00440537 |
| 7 | 8.3189 | 1.0140 | 1.01635076 | 0.00235076 | 1.01633550 | 0.00233550 |
| 8 | 9.3097 | 1.0100 | 1.01049137 | 0.00049137 | 1.01047529 | 0.00047529 |
| 9 | 10.2163 | 1.0035 | 1.00067872 | 0.00282128 | 1.00066456 | 0.00283544 |
| 10 | 11.0449 | 0.9880 | 0.98465339 | 0.00334661 | 0.98464377 | 0.00335623 |
| 11 | 11.8018 | 0.9630 | 0.95969770 | 0.00330230 | 0.95969440 | 0.00330560 |
| 12 | 12.4929 | 0.9255 | 0.92304878 | 0.00245122 | 0.92305206 | 0.00244794 |
| 13 | 13.1231 | 0.8725 | 0.87258820 | 0.00008820 | 0.87259659 | 0.00009659 |
| 14 | 13.6983 | 0.8075 | 0.80731017 | 0.00018983 | 0.80732090 | 0.00017910 |
| 15 | 14.2221 | 0.7265 | 0.72795786 | 0.00145786 | 0.72796791 | 0.00146791 |
| 16 | 14.6995 | 0.6345 | 0.63646667 | 0.00196667 | 0.63647370 | 0.00197370 |
| 17 | 15.1346 | 0.5345 | 0.53569608 | 0.00119608 | 0.53569897 | 0.00119897 |
| 18 | 15.5311 | 0.4275 | 0.42881624 | 0.00131624 | 0.42881506 | 0.00131506 |
| 19 | 15.8929 | 0.3185 | 0.31866863 | 0.00016863 | 0.31866436 | 0.00016436 |
| 20 | 16.2229 | 0.2085 | 0.20785708 | 0.00064292 | 0.20785117 | 0.00064883 |
| 21 | 16.5241 | 0.1010 | 0.09835419 | 0.00264581 | 0.09834825 | 0.00265175 |
| 22 | 16.7987 | −0.0080 | −0.00816923 | 0.00016923 | −0.00817364 | 0.00017364 |
| 23 | 17.0499 | −0.1110 | −0.11096847 | 0.00003153 | −0.11096996 | 0.00003004 |
| 24 | 17.2793 | −0.2090 | −0.20911761 | 0.00011761 | −0.20911505 | 0.00011505 |
| 25 | 17.4885 | −0.3030 | −0.30202234 | 0.00097766 | −0.30201487 | 0.00098513 |
| SIAE of MCSWOA | 0.04178694 | 0.04174098 | ||||
| SIAE of WOA | 0.04521107 | 0.04308364 | ||||
| Item | VL (V) | IL Measured (A) | SDM (Case 5) | DDM (Case 6) | ||
|---|---|---|---|---|---|---|
| IL Calculated (A) | IAE (A) | IL Calculated (A) | IAE (A) | |||
| 1 | 0.0000 | 1.6630 | 1.66345754 | 0.00045754 | 1.66335653 | 0.00035653 |
| 2 | 0.1180 | 1.6630 | 1.66325166 | 0.00025166 | 1.66316242 | 0.00016242 |
| 3 | 2.2370 | 1.6610 | 1.65955087 | 0.00144913 | 1.65966539 | 0.00133461 |
| 4 | 5.4340 | 1.6530 | 1.65391451 | 0.00091451 | 1.65427645 | 0.00127645 |
| 5 | 7.2600 | 1.6500 | 1.65056604 | 0.00056604 | 1.65099325 | 0.00099325 |
| 6 | 9.6800 | 1.6450 | 1.64543105 | 0.00043105 | 1.64576715 | 0.00076715 |
| 7 | 11.5900 | 1.6400 | 1.63923502 | 0.00076498 | 1.63929611 | 0.00070389 |
| 8 | 12.6000 | 1.6360 | 1.63371634 | 0.00228366 | 1.63357235 | 0.00242765 |
| 9 | 13.3700 | 1.6290 | 1.62728896 | 0.00171104 | 1.62699263 | 0.00200737 |
| 10 | 14.0900 | 1.6190 | 1.61831553 | 0.00068447 | 1.61791078 | 0.00108922 |
| 11 | 14.8800 | 1.5970 | 1.60306755 | 0.00606755 | 1.60262830 | 0.00562830 |
| 12 | 15.5900 | 1.5810 | 1.58158496 | 0.00058496 | 1.58123166 | 0.00023166 |
| 13 | 16.4000 | 1.5420 | 1.54232802 | 0.00032802 | 1.54223011 | 0.00023011 |
| 14 | 16.7100 | 1.5240 | 1.52122491 | 0.00277509 | 1.52126131 | 0.00273869 |
| 15 | 16.9800 | 1.5000 | 1.49920537 | 0.00079463 | 1.49936328 | 0.00063672 |
| 16 | 17.1300 | 1.4850 | 1.48527079 | 0.00027079 | 1.48549479 | 0.00049479 |
| 17 | 17.3200 | 1.4650 | 1.46564287 | 0.00064287 | 1.46594489 | 0.00094489 |
| 18 | 17.9100 | 1.3880 | 1.38759918 | 0.00040082 | 1.38804424 | 0.00004424 |
| 19 | 19.0800 | 1.1180 | 1.11837322 | 0.00037322 | 1.11798671 | 0.00001329 |
| 20 | 21.0200 | 0.0000 | −0.00002144 | 0.00002144 | 0.00002509 | 0.00002509 |
| SIAE of MCSWOA | 0.02177346 | 0.02210631 | ||||
| SIAE of WOA | 0.04187370 | 0.04245192 | ||||
| Item | VL (V) | IL Measured (A) | SDM (Case 7) | DDM (Case 8) | ||
|---|---|---|---|---|---|---|
| IL Calculated (A) | IAE (A) | IL Calculated (A) | IAE (A) | |||
| 1 | 19.2100 | 0.0000 | 0.00117621 | 0.00117621 | 0.00114264 | 0.00114264 |
| 2 | 17.6500 | 3.8300 | 3.83225520 | 0.00225520 | 3.83236037 | 0.00236037 |
| 3 | 17.4100 | 4.2900 | 4.27391075 | 0.01608925 | 4.27398800 | 0.01601200 |
| 4 | 17.2500 | 4.5600 | 4.54627802 | 0.01372198 | 4.54633438 | 0.01366562 |
| 5 | 17.1000 | 4.7900 | 4.78582746 | 0.00417254 | 4.78586359 | 0.00413641 |
| 6 | 16.9000 | 5.0700 | 5.08193661 | 0.01193661 | 5.08194603 | 0.01194603 |
| 7 | 16.7600 | 5.2700 | 5.27377339 | 0.00377339 | 5.27376501 | 0.00376501 |
| 8 | 16.3400 | 5.7500 | 5.77683588 | 0.02683588 | 5.77678272 | 0.02678272 |
| 9 | 16.0800 | 6.0000 | 6.03752035 | 0.03752035 | 6.03744819 | 0.03744819 |
| 10 | 15.7100 | 6.3600 | 6.34875976 | 0.01124024 | 6.34867349 | 0.01132651 |
| 11 | 15.3900 | 6.5800 | 6.56796191 | 0.01203809 | 6.56787501 | 0.01212499 |
| 12 | 14.9300 | 6.8300 | 6.81488832 | 0.01511168 | 6.81481542 | 0.01518458 |
| 13 | 14.5800 | 6.9700 | 6.95847149 | 0.01152851 | 6.95841712 | 0.01158288 |
| 14 | 14.1700 | 7.1000 | 7.08815167 | 0.01184833 | 7.08812304 | 0.01187696 |
| 15 | 13.5900 | 7.2300 | 7.21776382 | 0.01223618 | 7.21777158 | 0.01222842 |
| 16 | 13.1600 | 7.2900 | 7.28412533 | 0.00587467 | 7.28415609 | 0.00584391 |
| 17 | 12.7400 | 7.3400 | 7.33147260 | 0.00852740 | 7.33152077 | 0.00847923 |
| 18 | 12.3600 | 7.3700 | 7.36325038 | 0.00674962 | 7.36330957 | 0.00669043 |
| 19 | 11.8100 | 7.3800 | 7.39585537 | 0.01585537 | 7.39592269 | 0.01592269 |
| 20 | 11.1700 | 7.4100 | 7.42024640 | 0.01024640 | 7.42031281 | 0.01031281 |
| 21 | 10.3200 | 7.4400 | 7.43907657 | 0.00092343 | 7.43912820 | 0.00087180 |
| 22 | 9.7400 | 7.4200 | 7.44670325 | 0.02670325 | 7.44673825 | 0.02673825 |
| 23 | 9.0600 | 7.4500 | 7.45253188 | 0.00253188 | 7.45254265 | 0.00254265 |
| 24 | 0.0000 | 7.4800 | 7.47109229 | 0.00890771 | 7.47066044 | 0.00933956 |
| SIAE of MCSWOA | 0.27780418 | 0.27832466 | ||||
| SIAE of WOA | 0.28272891 | 0.28498596 | ||||
| Item | VL (V) | IL Measured (A) | SDM (Case 9) | DDM (Case 10) | ||
|---|---|---|---|---|---|---|
| IL Calculated (A) | IAE (A) | IL Calculated (A) | IAE (A) | |||
| 1 | 0.0000 | 9.1500 | 9.14302743 | 0.00697257 | 9.14302768 | 0.00697232 |
| 2 | 7.7100 | 9.1400 | 9.14242378 | 0.00242378 | 9.14242403 | 0.00242403 |
| 3 | 10.9800 | 9.1200 | 9.14016661 | 0.02016661 | 9.14016685 | 0.02016685 |
| 4 | 14.5500 | 9.1100 | 9.12733899 | 0.01733899 | 9.12733920 | 0.01733920 |
| 5 | 16.3600 | 9.1000 | 9.10594093 | 0.00594093 | 9.10594110 | 0.00594110 |
| 6 | 18.0000 | 9.0700 | 9.06266719 | 0.00733281 | 9.06266730 | 0.00733270 |
| 7 | 19.1500 | 9.0200 | 9.00583091 | 0.01416909 | 9.00583095 | 0.01416905 |
| 8 | 20.0400 | 8.9500 | 8.93692097 | 0.01307903 | 8.93692095 | 0.01307905 |
| 9 | 20.8700 | 8.8600 | 8.84418281 | 0.01581719 | 8.84418274 | 0.01581726 |
| 10 | 21.6700 | 8.7300 | 8.71970414 | 0.01029586 | 8.71970401 | 0.01029599 |
| 11 | 22.3600 | 8.5800 | 8.57706890 | 0.00293110 | 8.57706873 | 0.00293127 |
| 12 | 23.0200 | 8.4000 | 8.40362835 | 0.00362835 | 8.40362815 | 0.00362815 |
| 13 | 23.6200 | 8.2000 | 8.20979996 | 0.00979996 | 8.20979975 | 0.00979975 |
| 14 | 24.1500 | 8.0000 | 8.00692218 | 0.00692218 | 8.00692197 | 0.00692197 |
| 15 | 24.6100 | 7.8000 | 7.80514823 | 0.00514823 | 7.80514802 | 0.00514802 |
| 16 | 25.0200 | 7.6000 | 7.60439716 | 0.00439716 | 7.60439697 | 0.00439697 |
| 17 | 25.3900 | 7.4000 | 7.40597697 | 0.00597697 | 7.40597679 | 0.00597679 |
| 18 | 25.7500 | 7.2000 | 7.19709834 | 0.00290166 | 7.19709818 | 0.00290182 |
| 19 | 26.3800 | 6.8000 | 6.79421478 | 0.00578522 | 6.79421466 | 0.00578534 |
| 20 | 26.9400 | 6.4000 | 6.39703240 | 0.00296760 | 6.39703233 | 0.00296767 |
| 21 | 27.4600 | 6.0000 | 5.99656297 | 0.00343703 | 5.99656293 | 0.00343707 |
| 22 | 27.9400 | 5.6000 | 5.60112090 | 0.00112090 | 5.60112090 | 0.00112090 |
| 23 | 28.4000 | 5.2000 | 5.20016085 | 0.00016085 | 5.20016088 | 0.00016088 |
| 24 | 28.8400 | 4.8000 | 4.79761966 | 0.00238034 | 4.79761971 | 0.00238029 |
| 25 | 29.2500 | 4.4000 | 4.40675456 | 0.00675456 | 4.40675462 | 0.00675462 |
| 26 | 29.6600 | 4.0000 | 4.00156633 | 0.00156633 | 4.00156640 | 0.00156640 |
| 27 | 30.0500 | 3.6000 | 3.60362789 | 0.00362789 | 3.60362796 | 0.00362796 |
| 28 | 30.4400 | 3.2000 | 3.19420724 | 0.00579276 | 3.19420732 | 0.00579268 |
| 29 | 30.8100 | 2.8000 | 2.79578571 | 0.00421429 | 2.79578579 | 0.00421421 |
| 30 | 31.1700 | 2.4000 | 2.39932544 | 0.00067456 | 2.39932550 | 0.00067450 |
| 31 | 31.5200 | 2.0000 | 2.00601421 | 0.00601421 | 2.00601426 | 0.00601426 |
| 32 | 31.8800 | 1.6000 | 1.59382496 | 0.00617504 | 1.59382498 | 0.00617502 |
| 33 | 32.2200 | 1.2000 | 1.19780705 | 0.00219295 | 1.19780706 | 0.00219294 |
| 34 | 32.5500 | 0.8000 | 0.80751916 | 0.00751916 | 0.80751914 | 0.00751914 |
| 35 | 32.8900 | 0.4000 | 0.39962407 | 0.00037593 | 0.39962402 | 0.00037598 |
| 36 | 33.2200 | 0.0000 | −0.00159760 | 0.00159760 | −0.00159769 | 0.00159769 |
| SIAE of MCSWOA | 0.21759970 | 0.21759985 | ||||
| SIAE of WOA | 0.24899579 | 0.26906430 | ||||
| Algorithm | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
| WOA | 3.3118 × 10−3±2.5700×10−3 † | 3.6217 × 10−3±2.7791×10−3 † | 9.6733 × 10−3±1.1794×10−2 † | 2.4505 × 10−2±2.2337×10−2 † | 2.8343 × 10−2±6.0554×10−2 † |
| WOAwM | 1.9296 × 10−3±8.6309×10−4 † | 2.3822 × 10−3±1.0539×10−3 † | 3.9812 × 10−3±2.0408×10−3 † | 1.9714 × 10−2±2.6652×10−2 † | 9.2314 × 10−3±8.1319×10−3 † |
| WOAwC | 1.7668 × 10−3±5.3337×10−4 † | 2.2107 × 10−3±6.2234×10−4 † | 3.0516 × 10−3±9.4430×10−4 † | 3.9044 × 10−3±1.4276×10−3 † | 3.4664 × 10−3±1.0919×10−3 † |
| WOAwS | 1.5324 × 10−3±6.0777×10−4 † | 1.6445 × 10−3±5.2751×10−4 † | 4.0862 × 10−3±4.2387×10−3 † | 9.1345 × 10−3±1.4631×10−2 † | 3.6344 × 10−2±9.2696×10−2 † |
| MCSWOAwoM | 1.3311 × 10−3±4.2360×10−4 † | 1.5667 × 10−3±5.5562×10−4 † | 2.9301 × 10−3±1.0113×10−3 † | 2.8068 × 10−3±6.8783×10−4 † | 2.6430 × 10−3±4.3694×10−4 † |
| MCSWOAwoC | 1.3425 × 10−3±3.5746×10−4 † | 1.3755 × 10−3±3.7302×10−4 † | 2.8885 × 10−3±9.4059×10−4 † | 7.6989 × 10−3±1.2735×10−2 † | 3.5022 × 10−2±9.4205×10−2 † |
| MCSWOAwoS | 1.5019 × 10−3±4.7279×10−4 † | 1.5784 × 10−3±4.6080×10−4 † | 2.7574 × 10−3±5.5040×10−4 † | 2.9587 × 10−3±9.4949×10−4 † | 2.9479 × 10−3±6.2242×10−4 † |
| MCSWOA | 9.8602 × 10−4±4.8373×10−10 | 1.0078 × 10−3±3.7224×10−5 | 2.4252 × 10−3±3.2927×10−7 | 2.4377 × 10−3±1.3424×10−5 | 1.7311 × 10−3±1.0774×10−6 |
| Algorithm | Case 6 | Case 7 | Case 8 | Case 9 | Case 10 |
| WOA | 1.2171 × 10−2±8.5449×10−3 † | 1.3390 × 10−1±3.3374×10−1 † | 3.8581 × 10−2±1.1413×10−2 † | 1.9117 × 10−1±5.2271×10−1 † | 3.4638 × 10−2±1.2972×10−2 † |
| WOAwM | 1.1827 × 10−2±1.0218×10−2 † | 1.4783 × 10−1±4.0155×10−1 † | 3.2690 × 10−2±1.2753×10−2 † | 9.2149 × 10−1±1.1998 † | 6.2633 × 10−1±1.1112 † |
| WOAwC | 3.8571 × 10−3±1.3413×10−3 † | 3.3596 × 10−2±1.2829×10−2 † | 3.5628 × 10−2±1.1472×10−2 † | 4.5812 × 10−2±1.0846×10−1 † | 2.8767 × 10−2±1.3194×10−2 † |
| WOAwS | 1.0220 × 10−2±4.3428×10−2 † | 3.0149 × 10−1±5.3225×10−1 † | 1.3955 × 10−1±3.3301×10−1 † | 8.6839 × 10−1±9.1094×10−1 † | 3.0201 × 10−1±5.5643×10−1 † |
| MCSWOAwoM | 2.7088 × 10−3±4.7905×10−4 † | 2.1776 × 10−2±3.9977×10−3 † | 2.2506 × 10−2±3.9073×10−3 † | 2.0330 × 10−2±7.6106×10−3 † | 2.4356 × 10−2±8.2859×10−3 † |
| MCSWOAwoC | 1.0494 × 10−2±4.3369×10−2 † | 8.8438 × 10−2±2.0395×10−1 † | 2.9647 × 10−2±1.4360×10−2 † | 3.0895 × 10−1±6.8799×10−1 † | 1.7716 × 10−1±3.7440×10−1 † |
| MCSWOAwoS | 2.9186 × 10−3±6.0366×10−4 † | 3.3319 × 10−2±8.6499×10−3 † | 3.0825 × 10−2±9.3727×10−3 † | 4.8567 × 10−2±1.1040×10−1 † | 3.2615 × 10−2±1.0742×10−2 † |
| MCSWOA | 1.7296 × 10−3±5.4724×10−6 | 1.6632 × 10−2±2.6486×10−5 | 1.6640 × 10−2±2.8956×10−5 | 1.1187 × 10−2±9.1358×10−6 | 1.1190 × 10−2±8.4623×10−6 |
| Algorithm | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
| CWOA | 6.5608 × 10−3±7.7906×10−3 † | 6.5015 × 10−3±8.3105×10−3 † | 4.0220 × 10−2±3.3878×10−2 † | 8.8557 × 10−2±1.2848×10−1 † | 7.3042 × 10−2±1.0974×10−1 † |
| IWOA | 1.3789 × 10−3±5.1312×10−4 † | 1.3881 × 10−3±2.9395×10−4 † | 2.7650 × 10−3±4.6827×10−4 † | 2.9409 × 10−3±6.7649×10−4 † | 2.8122 × 10−3±4.5910×10−4 † |
| Lion_Whale | 3.1843 × 10−3±2.2032×10−3 † | 4.1686 × 10−3±3.1841×10−3 † | 8.3281 × 10−3±1.0314×10−2 † | 3.5424 × 10−2±2.8837×10−2 † | 1.2740 × 10−2±8.5614×10−3 † |
| LWOA | 3.8223 × 10−3±2.5841×10−3 † | 3.7734 × 10−3±3.2433×10−3 † | 7.5580 × 10−3±1.0062×10−2 † | 2.9719 × 10−2±2.6177×10−2 † | 2.3724 × 10−2±5.9677×10−2 † |
| MWOA | 1.4352 × 10−3±3.8523×10−4 † | 1.6923 × 10−3±5.4619×10−4 † | 3.4700 × 10−3±1.4623×10−3 † | 4.9057 × 10−3±2.7372×10−3 † | 1.9707 × 10−1±9.6087×10−2 † |
| OBWOA | 3.0937 × 10−3±2.1925×10−3 † | 3.8497 × 10−3±2.0783×10−3 † | 1.1591 × 10−2±1.1474×10−2 † | 4.6378 × 10−2±3.6616×10−2 † | 4.1245 × 10−2±8.1091×10−2 † |
| PSO_WOA | 2.5317 × 10−3±1.0688×10−3 † | 3.1643 × 10−3±1.0202×10−3 † | 6.1397 × 10−3±2.5857×10−3 † | 4.4845 × 10−2±5.8766×10−2 † | 2.5510 × 10−2±4.2215×10−2 † |
| RWOA | 3.5386 × 10−3±2.5903×10−3 † | 3.5906 × 10−3±2.5699×10−3 † | 1.1432 × 10−2±1.2700×10−2 † | 3.7910 × 10−2±2.8936×10−2 † | 1.4016 × 10−2±8.1452×10−3 † |
| SAWOA | 3.9103 × 10−3±3.2763×10−3 † | 4.2854 × 10−3±2.7580×10−3 † | 1.0367 × 10−2±1.5587×10−2 † | 1.2186 × 10−1±6.1004×10−1 † | 1.0681 × 10−2±5.7482×10−3 † |
| WOA−CM | 1.8057 × 10−3±9.4142×10−4 † | 1.9303 × 10−3±6.4609×10−4 † | 3.0553 × 10−3±1.1304×10−3 † | 3.2230 × 10−3±1.0350×10−3 † | 2.7473 × 10−3±6.1670×10−4 † |
| WOABHC | 2.4830 × 10−3±1.4878×10−3 † | 3.2285 × 10−3±1.7139×10−3 † | 5.7079 × 10−3±5.9201×10−3 † | 1.2009 × 10−2±1.3695×10−2 † | 1.7371 × 10−2±7.5501×10−3 † |
| MCSWOA | 9.8602 × 10−4±4.8373×10−10 | 1.0078 × 10−3±3.7224×10−5 | 2.4252 × 10−3±3.2927×10−7 | 2.4377 × 10−3±1.3424×10−5 | 1.7311 × 10−3±1.0774×10−6 |
| Algorithm | Case 6 | Case 7 | Case 8 | Case 9 | Case 10 |
| CWOA | 4.1656 × 10−2±6.0841×10−2 † | 6.0298 × 10−1±7.0364×10−1 † | 2.4784 × 10−1±4.8707×10−1 † | 1.9090±1.0622 † | 1.1956±1.2143 † |
| IWOA | 2.8068 × 10−3±6.1560×10−4 † | 2.6344 × 10−2±6.5869×10−3 † | 2.4487 × 10−2±6.0914×10−3 † | 2.3385 × 10−2±1.1011×10−2 † | 2.0908 × 10−2±8.4553×10−3 † |
| Lion_Whale | 1.1758 × 10−2±7.4784×10−3 † | 3.2231 × 10−2±1.1794×10−2 † | 3.2987 × 10−2±1.2592×10−2 † | 9.8029 × 10−2±3.4184×10−1 † | 2.9543 × 10−2±1.3201×10−2 † |
| LWOA | 1.1983 × 10−2±7.8099×10−3 † | 8.9130 × 10−2±2.7403×10−1 † | 3.7172 × 10−2±1.5830×10−2 † | 1.7580 × 10−1±5.0999×10−1 † | 3.1649 × 10−2±1.4127×10−2 † |
| MWOA | 1.6428 × 10−1±7.9106×10−2 † | 3.7422 × 10−2±1.2357×10−2 † | 3.8979 × 10−2±1.0903×10−2 † | 4.8405 × 10−2±1.0824×10−1 † | 3.2497 × 10−2±1.2601×10−2 † |
| OBWOA | 1.7604 × 10−2±9.8420×10−3 † | 1.1870 × 10−1±3.3200×10−1 † | 9.8499 × 10−2±2.7722×10−1 † | 4.0964 × 10−1±8.0655×10−1 † | 2.9575 × 10−2±1.2568×10−2 † |
| PSO_WOA | 2.0718 × 10−2±1.1155×10−2 † | 4.6616 × 10−1±6.7103×10−1 † | 1.2651 × 10−1±1.2418×10−1 † | 2.1068±1.1111 † | 2.1078±1.0319 † |
| RWOA | 1.3841 × 10−2±8.0800×10−3 † | 3.8377 × 10−2±2.1557×10−2 † | 3.5678 × 10−2±1.2714×10−2 † | 1.7159 × 10−1±5.0952×10−1 † | 2.7693 × 10−2±1.2816×10−2 † |
| SAWOA | 1.3133 × 10−2±8.9981×10−3 † | 6.3576 × 10−2±1.9534×10−1 † | 3.8696 × 10−2±3.0127×10−2 † | 2.2969 × 10−1±5.8559×10−1 † | 3.7130 × 10−2±1.2907×10−2 † |
| WOA−CM | 2.9571 × 10−3±6.6077×10−4 † | 2.7691 × 10−2±1.0487×10−2 † | 2.7232 × 10−2±1.0768×10−2 † | 2.6774 × 10−2±1.6707×10−2 † | 2.9099 × 10−2±1.3264×10−2 † |
| WOABHC | 1.7284 × 10−2±8.0367×10−3 † | 4.9880 × 10−2±7.6648×10−3 † | 4.6525 × 10−2±1.1413×10−2 † | 8.4911 × 10−2±2.9295×10−1 † | 4.1759 × 10−2±1.0658×10−2 † |
| MCSWOA | 1.7296 × 10−3±5.4724×10−6 | 1.6632 × 10−2±2.6486×10−5 | 1.6640 × 10−2±2.8956×10−5 | 1.1187 × 10−2±9.1358×10−6 | 1.1190 × 10−2±8.4623×10−6 |
| Algorithm | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
| BLPSO | 1.9021 × 10−3±1.8505×10−4 † | 2.0514 × 10−3±2.7912×10−4 † | 2.4898 × 10−3±2.7678×10−5 † | 2.5112 × 10−3±5.4421×10−5 † | 5.2325 × 10−3±1.1639×10−3 † |
| CLPSO | 1.1194 × 10−3±1.0940×10−4 † | 1.2102 × 10−3±1.2533×10−4 † | 2.4833 × 10−3±3.3208×10−5 † | 2.5561 × 10−3±6.5265×10−5 † | 3.9131 × 10−3±9.9804×10−4 † |
| CSO | 1.7135 × 10−3±3.7256×10−4 † | 2.3968 × 10−3±5.0421×10−4 † | 2.4779 × 10−3±6.1374×10−5 † | 2.4703 × 10−3±3.3601×10−5 † | 3.6956 × 10−2±5.2404×10−2 † |
| DBBO | 1.2829 × 10−3±2.5357×10−4 † | 1.0515 × 10−3±1.0529×10−4 † | 2.4255 × 10−3±1.8443×10−6 † | 2.4257 × 10−3±2.1496×10−6 ‡ | 1.5373 × 10−2±1.3834×10−2 † |
| DE/BBO | 1.1196 × 10−3±1.1647×10−4 † | 1.1190 × 10−3±1.5390×10−4 † | 2.4332 × 10−3±5.3545×10−5 † | 2.4536 × 10−3±5.7504×10−5 † | 3.7298 × 10−3±2.9966×10−3 † |
| GOTLBO | 1.0777 × 10−3±1.0248×10−4 † | 1.1211 × 10−3±1.1785×10−4 † | 2.4710 × 10−3±8.6113×10−5 † | 2.5120 × 10−3±1.4228×10−4 † | 2.7002 × 10−3±2.9037×10−4 † |
| IJAYA | 1.0116 × 10−3±3.9701×10−5 † | 1.0375 × 10−3±6.5079×10−5 † | 2.4402 × 10−3±1.7719×10−5 † | 2.4547 × 10−3±2.8211×10−5 † | 2.2691 × 10−3±3.7081×10−4 † |
| LETLBO | 1.0118 × 10−3±2.9676×10−5 † | 1.0565 × 10−3±1.0299×10−4 † | 2.4517 × 10−3±4.1189×10−5 † | 2.4607 × 10−3±4.1340×10−5 † | 2.3621 × 10−3±3.3351×10−4 † |
| MABC | 1.1217 × 10−3±1.5006×10−4 † | 1.1301 × 10−3±1.1174×10−4 † | 2.4592 × 10−3±3.4902×10−5 † | 2.4913 × 10−3±4.6322×10−5 † | 1.2849 × 10−2±7.4066×10−3 † |
| ODE | 1.1306 × 10−3±1.3390×10−4 † | 1.0152 × 10−3±7.3670×10−5 † | 2.4265 × 10−3±7.2112×10−6 † | 2.4255 × 10−3±1.5214×10−6 ‡ | 3.2435 × 10−3±1.6449×10−3 † |
| SATLBO | 9.9236 × 10−4±7.7023×10−6 † | 1.0196 × 10−3±4.4399×10−5 † | 2.4503 × 10−3±8.8712×10−5 † | 2.5334 × 10−3±2.4232×10−4 † | 1.9681 × 10−3±1.6428×10−4 † |
| SLPSO | 1.6741 × 10−3±3.8943×10−4 † | 2.2540 × 10−3±6.0816×10−4 † | 2.5069 × 10−3±1.8101×10−4 † | 2.4713 × 10−3±4.0124×10−5 † | 1.2625 × 10−2±5.1388×10−3 † |
| TLABC | 9.9237 × 10−4±1.5009×10−5 † | 1.0325 × 10−3±6.4577×10−5 † | 2.4255 × 10−3±9.5526×10−7 † | 2.4339 × 10−3±9.0969×10−6 ≈ | 1.8665 × 10−3±1.0099×10−4 † |
| MCSWOA | 9.8602 × 10−4±4.8373×10−10 | 1.0078 × 10−3±3.7224×10−5 | 2.4252 × 10−3±3.2927×10−7 | 2.4377 × 10−3±1.3424×10−5 | 1.7311 × 10−3±1.0774×10−6 |
| Algorithm | Case 6 | Case 7 | Case 8 | Case 9 | Case 10 |
| BLPSO | 5.0586 × 10−3±1.2686×10−3 † | 4.7472 × 10−2±3.2271×10−3 † | 4.4430 × 10−2±5.2342×10−3 † | 4.4674 × 10−2±5.5602×10−3 † | 4.3783 × 10−2±4.7164×10−3 † |
| CLPSO | 4.2857 × 10−3±1.0083×10−3 † | 2.6297 × 10−2±6.0504×10−3 † | 3.0761 × 10−2±8.4038×10−3 † | 1.2006 × 10−1±7.4285×10−2 † | 1.2302 × 10−1±8.9533×10−2 † |
| CSO | 1.5507 × 10−2±7.6428×10−3 † | 3.8608 × 10−1±4.6849×10−1 † | 1.3560 × 10−1±2.4327×10−1 † | 1.3952±6.9328×10−1 † | 9.5533 × 10−1±8.0496×10−1 † |
| DBBO | 1.3809 × 10−2±9.4018×10−3 † | 1.5307 × 10−1±2.0137×10−1 † | 7.4939 × 10−2±8.1393×10−2 † | 3.5746×10−2±2.0978×10−2 † | 3.4309 × 10−2±8.1225×10−3 † |
| DE/BBO | 4.6286 × 10−3±3.1740×10−3 † | 3.2601 × 10−2±7.9176×10−3 † | 3.2281 × 10−2±7.4126×10−3 † | 3.3622 × 10−1±5.2313×10−1 † | 2.7941 × 10−1±4.3527×10−1 † |
| GOTLBO | 3.3486 × 10−3±6.6655×10−4 † | 2.1023 × 10−2±2.9156×10−3 † | 2.6143 × 10−2±6.4333×10−3 † | 1.9831 × 10−2±5.5072×10−3 † | 2.5341 × 10−2±9.1729×10−3 † |
| IJAYA | 2.5200 × 10−3±5.1689×10−4 † | 1.7273 × 10−2±4.0886×10−4 † | 1.7915 × 10−2±1.6640×10−3 † | 1.2786 × 10−2±1.5584×10−3 † | 1.3658 × 10−2±2.4658×10−3 † |
| LETLBO | 2.8076 × 10−3±8.0176×10−4 † | 2.2716 × 10−2±1.9207×10−2 † | 1.9306 × 10−2±2.8808×10−3 † | 3.1644 × 10−2±3.5249×10−2 † | 2.4674 × 10−2±1.9033×10−2 † |
| MABC | 1.1607 × 10−2±7.3824×10−3 † | 4.1445 × 10−2±1.0439×10−2 † | 4.0201 × 10−2±1.1824×10−2 † | 3.7567 × 10−2±8.9141×10−3 † | 3.4091 × 10−2±1.1119×10−2 † |
| ODE | 3.0783 × 10−3±1.3525×10−3 † | 4.5691 × 10−2±5.5273×10−2 † | 3.4596 × 10−2±3.5109×10−2 † | 1.2531±4.2568×10−1 † | 1.2490±3.5744×10−1 † |
| SATLBO | 2.0176 × 10−3±1.6428×10−4 † | 1.7206 × 10−2±9.1397×10−4 † | 1.7356 × 10−2±9.3366×10−4 † | 1.6181×10−2±9.9094×10−3 † | 1.9837 × 10−2±1.2493×10−2 † |
| SLPSO | 9.5470 × 10−3±5.4545×10−3 † | 1.3935 × 10−1±1.8024×10−1 † | 6.4134 × 10−2±7.0877×10−2 † | 3.6172 × 10−1±3.2445×10−1 † | 3.9282 × 10−1±3.9592×10−1 † |
| TLABC | 1.9030 × 10−3±1.0096×10−4 † | 1.6806 × 10−2±2.3608×10−4 † | 1.6773 × 10−2±9.1609×10−5 † | 1.1691 × 10−2±7.1799×10−4 † | 1.1892 × 10−2±1.3444×10−3 † |
| MCSWOA | 1.7296 × 10−3±5.4724×10−6 | 1.6632 × 10−2±2.6486×10−5 | 1.6640 × 10−2±2.8956×10−5 | 1.1187 × 10−2±9.1358×10−6 | 1.1190 × 10−2±8.4623×10−6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, G.; Zhang, J.; Shi, D.; Zhu, L.; Yuan, X.; Yao, G. Modified Search Strategies Assisted Crossover Whale Optimization Algorithm with Selection Operator for Parameter Extraction of Solar Photovoltaic Models. Remote Sens. 2019, 11, 2795. https://doi.org/10.3390/rs11232795
Xiong G, Zhang J, Shi D, Zhu L, Yuan X, Yao G. Modified Search Strategies Assisted Crossover Whale Optimization Algorithm with Selection Operator for Parameter Extraction of Solar Photovoltaic Models. Remote Sensing. 2019; 11(23):2795. https://doi.org/10.3390/rs11232795
Chicago/Turabian StyleXiong, Guojiang, Jing Zhang, Dongyuan Shi, Lin Zhu, Xufeng Yuan, and Gang Yao. 2019. "Modified Search Strategies Assisted Crossover Whale Optimization Algorithm with Selection Operator for Parameter Extraction of Solar Photovoltaic Models" Remote Sensing 11, no. 23: 2795. https://doi.org/10.3390/rs11232795
APA StyleXiong, G., Zhang, J., Shi, D., Zhu, L., Yuan, X., & Yao, G. (2019). Modified Search Strategies Assisted Crossover Whale Optimization Algorithm with Selection Operator for Parameter Extraction of Solar Photovoltaic Models. Remote Sensing, 11(23), 2795. https://doi.org/10.3390/rs11232795