An Enhanced Deep Convolutional Model for Spatiotemporal Image Fusion

Abstract

Earth observation data with high spatiotemporal resolution are critical for dynamic monitoring and prediction in geoscience applications, however, due to some technique and budget limitations, it is not easy to acquire satellite images with both high spatial and high temporal resolutions. Spatiotemporal image fusion techniques provide a feasible and economical solution for generating dense-time data with high spatial resolution, pushing the limits of current satellite observation systems. Among existing various fusion algorithms, deeplearningbased models reveal a promising prospect with higher accuracy and robustness. This paper refined and improved the existing deep convolutional spatiotemporal fusion network (DCSTFN) to further boost model prediction accuracy and enhance image quality. The contributions of this paper are twofold. First, the fusion result is improved considerably with brand-new network architecture and a novel compound loss function. Experiments conducted in two different areas demonstrate these improvements by comparing them with existing algorithms. The enhanced DCSTFN model shows superior performance with higher accuracy, vision quality, and robustness. Second, the advantages and disadvantages of existing deeplearningbased spatiotemporal fusion models are comparatively discussed and a network design guide for spatiotemporal fusion is provided as a reference for future research. Those comparisons and guidelines are summarized based on numbers of actual experiments and have promising potentials to be applied for other image sources with customized spatiotemporal fusion networks.

1. Introduction

Remote sensing images with simultaneous high spatial and high temporal resolution play a critical role in land surface dynamics research [1], such as crop and forest monitoring [2,3], and land-use and land-cover changes detection [4]. These applications require dense time-series data to capture ground changes and also finespatialresolution surface details, such as textures and structures of ground objects, to perform accurate classification and identification or some advanced quantitative calculation. Even though advances of sensor technology in recent years have greatly prompted the precision of satellite observation, due to some inevitable technical and budget limitations, there is always a tradeoff among spatial, temporal, and spectral resolutions for Earth observation data [5,6]. Fortunately, this problem that it is not easy to directly acquire high spatiotemporal resolution images from existing satellite observation systems can be partly alleviated by some data post-processing processes [7,8,9]. Among them, spatiotemporal remote sensing image fusion is a class of techniques used to synthesize dense-time images with high spatial resolution from at least two different data sources [1,5,10]. In most cases, one is the coarsespatialresolution image with high temporal but low spatial resolution (HTLS), while the other is the finespatialresolution image with low temporal but high spatial resolution (LTHS). A typical example is to fuse Landsat and Moderate Resolution Image Spectroradiometer (MODIS) images to derive high spatial resolution images in a dense time sequence. The spatial resolution of Landsat for most spectral bands is 30 m and its temporal resolution is around 16 days [11]. MODIS images, in contrast, are acquired daily but only with a coarse spatial resolution ranging from 250 to 1000 m for different bands [12]. By fusing these two data sources, composite images can gain the spatial resolution of Landsat and the temporal resolution of MODIS within a certain error tolerance.

Generally speaking, the existing algorithms for spatiotemporal data fusion can be classified into four categories: (1) transformationbased; (2) reconstructionbased; (3) Bayesian-based; and (4) learning-based models [5,10,13]. Transformationbased models use some advanced mathematical transformations, such as wavelet transformation, to integrate multi-source information in a transformed space [5]. This type of method not only can be applied in spatiotemporal fusion [14] but also is widely employed in the fusion of panchromatic and multispectral images (referred to as pansharpening) [15]. Reconstructionbased methods are the most prosperous branch according to the statistics [5]. Generally, there are two major subbranches of reconstructionbased methods: weightfunctionbased and unmixingbased [5]. The weightfunctionbased methods evaluate LTHS images as well as the corresponding HTLS images through a local moving window with some hand-crafted weighting functions, such as the Spatial and Temporal Adaptive Reflectance Fusion Model (STARFM) [7] and the Spatial and Temporal Adaptive Algorithm for Mapping Reflectance Change (STAARCH) [16]. The unmixing-based methods estimate the selected end-member fractions of HTLS image pixels to reconstruct the corresponding LTHS image with spectral unmixing theory, such as the flexible spatiotemporal data fusion (FSDAF) method [17] and the spatial attraction model [18]. Bayesian-based models utilize Bayesian statistical inference to perform prediction with multiple reference images, such as the unified fusion method proposed by [19] and the Bayesian fusion approach proposed by [20]. The biggest advantage of Bayesian-based models is that they can handle the uncertainty of input images and produce the most probable predictions naturally [10]. At present, some of these models have been applied in practical applications, such as crop monitoring, forest phenology analysis, and daily evapotranspiration evaluation, and achieved desirable results [2,3,21]. However, theoretically speaking, a conventional model with hand-crafted fusion rules, even though elaborately designed with enormous complexity, cannot handle all situations well considering spatial heterogeneity of ground surfaces and uneven quality of acquired data. As a result, the conventional fusion algorithm may be performed well in some areas for some data, but cannot always maintain high accuracy.

Today, the learning-based model has become a new research hotspot with comparatively higher accuracy and robustness. In general, learning-based fusion models do not or seldom need to manually design fusion rules and can automatically learn essential features from massive archived data and generate dense-time images with fine spatial resolution. Current learning-based methods mostly employ sparse representation and deep learning techniques to establish their domain-specific models [13,22,23]. The theoretical assumption of sparserepresentationbased methods is the HTLS and LTHS image pair acquired on the same day share the same sparse codes. By jointly learning two dictionaries corresponding to HTLS and LTHS image patches in advance, the LTHS images for prediction can be reconstructed with the learned dictionaries as well as sparse encoding algorithms [22,24]. The deep learning approach simulates the way in which human neurons work and tries to establish a complex, nonlinear relation mapping between input(s) and output(s) with several hidden layers, potentially containing massive amounts of learnable parameters [25,26]. There are various building blocks to construct a deep learning network for a specific task, among which convolutional neural network (CNN) turns to be an effective and efficient architecture for image feature extraction and recognition problems [25]. As the study goes on, CNN-based models are gradually applied in data fusion domain, and relevant research is being undertaken [13,23,27,28,29].

There have been many studies, so far, concentrating on remote sensing image fusion with deep convolutional networks. Some research applied CNN models to pansharpening fusion for panchromatic and multispectral images [29,30]; some introduced CNNs to multispectral and hyperspectral image fusion [31]; some utilized CNNs to blend optical and microwave remote sensing images to improve optical image quality [32]. However, the exploration of the deep learning approach for spatiotemporal data fusion is still limited and preliminary. [23] proposed a hybrid approach for spatiotemporal image fusion named STFDCNN. First, a nonlinear mapping between HTLS and resampled low-spatial-resolution LTHS is learned with a CNN (NLMCNN), then a second super-resolution CNN (SRCNN) is established between the low-spatial-resolution LTHS and original LTHS. For best results, the output of the first CNN on prediction date is not directly fed into the SRCNN model, but is tweaked with a high-pass modulation. [13] proposed a CNN-based, one-stop method termed Deep Convolutional SpatioTemporal Fusion Network (DCSTFN) to perform MODIS-Landsat image fusion. The inputs are one pair of LTHS and HTLS images for reference and another HTLS for prediction. Information is merged in the form of extracted feature maps, then the merged features are reconstructed to the predicted image. [33] proposed a residual fusion network termed StfNet by learning pixel differences between reference and prediction dates. The fusion process of StfNet is performed at raw pixel level instead of feature level, therefore, the StfNet model can preserve abundant texture details.

These aforementioned work initially introduces CNN approach to spatiotemporal data fusion domain for remote sensing images and improves fusion accuracy considerably compared with conventional methods. Still, there are some shortcomings of existing CNN-based fusion models. First, predicted images from CNN models are not as sharp and clear as actual observations for feature-level fusion. This is partly because a convolutional network minimizes its losses to make predictions as close to ground truths as possible, therefore, errors are balanced among each pixel to reach a global optimum. Moreover, practices indicate that the de-factor loss function—$l_2$ loss (i.e., mean squared error (MSE)) for image reconstruction renders it much likely to yield blurry images [34]. Second, it is crucial to select appropriate LTHS reference images in spatiotemporal fusion, from which all the detailed high-frequency information comes, thus, predictions are necessarily affected by their references causing fusion results to resemble the references to some degree. It could be much worse when there are significant ground changes during the reference and prediction period. These problems should be resolved or mitigated so that image quality of prediction can be further improved.

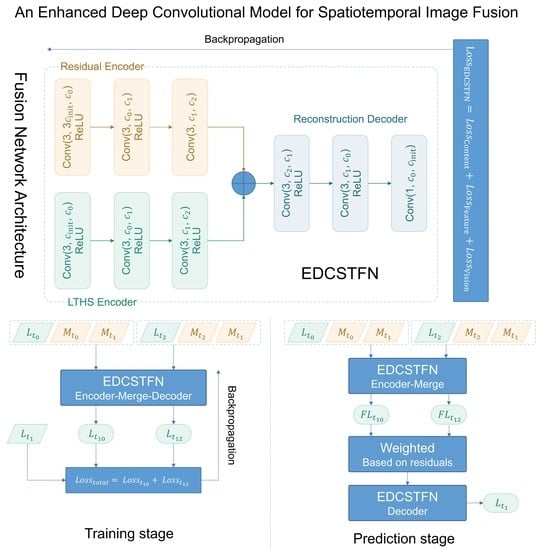
This paper continues previous work on CNN-based spatiotemporal fusion model to further explore possibilities to improve the DCSTFN model. By redesigning network architecture, an enhanced deep convolutional spatiotemporal fusion network (EDCSTFN) was developed to alleviate the aforementioned problems. The EDCSTFN model needs at least one pair of MODIS-Landsat images as fusion references, and spectral information of prediction is derived based on spectrum changes between the reference and prediction dates. The novelty of the EDCSTFN model is that differences between reference and prediction dates are completely learned from actual data, not like the DCSTFN model in which the relation between inputs and output is established on a hypothetical equation. Second, high-frequency information is preserved as much as possible by using a new compound loss function, which combines the accuracy and vision loss to generate sharp and clear images. Third, two pairs of references, usually from the time before and after the prediction date, are supported to make predictions less reliant on a single reference and thus to improve the accuracy and robustness of the model. In the experiments, by taking MODIS and Landsat 8 Operational Land Imager (OLI) data fusion as an example, a series of comparative evaluations were performed. The results demonstrate that not only fusion accuracy is improved, and also the predicted result gains more clarity and sharpness, significantly improving fusion image quality.

The rest of this paper is organized as follows. The former DCSTFN model is briefly recalled and the new EDCSTFN model is introduced in Section 2. Section 3 dives into the details of the experiments, and the corresponding results and discussion are presented in Section 4. Conclusion and future work are summarized in Section 5.

2. Methods

2.1. DCSTFN Introduction

Taking MODIS and Landsat image fusion as an example, let L and M denote Landsat and MODIS images respectively. There are MODIS images acquired at time of $t_0$, $t_1$ and $t_2$, and Landsat images acquired at time $t_0$ and $t_2$ within the same geographic area corresponding to the MODIS. The objective of spatiotemporal fusion is to predict Landsat-like images with fine-spatial resolution at time $t_1$. Mathematically, it can be abstracted to a problem of establishing a mapping f between the Landsat-like image $L_{t_1}$ on prediction date and the relevant acquired data, including MODIS image $M_{t_1}$ and other reference images $M_{t_k}$ and $L_{t_k}$ (k ≠ 1). Particularly, the $t_0$ and $t_2$ indicate the reference dates before and after prediction date $t_1$. The mapping function f can be formulated as Equation (1).

$$L_{t_1}=f(M_{t_1},L_{t_k},M_{t_k}|\Theta )(k\ne 1)$$

(1)

In summary, the deep learning approach is to establish a complex nonlinear mapping with a set of learnable parameters $\Theta$ from archived satellite images to approximate the actual f function.

Generally, the primitive DCSTFN model adopts an “encoder–merge–decoder” architecture to address this problem. In the DCSTFN fusion model, the HTLS subnet and LTHS subnet function as Encoders extracting features from MODIS and Landsat images respectively. The fusion process is performed in a high-level abstract feature space to merge features from different data sources. To be specific, the extracted features are merged according to an assumption that ground feature changes observed from MODIS and Landsat images between the reference and prediction dates are nearly identical, which can be formulated as Equation (2).

$$F{L}_{t_1}=F{L}_{t_k}+F{M}_{t_1}-F{M}_{t_k}(k\ne 1).$$

(2)

$FL$ and $FM$ denotes the extracted feature maps from Landsat and MODIS images. The subscript indicates the data acquisition time. Transposed convolution [35] is employed in the HTLS subnet to upsample MODIS image features to match the feature size of Landsat produced by the LTHS subnet. Finally, the fused high-level features are entered into a reconstruction subnet—the decoder—and are restored to the raw pixel space. Figure 1a illustrates the general architecture of DCSTFN model. The reference MODIS data at time $t_k$ and the MODIS data on prediction date $t_1$ share the same HTLS Encoder and the reference Landsat data are fed into the LTHS Encoder. The final prediction is directly produced by the reconstruction decoder.

2.2. EDCSTFN Architecture

2.2.1. Overall Architecture

The EDCSTFN employs this similar “encoder–merge–decoder” architecture with three subnets. The first Encoder termed as LTHS Encoder is used for Landsat feature extraction; the second Encoder termed as Residual Encoder is utilized to learn feature differences between the reference and prediction dates. By adding feature maps from these two Encoders, then features on prediction can be generated, and finally, the reconstruction decoder restores these high-level features to the original pixel space deriving prediction. The whole process can be formulated as Equation (3),

$$L_{t_1}=f(g(L_{t_k})+h(L_{t_k},M_{t_1},M_{t_k}))(k\ne 1),$$

(3)

where g denotes the LTHS encoder and its input is Landsat image on reference date $t_k$; h denotes the residual encoder and the inputs are reference image pair on $t_k$ and MODIS image on $t_1$ for prediction; and f denotes the reconstruction decoder and its inputs are the merged features from the preceding stage. Compared with DCSTFN model, the relation between reference and prediction images is implicitly established with the residual encoder, automatically learned from actual data without additional assumption. Figure 1b illustrates the general architecture of the EDCSTFN model.

2.2.2. Compound Loss Function

To enhance prediction image sharpness, the $l_2$ loss is replaced with a customized compound loss function considering prediction accuracy and image quality. This new comprehensive loss function is composed of content loss, feature loss and vision loss, formulated as Equation (4),

$${\mathcal{L}}_{EDCSTFN}={\mathcal{L}}_{Content}+{\mathcal{L}}_{Feature}+\alpha ·{\mathcal{L}}_{Vision},$$

(4)

where $\alpha$ is a scaling factor to balance the weight of vision loss in the compound loss. The $\alpha$ is empirically set to 0.5 in the following experiment. The content loss is the fundamental requirement for an image reconstruction model ensuring overall image content, such as texture and tone. It can be calculated based on raw image pixel errors with MSE, the same as the DCSTFN model.

The feature loss is first proposed in [36] for image super-resolution to preserve the essential information of images. As the name implies, feature loss is performed in feature space instead of raw pixels. In our model, it is calculated by comparing the MSE losses of derived features from a pre-trained model. The pre-trained model in our experiment is the classical “hourglass” AutoEncoder with one encoder followed by one decoder [37]. The Encoder is intended to extract compressed features from Landsat images and thus to acquire essentials of detailed textures, while the Decoder can fairly restore the extracted essentials to the original inputs. Practically, the detailed architecture of this pre-trained AutoEncoder can be arbitrary. In this paper, the pre-trained AutoEncoder is architected as Figure 2. Conv denotes the standard convolution layers, and the four parameters attached are convolution kernel size, input and output channels, and convolution stride. The convolution layer with a stride of 2 in the Encoder can shrink the feature size by half, while the Upsample in the Decoder with the scale of 2 can double the feature size. The nonlinear activation used in network is the rectified linear units (ReLU) [26]. With this pre-trained model for Landsat images, the feature loss can be formulated as Equation (5).

$${\mathcal{L}}_{Feature}=\frac{1}{N}\sum _{i=1}^N{({\widehat{FL}}_{t_1}-F{L}_{t_1})}^2$$

(5)

N denotes the element numbers of the feature maps; ${\widehat{FL}}_{t_1}$ denotes the extracted features from the EDCSTFN prediction with the pre-trained encoder; $F{L}_{t_1}$ denotes the features extracted from observed data on prediction date $t_1$.

Vision loss is an auxiliary component designed for improving whole image quality from the perspective of computer vision. It can be evaluated with the multi-scale structural similarity (MS-SSIM) index that is widely used in image reconstruction models [34]. SSIM index comprehensively evaluates image similarity from three components: luminance, contrast, and structure, embodied by the statistics of mean, standard deviation and correlation coefficient of two corresponding images [38]. It can be denoted as Equation (6),

$$SSIM(y,\widehat{y})=\frac{(2{\mu }_y{\mu }_{\widehat{y}}+C_1)(2{\sigma }_{y\widehat{y}}+C_2)}{({\mu }_y^2+{\mu }_{\widehat{y}}^2+C_1)({\sigma }_y^2+{\sigma }_{\widehat{y}}^2+C_2)},$$

(6)

where y and $\widehat{y}$ indicate observation and predication images; ${\mu }_i$ and ${\sigma }_i$ denote mean value and standard deviation of image i respectively; ${\sigma }_{xy}$ stands for covariance of image x and y; constant $C_i$ is added to stabilize the equation. The value range of SSIM is between −1 and 1 theocratically. The SSIM of two identical images equals to 1 and a value of 0 indicates no structural similarity. MS-SSIM extends the original SSIM by evaluating SSIM at multiple scale levels with multiple image resolutions to gain higher accuracy. The MS-SSIM loss is defined as Equation (7) to penalize the low MS-SSIM derived from the prediction image patch P.

$${\mathcal{L}}_{Vision}=1-MS-SSIM(P)$$

(7)

Studies show that MS-SSIM can effectively preserve the high-frequency details of images [34]. So by involving the MS-SSIM, the compound loss function can urge the network to generate clear and sharp predictions.

2.2.3. Enhanced Data Strategy

Besides the image quality enhancement, prediction accuracy should be paid more attention to and further improved. Because MODIS data lack high-frequent details of ground surface, many predicted details need to be extrapolated from reference images. If there are significant ground changes during the reference and prediction period or the only Landsat reference image is acquired with poor data quality, the prediction result tends to be less accurate. To address this issue, the EDCSTFN model is extended to support two pairs of references. Not only can additional reference data generalize the model, but also weighted predictions from different references can improve the prediction reliability to some degree. Unlike the existing deeplearningbased methods where two references are mandatory in training and prediction, a flexible training-prediction data strategy is proposed in this paper. The number of reference pair(s) can be either one or two in training and is not restricted to be the same in training and prediction phases. For example, two pairs of references can be used to train the model and one pair of references can be used for prediction, and vice versa. Since the revisit period of Landsat satellite spans 16 days and according to the statistics, 35% of the acquired images are contaminated by clouds and mist on average [39], it may be quite challenging to collect two applicable reference images in production practice. This data strategy offers an opportunity to choose input data flexibly according to the actual data condition of the study area.

Specifically, there are four cases concerning the inputs of the model in training and prediction. When a training model with only one pair of references, the process is just the same as the DCSTFN. If two pairs of references are involved in training, the two references are still separated as two independent groups to be entered into the model. In other words, the model should satisfy the two different training data groups simultaneously, which can regularize the model in effect and prevent overfitting to a large extent, shown in Figure 3a. In this case, the EDCSTFN model updates the network learnable parameters with the backpropogation algorithm based on the sum total of losses from these two data groups. Owing to the independence of input data groups in model training, input group(s) with neither one or two reference(s) can be fed into the model in the prediction phase. If there is only one reference for prediction, then no extra process is needed and prediction results can be directly obtained from the trained network. If there are two references for prediction, the two intermediate feature maps from the feature merge layer, shown in Figure 1, need to be further weighted and then are entered into the reconstruction decoder to produce the final result, shown in Figure 3b. This also explains why residuals between reference and prediction are needed to be learned in the first place. The weighting method is built based on the inversion differences between reference and prediction, namely the output of residual encoder. It can be reasonably assumed that a larger distance represents a more significant ground change and the greater the change is, the less accurate the prediction becomes. Hence, by employing the inverse distance weighted method, both of the predictions can contribute to the final result based on their reliability. Equation (8) initially calculates weights regarding to the prediction with reference at time $t_0$.

$$W_{10}=\frac{\frac{1}{D_{10}}}{\frac{1}{D_{10}}+\frac{1}{D_{12}}},$$

(8)

where $D_{10}$ and $D_{12}$ denote the absolute differences between prediction at time $t_1$ and two references at time $t_0$ and $t_2$ from the residual encoder. Equations (9) and (10) formulate the weighting process,

$$W_{12}=I-W_{10}$$

(9)

$$L_{t_1}=L_{t_1}^{t_0}·W_{10}+L_{t_1}^{t_2}·W_{12},$$

(10)

where $L_{t_1}^{t_0}$ and $L_{t_1}^{t_2}$ are the predicted feature maps based on the references at time $t_0$ and $t_2$ respectively. I is an all-ones multi-dimensional array with the same size of $W_{10}$. The sum of $W_{10}$ and $W_{12}$ should be constantly equal to I. Notably, the weighing process is performed on high-level features instead of raw image pixels and this process only happens in the prediction phase with two pairs of references.

2.2.4. Detailed Design

Figure 4 illustrates the detailed design of each subnet in the EDCSTFN model. To maintain texture details as many as possible, the classical hourglass-shaped AutoEncoder is not used here, instead, feature maps keep their original spatial resolution through all the layers. Structures of LTHS Encoder and residual encoder are nearly identical. The only difference is that the input channels of the LTHS Encoder is $c_{\mathrm{init}}$ corresponding to the number of spectral bands, while the input channels of residual encoder is three times than LTHS Encoder’s, because three images including a pair of reference images and a MODIS image on prediction are stacked as a whole to enter the residual encoder. Notably, MODIS images need to be upsampled with interpolation in the first place to gain the same size of Landsat images. This is also one of the differences between the new and original designs. In the DCSTFN model, MODIS images are upsampled with multiple transposed convolution layers, thus the HTLS Encoder of DCSTFN is equipped with more layers than EDCSTFN Encoder. However, the use of transposed convolution in image reconstruction tasks can easily cause the “checkerboard artifacts” [40], leading to severely deteriorated image quality. Here, bicubic interpolation is used to upsample MODIS images in the beginning, and the building layers of the network are reduced accordingly. After raw images are encoded, the extracted feature maps from the two encoders are added in an element-wise manner, then directly flow into the reconstruction decoder. In the experiment, convolution kernel size is empirically set to $3\times 3$ and stride is set to 1 for most of the convolution layers. The other two hyper-parameters of a convolution layer are channels of input and output features, denoted with $c_i(i=0,1,2)$ in Figure 4. Usually, many features bring many learnable parameters and improve the model accuracy within limits, but too many parameters tend to cause overfitting. There is a balance in hyper-parameter selection. Here the three hyper-parameters are empirically set to 32, 64, and 128 for different layers. The last layer is still a convolution layer with a filter size of 1 and it functions similar to the linear transformation in the DCSTFN model.

3. Experiments

3.1. Study Area and Datasets

In this experiment, the level-2 Landsat 8 OLI and MODIS surface reflectance products were employed to evaluate the fusion model. The eight-day composite MODIS data product–MOD09A1–is selectively used because there is no sufficient daily data in our study areas due to a massive amount of data missing and cloud contamination. The eight-day product significantly lessens the impact of atmosphere and clouds, repairs missing data as much as possible, and provides a fairly high image quality [41]. Theoretically, the eight-day product may not always present the actual ground truth on a specific date, especially in some places where there are significant ground changes during the eight days, while the daily product, of course, can offer a more accurate representation of ground changes. If there are daily data with good quality available in the study area, it is recommended to use the daily product to perform the fusion. To verify the generality of the EDCSTFN model, it is tested in two different regions of China: Guangdong and Shandong, spanning from January 2013 to December 2017, shown in Figure 5. All the data with cloud coverage greater than 5% for Landsat and “no data" pixel amount greater than 1% for MODIS are discarded to guarantee fusion accuracy. For Guangdong province, coordinates of the selected experiment area in Landsat Worldwide Reference System (WRS) are denoted with P122R043, P123R043, and P123R044; and the corresponding area in MODIS Sinusoidal Tile Grid is located in h28v06. Since Guangdong is in the subtropical coastal region, the humid climate causes this area to be covered with clouds most of the time. As a result, it is inaccessible to obtain two favorable references after data filtering. Besides, Guangdong presents a more heterogeneous landscape than Shandong. Given this fact, data of this area were mainly used to test the improvement in image sharpness with only one reference. For Shandong province, two scenes of Landsat images with the WRS coordinate of P122R034 and P122R035 were used and the corresponding MODIS grid is located in h27v05. Guangdong is a large province in agriculture growing a variety of crops. Data of this area were used to test fusion accuracy improvement with the enhanced data strategy. In the following experiments, since the entire scene of Landsat image is used for fusion, for clarity, the WRS coordinate and the calendar date are used to mark the location and time of the acquired image.

Data preprocessing for spatiotemporal fusion still followed the procedures conducted in the DCSTFN experiment. First, preliminary radiometric calibration and atmospheric correction should be performed. The level-2 data product already has undergone these routines. Then, Landsat image of each scene was cropped to the same size (4800 × 4800) to remove “no data” regions from the edge. Third, the corresponding MODIS data were resampled from MODIS sinusoidal projection to the Universal Transverse Mercator (UTM) and cropped to obtain the same geographical extent as the Landsat (the resampled image size of MODIS is 300 × 300 and the spatial resolution is 480 m). Finally, these processed MODIS and Landsat data were organized and grouped according to the acquisition date. The basic rule is that reference and prediction dates should be as close as possible, better within a quarter. For the model trained with one reference pair, each training data group consists of two MODIS images and two Landsat images on prediction and reference date respectively; for the model trained with two reference pairs, there are three MODIS and Landsat pairs. It should be also aware that the spectral range of each band should be matched in the fusion process, which means the spectral band of Landsat and MODIS to be merged should be within the approximate same range (see [7]). After data filtering, preprocessing and grouping, there were fourteen data groups for each area. For each area, all groups are needed to be split into training and validation datasets randomly. Validation data are not involved in the training process, only used for testing. The minimum requirement for training data volume is related to the complexity of the model. In practice, it could be considered to have met the requirement as long as the model can reach convergence and does not overfit. During training, images were further subdivided into small patches considering the computer memory consumption and entered into the network batch by batch. In our experiment, the patch size for MODIS was 50 × 50 and the sliding stride for subsetting was 30 × 30. Accordingly, the settings of Landsat are sixteen times as MODIS. In the prediction phase, small patches are processed through the trained network and then stitched together to form the whole scene.

3.2. Experiment Settings

Corresponding to the study areas, the experiments were also separated into two main groups. The first was meant to verify the improvements of EDCSTFN regarding prediction accuracy and image sharpness by using three scenes data of Guangdong province. Besides, the impact of input spectral bands for fusion models was also explored in this group. Since experiment data of Guangdong are only equipped with one pair of references, conventional spatiotemporal fusion algorithms supporting one reference such as STARFM and FSDAF and the former deeplearningbased model DCSTFN are tested here. The second group was intended to test the prediction accuracy improvements with the enhanced data strategy by using two scenes data of Shandong province. Also, the conventional models including STARFM and ESTARFM and deeplearningbased models including DCSTFN, StfNet were comparatively tested here. Among them, STARFM and EDCSTFN can support one or two pair(s) of references and ESTARFM and StfNet need two references mandatorily.

All the deeplearningbased models in the experiment were implemented with PyTorch [42] deep learning framework using Python programming language. To ensure the reproducibility of the experiment and contribute to the geoscience community, the source code is unclosed via GitHub (https://github.com/theonegis/edcstfn). There are 408961, 95972 and 281764 learnable parameters for DCSTFN, StfNet and EDCSTFN models respectively. StfNet only consists of three layers, much shallower than DCSTFN and EDCSTFN, thus, it has fewer parameters than the other two. The total parameters of the EDCSTFN model are decreased by nearly half with this new architecture compared with the DCSTFN model. The Adam [43] optimization algorithm was used for all the fusion networks to optimize and update the learnable parameters. The initial learning rate was set to $8\times {10}^{-4}$ for single-band training and $1\times {10}^{-3}$ for multi-band training including blue, green, red and near-infrared (NIR) bands. Sixty epochs training was performed for every experiment group and the learning rate was decayed by 0.1 when validation losses stop improving after five epochs. In our hardware environment, the batch size for training was set to 8 for the testing with one reference and 4 for the model with two references. All these settings depend on actual hardware and training data and should be adjusted accordingly. The settings, such as training batch size, image patch and stride size, do affect the result, but the influence is not so evident in our test that it could be ignored for the fusion experiment.

4. Results and Discussion

4.1. Evaluation Indices

Currently, there is no internationally-accepted standard that can uniquely determine the quality of fused images [44]. Different fusion metrics have their limitations and can only reveal some parts of the fused image quality [45], thus, several metrics are selected for the evaluation in this experiment, including the root mean square error (RMSE), structural similarity index (SSIM), spectral angle mapper (SAM) [46], and relative dimensionless global error (ERGAS) [47]. The RMSE, formulated as Equation (11), measures the distance between ground truth and prediction. A small RMSE shows high accuracy.

$$\mathrm{RMSE}=\sqrt{\frac{{\sum }_{i=1}^N{(y_i-{\widehat{y}}_i)}^2}{N}}.$$

(11)

In Equation (11) and following equations, M denotes the number of spectral bands; N denotes the total number of pixels of the image; $y_i$ and ${\widehat{y}}_i$ denote the ith observed value and predicted value. The SSIM, formulated as Equation (7), is a visual indicator to measure the similarity between two images, and a higher value shows higher similarity. The SAM, formulated as Equation (12), evaluates spectral distortion by spectral angle and a small SAM indicates a better result.

$$\mathrm{SAM}=\frac{1}{N}\sum _{i=1}^{N}arccos\frac{{\sum }_{j=1}^M(y_i^j{\widehat{y}}_i^j)}{\sqrt{{\sum }_{j=1}^M{(y_i^j)}^2{\sum }_{j=1}^M{({\widehat{y}}_i^j)}^2}}.$$

(12)

The ERGAS, formulated as Equation (13), comprehensively evaluates fusion results based on prediction errors, and a smaller ERGAS indicates a better result. The h and l in Equation (13) denote the spatial resolution of LTHS and HTLS images; ${\mathrm{RMSE}}_i$ stands for the RMSE of the ith band.

$$\mathrm{ERGAS}=100\frac{h}{l}\sqrt{\frac{1}{M}\sum _{i=1}^M{(\frac{{\mathrm{RMSE}}_i}{{\mu }_i})}^2}.$$

(13)

4.2. Experimental Results

4.2.1. The Guangdong Region

Guangdong was selected to test the improvement for image sharpness because of its heterogenous ground features, especially for the rapidly-developed city areas. Meanwhile, the impact of input image bands for the EDCSTFN model was also explored with this dataset. For these purposes, the STARFM, FSDAF, DCSTFN, EDCSTFN with single-band inputs (EDCSTFN-S), and EDCSTFN with multi-band inputs (EDCSTFN-M) were comparatively tested. Figure 6 gives the learning curve showing the MSE losses over epochs for the deeplearningbased fusion models in Guangdong test area. The errors are summarized over all image patches with the moving window for the training and validation datasets. For the model trained with a single spectrum band, the errors are averaged among all the bands. The solid line and dashed line indicate error curves for the training and validation datasets respectively. From Figure 6, it can be seen that the models are converged after 40 epochs around. The EDCSTFN model outperforms DCSTFN and the EDCSTFN-M shows slight superiority over EDCSTFN-S. Figure 7 presents the quantitative metrics on the five validation data groups. The metrics are calculated across the entire image for each group. Generally, the EDCSTFN model can generate much better results than the DCSTFN model whether from the perspective of statistic errors or vision index. Second, the EDCSTFN predictions for most of the tests have higher accuracy than conventional methods, except for the last one (the group on 30 October 2017 in P123R044 tile) with a tiny lag difference. Third, there is little difference between the quantitative metrics of EDCSTFN-S and EDCSTFN-M, which means the input spectral bands have some influence on fusion results, but not significantly. Last, the EDCSTFN prediction results remain comparatively stable than other methods, showing strong robustness.

Table 1. The averaged quantitative metrics for Guangdong area on validation dataset.

	STARFM	FSDAF	DCSTFN	EDCSTFN-S	EDCSTFN-M
RMSE	0.0220	0.0226	0.0201	0.0176	0.0174
ERGAS	2.2708	2.3424	1.8838	1.5199	1.5268
SAM	0.0678	0.0681	0.0689	0.0562	0.0562
SSIM	0.9079	0.9001	0.9060	0.9294	0.9290

lists the averaged quantitative metrics of Guangdong areas on the whole validation dataset. The columns of EDCSTFN models are in bold. Every quantitative index shows the EDCSTFN model outperforms other methods, which demonstrates the proposed model does improve the fusion accuracy.

Figure 8 illustrates part of the results on December 7th, 2016 in the P122R043 region. The first column exhibits the standard true color composite images for the ground truth, predictions of STARFM, FSDAF, DCSTFN, EDCSTFN-S, and EDCSTFN-M. The second column gives the bias between fusion results and ground truth corresponding to the first column. The values are stretched between 0.0 and 0.1 to highlight the differences. The third column shows the zoomed-in details of the red rectangles marked in the first column. The last column is the calculated normalized difference vegetation index (NDVI), a commonly-used vegetation indicator in remote sensing, corresponding to the third column. First, the second row demonstrates that prediction errors from conventional methods are much more significant than deeplearningbased models. Second, the third column shows the EDCSTFN model sharpens miscellaneous ground features compared with the DCSTFN model, nearly as clear as the observed ground truth. This also implies the comprehensive compound loss function works quite well for image fusion tasks. Third, distinct white flakes are scattering in the results of STARFM and FSDAF, showing they failed to predict ground features in heterogeneous city areas. Fourth, the results of EDCSTFN-S and EDCSTFN-M do have some differences visually, but not significantly. Theoretically, four individual networks are trained for the EDCSTFN-S corresponding to the four spectral bands, and each network is specially optimized catering for the characteristics of each unique band, while the EDCSTFN-M is a one-size-fit-all network where all the bands are treated equally and some common features may be highlighted in this case. Training an EDCSTFN-S model for production is much more time-consuming than EDCSTFN-M does, and the accuracy improvement is not obvious, so multiple-band images can be safely used for training in normal cases. Last, the calculated NDVIs from CNN-based models are more close to the actual observation visually.

Figure 9 exhibits part of the results on 30 October 2017 in the P123R044 region, where the predictions of conventional methods produced fewer errors than the DCSTFN model. The arrangement of the subfigures is the same as above. It can be seen there are some distinguishable small abnormal blue patterns in the results of STARMF and FSDAF from the first column. Overall, the prediction of EDCSTFN-M resembles ground truth best visually. From the third column, there are noticeable abnormal patterns produced by STARMF and FSDAF marked with yellow rectangles, while the EDCSTFN model yield quite reliable results for heterogeneous city areas. From the last NDVI results, still, the EDCSTFN model represents the most accurate results compared with others. In brief, although the conventional methods produce smaller errors averagely in this data group, there are some obvious mistakes in the fusion results, which means the conventional model is not so robust as the EDCSTFN model. Moreover, the outlines of the city are much more clear with the EDCSTFN model seen from the third column, which means the EDCSTFN model significantly improves image sharpness compared with the DCSTFN model.

4.2.2. The Shandong Region

The climate of Shandong is not humid as Guangdong’s, thus more Landsat data with little or without cloud coverage are available. For this reason, the enhanced data strategy was tested here and comparisons between DCSTFN and other models that need two reference images were performed in this area. Five models, including seven cases: STARFM with one reference (STARFM-I), STARFM with two references (STARFM-II), ESTARFM, DCSTFN, StfNet, EDCSTFN with one reference (EDCSTFN-I) and EDCSTFN with two references (EDCSTFN-II), were tested here. Figure 10 gives the learning curve of the deeplearningbased fusion models in the Shandong test area. Clearly, the average errors of StfNet over validation patches are significantly larger than the EDCSTFN model. The prediction accuracy of EDCSTFN-II is pretty higher than EDCSTFN-I, showing the improvement with the two-reference-enhanced strategy. Figure 11 shows the quantitative metrics on the five validation data groups. Generally, EDCSTFN-II outperforms other models. For one thing, the EDCSTFN model shows significant high-score metrics than others; for another, the prediction of EDCSTFN remains stable for all the data groups. The classical ESTARFM and recently-proposed StfNet fluctuate heavily for different data groups, showing they are not so robust as EDCSTFN. With respect to the effect of reference data pairs on prediction, in most cases, the two-reference strategy can contribute to the improvement of model accuracy both for the STARFM and the EDCSTFN, but this is not always the case. It may relate to the reference image quality as well as significant ground changes.

Table 2. The averaged quantitative metrics for the Shandong area on validation dataset.

	STARFM-I	STARFM-II	ESTARFM	DCSTFN	StfNet	EDCSTFN-I	EDCSTFN-II
RMSE	0.0243	0.0221	0.0260	0.0230	0.0206	0.0172	0.0154
ERGAS	1.2541	1.1436	1.4637	1.2242	1.1737	0.9249	0.8353
SAM	0.0738	0.0676	0.0624	0.0783	0.0792	0.0616	0.0507
SSIM	0.8963	0.8948	0.9216	0.8472	0.9161	0.9161	0.9352

lists the averaged quantitative metrics of Shandong areas on the whole validation dataset. The columns of EDCSTFN models are in bold. Every quantitative index shows the EDCSTFN-II model outperforms other methods, which further demonstrates the enhanced data strategy can truly boost the fusion accuracy.

Figure 12 demonstrates part of the fusion results on 24 November 2017 in P122R035 region. The first column exhibits the overview of the whole scene. The second column shows the zoomed-in details of the red rectangles marked in the first column. The third column gives the bias between fusion results and ground truth corresponding to the second column. The fourth column presents the zoomed-in details of the yellow rectangles in the second column. The last column is the calculated NDVI corresponding to the fourth column. Generally, the EDCSTFN and StfNet show the best results from the overview. The third column shows the EDCSTFN-II produces minimum errors. The fourth column shows that the result of DCSTFN lacks clarity and sharpness, while the other models can preserve more texture details. From the NDVI view of the last column, the EDCSTFN-II predictions are the closest to the ground truth. Overall, EDCSTFN-II produces better results than others. Figure 13 illustrates part of the fusion results on 10 December 2017 in P122R034 region. The arrangement of the subfigures is the same as Figure 12. Obviously, the conventional methods fail to make the right prediction on the bottom left areas of the images in the first column. From the third and fourth columns, it clearly demonstrates the results of EDCSTFN-II matches the ground truth best for areas covering fields and villages and predict the changes in crops with considerable accuracy. Besides, the image tone of DCSTFN and StfNet is strikingly different from the ground truth seen from the fourth column. In conclusion, the EDCSTFN model outperforms other models from statistical metrics and visual observation in Shandong province. The two-reference-enhanced strategy can reduce fusion errors on a large scale.

4.3. Discussion

First, the experiments performed in Guangdong province reveal that by the new architecture and the comprehensive compound loss function, the EDCSTFN model can sharpen predicted images and remedy the defects of DCSTFN model. Also the prediction accuracy is significantly improved compared with DCSTFN model, which renders quantitative analysis in remote sensing applications more reliable. The input image bands also have a certain impact on prediction, but it is not that obvious, so training a fusion network using multiple-band images is doable in practice with less time consumption.

Second, the experiments of Shandong province prove that the EDCSTFN model outperforms other spatiotemporal fusion models. By applying the enhanced data strategy in the experiments, it can be seen that additional reference data do gain performance improvement in most cases, but the accuracy is also strongly influenced by the data quality. If one of the references is not in good quality, the result is even worse than prediction with one reference. In practice, it may be not always easy to collect source data with high quality for some areas. Our model supports both one and two data references no matter in training or prediction and allows limited existence of clouds and missing data, which shows the EDCSTFN model is quite flexible and has a fair fault-tolerant capacity.

Third, three deeplearningbased fusion models are compared and the EDCSTFN model achieves state-of-the-art results. Not only is the prediction accuracy improved considerably, but also the image sharpness and clarity is highly enhanced compared with the DCSTFN model. Moreover, the EDCSTFN model shows more robustness when handling poor-quality data compared with the StfNet. This is because the EDCSTFN model performs the fusion in abstract feature space, while StfNet does the fusion in the raw pixel space. If there are a small number of noisy pixels or missing values, the EDCSTFN decoder have partial ability to denoise prediction images and try to restore clean pixels. If the fusion process directly performed on pixels, then input noises definitely will be transmitted to prediction results.

Despite the aforementioned improvements, there are still some inadequacies in our work. First, daily MODIS data should be further used for model validation. Second, the prediction accuracy for areas with significant ground changes during the reference and prediction needs to be tested in future work. Once sufficient qualified data are collected and reasonable comparative cases can be designed to perform advanced analysis.

In general, the research on spatiotemporal image fusion with a deep learning approach is still limited. This paper compares the basic ideas of the existing models to provide a reference for further study. First, the STFDCNN model is based on superresolution approach to gradually upsample HTLS images. The advantage of superresolutionbased models is that they can preserve the correctness of spectral information maximally. However, because of lacking the injection of high-frequency information with super-resolution, the output images turn to be somewhat blurry. Second, the StfNet model performs fusion in raw pixel level by learning pixel differences between reference and prediction. The advantage of this approach is that all the texture information can be preserved. However, since this type of method directly merges information with pixel values, input data in poor quality is unacceptable. If there are two reference data available, this limitation can be abated partially. But still, how to automatically select good-quality pixels from the two candidates becomes a problem. Third, the DCSTFN and EDCSTFN models perform fusion in a high-level abstract feature space level. This type of method turns to be less sensitive to input data quality than the second approach. Because information merges in a high-level feature space, the network can take full advantage of CNNs and be trained to automatically fix small input data errors.

In the end, this paper summarizes some practical tricks when designing and implementing a spatiotemporal fusion network: (1) input data quality is the most important factor for a fusion network. When collected data are not in good quality, it is recommended to use two references to eliminate prediction errors. (2) Too-deep networks may easily lead to overfitting, and networks with too deeper layers are not doable in the current situation. (3) Normalization, such as batch normalization [48] or instance normalization [49], do no good for the aforementioned fusion networks, because the normalization will destroy the original data distribution and thus it will reduce the fusion accuracy. (4) The input data of models would better include high-frequency information, otherwise the output image turns to be less sharp. (5) The fusion process is recommended to be performed in high-level feature space instead of raw pixel space to provide much more robustness. (6) Transposed convolution should be avoided for up-sampling, because the transposed convolution in image reconstruction easily leads to the “checkerboard artifacts” [40]. (7) The $l_2$ loss function can easily lead to a blurry output, but it is more sensitive for outliers. So it is of much importance to design a comprehensive loss function for remote sensing image reconstruction tasks. Above are some empirical rules provided for a reference when designing a new spatiotemporal fusion network.

5. Conclusions and Prospects

This paper is devoted to improving prediction accuracy and result image quality using deep learning techniques for spatiotemporal remote sensing image fusion. The contribution of this paper is twofold. First, an improved spatiotemporal fusion network is proposed. With this brand-new architecture, compound loss function and enhanced data strategy, not only does the predicted image gain more sharpness and clarity, but also the prediction accuracy is highly boosted. A series of experiments in two different areas demonstrate the superiority of our EDCSTFN model. Second, the advantages and disadvantages of existing fusion methods are discussed, and a succinct guideline is presented to offer some practical tricks when designing a workable spatiotemporal fusion network.

In spatiotemporal image fusion, much of detailed information needs to be inferred from coarsespatialresolution images as well as extra auxiliary data, especially for the MODIS-Landsat image fusion with the upsampling factor of sixteen. It cannot be denied that there must be a limit regarding prediction accuracy for this ill-posed problem and further improvement may not be easy. Generative adversarial networks (GANs), a class of generative models in deep learning domain, [36,50], present a promising prospect in solving the spatiotemporal fusion problem because they specialize in generating information with higher reliability and fidelity. As a matter of fact, GANs have been applied to image super-resolution with an upsampling factor of four and outperformed other models generating photorealistic images with more details [36,51]. In addition, the prediction accuracy of each pixel for a certain model varies extensively, so the reliability of the fusion result should be concerned. By interacting Bayesian networks into deep learning technologies, it would be possible to solve this uncertainty problem. Currently, limited researches are using Bayesian CNN for computer vision [52], which could be explored to apply in spatiotemporal image fusion.

Except for concentrating on fusion model accuracy, on the other hand, more efforts should be focused on the usability and robustness of fusion models. First, the transplantability of the model needs to be explored. In our experiment, different models are trained for different areas, which means each area owns its unique model with different parameters. If a model is trained for one place and used in another place, currently the accuracy is unknown. The idea of transfer learning [53] could be borrowed to study the transplantability of CNN-based spatiotemporal fusion models. Second, input image quality has a significant impact on the predicted results. A good model should lessen the impact of input data quality. For example, a model needs to handle the situation automatically where there are fairly notable changes during the reference and predation period. The model should have a high tolerance for inputs with limited clouds or missing data because this is a common situation in practical applications. Third, reference images are usually needed for most spatiotemporal data fusion models, and it is often not easy to collect appropriate data pairs in practice. Hence, it is quite necessary to develop models that can map HTLS images to LTHS images without references in the prediction phase and the key question is how to fabricate enough ground details without losing accuracy for this type of model. Last but not least, the existing spatiotemporal fusion networks all adopt a supervised learning approach, while the acquired appropriate training dataset in some study areas is not easy. Hence, it will be beneficial to devise some training schemes for unsupervised learning. All of these questions need further exploration.