Optimising Sampling Strategies in Coral Reefs Using Large-Area Mosaics
Abstract
:1. Introduction and Background
2. Materials and Methods
2.1. Study Site and Image Acquisition
2.2. Model and Mosaics Generation
2.3. Digital Annotation of Benthic Organisms
2.4. Testing Different Sampling Efforts
2.5. Data Analyses
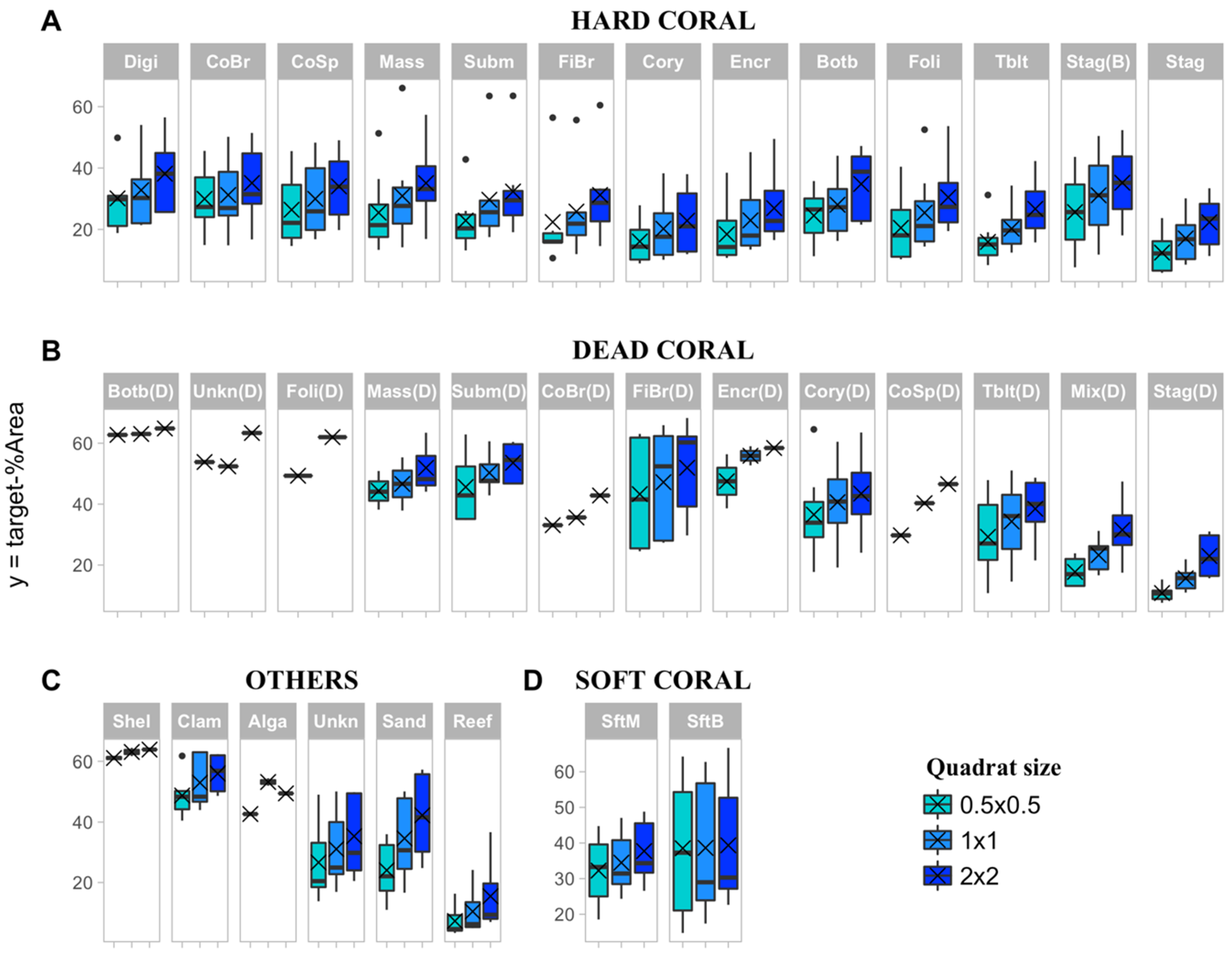
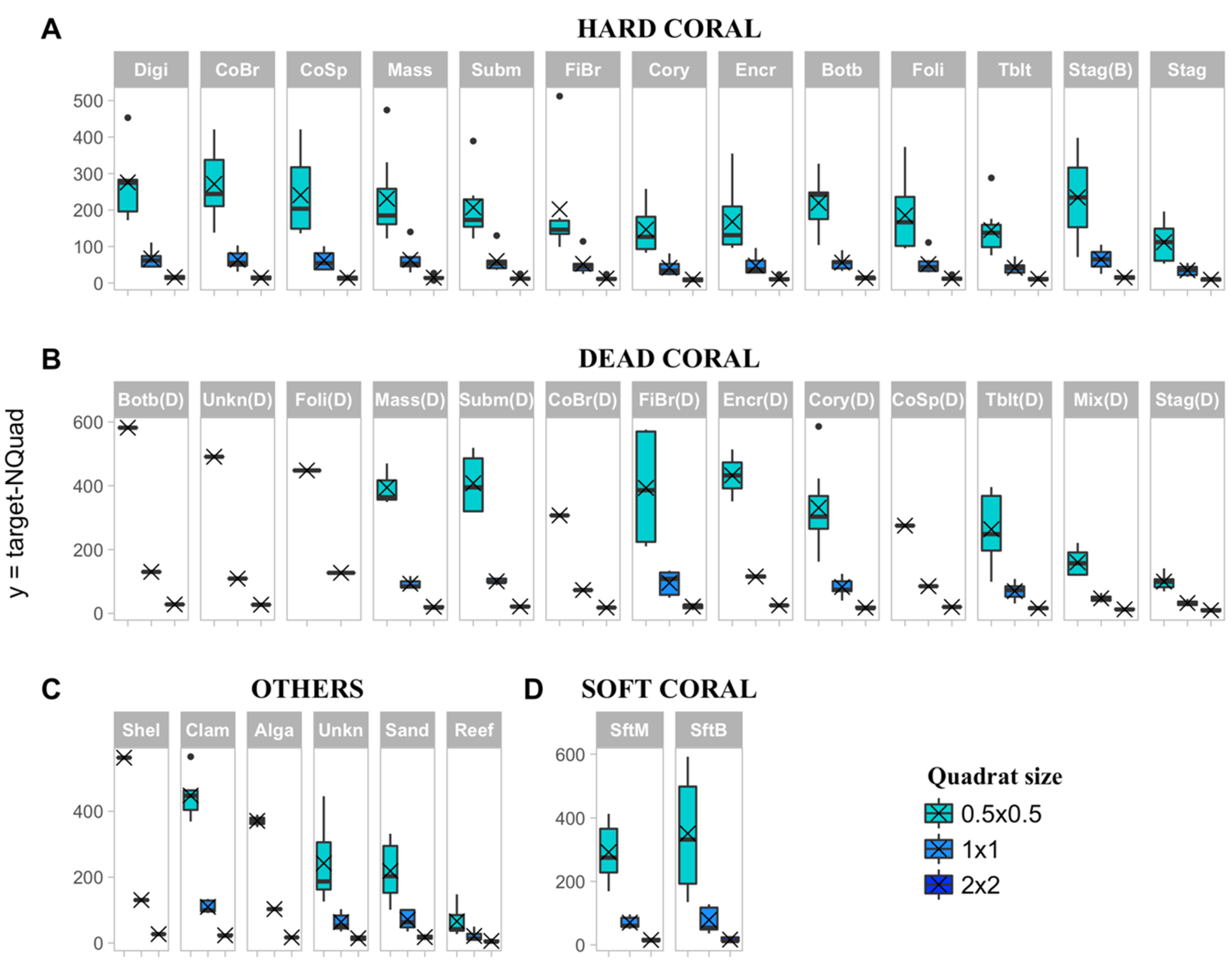
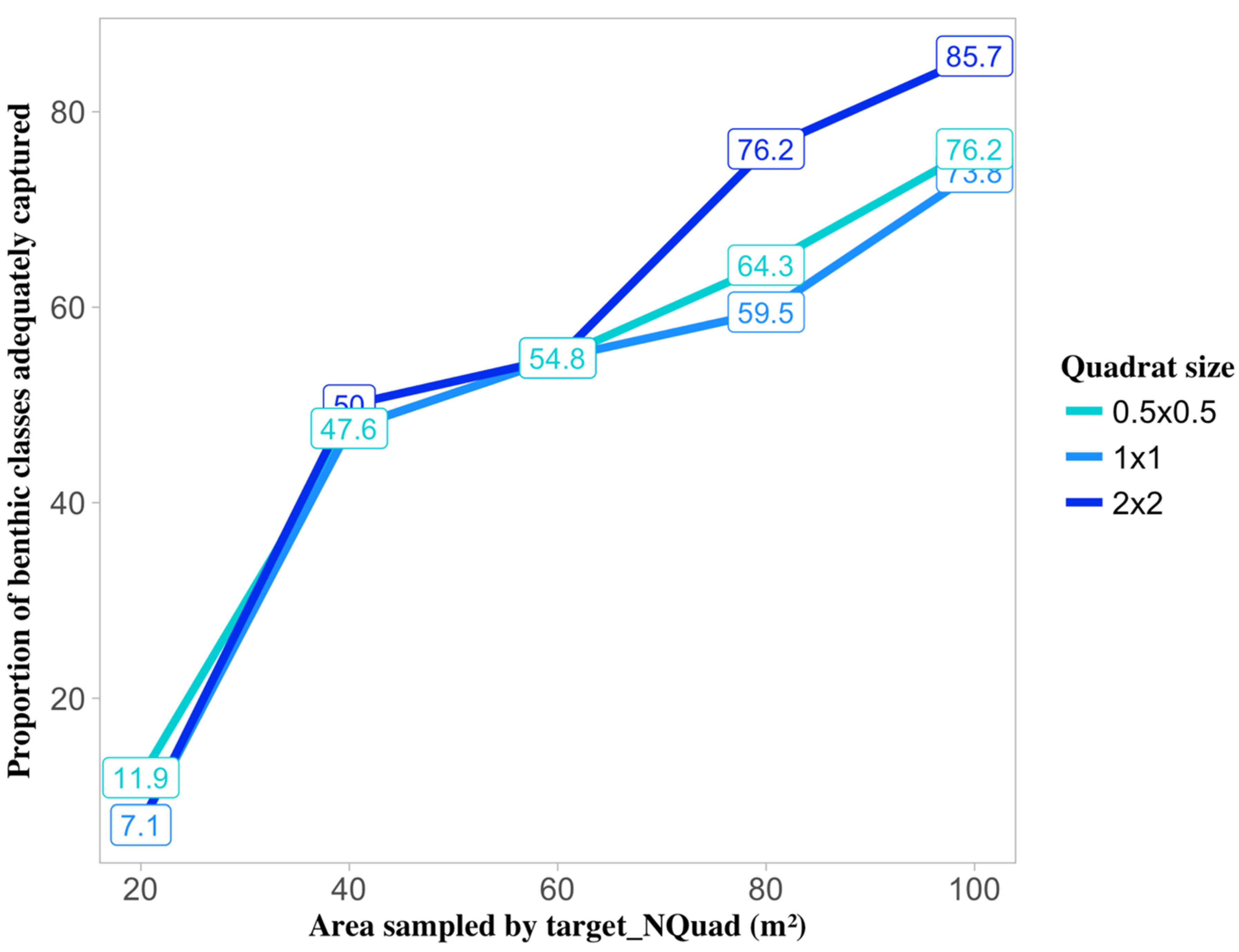
2.5.1. Precision Level of Cover Estimates
2.5.2. Effect of Quadrat Type, Benthic Class, and Cover on Target Sample Size
3. Results
3.1. Percent Cover and Precision Target
3.2. Effect of Sampling Strategy and Benthic Class on Target Sample Size
3.3. Effect of Sampling Strategy and Cover on Target Sample Size
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Target Sample size | Percent Area | No. of Quadrats | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Df | Sum Sq | Mean Sq | F | p | Df | Sum Sq | Mean Sq | F | p | |||
| Botb | Quadrat size | 2 | 275.22 | 137.61 | 1.1544 | 0.3479 | 2 | 117674 | 58837 | 23.361 | 7.28E-05 | |
| Residuals | 12 | 1430.45 | 1.565 | 119.2 | 12 | 30224 | 2519 | |||||
| Clam | Quadrat size | 2 | 146.07 | 73.034 | 1.2123 | 0.329 | 2 | 564160 | 282080 | 146.11 | 1.23E-09 | |
| Residuals | 13 | 783.15 | 60.242 | 13 | 25098 | 1931 | ||||||
| CoBr | Quadrat size | 2 | 102.27 | 51.135 | 0.3399 | 0.7163 | 2 | 260553 | 130277 | 32.592 | 1.04E-06 | |
| Residuals | 18 | 2708.13 | 150.452 | 18 | 71950 | 3997 | ||||||
| Cory | Quadrat size | 2 | 186.7 | 93.352 | 1.048 | 0.3683 | 2 | 82133 | 41066 | 25.044 | 2.75E-06 | |
| Residuals | 21 | 1870.6 | 89.075 | 21 | 34436 | 1640 | ||||||
| CoSp | Quadrat size | 2 | 233.68 | 116.84 | 0.8117 | 0.4576 | 2 | 228353 | 114177 | 26.698 | 1.71E-06 | |
| Residuals | 21 | 3022.86 | 143.95 | 21 | 89809 | 4277 | ||||||
| Digi | Quadrat size | 2 | 166.88 | 83.438 | 0.4972 | 0.6203 | 2 | 189489 | 94744 | 22.005 | 9.67E-05 | |
| Residuals | 12 | 2013.99 | 167.832 | 12 | 51667 | 4306 | ||||||
| Encr | Quadrat size | 2 | 287.71 | 143.85 | 1.285 | 0.2975 | 2 | 107546 | 53773 | 18.836 | 2.06E-05 | |
| Residuals | 21 | 2350.89 | 111.95 | 21 | 59950 | 2855 | ||||||
| FiBr | Quadrat size | 2 | 238.5 | 119.25 | 0.4608 | 0.6394 | 2 | 119947 | 59974 | 7.2632 | 0.006225 | |
| Residuals | 15 | 3881.6 | 258.77 | 15 | 123858 | 8257 | ||||||
| Foli | Quadrat size | 2 | 397.02 | 198.51 | 1.3882 | 0.2715 | 2 | 131277 | 65639 | 18.451 | 2.37E-05 | |
| Residuals | 21 | 3002.9 | 143 | 21 | 74707 | 3557 | ||||||
| FoLt | Quadrat size | 2 | 6.88 | 3.44 | 0.1784 | 0.8449 | 2 | 218961 | 109481 | 7914.3 | 2.61E-06 | |
| Residuals | 3 | 57.855 | 19.285 | 3 | 41 | 14 | ||||||
| Mass | Quadrat size | 2 | 374.7 | 187.33 | 0.9875 | 0.3892 | 2 | 206114 | 103057 | 20.685 | 1.09E-05 | |
| Residuals | 21 | 3983.9 | 189.71 | 21 | 104628 | 4982 | ||||||
| SftB | Quadrat size | 2 | 2.5 | 1.24 | 0.0032 | 0.9968 | 2 | 461072 | 230536 | 15.881 | 0.000106 | |
| Residuals | 18 | 6933.1 | 385.17 | 18 | 261301 | 14517 | ||||||
| SftM | Quadrat size | 2 | 104.96 | 52.478 | 0.6492 | 0.5343 | 2 | 300646 | 150323 | 52.69 | 2.99E-08 | |
| Residuals | 18 | 1454.96 | 80.831 | 18 | 51353 | 2853 | ||||||
| Solt | Quadrat size | 2 | 341.54 | 170.77 | 2.4406 | 0.129 | 2 | 374506 | 187253 | 354.27 | 2.13E-11 | |
| Residuals | 12 | 839.64 | 69.97 | 12 | 6343 | 529 | ||||||
| Stag | Quadrat size | 2 | 391.59 | 195.796 | 3.5357 | 0.04748 | 2 | 45476 | 22738 | 22.9 | 5.29E-06 | |
| Residuals | 21 | 1162.91 | 55.377 | 21 | 20851 | 992.9 | ||||||
| Subm | Quadrat size | 2 | 333.6 | 166.79 | 0.8934 | 0.4266 | 2 | 143260 | 71630 | 23.342 | 1.00E-05 | |
| Residuals | 18 | 3360.4 | 186.69 | 18 | 55237 | 3069 | ||||||
| Tblt | Quadrat size | 2 | 469.28 | 234.638 | 3.8217 | 0.03842 | 2 | 78552 | 39276 | 24.79 | 2.97E-06 | |
| Residuals | 21 | 1289.3 | 61.395 | 21 | 33272 | 1584 | ||||||
| Unkn | Quadrat size | 2 | 263.21 | 131.6 | 0.7905 | 0.4688 | 2 | 201303 | 100651 | 20.658 | 2.18E-05 | |
| Residuals | 18 | 2996.82 | 166.49 | 18 | 87701 | 4872 | ||||||
| Cory(B) | Quadrat size | 2 | 27.49 | 13.745 | 0.5348 | 0.6329 | 2 | 195406 | 97703 | 130.47 | 0.001212 | |
| Residuals | 3 | 77.11 | 25.703 | 3 | 2246 | 749 | ||||||
| Stag(B) | Quadrat size | 2 | 91.9 | 45.95 | 0.0695 | 0.9344 | 2 | 52940 | 26470 | 1.399 | 0.3722 | |
| Residuals | 3 | 1984.9 | 661.64 | 3 | 56762 | 18921 | ||||||
| Cory(D) | Quadrat size | 2 | 168.6 | 84.303 | 0.4365 | 0.6529 | 2 | 382833 | 191416 | 29.018 | 2.34E-06 | |
| Residuals | 18 | 3476.3 | 193.127 | 18 | 118735 | 6596 | ||||||
| FiBr(D) | Quadrat size | 2 | 187.3 | 93.63 | 0.2898 | 0.7535 | 2 | 387327 | 193663 | 17.416 | 0.0002831 | |
| Residuals | 12 | 3876.6 | 323.05 | 12 | 133441 | 11120 | ||||||
| Mass(D) | Quadrat size | 2 | 89.63 | 44.813 | 0.607 | 0.5754 | 2 | 235661 | 117830 | 73.313 | 6.08E-05 | |
| Residuals | 6 | 442.99 | 73.832 | 6 | 9643 | 1607 | ||||||
| Mix(D) | Quadrat size | 2 | 676.97 | 338.49 | 6.961 | 0.005763 | 2 | 83397 | 41698 | 66.709 | 4.74E-09 | |
| Residuals | 18 | 875.27 | 48.63 | 18 | 11251 | 625 | ||||||
| Stag(D) | Quadrat size | 2 | 374.79 | 187.395 | 7.0763 | 0.009332 | 2 | 21892.8 | 10946.4 | 38.776 | 5.79E-06 | |
| Residuals | 12 | 317.78 | 26.482 | 12 | 3387.6 | 282.3 | ||||||
| Subm(D) | Quadrat size | 2 | 159.11 | 79.553 | 1.0112 | 0.3928 | 2 | 416424 | 208212 | 72.214 | 2.04E-07 | |
| Residuals | 12 | 944.05 | 78.671 | 12 | 34599 | 2883 | ||||||
| Tblt(D) | Quadrat size | 2 | 339.76 | 169.88 | 1.2176 | 0.316 | 2 | 271546 | 135773 | 33.733 | 2.77E-07 | |
| Residuals | 21 | 2929.86 | 139.52 | 21 | 84523 | 4025 | ||||||
References
- Pandolfi, J.M.; Bradbury, R.H.; Sala, E.; Hughes, T.P.; Bjorndal, K.A.; Cooke, R.G.; McArdle, D.; McClenachan, L.; Newman, M.J.H.; Paredes, G. Global trajectories of the long-term decline of coral reef ecosystems. Science 2003, 301, 955–958. [Google Scholar] [CrossRef] [Green Version]
- Hughes, T.P.; Kerry, J.T.; Alvarez-Noriega, M.; Alvarez-Romero, J.G.; Anderson, K.D.; Baird, A.H.; Babcock, R.C.; Beger, M.; Bellwood, D.R.; Berkelmans, R.; et al. Global warming and recurrent mass bleaching of corals. Nature 2017, 543, 373–377. [Google Scholar] [CrossRef] [PubMed]
- De’ath, G.; Fabricius, K.E.; Sweatman, H.; Puotinen, M. The 27-year decline of coral cover on the Great Barrier Reef and its causes. Proc. Natl. Acad. Sci. USA 2012, 109, 17995–17999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hughes, T.P.; Rodrigues, M.J.; Bellwood, D.R.; Ceccarelli, D.; Hoegh-Guldberg, O.; McCook, L.; Moltschaniwskyj, N.; Pratchett, M.S.; Steneck, R.S.; Willis, B.L. Phase shifts, herbivory, and the resilience of coral reefs to climate change. Curr. Biol. 2007, 17, 360–365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferrari, R.; Bryson, M.; Bridge, T.; Hustache, J.; Williams, S.B.; Byrne, M.; Figueira, W. Quantifying the response of structural complexity and community composition to environmental change in marine communities. Glob. Chang. Biol. 2016, 22, 1965–1975. [Google Scholar] [CrossRef] [PubMed]
- Hedley, J.D.; Roelfsema, C.M.; Chollett, I.; Harborne, A.R.; Heron, S.F.; Weeks, S.; Skirving, W.J.; Strong, A.E.; Eakin, C.M.; Christensen, T.R. Remote sensing of coral reefs for monitoring and management: A review. Remote Sens. 2016, 8, 118. [Google Scholar] [CrossRef] [Green Version]
- Boström, C.; Pittman, S.J.; Simenstad, C.; Kneib, R.T. Seascape ecology of coastal biogenic habitats: Advances, gaps, and challenges. Mar. Ecol. Prog. Ser. 2011, 427, 191–217. [Google Scholar] [CrossRef] [Green Version]
- Jonker, M.M.; Johns, K.K.; Osborne, K.K. Surveys of benthic reef communities using underwater digital photography and counts of juvenile corals. In Long--term Monitoring of the Great Barrier Reef. Standard Operational Procedure. 2008. Available online: https://www.aims.gov.au/docs/research/monitoring/reef/sops.html (accessed on 13 November 2019).
- Palma, M.; Rivas Casado, M.; Pantaleo, U.; Cerrano, C. High Resolution Orthomosaics of African Coral Reefs: A Tool for Wide-Scale Benthic Monitoring. Remote Sens. 2017, 9, 705. [Google Scholar] [CrossRef] [Green Version]
- Pizarro, O.; Friedman, A.; Bryson, M.; Williams, S.B.; Madin, J. A simple, fast, and repeatable survey method for underwater visual 3D benthic mapping and monitoring. Ecol. Evol. 2017, 7, 1770–1782. [Google Scholar] [CrossRef]
- Edwards, C.B.; Eynaud, Y.; Williams, G.J.; Pedersen, N.E.; Zgliczynski, B.J.; Gleason, A.C.; Smith, J.E.; Sandin, S.A. Large-area imaging reveals biologically driven non-random spatial patterns of corals at a remote reef. Coral Reefs 2017, 36, 1291–1305. [Google Scholar] [CrossRef] [Green Version]
- González-Rivero, M.; Beijbom, O.; Rodriguez-Ramirez, A.; Holtrop, T.; González-Marrero, Y.; Ganase, A.; Roelfsema, C.; Phinn, S.; Hoegh-Guldberg, O. Scaling up ecological measurements of coral reefs using semi-automated field image collection and analysis. Remote Sens. 2016, 8, 30. [Google Scholar] [CrossRef] [Green Version]
- Bryson, M.; Ferrari, R.; Figueira, W.; Pizarro, O.; Madin, J.; Williams, S.B.; Byrne, M. Characterization of measurement errors using structure-from-motion and photogrammetry to measure marine habitat structural complexity. Ecol. Evol. 2017, 7, 5669–5681. [Google Scholar] [CrossRef] [PubMed]
- Burns, J.H.R.; Delparte, D.; Kapono, L.; Belt, M.; Gates, R.D.; Takabayashi, M. Assessing the impact of acute disturbances on the structure and composition of a coral community using innovative 3D reconstruction techniques. Methods Oceanogr. 2016, 15–16, 49–59. [Google Scholar] [CrossRef] [Green Version]
- Figueira, W.; Ferrari, R.; Weatherby, E.; Porter, A.; Hawes, S.; Byrne, M. Accuracy and Precision of Habitat Structural Complexity Metrics Derived from Underwater Photogrammetry. Remote Sens. 2015, 7, 16883–16900. [Google Scholar] [CrossRef] [Green Version]
- Beijbom, O.; Edmunds, P.J.; Roelfsema, C.; Smith, J.; Kline, D.I.; Neal, B.P.; Dunlap, M.J.; Moriarty, V.; Fan, T.-Y.; Tan, C.-J. Towards automated annotation of benthic survey images: Variability of human experts and operational modes of automation. PLoS ONE 2015, 10, e0130312. [Google Scholar] [CrossRef] [PubMed]
- Leujak, W.; Ormond, R.F.G. Comparative accuracy and efficiency of six coral community survey methods. J. Exp. Mar. Biol. Ecol. 2007, 351, 168–187. [Google Scholar] [CrossRef]
- Perkins, N.R.; Foster, S.D.; Hill, N.A.; Barrett, N.S. Image subsampling and point scoring approaches for large-scale marine benthic monitoring programs. Estuar. Coast. Shelf Sci. 2016, 176, 36–46. [Google Scholar] [CrossRef]
- Brown, E.K.; Cox, E.; Jokiel, P.; Rodgers, S.K.u.; Smith, W.R.; Tissot, B.N.; Coles, S.L.; Hultquist, J. Development of benthic sampling methods for the Coral Reef Assessment and Monitoring Program (CRAMP) in Hawai’i. Pac. Sci. 2004, 58, 145–158. [Google Scholar] [CrossRef] [Green Version]
- Mapstone, B.D.; Ayling, T. An Investigation of Optimum Methods and Unit Sizes for the Visual Estimation of Abundances of Some Coral Reef Organisms (No. 47); Great Barrier Reef Marine Park Authority: Townsville, Australia, 1998.
- Brown, C.J.; Smith, S.J.; Lawton, P.; Anderson, J.T. Benthic habitat mapping: A review of progress towards improved understanding of the spatial ecology of the seafloor using acoustic techniques. Estuar. Coast. Shelf Sci. 2011, 92, 502–520. [Google Scholar] [CrossRef]
- Lecours, V.; Devillers, R.; Schneider, D.C.; Lucieer, V.L.; Brown, C.J.; Edinger, E.N. Spatial scale and geographic context in benthic habitat mapping: Review and future directions. Mar. Ecol. Prog. Ser. 2015, 535, 259–284. [Google Scholar] [CrossRef] [Green Version]
- GBRMPA. Great Barrier Reef Marine Park Authority Spatial Data Geoportal. Available online: http://www.gbrmpa.gov.au/geoportal/catalog/download/download.page (accessed on 31 May 2017).
- Agisoft LLC. Agisoft Photoscan User Manual; Professional Edition v. 1. 3; Agisoft LLC: St Petersburg, Russia, 2014. [Google Scholar]
- ESRI Inc. ArcGIS 10.3; ESRI Inc.: Redlands, CA, USA, 2004. [Google Scholar]
- Althaus, F.; Hill, N.; Ferrari, R.; Edwards, L.; Przeslawski, R.; Schönberg, C.H.; Stuart-Smith, R.; Barrett, N.; Edgar, G.; Colquhoun, J. A standardised vocabulary for identifying benthic biota and substrata from underwater imagery: The CATAMI classification scheme. PLoS ONE 2015, 10, e0141039. [Google Scholar] [CrossRef]
- Jokiel, P.L.; Rodgers, K.S.; Brown, E.K.; Kenyon, J.C.; Aeby, G.; Smith, W.R.; Farrell, F. Comparison of methods used to estimate coral cover in the Hawaiian Islands. PeerJ 2015, 3, e954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roberts, T.; Moloney, J.; Sweatman, H.; Bridge, T. Benthic community composition on submerged reefs in the central Great Barrier Reef. Coral Reefs 2015, 34, 569–580. [Google Scholar] [CrossRef]
- R Core Team. The R Project for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 31 May 2017).
- Kendall, W.L.; White, G.C. A cautionary note on substituting spatial subunits for repeated temporal sampling in studies of site occupancy. J. Appl. Ecol. 2009, 46, 1182–1188. [Google Scholar] [CrossRef]
- TIBCO Software Inc. Statistica v. 12.1; TIBCO Software Inc.: Palo Alto, CA, USA, 2017. [Google Scholar]
- Kowalewski, L.K.; Chizinski, C.J.; Powell, L.A.; Pope, K.L.; Pegg, M.A. Accuracy or precision: Implications of sample design and methodology on abundance estimation. Ecol. Model. 2015, 316, 185–190. [Google Scholar] [CrossRef] [Green Version]
- Pringle, J. Efficiency estimates for various quadrat sizes used in benthic sampling. Can. J. Fish. Aquat. Sci. 1984, 41, 1485–1489. [Google Scholar] [CrossRef]
- Roelfsema, C.; Phinn, S.; Udy, N.; Maxwell, P. An integrated field and remote sensing approach for mapping seagrass cover, Moreton Bay, Australia. J. Spat. Sci. 2009, 54, 45–62. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.M.; Phinn, S.R.; Mumby, P.J. Environmental and sensor limitations in optical remote sensing of coral reefs: Implications for monitoring and sensor design. Remote Sens. 2012, 4, 271–302. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, R.; Malcolm, H.; Neilson, J.; Lucieer, V.; Jordan, A.; Ingleton, T.; Figueira, W.; Johnstone, N.; Hill, N. Integrating distribution models and habitat classification maps into marine protected area planning. Estuar. Coast. Shelf Sci. 2018, 212, 40–50. [Google Scholar] [CrossRef] [Green Version]
- Roelfsema, C.; Kovacs, E.; Ortiz, J.C.; Wolff, N.H.; Callaghan, D.; Wettle, M.; Ronan, M.; Hamylton, S.M.; Mumby, P.J.; Phinn, S. Coral reef habitat mapping: A combination of object-based image analysis and ecological modelling. Remote Sens. Environ. 2018, 208, 27–41. [Google Scholar] [CrossRef]

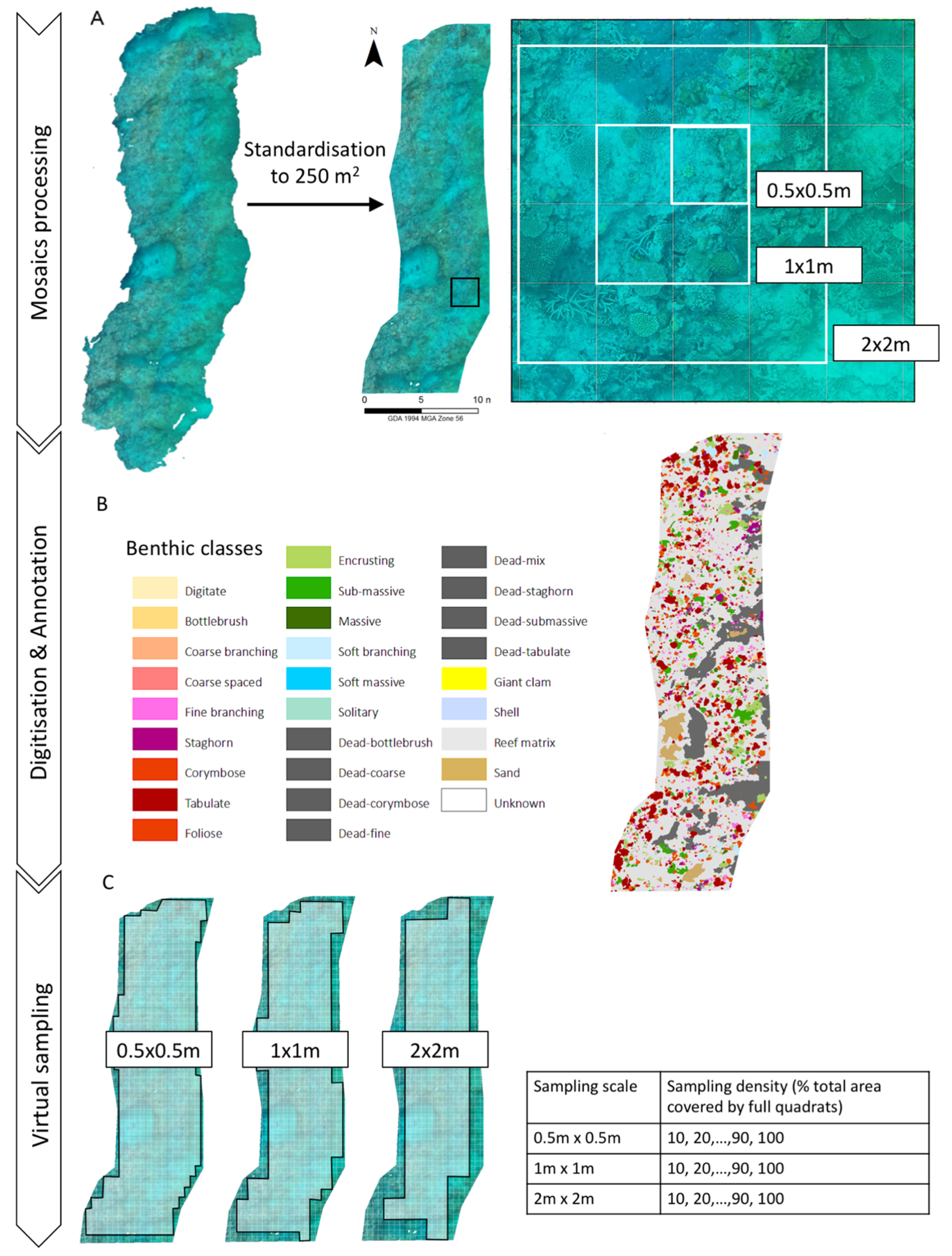


| Process | Settings | Comments |
|---|---|---|
| Photo alignment | High accuracy, pair selection enabled, key point limit 40000, tie point limit 4000, do not constrain features by mask | Align photos by common invariant key points resulting in a 3D sparse point cloud |
| Sparse point cloud | All optimisation properties yes except fit b1, b2; k4, p3, p4, rolling shutter | Optimisation of alignment based on camera and lenses properties |
| Dense point cloud | Medium quality, moderate depth filtering, do not reuse depth maps | Fill the sparse point cloud based on common points in the photos and camera locations |
| Mesh | Arbitrary surface type, source data-dense cloud face, count medium, interpolation enabled, all point classes | Create continuous 3D surface over dense cloud |
| Texture | Generic mapping mode, texture from all cameras, mosaic blending mode, texture size 8192, texture count 1, no color correction | Drape the original photos over the mesh |
| Mosaic building | Mesh surface type, mosaic blending mode, no color correction, hole filling enabled | Generate mosaic from mesh surface |
| Quadrat Size | ||||||
|---|---|---|---|---|---|---|
| 0.5 × 0.5 m | 1 × 1 m | 2 × 2 m | ||||
| Sites | NQuad | Area | NQuad | Area | NQuad | Area |
| BE | 928 | 232 | 206 | 206 | 43 | 172 |
| BP | 826 | 206.5 | 181 | 181 | 35 | 140 |
| BT | 914 | 228.5 | 205 | 205 | 41 | 164 |
| CA | 908 | 227 | 205 | 205 | 39 | 156 |
| HB | 922 | 230.5 | 204 | 204 | 42 | 168 |
| HE | 924 | 231 | 212 | 212 | 47 | 188 |
| JT | 912 | 228 | 208 | 208 | 42 | 168 |
| PP | 923 | 230.75 | 212 | 212 | 43 | 172 |
| Coarse Categories | Benthic Classes | Codes | Mean Cover (%) | SE | Presence (No. of Sites) |
|---|---|---|---|---|---|
| Abiotic | Reef matrix | Reef | 40.587 | 10.517 | 7 |
| Sand | Sand | 3.038 | 1.442 | 7 | |
| Macroalgae | Algae | Alga | 0.066 | - | 2 |
| Hard corals | Bottlebrush | Btb | 2.466 | 2.231 | 5 |
| Coarse branching | CoBr | 0.151 | 0.042 | 7 | |
| Coarse spaced | CoSp | 0.418 | 0.120 | 8 | |
| Columnar | Colu | 0.039 | 0.029 | 2 | |
| Corymbose | Cory | 2.367 | 0.659 | 8 | |
| Digitate | Figi | 0.139 | 0.042 | 5 | |
| Encrusting | Encr | 2.654 | 0.734 | 8 | |
| Fine branching | FiBr | 1.618 | 0.889 | 6 | |
| Foliose | Foli | 4.372 | 1.713 | 8 | |
| Foliose lettuce | FoLt | 0.070 | 0/013 | 2 | |
| Massive | Mass | 0.899 | 0.260 | 8 | |
| Solitary | Solt | 0.012 | 0.001 | 5 | |
| Staghorn | Stag | 21.266 | 7.948 | 8 | |
| Submassive | Subm | 1.035 | 0.384 | 7 | |
| Tabulate | Tblt | 5.362 | 2.027 | 8 | |
| Soft corals | Soft branching | SftB | 0.444 | 0.185 | 8 |
| Soft massive | SftM | 0.274 | 0.136 | 7 | |
| Bleached corals | Bottlebrush | Btb(B) | 0.031 | - | 1 |
| Coarse branching | CoBr(B) | 0.003 | - | 1 | |
| Corymbose | Cory(B) | 0.031 | 0.009 | 2 | |
| Fine branching | FiBr(B) | 0.010 | - | 1 | |
| Staghorn | Stag(B) | 17.322 | 17.131 | 2 | |
| Soft massive | SftM(B) | 0.014 | - | 1 | |
| Dead corals | Bottlebrush | Btb(D) | 0.004 | - | 1 |
| Coarse branching | CoBr(D) | 0.039 | - | 1 | |
| Coarse spaced | CoSp(D) | 0.561 | - | 1 | |
| Corymbose | Cory(D) | 0.213 | 0.089 | 7 | |
| Encrusting | Encr(D) | 0.185 | 0.096 | 2 | |
| Fine branching | FiBr(D) | 0.088 | 0.043 | 5 | |
| Foliose | Foli(D) | 0.039 | - | 1 | |
| Massive | Mass(D) | 0.030 | 0.014 | 3 | |
| Mix | Mix(D) | 3.033 | 1.001 | 7 | |
| Staghorn | Stag(D) | 15.530 | 4.2 | 5 | |
| Submassive | Subm(D) | 0.093 | 0.037 | 5 | |
| Tabulate | Tblt(D) | 2.023 | 1.571 | 8 | |
| Unknown | Unkn(D) | 0.006 | - | 1 | |
| Molluscs | Giant clam | Clam | 0.011 | 0.003 | 6 |
| Shell | Shel | 0.001 | 1.28E-05 | 2 | |
| Unknown | Unknown | Unkn | 0.799 | 0.292 | 7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lechene, M.A.A.; Haberstroh, A.J.; Byrne, M.; Figueira, W.; Ferrari, R. Optimising Sampling Strategies in Coral Reefs Using Large-Area Mosaics. Remote Sens. 2019, 11, 2907. https://doi.org/10.3390/rs11242907
Lechene MAA, Haberstroh AJ, Byrne M, Figueira W, Ferrari R. Optimising Sampling Strategies in Coral Reefs Using Large-Area Mosaics. Remote Sensing. 2019; 11(24):2907. https://doi.org/10.3390/rs11242907
Chicago/Turabian StyleLechene, Marine Anna Alice, Anna Julia Haberstroh, Maria Byrne, Will Figueira, and Renata Ferrari. 2019. "Optimising Sampling Strategies in Coral Reefs Using Large-Area Mosaics" Remote Sensing 11, no. 24: 2907. https://doi.org/10.3390/rs11242907
APA StyleLechene, M. A. A., Haberstroh, A. J., Byrne, M., Figueira, W., & Ferrari, R. (2019). Optimising Sampling Strategies in Coral Reefs Using Large-Area Mosaics. Remote Sensing, 11(24), 2907. https://doi.org/10.3390/rs11242907







