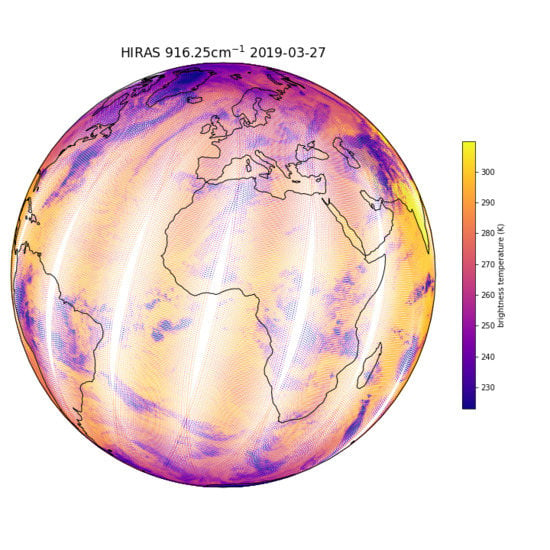
Assessment of the Hyperspectral Infrared Atmospheric Sounder (HIRAS)
Abstract
:1. Introduction
2. Methodology
2.1. Assessment of HIRAS FSR
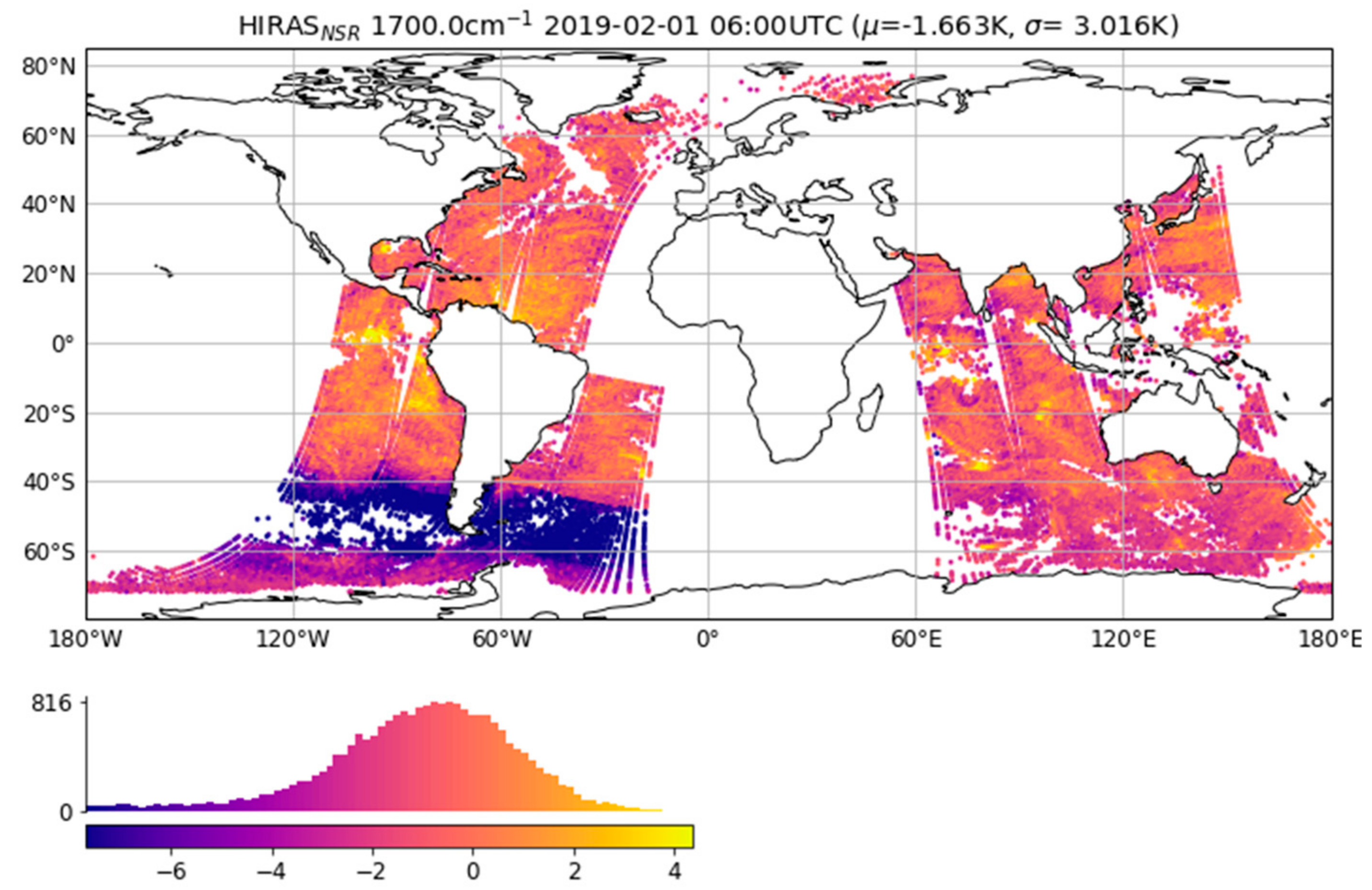
2.2. Assessment of HIRAS NSR
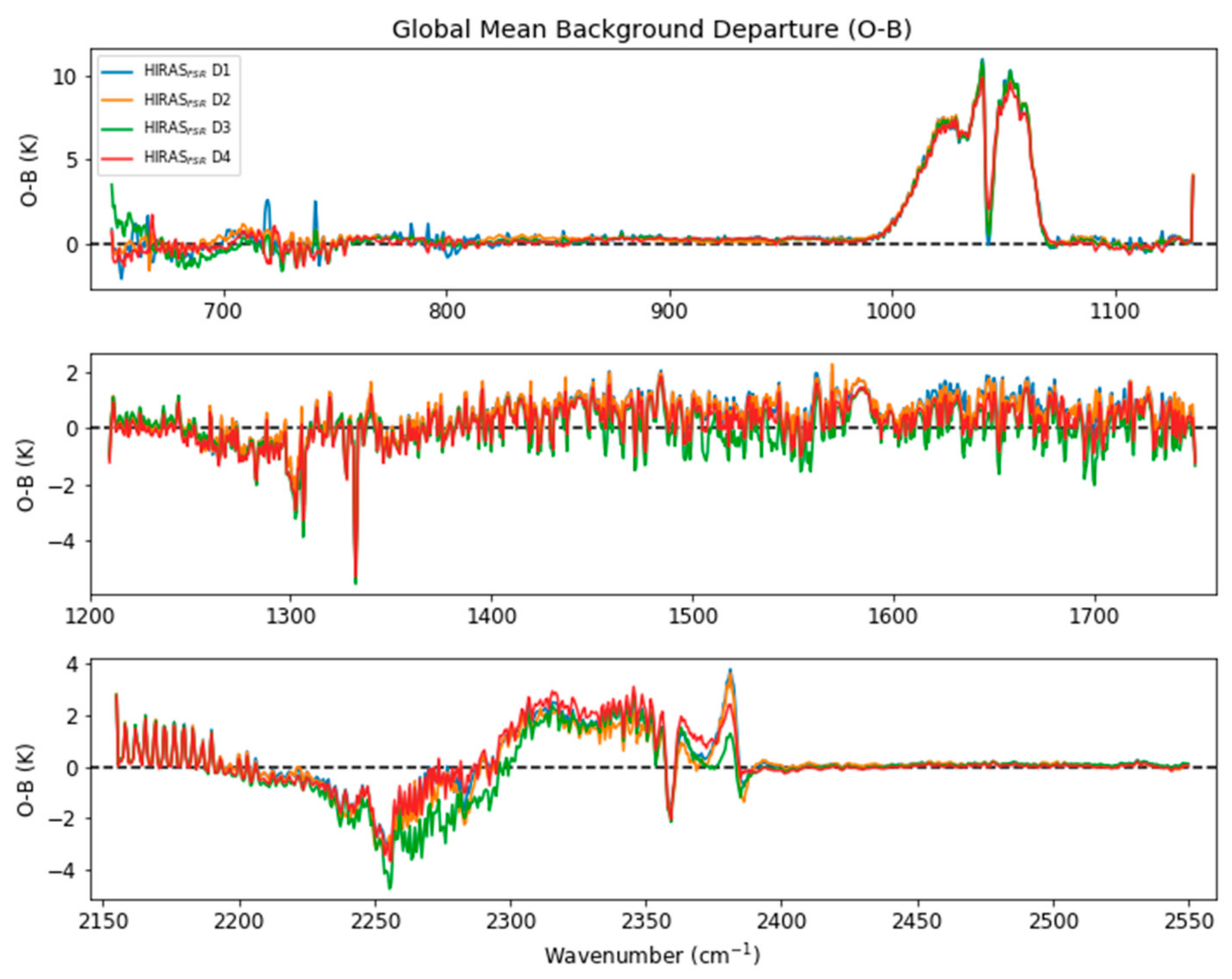
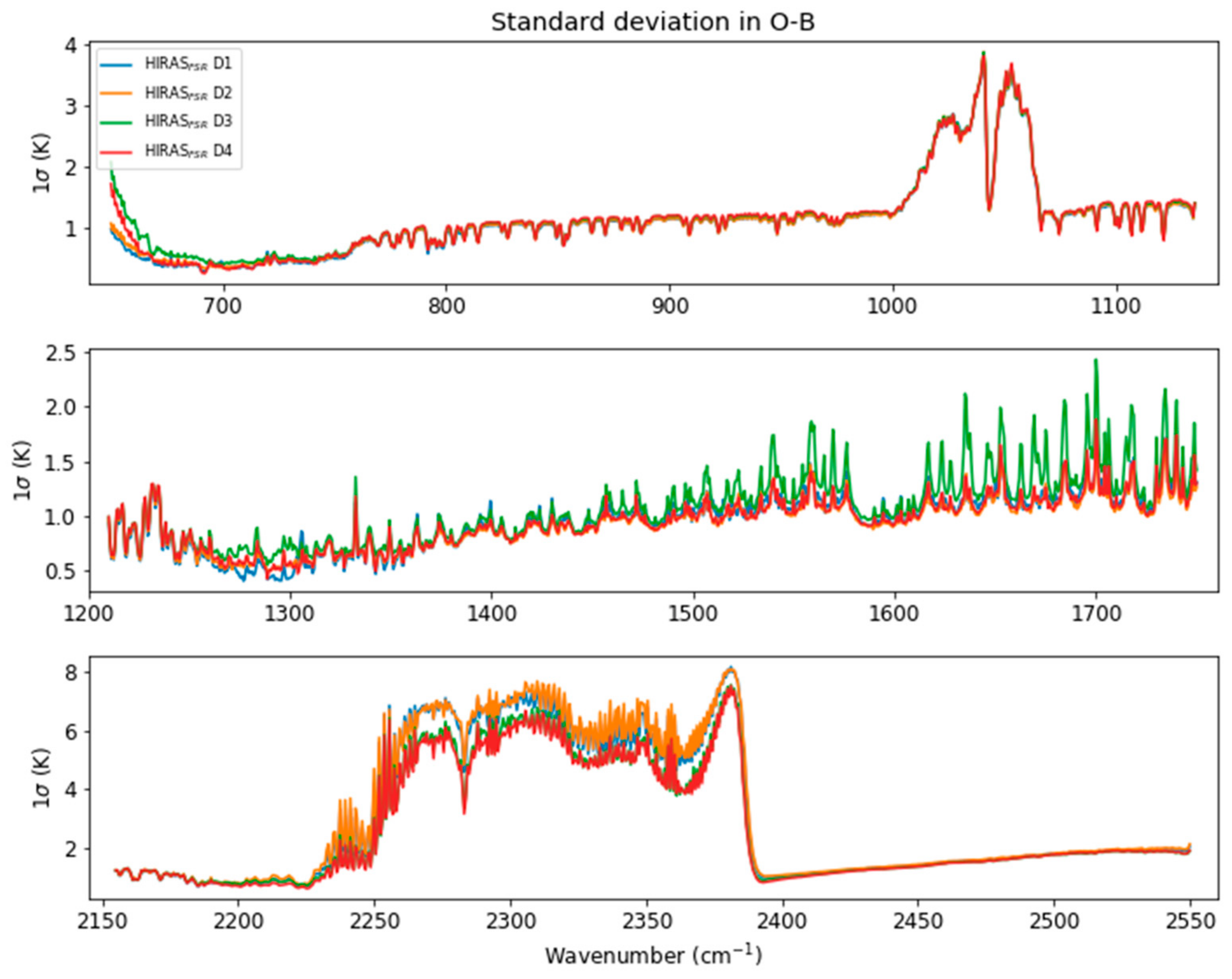
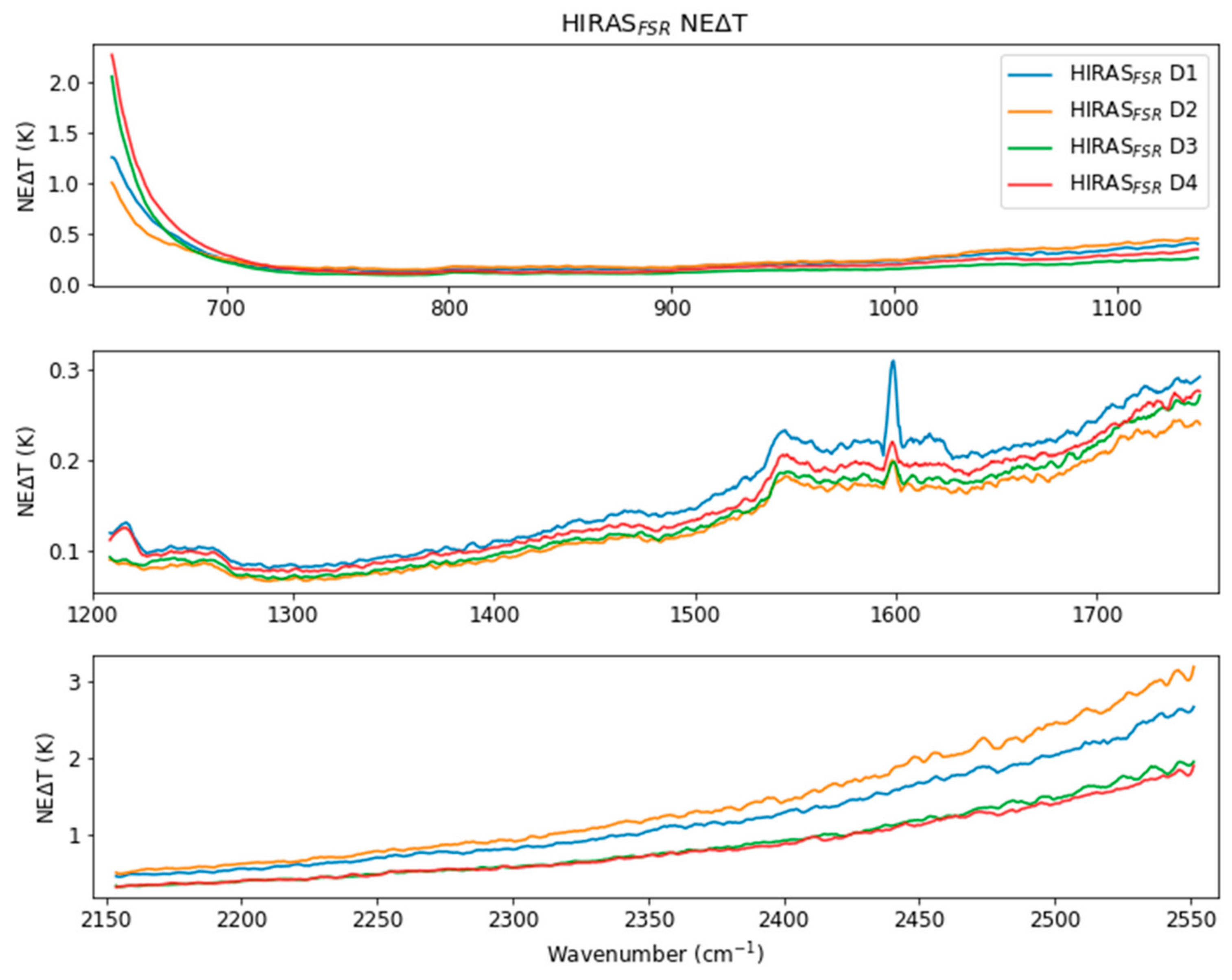
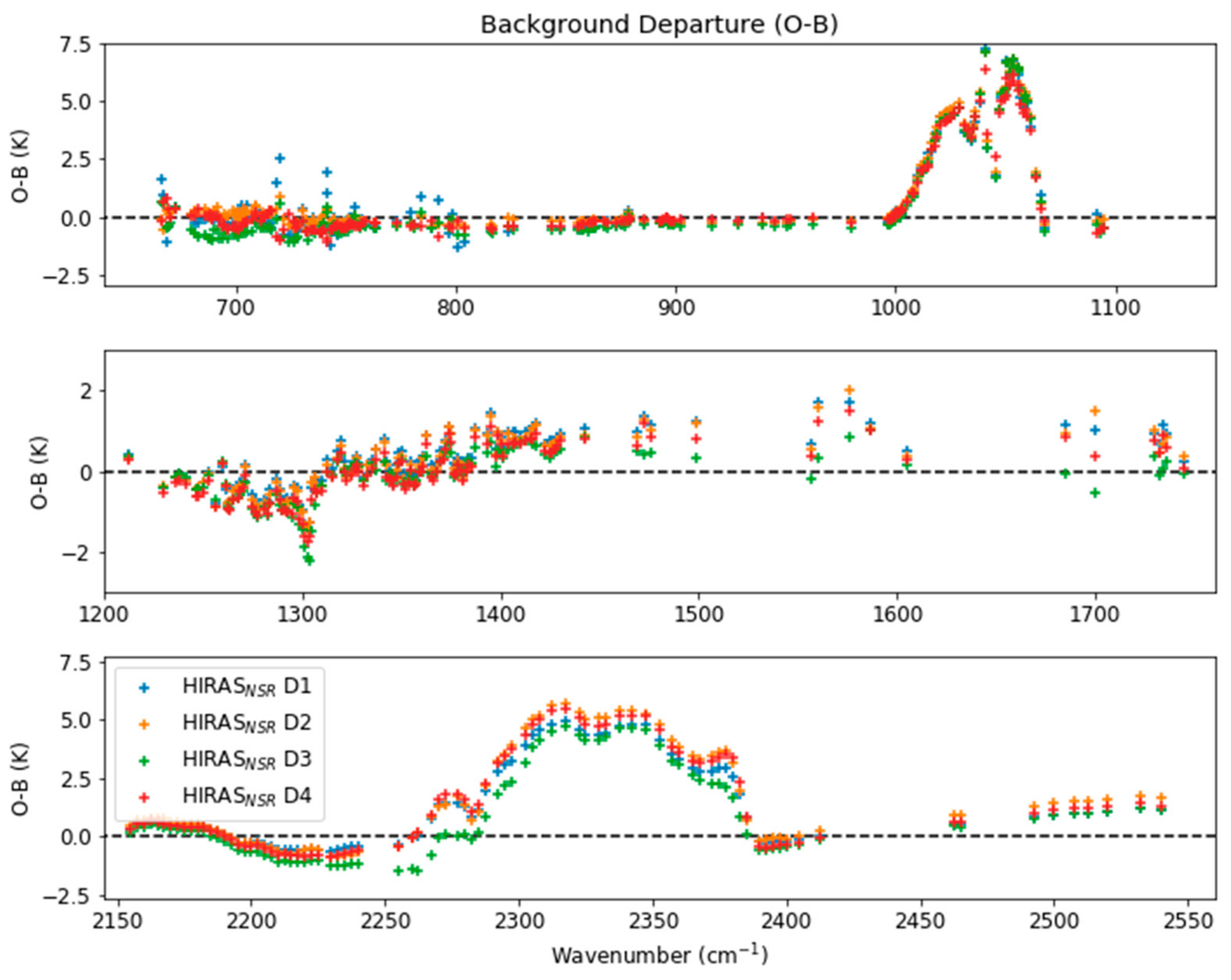
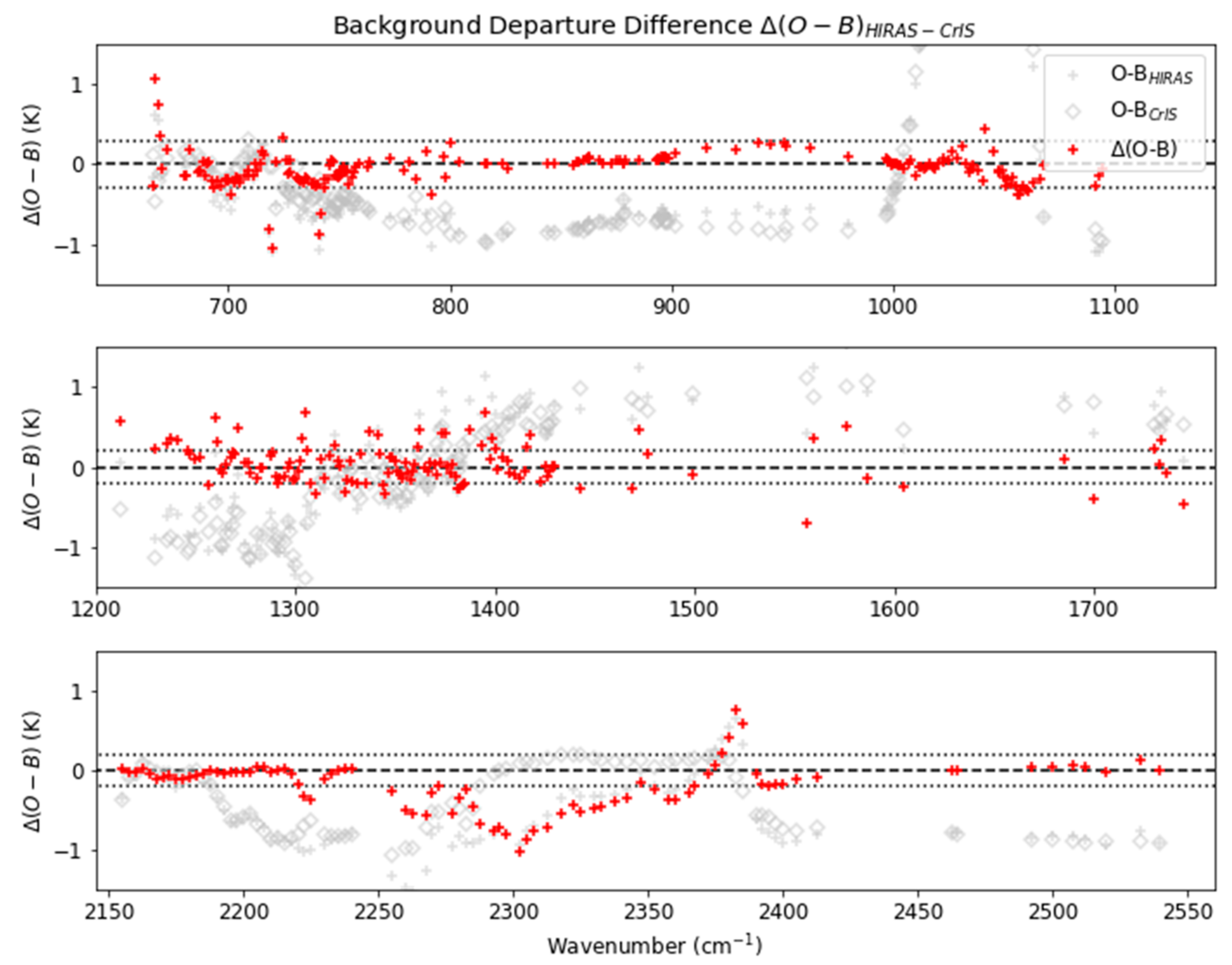
3. Results
4. Discussion
4.1. Surface Emissivity
4.2. Spectroscopy
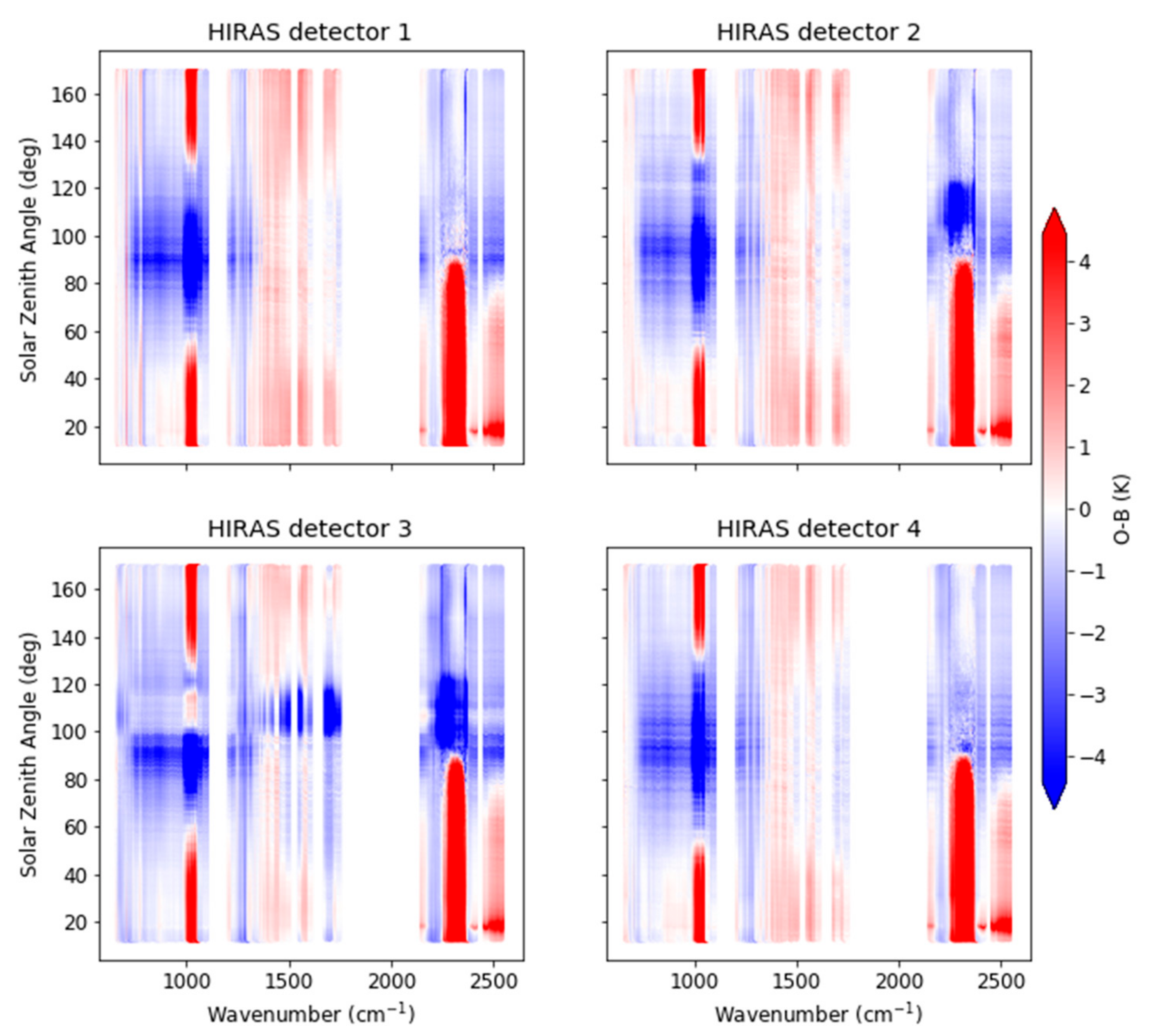
4.3. Solar Contamination
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aumann, H.H.; Gregorich, D.T.; Gaiser, S.L.; Chahine, M.T. Application of Atmospheric Infrared Sounder (AIRS) data to climate research. In Sensors, Systems, and Next-Generation Satellites VIII. Int. Soc. Opt. Photonics 2004, 5570, 202–208. [Google Scholar]
- Blumstein, D.; Tournier, B.; Cayla, F.R.; Phulpin, T.; Fjortoft, R.; Buil, C.; Ponce, G. In-flight performance of the infrared atmospheric sounding interferometer (IASI) on Metop-A. Proc. SPIE 2007, 6684, 66840H-1–66840H-12. [Google Scholar]
- Han, Y.; Revercomb, H.; Cromp, M.; Gu, D.; Johnson, D.; Mooney, D.; Scott, D.; Strow, L.; Bingham, G.; Borg, L.; et al. Suomi NPP CrIS measurements, sensor data record algorithm, calibration and validation activities, and record data quality. J. Geophys. Res. Atmos. 2013, 118, 12734–12748. [Google Scholar] [CrossRef]
- Cameron, J.R.N.; Collard, A.D.; English, S.J. Operational use of AIRS observations at the Met Office. In Proceedings of the ITSC-XIV, Beijing, China, 25–31 May 2005. [Google Scholar]
- Hilton, F.; Atkinson, N.C.; English, S.J.; Eyre, J.R. Assimilation of IASI at the Met Office and assessment of its impact through observing system experiments. Q. J. R. Meteorol. Soc. 2009, 135, 495–505. [Google Scholar] [CrossRef]
- Cardinali, C. Monitoring the observation impact on the short-range forecast. Q. J. R. Meteorol. Soc. 2009, 135, 239–250. [Google Scholar] [CrossRef]
- Hilton, F.; Armante, R.; August, T.; Barnet, C.; Bouchard, A.; Camy-Peyret, C.; Capelle, V.; Clarisse, L.; Clerbaux, C.; Coheur, P.F.; et al. Hyperspectral Earth observation from IASI: Five years of accomplishments. Bull. Am. Meteorol. Soc. 2012, 93, 347–370. [Google Scholar] [CrossRef]
- Smith, A.; Atkinson, N.; Bell, W.; Doherty, A. An initial assessment of observations from the Suomi-NPP satellite: Data from the Cross-track Infrared Sounder (CrIS). Atmos. Sci. Lett. 2015, 16, 260–266. [Google Scholar] [CrossRef]
- Strow, L.L.; Motteler, H.; Tobin, D.; Revercomb, H.; Hannon, S.; Buijs, H.; Predina, J.; Suwinski, L.; Glumb, R. Spectral calibration and validation of the Cross-track Infrared Sounder (CrIS) on the Suomi NPP satellite. J. Geophys. Res. Atmos. 2013, 118, 12486–12496. [Google Scholar] [CrossRef]
- Tobin, D.; Revercomb, H.; Knuteson, R.; Taylor, J.; Best, F.; Borg, L.; DeSlover, D.; Martin, G.; Buijs, H.; Esplin, M.; et al. Suomi-NPP CrIS radiometric calibration uncertainty. J. Geophys. Res. Atmos. 2013, 118, 10589–10600. [Google Scholar] [CrossRef]
- Wang, L.; Tremblay, D.A.; Han, Y.; Esplin, M.; Hagan, D.E.; Predina, J.; Suwinski, L.; Jin, X.; Chen, Y. Geolocation assessment for CrIS sensor data records. J. Geophys. Res. Atmos. 2013, 118, 12690–12704. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, B.; Tremblay, D.; Han, Y. Improved scheme for Cross-track Infrared Sounder geolocation assessment and optimization. J. Geophys. Res. Atmos. 2017, 122, 519–536. [Google Scholar] [CrossRef]
- Larar, A.M.; Smith, W.L.; Zhou, D.K.; Liu, X.; Revercomb, H.; Taylor, J.P.; Newman, S.M.; Schlüssel, P. IASI spectral radiance validation inter-comparisons: Case study assessment from the JAIVEx field campaign. Atmos. Chem. Phys. 2010, 10, 411–430. [Google Scholar] [CrossRef] [Green Version]
- Newman, S.M.; Larar, A.M.; Smith, W.L.; Ptashnik, I.V.; Jones, R.L.; Mead, M.I.; Revercomb, H.; Tobin, D.C.; Taylor, J.K.; Taylor, J.P. The Joint Airborne IASI Validation Experiment:An evaluation of instrument and algorithms. J. Quant. Spectrosc. Ra. 2012, 113, 1372–1390. [Google Scholar] [CrossRef]
- Wang, L.; Wu, X.; Goldberg, M.; Cao, C.; Li, Y.; Sohn, S. Comparison of AIRS and IASI Radiances Using GOES Imagers as Transfer Radiometers toward Climate Data Records. J. Appl. Meteor. Clim. 2010, 49, 478–492. [Google Scholar] [CrossRef]
- Wang, L.; Han, Y.; Jin, X.; Chen, Y.; Tremblay, D.A. Radiometric consistency assessment of hyperspectral infrared sounders. Atmos. Meas. Tech. 2015, 8, 4831–4844. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Chen, Y. Inter-Comparing SNPP and NOAA-20 CrIS Toward Measurement Consistency and Climate Data Records. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2024–2031. [Google Scholar] [CrossRef]
- Cao, C.; Weinreb, M.; Xu, H. Predicting Simultaneous Nadir Overpasses among Polar-Orbiting Meteorological Satellites for the Intersatellite Calibration of Radiometers. J. Atmos. Ocean. Technol. 2014, 21, 537–542. [Google Scholar] [CrossRef]
- Wang, L.; Goldberg, M.; Wu, X.; Cao, C.; Iacovazzi, R.A.; Yu, F.; Li, Y. Consistency assessment of Atmospheric Infrared Sounder and Infrared Atmospheric Sounding Interferometer radiances: Double differences versus simultaneous nadir overpasses. J. Geophys. Res. 2011, 116, D11111. [Google Scholar] [CrossRef]
- Saunders, R.W.; Blackmore, T.A.; Candy, B.; Francis, P.N.; Hewison, T.J. Monitoring Satellite Radiance Biases Using NWP Models. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1124–1138. [Google Scholar] [CrossRef]
- Bormann, N.; Fouilloux, A.; Bell, W. Evaluation and assimilation of ATMS data in the ECMWF system. J. Geophys. Res. Atmos. 2013, 118, 12970–12980. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A.; et al. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef] [Green Version]
- Loew, A.; Bell, W.; Brocca, L.; Bulgin, C.E.; Burdanowitz, J.; Calbet, X.; Donner, R.V.; Ghent, D.; Gruber, A.; Kaminski Tand Kinzel, J.; et al. Validation practices for satellitebased earth observation data across communities. Rev. Geophys. 2017, 55, 779–817. [Google Scholar] [CrossRef] [Green Version]
- Carminati, F.; Migliorini, S.; Ingleby, B.; Bell, W.; Lawrence, H.; Newman, S.; Hocking, J.; Smith, A. Using reference radiosondes to characterise NWP model uncertainty for improved satellite calibration and validation. Atmos. Meas. Tech. 2019, 12, 83–106. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Lu, N.; Shi, J.; Zhang, P.; Dong, C.; Yang, J. Overview of FY-3 Payload and Ground Application System. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4846–4853. [Google Scholar] [CrossRef]
- Qi, C.; Gu, M.; Wu, C.; Hu, X. Calibration Method of High Spectral Infrared Atmospheric Sounder Onboard FY-3D Satellite. In Proceedings of the 3rd International Symposium of Space Optical Instruments and Applications, Beijing, China, 26–29 June 2016; Volume 192. [Google Scholar]
- Smith, A.; Hocking, J. Radiance Simulator v2.2User Guide, NWPSAF-MO-UD-040, Version 0.5, 2019. Available online: https://www.nwpsaf.eu/site/download/documentation/rad_sim/user_documentation/RadSim_UserGuide.pdf (accessed on 9 December 2019).
- Lorenc, A.C.; Ballard, S.P.; Bell, R.S.; Ingleby, N.B.; Andrews, P.L.F.; Barker, D.M.; Bray, J.R.; Clayton, A.M.; Dalby, T.; Li, D.; et al. The Mat. Office global three-dimensional variational data assimilation scheme. Q. J. R. Meteorol. Soc. 2000, 126, 2991–3012. [Google Scholar] [CrossRef]
- Rawlins, F.; Ballard, S.; Bovis, K.; Clayton, A.; Li, D.; Inverarity, G.; Lorenc, A.; Payne, T. The Met Office global four dimensional variational data assimilation scheme. Q. J. R. Meteor. Soc. 2007, 133, 347–362. [Google Scholar] [CrossRef]
- Auligné, T.; McNally, A.P.; Dee, D.P. Adaptive bias correction for satellite data in a numerical weather prediction system. Q. J. R. Meteorol. Soc. 2007, 133, 631–642. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Rundle, D.; Rayer, P.; Havemann, S.; Matricardi, M.; Geer, A.; Lupu, C.; Brunel, P.; Vidot, J. RTTOV-12 Science and Validation Report, NWPSAF-MO-TV-41, Version 1.0, 2017. Available online: https://www.nwpsaf.eu/site/download/documentation/rtm/docs_rttov12/rttov12_svr.pdf (accessed on 9 December 2019).
- Joint Polar Satellite System (JPSS). Cross Track Infrared Sounder (CrIS) Sensor Data Records (SDR) Algorithm Theoretical Basis Document (ATBD), 2018. Available online: https://www.star.nesdis.noaa.gov/jpss/documents/ATBD/D0001-M01-S01-002_JPSS_ATBD_CRIS-SDR_fsr_20180614.pdf (accessed on 9 December 2019).
- Eyre, J.R.; Menzel, W.P. Retrieval of cloud parameters from satellite sounder data: A simulation study. J. Appl. Meteorol. 1989, 28, 267–275. [Google Scholar] [CrossRef] [Green Version]
- Labrot, T.; Atkinson, N.; Roquet, P. AAPP Documentation Software Description, NWPSAF-MF-UD-002, Version 8.1, 2019. Available online: https://www.nwpsaf.eu/site/software/aapp/documentation/ (accessed on 9 December 2019).
- Gambacorta, A.; Barnet, C.D. Methodology and information content of the NOAA NESDIS operational channel selection for the Cross-Track Infrared Sounder (CrIS). IEEE Trans. Geosci. Remote Sens. 2013, 51, 3207–3216. [Google Scholar] [CrossRef]
- Li, X.; Zou, X. Bias characterization of CrIS radiances at 399 selected channels with respect to NWP model simulations. Atmos. Res. 2017, 196, 164–181. [Google Scholar] [CrossRef]
- Walters, D.; Boutle, I.; Brooks, M.; Melvin, T.; Stratton, R.; Vosper, S.; Wells, H.; Williams, K.; Wood, N.; Allen, T.; et al. The Met Office Unified Model Global Atmosphere 6.0/6.1 and JULES Global Land 6.0/6.1 configurations. Geosci. Model Dev. 2017, 10, 1487–1520. [Google Scholar] [CrossRef] [Green Version]
- Cao, C.; Weinreb, M.; Sullivan, J. Solar contamination effects on the infrared channels of the advanced very high resolution radiometer (AVHRR). J. Geophys. Res. 2001, 106, 33463–33469. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurements of the roughness of the sea surface from photographs of the sun’s glitter. J. Opt. Soc. Am. 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Optical constants of water in the 200nm to 200μm wavelength region. Appl. Opt. 1973, 12, 555–563. [Google Scholar] [CrossRef]
- Friedman, D. Infrared characteristics of ocean water (1.5–15μm). Appl. Opt. 1969, 8, 2073–2078. [Google Scholar] [CrossRef]
- Ebuchi, N.; Kizu, S. Probability distribution of surface wave slope derived using sun glitter images from geostationary meteorological satellite and surface vector winds from scatterometers. J. Oceanogr. 2002, 58, 477–486. [Google Scholar] [CrossRef]
- Hocking, J.; Rayer, P.; Rundleand, D.; Saunders, R.; Matricardi, M.; Geer, A.; Brunel, P.; Vidot, J. RTTOV v12 Users Guide, NWPSAF-MO-UD-037, Version: 1.3, 2019. Available online: https://www.nwpsaf.eu/site/download/documentation/rtm/docs_rttov12/users_guide_rttov12_v1.3.pdf (accessed on 9 December 2019).
- Chen, Y.; Han, Y.; van Delst, P.; Weng, F. Assessment of Shortwave Infrared Sea Surface Reflection and Nonlocal Thermodynamic Equilibrium Effects in the Community Radiative Transfer Model Using IASI Data. J. Atmos. Ocean. Technol. 2013, 30, 2152–2160. [Google Scholar] [CrossRef]
- Qi, C.; Wu, C.; Hu, X.; Xu, H.; Li, L.; Zhou, F. 2019: FY-3D/HIRAS On-Orbit Performance and Validation, Presentation at 2019 GSICS Data & Research Working Groups Annual Meeting, Frascati. Available online: http://gsics.atmos.umd.edu/pub/Development/AnnualMeeting2019/7c_Chengli_Qi_GSICS%202019_HIRAS.pptx (accessed on 9 December 2019).
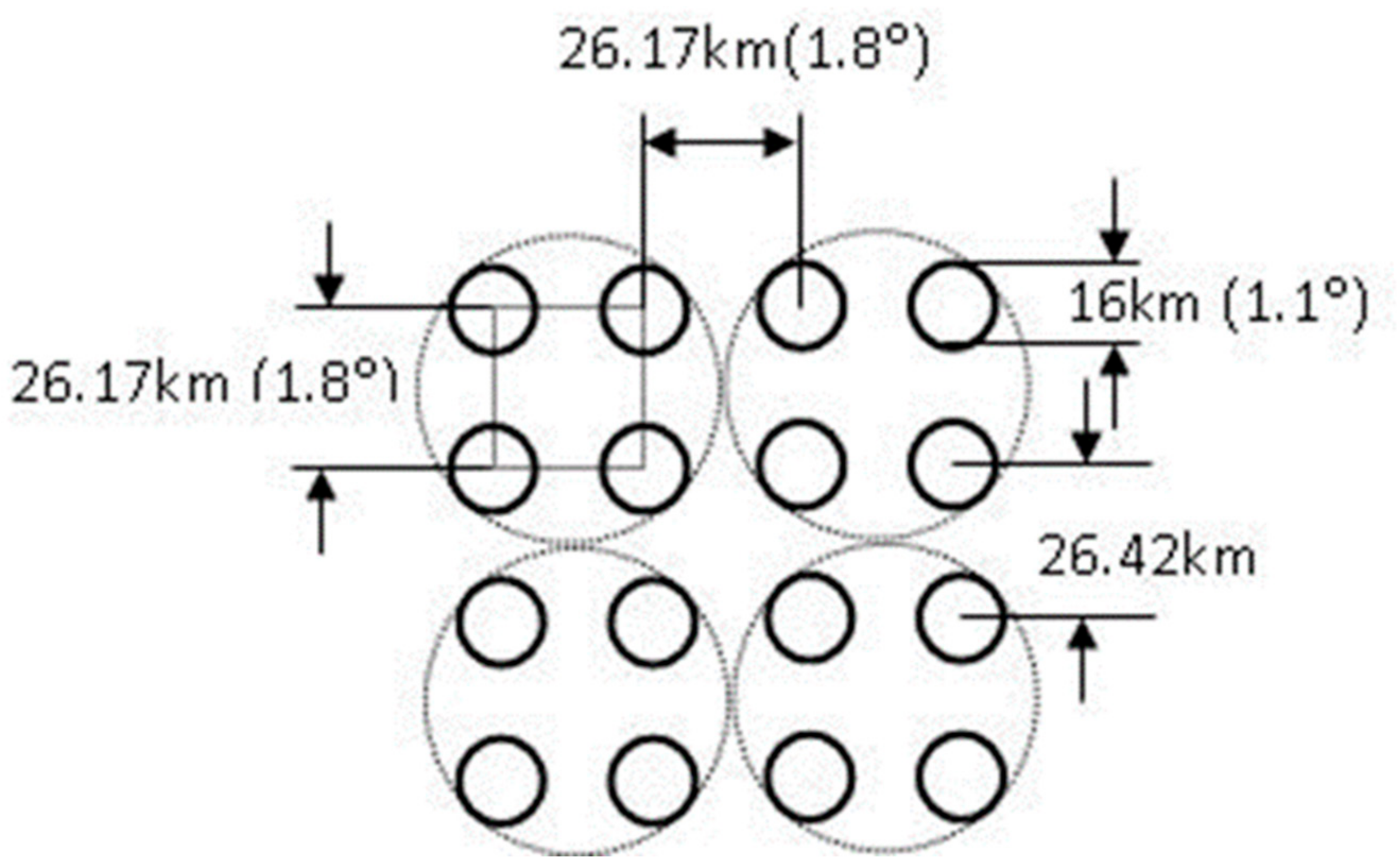


| Parameters | Specification |
|---|---|
| Scan Period (s) | 10 |
| View angle (°) | 1.1 |
| Scan angle (°) | ±50.4 |
| Radiative calibration accuracy (K) | 0.7 |
| Spectral calibration accuracy (ppm) | 7 |
| Direction pointing bias (°) | ± 0.25 |
| Pixels per scan | 116 |
| Band | Spectral Range (cm−1) | Spectral Resolution (cm−1) | NE△T at 250 K (K) | No of Channels |
|---|---|---|---|---|
| Long-wave | 650–1136 | 0.625 | 0.15 to 0.4 K | 777 |
| Mid-wave | 1210–1750 | 0.625 | 0.1 to 0.7 K | 865 |
| Short-wave | 2155–2550 | 0.625 | 0.3 to 1.2 K | 633 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carminati, F.; Xiao, X.; Lu, Q.; Atkinson, N.; Hocking, J. Assessment of the Hyperspectral Infrared Atmospheric Sounder (HIRAS). Remote Sens. 2019, 11, 2950. https://doi.org/10.3390/rs11242950
Carminati F, Xiao X, Lu Q, Atkinson N, Hocking J. Assessment of the Hyperspectral Infrared Atmospheric Sounder (HIRAS). Remote Sensing. 2019; 11(24):2950. https://doi.org/10.3390/rs11242950
Chicago/Turabian StyleCarminati, Fabien, Xianjun Xiao, Qifeng Lu, Nigel Atkinson, and James Hocking. 2019. "Assessment of the Hyperspectral Infrared Atmospheric Sounder (HIRAS)" Remote Sensing 11, no. 24: 2950. https://doi.org/10.3390/rs11242950
APA StyleCarminati, F., Xiao, X., Lu, Q., Atkinson, N., & Hocking, J. (2019). Assessment of the Hyperspectral Infrared Atmospheric Sounder (HIRAS). Remote Sensing, 11(24), 2950. https://doi.org/10.3390/rs11242950