Analysis of Stochastic Distances and Wishart Mixture Models Applied on PolSAR Images
Abstract
:1. Introduction
- (a)
- Data set type (numerical real, numerical complex, categorical);
- (b)
- Data set normalization need;
- (c)
- Outliers, and how to deal with them;
- (d)
- Number of clusters;
- (e)
- Cluster shape;
- (f)
- Similarity measure;
- (g)
- The initial centroid location choice.
2. PolSAR Image Representation
3. Stochastic Distances
- Bhattacharyya
- Kullback-Leibler
- Hellinger
- Rényi of order
- Chi-square
4. Stochastic Clustering Algorithm
5. Expectation Maximization of Wishart Mixture Model
- The Expectation or E-step. In E-step the log-likelihood of the observed data , given the estimated parameter , is calculated as:
- The Maximization or M-step. The M-step finds the new estimation by maximizing :Since the parameter is composed of and , the parameter optimization is done by setting the respective partial derivative to zero. The optimization with respect to can be summarized as:and the new estimation for is given by:
6. Applications
- Expectation-Maximization for Wishart mixture model distribution (EM-W);
- Stochastic Clustering using Bhattacharyya distance (SC-B);
- Stochastic Clustering using Kullback-Leibler distance (SC-KL);
- Stochastic Clustering using Hellinger distance (SC-H);
- Stochastic Clustering using Rényi of order distance (SC-R). The selected value of the Rényi’s order () was 0.9;
- Stochastic Clustering using Chi-square distance (SC-C).
- K-means using Euclidean distance (KM-E);
6.1. Experiment I
6.1.1. Image Simulation
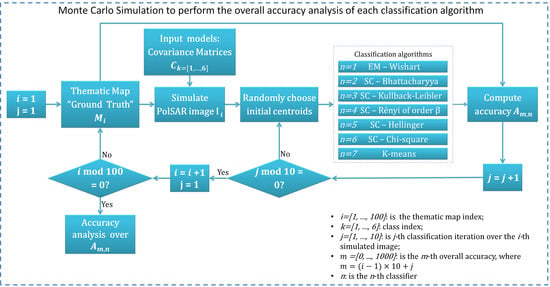
6.1.2. Monte Carlo Simulation Results
- S01: All six initial centroids were selected from the one class;
- S02: The six initial centroids are distributed over three class;
- S03: The six initial centroids were picked from the borders of two classes;
- S04: Three initial centroids were selected in three different class, and the other three comes from the borders of two classes;
- S05: All initial centroids comes from overlays;
- S06: One initial centroid were picked per class.
6.2. Experiment II
6.2.1. ALOS PALSAR Image Description
6.2.2. Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Song, H.; Yang, W.; Xu, X.; Liao, M. Unsupervised PolSAR imagery classification based on jensen-bregman logdet divergence. In Proceedings of the 10th European Conference on Synthetic Aperture Radar (EUSAR 2014), Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Frery, A.C.; Cintra, R.J.; Nascimento, A.D. Entropy-based statistical analysis of PolSAR data. IEEE Trans. Geosci. Remote Sens. 2012, 51, 3733–3743. [Google Scholar] [CrossRef]
- Silva, W.; Freitas, C.; Sant’Anna, S.; Frery, A.C. PolSAR region classifier based on stochastic distances and hypothesis tests. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1473–1476. [Google Scholar]
- Frery, A.C.; Nascimento, A.D.; Cintra, R.J. Analytic expressions for stochastic distances between relaxed complex Wishart distributions. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1213–1226. [Google Scholar] [CrossRef] [Green Version]
- Frery, A.C.; Correia, A.; Rennó, C.D.; Freitas, C.; Jacobo-Berlles, J.; Mejail, M.; Vasconcellos, K.; Sant’anna, S. Models for synthetic aperture radar image analysis. Resenhas (IME-USP) 1999, 4, 45–77. [Google Scholar]
- Gao, G. Statistical modeling of SAR images: A survey. Sensors 2010, 10, 775–795. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, A.D.C.D. Teoria EstatíStica da InformaçãO Para Dados de Radar de Abertura SintéTica Univariados E PolariméTricos. Ph.D. Thesis, Federal University of Pernambuco, Recife, Pernambuco, Brazil, 2012. [Google Scholar]
- Torres, L.; Sant’Anna, S.J.; da Costa Freitas, C.; Frery, A.C. Speckle reduction in polarimetric SAR imagery with stochastic distances and nonlocal means. Pattern Recognit. 2014, 47, 141–157. [Google Scholar] [CrossRef] [Green Version]
- Saldanha, M.F.S. Um Segmentador Multinível Para Imagens SAR PolariméTricas Baseado na DistribuiçãO Wishart. Ph.D. Thesis, National Institute for Space Research, São José dos Campos, São Paulo, Brazil, 2013. [Google Scholar]
- Doulgeris, A.P. An Automatic U-Distribution and Markov Random Field Segmentation Algorithm for PolSAR Images. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1819–1827. [Google Scholar] [CrossRef] [Green Version]
- Doulgeris, A.P.; Eltoft, T. PolSAR image segmentation—Advanced statistical modelling versus simple feature extraction. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 1021–1024. [Google Scholar]
- Yang, W.; Liu, Y.; Xia, G.S.; Xu, X. Statistical mid-level features for building-up area extraction from high-resolution PolSAR imagery. Prog. Electromagn. Res. 2012, 132, 233–254. [Google Scholar] [CrossRef]
- Silva, W.B.; Freitas, C.C.; Sant’Anna, S.J.; Frery, A.C. Classification of segments in PolSAR imagery by minimum stochastic distances between Wishart distributions. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1263–1273. [Google Scholar] [CrossRef] [Green Version]
- Braga, B.C.; Freitas, C.C.; Sant’Anna, S.J. Multisource classification based on uncertainty maps. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 13–18 July 2015; pp. 1630–1633. [Google Scholar]
- Formont, P.; Pascal, F.; Vasile, G.; Ovarlez, J.P.; Ferro-Famil, L. Statistical classification for heterogeneous polarimetric SAR images. IEEE J. Sel. Top. Signal Process. 2010, 5, 567–576. [Google Scholar] [CrossRef] [Green Version]
- Negri, R.G.; Frery, A.C.; Silva, W.B.; Mendes, T.S.; Dutra, L.V. Region-based classification of PolSAR data using radial basis kernel functions with stochastic distances. Int. J. Digit. Earth 2019, 12, 699–719. [Google Scholar] [CrossRef] [Green Version]
- Deng, X.; López-Martínez, C.; Chen, J.; Han, P. Statistical modeling of polarimetric SAR data: A survey and challenges. Remote Sens. 2017, 9, 348. [Google Scholar] [CrossRef] [Green Version]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Salicru, M.; Menendez, M.; Morales, D.; Pardo, L. Asymptotic distribution of (h, φ)-entropies. Commun. Stat. Theory Methods 1993, 22, 2015–2031. [Google Scholar] [CrossRef]
- Seghouane, A.K.; Amari, S.I. The AIC criterion and symmetrizing the Kullback–Leibler divergence. IEEE Trans. Neural Netw. 2007, 18, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-H.; Han, C.-Z. Polsar image segmentation by mean shift clustering in the tensor space. Acta Autom. Sin. 2010, 36, 798–806. [Google Scholar] [CrossRef] [Green Version]
- Pakhira, M.K. A linear time-complexity k-means algorithm using cluster shifting. In Proceedings of the 2014 International Conference on Computational Intelligence and Communication Networks, Bhopal, India, 14–16 November 2014; pp. 1047–1051. [Google Scholar]
- Hidot, S.; Saint-Jean, C. An Expectation–Maximization algorithm for the Wishart mixture model: Application to movement clustering. Pattern Recognit. Lett. 2010, 31, 2318–2324. [Google Scholar] [CrossRef]
- Silva, W.B. Classificação de RegiãO de Imagens Utilizando Teste de HipóTese Baseado em DistâNcias EstocáSticas: AplicaçãO a Dados PolariméTricos. Ph.D. Thesis, National Institute for Space Research São José dos Campos, São Paulo, Brazil, 2013. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Frery, A.C.; Nascimento, A.D.; Cintra, R.J. Information theory and image understanding: An application to polarimetric SAR imagery. arXiv 2014, arXiv:1402.1876. [Google Scholar]
- Celebi, M.E.; Kingravi, H.A.; Vela, P.A. A comparative study of efficient initialization methods for the k-means clustering algorithm. Expert Syst. Appl. 2013, 40, 200–210. [Google Scholar] [CrossRef] [Green Version]















| Class Name | Covariance Matrix |
|---|---|
| Class 1 | |
| Class 2 | |
| Class 3 | |
| Class 4 | |
| Class 5 | |
| Class 6 |
| EM-W | SC-B | SC-KL | SC-H | SC-R | SC-C | KM-E | |
|---|---|---|---|---|---|---|---|
| Average Accuracy | 54.34 | 72.21 | 70.91 | 72.29 | 35.22 | 41.72 | 57.99 |
| Average STD | 15.98 | 17.05 | 16.79 | 17.06 | 6.15 | 5.22 | 10.48 |
| EM-W | SC-B | SC-KL | SC-H | SC-R | SC-C | KM-E | |
|---|---|---|---|---|---|---|---|
| S01 | 36.41 | 48.13 | 31.20 | 48.23 | 41.36 | 40.14 | 47.37 |
| S02 | 36.06 | 48.02 | 34.45 | 48.12 | 45.46 | 30.74 | 45.72 |
| S03 | 49.03 | 64.26 | 65.49 | 63.26 | 46.86 | 33.95 | 59.17 |
| S04 | 65.30 | 58.68 | 60.62 | 58.78 | 30.35 | 35.77 | 56.67 |
| S05 | 55.72 | 51.21 | 54.75 | 51.31 | 45.23 | 31.81 | 47.20 |
| S06 | 95.29 | 94.67 | 93.91 | 94.77 | 47.79 | 44.15 | 62.97 |
| EM-W | SC-B | SC-KL | SC-H | SC-R | SC-C | KM-E | |
|---|---|---|---|---|---|---|---|
| Time | 30.35 | 22.93 | 24.47 | 24.07 | 23.95 | 26.522 | 21.52 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, N.C.R.L.; Sant’Anna Bins, L.; Siqueira Sant’Anna, S.J. Analysis of Stochastic Distances and Wishart Mixture Models Applied on PolSAR Images. Remote Sens. 2019, 11, 2994. https://doi.org/10.3390/rs11242994
Carvalho NCRL, Sant’Anna Bins L, Siqueira Sant’Anna SJ. Analysis of Stochastic Distances and Wishart Mixture Models Applied on PolSAR Images. Remote Sensing. 2019; 11(24):2994. https://doi.org/10.3390/rs11242994
Chicago/Turabian StyleCarvalho, Naiallen Carolyne Rodrigues Lima, Leonardo Sant’Anna Bins, and Sidnei João Siqueira Sant’Anna. 2019. "Analysis of Stochastic Distances and Wishart Mixture Models Applied on PolSAR Images" Remote Sensing 11, no. 24: 2994. https://doi.org/10.3390/rs11242994
APA StyleCarvalho, N. C. R. L., Sant’Anna Bins, L., & Siqueira Sant’Anna, S. J. (2019). Analysis of Stochastic Distances and Wishart Mixture Models Applied on PolSAR Images. Remote Sensing, 11(24), 2994. https://doi.org/10.3390/rs11242994