Hyperspectral Anomaly Detection with Harmonic Analysis and Low-Rank Decomposition

Abstract

Hyperspectral anomaly detection methods are often limited by the effects of redundant information and isolated noise. Here, a novel hyperspectral anomaly detection method based on harmonic analysis (HA) and low rank decomposition is proposed. This paper introduces three main innovations: first and foremost, in order to extract low-order harmonic images, a single-pixel-related HA was introduced to reduce dimension and remove redundant information in the original hyperspectral image (HSI). Additionally, adopting the guided filtering (GF) and differential operation, a novel background dictionary construction method was proposed to acquire the initial smoothed images suppressing some isolated noise, while simultaneously constructing a discriminative background dictionary. Last but not least, the original HSI was replaced by the initial smoothed images for a low-rank decomposition via the background dictionary. This operation took advantage of the low-rank attribute of background and the sparse attribute of anomaly. We could finally get the anomaly objectives through the sparse matrix calculated from the low-rank decomposition. The experiments compared the detection performance of the proposed method and seven state-of-the-art methods in a synthetic HSI and two real-world HSIs. Besides qualitative assessment, we also plotted the receiver operating characteristic (ROC) curve of each method and report the respective area under the curve (AUC) for quantitative comparison. Compared with the alternative methods, the experimental results illustrated the superior performance and satisfactory results of the proposed method in terms of visual characteristics, ROC curves and AUC values.

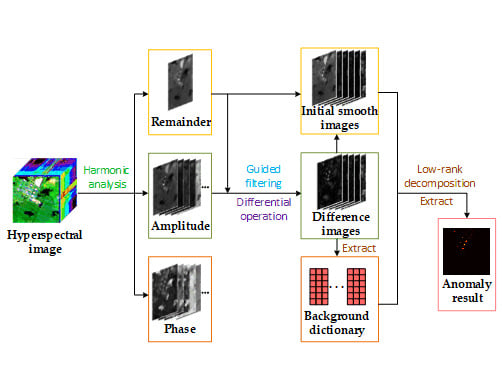
1. Introduction

Hyperspectral image (HSI), which is an image cube that simultaneously acquires spatial information and rich spectral information of the objects, has high spectral resolution (10 nm or less) and a wide spectral coverage (from visible to short-wave infrared) [1]. The recorded spectral reflection characteristics of the objects can fully reflect the inherent nature of the objects [2,3]. Therefore, target detection and recognition can be performed by the spatial-spectral information provided by the HSI [4,5]. According to whether priori information is used, the target detection methods are classified into two categories: supervised and unsupervised [6]. Anomaly detection is an unsupervised method, which is more practical than supervised target detection because it does not require the prior information of the target. Anomaly detection has been widely applied to the fields of maritime search and rescue, geological survey, fire disaster monitoring and battlefield target detection [7].

At present, many anomaly detection methods have been developed. The iconic hyperspectral anomaly detection method is proposed by Reed-Xiaoli (RX) [8,9], and its variant, the local RX (LRX) method [10]. However, its assumptions on the background model are too simple, which limits the detection performance [11]. Moreover, it is difficult to avoid the contamination of the anomaly and noise when calculating the statistical distribution characteristics of the background. As a result, many improved methods have been proposed [12]. For example, the subspace-based RX (SSRX) method [13] made the background statistical characteristic evaluation more robust by a projection transformation of the covariance matrix. The random-selection-based anomaly detector (RSAD) [14] iteratively selected a set of robust background feature pixels in HSI by adopting a random approach. The method could obtain background statistical characteristic evaluation parameters that exclude the interference of anomaly. Due to the fact that anomaly and background are linearly inseparable, Kown et al. [15] suggested that the kernel method was worked to project the traditional RX (KRX) method into the high-dimensional kernel feature space. Then, the anomaly could be separated from the background. Traditional RX-based improved methods typically model the background before performing the complex calculations. Therefore, the performance of such methods was limited due to anomaly and noise contamination that may violate the assumption on background. As a consequence, other types of methods have also been explored.

In recent years, harmonic analysis (HA) [16], which was first proposed by Jakubauskas et al., has attracted broad attention in the image process area. In the field of remote sensing data processing, HA was initially exploited to analyze time series data [17]. A curve fitting method based on HA [18] was proposed to better understand the change of natural land cover. In hyperspectral unmixing, a mixture model based on harmonic combination description was introduced [19]. An HSI classification method called HA-PSO-SVM [20] was proposed by combining HA and particle swarm optimization (PSO) optimized support vector machine (SVM). It is shown that, through the above analysis, harmonic analysis can be used for hyperspectral anomaly detection.

More recently, filtering-based methods have been introduced into anomaly detection. To solve the unreasonable problem of the assumptions of the RX method, whitening spatial correlation filtering (WSCF) [21] was described by Gaucel et al. Anomaly detector based on attribute and edge-preserving filters (AED) [22] was examined by Kang et al. The AED method detected anomalies by introducing local morphological attribute filtering after dimensionality reduction. The domain transform recursive filter as a follow-up operation had been proved to be able to remove the noise and maintain the edges. Multiscale attribute and edge preserving filters-based method [23] was discussed by Li et al. to consider multiscale information in HSI. This method concentrated on the spatial structure information of anomaly targets in HSI. To solve redundant data and noise bands in HSI, structure tensor and guided filtering (STGF)-based anomaly detection method [24] was proposed by combining attribute filtering.

In addition to the above methods, the representation based has gained much attention of researchers. For the first time, Chen et al. [25] introduced sparse representations into the hyperspectral target detection and achieved extraordinary results. This method represented the pixel under test by a few pixels in the neighborhood. After this, Li et al. originally proposed a collaborative representation-based [26] anomaly detection method (CRD). Unlike the sparse representation, the pixels under test were represented by all the pixels in the neighborhood in the collaborative representation. Another type of representation-based approach that has been applied to anomaly detection is based on low-rank decomposition. Xu et al. [27] separated the anomaly from the low rank background through robust principal component analysis (RPCA) [28]. In order to take advantage of neglected low rank background information and reduce false alarm rate, Zhang et al. [29] combined low-rank and sparse decomposition based on Go Decomposition (GoDec) with Mahalanobis distance (LSMAD). The difference between this method and others is that the statistical characteristic of the decomposed low-rank component was added to the Mahalanobis distance detection. Xu et al. first developed an anomaly detection method based on low-rank and sparse representation (LRASR) [30] by combining local and global structure information in HSI. The LRASR method established a background dictionary by k-means clustering. Niu et al. [31] argued that the background dictionary constructed by adding a random selection method to the iterative update of dictionary exhibits more excellent performance in low-rank decomposition. This one made low-rank decomposition more robust by avoiding the contamination of anomaly. To alleviate the effect of noise and mixed pixels, Qu et al. [32] performed abundance and dictionary-based low-rank decomposition (ADLR) to obtain the residual matrix. Thus, anomaly was detected from the residual matrix. The advantage of the ADLR method was that the abundance vector obtained by spectral unmixing, whose low-rank decomposition was more accurate. However, most anomaly detection methods do not take into account the redundant information and isolated noise in HSI.

In this paper, we propose a novel hyperspectral anomaly detection method based on HA and low rank decomposition (HALR) to overcome the above problems. There are three main contributions in the proposed HALR method. Initially, low-order harmonic images of the HSI are extracted by performing HA in a single pixel. The HA can reduce the dimension of HSI and remove the redundant information in HSI. Moreover, in order to reduce the effects of isolated noise and suppress background, the low-order harmonic images are filtered by the guided filtering (GF). Hence, the initial smoothed images that were obtained by the differential operation replace the original HSI to detect anomalies. At the same time, a novel background dictionary construction method is proposed. The extracted background dictionary can fully represent background features. Eventually, anomalies can be obtained by performing dictionary-based low-rank decomposition on the initial smoothed images. The low-rank decomposition takes full advantage of the fact that the background is low-rank and the anomaly is sparse. The experimental results verify the superiority of the proposed HALR method in terms of detection performance.

The rest of this paper is organized as follows. The second part describes the proposed HALR method. The third part illustrates the experimental results. The fourth part is the parameter setting discussion. The fifth draws the conclusions.

2. Harmonic Analysis and Low-Rank Decomposition

The flowchart of the proposed HALR-based method is shown in Figure 1. The proposed HALR method mainly includes three strategies. In the beginning, low-order harmonic images are obtained by HA. Then, the initial smooth images are gained by GF and differential operation. At the same time, a background dictionary is obtained through a new background dictionary construction method. Finally, anomaly can be acquired by the low-rank decomposition.

2.1. Hyperspectral Harmonic Analysis

HSI has a lot of redundant information because of the high correlation of adjacent bands. Due to the influence of noise and the atmosphere, not all bands can provide valid information [33]. Because of this, the hyperspectral data are regarded as the timing signal from the perspective of time domain signals. Then, HA is introduced to perform time-frequency space conversion on the timing signal. The theory of HA is to represent any time-series function f(t) with respect to time t by superposition of sine or cosine waves (harmonics) [34].

Different from the traditional Fourier transform [35] than from the spatial domain to the frequency domain, HA utilizes spectral information and correlation between bands in the HSI to transform from time domain to spatial domain. By making full use of the hyperspectral spectral characteristics, the hyperspectral data is transformed into a set of components that is composed of energy spectral characteristic components by the harmonic analysis, while the spatial characteristics of the hyperspectral data remain unchanged. Specifically for a single pixel, multiple harmonic analysis can express the spectral information of each pixel as the sum of the superposition of the sine waves (cosine waves), which is composed of a series of harmonic energy characteristic parameter components. In this way, the spectrum of each pixel can be represented as a complex, continuous and smooth curve.

When HA is employed to process spectral data, the approximately continuous spectral curve composed of B bands can be treated as a function of period B. After harmonic decomposition, the spectral curve of each pixel in the HSI can be expressed as the sum of the superposition of the sine waves (cosine waves) composed of a series of harmonic energy characteristic parameter components, including harmonic remainder, amplitude and phase [20]. If it is known that the spectral vector consisting of B bands can be represented as Y_i = [y₁, y₂, …, y_n, …, y_B]^T, the spectral value of each band is recorded as y_n, where n is the band serial number (n = 1, 2, …, B). Therefore, the harmonic decomposition expansion of the h-th harmonic analysis of the spectral vector Y_i is:

$$\begin{array}{ll}{Y}_i^{\prime }& =\frac{R_0}{2}+{\displaystyle {\displaystyle \sum }_{h=1}^{h_{max}{{\displaystyle \sum }}^{}}}\left[C_{h}cos(\frac{2\pi hn}{B}\right)+S_{h}sin(\frac{2\pi hn}{B})]\\ & =R_e+{\displaystyle {\displaystyle \sum }_{h=1}^{h_{max}{{\displaystyle \sum }}^{}}}{H}_{h}sin(\frac{2\pi hn}{B}+P_h)\end{array}$$

(1)

The harmonic energy characteristic parameter components of the h-th harmonic decomposition of Y_i are calculated as:

$$R_e=R_0/2=\frac{1}{B}{\displaystyle \sum }_{n=1}^B{y}_n$$

(2)

$$C_h=\frac{2}{B}{\displaystyle \sum }_{n=1}^B{y}_{n}cos(\frac{2\pi hn}{B})$$

(3)

$$S_h=\frac{2}{B}{\displaystyle \sum }_{n=1}^B{y}_{n}sin(\frac{2\pi hn}{B})$$

(4)

$$H_h=\sqrt{\left(C_h^2+S_h^2\right)}$$

(5)

$$P_h={tan}^{-1}(\frac{C_h}{S_h})$$

(6)

where h (h = 1, 2, 3, …) is the number of harmonic decompositions; R_e is the remainder of the harmonic; $H_{h}sin(\frac{2\pi hn}{B}+P_h)$ is the h-th harmonic component; C_h, S_h, H_h and P_h are the cosine amplitude, sine amplitude, harmonic component amplitude and harmonic component phase of the h-th harmonic decomposition, respectively. Here, the remainder represents the average of the spectral, the amplitude and phase respectively reflect energy changes in different bands and the position of the band where the amplitude of the energy appears [36]. The detailed steps of hyperspectral HA are described in Algorithm 1.

In the HA, the lower harmonics contain the main energy characteristics of the spectral and the higher harmonics are usually mixed with noise information. Therefore, harmonic analysis has better noise cancellation and main energy extraction capabilities, and it can also preserve the spatial feature information of hyperspectral data.

Since the low-order harmonics contain most of the energy of the HSI, not all harmonic images can provide crucial information. As such, we can select the first few low-order harmonic images as the subsequent test images. However, not all images in low-order harmonic images are suitable for anomaly detection. As shown in Figure 2, it can be clearly seen that the phase in low-order harmonic images contains a lot of interference and useless information. Thus, the phase in low-order harmonic images is directly discarded. The remainder and amplitude are preserved. Finally, the remainder and the first five amplitude images are adopted for subsequent test images. In this way, the ultimate goal of hyperspectral HA in this part is to reduce dimensionality and remove redundant information.

Algorithm 1. Harmonic analysis

1. Input: Hyperspectral matrix Y = [Y1, Y2, …, YM] ∈ RB×M, maximum harmonic number hmax.

2. Transformation process

for each pixel Yi do

(1) calculate remainder Re by Equation (2);

for h = 1 to hmax do

(2) Calculate coefficients of HA by Equations (3)–(6);

end for

(3) Get the reconstructed pixel Y′i by Equayion (1);

end for

3. Output: remainder Re, amplitude Hh and phase Ph.

2.2. Guided Filtering and Dictionary Construction

Although HA achieves dimensionality reduction and removes redundant information in the HSI, the resulting image still retains some isolated noise. Next, GF and differential operation is applied to further reduce the isolated noise and enhance the detail in the image [37,38]. In addition, it should be mentioned that the GF can also smooth the background to a certain extent.

2.2.1. Guided Filtering

In GF, it is crucial to choose the guidance image sensibly [39]. The guidance image directly affects the result of the filtered output. In this part, the remainder R_e is taken as the guide image. The five amplitude images H_j (j = 1, 2, …,5) are recorded as input images, and G_j are recorded as output images. The GF output images G_j can be obtained as follows:

$$\begin{array}{cc}{G}_{j,x}=a_k{(R_e)}_x+b_k& \forall x\in W_k\end{array}$$

(7)

where W_k represents a window of (2r + 1) × (2r + 1); k is the center of the window W_k; x is the pixel index in window W_k; a_k and b_k are the fixed coefficients of the linear function in the window W_k, respectively.

In order to minimize the difference between the output image and the input image, the minimum cost function expression is as follows:

$$E\left(a_k,b_k\right)={\displaystyle \sum }_{x\in W_k}[(a_k\left(R_e{)}_x+b_k-H_j{)}^2+\epsilon a_k^2\right]$$

(8)

where ε is the regularization coefficient. The expressions for a_k and b_k are as follows:

$$\{\begin{array}{l}{a}_k=\frac{\frac{1}{|w|}{{\displaystyle \sum }}_{x\in W_k}{(R_e)}_x{H}_{j,x}-u_k{V}_k}{{\delta }_k+\epsilon }\\ b_k=V_k-a_k{u}_k\end{array}$$

(9)

where u_k and δ_k are the mean and variance of the image R_e in the window W_k; |w| is the total number of elements in the window W_k; V_k is the mean of the image H_j in the window W_k, respectively.

Some examples of GF are illustrated in Figure 3. Figure 3a shows the remainder R_e as a guide image. Figure 3b,d show the first-order amplitude image H₁ and H₂ as GF input images, respectively. Figure 3c,e denote the output images G₁ and G₂ of Figure 3b,d, respectively. It can be seen from Figure 3 that the background is smoothed by the GF.

After getting the output images G_j of the GF, differential operation is introduced to calculate the difference between the input images H_j and the output images G_j:

$$I_j=|H_j-G_j|,j=1,2,\cdots ,5$$

(10)

where I_j is the difference image. This differential operation can alleviate the isolated noise [40,41] in the input image to a certain extent. Although anomalies are also suppressed after GF and differential operations, background and isolated noise are simultaneously suppressed. It can highlight anomaly and enhance the detail while suppressing the background. A wealth of information with respect to anomaly is to be found in the difference image. Figure 4 is shown as an example, where Figure 4a,d are difference images I₁ and I₂, respectively.

In order to make use of distinctive characteristics of differential images in detecting anomalies, the harmonic remainder R_e and the difference image I_j replaces the original HSI as initial smooth images S $\in$ R^l×M for low rank decomposition. l indicates that each pixel in the initial smooth images S is an l-dimensional column vector.

Figure 5 reveals an example of the formation of the initial smooth images S. The initial smooth images S can be obtained by transforming the three-dimensional cube composed of the harmonic remainder R_e and the difference image I_j into a two-dimensional matrix.

2.2.2. Dictionary Construction

In the low-rank decomposition, the background dictionary is of great importance. A satisfactory background dictionary usually contains various background categories in the image under test, while eliminating interference from anomaly and noise [42,43]. In this section, a rational method is studied instead of directly using original HSI or dictionary learning method to establish a background dictionary.

In order to extract a suitable background dictionary from the initial smooth images S, the difference image I is first fused. To further reduce the interference of anomalies and noise on the background dictionary, pixels in the fused image are sorted in ascending order and segmented. Then, for the sorted pixels after segmentation, the part with a large pixel value is considered to be an anomaly and noise pixel set, and the part with a small pixel value is considered to be a background pixel set. Finally, in order to ensure that the background dictionary atoms contain as many different background categories as possible, we randomly select some pixels from the background pixel set as representative and discriminative background dictionary atoms. The extracted background dictionary is applied for subsequent low-rank decomposition.

We take the column vectors of the initial smooth images S as samples. Firstly, the resulting difference images are merged together. The fusion method is denoted as:

$$d=\frac{{{\displaystyle \sum }}_{j=1}^5{I}_j}{5}$$

(11)

where d is the merged image, which will be used as the basis for dictionary extraction.

After merging, anomaly pixels and edges in the image will be highlighted. Consequently, these highlighted points in the image will be numerically larger than background values. After that, the pixels in the fused image d are sorted in ascending order. For sorted pixels, the background pixels will be more forward.

Finally, a part of the pixels φ is randomly selected from the first ξ of the sorted pixels to build background dictionary, where φ is dictionary atom selection percentage and ξ is separated value. Both φ and ξ are percentages. Among them, the value of φ is not fixed, and the value of ξ is 90%. The number of the selected pixels and the value of ξ will be analyzed later. The main objective of random selection is to choose as many categories of background pixels as possible. An example of the background dictionary constructed is displayed in Figure 6.

Through this method, a representative background dictionary D$\in$R^l×m is obtained, where m represents the total number of atoms in the background dictionary D.

2.3. Low-Rank Decomposition

Since the anomaly is sparse and the background is low-rank in hyperspectral data, the low-rank decomposition in the field of visible light image processing is also applicable to HSI [44,45,46]. However, most of these methods directly implement low-rank decomposition on the original HSI without considering the redundant information of HSI, the correlation between bands and the isolated noise. In this respect, we proposed a novel low-rank decomposition strategy. Here, instead of the original HSI, we performed the low-rank decomposition on the initial smooth images S, which is identified as the object of low-rank decomposition. Then, the decomposition formula is represented as follows:

$$S=DF+A$$

(12)

where F$\in$R^m×M is a m × M coefficient matrix of all pixels in S; A$\in$R^l×M is a l × M sparse matrix, respectively. Here, m represents the total number of atoms in the background dictionary D, M represents the total number of pixels in the HIS, and l indicates that each pixel in the initial smooth images S is a l-dimensional column vector.

For the low-rank decomposition problem, there are several solutions. RPCA [28] could decompose the hyperspectral data into the low rank part and the sparse residual part. However, RPCA does not consider the noise of hyperspectral data making the detection results prone to false alarms. The GoDec method [47,48] divides the hyperspectral data into low rank matrix, sparse matrix and noise matrix, taking into account the noise. The LRASR method [30] solves the low rank representation (LRR) [49] problem with low rank and sparse regularization constraints by the linearized alternating direction method with adaptive penalty (LADMAP) [50]. This method implants the l₂₁ regularization constraint to make the majority of the columns in matrix F equal to 0. However, due to the characteristic difference of anomaly in practice, there are some non-zero values in the column of the sparse matrix A. Therefore, the ADLR method [32] replaces the l₂₁ regularization constraint with the l₁ regularization constraint. In addition, this l₁ regularization constraint can further reduce the impact of isolated noise on anomaly detection. Since the isolated noise has no sparse attributes in the image, they will be clustered into a group because of their similar coefficients. The l₂₁ regularization is the l₂₁ norm of a matrix, which is defined as the sum of the l₂ norm of each column in the matrix. The l₁ regularization is the l₁ norm of a matrix, which is defined as the sum of the absolute values of all the elements of the matrix.

Through the above analysis and comparison, we exploited the ADLR method with the l₁ regularization constraint for the low-rank decomposition. In the low-rank decomposition, the coefficient matrix F is low-rank and the sparse matrix A is sparse. After introducing the l₁ regularization constraint, the objective function is as follows:

$$\begin{array}{ll}\underset{F,A}{min}& rank\left(F\right)+\lambda ||A|{|}_1\\ s.t.& S=DF+A\end{array}$$

(13)

where rank(·) represents the rank function; λ > 0 is the tradeoff parameter used to adjust the low rank part and the sparse part; ||·||₁ is the l₁ norm, respectively. The abbreviation s.t. refers to “subject to”, which indicating that the constraint is S = DF + A. ||A||₁ is specifically expressed as:

$$||A|{|}_1={\displaystyle \sum }_{r_{ow}}^l{\displaystyle \sum }_{c_{ol}}^M|A_{r_{ow},c_{ol}}|$$

(14)

where l indicates that each pixel in the initial smooth images S is a l-dimensional column vector, M represents the total number of pixels in the HIS and $|A_{r_{ow},c_{ol}}|$ is the absolute value of the element in the r_ow-th row and c_ol-th column of the matrix A.

To solve the objective function, the rank function is replaced by the matrix nuclear norm ||·||_* [51]. Therefore, the objective function can be optimized to:

$$\begin{array}{ll}\underset{F,A}{min}& ||F|{|}_{*}+\lambda ||A|{|}_1\\ s.t.& S=DF+A\end{array}$$

(15)

In order to decouple the objective function (15), an auxiliary variable U is introduced instead of F [52]. The Lagrange equation of the objective function is;

$$\begin{array}{ll}\underset{F,A,U,L_1,L_2}{min}& ||U|{|}_{*}+\lambda ||A|{|}_1+tr\left[L_1^T\left(S-DF-A\right)\left]+tr\right[L_2^T\left(F-U\right)\right]\\ & +\frac{\tau }{2}\left(||S-DF-A|{|}_F^2+||F-U|{|}_F^2\right)\end{array}$$

(16)

where tr[·] represents the trace of matrix, which is the sum of the diagonal elements of matrix; L₁ and L₂ are Lagrange multipliers; τ > 0 is the penalty parameter; ||·||_F is the F norm, respectively. Since Equation (16) contains multiple variables, it can be solved by alternate iterative update methods. When solving one of the variables, keep the other variables unchanged. Accordingly, the solution process can be broken down into the following form.

(1) Update U when keeping F and A unchanged, the objective function can be reformulated as:

$$\begin{array}{ll}U& =argmin||U|{|}_{*}+tr\left[L_2^T\left(F-U\right)\right]+\frac{\tau }{2}||F-U|{|}_F^2\\ & =argmin\frac{1}{\tau }||U|{|}_{*}+\frac{1}{2}||U-\left(F+\frac{L_2}{\tau }\right)|{|}_F^2\end{array}$$

(17)

where arg is the abbreviation of argument. The arg min refers to the value of the variable U when the equation behind it reaches the minimum value.

(2) Update F when keeping U and A unchanged, the objective function can be reformulated as:

$$\begin{array}{cc}\underset{F}{min}& tr\left[L_1^T\left(S-DF-A\right)\left]+tr\right[L_2^T\left(F-U\right)\right]\hfill \\ & +\frac{\tau }{2}\left(||S-DF-A|{|}_F^2+||F-U|{|}_F^2\right)\hfill \\ F=& {(D^{T}D+I)}^{-1}\left[\frac{1}{\tau }\left(D^T{L}_1-L_2\right)+D^{T}S-D^{T}A+U\right]\end{array}$$

(18)

(3) Update A when keeping F and U unchanged, the objective function can be reformulated as:

$$\begin{array}{ll}A& =argmin\lambda ||A|{|}_1+tr\left[L_1^T\left(S-DF-A\right)\right]+\frac{\tau }{2}||S-DF-A|{|}_F^2\\ & =argmin\frac{\lambda }{\tau }||A|{|}_1+\frac{1}{2}||A-\left(S-DF-\frac{L_1}{\tau }\right)|{|}_F^2\end{array}$$

(19)

Equations (17) and (19) can be optimized by utilizing the singular value thresholding operator [53] and Lemma 1 in literature [54], respectively. In the iterative process, the Lagrange multipliers update formulas are as follows:

$$\begin{array}{l}{L}_1=L_1+\tau \left(S-DF-A\right)\\ L_2=L_2+\tau \left(F-U\right)\end{array}$$

(20)

The iterative convergence condition is expressed as:

$$||S-DF-A|{|}_{\infty }<\eta and||U-F|{|}_{\infty }<\eta$$

(21)

where η is the decomposition error; ||·||_∞ is the infinite norm. After the sparse matrix A is obtained by low-rank decomposition, we get the anomaly by the l₂ norm. The l₂ norm is the square root of the sum of the squares of all the elements in each column of pixels in the matrix. The specific equation is as follows:

$$T\left(i\right)=\sqrt{{{\displaystyle \sum }}^{}{(A_{:,i})}^2}i=1,2,\cdots ,M$$

(22)

where T(i) represents the anomaly detection result of the i-th pixel. A:,_i represents the i-th column of pixels in the matrix A, and M represents the total number of pixels in the HSI.

The complete steps of the low-rank decomposition are presented in Algorithm 2.

Algorithm 2. Low-rank Decomposition

Input: Initial smooth image S, background dictionary D.

Initialization: Give λ according to different input data, τ = 10−6, η = 10−6, τmax = 1010, ζ = 1.1, F = U = A = L1 = L2 = 0.

while not satisfy the convergence condition (21) do

(1) Update variable U according to Equation (17);

(2) Update variable F according to Equation (18);

(3) Update variable A according to Equation (19);

(4) Update Lagrange multipliers L1 and L2 according to Equation (20);

(5) Update variable τ, where τ = min(τmax, τ*ζ);

end while

Return: Coefficient matrix F, sparse matrix A.

Calculate anomaly result T according to Equation (22);

Output: Anomaly result T.

3. Experimental Results

To verify the validity of the proposed HALR method, the following methods, including the RX method [8], LRX method [10], WSCF method [21], LSMAD method [29], CRD method [26], RPCA-RX method [55] and AED method [22], are selected for comparison. In order to evaluate the detection results quantitatively, the receiver operating characteristic (ROC) and the area under the curve (AUC) are adopted [56]. The ROC curve shows the corresponding relationship between the false alarm rate and the probability of detection under each threshold segmentation result. The AUC value is obtained by calculating the area under the ROC curve of anomaly detector. At the same false alarm rate, the larger the value of AUC is, the better the performance of the detector. In addition, we select the optimal parameters of the alternative methods from original author in term of AUC value or the parameters. Since the background dictionary is randomly chosen, we repeated it 10 times for each experiment and reported the averaged result. Moreover, in order to verify the stability of the proposed HALR method, we also provided the standard deviation of the results of 10 experiments.

3.1. Data Sets

Synthetic Data Set: the synthetic data is generated by a real-world HSI Salinas [44]. This Salinas scene is acquired by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Some parameters of this HSI are shown in

Table 1. HSI data parameters.

Data Set	Salinas	San Diego	Beach
Sensor	AVIRISa	AVIRISa	ROSISb
Captured place	Salinas Valley, CA, USA	San Diego, CA, USA	Pavia, Italy
Spatial resolution	3.7 m	3.5 m	1.3 m
Total band	224	224	102
Available band	204	189	102
Test image size	150 × 150	100 × 100	100 × 100

^a AVIRIS is Airborne Visible/Infrared Imaging Spectrometer. ^b ROSIS is Reflective Optics System Imaging Spectrometer.

. As shown in Figure 7a, a 150 × 150 size area is selected from the original image of 512 × 217 size as the background of the synthetic data. 204 bands (1–107, 113–153, 168–223) were retained after removing water absorption bands and low signal-to-noise ratio (SNR) bands in the experiment. In the synthetic data, the anomaly target is embedded by the target implantation method [57]. Anomaly X_ea is specifically embedded as follows:

$$X_{ea}=J_{bg}\times \left(1-p\right)+X_{ia}\times p$$

(23)

where J_bg represents the spectral of the background pixel at the implantation location; X_ia indicates the spectral of the implanted anomaly; p is the percentage coefficient of the anomaly. In the synthetic data, the embedded anomaly spectral is also extracted from the Salinas scene. As shown in Figure 7b, six rows and three columns of targets with different size have been embedded obliquely. From left to right, the corresponding p values for each column are 0.6, 0.8 and 1, respectively. The ground truth map of the synthetic data is shown in Figure 7c. The ground truth is labeled with the help of the Environment for Visualizing Images (ENVI) software.

San Diego Data Set: one of the real-world test image in the experiment is a 100 × 100 image cropped from the original 400 × 400 San Diego HSI [46]. The HSI has a spectral range from 0.37 um to 2.51 um. 189 bands (7–32, 36–96, 98–106, 114–152, 167–220) were retained after removing water absorption bands and low SNR bands in the experiment. Other parameters about the San Diego data set are illustrated in Table 1. Three aircraft in the scene are considered to be anomaly targets to detect. The image under test and the corresponding ground truth map are shown in Figure 8. The ground truth is labeled with the help of the ENVI software.

Beach Data Set: this HSI [22,24] was taken by Reflective Optics System Imaging Spectrometer (ROSIS) sensor. Its wavelength ranges from 0.43 um to 0.86 um. Additional information about this data set is displayed in Table 1. In the experiment, a 100 × 100 area is chosen for the experiment. As shown in Figure 9, the background in the scene is mainly water and bridge. The vehicles on the bridge are considered to be anomaly targets. The ground truth is labeled with the help of the ENVI software.

3.2. Detection Performance Analysis

For the synthetic HSI, the visual detection results of different anomaly detection methods are displayed in Figure 10. It is obvious that the RX method, the WSCF method, the RPCA-RX method and the LSMAD method have poor detection performance in visual effect. We could see in Figure 10 that the RX method, the WSCF method, the RPCA-RX method and the LSMAD method have failed to separate the anomaly from background. Moreover, there are many false alarms in the results of the RPCA-RX method. The visual effect of the AED and CRD detection results are roughly close to the proposed HALR method. However, the false alarm of the proposed HALR method and the CRD method are slightly less than the AED method. The background suppression effect of the CRD method is also similar to that of the AED method and the HALR method. In terms of the ROC curves in Figure 11, the proposed HALR method is still excellent. The AUC values of the respective methods are reported in

Table 2. Performance evaluation based on AUC values corresponding to different anomaly detection methods.

Datasets	Methods
	RX	LRX	WSCF	CRD	RPCA-RX	LSMAD	AED	HALR
Synthetic	0.1370	0.9823	0.9072	0.9998	0.9602	0.9836	0.9997	0.9998
San Diego	0.9832	0.8467	0.9855	0.9875	0.9799	0.9867	0.9871	0.9939
Beach	0.9855	0.9347	0.9819	0.9716	0.9758	0.9828	0.7594	0.9920

. The AUC values of the CRD method and the HALR method both reach a maximum value of 0.9998. The AUC value of the AED method reaches 0.9997, which is substantially equal to the AUC value of the HALR method. From the AUC values in Table 2, the RX method has the worst detection effect. Combined with visual detection results, ROC curves and AUC values, our proposed HALR method is a significant and effective method.

For the San Diego HSI, the false color maps of the detection results of different methods are illustrated in Figure 12. The LRX method has the worst detection result in Figure 12. The size of the aircraft is one of the main reasons that affect the detection result of the LRX method. The RX, WSCF, CRD and RPCA-RX method are not very effective in suppressing background. In consequence, there are numerous false targets in their detection results. The detection results of the proposed HALR method has clearer outline and fewer false alarms than the LSMAD method and the AED method. In Figure 13 shows that the ROC curves of the RX method, the WSCF method, the CRD method, the RPCA-RX method the LSMAD method and the AED method are almost same, while the performance of the HALR method is more remarkable. Above all, the ROC curve of the proposed HALR method is mostly higher than the other curves. Moreover, Table 2 indicates that the AUC value of the proposed HALR method, 0.9939, is the largest. In brief, the proposed HALR method achieved exceptional performance.

For the Beach HSI, the false color maps of the detection results of different methods are illustrated in Figure 14. In terms of visual effects, the CRD method yields the worst detection result. The AED method and the WSCF method do not separate the anomaly targets from the background very well. The detection results of the LSMAD method and the RPCA-RX method are stable, but some false alarms also exist for the RPCA-RX method. The detection results of the RX method, the LRX method and the LSMAD method are similar. Compared to them, the proposed HALR method not only effectively detects the vehicle, but also successfully suppresses the bridge and other backgrounds. We could see that the separation of background and anomaly in the detection result of the proposed HALR method are successful. It is obvious from the ROC curves in Figure 15 that the performance of the AED method is the worst. The ROC curve of the proposed HALR method is lower than the curves of the WSCF method and the RPCA-RX method in a small region. However, under the same false alarm rate, the detection probability of the proposed HALR method reaches 1 the first. Additionally, the curves show that the proposed HALR method has a higher detection probability at a lower false alarm rate than other methods. The AUC values of different methods are presented in Table 2. The AUC value of the proposed HALR method is 0.9920, the largest among all. In summary, the performance of the proposed HALR method is very outstanding.

We reintroduced the standard deviation to further evaluate the effectiveness and stability of the proposed HALR method. In another set of experiment, the AUC value is still the average of the 10 results. At the same time, the standard deviation is calculated. Table 1 shows the 10 AUC values, average AUC values, and standard deviations of the proposed HALR method on three datasets. In the original paper, the average values of AUC on the three datasets were 0.9998, 0.9939 and 0.9920, respectively. As shown in

Table 3. Performance evaluation based on AUC value and standard deviation on the Synthetic, the San Diego and the Beach datasets.

Datasets		Synthetic	San Diego	Beach
AUC	1	0.9999	0.9934	0.9899
	2	0.9996	0.9969	0.9949
	3	0.9998	0.9886	0.9899
	4	0.9999	0.9832	0.9939
	5	0.9998	0.9956	0.9928
	6	0.9997	0.9944	0.9915
	7	0.9998	0.9939	0.9932
	8	0.9999	0.9936	0.9898
	9	0.9997	0.9898	0.9942
	10	0.9999	0.9968	0.9931
Average AUC		0.9998	0.9926	0.9922
Standard deviation		0.00011	0.0043	0.002

, the average AUC of the 10 results in another experiment were 0.9998, 0.9926 and 0.9922, respectively. They are very close to the results in the first set of experiments. In addition, the standard deviations of the 10 results on each dataset are 0.00011, 0.0043 and 0.002, respectively. It can be seen from the standard deviations that the performance of our proposed HALR method is still relatively stable.

4. Discussion

The proposed HALR method contains a total of four sensitive parameters. They are the window radius r and the regularization coefficient ε in GF, dictionary atom selection percentage φ, and the tradeoff parameter λ in low-rank decomposition, respectively. The AUC value will be utilized to distinguish the influence of each sensitive parameter on the performance of the HALR method. When analyzing one parameter, the others are fixed as default parameters. As has been noted, the atoms in the background dictionary are selected randomly. Hence, to eliminate the effects of random dictionary, we repeated the test for each value 10 times to report the average score.

For the synthetic hyperspectral dataset, the default parameters are r = 60, ε = 1, φ = 0.001 and λ = 6 × 10⁻⁴, respectively. For the San Diego dataset, the default parameters are r = 20, ε = 0.1², φ = 0.002 and λ = 3 × 10⁻³, respectively. For the Beach dataset, the default parameters are r = 2, ε = 0.3², φ = 0.001 and λ = 1 × 10⁻¹, respectively. The default parameters were selected in order to make the HALR method to achieve optimal performance on the corresponding dataset.

The influence of each sensitive parameter on the AUC performance of the HALR method is demonstrated in Figure 16. When the window radius r parameter is analyzed, due to the different image sizes, the parameter r shows values of only up to 40 in the San Diego HSI and the Beach HSI. For the tradeoff parameter λ, when the parameter λ is greater than or equal to 0.01 while other parameters are fixed, the iterative process of the low-rank decomposition does not converge in the Synthetic HSI and the San Diego HSI. Though there is some variance due to randomness in selecting the atoms in the background dictionary, in general, it can be verified from Figure 16 that the HALR method achieves optimal detection performance under the default parameter settings.

For the parameter h_max, it determines the number of harmonic analysis. In the hyperspectral harmonic analysis, the parameter h_max determines the number of lower harmonics that we should choose. When analyzing the parameter h_max, the other parameters are fixed, the AUC value is used as the evaluation standard. Figure 17 shows the impact of the parameter h_max on the detection results. It can be seen that, for the synthetic dataset, when the parameter h_max is equal to 3 or 5, the detection performance of the proposed HALR method is optimal. For the San Diego and Beach datasets, when the parameter h_max is equal to 3 or 7, respectively, the AUC value of the proposed HALR method reaches the maximum. However, they are slightly larger than the AUC values when the parameter h_max is equal to 5. In order to unify the parameters, the parameter h_max is set as 5. Hence, we finally select the first 5 amplitude images of lower harmonics in the experiment.

Finally, the effect of the separated value ξ on the performance of the proposed HALR method is analyzed. As shown in Figure 18, when the separated value ξ is 90%, the proposed HALR method has the highest performance on all three data sets.

In the experiment, these uncertain parameters are empirically selected which limits the application of the proposed HALR method to some extent. In the future, we will work on the adaptive determination of the various parameters of the proposed HALR method.

5. Conclusions

In this paper, we proposed a novel hyperspectral anomaly detection based on harmonic analysis (HA) and low-rank decomposition. The proposed approach mainly comprises three stages, i.e., HA, guided filter (GF) and low-rank decomposition. In order to deal with large data and redundant information in the original hyperspectral image (HSI), we applied a single-pixel-based HA. Subsequently, we introduced GF on the images after HA, not only to reduce the impact of isolated noise to some extent, but also to make the dictionary more discriminative on the low-rank decomposition. Ultimately, the low-rank decomposition was adopted to extract anomaly objects. The primary goal of this low-rank decomposition was to consider the low-rank features of background and the sparse features of anomaly. Furthermore, both the visual and the quantitative results (receiver operating characteristic (ROC) curves and area under the curve (AUC)) indicate that the proposed approach achieves a more competitive detection performance than alternatives. In the future, we will work on the automatic determination of the optimal parameter.