Improving Estimation of Gross Primary Production in Dryland Ecosystems by a Model-Data Fusion Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. In Situ Meteorological Observations and Carbon Flux Data
2.2. MODIS Datasets
2.3. Description of MOD17A2H Algorithm
2.4. Parameter Optimization and Uncertainty Analysis
2.5. Experiment Configuration and Validation
2.6. Statistical Analyses and Model Evaluation
3. Results
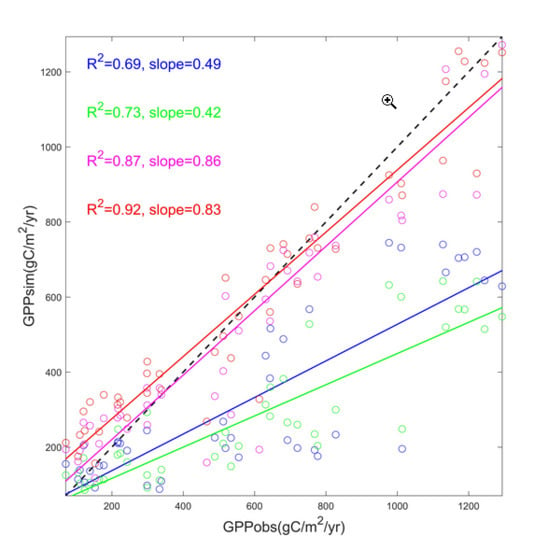
3.1. Evaluation of MODIS GPP Products and MOD17 Algorithm in the Arid Region
3.1.1. Site-Specific Evaluation of MODIS GPP Products and MOD17 Algorithm
3.1.2. Biome-Specific Evaluation of MODIS GPP Product and MOD17 Algorithm
3.1.3. Site-Specific Evaluation of MODIS GPP Products and MOD17 Algorithms
3.2. Uncertainty of Satellite Data in MODIS GPP Simulation over Ecosystems in the Arid Region
3.2.1. Impacts of the Accuracy of the Land Cover Classification on MODIS GPP Simulation
3.2.2. Impacts of Uncertainty of FPAR Data on MODIS GPP Simulation
3.3. Uncertainty and Variability of Biophysical Parameters for Diversity Ecosystems in Arid Regions
4. Discussion
4.1. Evaluations of the MOD17A2H Products over Diversity Ecosystems in the Arid Region
4.2. Uncertainty of Input Data in MODIS GPP Estimation in Diversity Ecosystems in the Arid Region
4.3. Uncertainty and Variability of Biophysical Parameters in Modelling GPP over Diversity Ecosystems in Arid Regions
4.4. Uncertainty of GPP Modelling of the Desert Ecosystems and Its Implications for GPP Simulation in Arid Regions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Asner, G.P.; Archer, S.; Hughes, R.F. Net changes in regional woody vegetation cover and carbon storage in Texas dry-lands, 1937–1999. Glob. Chang. Biol. 2003, 9, 316–335. [Google Scholar] [CrossRef]
- Bastin, J.F.; Berrahmouni, N.; Grainger, A.; Maniatis, D.; Mollicone, D.; Moore, R.; Patriarca, C.; Picard, N.; Sparrow, B.; Abraham, E.M.; et al. The extent of forest in dryland biomes. Science 2017, 356, 635–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahlström, A.; Raupach, M.R.; Schurgers, G.; Smith, B.; Arneth, A.; Jung, M.; Reichstein, M.; Canadell, J.G.; Friedlingstein, P.; Jain, A.K.; et al. The dominant role of semi-arid ecosystems in the trend and variability of the land CO2 sink. Science 2015, 348, 895–899. [Google Scholar] [CrossRef] [PubMed]
- Poulter, B.; Frank, D.; Ciais, P.; Myneni, R.B.; Andela, N.; Bi, J.; Broquet, G.; Canadell, J.G.; Chevallier, F.; Liu, Y.Y.; et al. Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 2014, 509, 600–603. [Google Scholar] [CrossRef] [PubMed]
- Lal, R. Carbon sequestration in dryland ecosystems. Environ. Manag. 2004, 33, 528–544. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, J.F.; Smith, D.M.; Lambin, E.F.; Turner, B.L.; Mortimore, M.; Batterbury, S.P.; Downing, T.E.; Dowlatabadi, H.; Fernández, R.J.; Herrick, J.E.; et al. Global desertification: Building a science for dryland development. Science 2007, 316, 847–851. [Google Scholar] [CrossRef] [PubMed]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Xiao, X.M.; Zhang, Q.Y.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Berrien, M.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Yuan, W.P.; Liu, S.G.; Zhou, G.S.; Zhou, G.Y.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. Forest Meteorol. 2007, 143, 189207. [Google Scholar] [CrossRef]
- Ma, X.; Huete, A.; Moran, S.; Ponce-Campos, G.; Eamus, D. Abrupt shifts in phenology and vegetation productivity under climate extremes. J. Geophys. Res. Biogeosci. 2015, 120, 2036–2052. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.S.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- Biederman, J.A.; Scott, R.L.; Bell, T.W.; Bowling, D.R.; Dore, S.; Garatuza-Payan, J.; Kolb, T.E.; Krishnan, P.; Krofcheck, D.J.; Litvak, M.E.; et al. CO2 exchange and evapotranspiration across dryland ecosystems of southwestern North America. Glob. Chang. Biol. 2017, 23, 4204–4221. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Running, S.W.; Nemani, R.R. Sensitivity of Moderate Resolution Imaging Spectroradiometer (MODIS) terrestrial primary production to the accuracy of meteorological reanalyses. J. Geophys. Res. 2006, 111, G01002. [Google Scholar] [CrossRef]
- Running, S.W.; Zhao, M. Daily GPP and Annual NPP (MOD17A2/A3) Products NASA Earth Observing System MODIS Land Algorithm; MOD17 User’s Guide; University of Montana: Missoula, MT, USA, 2015; pp. 1–28. [Google Scholar]
- Chasmer, L.; Barr, A.; Hopkinson, C.; McCaughey, H.; Treitz, P.; Black, A.; Shashkov, A. Scaling and assessment of GPP from MODIS using a combination of airborne lidar and eddy covariance measurements over jack pine forests. Remote Sens. Environ. 2009, 113, 82–93. [Google Scholar] [CrossRef]
- Running, S.W.; Zhao, M. MOD17A2H MODIS/Terra Gross Primary Productivity 8-Day L4 Global 500 m SIN Grid V006; USGS: Reston, VA, USA, 2015.
- Heinsch, F.A.; Zhao, M.; Running, S.W.; Kimball, J.S.; Nemani, R.R.; Davis, K.J.; Bolstad, P.V.; Cook, B.D.; Desai, A.R.; Ricciuto, D.M.; et al. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Trans. Geosci. Remote Sens. 2006, 7, 1908–1925. [Google Scholar] [CrossRef]
- Tang, X.; Li, H.; Huang, N.; Li, X.; Xu, X.; Ding, Z.; Xie, J. A comprehensive assessment of MODIS-derived GPP for forest ecosystems using the site-level FLUXNET database. Environ. Earth Sci. 2015, 74, 5907–5918. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Niu, B.; He, Y.T.; Zhang, X.Z.; Fu, G.; Shi, P.L.; Du, M.Y.; Zhang, Y.J.; Zong, N. Tower-Based Validation and Improvement of MODIS Gross Primary Production in an Alpine Swamp Meadow on the Tibetan Plateau. Remote Sens. 2016, 8, 592. [Google Scholar] [CrossRef]
- Fu, G.; Zhang, J.; Shen, Z.X.; Shi, P.L.; He, Y.T.; Zhang, X.Z. Validation of collection of 6 MODIS/Terra and MODIS/Aqua gross primary production in an alpine meadow of the Northern Tibetan Plateau. Int. J. Remote Sens. 2017, 38, 4517–4534. [Google Scholar] [CrossRef]
- Kanniah, K.D.; Beringer, J.; Hutley, L.B.; Tapper, N.J.; Zhu, X. Evaluation of Collections 4 and 5 of the MODIS Gross Primary Productivity Product and Algorithm Improvement at a Tropical Savanna Site in Northern Australia. Remote Sens. Environ. 2009, 113, 1808–1822. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Yu, Q.; Jiang, J.; Tang, Y.H. Calibration of Terra/MODIS gross primary production over an irrigated cropland on the North China Plain and an alpine meadow on the Tibetan Plateau. Glob. Chang. Biol. 2008, 14, 757–767. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Shao, Q.; Liu, J. The performances of MODIS-GPP and-ET products in China and their sensitivity to input data (FPAR/LAI). Remote Sens. 2014, 7, 135–152. [Google Scholar] [CrossRef]
- Zhu, H.; Lin, A.; Wang, L.; Xia, Y.; Zou, L. Evaluation of MODIS gross primary production across multiple biomes in China using eddy covariance flux data. Remote Sens. 2016, 8, 395. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, H.; Lin, A.; Zou, L.; Qin, W.; Du, Q. Evaluation of the Latest MODIS GPP Products across Multiple Biomes Using Global Eddy Covariance Flux Data. Remote Sens. 2017, 9, 418. [Google Scholar] [CrossRef]
- Gilabert, M.A.; Moreno, A.; Maselli, F.; Martinez, B.; Chiesi, M.; Sanchez-Ruiz, S.; Garcia-Haro, F.J.; Pérez-Hoyos, A.; Campos-Taberner, M.; Pérez-Priego, O.; et al. Daily GPP Estimates in Mediterranean Ecosystems by Combining Remote Sensing and Meteorological Data. ISPRS J. Photogramm. 2015, 102, 184–197. [Google Scholar] [CrossRef]
- Verbeeck, H.; Samson, R.; Verdonck, F.; Lemeur, R. Parameter sensitivity and uncertainty of the forest carbon flux model FORUG: A Monte Carlo analysis. Tree Physiol. 2006, 26, 807–817. [Google Scholar] [CrossRef]
- Kang, X.; Liang, Y.; Zhang, X.; Li, Y.; Tian, D.; Peng, C.; Wu, H.; Wang, J.; Zhong, L. Modeling gross primary production of a typical coastal wetland in china using MODIS time series and CO2 eddy flux tower data. Remote Sens. 2018, 10, 708. [Google Scholar] [CrossRef]
- Jin, C.; Xiao, X.; Wagle, P.; Griffis, T.; Dong, J.; Wu, C.; Qin, Y.; Cook, D.R. Effects of in-situ and reanalysis climate data on estimation of cropland gross primary production using the Vegetation Photosynthesis Model. Agric. Forest Meteorol. 2015, 213, 240–250. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.F.; Ma, M.G.; Li, X.; Song, Y.; Tan, J.L.; Huang, G.H.; Zhang, Z.H.; Zhao, T.B.; Feng, J.M.; Ma, Z.G.; et al. Validation of MODIS-GPP product at 10 flux sites in northern China. Int. J. Remote Sens. 2013, 34, 587–599. [Google Scholar] [CrossRef]
- Braswell, B.H.; Sacks, W.J.; Linder, E.; Schimel, D.S. Estimating diurnal to annual ecosystem parameters by synthesis of a carbon flux model with eddy covariance net ecosystem exchange observations. Glob. Chang. Biol. 2005, 11, 335–355. [Google Scholar] [CrossRef]
- Ricciuto, D.M.; Davis, K.J.; Keller, K. A Bayesian calibration of a simple carbon cycle model: The role of observations in estimating and reducing uncertainty. Glob. Biogeochem. Cycles 2008, 22, GB2030. [Google Scholar] [CrossRef]
- Li, X. Characterization, controlling, and reduction of uncertainties in the modeling and observation of land-surface systems. Sci. China Earth Sci. 2014, 57, 80–87. [Google Scholar] [CrossRef]
- Wang, H.B.; Ma, M.G.; Xie, Y.M.; Wang, X.F.; Wang, J. Parameter inversion estimation in photosynthetic models: Impact of different simulation methods. Photosynthetica 2014, 52, 233–246. [Google Scholar] [CrossRef]
- van Oijen, M.; Rougier, J.; Smith, R. Bayesian calibration of process-based forest models: Bridging the gap between models and data. Tree Physiol. 2005, 25, 915–927. [Google Scholar] [CrossRef]
- Wang, H.B.; Ma, M.G. Comparing the seasonal variation of parameter estimation of ecosystem carbon exchange between alpine meadow and cropland in Heihe River Basin, northwestern China. Sci. Cold Arid Reg. 2015, 7, 216–228. [Google Scholar]
- Knorr, W.; Kattge, J. Inversion of terrestrial biosphere model parameter values against eddy covariance measurements using Monte Carlo sampling. Glob. Chang. Biol. 2005, 11, 1333–1351. [Google Scholar] [CrossRef]
- Groenendijk, M.; Dolman, A.J.; Van der Molen, M.K.; Leuning, R.; Arneth, A.; Delpierre, N.; Gash, J.H.C.; Richardson, A.D.; Verbeeck, H.; Wohlfahrt, G. Assessing parameter variability in a photosynthesis model within and between plant functional types using global Fluxnet eddy covariance data. Agric. Forest Meteorol. 2011, 151, 22–38. [Google Scholar] [CrossRef]
- Cheng, G.; Li, X.; Zhao, W.; Xu, Z.; Feng, Q.; Xiao, S.; Xiao, H. Integrated study of the water–ecosystem–economy in the Heihe River Basin. Natl. Sci. Rev. 2014, 1, 413–428. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Cheng, G.D.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Liu, Q.H.; Wang, W.Z.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Wang, W.Z.; Hu, X.L.; Xu, Z.W.; Wen, J.G.; et al. A multiscale dataset for understanding complex eco-hydrological processes in a heterogeneous oasis system. Sci. Data 2017, 4, 170083. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Z.W.; Liu, S.M.; Li, X.; Shi, S.J.; Wang, J.M.; Zhu, Z.L.; Xu, T.R.; Wang, W.Z.; Ma, M.G. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. Atmos. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Wang, X.F.; Wang, H.B.; Li, X.; Ran, Y.H. Photosynthesis (NPP, NEP, Respiration). In Observation and Measurement of Ecohydrological Processes; Li, X., Vereecken, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–30. [Google Scholar]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Ma, M.G.; Veroustraete, F. Reconstructing Pathfinder AVHRR Land NDVI Time-Series Data for the Northwest of China. Adv. Space Res. 2006, 37, 835–840. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El-Masri, B.Z.; Baldocchi, D.D.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; Monson, R.K.; et al. On the use of MODIS EVI to assess gross primary productivity of North American ecosystems. J. Geophys. Res 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Reeves, M.; Votava, P.; Kang, S.; Milesi, C.; Zhao, M.; Glassy, J.; Jolly, W.M.; Loehman, R.; Bowker, C.F.; et al. User’s Guide: GPP and NPP (MOD17A2/A3) Products NASA MODIS Land Algorithm; University of Montana: Missoula, MT, USA, 2003; pp. 1–57. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equations of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chain and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Liu, S.; Dong, W.; Chen, J.; Arain, M.A.; Blanken, P.D.; Cescatti, A.; Wohlfahrt, G.; Georgiadis, T.; et al. Vegetation-specific model parameters are not required for estimating gross primary production. Ecol. Model. 2014, 292, 1–10. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Zhao, M.; Running, S.W.; Wofsy, S.C.; Urbanski, S.; Dunn, A.L.; Munger, J.W. Scaling Gross Primary Production (GPP) over boreal and deciduous forest landscapes in support of MODIS GPP product validation. Remote Sens. Environ. 2003, 88, 256–270. [Google Scholar] [CrossRef] [Green Version]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Mu, X.; Song, W.; Gao, Z.; McVicar, T.R.; Donohue, R.J.; Yan, G. Fractional vegetation cover estimation by using multi-angle vegetation index. Remote Sens. Environ. 2018, 216, 44–56. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Heinsch, F.A.; Liu, M.; Tian, H.; Running, S.W. Evaluating water stress controls on primary production in biogeochemical and remote sensing based models. J. Geophys. Res. 2007, 112, G01012. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.G.; Houghton, R.A.; Tang, L.S. Hidden carbon sink beneath desert. Geophys. Res. Lett. 2015, 42, 5880–5887. [Google Scholar] [CrossRef] [Green Version]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- He, M.; Ju, W.; Zhou, Y.; Chen, J.; He, H.; Wang, S.; Wang, H.; Guan, D.; Yan, J.; Li, Y.; et al. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary productivity. Agric. Forest Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Propastin, P.; Ibrom, A.; Knohl, A.; Erasmi, S. Effects of canopy photosynthesis saturation on the estimation of gross primary productivity from MODIS data in a tropical forest. Remote Sens. Environ. 2012, 121, 252–260. [Google Scholar] [CrossRef]
- Chu, H.; Baldocchi, D.D.; John, R.; Wolf, S.; Reichstein, M. Fluxes all of the time? A primer on the temporal representativeness of FLUXNET. J. Geophys. Res. 2017, 122, 289–307. [Google Scholar] [CrossRef]









| Site Code | PFTs | Year Used | Vegetation Cover | Longitude | Latitude | MAT (°C) | MAP (mm) | PET (mm) |
|---|---|---|---|---|---|---|---|---|
| A’rou(ARZ) | Grassland | 2013–2016 | alpine grassland | 38.0473 | 100.4643 | −0.29 | 444.70 | 636.18 |
| Dashalong(DSL) | Grassland | 2013–2016 | alpine meadow | 38.8399 | 98.9406 | −3.91 | 314.43 | 698.07 |
| Yakou(YKZ) | Grassland | 2015–2016 | alpine meadow | 38.0142 | 100.2421 | −4.68 | 500.79 | 653.16 |
| Huazhaizi(HZZ) | Desert steppe | 2012–2016 | desert steppe | 38.76519 | 100.3186 | 8.89 | 139.68 | 590.93 |
| Gobi(GBZ) | Desert steppe | 2012–2015 | desert steppe | 38.91496 | 100.3042 | 9.07 | 102.25 | 575.72 |
| Luodi(LDZ) | Desert steppe | 2013–2015 | desert steppe | 41.9993 | 101.1326 | 12.32 | 24.80 | 727.68 |
| Daman(DMZ) | Cropland | 2012–2016 | maize | 38.85551 | 100.3722 | 6.93 | 135.70 | 828.04 |
| Nongtian(NTZ) | Cropland | 2012–2016 | cantaloupe | 42.0048 | 101.1338 | 9.39 | 35.55 | 727.68 |
| Shidi(SDZ) | Cropland | 2012–2016 | reed | 38.97514 | 100.4464 | 9.19 | 119.9 | 1249.35 |
| Huyanglin(HYL) | Forest | 2013–2015 | populus euphratica | 41.9928 | 101.1236 | 10.33 | 26.00 | 922.91 |
| Hunhelin(HHL) | Forest | 2013–2016 | mixed forest | 41.9903 | 101.1335 | 10.04 | 35.53 | 1043.34 |
| Sidaoqiao(SDQ) | Forest | 2013–2016 | tamarix forest | 42.0012 | 101.1374 | 10.06 | 37.13 | 977.95 |
| GPP_MODIS | GPP_Insitu | GPP_LUE | GPP_Fiveopt | |||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| ARZ | 0.85 | 1.13 | 0.92 | 1.58 | 0.92 | 1.58 | 0.92 | 0.82 |
| DSL | 0.79 | 1.01 | 0.86 | 1.18 | 0.85 | 0.74 | 0.82 | 0.59 |
| YKZ | 0.72 | 0.41 | 0.76 | 0.30 | 0.76 | 0.58 | 0.78 | 0.65 |
| HZZ | 0.38 | 0.42 | 0.40 | 0.32 | 0.40 | 0.53 | 0.40 | 0.54 |
| GBZ | 0.37 | 0.28 | 0.41 | 0.27 | 0.41 | 0.60 | 0.42 | 0.68 |
| LDZ | 0.50 | 0.44 | 0.73 | 0.41 | 0.73 | 0.59 | 0.72 | 0.61 |
| DMZ | 0.86 | 3.43 | 0.94 | 3.69 | 0.94 | 1.27 | 0.96 | 0.96 |
| NTZ | - | - | 0.63 | 2.30 | 0.55 | 1.82 | 0.63 | 1.42 |
| SDZ | 0.85 | 1.55 | 0.88 | 1.76 | 0.88 | 1.16 | 0.91 | 0.98 |
| HHL | 0.57 | 2.48 | 0.77 | 2.30 | 0.68 | 1.21 | 0.87 | 0.75 |
| SDQ | 0.56 | 1.68 | 0.81 | 1.46 | 0.74 | 0.85 | 0.85 | 0.66 |
| HYL | 0.54 | 2.14 | 0.76 | 1.86 | 0.67 | 1.10 | 0.89 | 0.65 |
| Sites | εmax | Tmin_min | Tmin_max | VPDmin | VPDmax |
|---|---|---|---|---|---|
| Prior range | (0.3,3) | (−35,−2) | (6,30) | (60,1000) | (1500,6500) |
| ARZ | 1.044, 2.10(1.62,2.94) | −8, −10.29(−11.33,−9.29) | 12.02, 15.52(10.16, 26.63) | 650, 151.37(64.48,296.64) | 4300, 3252.21(2801.68, 4009.33) |
| DSL | 1.044, 1.24(0.90,1.75) | −8, −30.28(−34.79,−22.79) | 12.02, 18.84(6.78, 29.44) | 650, 430.98(81.46,961.71) | 4300, 3960.64(1732.84, 6361.79) |
| YKZ | 1.044, 1.80(0.97, 2.53) | −8, −15.30(−32.13,−3.62) | 12.02, 20.49(6.94, 29.58) | 650, 567.33(96.08,978.23) | 4300, 4136.91(1760.66, 6397.26) |
| HZZ | 1.044, 1.68(1.21, 2.42) | −8, −20.76(−34.33,−3.14) | 12.02, 22.62(7.30, 29.53) | 650, 608.86(81.31,977.20) | 4300, 4936.72(3135.86, 6400.44) |
| GBZ | 1.044, 2.46(1.87, 2.95) | −8, −18.93(−34.14, −2.95) | 12.02, 13.71(6.47, 27.14) | 650, 592.37(92.14,982.30) | 4300, 4654.96(3150.60, 6424.90) |
| LDZ | 1.044, 1.16(0.89, 2.04) | −8, −17.23(−34.07, −2.79) | 12.02, 13.83(6.39, 28.65) | 650, 568.79(98.05,977.54) | 4300, 5006.36(3050.36, 6436.59) |
| DMZ | 0.860, 2.89(2.73, 2.99) | −8, −3.91(−4.82,−3.08) | 12.02, 16.37(15.66, 17.58) | 650, 176.02(66.63,377.42) | 5300, 6089.55(5664.46, 6457.04) |
| NTZ | 0.860, 3.0(2.98, 3.0) | −8, −28.59 (−34.78, −11.21) | 12.02, 8.27(6.14, 11.13) | 650, 991.88(961.92,999.73) | 5300, 6486.19(6432.50, 6499.42) |
| SDZ | 0.860, 1.59(1.41, 1.74) | −8, −32.82(−34.91,−27.88) | 12.02, 25.76(19.61, 29.68) | 650, 237.30(66.65,519.04) | 5300, 6329.98(5928.29, 6492.67) |
| HHL | 1.051, 2.89(2.63, 3.0) | −8, −18.54(−26.41, −10.64) | 8.61, 22.26(19.30, 26.62) | 650, 771.23(229.59,992.57) | 4800, 6435.17(6233.17, 6497.78) |
| SDQ | 1.268, 2.33(1.80, 2.94) | −8, −18.07(−33.83, −2.82) | 9.09, 20.25(11.59, 29.25) | 800, 523.27(82.79,972.83) | 3100, 5947.81(5274.70, 6461.10) |
| HYL | 1.165, 2.71(2.28, 2.98) | −6, −6.20(−13.10,−2.44) | 9.94, 25.11(21.11, 29.50) | 650, 619.61(108.53,980.37) | 1650, 6410.51(6143.55, 6496.60) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Li, X.; Ma, M.; Geng, L. Improving Estimation of Gross Primary Production in Dryland Ecosystems by a Model-Data Fusion Approach. Remote Sens. 2019, 11, 225. https://doi.org/10.3390/rs11030225
Wang H, Li X, Ma M, Geng L. Improving Estimation of Gross Primary Production in Dryland Ecosystems by a Model-Data Fusion Approach. Remote Sensing. 2019; 11(3):225. https://doi.org/10.3390/rs11030225
Chicago/Turabian StyleWang, Haibo, Xin Li, Mingguo Ma, and Liying Geng. 2019. "Improving Estimation of Gross Primary Production in Dryland Ecosystems by a Model-Data Fusion Approach" Remote Sensing 11, no. 3: 225. https://doi.org/10.3390/rs11030225
APA StyleWang, H., Li, X., Ma, M., & Geng, L. (2019). Improving Estimation of Gross Primary Production in Dryland Ecosystems by a Model-Data Fusion Approach. Remote Sensing, 11(3), 225. https://doi.org/10.3390/rs11030225