Disassociation of the Kuroshio Current with the Pacific Decadal Oscillation Since 1999
Abstract
1. Introduction
2. Materials and Methods
3. Results
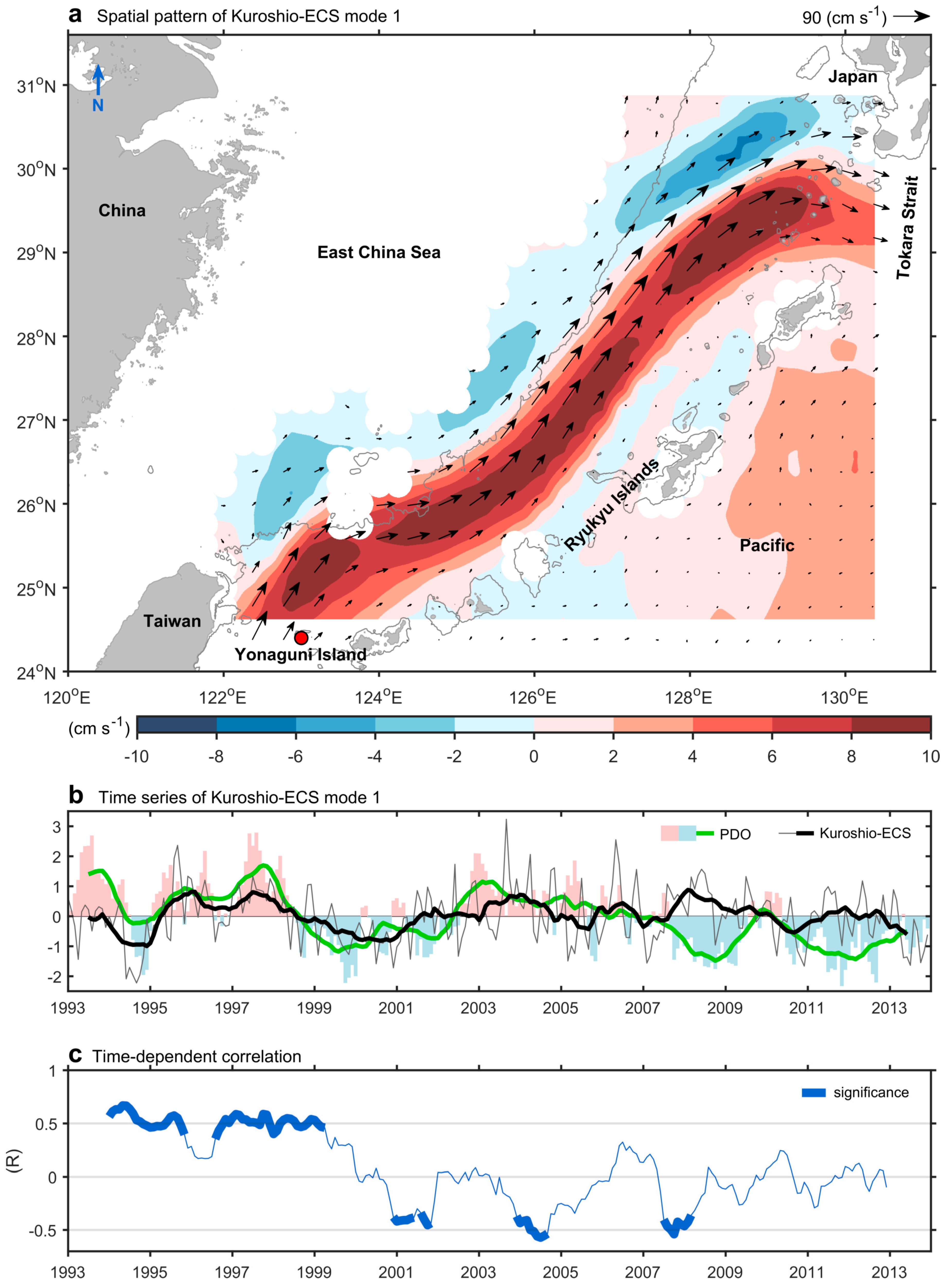
3.1. Principal Component Analysis of the Kuroshio-ECS
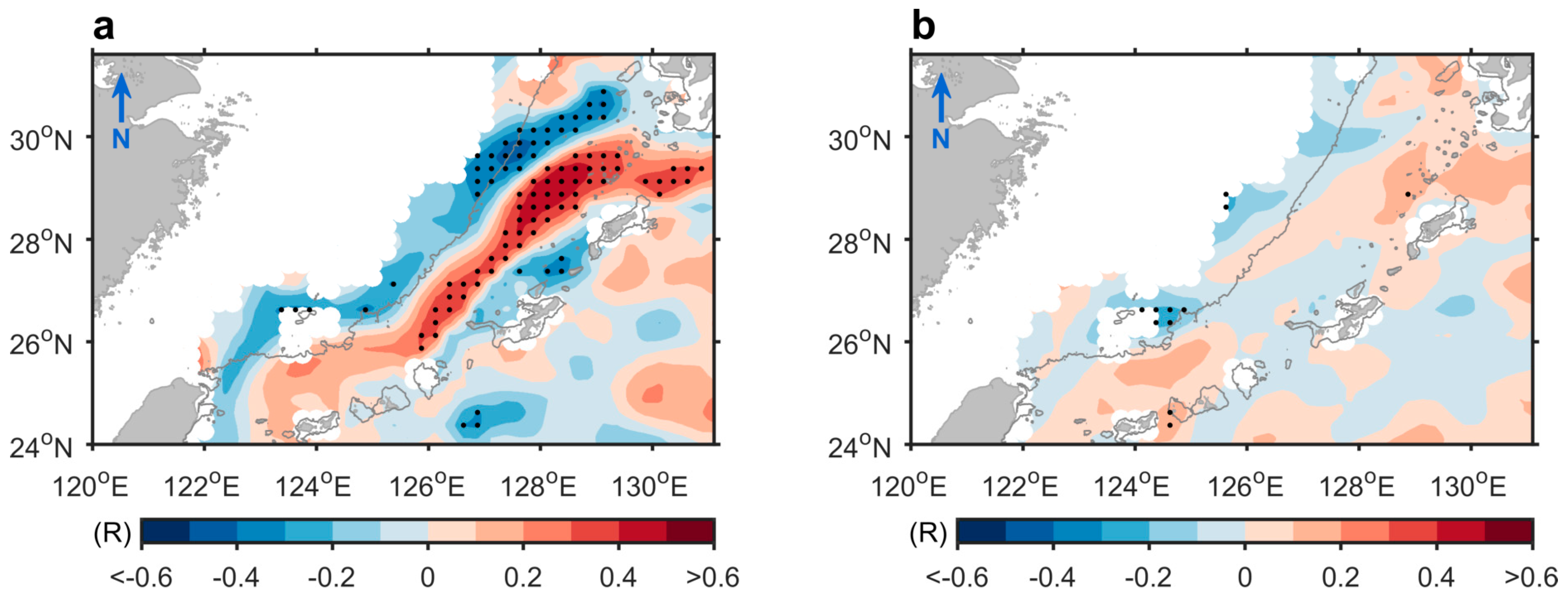
3.2. Leading Mode Succession
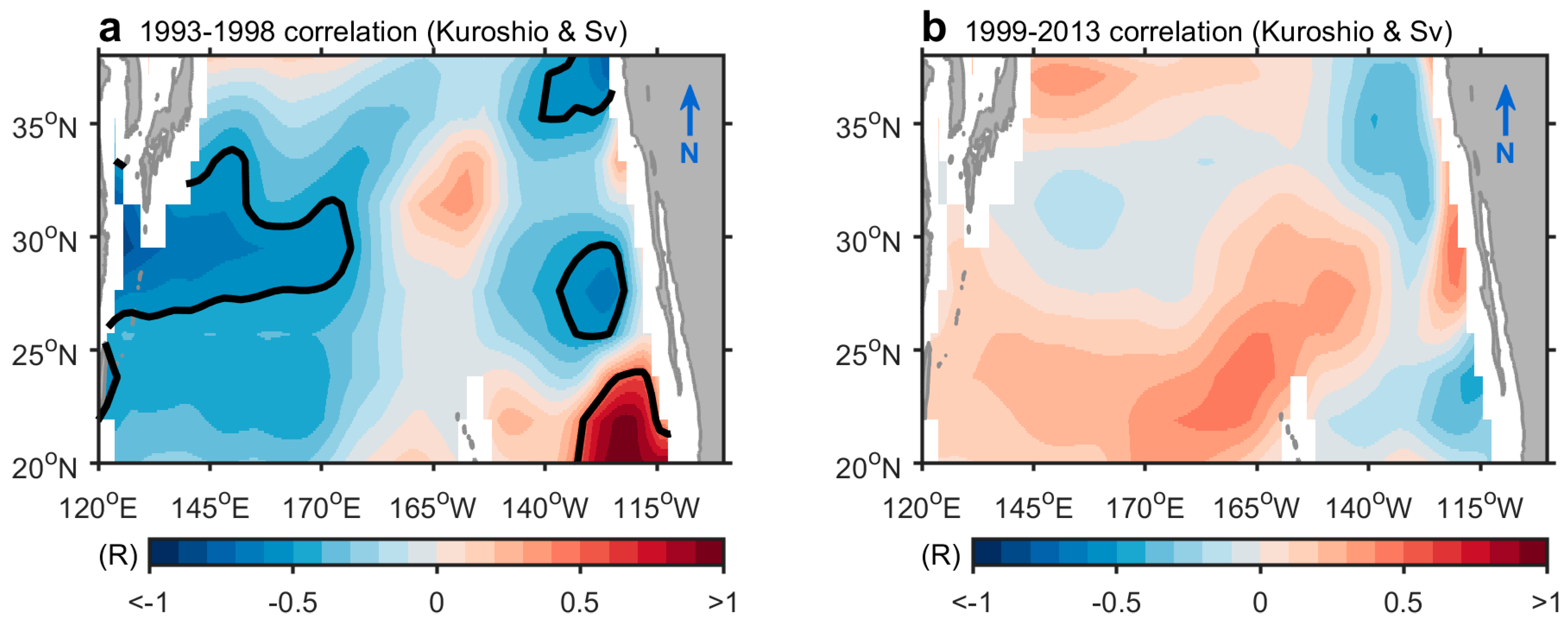
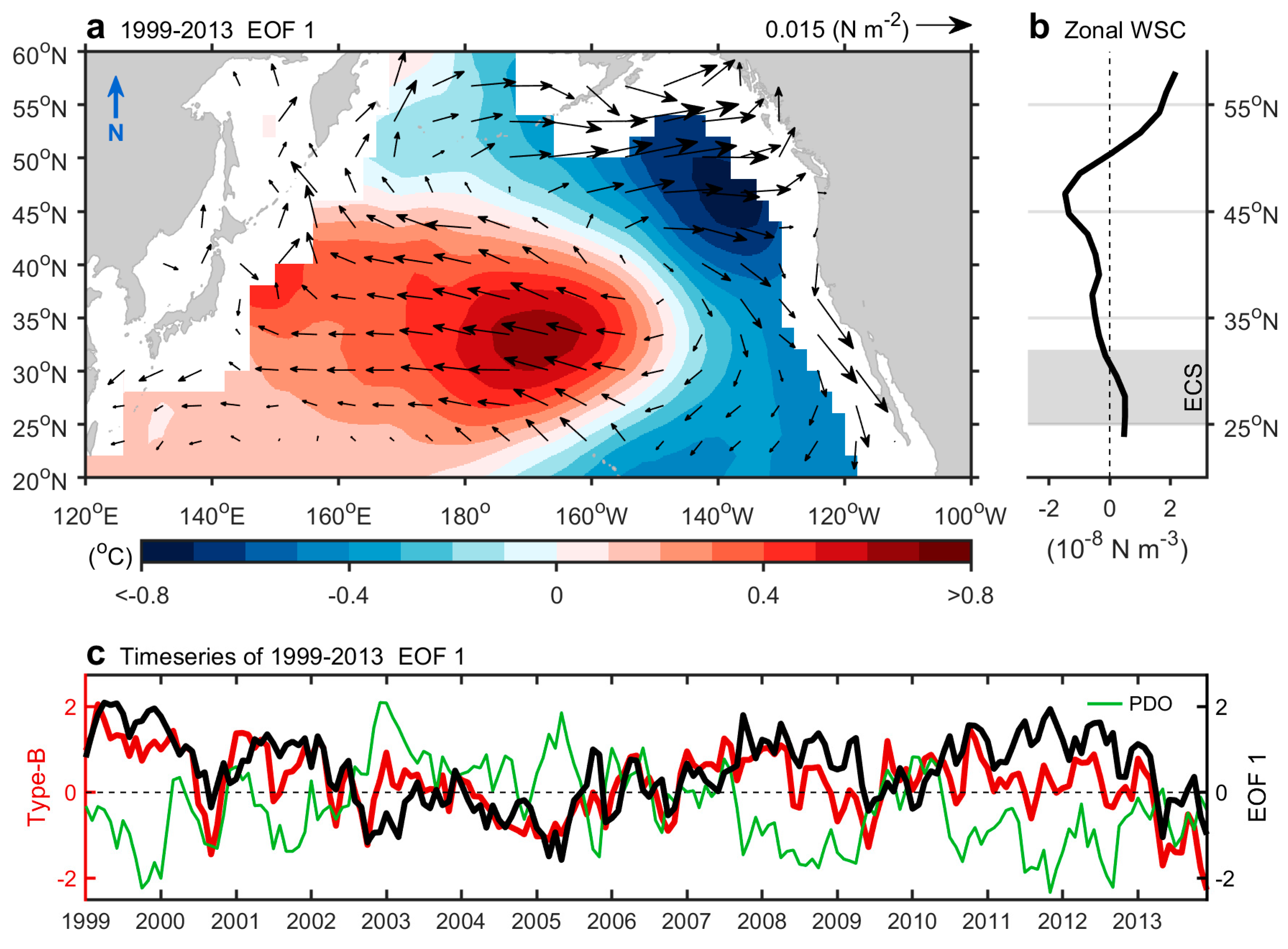
3.3. Baroclinic Responses
4. Summary
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tang, T.Y.; Tai, J.H.; Yang, Y.J. The flow pattern north of Taiwan and the migration of the Kuroshio. Cont. Shelf Res. 2000, 20, 349–371. [Google Scholar] [CrossRef]
- Hsin, Y.-C.; Wu, C.-R.; Shaw, P.-T. Spatial and temporal variations of the Kuroshio east of Taiwan, 1982–2005: A numerical study. J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef]
- Nitani, H. Beginning of the Kuroshio. In Kuroshio, Its Physical Aspects; University of Tokyo Press: Tokyo, Japan, 1972; pp. 129–163. [Google Scholar]
- Isobe, A. Recent advances in ocean-circulation research on the Yellow Sea and East China Sea shelves. J. Oceanogr. 2008, 64, 569–584. [Google Scholar] [CrossRef]
- Liu, Z.; Gan, J. Variability of the Kuroshio in the East China Sea derived from satellite altimetry data. Deep Sea Res. Part I 2012, 59, 25–36. [Google Scholar] [CrossRef]
- Guo, X.; Miyazawa, Y.; Yamagata, T. The Kuroshio Onshore Intrusion along the Shelf Break of the East China Sea: The Origin of the Tsushima Warm Current. J. Phys. Oceanogr. 2006, 36, 2205–2231. [Google Scholar] [CrossRef]
- Ichikawa, K.; Tokeshi, R.; Kashima, M.; Sato, K.; Matsuoka, T.; Kojima, S.; Fujii, S. Kuroshio variations in the upstream region as seen by HF radar and satellite altimetry data. Int. J. Remote Sens. 2008, 29, 6417–6426. [Google Scholar] [CrossRef]
- Wu, C.-R.; Lu, H.-F.; Chao, S.-Y. A numerical study on the formation of upwelling off northeast Taiwan. J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef]
- Hsin, Y.-C.; Chiang, T.-L.; Wu, C.-R. Fluctuations of the thermal fronts off northeastern Taiwan. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Wong, G.T.F.; Hung, C.-C.; Gong, G.-C. Dissolved iodine species in the East China Sea—A complementary tracer for upwelling water on the shelf. Cont. Shelf Res. 2004, 24, 1465–1484. [Google Scholar] [CrossRef]
- Hwang, C.; Kao, R. TOPEX/POSEIDON-derived space–time variations of the Kuroshio Current: Applications of a gravimetric geoid and wavelet analysis. Geophys. J. Int. 2002, 151, 835–847. [Google Scholar] [CrossRef]
- Han, G.; Huang, W. Pacific Decadal Oscillation and Sea Level Variability in the Bohai, Yellow, and East China Seas. J. Phys. Oceanogr. 2008, 38, 2772–2783. [Google Scholar] [CrossRef]
- Andres, M.; Park, J.-H.; Wimbush, M.; Zhu, X.-H.; Nakamura, H.; Kim, K.; Chang, K.-I. Manifestation of the Pacific Decadal Oscillation in the Kuroshio. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Gordon, A.L.; Giulivi, C.F. Pacific decadal oscillation and sea level in the Japan/East sea. Deep Sea Res. Part I 2004, 51, 653–663. [Google Scholar] [CrossRef]
- Newman, M.; Alexander, M.A.; Ault, T.R.; Cobb, K.M.; Deser, C.; Di Lorenzo, E.; Mantua, N.J.; Miller, A.J.; Minobe, S.; Nakamura, H. The Pacific decadal oscillation, revisited. J. Clim. 2016, 29, 4399–4427. [Google Scholar] [CrossRef]
- Schneider, N.; Cornuelle, B.D. The Forcing of the Pacific Decadal Oscillation. J. Clim. 2005, 18, 4355–4373. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R. The Pacific Decadal Oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Seager, R.; Kushnir, Y.; Naik, N.H.; Cane, M.A.; Miller, J. Wind-Driven Shifts in the Latitude of the Kuroshio–Oyashio Extension and Generation of SST Anomalies on Decadal Timescales. J. Clim. 2001, 14, 4249–4265. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Wu, C.-R.; Chao, S.-Y. Warming and weakening trends of the Kuroshio during 1993–2013. Geophys. Res. Lett. 2016, 43, 9200–9207. [Google Scholar] [CrossRef]
- Hu, D.; Wu, L.; Cai, W.; Gupta, A.S.; Ganachaud, A.; Qiu, B.; Gordon, A.L.; Lin, X.; Chen, Z.; Hu, S.; et al. Pacific western boundary currents and their roles in climate. Nature 2015, 522, 299–308. [Google Scholar] [CrossRef]
- Andres, M.; Kwon, Y.-O.; Yang, J. Observations of the Kuroshio’s barotropic and baroclinic responses to basin-wide wind forcing. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Deser, C.; Alexander, M.A.; Xie, S.-P.; Phillips, A.S. Sea surface temperature variability: Patterns and mechanisms. Annu. Rev. Mar. Sci. 2010, 2, 115–143. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Delworth, T.L. Impact of the Atlantic multidecadal oscillation on North Pacific climate variability. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Medhaug, I.; Stolpe, M.B.; Fischer, E.M.; Knutti, R. Reconciling controversies about the ‘global warming hiatus’. Nature 2017, 545, 41. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Fedorov, A.V. The extreme El Niño of 2015–2016 and the end of global warming hiatus. Geophys. Res. Lett. 2017, 44, 3816–3824. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Branstator, G.; Phillips, A.S. Seasonal aspects of the recent pause in surface warming. Nat. Clim. Chang. 2014, 4, 911–916. [Google Scholar] [CrossRef]
- England, M.H.; McGregor, S.; Spence, P.; Meehl, G.A.; Timmermann, A.; Cai, W.; Gupta, A.S.; McPhaden, M.J.; Purich, A.; Santoso, A. Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus. Nat. Clim. Chang. 2014, 4, 222–227. [Google Scholar] [CrossRef]
- Nakamura, H.; Nishina, A.; Tabata, K.; Higashi, M.; Habano, A.; Yamashiro, T. Surface velocity time series derived from satellite altimetry data in a section across the Kuroshio southwest of Kyushu. J. Oceanogr. 2012, 68, 321–336. [Google Scholar] [CrossRef]
- Soeyanto, E.; Guo, X.; Ono, J.; Miyazawa, Y. Interannual variations of Kuroshio transport in the East China Sea and its relation to the Pacific Decadal Oscillation and mesoscale eddies. J. Geophys. Res. Oceans 2014, 119, 3595–3616. [Google Scholar] [CrossRef]
- Ichikawa, K. Variation of the Kuroshio in the Tokara Strait induced by meso-scale eddies. J. Oceanogr. 2001, 57, 55–68. [Google Scholar] [CrossRef]
- Nagano, A.; Ichikawa, K.; Ichikawa, H.; Tomita, H.; Tokinaga, H.; Konda, M. Stable volume and heat transports of the North Pacific subtropical gyre revealed by identifying the Kuroshio in synoptic hydrography south of Japan. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Rio, M.; Mulet, S.; Picot, N. New global Mean Dynamic Topography from a GOCE geoid model, altimeter measurements and oceanographic in-situ data. In Proceedings of the ESA Living Planet Symposium, Edinburgh, UK, 9–13 September 2013. [Google Scholar]
- Hsin, Y.-C.; Qu, T.; Wu, C.-R. Intra-seasonal variation of the Kuroshio southeast of Taiwan and its possible forcing mechanism. Ocean Dyn. 2010, 60, 1293–1306. [Google Scholar] [CrossRef]
- Manly, B.F. Randomization, Bootstrap and Monte Carlo Methods in Biology; CRC Press: Boca Raton, FL, USA, 2006; Volume 70. [Google Scholar]
- Kawabe, M. Variability of Kuroshio velocity assessed from the sea-level difference between Naze and Nishinoomote. J. Oceanogr. 1988, 44, 293–304. [Google Scholar] [CrossRef]
- Sun, X. Analysis of the surface path of the Kuroshio in the East China Sea. In Essays on the Investigation of Kuroshio; China Ocean Press: Beijing, China, 1987; pp. 1–14. [Google Scholar]
- Di Lorenzo, E.; Schneider, N.; Cobb, K.M.; Franks, P.J.S.; Chhak, K.; Miller, A.J.; McWilliams, J.C.; Bograd, S.J.; Arango, H.; Curchitser, E.; et al. North Pacific Gyre Oscillation links ocean climate and ecosystem change. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- McGregor, S.; Timmermann, A.; Stuecker, M.F.; England, M.H.; Merrifield, M.; Jin, F.-F.; Chikamoto, Y. Recent Walker circulation strengthening and Pacific cooling amplified by Atlantic warming. Nat. Clim. Chang. 2014, 4, 888–892. [Google Scholar] [CrossRef]
- Easterling, D.R.; Wehner, M.F. Is the climate warming or cooling? Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Stommel, H. The westward intensification of wind-driven ocean currents. Eos Trans. Am. Geophys. Union 1948, 29, 202–206. [Google Scholar] [CrossRef]
- Walker, G.T.; Bliss, E. World Weather V. Memoirs of the Royal Meteorological Society 1932, 4, 53–84. [Google Scholar]
- Chhak, K.C.; Di Lorenzo, E.; Schneider, N.; Cummins, P.F. Forcing of Low-Frequency Ocean Variability in the Northeast Pacific. J. Clim. 2009, 22, 1255–1276. [Google Scholar] [CrossRef]
- Newman, M.; Compoew, G.P.; Alexander, M.A. ENSO-Forced Variability of the Pacific Decadal Oscillation. J. Clim. 2003, 16, 3853–3857. [Google Scholar] [CrossRef]
- Miller, A.J.; Cayan, D.R.; White, W.B. A westward-intensified decadal change in the North Pacific thermocline and gyre-scale circulation. J. Clim. 1998, 11, 3112–3127. [Google Scholar] [CrossRef]
- Deser, C.; Alexander, M.A.; Timlin, M.S. Evidence for a wind-driven intensification of the Kuroshio Current Extension from the 1970s to the 1980s. J. Clim. 1999, 12, 1697–1706. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Wu, C.-R. Enhanced warming and intensification of the Kuroshio Extension, 1999–2013. Remote Sens. 2019, 11, 101. [Google Scholar] [CrossRef]
- Kosaka, Y.; Xie, S.P. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 2013, 501, 403–407. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-L.; Wu, C.-R. Discordant multi-decadal trend in the intensity of the Kuroshio along its path during 1993–2013. Sci. Rep. 2018, 8, 14633. [Google Scholar] [CrossRef] [PubMed]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-R.; Wang, Y.-L.; Chao, S.-Y. Disassociation of the Kuroshio Current with the Pacific Decadal Oscillation Since 1999. Remote Sens. 2019, 11, 276. https://doi.org/10.3390/rs11030276
Wu C-R, Wang Y-L, Chao S-Y. Disassociation of the Kuroshio Current with the Pacific Decadal Oscillation Since 1999. Remote Sensing. 2019; 11(3):276. https://doi.org/10.3390/rs11030276
Chicago/Turabian StyleWu, Chau-Ron, You-Lin Wang, and Shenn-Yu Chao. 2019. "Disassociation of the Kuroshio Current with the Pacific Decadal Oscillation Since 1999" Remote Sensing 11, no. 3: 276. https://doi.org/10.3390/rs11030276
APA StyleWu, C.-R., Wang, Y.-L., & Chao, S.-Y. (2019). Disassociation of the Kuroshio Current with the Pacific Decadal Oscillation Since 1999. Remote Sensing, 11(3), 276. https://doi.org/10.3390/rs11030276






