Use of SMAP Soil Moisture and Fitting Methods in Improving GPM Estimation in Near Real Time
Abstract
1. Introduction
2. Study Area and Data Sets
2.1. China Merged Perception Analysis (CMPA)
2.2. GPM IMERG
2.3. SMAP Soil Moisture
2.4. Additional Datasets
3. Model and Method
3.1. API Model
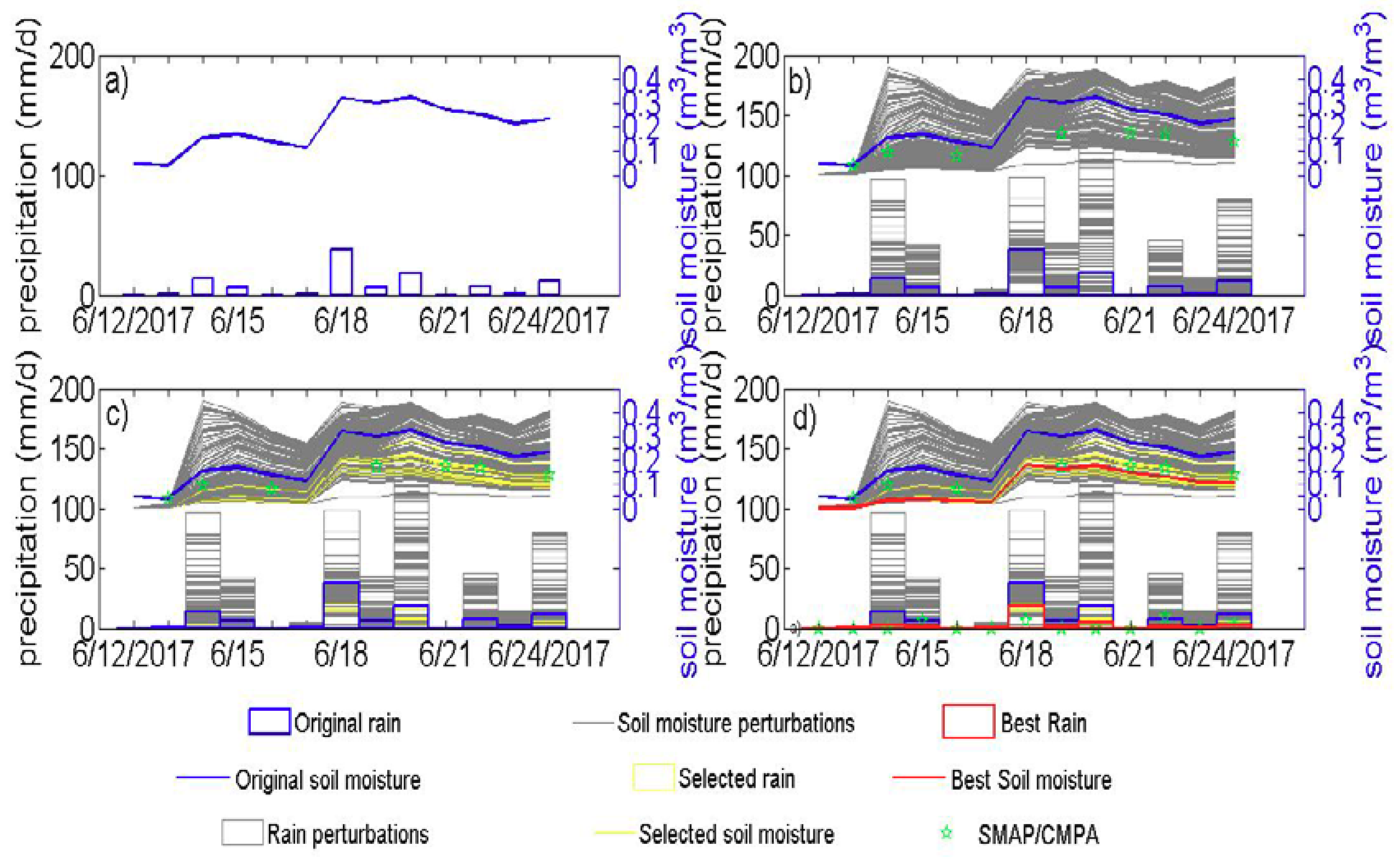
3.2. Assimilation Algorithm
3.3. Fitting Correction Methods
3.3.1. Linear Fitting Correction
3.3.2. Nonlinear Fitting Correction
3.3.3. CDF Fitting Correction
3.3.4. Performance Metrics
4. Results
4.1. Parameter Values for Seven Correction Methods
4.2. Performance Assessment
4.2.1. Statistics
4.2.2. Monthly Series Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brocca, L.; Pellarin, T.; Crow, W.T.; Ciabatta, L.; Massari, C.; Ryu, D.; Su, C.H.; Rüdiger, C.; Kerr, Y. Rainfall estimation by inverting SMOS soil moisture estimates: A comparison of different methods over Australia. J. Geophys. Res. Atmos. 2016, 121, 12,062–12,079. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Dijk, A.I.J.M.V.; Beck, H.E.; Crosbie, R.S.; Jeu, R.A.M.D.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The Millennium Drought in southeast Australia (2001–2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
- Herold, N.; Alexander, L.V.; Donat, M.G.; Contractor, S.; Becker, A. How much does it rain over land? Geophys. Res. Lett. 2016, 43, 341–348. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Sheffield, J.; Pan, M.; Wood, E.F. Evaluation of the Tropical Rainfall Measuring Mission Multi-Satellite Precipitation Analysis (TMPA) for assessment of large-scale meteorological drought. Remote Sens. Environ. 2015, 159, 181–193. [Google Scholar] [CrossRef]
- Rinaldo, A.; Bertuzzo, E.; Mari, L.; Righetto, L.; Blokesch, M.; Gatto, M.; Casagrandi, R.; Murray, M.; Vesenbeckh, S.M.; Rodrigueziturbe, I. Reassessment of the 2010–2011 Haiti cholera outbreak and rainfall-driven multiseason projections. Proc. Natl. Acad. Sci. USA 2012, 109, 6602–6607. [Google Scholar] [CrossRef] [PubMed]
- Scholthof, K.B.G. The disease triangle: pathogens, the environment and society. Nat. Rev. Microbiol. 2007, 5, 152–156. [Google Scholar] [CrossRef] [PubMed]
- Casse, C.; Gosset, M.; Peugeot, C.; Pedinotti, V.; Boone, A.; Tanimoun, B.A.; Decharme, B. Potential of satellite rainfall products to predict Niger River flood events in Niamey. Atmos. Res. 2015, 163, 162–176. [Google Scholar] [CrossRef]
- Jongman, B.; Hochrainerstigler, S.; Feyen, L.; Aerts, J.C.J.H.; Mechler, R.; Botzen, W.J.W.; Bouwer, L.M.; Pflug, G.; Rojas, R.; Ward, P.J. Increasing stress on disaster-risk finance due to large floods. Nat. Clim. Chang. 2014, 4, 264–268. [Google Scholar] [CrossRef]
- Wake, B. Flooding costs. Nat. Clim. Chang. 2013, 3, 778. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Tian, Y.; Huffman, G.J.; Li, H.; Wang, J.J. Real-time global flood estimation using satellite-based precipitation and a coupled land surface and routing model. Water Resour. Res. 2014, 50, 2693–2717. [Google Scholar] [CrossRef]
- Lievens, H.; Tomer, S.K.; Bitar, A.A.; Lannoy, G.J.M.D.; Drusch, M.; Dumedah, G.; Franssen, H.J.H.; Kerr, Y.H.; Martens, B.; Pan, M. SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia. Remote Sens. Environ. 2015, 168, 146–162. [Google Scholar] [CrossRef]
- Pennington, C.; Dijkstra, T.; Lark, M.; Dashwood, C.; Harrison, A.; Freeborough, K. Antecedent Precipitation as a Potential Proxy for Landslide Incidence in South West United Kingdom; Springer: Nottinghamshire, UK, 2014; pp. 253–259. [Google Scholar]
- Lanza, L.G.; Stagi, L. High resolution performance of catching type rain gauges from the laboratory phase of the WMO Field Intercomparison of Rain Intensity Gauges. Atmos. Res. 2009, 94, 555–563. [Google Scholar] [CrossRef]
- Kucera, P.A.; Ebert, E.E.; Turk, F.J.; Levizzani, V.; Kirschbaum, D.; Tapiador, F.J.; Loew, A.; Borsche, M. Precipitation from Space: Advancing Earth System Science. Bull. Am. Meteorol. Soc. 2013, 94, 365–375. [Google Scholar] [CrossRef]
- Schamm, K.; Ziese, M.; Becker, A.; Finger, P.; Meyerchristoffer, A.; Schneider, U.; Schröder, M.; Stender, P. Global gridded precipitation over land: a description of the new GPCC First Guess Daily product. Earth Syst. Sci. Data 2014, 6, 49–60. [Google Scholar] [CrossRef]
- Ali, A.; Lebel, T. The Sahelian standardized rainfall index revisited. Int. J. Clim. 2010, 29, 1705–1714. [Google Scholar] [CrossRef]
- Delrieu, G.; Braud, I.; Berne, A.; Borga, M.; Boudevillain, B.; Fabry, F.; Freer, J.; Gaume, E.; Nakakita, E.; Seed, A. Weather radar and hydrology. Adv. Water Res. 2009, 32, 969–974. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Smith, J.A. Radar hydrology: rainfall estimation. Adv. Water Res. 2002, 25, 1387–1394. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, S.; You, S.; Huang, Y.; Wang, Q.; Zhou, Q. Comprehensive Evaluation of Two Successive V3 and V4 IMERG Final Run Precipitation Products over Mainland China. Remote Sens. 2018, 10, 34. [Google Scholar] [CrossRef]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.; Sorooshian, S.; Wang, J.; Xie, P. First Results from the Integrated Multi-Satellite Retrievals for GPM (IMERG). In Proceeding of EGU General Assembly Conference, Vienna, Austria, 12–17 April 2015. [Google Scholar]
- Cai, Y.; Jin, C.; Wang, A.; Guan, D.; Wu, J.; Yuan, F.; Xu, L. Spatio-Temporal Analysis of the Accuracy of Tropical Multisatellite Precipitation Analysis 3B42 Precipitation Data in Mid-High Latitudes of China. PLoS ONE 2015, 10, e0120026. [Google Scholar] [CrossRef] [PubMed]
- Pipunic, R.C.; Ryu, D.; Costelloe, J.F.; Su, C.H. An evaluation and regional error modeling methodology for near-real-time satellite rainfall data over Australia. J. Geophys. Res. Atmos. 2015, 120, 135–141. [Google Scholar] [CrossRef]
- Prasetia, R.; As-syakur, A.R. Validation of TRMM Precipitation Radar satellite data over Indonesian;region. Theoret. Appl. Clim. 2013, 112, 575–587. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.T.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104–105, 70–97. [Google Scholar] [CrossRef]
- Yin, X.; Gruber, A. Validation of the abrupt change in GPCP precipitation in the Congo River Basin. Int. J. Clim. 2010, 30, 110–119. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W. A new method for rainfall estimation through soil moisture observations. Geophys. Res. Lett. 2013, 40, 853–858. [Google Scholar] [CrossRef]
- Pellarin, T.; Ali, A.; Chopin, F.; Jobard, I.; Bergès, J.C. Using spaceborne surface soil moisture to constrain satellite precipitation estimates over West Africa. Geophys. Res. Lett. 2008, 35, 244–255. [Google Scholar] [CrossRef]
- Mccoll, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.; Entekhabi, D. The global distribution and dynamics of surface soil moisture. Nat. Geosci. 2017, 10, 100–104. [Google Scholar] [CrossRef]
- Crow, W.T.; Bolten, J.D. Estimating precipitation errors using spaceborne surface soil moisture retrievals. Geophys. Res. Lett. 2007, 34, 402–420. [Google Scholar] [CrossRef]
- Crow, W.T.; Huffman, G.J.; Bindlish, R.; Jackson, T.J. Improving satellite-based rainfall accumulation estimates using spaceborne surface soil moisture retrievals. J. Hydrometeorol. 2007, 10, 199–212. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, M.J.V.D.; Huffman, G.J.; Pellarin, T. Correcting rainfall using satellite-based surface soil moisture retrievals: The Soil Moisture Analysis Rainfall Tool (SMART). Water Resour. Res. 2011, 47, 2924–2930. [Google Scholar] [CrossRef]
- Brocca, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Wanders, N.; Pan, M.; Wood, E.F. Correction of real-time satellite precipitation with multi-sensor satellite observations of land surface variables. Remote Sens. Environ. 2015, 160, 206–221. [Google Scholar] [CrossRef]
- Pellarin, T.; Tran, T.; Cohard, J.M.; Galle, S.; Laurent, J.P.; Rosnay, P.D.; Vischel, T. Soil moisture mapping over West Africa with a 30-min temporal resolution using AMSR-E observations and a satellite-based rainfall product. Hydrol. Earth Syst. Sci. 2009, 13, 1887–1893. [Google Scholar] [CrossRef]
- Pellarin, T.; Louvet, S.; Gruhier, C.; Quantin, G.; Legout, C. A simple and effective method for correcting soil moisture and precipitation estimates using AMSR-E measurements. Remote Sens. Environ. 2013, 136, 28–36. [Google Scholar] [CrossRef]
- Román-Cascón, C.; Pellarin, T.; Gibon, F.; Brocca, L.; Cosme, E.; Crow, W.; Fernández-Prieto, D.; Kerr, Y.H.; Massari, C. Correcting satellite-based precipitation products through SMOS soil moisture data assimilation in two land-surface models of different complexity: API and SURFEX. Remote Sens. Environ. 2017, 200, 295–310. [Google Scholar] [CrossRef]
- Deng, P.; Zhang, M.; Guo, H.; Xu, C.; Bing, J.; Jia, J. Error analysis and correction of the daily GSMaP products over Hanjiang River Basin of China. Atmos. Res. 2018, 214, 121–134. [Google Scholar]
- Sheffield, J.; Wood, E.F.; Chaney, N.; Guan, K.; Sadri, S.; Yuan, X.; Olang, L.; Amani, A.; Ali, A.; Demuth, S. A Drought Monitoring and Forecasting System for Sub-Sahara African Water Resources and Food Security. Bull. Am. Meteorol. Soc. 2014, 95, 861–882. [Google Scholar] [CrossRef]
- Xie, P.; Xiong, A.Y. A conceptual model for constructing high-resolution gauge-satellite merged precipitation analyses. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Shen, Y.; Yu, Y.P.A. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res. Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, Q. Combining satellite precipitation and long-term ground observations for hydrological monitoring in China. J. Geophys. Res. Atmos. 2015, 120, 6426–6443. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates From Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 287–296. [Google Scholar] [CrossRef]
- Jingjing, Y.U.; Yan, S.; Yang, P.; Xiong, A. Comparative assessment between the daily merged precipitation dataset over China and the worlds popular counterparts. Acta Meteorol. Sin. 2015, 73, 394–410. [Google Scholar]
- Babar, Z.A.; Zhi, X.F.; Fei, G. Precipitation assessment of Indian summer monsoon based on CMIP5 climate simulations. Arab. J. Geosci. 2015, 8, 4379–4392. [Google Scholar] [CrossRef]
- Chen, H.; Rucong, Y.U.; Yan, S. A New Method to Compare Hourly Rainfall between Station Observations and Satellite Products over Central-Eastern China. J. Meteorol. Res. 2016, 30, 737–757. [Google Scholar] [CrossRef]
- Wang, D.; Wang, X.; Liu, L.; Huang, H.; Pan, C. Evaluation of CMPA precipitation estimate in the evolution of typhoon-related storm rainfall in Guangdong, China. J. Hydroinf. 2016, 18, 1055–1068. [Google Scholar] [CrossRef]
- Wang, H.; Luo, J.; Ye, J.; Li, Z. Comparative analysis of area rainfall in Huaihe River Basin estimated by CMORPH-Gauge merged data and observed rain gauge data. J. Hohai Univ. 2014, 42, 189–194. [Google Scholar]
- Yang, J.; Shi, L.; Miao, Q.; Zhang, D.; Wan, Y. Precision evaluation of three sets of remote sensing precipitation data in Qinling-Daba Mountains. J. Jiangsu Normal Univ. 2017, 2, 77–82. [Google Scholar]
- Zhu, Y.; Lin, Z.; Zhao, Y.; Li, H.; He, F.; Zhai, J.; Wang, L.; Wang, Q. Flood Simulations and Uncertainty Analysis for the Pearl River Basin Using the Coupled Land Surface and Hydrological Model System. Water 2017, 9, 391. [Google Scholar] [CrossRef]
- Huffman, G.A.; Adler, R.; Bolvin, D.T.; Gu, G.; Nelkin, E.; Bowman, K.; Hong, Y.; Stocker, T.; Wolff, D. The TRMM multi-satellite precipitation analysis (TMPA): quasi-global, multiyear, combined-sensor precipitation estimates at fine scale. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; Iwanami, K. Global Precipitation Map Using Satellite-Borne Microwave Radiometers by the GSMaP Project: Production and Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Joyce, R.J.; Xie, P. Kalman Filter-Based CMORPH. J. Hydrometeorol. 2011, 12, 1547–1563. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Sorooshian, S.; Gao, X. Precipitation Estimation from Remotely Sensed Imagery Using an Artificial Neural Network Cloud Classification System. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.L.; Gao, X.; Gupta, H.V.; Imam, B.; Dan, B. Evaluation of PERSIANN system satellite-based estimates of tropical rainfall. Bull. Am. Meteor. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Dan, B.; Hsu, K.; Joyce, R.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG). 2014. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V5.2_0.pdf (accessed on 7 February 2018).
- Bosilovich, M.G.; Lucchesi, R.; Suarez, M. MERRA-2: File Specification. 2015. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20150019760.pdf (accessed on 25 September 2015).
- Yuan, H.; Dai, Y.; Xiao, Z.; Ji, D.; Shangguan, W. Reprocessing the MODIS Leaf Area Index products for land surface and climate modelling. Remote Sens. Environ. 2011, 115, 1171–1187. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. TIMESAT—a program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Shangguan, W.; Dai, Y.; Liu, B.; Zhu, A.; Duan, Q.; Wu, L.; Ji, D.; Ye, A.; Yuan, H.; Zhang, Q. A China data set of soil properties for land surface modeling. J. Adv. Model. Earth Syst. 2013, 5, 212–224. [Google Scholar] [CrossRef]
- Cordery, I. Antecedent wetness for design flood estimation. Civil Eng. Trans. 1970, 12, 181–184. [Google Scholar]
- Yan, H.; Dechant, C.M.; Moradkhani, H. Improving Soil Moisture Profile Prediction With the Particle Filter-Markov Chain Monte Carlo Method. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6134–6147. [Google Scholar] [CrossRef]
- Marsaglia, G.; Tsang, W.W. A simple method for generating gamma variables. Acm Trans. Math. Softw. 2000, 26, 363–372. [Google Scholar] [CrossRef]
- Tan, M.L.; Tan, K.C.; Chua, V.P.; Chan, N.W. Evaluation of TRMM Product for Monitoring Drought in the Kelantan River Basin, Malaysia. Water 2017, 9, 57. [Google Scholar] [CrossRef]
- Koster, R.D.; Brocca, L.; Crow, W.T.; Burgin, M.S.; De Lannoy, G.J.M. Precipitation estimation using L-band and C-band soil moisture retrievals. Water Resour. Res. 2016, 52, 7213–7225. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Li, X.; Wei, L.; Wang, W. Multi-Scale Validation of SMAP Soil Moisture Products over Cold and Arid Regions in Northwestern China Using Distributed Ground Observation Data. Remote Sens. 2017, 9, 327. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, S.; Ma, J.; Li, J.; Li, X.; Wang, H.; Chen, S.; Zang, W. Preliminary Evaluation of the SMAP Radiometer Soil Moisture Product over China Using In Situ Data. Remote Sens. 2017, 9, 292. [Google Scholar] [CrossRef]
- Tian, Y.D.; Peterslidard, C.D.; Eylander, J.B. Real-time bias reduction for satellite-based precipitation estimates. J. Hydrometeorol. 2010, 11, 1275–1285. [Google Scholar] [CrossRef]






| Product | Parameters | Median | σ | 25th | 75th |
|---|---|---|---|---|---|
| SMP | NSMAP,opt | 5 | 1.47 | 4 | 7 |
| Pthreshold (mm/day) | 25 | 13.57 | 15 | 35 | |
| GPM-Linear | a1 | 0.67 | 1.08 | 0.48 | 1.07 |
| GPM-Nonlinear | b1 | 2.3 | 1.66 | 1.43 | 3.40 |
| c1 | 0.57 | 0.94 | 0.46 | 0.71 | |
| GPM-CDF | k1,o (k1,m) | 0.127(0.104) | 0.097(0.054) | 0.073(0.075) | 0.200(0.141) |
| θ1,o (θ1,m) | 12.69(13.65) | 12.18(18.44) | 8.18(3.56) | 21.11(29.65) | |
| SMP-Linear | a2 | 0.91 | 0.38 | 0.63 | 1.12 |
| SMP-Nonlinear | b2 | 1.46 | 1.21 | 0.83 | 2.30 |
| c2 | 0.74 | 0.89 | 0.56 | 0.97 | |
| SMP-CDF | K2,o (k2,m) | 0.127(0.163) | 0.097(0.091) | 0.073(0.101) | 0.200(0.223) |
| Θ2,o (θ2,m) | 12.69(8.99) | 12.18(7.91) | 8.18(5.47) | 21.11(14.19) |
| Product | R | RMSE (mm/day) | BIAS (mm/day) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 10th | 50th | 90th | 10th | 50th | 90th | 10th | 50th | 90th | |
| GPM | 0.24 | 0.49 | 0.69 | 1.37 | 5.25 | 13.43 | 0.37 | 2.03 | 5.46 |
| SMP | 0.28b | 0.49b | 0.67 | 1.4 | 4.32b | 10.15b | 0.41 | 1.76b | 4.63b |
| GPM-Linear | 0.24b | 0.49bc | 0.69bc | 0.86bc | 5.04b | 12.39b | 0.23bc | 1.85b | 5.14b |
| GPM-Nonlinear | 0.32bc | 0.51bc | 0.66 | 0.86bc | 4.64b | 11.15b | 0.31bc | 2.19 | 5.61 |
| GPM-CDF | 0.27b | 0.50bc | 0.69bc | 2.14 | 6.92 | 18.55 | 0.58 | 2.73 | 7.57 |
| SMP-Linear | 0.28bc | 0.49bc | 0.67c | 0.67bc | 4.00bc | 10.40b | 0.18bc | 1.69bc | 4.83bc |
| SMP-Nonlinear | 0.31bc | 0.49bc | 0.65 | 0.70bc | 4.07bc | 10.52b | 0.23bc | 1.81b | 5.23b |
| SMP-CDF | 0.28bc | 0.49bc | 0.67c | 1.54 | 5.32 | 12.46b | 0.38c | 2.14 | 5.77 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, D.; Wang, G.; Qiu, J.; Liao, W. Use of SMAP Soil Moisture and Fitting Methods in Improving GPM Estimation in Near Real Time. Remote Sens. 2019, 11, 368. https://doi.org/10.3390/rs11030368
Zhang Z, Wang D, Wang G, Qiu J, Liao W. Use of SMAP Soil Moisture and Fitting Methods in Improving GPM Estimation in Near Real Time. Remote Sensing. 2019; 11(3):368. https://doi.org/10.3390/rs11030368
Chicago/Turabian StyleZhang, Zhi, Dagang Wang, Guiling Wang, Jianxiu Qiu, and Weilin Liao. 2019. "Use of SMAP Soil Moisture and Fitting Methods in Improving GPM Estimation in Near Real Time" Remote Sensing 11, no. 3: 368. https://doi.org/10.3390/rs11030368
APA StyleZhang, Z., Wang, D., Wang, G., Qiu, J., & Liao, W. (2019). Use of SMAP Soil Moisture and Fitting Methods in Improving GPM Estimation in Near Real Time. Remote Sensing, 11(3), 368. https://doi.org/10.3390/rs11030368







