Self-Paced Convolutional Neural Network for PolSAR Images Classification
Abstract
:1. Introduction
2. Methodology
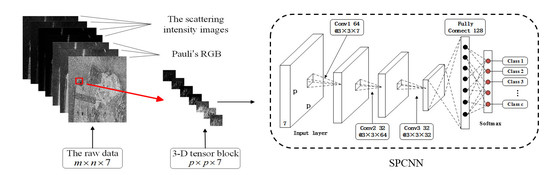
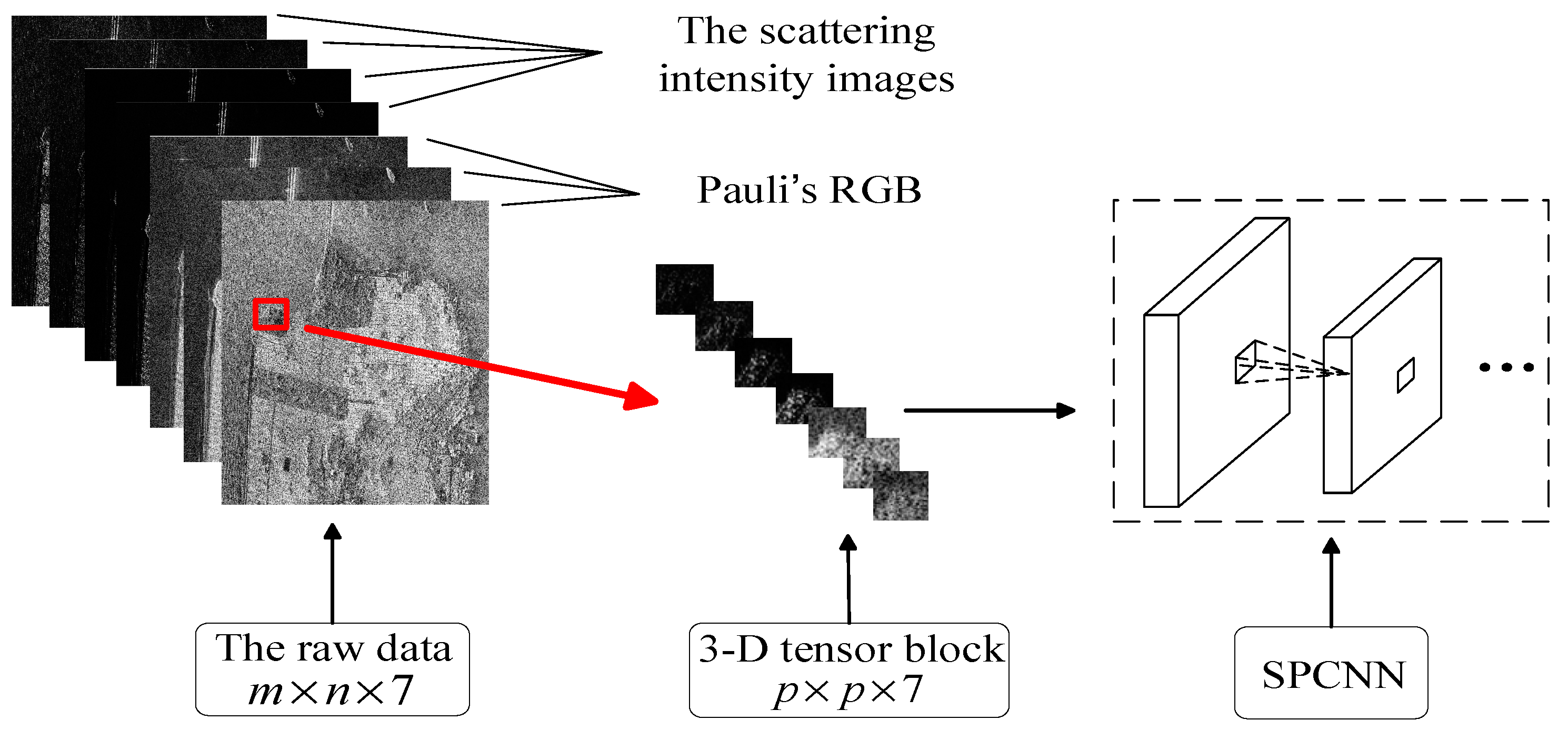
2.1. 3-Dimensional Tensor Block Representation of PolSAR Data
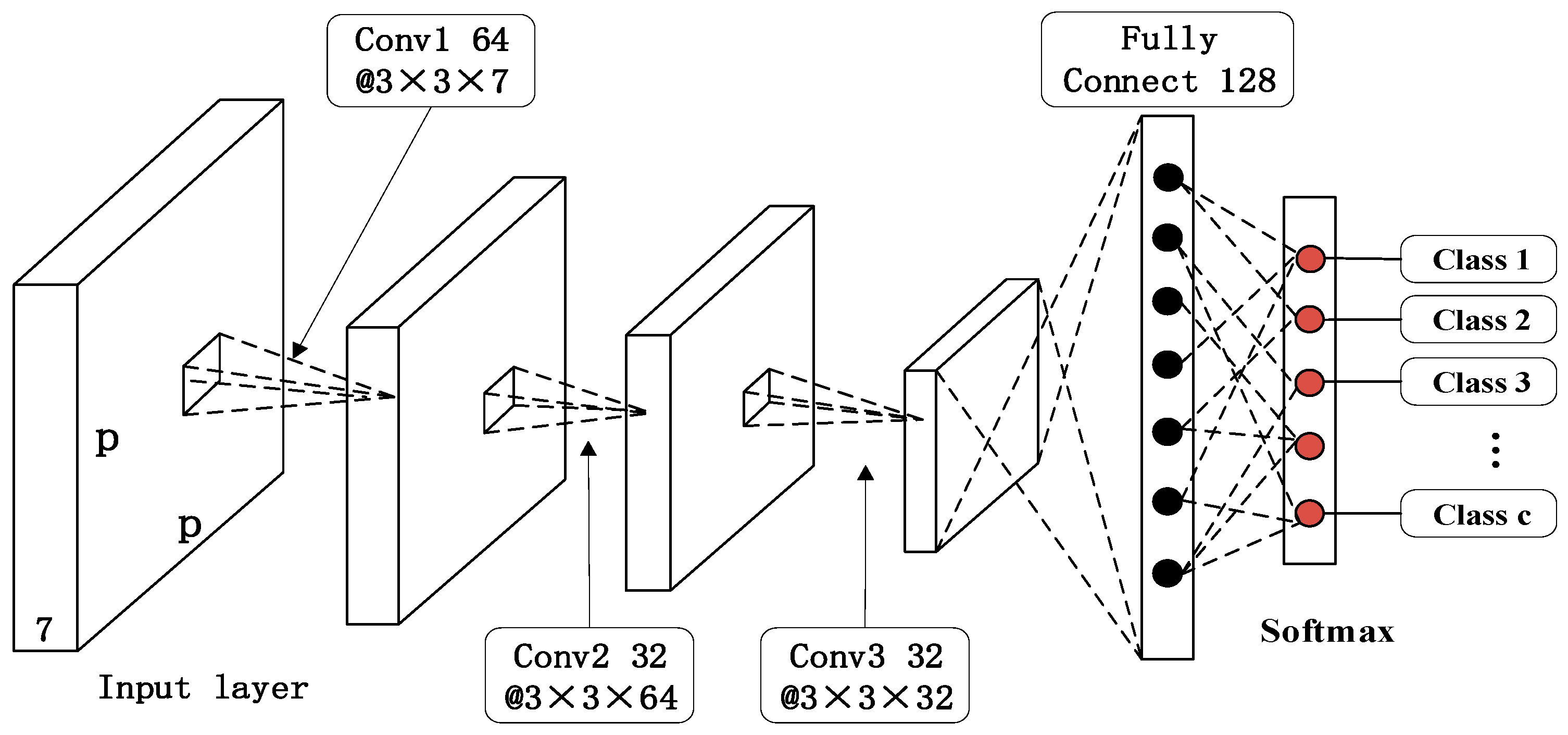
2.2. Network Architecture
2.3. Training SPCNN
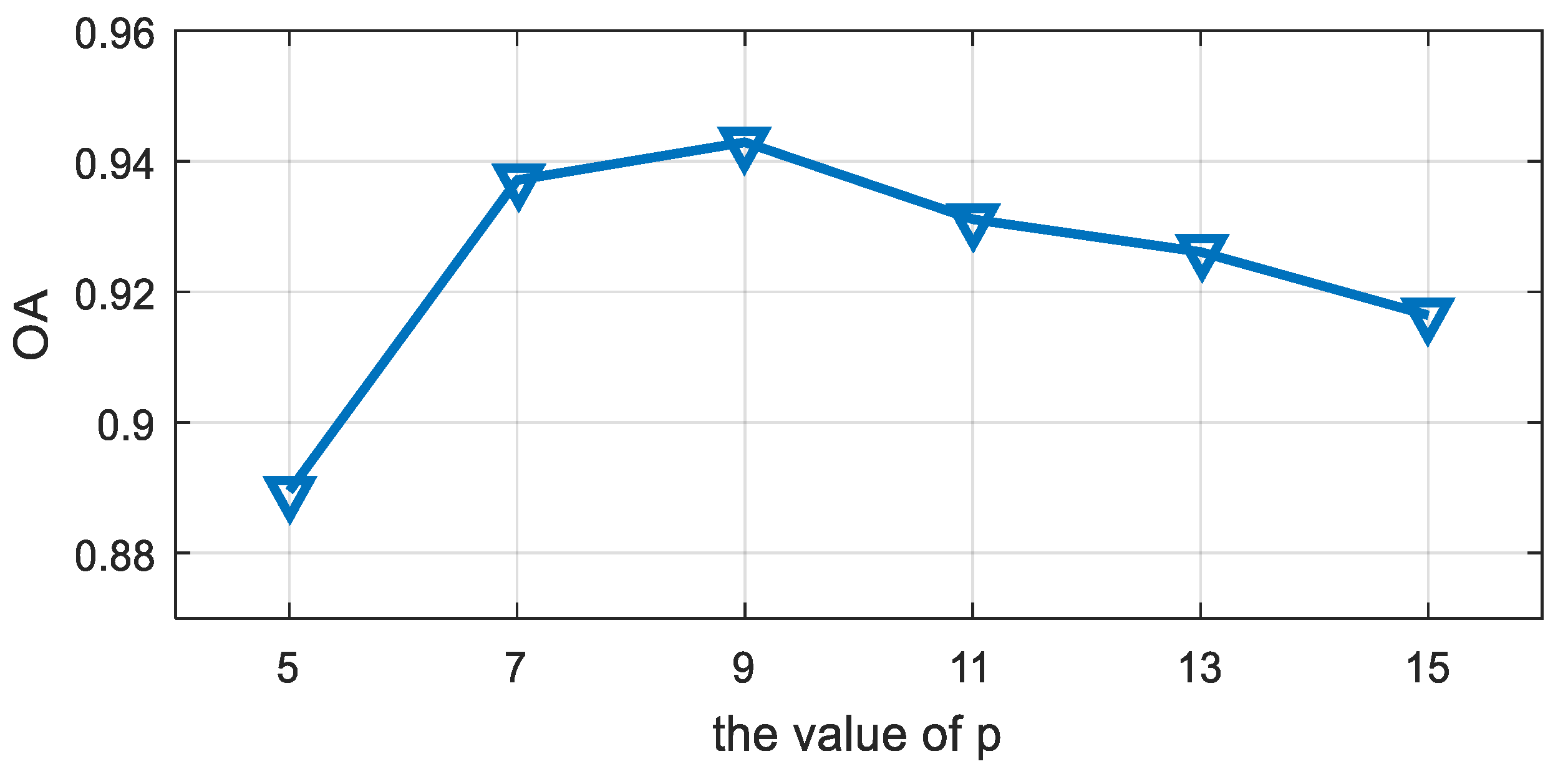
3. Experiments
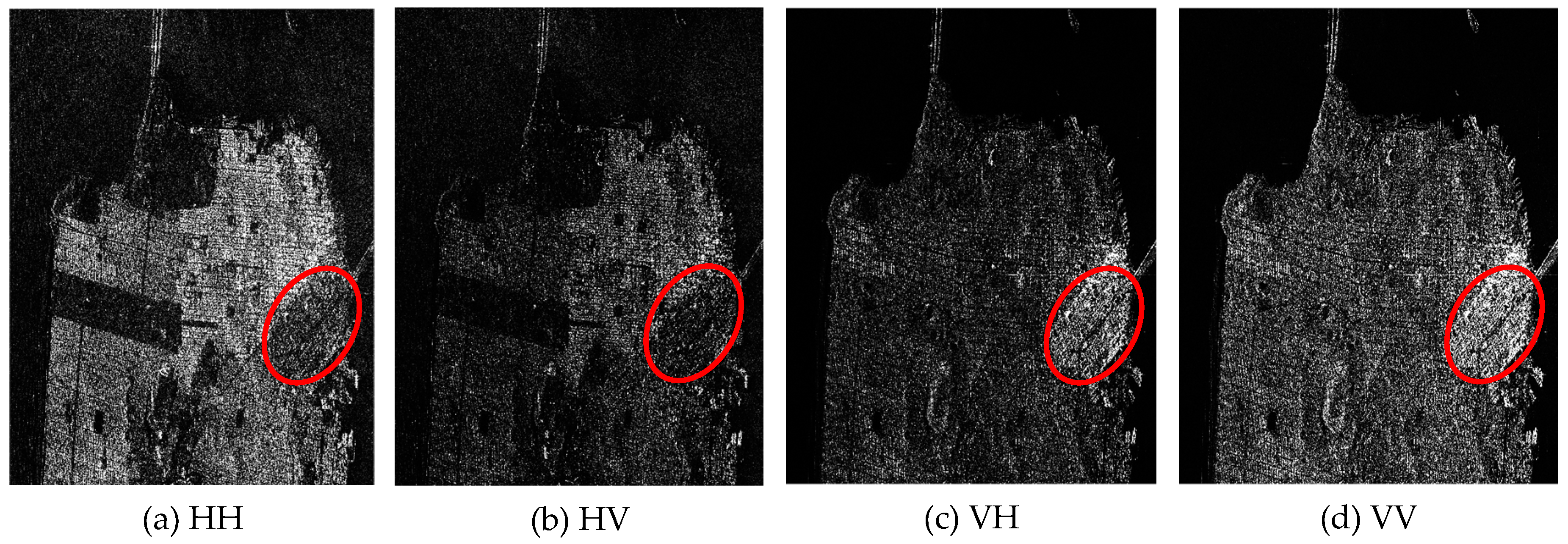
3.1. Experiment on Flevoland Dataset from AIRSAR
3.2. Experiment on San Francisco Dataset
3.3. Experiment on the Flevoland Dataset from RADARSAT-2
3.4. Experiment on the Yellow River Dataset from ALOS-2
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cloude, S.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Lee, J.; Grunes, M.; Ainsworth, T.; Du, L.-J.; Schuler, D.L.; Cloude, S.R. Unsupervised classification using polarimetric decomposition and the complex Wishart classifier. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2249–2258. [Google Scholar]
- Ferro-Famil, L.; Pottier, E.; Lee, J.S. Unsupervised classification of multifrequency and fully polarimetric SAR images based on the H/A/Alpha-Wishart classifier. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2332–2342. [Google Scholar] [CrossRef]
- Zhang, L.; Zou, B.; Zhang, J.; Zhang, Y. Classification of polarimetric SAR image based on support vector machine using multiple-component scattering model and texture features. EURASIP J. Adv. Signal Process. 2010, 2010, 960831. [Google Scholar] [CrossRef]
- Du, P.; Samat, A.; Waske, B.; Liu, S.; Li, Z. Random forest and rotation forest for fully polarized SAR image classification using polarimetric and spatial features. ISPRS J. Photogramm. Remote Sens. 2015, 105, 38–53. [Google Scholar] [CrossRef]
- Lardeux, C.; Frison, P.L.; Tison, C.; Souyris, J.-C.; Stoll, B.; Fruneau, B.; Tison, C.; Rudant, J.-P. Support vector machine for multifrequency SAR polarimetric data classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4143–4152. [Google Scholar] [CrossRef]
- Wang, H.; Han, J.; Deng, Y. PolSAR image classification based on Laplacian Eigenmaps and superpixels. EURASIP J. Wirel. Commun. Netw. 2017, 2017, 198. [Google Scholar] [CrossRef]
- Han, C.; Zhang, L.; Wang, X. Polarimetric SAR image classification based on selective ensemble learning of sparse representation. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 4964–4967. [Google Scholar]
- Pajares, G.; López-Martínez, C.; Sánchez-Lladó, F.J.; Molina, I. Improving Wishart classification of polarimetric SAR data using the Hopfield Neural Network optimization approach. Remote Sens. 2012, 4, 3571–3595. [Google Scholar] [CrossRef]
- Dargahi, A.; Maghsoudi, Y.; Abkar, A.A. Supervised Classification of Polarimetric SAR Imagery Using Temporal and Contextual Information. In Proceedings of the ISPRS—International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Tehran, Iran, 5–8 October 2013; Volume XL-1/W3, pp. 107–110. [Google Scholar]
- Feng, J.; Cao, Z.; Pi, Y. Polarimetric Contextual Classification of PolSAR Images Using Sparse Representation and Superpixels. Remote Sens. 2014, 6, 7158–7181. [Google Scholar] [CrossRef]
- Zhang, F.; Ni, J.; Yin, Q.; Li, W.; Li, Z.; Liu, Y.; Hong, W. Nearest-Regularized Subspace Classification for PolSAR Imagery Using Polarimetric Feature Vector and Spatial Information. Remote Sens. 2017, 9, 1114. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, Q.; Yang, S.; Liu, X. Superpixel-Based Classification Using K Distribution and Spatial Context for Polarimetric SAR Images. Remote Sens. 2016, 8, 619. [Google Scholar] [CrossRef]
- Ioannidou, A.; Chatzilari, E.; Nikolopoulos, S.; Kompatsiaris, I. Deep Learning Advances in Computer Vision with 3D Data: A Survey. ACM Comput. Surv. 2017, 50, 20. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, South Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- He, X.; Gao, J.; Deng, A.L. Deep Learning for Natural Language Processing: Theory and Practice (Tutorial). In Proceedings of the CIKM ‘14 2014 ACM Conference on Information and Knowledge Management, Shanghai, China, 3–7 November 2014. [Google Scholar]
- Bengio, Y.; Ducharme, R.; Vincent, P.; Jauvin, C. A neural probabilistic language model. J. Mach. Learn. Res. 2003, 3, 1137–1155. [Google Scholar]
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the IEEE International Conference Acoustics Speech Signal Process, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Seide, F.; Li, G.; Yu, D. Conversational Speech Transcription Using Context-Dependent Deep Neural Networks. In Proceedings of the Automatic Speech Recognition and Understanding, Waikoloa, HI, USA, 11–15 December 2011; pp. 24–29. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Xu, F.; Jin, Y.Q. Polarimetric SAR Image Classification Using Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2017, 13, 1935–1939. [Google Scholar] [CrossRef]
- Duan, Y.; Liu, F.; Jiao, L.; Zhao, P.; Zhang, L. SAR Image segmentation based on convolutional-wavelet neural network and markov random field. Pattern Recognit. 2016, 64, 255–267. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-Valued Convolutional Neural Network and Its Application in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Wang, L.; Xu, X.; Dong, H.; Gui, R.; Pu, F. Multi-Pixel Simultaneous Classification of PolSAR Image Using Convolutional Neural Networks. Sensors 2018, 18, 769. [Google Scholar] [CrossRef]
- Liu, X.; Jiao, L.; Tang, X.; Sun, Q.; Zhang, D. Polarimetric Convolutional Network for PolSAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2018. [Google Scholar] [CrossRef]
- Chen, S.; Tao, C. PolSAR Image Classification Using Polarimetric-Feature-Driven Deep Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2018, 15, 627–631. [Google Scholar] [CrossRef]
- Kumar, M.P.; Packer, B.; Koller, D. Self-paced learning for latent variable models. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; pp. 1189–1197. [Google Scholar]
- Tang, Y.; Yang, Y.B.; Gao, Y. Self-paced dictionary learning for image classification. In Proceedings of the ACM International Conference Multimedia, Hong Kong, China, 5–8 January 2012; pp. 833–836. [Google Scholar]
- Basu, S.; Christensen, J. Teaching classification boundaries to humans. In Proceedings of the AAAI Conference Artificial Intelligence, Bellevue, WC, USA, 14–18 July 2013; pp. 109–115. [Google Scholar]
- Jiang, L.; Meng, D.; Mitamura, T.; Hauptmann, A.G. Easy samples first: Self-paced reranking for zero-example multimedia search. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 547–556. [Google Scholar]
- Supancic, J.; Ramanan, D. Self-paced learning for long-term tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2379–2386. [Google Scholar]
- Yong, J.L.; Grauman, K. Learning the easy things first: Self-paced visual category discovery. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 1721–1728. [Google Scholar]
- Shang, R.; Yuan, Y.; Jiao, L.; Meng, Y.; Ghalamzan, A.M. A self-paced learning algorithm for change detection in synthetic aperture radar images. Signal Process. 2018, 142, 375–387. [Google Scholar] [CrossRef]
- Li, H.; Gong, M. Self-paced convolutional neural networks. In Proceedings of the Twenty-Sixth International Joint Conferences Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 2110–2116. [Google Scholar]
- Bai, Y.; Yang, W.; Xia, G.; Liao, M. A novel polarimetric-texture-structure descriptor for high-resolution PolSAR image classification. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1136–1139. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Meng, D.; Zhao, Q.; Jiang, L. What objective does self-paced learning indeed optimize? arXiv, 2015; arXiv:1511.06049. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learn. Res. 2010, 9, 249–256. [Google Scholar]
- Xie, W.; Jiao, L.; Hou, B.; Ma, W.; Zhao, J.; Zhang, S.; Liu, F. PolSAR image classification via Wishart-AE model or Wishart-CAE model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3604–3615. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Uhlmann, S.; Kiranyaz, S. Integrating Color Features in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2197–2216. [Google Scholar] [CrossRef]
- Buono, A.; Nunziata, F.; Migliaccio, M.; Yang, X.; Li, X. Classification of the Yellow River delta area using fully polarimetric SAR measurements. Int. J. Remote Sens. 2017, 38, 6714–6734. [Google Scholar] [CrossRef]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv, 2015; arXiv:1511.07122. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]













| Scene | System & Band | Date | Resolution | Size | #Class |
|---|---|---|---|---|---|
| Flevoland | AIRSAR L | August 1989 | 12 × 6 m | 1024 × 750 | 15 |
| San Francisco bay | RADARSAT-2 C | April 2008 | 10 × 5 m | 1800 × 1380 | 5 |
| Flevoland | RADARSAT-2 C | April 2008 | 10 × 5 m | 1200 × 1400 | 4 |
| Yellow River | ALOS-2 L | May 2015 | 3.125m | 960 × 690 | 4 |
| Class | CNN [21] | CV-CNN [23] | SPCNN-6.4% | SPCNN-9% | H/α-Wishart [2] |
|---|---|---|---|---|---|
| Stembeans | 0.926 | 0.988 | 0.976 | 0.991 | 0.951 |
| Rapeseed | 0.931 | 0.920 | 0.926 | 0.958 | 0.748 |
| Bare soil | 0.999 | 0.988 | 0.984 | 0.975 | 0.992 |
| Potatoes | 0.872 | 0.967 | 0.934 | 0.922 | 0.878 |
| Beet | 0.897 | 0.976 | 0.955 | 0.966 | 0.951 |
| Wheat 2 | 0.918 | 0.942 | 0.859 | 0.943 | 0.827 |
| Peas | 0.889 | 0.987 | 0.978 | 0.975 | 0.963 |
| Wheat 3 | 0.945 | 0.946 | 0.982 | 0.992 | 0.886 |
| Lucerne | 0.922 | 0.981 | 0.967 | 0.977 | 0.929 |
| Barley | 0.969 | 0.945 | 0.993 | 0.980 | 0.953 |
| Wheat | 0.936 | 0.950 | 0.992 | 0.985 | 0.862 |
| Grasses | 0.792 | 0.900 | 0.899 | 0.920 | 0.725 |
| Forest | 0.940 | 0.968 | 0.980 | 0.978 | 0.879 |
| Water | 0.989 | 0.994 | 0.901 | 0.989 | 0.518 |
| Building | 0.872 | 0.832 | 0.891 | 0.831 | 0.834 |
| OA | 0.925 | 0.962 | 0.953 | 0.969 | 0.850 |
| Class | H/α-Wishart [2] | Wishart-CAE [42] | SVM | CNN | SPCNN |
|---|---|---|---|---|---|
| High-density | 0.496 | 0.929 | 0.773 | 0.826 | 0.945 |
| Water | 0.971 | 0.996 | 0.975 | 0.999 | 1.000 |
| Vegetation | 0.926 | 0.938 | 0.905 | 0.926 | 0.926 |
| Developed | 0.578 | 0.863 | 0.533 | 0.887 | 0.882 |
| Low-density | 0.742 | 0.917 | 0.453 | 0.972 | 0.922 |
| OA | 0.750 | 0.958 | 0.813 | 0.952 | 0.961 |
| Class | SVM | CNN | H/α-Wishart [2] | SPCNN |
|---|---|---|---|---|
| Urban | 0.805 | 0.830 | 0.602 | 0.847 |
| Water | 0.969 | 0.980 | 0.985 | 0.981 |
| Forest | 0.921 | 0.958 | 0.848 | 0.959 |
| Cropland | 0.937 | 0.918 | 0.807 | 0.946 |
| OA | 0.923 | 0.934 | 0.838 | 0.945 |
| Class | H/α-Wishart [2] | SVM | CNN | SPCNN |
|---|---|---|---|---|
| Reservoir pits (1) | 0.359 | 0.927 | 0.858 | 0.917 |
| Saline-alkali soil (2) | 0.897 | 0.804 | 0.550 | 0.839 |
| Marshland (3) | 0.735 | 0.681 | 0.873 | 0.840 |
| Shoaly land (4) | 0.034 | 0.063 | 0.193 | 0.530 |
| OA | 0.481 | 0.681 | 0.651 | 0.807 |
| Methods | SVM | H/α-Wishart | CNN | SPCNN |
|---|---|---|---|---|
| Time | 64.65s | 46.19s | 148.78s | 215.18s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, C.; Wang, X.; Gou, S.; Chen, W.; Li, D.; Chen, C.; Li, X. Self-Paced Convolutional Neural Network for PolSAR Images Classification. Remote Sens. 2019, 11, 424. https://doi.org/10.3390/rs11040424
Jiao C, Wang X, Gou S, Chen W, Li D, Chen C, Li X. Self-Paced Convolutional Neural Network for PolSAR Images Classification. Remote Sensing. 2019; 11(4):424. https://doi.org/10.3390/rs11040424
Chicago/Turabian StyleJiao, Changzhe, Xinlin Wang, Shuiping Gou, Wenshuai Chen, Debo Li, Chao Chen, and Xiaofeng Li. 2019. "Self-Paced Convolutional Neural Network for PolSAR Images Classification" Remote Sensing 11, no. 4: 424. https://doi.org/10.3390/rs11040424
APA StyleJiao, C., Wang, X., Gou, S., Chen, W., Li, D., Chen, C., & Li, X. (2019). Self-Paced Convolutional Neural Network for PolSAR Images Classification. Remote Sensing, 11(4), 424. https://doi.org/10.3390/rs11040424