Drought Evaluation with CMORPH Satellite Precipitation Data in the Yellow River Basin by Using Gridded Standardized Precipitation Evapotranspiration Index
Abstract
1. Introduction
2. Materials and Methods
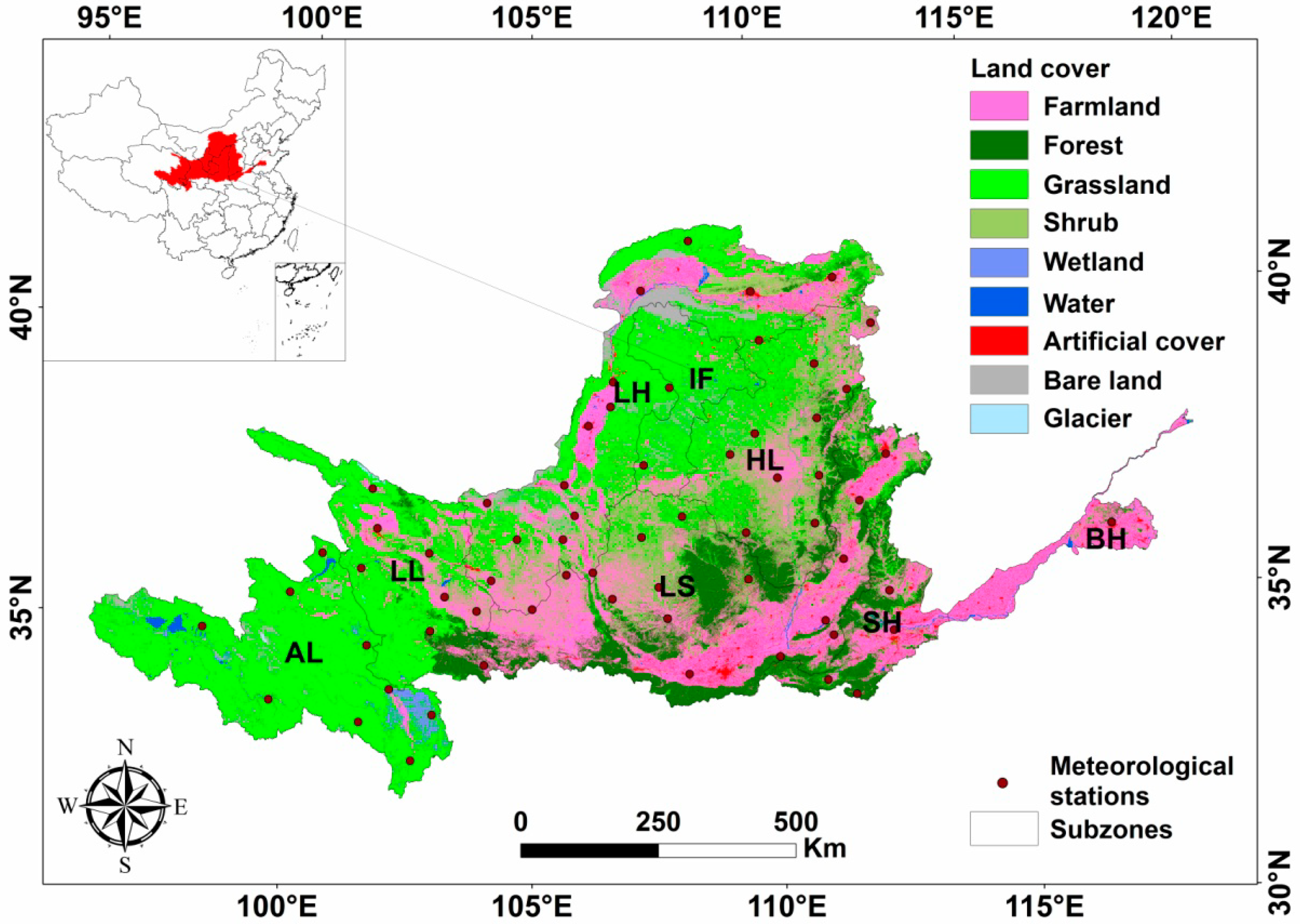
2.1. Study Area
2.2. Dataset
2.2.1. CMORPH Precipitation Data
2.2.2. Rain Gauge Data
2.3. Gridded Standardized Precipitation Evapotranspiration Index (GSPEI)
2.4. Statistical Methods
2.4.1. Evaluation Indicators
2.4.2. Extreme-Point Symmetric Mode Decomposition (ESMD)
2.4.3. The Modified Mann–Kendall (MMK) Trend Test Method
3. Results
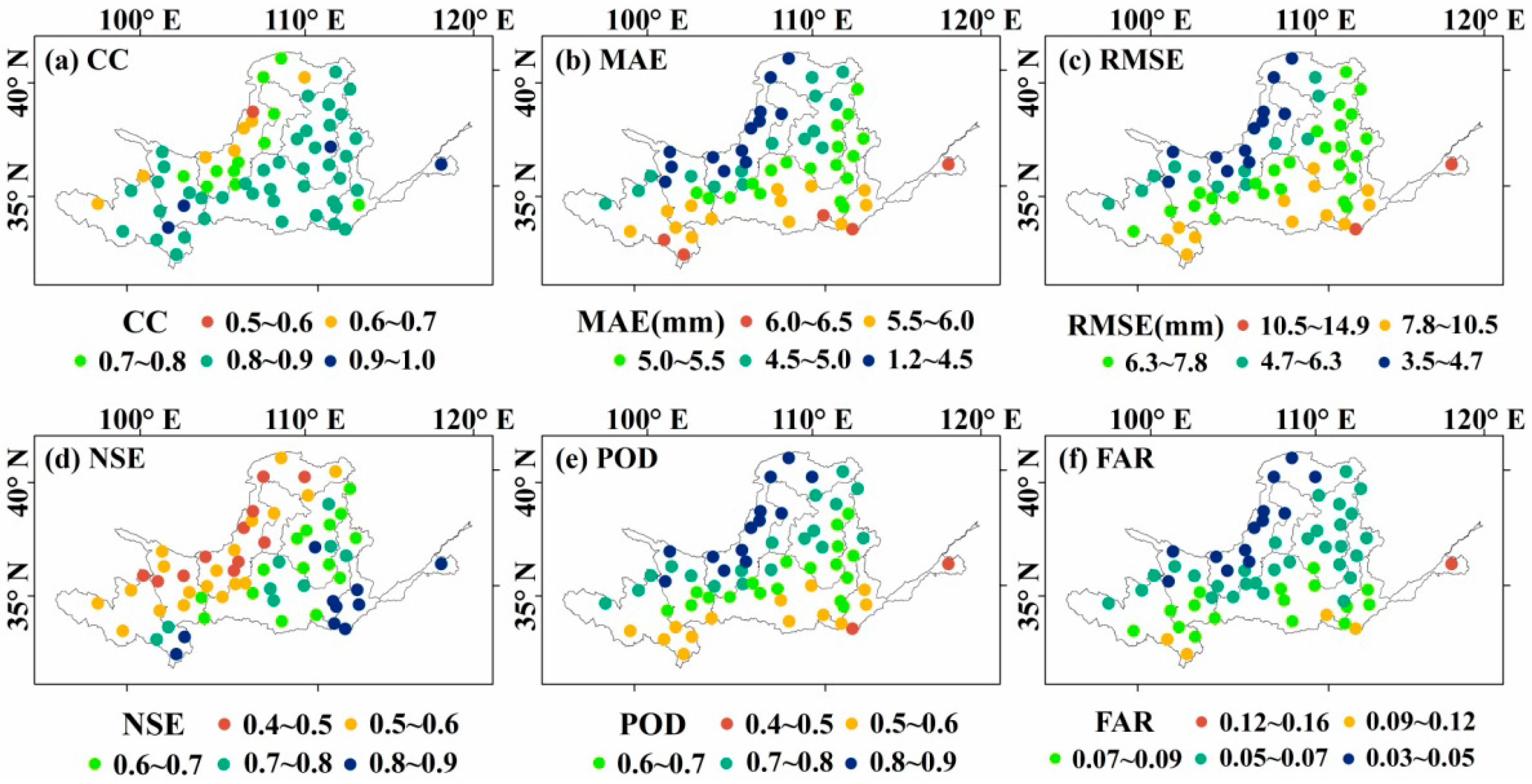
3.1. Accuracy Assessment
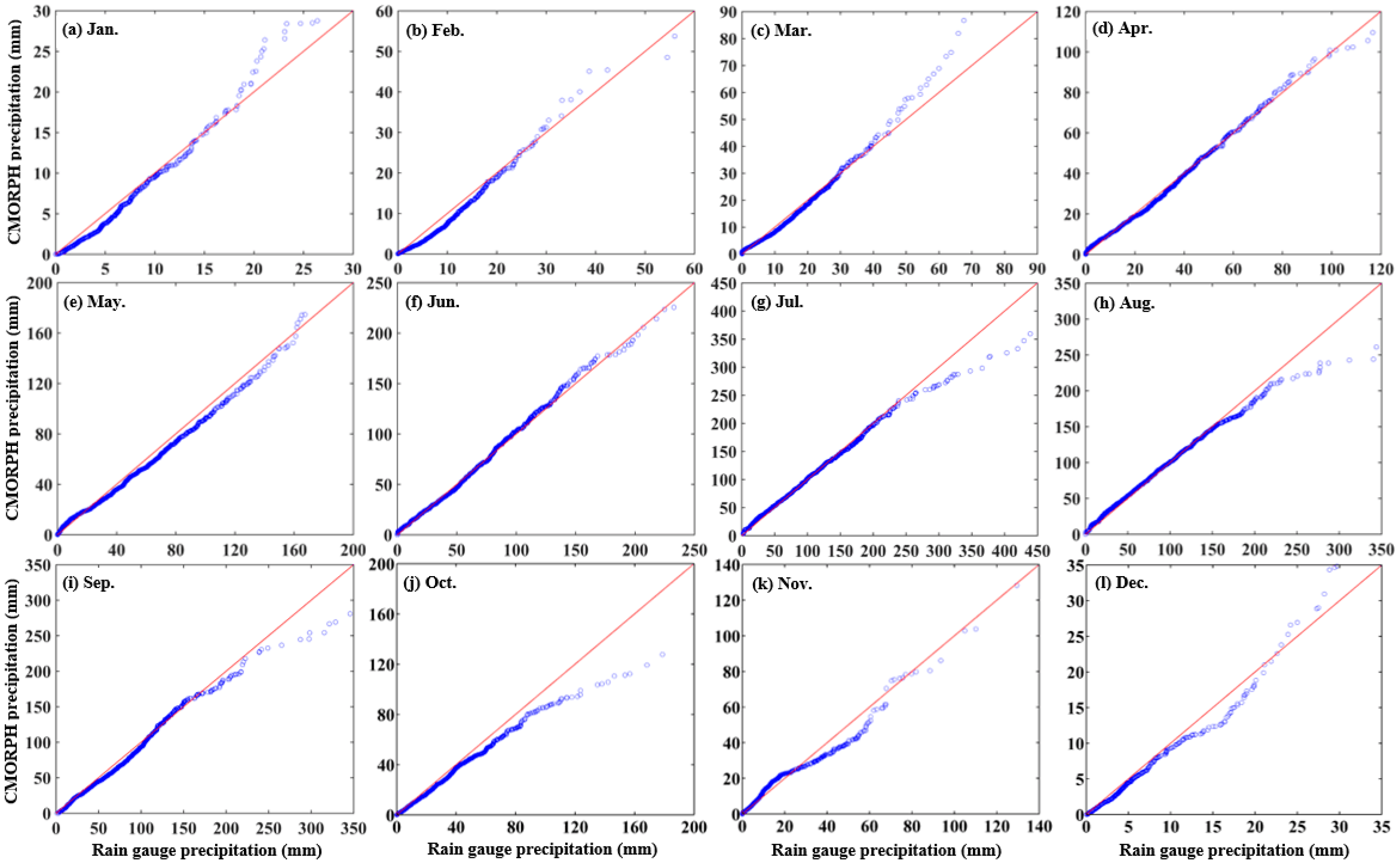
3.1.1. Temporal and Spatial Validation of CMORPH
3.1.2. Accuracy Assessment of GSPEI
3.2. GSPEI-Based Drought Characteristics
3.2.1. Temporal Evolution of Drought
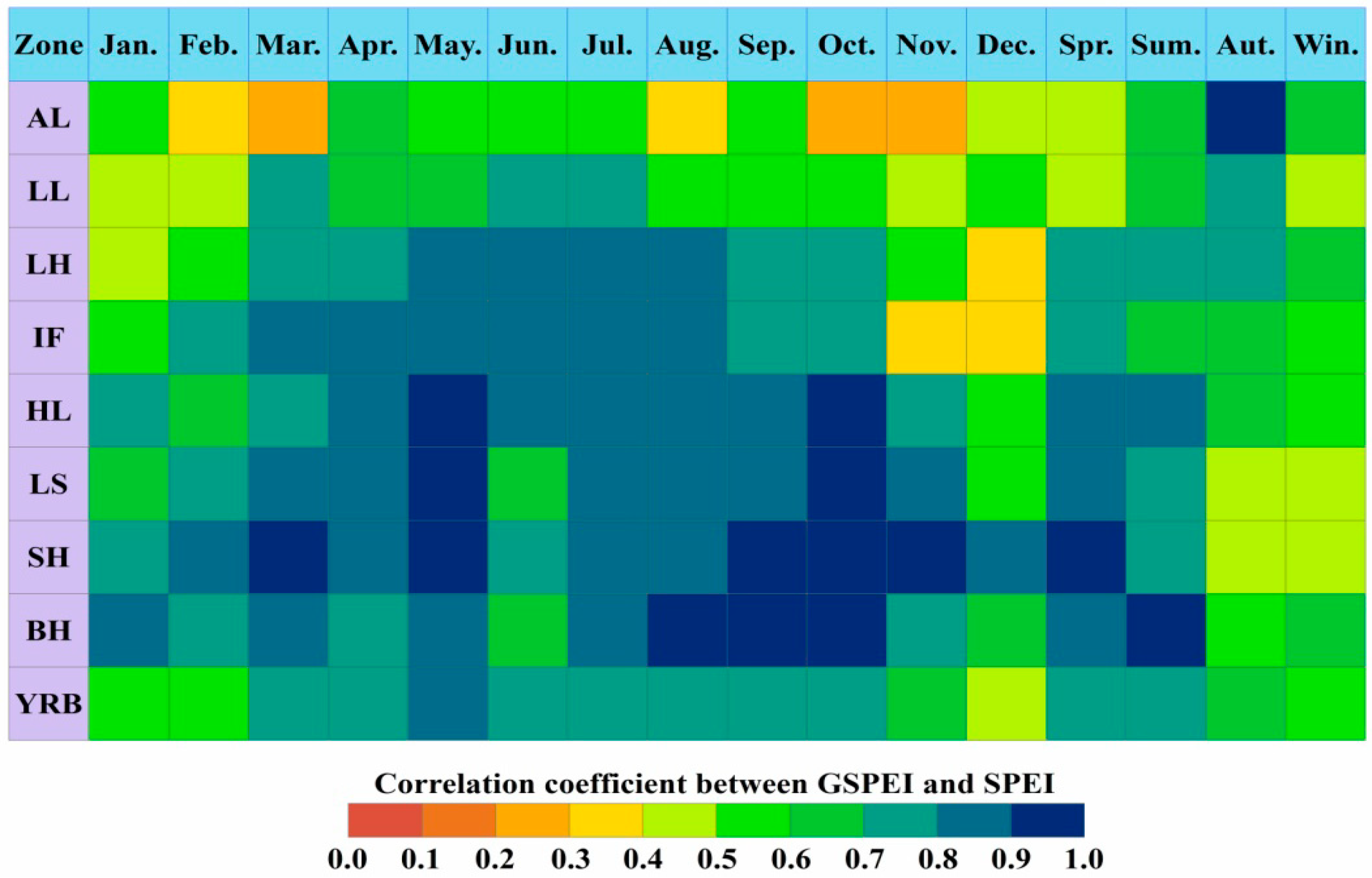
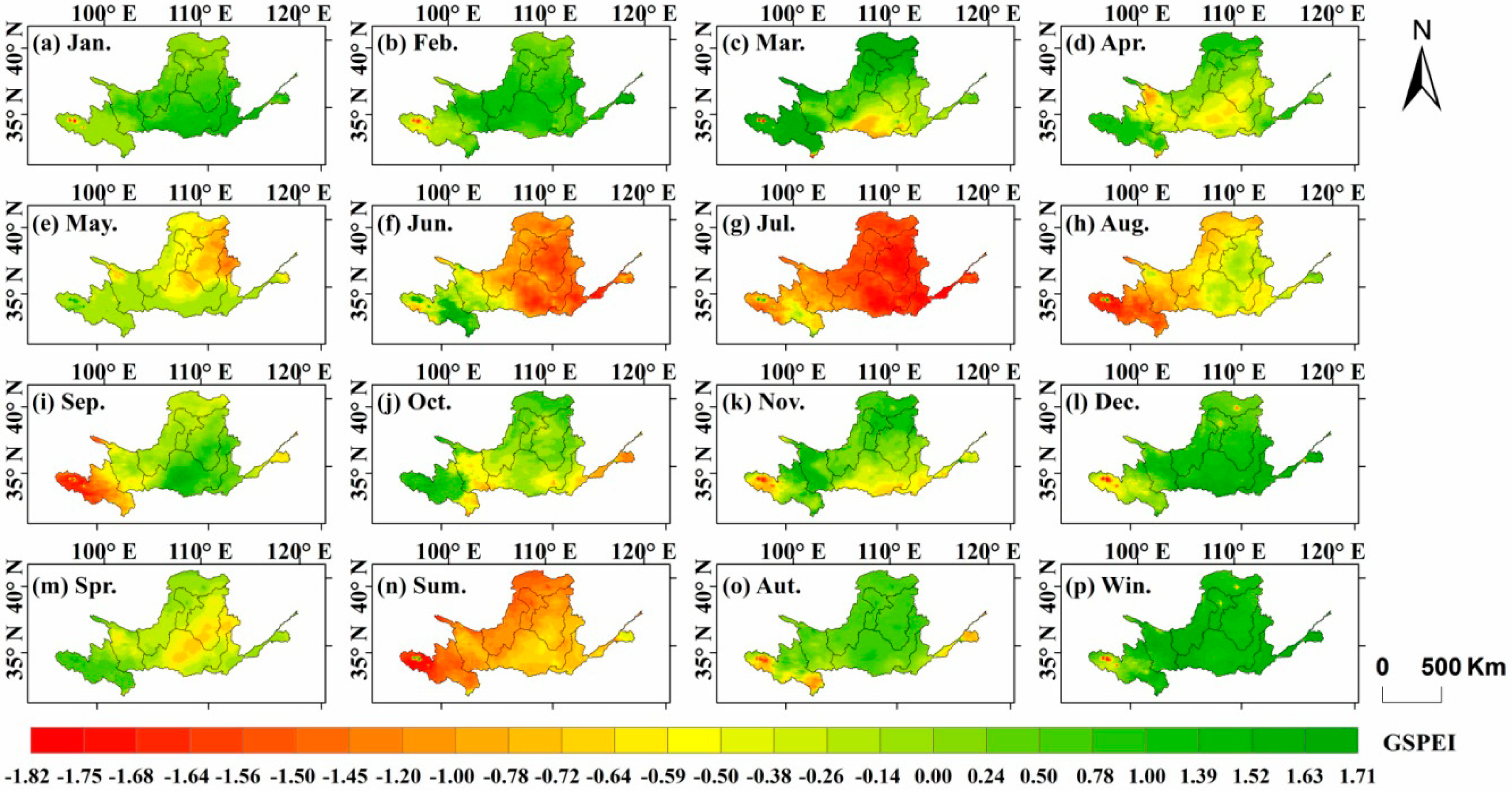
3.2.2. Spatial Distribution of Drought
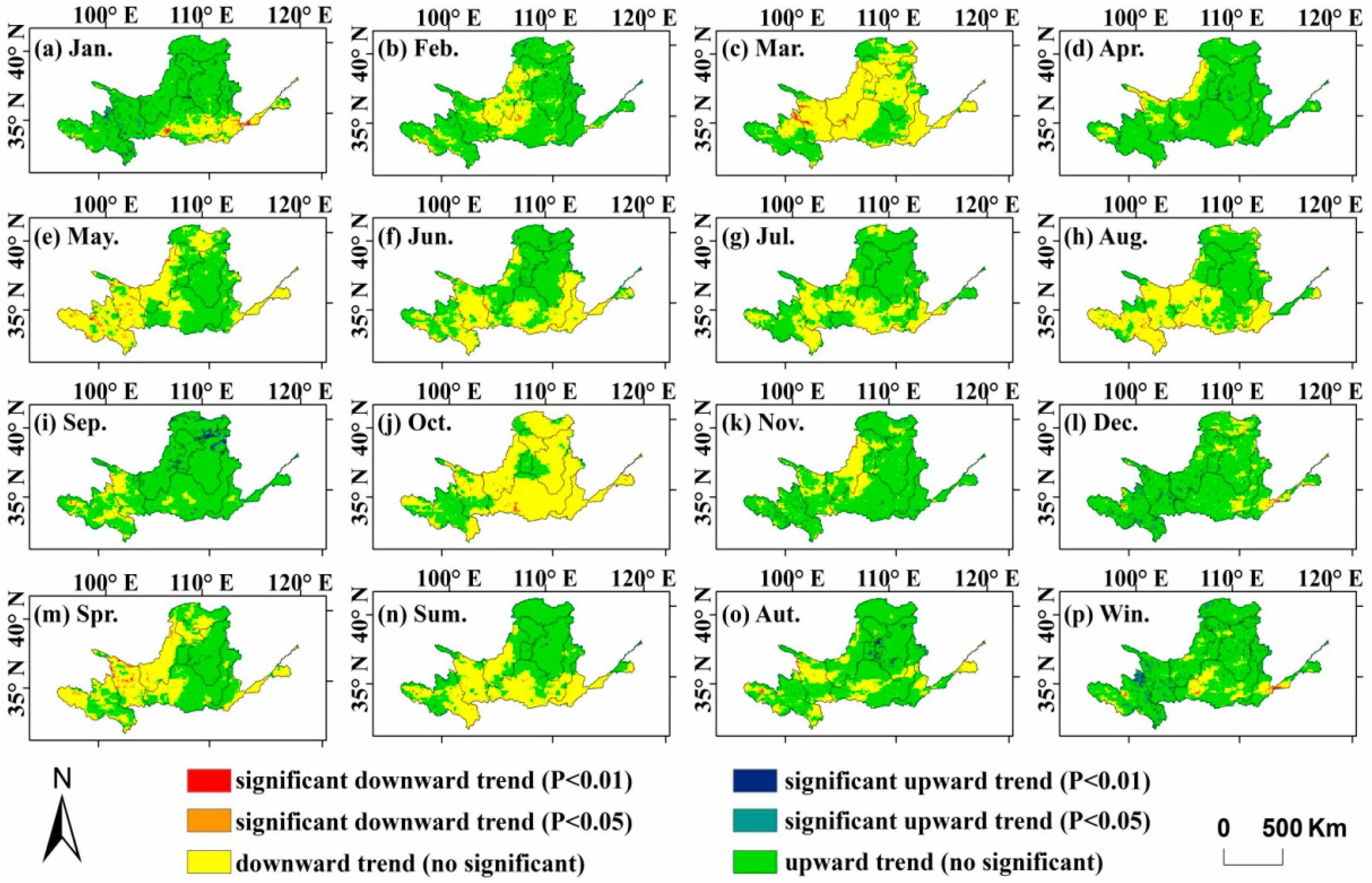
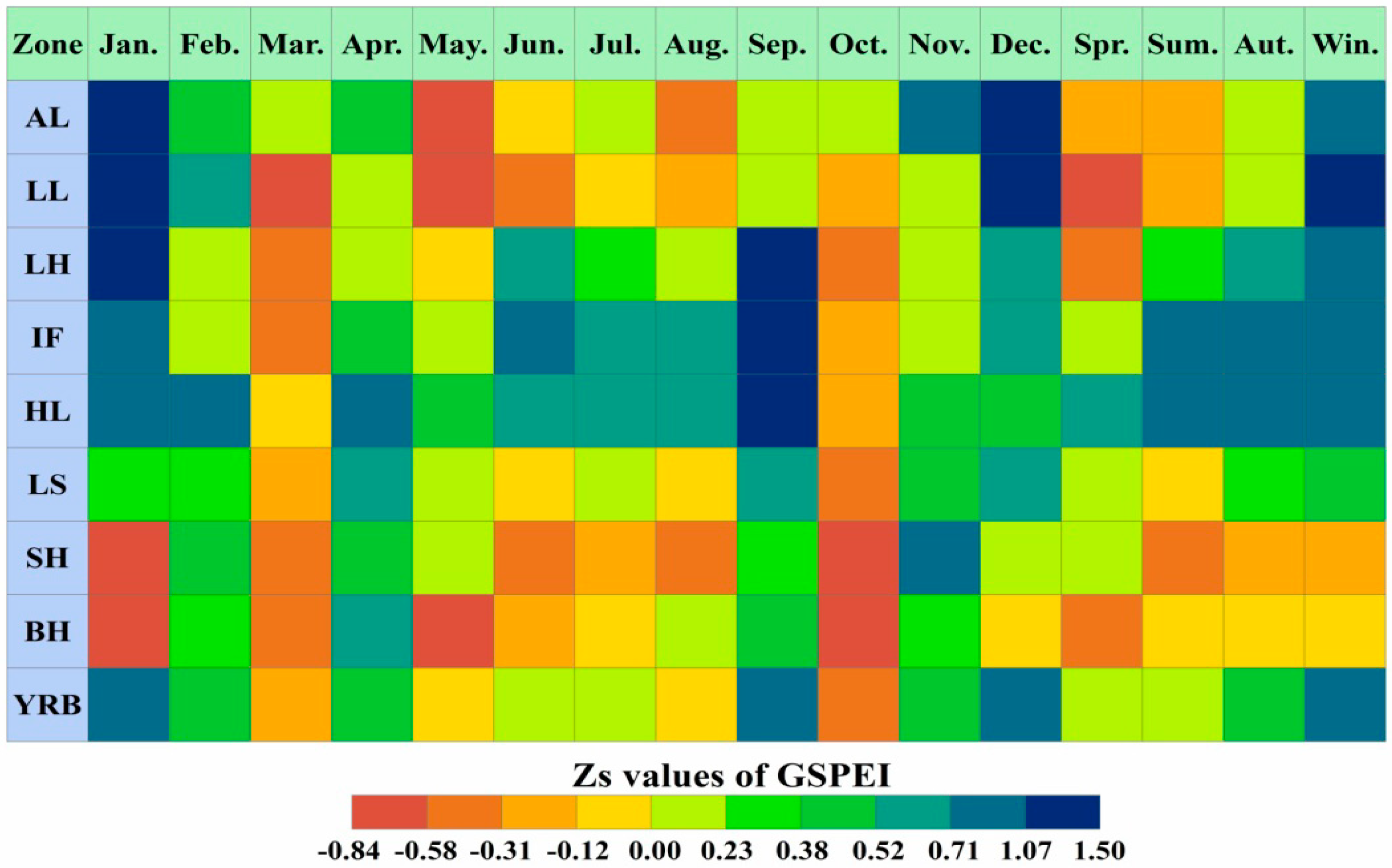
3.3. Drought Trend Characteristics at the Grid Scale
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yao, J.Q.; Zhao, Y.; Chen, Y.N.; Yu, X.J.; Zhang, R.B. Multi–scale assessments of droughts: A case study in Xinjiang, China. Sci. Total Environ. 2018, 630, 444–452. [Google Scholar] [CrossRef] [PubMed]
- Ahmadalipour, A.; Moradkhani, H. Multi–dimensional assessment of drought vulnerability in Africa: 1960–2100. Sci. Total Environ. 2018, 644, 520–535. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Yu, H.Q.; Sun, P.; Singh, V.P.; Shi, P.J. Multisource data based agricultural drought monitoring and agricultural loss in China. Glob. Planet. Chang. 2019, 172, 298–306. [Google Scholar] [CrossRef]
- Tang, G.Q.; Zeng, Z.Y.; Long, D.; Guo, X.L.; Yong, B.; Zhang, W.H.; Hong, Y. Statistical and hydrological comparisons between TRMM and GPM Level–3 products over a midlatitude basin: Is Day–1 IMERG a good successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Sun, Q.H.; Miao, C.Y.; Duan, Q.Y.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A review of global precipitation datasets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Tao, H.; Fischer, T.; Zeng, Y.; Fraedrich, K. Evaluation of TRMM 3B43 precipitation data for drought monitoring in Jiangsu Province, China. Water 2016, 8, 221. [Google Scholar] [CrossRef]
- Wu, J.W.; Miao, C.Y.; Zheng, H.Y.; Duan, Q.Y.; Lei, X.H.; Li, H. Meteorological and hydrological drought on the Loess Plateau, China: Evolutionary characteristics, impact, and propagation. J. Geophys. Res–Atmos. 2018, 123, 11569–11584. [Google Scholar] [CrossRef]
- Duan, Z.; Liu, J.Z.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of eight high spatial resolution gridded precipitation products in Adige Basin (Italy) at multiple temporal and spatial scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef] [PubMed]
- Zhong, R.D.; Chen, X.H.; Lai, C.G.; Wang, Z.L.; Lian, Y.Q.; Yu, H.J.; Wu, X.Q. Drought monitoring utility of satellite–based precipitation products across mainland China. J. Hydrol. 2019, 568, 343–359. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P.P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Chen, S.; Li, W.B.; Du, Y.D.; Mao, C.Y.; Zhang, L. Urbanization effect on precipitation over the Pearl River Delta based on CMORPH data. Adv. Clim. Chang. Res. 2015, 6, 16–22. [Google Scholar] [CrossRef]
- Lai, C.G.; Zhong, R.D.; Wang, Z.L.; Wu, X.Q.; Chen, X.H.; Wang, P.; Lian, Y.Q. Monitoring hydrological drought using long–term satellite–based precipitation data. Sci. Total Environ. 2019, 649, 1198–1208. [Google Scholar] [CrossRef] [PubMed]
- Zeweldi, D.A.; Gebremichael, M. Evaluation of CMORPH precipitation products at fine space–time scales. J. Hydrometeorol. 2009, 10, 300–307. [Google Scholar] [CrossRef]
- Xu, S.G.; Niu, Z.; Shen, Y.; Kuang, D. A research into the characters of CMORPH remote sensing precipitation error in China. Remote Sens. Technol. Appl. 2014, 29, 189–194. (In Chinese) [Google Scholar]
- Wang, Y.D.; Chen, H.; Liu, C.R.; Ding, Y.J. Applicability of ITPCAS and CMORPH precipitation datasets over Shaanxi Province. Arid Zone Res. 2018, 35, 579–588. [Google Scholar]
- Jiang, S.H.; Zhou, M.; Ren, L.L.; Cheng, X.R.; Zhang, P.J. Evaluation of latest TMPA and CMORPH satellite precipitation products over Yellow River Basin. Water Sci. Eng. 2016, 9, 87–96. [Google Scholar] [CrossRef]
- Lu, J.; Jia, L.; Menenti, M.; Yan, Y.P.; Zheng, C.L.; Zhou, J. Performance of the Standardized Precipitation Index based on the TMPA and CMORPH precipitation products for drought monitoring in China. IEEE J.–STARS. 2018, 11, 1387–1396. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Singh, V.P.; Mishra, A.K. Multivariate drought index: An information theory based approach for integrated drought assessment. J. Hydrol. 2015, 526, 164–182. [Google Scholar] [CrossRef]
- Tan, C.P.; Yang, J.P.; Li, M. Temporal–spatial variation of drought indicated by SPI and SPEI in Ningxia Hui Autonomous Region, China. Atmosphere 2015, 6, 1399–1421. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Alam, N.M.; Sharma, G.C.; Moreira, E.; Jana, C.; Mishra, P.K.; Sharma, N.K.; Mandal, D. Evaluation of drought using SPEI drought class transitions and log–linear models for different agro–ecological regions of India. Phys. Chem. Earth 2017, 100, 31–43. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Yu, Z.S.; Niu, H.S. Standardized Precipitation Evapotranspiration Index is highly correlated with total water storage over China under future climate scenarios. Atmos. Environ. 2018, 194, 123–133. [Google Scholar] [CrossRef]
- Tirivarombo, S.; Osupile, D.; Eliasson, P. Drought monitoring and analysis: Standardised Precipitation Evapotranspiration Index (SPEI) and Standardised Precipitation Index (SPI). Phys. Chem. Earth 2018, 106, 1–10. [Google Scholar] [CrossRef]
- Gao, X.R.; Zhao, Q.; Zhao, X.N.; Wu, P.T.; Pan, W.X.; Gao, X.D.; Sun, M. Temporal and spatial evolution of the standardized precipitation evapotranspiration index (SPEI) in the Loess Plateau under climate change from 2001 to 2050. Sci. Total Environ. 2017, 595, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.Y.; Gao, G.; An, W.; Zou, X.K.; Li, H.T.; Hou, M.T. Timescale differences between SC–PDSI and SPEI for drought monitoring in China. Phys. Chem. Earth. 2015, 10, 1–11. [Google Scholar] [CrossRef]
- Wu, D.; Yan, D.H.; Yang, G.Y.; Wang, X.G.; Xiao, W.H.; Zhang, H.T. Assessment on agricultural drought vulnerability in the Yellow River basin based on a fuzzy clustering iterative model. Nat. Hazards 2013, 67, 919–936. [Google Scholar] [CrossRef]
- Liang, K.; Liu, S.; Bai, P.; Nie, R. The Yellow River basin becomes wetter or drier? The case as indicated by mean precipitation and extremes during 1961–2012. Theor. Appl. Climatol. 2015, 119, 701–722. [Google Scholar] [CrossRef]
- Huang, S.Z.; Chang, J.X.; Leng, G.Y.; Huang, Q. Integrated index for drought assessment based on variable fuzzy set theory: A case study in the Yellow River basin, China. J. Hydrol. 2015, 527, 608–618. [Google Scholar] [CrossRef]
- She, D.X.; Xia, J. The spatial and temporal analysis of dry spells in the Yellow River basin, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 29–42. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.Y.; Wang, Y.; Xie, P.P. Performance of high–resolution satellite precipitation products over China. J. Geophys. Res. 2010, 115, D02114. [Google Scholar] [CrossRef]
- Buarque, D.C.; Paiva, R.C.D.; Clarke, R.T.; Mendes, C.A.B. A comparison of Amazon rainfall characteristics derived from TRMM, CMORPH, and the Brazilian national rain gauge network. J. Geophys. Res. Atmos. 2011, 116, D19105. [Google Scholar] [CrossRef]
- Zhang, B.Q.; He, C.S.; Morey, B.; Zhang, L.H. Evaluating the coupling effects of climate aridity and vegetation restoration on soil erosion over the Loess Plateau in China. Sci. Total Environ. 2016, 539, 436–449. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Liu, X.; Ma, X.Y. Spatio–temporal evolutions of precipitation in the Yellow River basin of China from 1981 to 2013. Water Sci. Tech.–Water Supply 2016, 16, 1441–1450. [Google Scholar] [CrossRef]
- Li, X.; He, B.B.; Quan, X.W.; Liao, Z.M.; Bai, X.J. Use of the Standardized Precipitation Evapotranspiration Index (SPEI) to characterize the drying trend in Southwest China from 1982–2012. Remote Sens. 2015, 7, 10917–10937. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.M.; Yang, H.B.; Zhao, Y. Study of the temporal and spatial patterns of drought in the Yellow River basin based on SPEI. Sci. China Earth Sci. 2018, 61, 1098–1111. [Google Scholar] [CrossRef]
- Wang, Q.F.; Shi, P.J.; Lei, T.J.; Geng, G.P.; Liu, J.H.; Mo, X.Y.; Li, X.H.; Zhou, H.K.; Wu, J.J. The alleviating trend of drought in the Huang–Huai–Hai Plain of China based on the daily SPEI. Int. J. Climatol. 2015, 35, 3760–3769. [Google Scholar] [CrossRef]
- Jiang, S.H.; Ren, L.L.; Yong, B.; Yang, X.L.; Shi, L. Evaluation of high–resolution satellite precipitation products with surface rain gauge observations from Laohahe Basin in northern China. Water Sci. Eng. 2010, 3, 405–417. [Google Scholar]
- Zhang, Y.Y.; Li, Y.G.; Ji, X.; Luo, X.; Li, X. Evaluation and hydrologic validation of three satellite–based precipitation products in the upper catchment of the Red River Basin, China. Remote Sens. 2018, 10, 1881. [Google Scholar] [CrossRef]
- Wang, J.L.; Li, Z.J. The ESMD method for climate data analysis. Clim. Chang. Res. Lett. 2014, 3, 1–5. [Google Scholar] [CrossRef]
- Li, H.F.; Wang, J.L.; Li, Z.J. Application of ESMD method to air–sea flux investigation. Int. J. Geosci. 2013, 4, 8–11. [Google Scholar] [CrossRef]
- Huang, S.Z.; Chang, J.X.; Huang, Q.; Chen, Y.T. Spatio–temporal changes and frequency analysis of drought in the Wei River basin, China. Water Resour. Manag. 2014, 28, 3095–3110. [Google Scholar] [CrossRef]
- Huang, S.Z.; Huang, Q.; Zhang, H.B.; Chen, Y.T.; Leng, G.Y. Spatio–temporal changes in precipitation, temperature and their possibly changing relationship: A case study in the Wei River Basin, China. Int. J. Climatol. 2016, 36, 1160–1169. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H.; Nadoushani, S.S.M.; Willems, P.; Marchetto, A. A survey of temperature and precipitation based aridity indices in Iran. Quat. Int. 2014, 345, 158–166. [Google Scholar] [CrossRef]
- Oertel, M.; Meza, F.J.; Gironás, J.; Scott, C.A.; Rojas, F.; Pineda–Pablos, N. Drought propagation in semi–arid river basins in Latin America: Lessons from Mexico to the Southern Cone. Water 2018, 10, 1564. [Google Scholar] [CrossRef]
- Li, B.Q.; Zhou, W.; Zhao, Y.Y.; Ju, Q.; Yu, Z.B.; Liang, Z.M.; Acharya, K. Using the SPEI to assess recent climate change in the Yarlung Zangbo River Basin, South Tibet. Water 2015, 7, 5474–5486. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, Q.Y.; Jiao, M.Y.; Wu, P.T.; Gao, X.R.; Ma, M.H.; Hong, Y. The temporal–spatial characteristics of drought in the Loess Plateau using the remote–sensed TRMM precipitation data from 1998 to 2014. Remote Sens. 2018, 10, 838. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.M.; Yang, H.B.; Zhao, Y.; Li, Z.H.; Wu, J.P. Capability of remotely sensed drought indices for representing the spatio–temporal variations of the meteorological droughts in the Yellow River Basin. Remote Sens. 2018, 10, 1834. [Google Scholar] [CrossRef]
- Jiang, W.G.; Yuan, L.H.; Wang, W.J.; Cao, R.; Zhang, Y.F.; Shen, W.M. Spatio–temporal analysis of vegetation variation in the Yellow River Basin. Ecol. Indic. 2015, 51, 117–126. [Google Scholar] [CrossRef]
- Huang, S.Z.; Huang, Q.; Chang, J.X.; Zhu, Y.L.; Leng, G.Y.; Xing, L. Drought structure based on a nonparametric multivariate standardized drought index across the Yellow River basin, China. J. Hydrol. 2015, 530, 127–136. [Google Scholar] [CrossRef]
- Liu, Q.; Yan, C.R.; He, W.Q. Drought variation and its sensitivity coefficients to climatic factors in the Yellow River Basin. Chin. J. Agrometeorol. 2016, 37, 623–632. (In Chinese) [Google Scholar]
- Sun, R.C.; Yuan, H.L.; Liu, X.L.; Jiang, X.M. Evaluation of the latest satellite–gauge precipitation products and their hydrologic applications over the Huaihe River basin. J. Hydrol. 2016, 536, 302–319. [Google Scholar] [CrossRef]
- Haile, A.T.; Yan, F.; Habib, E. Accuracy of the CMORPH satellite–rainfall product over Lake Tana Basin in Eastern Africa. Atmos. Res. 2015, 163, 177–187. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, X.; Shao, H.; Chen, S.Y.; Liu, T.; Chen, C.B.; Ding, Q.; Du, H.Y. Evaluation and intercomparison of high–resolution satellite precipitation estimates–GPM, TRMM, and CMORPH in the Tianshan Mountain Area. Remote Sens. 2018, 10, 1543. [Google Scholar] [CrossRef]
- Liao, R.W.; Zhang, D.B.; Shen, Y. Validation of six satellite–derived rainfall estimates over China. Meteorol. Mon. 2015, 41, 970–979. (In Chinese) [Google Scholar]
- Jiang, S.H.; Liu, S.Y.; Ren, L.L.; Yong, B.; Zhang, L.Q.; Wang, M.H.; Lu, Y.J.; He, Y.Q. Hydrologic evaluation of six high resolution satellite precipitation products in capturing extreme precipitation and streamflow over a medium–sized basin in China. Water 2018, 10, 25. [Google Scholar] [CrossRef]
- Cheng, L.; Shen, R.P.; Shi, C.X.; Bai, L.; Yang, Y.H. Evaluation and verification of CMORPH and TRMM 3B42 precipitation estimation products. Meteorol. Mon. 2014, 40, 1372–1379. (In Chinese) [Google Scholar]
- Li, Q.L.; Zhang, W.C.; Yi, L.; Liu, J.P.; Chen, H. Accuracy evaluation and comparison of GPM and TRMM precipitation product over Mainland China. Adv. Water Sci. 2018, 29, 303–313. [Google Scholar]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Yang, Y.F.; Luo, Y. Evaluating the performance of remote sensing precipitation products CMORPH, PERSIANN, and TMPA, in the arid region of northwest China. Theor. Appl. Climatol. 2014, 118, 429–445. [Google Scholar] [CrossRef]
- Zeng, Q.L.; Wang, Y.Q.; Chen, L.F.; Wang, Z.F.; Zhu, H.; Li, B. Inter–comparison and evaluation of remote sensing precipitation products over China from 2005 to 2013. Remote Sens. 2018, 10, 168. [Google Scholar] [CrossRef]


| Interpolation Methods | RMSE | MRE | CC | |
|---|---|---|---|---|
| Kriging Interpolation | Ordinary Kriging | 0.19 | 0.03 | 0.98 |
| Universal Kriging | 1.35 | 1.87 | 0.82 | |
| Inverse Distance Weighting | IDW | 0.77 | 0.91 | 0.91 |
| Polynomial Interpolation | Global PI | 1.75 | 2.60 | 0.75 |
| Local PI | 1.05 | 1.11 | 0.89 | |
| Radial Basis Function | Completely Regularized Spline | 0.22 | 0.05 | 0.94 |
| Spline with Tension | 0.25 | 0.07 | 0.92 | |
| Thin Plate Spline | 0.22 | 0.05 | 0.94 | |
| Grade | Classification | GSPEI |
|---|---|---|
| I | No drought | −0.5 < GSPEI |
| II | Mild drought | −1.0 < GSPEI ≤ −0.5 |
| III | Moderate drought | −1.5 < GSPEI ≤ −1.0 |
| IV | Severe drought | −2.0 < GSPEI ≤ −1.5 |
| V | Extreme drought | GSPEI ≤ −2.0 |
| Evaluation Indicators | Unit | Formula | Range | Perfect Value | Reference |
|---|---|---|---|---|---|
| CC | NA | [−1,1] | 1 | [37] | |
| MAE | mm | [0,+∞) | 0 | [37] | |
| RMSE | mm | [0,+∞) | 0 | [38] | |
| NSE | NA | (−∞,1] | 1 | [38] | |
| POD | NA | [0,1] | 1 | [38] | |
| FAR | NA | [0,1] | 0 | [38] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Yang, H.; Wang, Z.; Zhang, Z.; Li, Z. Drought Evaluation with CMORPH Satellite Precipitation Data in the Yellow River Basin by Using Gridded Standardized Precipitation Evapotranspiration Index. Remote Sens. 2019, 11, 485. https://doi.org/10.3390/rs11050485
Wang F, Yang H, Wang Z, Zhang Z, Li Z. Drought Evaluation with CMORPH Satellite Precipitation Data in the Yellow River Basin by Using Gridded Standardized Precipitation Evapotranspiration Index. Remote Sensing. 2019; 11(5):485. https://doi.org/10.3390/rs11050485
Chicago/Turabian StyleWang, Fei, Haibo Yang, Zongmin Wang, Zezhong Zhang, and Zhenhong Li. 2019. "Drought Evaluation with CMORPH Satellite Precipitation Data in the Yellow River Basin by Using Gridded Standardized Precipitation Evapotranspiration Index" Remote Sensing 11, no. 5: 485. https://doi.org/10.3390/rs11050485
APA StyleWang, F., Yang, H., Wang, Z., Zhang, Z., & Li, Z. (2019). Drought Evaluation with CMORPH Satellite Precipitation Data in the Yellow River Basin by Using Gridded Standardized Precipitation Evapotranspiration Index. Remote Sensing, 11(5), 485. https://doi.org/10.3390/rs11050485









