Homogeneity Distance Classification Algorithm (HDCA): A Novel Algorithm for Satellite Image Classification

Abstract

Image classification is one of the most common methods of information extraction from satellite images. In this paper, a novel algorithm for image classification based on gravity theory was developed, which was called “homogeneity distance classification algorithm (HDCA)”. The proposed HDCA used texture and spectral information for classifying images in two iterative supplementary computing stages: (1) merging, (2) traveling and escaping operators. The HDCA was equipped by a new concept of distance, the weighted Manhattan distance (WMD). Moreover, an improved gravitational search algorithm (IGSA) was applied for selecting features and determining optimal feature space scale in HDCA. In the case of multispectral satellite image classification, the proposed method was compared with two well-known classification methods, Maximum Likelihood classifier (MLC) and Support Vector Machine (SVM). The results of the comparison indicated that overall accuracy values for HDCA, MLC, and SVM are 95.99, 93.15, and 95.00, respectively. Furthermore, the proposed HDCA method was also used for classifying hyperspectral reference datasets (Indian Pines, Salinas and Salinas-A scene). The classification results indicated substantial improvement over previous algorithms and studies by 2% in Indian Pines dataset, 0.7% in the Salinas dataset and 1.2% in the Salinas-A scene. These experimental results demonstrate that the proposed algorithm can classify both multispectral and hyperspectral remote sensing images with reliable accuracy because this algorithm uses the WMD in the classification process and the IGSA to select automatically optimal features for image classification based on spectral and texture information.

1. Introduction

Image classification is one of the most common methods of information extraction from satellite images. Various methods have been developed for satellite image classification. Generally, these methods can be divided into supervised and unsupervised categories [1]. With the development of remote sensing and image processing techniques, a wide variety of supervised and unsupervised methods have been proposed to improve the accuracy of classification, which include Maximum likelihood [2], Artificial neural network [3], Support vector machine [4], Alternating decision tree [5], Attribute bagging [6], Large margin nearest neighbor [7], Nearest centroid classifier [8] and tensor-based methods [9,10]. All methods of image classification for implementation require image features, which denotes types of homogeneity classes; in other words, classification is performed based on feature measurements taken from an image that could be spectral, texture, spatial, shape, geometric properties, and/or some statistical measures [11]. Image classification can be done using a combination of several features. Selecting the proper combination of features for implementation is a major challenge in classification [12]. It is worth noting that most conventional methods of image classification have no obvious strengths to classify images with different spatial and spectral features [13].

Recently, there has been a great interest in heuristic and meta-heuristic algorithms for image classification and related fields [14]. The majority of heuristic and metaheuristic algorithms are inspired by natural or biological phenomena [11]. A comprehensive review of heuristic and metaheuristic algorithms can be found in [11,15,16]. Genetic Algorithm has been applied to image classification in [17]. In [18] Ant Colony Optimization has been presented as a method for clustering analysis. In [19], for clustering problem, a genetic k-means algorithm has been proposed. Clustering approaches based on a neural gas algorithm have been presented in [20]. Particle Swarm Optimization has been proposed for image classification in [21]. Recently, convolutional neural networks (CNN) and deep CNN are of interest to researchers in the field of image classification [22,23,24,25,26,27,28].

In the present study, a novel image classification algorithm based on natural gravity, which is inspired by Newton’s physics theory, is presented, which is called s “homogeneity distance classification algorithm (HDCA)”. The proposed HDCA uses texture and spectral information for classifying images. Some distinct features of the proposed HDCA include:

(i)

Some HDCA operators are combined with stochastic features; therefore, the algorithm can consider more similar pixels for assigning to a class;

(ii)

In order to achieve the high accuracy in classification of different images, a new and unique concept of distance in classification process is used;

(iii)

Automatic selection of optimal features for image classification based on spectral and texture information; and

(iv)

It is possible to separate more homogeneous classes by determining the optimal scale of feature space with the new optimization method.

The remainder of the paper is organized as follows. Section 2 introduces relevant works and a brief introduction about the law of gravity. Also, in Section 2 the proposed HDCA is introduced and the optimization of features space scale is described. Experimental results are presented in Section 3. The discussion is reported in Section 4, followed by conclusions in Section 5.

2. Data and Method

2.1. Data

To evaluate and validate the performance of the HDCA algorithm, two categories of satellite imagery (multispectral and hyperspectral images) were used. IKONOS satellite image for the Shahriar region (Tehran), 2013, which has 4 spectral bands Red, Green, Blue and Near Infrared with spatial resolution of 4 meter and the size of 400 × 400 pixels was used. Also, hyperspectral reference datasets including the Indian Pines dataset, Salinas, and Salinas-A dataset, acquired by the Airborne Visible/ Infrared Imaging Spectrometer (AVIRIS) sensor, were used. The Indian Pines hyperspectral dataset consisted of a 2.9 × 2.9 km² (145 × 145 pixels) land of Northwest Tippecanoe County in the Indian Pine region and was collected on 12 June 1992. The Salinas dataset contained 224 spectral bands with a spatial resolution of 3.7 m and was acquired by the AVIRIS sensor over Salinas Valley, California, USA. The size of image is 512 × 217 pixels. The Salinas-A scene dataset is a subset of the Salinas dataset which includes 224 spectral bands. The size of image is 86 × 83 pixels.

2.2. Background

According to Newton’s law of universal gravitation, all objects attract each other with a force of gravitational attraction [29,30]. The force of gravitational attraction between two objects has an effect on the joint line of two particles, which is dependent upon the mass of both objects directly and is related to the square of the distance between two objects inversely [30]. Newton’s conclusion about the amount of these forces is expressed as Equation (1).

$${\mathrm{Force}}_{ij}=G\frac{M_i{M}_j}{R_{ij}{}^2}$$

(1)

where ${\mathrm{Force}}_{ij}$ is the magnitude of gravitational force between two objects i and j, and $M_i$ and $M_j$ are the masses of objects i and j, respectively. G is the universal gravitational constant, and $R_{ij}$ is the distance separating i and j objects’ centers.

Inspired by the Newtonian law of gravity, a gravitational clustering algorithm was first suggested by Wright (1977) [31] and has been studied substantially in [11,32,33,34,35,36,37]. One of these studies is reviewed in this section, which our proposed method is similar to. In Rashedi and Nezamabadi-pour (2013) [11], a model of the gravitational clustering in RGB space was used for color image segmentation. In the process of segmentation, image pixels were mapped to RGB color space, context and spatial information of pixel, and each pixel was considered a particle equal to the mass of one. All particles exert gravitational force with respect to each other. The gravitational attraction model between two particles i and j was defined as (Equation (2)):

$${\mathrm{Force}}_{ij}=G\frac{M_i{M}_j}{R_{ij}+\epsilon }\left(\overrightarrow{z_j}-\overrightarrow{z_i}\right)$$

(2)

where $\overrightarrow{z_i}$ and $\overrightarrow{z_j}$ are the feature vector of particle i and j, respectively. This causes particles (pixels) to move in RGB space. Particles moving to one place are merged into a new particle, whose mass is considered as the sum of the two particles mass. This method is an unsupervised segmentation algorithm for color images based on gravitational law. It is an iterative method which contains three operators called traveling, merging, and escaping. Executing these operators is continued until the certain number of iterations is reached. Our proposed algorithm has some similarities to this algorithm theoretically, but there are major differences in calculation and operator performance that will be discussed below.

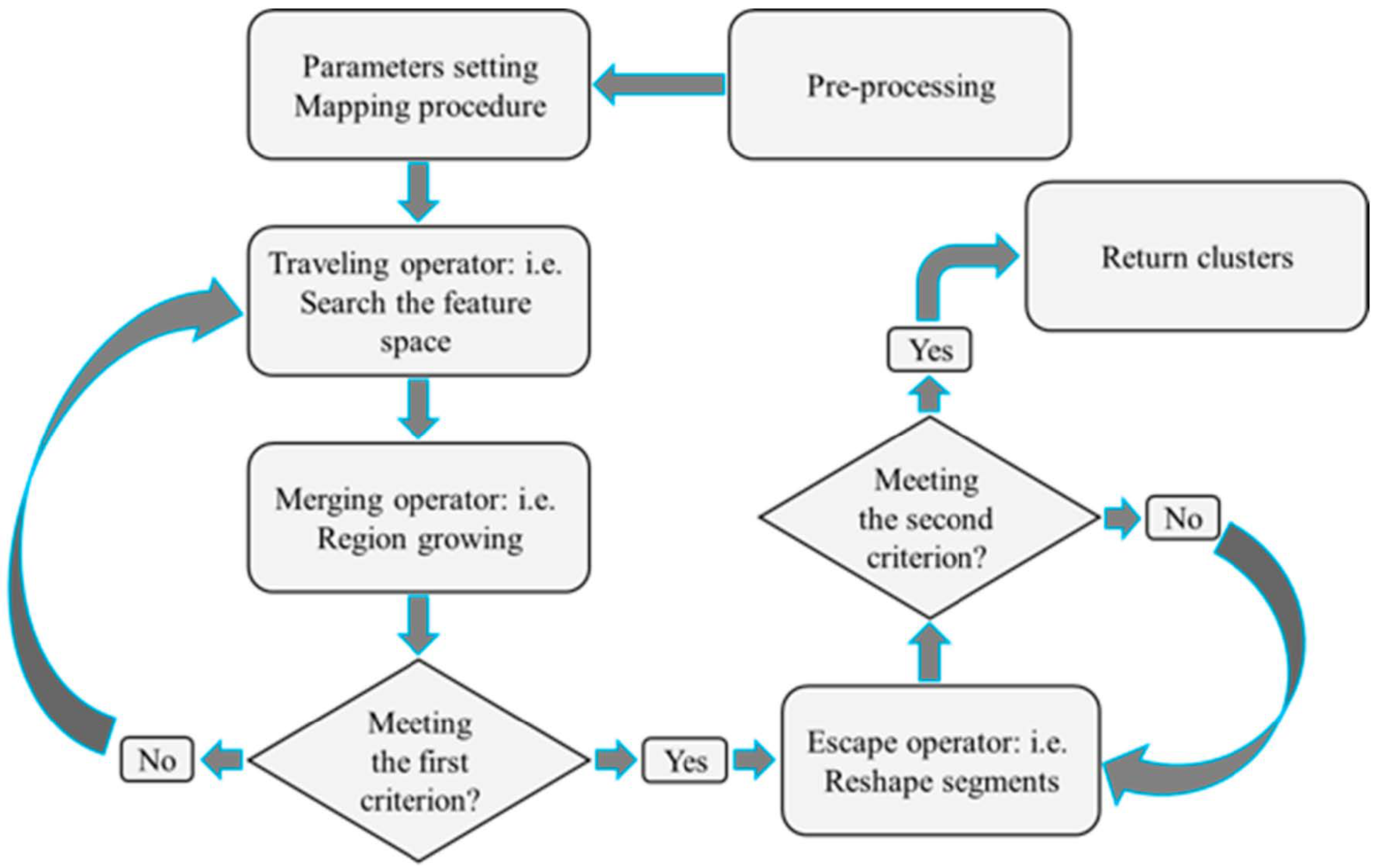
2.3. The Proposed Algorithm: HDCA

HDCA is a supervised classification for remote sensing images based on the gravity law. The proposed algorithm is an iterative method which contains three operators called traveling, merging, and escaping. The implementation of these operators is repeated in two supplementary computing stages until stopping criteria are met for every stage. Based on traveling operator, agents (pixels) move in the feature space under the influence of training pixels gravitational force. They can find other similar agents by traveling. In the merging operator, the agents are merged with the nearest agents to each other based on the rule that only one of these agents contains training data. In other words, the merging operator will merge unlabeled pixels with agents that are included in the training data. Finally, using the escaping operator, unlabeled pixels escape from their clusters with a probability that is proportional to their distance from their cluster’s center. The escaped pixels are absorbed by nearest clusters. It is noted that the algorithm does not cycle as repeating traveling- merging-escaping consecutively, but two traveling and merging operators repeat consecutively as long as the first stopping criterion is met and then the escaping operator begins to repeat until the second stopping criterion is met. The overall flowchart of the proposed method is shown in Figure 1.

2.3.1. The Procedure of Image Mapping into Feature Space

First, a satellite image is mapped into a feature space in which the masses move to find similar pixels. As mentioned before, in order to acquire an accurate classification, the use of different features, in addition to spectral information, is essential. In the proposed HDCA method, we define a feature space containing three features (dimensions) per spectral band. The first dimension indicates the spectral information in each band of the original image. The next two dimensions are the variance and inertia of pixels located in a small region (window) around a pixel in each band of the original image.

In other words, each agent i (pixel) in an image with an L band is described as follows:

$$Z_i=\left(S_i^d{\mathrm{Var}}_i^d{\mathrm{Inr}}_i^d\mathrm{for}d=1,\dots ,L\right)\mathrm{for}i=1,\dots ,N$$

(3)

where N is the total number of pixels in the image, $S_i^d$ represents th spectral component values of agent i (pixel) in band d, and ${\mathrm{Var}}_i^d$, ${\mathrm{Inr}}_i^d$ represent variance and inertia of agent i in band d, respectively. Each pixel is first considered as a particle or an agent. By the traveling operator, particles move under the gravitational force of the particles that contain training data. The number of agents is decreased after each iteration by the merging operation.

2.3.2. Traveling Operator

At the traveling stage, particles move based on the gravity force and search the feature space to find a similar agent. This step is performed based on the gravitational and motion laws. In order to calculate the agent acceleration, the sum of forces that other particles applied on an agent is calculated using Equation (4), followed by the agent acceleration calculated by using the law of motion (Equation (5)). Theoretically, three types of masses can be defined for each object: (1) Active gravitational mass (Ma) is a measure of the power of the gravitational field related to a particular object. (2) Passive gravitational mass (Mp) is a measure of the strength of an object’s interaction with the gravitational field. An object with a smaller passive gravitational mass faces a smaller force compared to an object with a larger passive gravitational mass in the same gravitational field. (3) Inertial mass (Mi) is a mass parameter giving the inertial resistance to acceleration of the object when a force is applied. An object with large and small inertial masses changes its motion more slowly and rapidly, respectively [37].

It is noted that active gravitational mass is considered only for training pixels in these methods. Particles without labels have Passive gravitational mass. As a result, unlabeled particles have no force applied onto other particles; therefore, only training pixels can attract other particles. The active gravitational mass is calculated through Equation (6) for training pixels. According to Equation (6), the similarity between features of agents is the only criterion for traveling, and the feature space which is followed by merging, rather than the number of training data for the different classes. Therefore, the difference in the number of training data in different classes does not affect the performance of the algorithm. Finally, the velocity of each dimension of an agent is calculated by adding the current acceleration to a fraction of previous velocity (Equation (7)). One of the characteristics of heuristic search algorithms is stochastic search. By adding the stochastic search, the proposed algorithm will have the ability to some extent overcome the weakness of the inadequate training data and search the image to find the best areas for the proper merge. Also, this stochasticity facilitates the algorithm to avoid local minima and explore in a more efficient way the space. In order to keep the random characteristic in Relation (7), the random fraction has been used. Finally, the agent position is updated using Equation (8).

$${\mathrm{force}}_i^d\left(t\right)={\displaystyle \sum }_{j\in k_{close}\ne i}G\left(t\right)\frac{M_{aj}\left(t\right)M_{pi}\left(t\right)}{{(1+R_{ij}\left(t\right))}^2}(z_j^d\left(t\right)-z_i^d\left(t\right))$$

(4)

$$a_i^d\left(t\right)=\frac{{\mathrm{force}}_i^d\left(t\right)}{M_{ii}\left(t\right)}={\displaystyle \sum }_{j\in k_{close}\ne i}G\left(t\right)\frac{M_{aj}\left(t\right)}{{(1+R_{ij}\left(t\right))}^2}(z_j^d\left(t\right)-z_i^d\left(t\right))$$

(5)

$$M_j\left(t\right)=\frac{1}{n_{c_j}}$$

(6)

$$v_i^d\left(t+1\right)={\mathrm{rand}}_i·v_i^d\left(t\right)+a_i^d\left(t\right)$$

(7)

$$z_i^d\left(t+1\right)=z_i^d\left(t\right)+v_i^d\left(t+1\right)$$

(8)

where $M_{aj}$ is the active gravitational mass of agent j, $M_{pi}$ is the passive gravitational mass of agent i, $M_{ii}$ is the inertial mass of ith agent and $R_{ij}\left(t\right)$ is unique concept of the Manhattan distance between two agents i and j in the feature space, which is called the Weighted Manhattan Distance (WMD) (Appendix A proves why WMD is more appropriate than other distance metrics). However, it is important to note that the feature space should be normalized (the feature space should be transferred to the range between 0 and 1), then the distance between agents is calculated by Equation (9). $k_{close}$ is a set of $k$ closest agents containing training data relative to agent i which apply forces on the ith agent and pulls it. $n_{c_j}$ is the total number of training pixels assigned to the class related to agent j. The use of the unique concept of distance is additional distinctive properties of the proposed algorithm. In this paper, the gravitational constant, $G$, is assigned to a constant value during iterations.

$$R_{ij}\left(t\right)={\displaystyle \sum }_{d=1}^L{\mu }_1^d\frac{|S_j^d-S_i^d|}{{\delta }_{S_{c_j}^d}}+{\mu }_2^d\frac{|{\mathrm{Var}}_j^d-{\mathrm{Var}}_i^d|}{{\delta }_{{\mathrm{Var}}_{c_j}^d}}+{\mu }_3^d\frac{|{\mathrm{Inr}}_j^d-{\mathrm{Inr}}_i^d|}{{\delta }_{{\mathrm{Inr}}_{c_j}^d}}$$

(9)

where $S_j^d$ is the spectral value of pixel j in band d and ${\mathrm{Var}}_i^d$, ${\mathrm{Inr}}_i^d$ are variance and inertia values of pixels located in a small window surrounding pixel j in band d, respectively. ${\delta }_{S_{c_j}^d}$ is the standard deviation of spectral value of all training pixels assigned to class related to agent j in band d and ${\delta }_{{\mathrm{Var}}_{c_j}^d}$, ${\delta }_{{\mathrm{Inr}}_{c_j}^d}$ is the standard deviation of variance and inertia values in a small window around all training data assigned to class related to agent j in band d, respectively. ${\mu }_1^d$, ${\mu }_2^d$ and ${\mu }_3^d$ coefficients are the weight and scale of each feature, which uses a new optimization method to calculate its best values.

2.3.3. Merging Operator

In the merging operator, unlabeled agents or non-training agents will be merged with agents that include training data. At this stage, if the unlabeled agent and agent with training pixels are the closest agents to each other, they will be merged and create a new labelled agent. However, two agents cannot be merged together if both contain training data or if both contain no training data. Since unlabeled agents do not have mass, the location, mass, velocity, and label of the new agent are taken from the agent with training data.

During the merging operator, the number of agents is decreased by increasing iterations. A stopping criterion to controlling the iterative circle of traveling- merging is the number of agents. When the number of agents equals the total number of training data, iterative circles will stop; and after the final merging, the escaping stage will happen. In the final merging, all agents with same training data become a new agent. As a result of this process, the number of agents would equal to the number of classes.

2.3.4. Escaping Operator

One of the problems of image clustering and classification based on regional growth algorithms is to create incorrect sequential clusters due to incorrect merging [13]. To solve this problem, the random concept has been introduced to obtain the velocity of agents through the traveling process, but the classification accuracy is influenced by incorrect merging. In order to meaningfully remove this problem, the escaping operator is introduced in HDCA.

This stage starts after the end of the merging-traveling circles. It is necessary that before running this stage, pixels are returned from moved (transferred) features to the same initial features and then the center location of every cluster is determined. All training and unlabeled pixels have equal weight in computing the new center location of clusters. At the escaping stage, all calculations are done on the basis of initial features.

Each of the unlabeled pixels escaping from their corresponding clusters with a probability of $P{e}_i^k$ is calculated using the distances from their corresponding cluster centers, but training pixels cannot escape from their clusters. The escaped pixels are absorbed by the closest cluster in the feature space. The escape probability of pixel i to become free from cluster k is calculated by Equation (10), where $r_i^k$ is the distance between pixel $i$ and cluster center $k$ (agent $k$), and $d_{min}^k$, $d_{max}^k$ are the distances nearest and farthest pixel to the cluster center, respectively. Pixels close to the cluster center would be released with less probability, while the pixels far from the cluster center would escape with higher probability. It is noteworthy that the location of the cluster center is calculated two times during an iteration of escaping stage, before and after absorbing the escaped pixels.

$$P{e}_i^k={(\frac{r_{\min }^k-d_{\min }^k}{d_{\max }^k-d_{\min }^k})}^{\frac{1}{p}}$$

(10)

where $p$ is the escape power of pixels. Higher $p$ values lead to higher escape probability. The order of distance is WMD at the escaping stage. This distance is used to calculate standard deviations from the training data values of the cluster member. It should be noted that a pixel close to the center with the size of $d_{\min }$ would never escape and that far from the center with the size of $d_{\max }$ would be released. One advantage of the designed escaping operator is no need to determine the threshold by the user for pixels to become free, in addition to the random concept. The stopping criteria of escaping operator can be one of the conditions below.

(1)

Stopping after a certain number of iterations; and

(2)

Stopping after fixing classes: the operator stops when no change is observed in classes.

2.4. Optimization of Feature Space Scale

Optimization of the feature space is an important stage of pre-processing to accomplish image classification. In the gravitational classification, coefficients ${\mu }_1^d$, ${\mu }_2^d$ and ${\mu }_3^d$ determine the weight and scale of each feature, which are used to compute WMD in the feature space. For example, if ${\mu }_1^d$ increases, the spectral data weight of band $d$ will increase, which has more effect on the classification. Values of these coefficients in different images have different effects to achieve homogenous classes. To determine the optimum value of these coefficients, they should be chosen by considering images automatically. It is crucial that coefficients can be determined automatically to distinguish between classes, with the most similarity of elements within classes and the least similarity between classes. In this paper, the Improved Gravitational Search Algorithm (IGSA) is used to optimize coefficients as well as the particular feature management function in order to achieve accurate image classification. This method can calculate coefficient values ${\mu }_1^d$, ${\mu }_2^d$ and ${\mu }_3^d$ by considering training data to obtain the most separability of classes.

2.4.1. Background

The IGSA algorithm, like the GSA algorithm [37], is inspired by the law of gravity. According to the law of gravity, every object is able to understand location and situation of the other objects through the law of gravitational attraction. The optimum region attracts the objects like black holes. Thus, this force can be utilized as an instrument to exchange information. The designed optimum finder can be used to solve every optimization problem, in which each solution is defined as a situation in space, and its similarity to the other solutions is expressed as a distance. The amounts of masses are determined by the objective function. Major reasons for applying the IGSA algorithm instead of other algorithms are listed as follows.

• The efficiency of most optimization algorithm is determined by the initial position of particles. This means that if the initial population does not cover some parts of space, finding the optimum region will be difficult. Our proposed algorithm (IGSA) is able to remove this problem with negative mass.
• The time to achieve the optimum solution is short.
• Other benefits of our proposed algorithm is using a kind of memory. The memory helps find the optimum solution properly.
• The memory of the algorithm and using the negative mass dramatically decrease the possibility of trapping the algorithm in the local optimum, so the memory can be achieved the solution convergence in global optimum at a low number iterations.

2.4.2. The Proposed Algorithm (IGSA)

Consider a system with N agents that their performances are based on their masses. Each agent has the same coefficient, ${\mu }_1^d$, ${\mu }_2^d$ and ${\mu }_3^d$ ($ford=1,2,\dots ,M$ where $M$ is the number of bands), which is a point in the space or a solution of the problem. The position of the ith agent in the kth dimension is shown by $x_i^k$ (Equation (11)).

$$X_i=\left(x_{1i}^d{x}_{2i}^d{x}_{3i}^d\mathrm{for}d=1,\dots ,M\right)\mathrm{for}i=1,\dots ,N$$

(11)

where N is the total number of pixels in the image. In this system, the law of gravity is not only based on attraction but also uses the repulsion that is in the results of negative mass. In IGSA, in addition to positive force (attraction) where top members of the community (set of agents with greater mass) import each agent in each dimension, a negative force (distraction) also enters each agent in each dimension by the poorer members of community (set of agents with smaller mass). In order to give memory to this algorithm, the positive and negative force should be considered towards the best and worst position for each agent that receive the force. Agents with positive or negative mass apply their force to the other agents, which lead to their general motion toward objects that have the best solutions. In other words, during iterations, it is expect that masses be attracted by the heaviest mass on the positive side that presents an optimum solution in the search space.

In this system, at a specific time ‘$t$’, the force acting on agent ‘$i$’ from agent ‘$j$’ in dth dimension is $f_{ij}^d\left(t\right)$. the amount of this force can be calculated by Equation (12), where $M_{aj}$, $M_{pi}$ are active gravitational mass of particle j and passive gravitational mass of particle i, respectively, G(t) is the gravitational constant at time t, ε is a small constant and $R_{ij}$ is the Euclidian distance (2-norm distance) between two agents i and j which is calculated according to Equation (13).

$$f_{ij}^d\left(t\right)=G\left(t\right)\frac{M_{pi}\left(t\right)·M_{aj}\left(t\right)}{R_{ij}\left(t\right)+\epsilon }(x_j^d\left(t\right)-x_i^d\left(t\right))$$

(12)

$$R_{ij}\left(t\right)=\Vert X_i\left(t\right)·X_j\left(t\right)\Vert$$

(13)

According to Equation (14), the total force that acts on agent i in a dimension d at time t ($f_i^d\left(t\right)$) is equal to the randomly weighted sum of the positive forces from the better agents k, randomly weighted sum of the negative forces from the worst agents h, and the positive and negative forces from the best and worst position for each agent that receive the force, respectively. The force acting on the best (pbest) and worst (pworst) position for each agent in each dimension is calculated using Equations (15) and (16).

$$\begin{array}{cc}{f}_i^d\left(t\right)={\displaystyle \sum _{j\in kbest, j\ne i}}& {\mathrm{rand}}_j{f}_{ij}^d\left(t\right)\hfill \\ & +{\displaystyle \sum _{t\in hworst, t\ne i}}{\mathrm{rand}}_t{f}_{it}^d\left(t\right)+{\mathrm{rand}}_{pb}{f}_{i pb}^d\left(t\right)+{\mathrm{rand}}_{pw}{f}_{i pw}^d\left(t\right)\hfill \end{array}$$

(14)

$$f_{ipw}^d\left(t\right)=G\left(t\right)\frac{M_{pi}\left(t\right)·M_{apworst}\left(t\right)}{R_{ij}\left(t\right)+\epsilon }(x_{pworst}^d\left(t\right)-x_i^d\left(t\right))$$

(15)

$$f_{ipb}^d\left(t\right)=G\left(t\right)\frac{M_{pi}\left(t\right)·M_{apbest}\left(t\right)}{R_{ij}\left(t\right)+\epsilon }(x_{pbest}^d\left(t\right)-x_i^d\left(t\right))$$

(16)

In these Equations, rand is a uniformly distributed random number in the interval [0, 1], $M_{apworst}$, $M_{apbest}$ are active gravitational mass of the best and worst positions for each agent, respectively, and $M_{pi}$ is the passive gravitational mass of the agent i. The values of K and h are variable over time in order to control compromise between exploration and exploitation. The algorithm needs to do a proper search and exploration in the first iterations, but as time passes the population will achieve better results and the problem will require exploitation. Therefore, at the beginning, the K value is defined as almost all agents (95% of the best community), and as time passes, the number of absorbents decreases linearly until at the end there will be just one agent that attracts the others agents of the population.

The h value has different procedures, as at the beginning, only 5 percent of the worst population members repulse the others, and as time passes, the number of repellents is increased linearly until at 25 percent of iterations there will be 30 percent of the worst population members and after this iteration, the h value is decreased linearly until at 50 percent of iterations there will be none of the worst population members. Also, the total force from the best (pbest) and worst (pworst) positions acting on each agent are applied until at 75 percent of iterations and after this iteration, the total force from pbest and pworst positions is not applied on the agent. Implementation of this procedure leads to controlling exploration and exploitation ideally.

According to Newton’s second law, each agent in dimension d has an acceleration that is proportional to the entered force on it in dimension d and inversely proportional to inertia mass of it, that is expressed in Equation (17). The acceleration of the agent i in dimension d at time t and the inertial mass of agent i are shown as $a_i^d\left(t\right)$ and $M_{ii}$, respectively [37,38].

$$a_i^d\left(t\right)=\frac{f_i^d\left(t\right)}{M_{ii}\left(t\right)}$$

(17)

In the IGSA algorithm, all values of inertial mass, passive gravitational mass, and active gravitational mass for every agent are considered equal. These values are calculated by the objective (fitness) function for mass of each agents of kbest, hworst, pbest and pworst with separate equations (Equations (18)–(21)). In these equations, a greater mass is assigned to objects with e better fitness that leads to greater effectiveness. Thus, agents with better fitness have more mass in the positive direction, and can therefore attract the other agents, and vice versa.

$$M_{\mathrm{ikb}}\left(t\right)=\frac{{\mathrm{fit}}_i\left(t\right)-\left(\mathrm{worst}\_\mathrm{so}\_\mathrm{far}\right)}{{{\displaystyle \sum }}_{j\in \mathrm{kbest}}^{.}{\mathrm{fit}}_j\left(t\right)-\left(\mathrm{worst}\_\mathrm{so}\_\mathrm{far}\right)}$$

(18)

$$M_{\mathrm{ihw}}\left(t\right)=\frac{h}{k}\frac{{\mathrm{fit}}_i\left(t\right)-\left(\mathrm{best}\_\mathrm{so}\_\mathrm{far}\right)}{{{\displaystyle \sum }}_{j\in \mathrm{hworst}}^{.}\left(\mathrm{best}\_\mathrm{so}\_\mathrm{far}\right)-{\mathrm{fit}}_j\left(t\right)}$$

(19)

$$M_{\mathrm{ipb}}\left(t\right)=\frac{{\mathrm{fitbest}}_i-\left(\mathrm{worst}\_\mathrm{so}\_\mathrm{far}\right)}{{{\displaystyle \sum }}_{j=1}^N{\mathrm{fitbest}}_j-\left(\mathrm{worst}\_\mathrm{so}\_\mathrm{far}\right)}$$

(20)

$$M_{\mathrm{ipw}}\left(t\right)=\frac{{\mathrm{fitworst}}_i-\left(\mathrm{best}\_\mathrm{so}\_\mathrm{far}\right)}{{{\displaystyle \sum }}_{j=1}^N\left(\mathrm{best}\_\mathrm{so}\_\mathrm{far}\right)-{\mathrm{fitworst}}_j}$$

(21)

where the best-so-far and worst-so-far values are the best and the worst solutions of all population, respectively, the ${\mathrm{fitbest}}_i$ and ${\mathrm{fitworst}}_i$ values are the best and the worst solutions of the agent i, respectively, ${\mathrm{fit}}_i\left(t\right)$ represent the fitness value of agent i at time t. According to the equations, it is clear that values of masses of pworst and hworst ($M_{\mathrm{ipw}}$ and $M_{\mathrm{ihw}}$) are negative, which lead to repulsion.

Furthermore, the next velocity of an agent is considered as a fraction of its current velocity added to its acceleration. Therefore, the position and velocity of agent i in dimension d could be calculated as Equations (22) and (23) [37,38].

$$v_i^d\left(t+1\right)={\mathrm{rand}}_i·v_i^d\left(t\right)+a_i^d\left(t\right)$$

(22)

$$x_i^d\left(t+1\right)=x_i^d\left(t\right)+v_i^d\left(t+1\right)$$

(23)

where ${\mathrm{rand}}_i$, ${\mathrm{rand}}_j$ are uniform random variables in the interval [0, 1] that give a randomized characteristic to the search.

According to Equation (24), the gravitational constant, G, is a function of the initial value ($G_0$) and time (t). In the GSA algorithm, an exponential equation is used to reduce the gravitational constant (Equation (24)) [37].

$$G\left(t\right)=G_0{\mathrm{e}}^{-\alpha \frac{t}{T}}$$

(24)

where $G_0$ is the initial gravitational constant, α is a positive constant, and T is the total iterations of the algorithm or the total age of system. At the beginning of system formation, each object (agent) is placed in a point of space randomly that is a solution to the problem. At each iteration, the agents are evaluated and values of G, pbest, pworst, best-so-far and bad-so-far are updated. Then, the gravitational mass, the gravitational force acting, the acceleration and the velocity of each agent are calculated. Finally, the next position of each agent is calculated and objects are placed in new positions. Figure 2 shows the optimization algorithm.

2.4.3. The Objective Function (Fitness)

The objective function for optimization in IGSA is defined by Equation (25), which is considered to determine the scale of feature space, were $R_{i{M}_i}$ is the distance of the ith training sample from its cluster center and $R_{i{M}_{\mathrm{nearest}}}$ is the distance of the ith training sample from the nearest neighbor cluster center. These distances are WMD.

$$F_{\mathrm{obj}}={\displaystyle \sum }_{i=1:T}\frac{R_{i{M}_i}}{R_{i{M}_{\mathrm{nearest}}}}$$

(25)

where T is the total number of selected training samples. The purpose of this function is the search in space of all possible states for the coefficients ${\mu }_1^d$, ${\mu }_2^d$ and ${\mu }_3^d$ in order to optimize the objective function. This objective function can carry out the balance of feature space, as if the maximum homogeneity can be established among the members of a class and maximum heterogeneity among the members of different classes. Afterwards, effective feature vectors and their scale can be predicted. These help to access the high accuracy for classification.

2.5. Comparison with Other Methods

The accuracy assessment of the HDCA for the Indian Pines, Salinas, and Salinas-A datasets are compared with other traditional and deep learning-based classification methods. The same training dataset was used in the training phase for all the methods and the same test dataset was used in the test phase for a uniform comparison. The k-NN and SVM with random feature selection [39] were selected as traditional classifiers. For each dataset, k-NN was employed with k equal to the number of classes. SVM with random feature selection was applied according to Waske et al. [39] with RBF kernel. The RBF kernel parameters (i.e., C and γ) were set by cross validation. The multilayer perceptron (MLP), the CNN designed by Hu et al. [40], and the CNN with pixel-pair features (PPFs) designed by Li et al. [41] were selected as deep learning-based classifiers. The MLP was used with base learning rate 0.0005 and batch size 200. In the CNN, the algorithm parameters were set equal to the values noted in [40]. PPF was applied with the same settings described by Li et al. [41].

Finally, the results of the hyperspectral reference dataset classification using the HCDA algorithm were compared with the results of other algorithms in previous studies [13,42,43,44,45,46,47,48,49,50,51,52].

3. Experimental Results

3.1. Multispectral Image

In order to evaluate the accuracy of HDCA compared to MLC (Maximum Likelihood classifier) and SVM (Support Vector Machine), an IKONOS satellite image was used. MLC and SVM are the most common methods of satellite image classification [53,54]. The MLC is one of the most powerful parametric statistical methods, while the SVM is one of the non-parametric methods that has been applied successfully to image classification in recent years [55,56,57,58,59,60,61]. The SVM classifier was employed using a radial basis function (RBF) kernel. For the classification of IKONOS satellite image, RBF kernel parameters (i.e., C and γ) were set to 250 and 3. The IKONOS satellite image for the Shahriar region (Tehran), 2013, which has 4 spectral bands, Red, Green, Blue and Near Infrared with spatial resolution of 4 meter and the size of 400 × 400 pixels, was used. The color composite of original image is shown in Figure 3. The image was classified into 5 classes: bare land, building, road, tree and farmland. The bare land class includes lands composed of rock, sand, and soil surfaces. The building class includes residential buildings, administrative buildings, and small industrial and commercial buildings. The road class includes main streets, subways and alleys. The farmland class includes annual and perennial crops and grassland found in open flat areas. Another class is a tree class that includes trees in the study area. Thereafter, classification accuracy was examined against the ground truth data and a set of training (<100 pixels) and testing (>400 pixels) samples for each land use class were collected for this purpose.

In HDCA, the gravitational constant (G) for traveling operator was considered equal to 10 with the lapse of time. The maximum number for escaping operator was set to 100, and the number of iterations for optimization to 200. The escape power element of pixel which determined escape probability was set to 3. It should be noted that the distance vectors in four main directions with the length of a pixel ((1,1) (0,1) (1,0) (−1,1)) for the Co-occurrence Matrix [62] were considered. The feature of inertia was produced for each direction and their average served as the final inertia feature. The size of both kernels was determined to be 3 × 3. To reduce the computational load, features with weight near zero in the classification were omitted.

Figure 4 shows the image classification results by the three methods.

Table 1. User’s and Producer’s accuracy, Overall accuracy and Cohen’s Kappa of three classifiers.

HDCA	User’s Accuracy					Producer’s Accuracy
	Road	tree	farmland	building	Bare land	road	tree	farmland	building	bare land
Road	98.56%	0%	0%	1.44%	0%	90.51%	0%	0%	1.69%	0%
Tree	0.56%	99.22%	0.22%	0%	0%	0.51	99.00%	0.10%	0%	0%
farmland	0%	0.45%	99.55%	0%	0%	0%	1.00%	99.65%	0%	0%
building	9.78%	0%	0.44%	80.67%	9.11%	8.98%	0%	0.20%	94.53%	10.90
bare land	0%	0%	0.14%	4.14%	95.71%	0%	0%	0.05%	3.78%	89.10%
Overall Accuracy: 95.69%						Cohen’s Kappa Coefficient: 94.35%
SVM	User’s Accuracy					Producer’s Accuracy
	Road	tree	farmland	building	Bare land	Road	tree	farmland	building	bare land
Road	98.67%	0%	0.11%	1.22%	0%	88.62%	0%	0.04%	1.52%	0%
Tree	0.89%	98.56%	0.56%	0%	0%	0.80%	98.78%	0.25%	0%	0%
farmland	0%	0.50%	99.50%	0%	0%	0%	1.11%	99.25%	0%	0%
building	11.78%	0%	0.89%	76.78%	10.33%	10.58%	0%	0.40%	95.18%	12.13%
bare land	0%	0.14%	0.14%	3.43%	96.29%	0%	0.11%	0.04%	3.31%	87.87%
Overall Accuracy: 95.00%						Cohen’s Kappa Coefficient: 93.95%
MLC	User’s Accuracy					Producer’s Accuracy
	Road	tree	farmland	building	Bare land	road	tree	farmland	building	bare land
Road	97.89%	0.33%	0.11%	1.67%	0%	90.45%	0.32%	0.05%	2.07%	0%
Tree	0.44%	99.33%	0.22%	0%	0%	0.41%	93.91%	0.10%	0%	0%
farmland	0%	2.70%	95.55%	0.60%	1.15%	0%	5.67%	99.32%	1.66%	2.78%
building	9.89%	0%	1.11%	74.56%	14.44%	9.14%	0%	0.52%	92.68%	15.74%
bare land	0%	0.14%	0%	3.71%	96.14%	0%	0.11%	0%	3.59%	81.48%
Overall Accuracy: 93.15%						Cohen’s Kappa Coefficient: 91.06%

indicates Producer’s accuracy, User’s accuracy, Overall accuracy and Cohen’s Kappa coefficient for the classification results.

Results reported in Table 1 indicate that the classification accuracy of each method for the road class is nearly identical. Also, all methods classified tree and farmland classes with high accuracy except that the accuracy of HDCA was slightly better than the other two methods. On the other hand, a significant difference in the accuracy of the building class has been observed. HDCA is approximately 2.4 and 0.69 more accurate than MLC and SVM, respectively. The HDCA yielded much higher accuracy because the application of the WMD and the proposed IGSA optimization algorithm in algorithm operators. Comparison of the bare land class accuracy obtained from classifiers revealed the weakness of MLC to distinguish the pixels that should be included in the bare land class.

Based on the results obtained, the HDCA algorithm was better than two other methods in this comparison due to high performance in all classes. According to Overall accuracy and Cohen’s Kappa coefficient, which was reported in Table 1, it is comprehensible that our proposed method has obvious excellence against MLC and SVM methods in the intended image.

As shown in Figure 3, building and wasteland had high spectral similarity; the accuracy of classification in these classes was not high with MLC and SVM. These classes are distinguishable texturally such that it is feasible to separate these classes with visual interpretation. Statistical methods such as MLC cannot use multiple sources of features with different scales and different statistical distributions effectively because of the low flexibility (especially in the building class). Also, MLC depends on the Gaussian statistical distribution of data. SVM did not show high efficiency in extracting building class either because the separator hyperplane between classes, which is supposed to be at the middle of Support Vectors, did not account for the dispersion of training data within classes in this case. The classification accuracy of HDCA was slightly higher than two other methods in bare land class, but was substantially higher in the building class. This difference in accuracy was attributable to the impact of the Weighted Manhattan Distance (WMD) and IGSA optimization in algorithm operators. The differences between HDCA and SVM classification were illustrated in Figure 5.

As illustrated in Figure 5, most of the differences between two classifier are related to pixels suspected to be the building class. This is indicative of the different procedure of HDCA in the face of extracted texture features of the image compared with SVM. Visual assessment of HDCA results demonstrates the efficiency of this method in the building extraction.

The appropriate integration of the road network and relatively high accuracy of road extraction can be presumed by visual interpretation of the obtained image from the proposed method. It is also noteworthy that two types of vegetation cover were separated from each other with acceptable accuracy. In sum, the HDCA advantages in high spatial resolution image classification (i.e., IKONOS) are listed as follows.

• The algorithm well preserved the road network.
• The different vegetation covers were separated from each other effectively.
• It distinguished between the two classes of bare land and building properly.

3.2. Hyperspectral Images

To evaluate and validate the performance of the HDCA algorithm in hyperspectral image classification, hyperspectral reference datasets including the Indian Pines dataset, Salinas, and Salinas-A dataset, which were acquired by the Airborne Visible/ Infrared Imaging Spectrometer (AVIRIS) sensor, were used. To investigate the influence of the size of training set on the classification methods, the classification for each of the reference datasets was performed with different training sample sizes (1, 5, 10 and 12.5%), and four different schemes were considered. In scheme (a) 1% of the training samples of each class were used. In other schemes: (b) 5%, (c) 10%, (d) 12.5% of the training samples of each class were used to classify the reference datasets. HDCA samples were randomly selected as training pixels and the remaining pixels were used as the test set.

3.2.1. Indian Pines Dataset

The Indian Pines hyperspectral dataset consisted of a 2.9 × 2.9 km² (145 × 145 pixels) land of Northwest Tippecanoe County in the Indian Pine region, and was collected on 12 June 1992. Two-thirds of this land were covered by mixed agriculture lands and one-third was forest or other wildland. This dataset included 220 bands with a spectral resolution of 10 nm and a spatial resolution of 20 m. Twenty spectral bands were omitted because of noise and water absorption. The remaining bands were used in the experiment. The color composite image of this dataset was illustrated in Figure 6.

The original ground-truth image had 16 various classes.

Table 2. Type of classes and their respective labeled pixels number in the Indian Pines dataset.

No	Class	Pixels	No	Class	Pixels
1	Alfalfa	46	9	Hay-windowed	478
2	Bldg-Grass-Tree-Drives	386	10	Oats	20
3	Corn-no till	1428	11	Soybeans-no till	972
4	Corn-min till	830	12	Soybeans-min till	2455
5	Corn	237	13	Soybeans-clean	593
6	Grass/pasture	483	14	Stone-Steel-Towers	93
7	Grass/trees	730	15	Wheat	205
8	Grass/pasture-mowed	28	16	Woods	1265

indicates the type and the number of labeled pixels for each class. Two challenging issues of this dataset are that all classes contained mixed pixels and the number of labeled pixels per class was unequal [42,43].

The results of the classification of Indian Pines dataset using the HDCA method for different training sample sizes were shown in Figure 7.

The classification results for each of the schemes were examined with a set of test data. The results of the user’s and producer’s accuracy for the scheme (c) were shown in

Table 3. User’s and Producer’s accuracy results (using 10% of the available training sample for the dataset), Overall accuracy and Cohen’s Kappa of the HDCA with different schemes on the Indian Pines dataset.

Class	UA	PA	Class	UA	PA
Alfalfa	100	100	Oats	100	100
Corn-no till	97.92	95.25	Soybeans-no till	97.03	96.81
Corn-min till	96.67	97.05	Soybeans-min till	96.22	98.05
Corn	97.71	100	Soybeans-clean	98.3	97.38
Grass/pasture	99.77	99.77	Wheat	100	99.46
Grass/trees	100	100	Woods	99.30	99.30
Grass/pasture-mowed	100	92.00	Bldg-Grass-Tree	97.42	97.98
Hay-windowed	99.77	100	Stone-Steel-Towers	100	90.48
Scheme.	(a) 1%	(b) 5%	(c) 10%	(d) 12.5%
Overall Accuracy	74.89	94.94	97.88	98.09
Cohen’s Kappa	0.7075	0.9423	0.9759	0.9789

. Also, the overall accuracy and Cohen’s Kappa coefficient for each of the four schemes were presented in Table 3.

3.2.2. Salinas Dataset

The Salinas dataset contained 224 spectral bands with a spatial resolution of 3.7 m and was acquired by the AVIRIS sensor over Salinas Valley, California, USA. The size of the image is 512 × 217 pixels. The water absorption bands were removed and the 204 remaining spectral bands were used in the experiment. The color composite of this image was shown in Figure 8.

These data included 16 various classes with high similarity of spectral signatures [63]. These dataset has been used in many studies as reference data to evaluate classification methods.

Table 4. Type of classes and their respective labeled pixels number in the Salinas dataset.

No	Class	Pixels	No	Class	Pixels
1	BBrocoli_green_weeds_1	2009	9	Soil_vinyard_develop	6203
2	BBrocoli_green_weeds_2	3726	10	Corn_senesced_weeds	3278
3	Fallow	1976	11	Lettuce_romaine_4 wk	1068
4	Fallow_rough_plow	1394	12	Lettuce_romaine_5 wk	1927
5	Fallow_smooth	2678	13	Lettuce_romaine_6 wk	916
6	Stubble	3959	14	Lettuce_romaine_7 wk	1070
7	Celery	3579	15	Vinyard_untrained	7268
8	Grapes_untrained	11271	16	Vinyard_vertical_trellis	1807

elucidates the type and the number of labeled pixels of each class.

The results of the classification of the Salinas dataset using the HDCA method for different training sample sizes were shown in Figure 9.

The classification results for each of the schemes were examined with a set of test data. The results of the user’s and producer’s accuracy for the scheme (c) were illustrated in

Table 5. User’s and Producer’s accuracy results (using 10% of the available training sample for the dataset), Overall accuracy and Cohen’s Kappa of the HDCA with different schemes on the Salinas dataset.

Class	UA	PA	Class	UA	PA
BBrocoli_green_weeds_1	100	100	Soil_vinyard_develop	99.86	99.98
BBrocoli_green_weeds_2	100	100	Corn_senesced_weeds	99.66	99.76
Fallow	100	100	Lettuce_romaine_4 wk	100	98.86
Fallow_rough_plow	99.52	99.76	Lettuce_romaine_5 wk	99.88	99.83
Fallow_smooth	100	99.71	Lettuce_romaine_6 wk	100	100
Stubble	100	99.76	Lettuce_romaine_7 wk	100	100
Celery	100	99.88	Vinyard_untrained	98.89	99.26
Grapes_untrained	99.43	99.30	Vinyard_vertical_trellis	99.82	100
Scheme	(a) 1%	(b) 5%	(c) 10%	(d) 12.5%
Overall Accuracy	96.03	99.08	97.66	99.82
Cohen’s Kappa	0.9562	0.9903	0.9966	0.9983

. The overall accuracy and Cohen’s Kappa coefficient for each of the four schemes were presented in Table 5.

3.2.3. Salinas-A Scene Dataset

The Salinas-A scene dataset is a subset of the Salinas dataset which includes 224 spectral bands. The size of image is 86 × 83 pixels. Due to water absorption, 20 spectral bands were removed. The Salinas-A scene was located within the Salinas scene at (samples: 591–676, lines: 158–240) [64]. The color composite of this image was shown in Figure 10.

The Salinas-A scene includes 6 classes, most of which belong to a specific plant species (Romaine lettuce) and their only difference is the growth period. For this characteristic, the Salinas-A scene has been used in many studies as reference data to evaluate classification methods.

Table 6. Type of classes and their respective labeled pixels number in the Salinas-A scene.

No	Category	Pixels
1	BBrocoli_green_weeds_1	391
2	Corn_senesced_weeds	1343
3	Lettuce_romaine_4 wk	616
4	Lettuce_romaine_5 wk	1525
5	Lettuce_romaine_6 wk	674
6	Lettuce_romaine_7 wk	799

demonstrates the type and the number of labeled pixels of each class.

The results of the classification of Salinas-A scene dataset using the HDCA method for different training sample sizes were shown in Figure 11.

The classification results for each of the schemes were examined with a set of test data. The results of the User’s and Producer’s accuracy for the scheme where 10% of the training sample size of each class were used as training sample were shown in

Table 7. User’s and Producer’s accuracy results (using 10% of the available training sample for the dataset), Overall accuracy and Cohen’s Kappa of the HDCA with different schemes on the Salinas-A scene.

Class			UA	PA
BBrocoli_green_weeds_1			100	99.41
Corn_senesced_weeds			100	99.91
Lettuce_romaine_4 wk			100	99.63
Lettuce_romaine_5 wk			99.78	100
Lettuce_romaine_6 wk			99.66	100
Lettuce_romaine_7 wk			99.71	99.71
Scheme	(a) 1%	(b) 5%	(c) 10%	(d) 12.5%
Overall accuracy	96.22	99.46	99.85	99.91
Cohen’s Kappa	0.9526	0.9933	0.9981	0.9989

. Also, the overall accuracy and Cohen’s Kappa coefficient for each of the four schemes were presented in Table 7.

The accuracy assessment of the HDCA for the Indian Pines, Salinas, and Salinas-A datasets was compared with other traditional and deep learning-based classifiers in

Table 8. Overall accuracies of the proposed method compared to other traditional and deep learning-based classifiers.

Dataset	Training Samples (%)	k-NN	SVM	MLP	CNN	PPFs	Proposed (HDCA)
Indian Pines	1	65.2	73.44	68.53	70.3	75.89	74.90
	5	74.2	83.63	81.64	86.12	90.72	94.90
	10	80.6	87.97	85.35	90.6	95.11	97.81
	12.5	81.3	89.27	87.93	92.75	96.75	98.09
Salinas	1	68.3	75.94	72.57	74.28	86.37	96.03
	5	78.1	86.41	84.26	90.63	94.26	99.08
	10	83.8	89.68	88.61	93.52	96.91	99.66
	12.5	85.9	92.6	90.3	96.68	98.15	99.82
Salinas-A	1	71.83	77.37	74.42	76.78	90.34	96.03
	5	79.69	88.59	84.94	92.36	95.26	99.08
	10	85.75	92.36	90.65	94.61	97.97	99.66
	12.5	89.43	93.96	92.33	97.93	99.01	99.82

. The overall accuracy of the reference dataset classification for various algorithms indicates that HCDA results were better than results of other algorithms such as k-NN, SVM, MLP, CNN and PPFs.

To analyze the sensitivity of the results to the number of training samples, the overall accuracies of classification of the three Indian Pines, Salinas, and Salinas-A datasets, by using different classifiers related to 1% to 50% (1, 5, 10, 12.5, 15, 20, 25, 30, 35, 40, 45, and 50 percent) of the number of pixels in each class, were randomly selected for training samples and the rest of the pixels were selected as test samples.

Figure 12 compares the variation of overall accuracy over increasing the percentage of training based on Indian Pines, Salinas, and Salinas-A datasets for various methods. The samples were randomly selected as training pixels and the remaining pixels were used as the test set.

Figure 12 indicates that by increasing the number of training samples, classification accuracy increases with all algorithms. In all cases, the overall accuracy using the HDCA algorithm was higher than the overall accuracy with other classifiers. For training samples above 10%, the overall accuracy of all three Indian Pines, Salinas, and Salinas-A datasets is above 97%. By increasing the number of training samples, the overall accuracy for the HDCA algorithm was more stable than the overall accuracies obtained by other classifiers. Generally, HDCA results were closer to the results of CNN and PPF classifiers. The overall accuracies of HDCA, CNN and PPF for the Indian Pines dataset with the number of training samples more than 35% were equal. Also, the overall accuracies of HDCA, CNN and PPF for Salinas and Salinas-A datasets with the number of training samples more than 20% were also equal. Among the various classifiers, the overall accuracy of k-NN and MLP was lower than other classifiers. Furthermore, the sensitivity of classification accuracy to the number of training samples in these two classifiers was higher than that of other classifiers.

Lastly, a comparative assessment has been provided. The proposed algorithm was compared with some recent classification methods. The results of the hyperspectral reference dataset classification using the HCDA algorithm were compared with the results of other algorithms in previous studies [13,42,43,44,45,46,47,48,49,50,51,52]. The overall accuracy of the reference dataset classification for various algorithms indicates that HCDA results were better than results of other algorithms. The results of other methods have been derived from the relevant articles. Therefore, some results are incomplete. The comparison results were illustrated in

Table 9. Overall accuracies of the proposed method compared to the results of other algorithms in previous studies.

Dataset	Training samples (%)	RKS-RLS a	SUnSALEMAP b	SVM-CK c	GURLS d	OLDA e	BASS Net f	CNN-MFL g	HIS-CNN h	Proposed (HDCA)
Indian Pines	1	-	-	73.7	-	73.3	-	-	-	74.90
	5	-	95	91.4		94.5	-	-	-	94.90
	10	93.79	96.8	94.9	89.59	97.6	96.77	97.54	-	97.81
	12.5	-	-	95.8	-	97.8	-	-	99.09	98.09
Salinas	1	-	-	95.6	-	96	-	-	-	96.03
	5	-	-	98.7	-	99.4	-	-	-	99.08
	10	-	-	98.9	-	99.9	95.33	98.34	-	99.66
	12.5	-	-	99.1	-	99.9	-	-	98.95	99.82
Salinas-A	1	-	-	-	-	-	-	-	-	96.03
	5	-	-	-	-	-	-	-	-	99.08
	10	98.58	-	-	98.31	-	-	-	-	99.66
	12.5	-	-	-	-	-	-	-	-	99.82

^a: Taken from Haridas et al. (2015) [64]. ^b: Taken from Song et al. (2014) [42]. ^c: Taken from Camps-Valls et al. (2006) [51]. ^d: Taken from Haridas et al. (2015) [44]. ^e: Taken from Shahdoosti and Mirzapour (2017) [43]. ^f: Taken from Santara et al. (2017) [65]. ^g: Taken from Gao et al. (2018) [23]. ^h: Taken from Luo et al. (2018) [22].

.

4. Discussion

The proposed algorithm has a key goal of optimizing the feature space. Due to the complex nature of the objective function and huge size of some images as input data, it is vital to use an efficient algorithm to optimize the objective function. The IGSA optimization algorithm, due to having memory and negative mass usage, is caught in local optimum with the least possibility rather than other optimization algorithms, which is the main characteristic of using this algorithm. This algorithm is able to determine the feature space scale, especially in images with high spectral dimension. Also, the intended objective function depicts the separation between classes ideally. Because of the use of the powerful optimization algorithm and the objective function, we can easily classify different resolution images without the need to know the nature of the image and its computational complexity.

The other vital issue to be discussed is training data and the parameters of HDCA classifier. The proposed algorithm is not more strongly affected by the number of training samples and has no need to determine the parameters for classification. This method has a stable model and lower dependency on the spatial dimension of the input data because of normalization of the feature space.

In the present study, the characteristics of spectral component values, variance and inertia were used to implement the HDCA. To classify images with more heterogeneity, more types of features should be used. The results of the study show that HDCA has high capability for classification of images with different spatial and spectral resolutions.

Moreover, the computational time of the proposed method has been computed. In this research a standard notebook (Intel Core i7, 2.40 GHz and 16 GB of RAM) was used for different datasets (for each dataset the average of computational time of 10 repetitions has been computed). The average of the computational time of the proposed method for IKONOS image, Salinas-A dataset, Salinas dataset and Indian Pines dataset is 3.63, 5.72, 11.31 and 7.15 minutes, respectively (using 10% of the available training sample for hyperspectral datasets). In sum, the proposed method has a moderate computational complexity. The complexity of HDCA is lower than that of deep CNN algorithms. Also, the time to image classification using HDCA is lower than deep CNN algorithms.

5. Conclusions

In this paper, a novel classification method, HDCA, was proposed, and tested with different types of remote sensing images, i.e., high spatial resolution and high spectral resolution. The HDCA used texture and spectral information for classifying images in two iterative, supplemental computing stages. It was demonstrated as a method of effective image classification as well as an algorithm for optimizing the scale of feature space at the pre-processing stage. This optimization makes it possible to identify more homogeneous classes. Furthermore, the proposed algorithm with heuristic search has the ability of finding the best-suited pixels for a class. The experimental results indicate that HDCA possessed high capability to separate classes with different spatial and spectral resolutions. Future works were warranted to test this method with voluminous data and images with more extracted features. The designed optimization algorithm and the method of determining feature space can be used for applications, independent of the proposed classification method. Additionally, future studies can investigate the concept of fuzzification with this algorithm in order to achieve considerable classification accuracy in the areas of abundant mixed pixels.